13.2 : Séquences arithmétiques
- Page ID
- 194934
- Déterminez la différence commune pour une séquence arithmétique.
- Écrivez les termes d'une séquence arithmétique.
- Utilisez une formule récursive pour une séquence arithmétique.
- Utilisez une formule explicite pour une séquence arithmétique.
Les entreprises font souvent des achats importants, tels que des ordinateurs et des véhicules, à des fins professionnelles. La valeur comptable de ces fournitures diminue chaque année à des fins fiscales. Cette diminution de valeur est appelée dépréciation. L'une des méthodes de calcul de l'amortissement est l'amortissement linéaire, dans lequel la valeur de l'actif diminue du même montant chaque année.
Prenons l'exemple d'une femme qui lance une petite entreprise de sous-traitance. Elle achète un nouveau camion pour\($25,000\). Au bout de cinq ans, elle estime qu'elle sera en mesure de vendre le camion pour\($8,000\). La perte de valeur du camion sera donc de\($17,000\), soit\($3,400\) par an pendant cinq ans. Le camion aura de la valeur au\($21,600\) bout de la première année, au\($18,200\) bout de deux ans,\($14,800\) au\($11,400\) bout de trois ans, au bout de quatre ans et\($8,000\) au bout de cinq ans. Dans cette section, nous examinerons des types spécifiques de séquences qui nous permettront de calculer l'amortissement, tels que la valeur du camion.
Trouver les différences communes
Les valeurs du camion dans l'exemple sont censées former une séquence arithmétique car elles changent d'une quantité constante chaque année. Chaque terme augmente ou diminue selon la même valeur constante appelée différence commune de la séquence. Pour cette séquence, la différence commune est\(-3,400\).

La séquence ci-dessous est un autre exemple de séquence arithmétique. Dans ce cas, la différence constante est\(3\). Vous pouvez choisir n'importe quel terme de la séquence et l'ajouter\(3\) pour trouver le terme suivant.

Une séquence arithmétique est une séquence dont la propriété est que la différence entre deux termes consécutifs est une constante. Cette constante s'appelle la différence commune. Si\(a_1\) est le premier terme d'une suite arithmétique et si\(d\) c'est la différence commune, la séquence sera :
\[\{a_n\}=\{a_1,a_1+d,a_1+2d,a_1+3d,...\}\]
Chaque séquence est-elle arithmétique ? Si c'est le cas, trouvez la différence commune.
- \(\{1,2,4,8,16,...\}\)
- \(\{−3,1,5,9,13,...\}\)
Solution
Soustrayez chaque terme du terme suivant pour déterminer s'il existe une différence commune.
- La séquence n'est pas arithmétique car il n'y a pas de différence commune.
\(2-1={\color{red}1} \qquad 4-2={\color{red}2} \qquad 8-4={\color{red}4} \qquad 16-8={\color{red}8}\)
- La séquence est arithmétique car il existe une différence commune. La différence commune est\(4\).
\(1-(-3)={\color{red}4} \qquad 5-1={\color{red}4} \qquad 9-5={\color{red}4} \qquad 13-9={\color{red}4}\)
Analyse
Le graphique de chacune de ces séquences est illustré sur la figure\(\PageIndex{1}\). Nous pouvons voir sur les graphiques que, bien que les deux séquences montrent une croissance, (a) n'est pas linéaire alors que (b) est linéaire. Les séquences arithmétiques ont un taux de variation constant, de sorte que leurs graphes seront toujours des points sur une ligne.
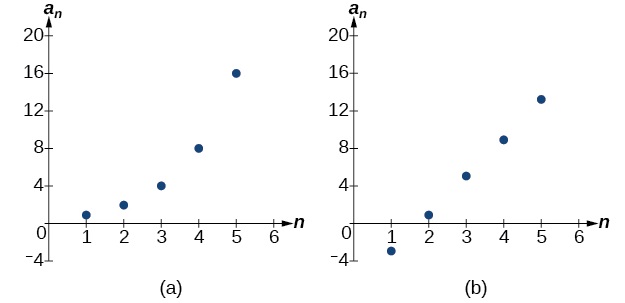
Figurine\(\PageIndex{1}\)
Si on nous dit qu'une séquence est arithmétique, devons-nous soustraire chaque terme du terme suivant pour trouver la différence commune ?
Non. Si nous savons que la séquence est arithmétique, nous pouvons choisir n'importe quel terme de la séquence et le soustraire du terme suivant pour trouver la différence commune.
La séquence donnée est-elle arithmétique ? Si c'est le cas, trouvez la différence commune.
\(\{18, 16, 14, 12, 10,…\}\)
- Réponse
-
La séquence est arithmétique. La différence commune est\(–2\).
La séquence donnée est-elle arithmétique ? Si c'est le cas, trouvez la différence commune.
\(\{1, 3, 6, 10, 15,…\}\)
- Réponse
-
La séquence n'est pas arithmétique car\(3−1≠6−3\).
Écrire des termes de séquences arithmétiques
Maintenant que nous pouvons reconnaître une séquence arithmétique, nous trouverons les termes si l'on nous donne le premier terme et la différence commune. Les termes peuvent être trouvés en commençant par le premier terme et en ajoutant la différence commune à plusieurs reprises. De plus, n'importe quel terme peut également être trouvé en insérant les valeurs de\(n\) et\(d\) dans la formule ci-dessous.
\[a_n=a_1+(n−1)d\]
- Ajoutez la différence commune au premier terme pour trouver le second terme.
- Ajoutez la différence commune au deuxième terme pour trouver le troisième terme.
- Continuez jusqu'à ce que tous les termes souhaités soient identifiés.
- Écrivez les termes séparés par des virgules entre crochets.
Écrivez les cinq premiers termes de la séquence arithmétique avec\(a_1=17\) et\(d=−3\).
Solution
Ajouter\(−3\) revient à soustraire\(3\). En commençant par le premier terme, soustrayez\(3\) de chaque terme pour trouver le terme suivant.
Les cinq premiers termes sont\(\{17,14,11,8,5\}\)
Analyse
Comme prévu, le graphique de la séquence se compose de points sur une ligne, comme indiqué sur la figure\(\PageIndex{2}\).
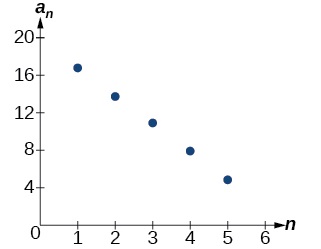
Figurine\(\PageIndex{2}\)
Répertoriez les cinq premiers termes de la séquence arithmétique avec\(a_1=1\) et\(d=5\).
- Réponse
-
\(\{1, 6, 11, 16, 21\}\)
- Remplacez les valeurs données pour\(a_1\)\(a_n\),\(n\) dans la formule\(a_n=a_1+(n−1)d\) à résoudre\(d\).
- Trouvez un terme donné en substituant les valeurs appropriées pour\(a_1\)\(n\), et\(d\) dans la formule\(a_n=a_1+(n−1)d\).
Donné\(a_1=8\) et\(a_4=14\), trouvez\(a_5\).
Solution
La séquence peut être écrite en fonction du terme initial\(8\) et de la différence commune\(d\).
\(\{8,8+d,8+2d,8+3d\}\)
Nous savons que le quatrième terme est égal\(14\) ; nous savons que le quatrième terme a la forme\(a_1+3d=8+3d\).
Nous pouvons trouver la différence commune\(d\).
\[\begin{align*} a_n&= a_1+(n-1)d \\ a_4&= a_1+3d \\ a_4&=8+3d\qquad \text{Write the fourth term of the sequence in terms of }a_1 \text{ and } d. \\ 14&=8+3d\qquad \text{Substitute }14 \text{ for } a_4. \\ d&=2\qquad \text{Solve for the common difference.} \end{align*}\]
Trouvez le cinquième terme en ajoutant la différence commune au quatrième terme.
\(a_5=a_4+2=16\)
Analyse
Notez que la différence commune est ajoutée au premier terme une fois pour trouver le deuxième terme, deux fois pour trouver le troisième terme, trois fois pour trouver le quatrième terme, etc. Le dixième terme peut être trouvé en ajoutant neuf fois la différence commune au premier terme ou en utilisant l'équation\(a_n=a_1+(n−1)d\).
Donné\(a_3=7\) et\(a_5=17\), trouvez\(a_2\).
- Réponse
-
\(a_2=2\)
Utilisation de formules récursives pour les séquences arithmétiques
Certaines séquences arithmétiques sont définies en fonction du terme précédent à l'aide d'une formule récursive. La formule fournit une règle algébrique pour déterminer les termes de la séquence. Une formule récursive permet de trouver n'importe quel terme d'une séquence arithmétique en utilisant une fonction du terme précédent. Chaque terme est la somme du terme précédent et de la différence commune. Par exemple, si la différence commune est\(5\), alors chaque terme est le terme précédent plus\(5\). Comme pour toute formule récursive, le premier terme doit être indiqué.
\(a_n=a_n−1+d\)
pour\(n≥2\)
La formule récursive pour une séquence arithmétique avec une différence commune\(d\) est la suivante :
\[a_n=a_n−1+d\]
pour\(n≥2\)
- Soustrayez n'importe quel terme du terme suivant pour trouver la différence commune.
- Indiquez le terme initial et remplacez la différence commune dans la formule récursive pour les séquences arithmétiques.
Écrivez une formule récursive pour la séquence arithmétique.
\(\{−18, −7, 4, 15, 26, …\}\)
Solution
Le premier terme est donné sous la forme\(−18\). La différence commune peut être trouvée en soustrayant le premier terme du second terme.
\(d=−7−(−18)=11\)
Remplacez le terme initial et la différence commune dans la formule récursive pour les séquences arithmétiques.
\(a_1=−18\)
\(a_n=a_{n−1}+11\)
pour\(n≥2\)
Analyse
Nous voyons que la différence commune est la pente de la droite formée lorsque nous tracons les termes de la séquence, comme le montre la figure\(\PageIndex{3}\). Le schéma de croissance de la séquence montre la différence constante de 11 unités.
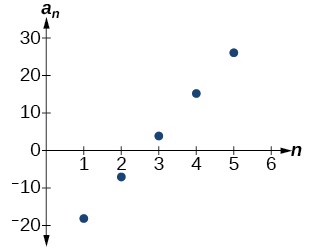
Figurine\(\PageIndex{3}\)
Faut-il soustraire le premier terme du second terme pour trouver la différence commune ?
Non. Nous pouvons soustraire n'importe quel terme de la séquence du terme suivant. Il est toutefois plus courant de soustraire le premier terme du second, car c'est souvent la méthode la plus simple pour trouver la différence commune.
Écrivez une formule récursive pour la séquence arithmétique.
\(\{25, 37, 49, 61, …\}\)
- Réponse
-
\(\begin{align*}a_1 &= 25 \\ a_n &= a_{n−1}+12 , \text{ for }n≥2 \end{align*}\)
Utilisation de formules explicites pour les séquences arithmétiques
Nous pouvons considérer une séquence arithmétique comme une fonction du domaine des nombres naturels ; c'est une fonction linéaire parce qu'elle a un taux de variation constant. La différence commune est le taux de variation constant, ou la pente de la fonction. Nous pouvons construire la fonction linéaire si nous connaissons la pente et l'intersection verticale.
\(a_n=a_1+d(n−1)\)
Pour trouver l'\(y\)intercept de la fonction, nous pouvons soustraire la différence commune au premier terme de la séquence. Considérez la séquence suivante.

La différence la plus courante est\(−50\) que la séquence représente une fonction linéaire avec une pente de\(−50\). Pour trouver le\(y\) -intercept, on soustrait\(−50\) de\(200\) :\(200−(−50)=200+50=250\). Vous pouvez également trouver le\(y\) -intercept en représentant graphiquement la fonction et en déterminant où une ligne reliant les points intersecterait l'axe vertical. Le graphique est illustré dans la figure\(\PageIndex{4}\).
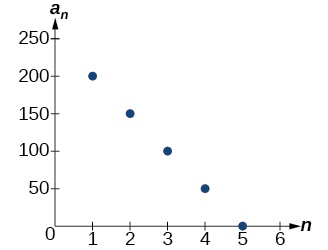
Figurine\(\PageIndex{4}\)
Rappelez-vous que la forme d'intersection inclinée d'une ligne est\(y=mx+b\). Lorsque nous traitons de séquences, nous utilisons\(a_n\) à la place\(y\) et\(n\) à la place de\(x\). Si nous connaissons la pente et l'intersection verticale de la fonction, nous pouvons les remplacer par\(m\) et\(b\) sous la forme d'intersection de pente d'une ligne. En remplaçant\(−50\) la pente et\(250\) l'intersection verticale, on obtient l'équation suivante :
\(a_n=−50n+250\)
Nous n'avons pas besoin de trouver l'intersection verticale pour écrire une formule explicite pour une séquence arithmétique. Une autre formule explicite pour cette séquence est\(a_n=200−50(n−1)\), qui simplifie à\(a_n=−50n+250\).
Une formule explicite pour le\(n^{th}\) terme d'une séquence arithmétique est donnée par
\[a_n=a_1+d(n−1)\]
- Trouvez la différence commune,\(a_2−a_1\).
- Remplacez la différence commune et le premier terme par\(a_n=a_1+d(n−1)\).
Écrivez une formule explicite pour la séquence arithmétique.
\(\{2, 12, 22, 32, 42, …\}\)
Solution
La différence commune peut être trouvée en soustrayant le premier terme du second terme.
\[\begin{align*} d &= a_2−a_1 \\ &= 12−2 \\ &= 10 \end{align*}\]
La différence commune est\(10\). Remplacez la différence commune et le premier terme de la séquence dans la formule et simplifiez.
\[\begin{align*}a_n &= 2+10(n−1) \\ a_n &= 10n−8 \end{align*}\]
Analyse
Le graphique de cette séquence, représenté sur la figure\(\PageIndex{5}\), montre une pente\(10\) et une intersection verticale de\(−8\).

Figurine\(\PageIndex{5}\)
Écrivez une formule explicite pour la séquence arithmétique suivante.
\(\{50,47,44,41,…\}\)
- Réponse
-
\(a_n=53−3n\)
Déterminer le nombre de termes dans une suite arithmétique finie
Des formules explicites peuvent être utilisées pour déterminer le nombre de termes dans une séquence arithmétique finie. Nous devons trouver la différence commune, puis déterminer combien de fois la différence commune doit être ajoutée au premier terme pour obtenir le terme final de la séquence.
- Trouvez la différence commune\(d\).
- Remplacez la différence commune et le premier terme par\(a_n=a_1+d(n–1)\).
- Remplacez le dernier terme par\(a_n\) et résolvez par\(n\).
Détermine le nombre de termes dans la suite arithmétique finie.
\(\{8, 1, –6, ..., –41\}\)
Solution
La différence commune peut être trouvée en soustrayant le premier terme du second terme.
\(1−8=−7\)
La différence commune est\(−7\). Remplacez la différence commune et le terme initial de la séquence dans la formule du nième terme et simplifiez.
\[\begin{align*} a_n &= a_1+d(n−1) \\ a_n &= 8+−7(n−1) \\ a_n &= 15−7n \end{align*}\]
Remplacez\(−41\)\(a_n\) et résolvez\(n\)
\[\begin{align*} -41&=15-7n\\ 8&=n \end{align*}\]
Il y a huit termes dans la séquence.
Détermine le nombre de termes dans la suite arithmétique finie.
\(\{6, 11, 16, ..., 56\}\)
- Réponse
-
Il y a\(11\) des termes dans la séquence.
Résolution de problèmes d'application avec des séquences arithmétiques
Dans de nombreux problèmes d'application, il est souvent judicieux d'utiliser un terme initial de\(a_0\) au lieu de\(a_1\). Dans ces problèmes, nous modifions légèrement la formule explicite pour tenir compte de la différence entre les termes initiaux. Nous utilisons la formule suivante :
\[a_n=a_0+dn\]
Un enfant de cinq ans reçoit une\($1\) allocation hebdomadaire. Ses parents lui promettent une augmentation annuelle\($2\) hebdomadaire.
- Rédigez une formule pour l'allocation hebdomadaire de l'enfant pour une année donnée.
- Quelle sera l'allocation pour enfant lorsqu'il aura\(16\) 6 ans ?
Solution
- La situation peut être modélisée par une séquence arithmétique avec un terme initial\(1\) et une différence commune de\(2\).
\(A\)Soit le montant de l'allocation et\(n\) le nombre d'années après l'âge\(5\). En utilisant la formule explicite modifiée pour une séquence arithmétique, nous obtenons :
\(A_n=1+2n\)
- Nous pouvons trouver le nombre d'années écoulées depuis l'âge\(5\) en soustrayant.
\(16−5=11\)
Nous cherchons à obtenir l'allocation pour enfant après des\(11\) années. \(11\)Substituez-le dans la formule pour trouver l'allocation pour enfant en fonction de l'âge\(16\).
\(A_{11}=1+2(11)=23\)
L'allocation pour enfant en fonction de son âge\(16\) sera calculée\($23\) par semaine.
Une femme décide de courir une\(10\) minute tous les jours cette semaine et prévoit d'augmenter la durée de sa course quotidienne de\(4\) quelques minutes par semaine. Écrivez une formule pour la durée de sa course après des\(n\) semaines. Dans combien de temps sa course quotidienne sera-t-elle dans\(8\) quelques semaines ?
- Réponse
-
La formule est\(T_n=10+4n\), et cela lui prendra\(42\) quelques minutes.
Accédez à cette ressource en ligne pour obtenir des instructions supplémentaires et vous entraîner à utiliser des séquences arithmétiques.
Équations clés
| formule récursive pour le nième terme d'une suite arithmétique | \(a_n=a_{n−1}+d\)\(n≥2\) |
| formule explicite pour le nième terme d'une séquence arithmétique | \(a_n=a_1+d(n−1)\) |
Key Concepts
- An arithmetic sequence is a sequence where the difference between any two consecutive terms is a constant.
- The constant between two consecutive terms is called the common difference.
- The common difference is the number added to any one term of an arithmetic sequence that generates the subsequent term. See Example \(\PageIndex{1}\).
- The terms of an arithmetic sequence can be found by beginning with the initial term and adding the common difference repeatedly. See Example \(\PageIndex{2}\) and Example \(\PageIndex{3}\).
- A recursive formula for an arithmetic sequence with common difference dd is given by \(a_n=a_{n−1}+d\), \(n≥2\). See Example \(\PageIndex{4}\).
- As with any recursive formula, the initial term of the sequence must be given.
- An explicit formula for an arithmetic sequence with common difference \(d\) is given by \(a_n=a_1+d(n−1)\). See Example \(\PageIndex{5}\).
- An explicit formula can be used to find the number of terms in a sequence. See Example \(\PageIndex{6}\).
- In application problems, we sometimes alter the explicit formula slightly to \(a_n=a_0+dn\). See Example \(\PageIndex{7}\).


