12.4 : Rotation des axes

Objectifs d'apprentissage

• Identifier les sections coniques non dégénérées en fonction de leurs équations de forme générales.
• Utilisez des formules de rotation des axes.
• Écrivez les équations des coniques pivotées sous une forme standard.
• Identifiez les coniques sans faire pivoter les axes.

Comme nous l'avons vu, les sections coniques se forment lorsqu'un plan croise deux cônes circulaires droits alignés bout à bout et s'étendant à l'infini dans des directions opposées, que nous appelons également cône. La manière dont nous découpons le cône déterminera le type de section conique formée à l'intersection. Un cercle est formé en tranchant un cône avec un plan perpendiculaire à l'axe de symétrie du cône. Une ellipse est formée en tranchant un cône unique avec un plan incliné qui n'est pas perpendiculaire à l'axe de symétrie. Une parabole est formée en tranchant le plan à travers le haut ou le bas du cône double, tandis qu'une hyperbole se forme lorsque le plan coupe à la fois le haut et le bas du cône (Figure$\PageIndex{1}$).

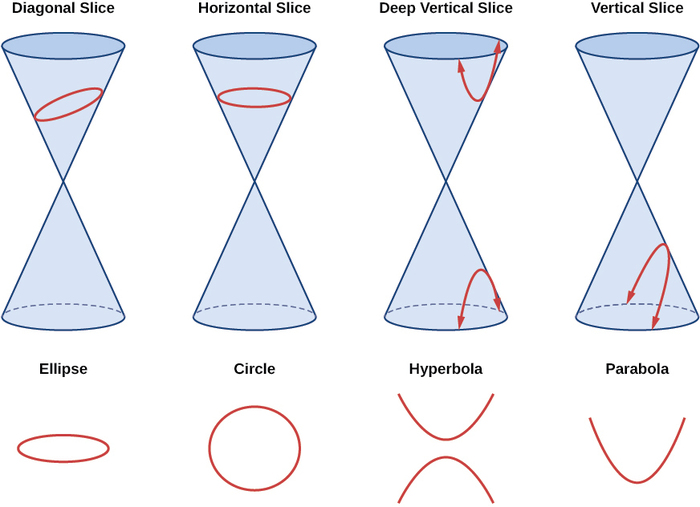
Figure$\PageIndex{1}$ : Les coupes coniques non dégénérées

Les ellipses, les cercles, les hyperboles et les paraboles sont parfois appelés sections coniques non dégénérées, contrairement aux sections coniques dégénérées, qui sont illustrées sur la figure$\PageIndex{2}$. Une conique dégénérée se produit lorsqu'un plan croise le double cône et passe par le sommet. Selon l'angle du plan, trois types de sections coniques dégénérées sont possibles : un point, une ligne ou deux lignes qui se croisent.

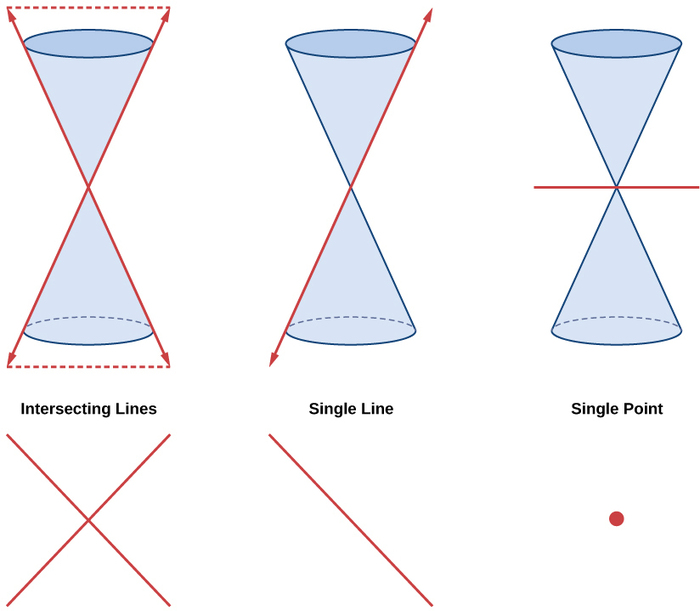
Figure$\PageIndex{2}$ : Sections coniques dégénérées

Identification des coniques non dégénérés sous forme générale

Dans les sections précédentes de ce chapitre, nous nous sommes concentrés sur les équations de forme standard pour les sections coniques non dégénérées. Dans cette section, nous allons nous concentrer sur l'équation de forme générale, qui peut être utilisée pour n'importe quelle conique. La forme générale est fixée à zéro et les termes et coefficients sont donnés dans un ordre particulier, comme indiqué ci-dessous.

$Ax^2+Bxy+Cy^2+Dx+Ey+F=0$

où$A$$B$, et ne$C$ sont pas tous nuls. Nous pouvons utiliser les valeurs des coefficients pour identifier quel type de conique est représenté par une équation donnée.

Vous remarquerez peut-être que l'équation de forme générale comporte un$xy$ terme que nous n'avons vu dans aucune des équations de forme standard. Comme nous le verrons plus loin, le$xy$ terme fait pivoter la conique chaque fois qu'$B$il n'est pas égal à zéro.

Tableau$\PageIndex{1}$

Sections coniques	Exemple
ellipse	$4x^2+9y^2=1$
encercler	$4x^2+4y^2=1$
hyperbole	$4x^2−9y^2=1$
parabole	$4x^2=9y$ou$4y^2=9x$
une ligne	$4x+9y=1$
lignes qui se croisent	$(x−4)(y+4)=0$
lignes parallèles	$(x−4)(x−9)=0$
un point	$4x^2+4y^2=0$
aucun graphique	$4x^2+4y^2=−1$

FORME GÉNÉRALE DES SECTIONS CONIQUES

Une section conique a la forme générale

$$Ax^2+Bxy+Cy^2+Dx+Ey+F=0 \label{gen}$$

où$A$$B$, et ne$C$ sont pas tous nuls. $\PageIndex{2}$Le tableau résume les différentes sections coniques où$B=0$, et$A$ et$C$ sont des nombres réels non nuls. Cela indique que la conique n'a pas été tournée.

Tableau$\PageIndex{2}$

ellipse	$Ax^2+Cy^2+Dx+Ey+F=0$,$A≠C$ et$AC>0$
encercler	$Ax^2+Cy^2+Dx+Ey+F=0$,$A=C$
hyperbole	$Ax^2−Cy^2+Dx+Ey+F=0$ou$−Ax^2+Cy^2+Dx+Ey+F=0$, où$A$ et$C$ sont positifs
parabole	$Ax^2+Dx+Ey+F=0$ou$Cy^2+Dx+Ey+F=0$

Comment : À partir de l'équation d'une conique, identifier le type de conique

1. Réécrivez l'équation sous forme générale (Équation \ ref {gen}),$Ax^2+Bxy+Cy^2+Dx+Ey+F=0$
2. Identifiez les valeurs de$A$ et$C$ à partir du formulaire général.
   • Si$A$ et$C$ sont différents de zéro, ont le même signe et ne sont pas égaux, alors le graphique peut être une ellipse.
   • Si$A$ et$C$ sont égaux et non nuls et ont le même signe, alors le graphique peut être un cercle.
   • Si$A$ et$C$ sont différents de zéro et ont des signes opposés, alors le graphique peut être une hyperbole.
   • Si l'$A$un des deux$C$ est égal à zéro, le graphique peut être une parabole.

Si$B=0$, la section conique aura un axe vertical et/ou horizontal. Si$B$ n'est pas égal à 0, comme indiqué ci-dessous, la section conique est tournée. Remarquez l'expression « peut être » dans les définitions. En effet, il se peut que l'équation ne représente pas du tout une section conique, selon les valeurs de$A$$B$$C$,$D$,$E$, et$F$. Par exemple, le cas dégénéré d'un cercle ou d'une ellipse est un point :

$$Ax^2+By^2=0,$$

quand$A$ et$B$ avoir le même signe.

Le cas dégénéré d'une hyperbole est constitué de deux lignes droites qui se croisent :$Ax^2+By^2=0$, quand$A$ et$B$ ont des signes opposés.

D'autre part, l'équation, quand$A$ et$B$ sont positifs$Ax^2+By^2+1=0$, ne représente pas du tout un graphe, puisqu'il n'existe pas de véritables paires ordonnées qui la satisfassent.

Exemple$\PageIndex{1}$: Identifying a Conic from Its General Form

Identifiez le graphe de chacune des sections coniques non dégénérées suivantes.

1. $4x^2−9y^2+36x+36y−125=0$
2. $9y^2+16x+36y−10=0$
3. $3x^2+3y^2−2x−6y−4=0$
4. $−25x^2−4y^2+100x+16y+20=0$

Solution

1. En réécrivant la forme générale (équation \ ref {gen}), nous avons $$\begin{align*} \color{red}{A} \color{black}x ^ { 2 } + \color{blue}{B} \color{black}x y + \color{red}{C} \color{black} y ^ { 2 } + \color{blue}{D} \color{black} x + \color{blue}{E} \color{black} y + \color{blue}{F} \color{black} &= 0 \\[4pt] 4 x ^ { 2 } + 0 x y + ( - 9 ) y ^ { 2 } + 36 x + 36 y + ( - 125 ) &= 0 \end{align*}$$ avec$A=4$ et$C=−9$, donc, nous observons cela$A$ et$C$ avons des signes opposés. Le graphique de cette équation est une hyperbole.
2. En réécrivant la forme générale (équation \ ref {gen}), nous avons $$\begin{align*} \color{red}{A} \color{black}x ^ { 2 } + \color{blue}{B} \color{black}x y + \color{red}{C} \color{black} y ^ { 2 } + \color{blue}{D} \color{black} x + \color{blue}{E} \color{black} y + \color{blue}{F} \color{black} &= 0 \\[4pt] 0 x ^ { 2 } + 0 x y + 9 y ^ { 2 } + 16 x + 36 y + ( - 10 ) &= 0 \end{align*}$$ avec$A=0$ et$C=9$. Nous pouvons déterminer que l'équation est une parabole, puisqu'elle$A$ est nulle.
3. En réécrivant la forme générale (équation \ ref {gen}), nous avons $$\begin{align*} \color{red}{A} \color{black}x ^ { 2 } + \color{blue}{B} \color{black}x y + \color{red}{C} \color{black} y ^ { 2 } + \color{blue}{D} \color{black} x + \color{blue}{E} \color{black} y + \color{blue}{F} \color{black} &= 0 \\[4pt] 3 x ^ { 2 } + 0 x y + 3 y ^ { 2 } + ( - 2 ) x + ( - 6 ) y + ( - 4 ) &= 0 \end{align*}$$ avec$A=3$ et$C=3$. Parce$A=C$ que le graphique de cette équation est un cercle.
4. En réécrivant la forme générale (équation \ ref {gen}), nous avons $$\begin{align*} \color{red}{A} \color{black}x ^ { 2 } + \color{blue}{B} \color{black}x y + \color{red}{C} \color{black} y ^ { 2 } + \color{blue}{D} \color{black} x + \color{blue}{E} \color{black} y + \color{blue}{F} \color{black} &= 0 \\[4pt] ( - 25 ) x ^ { 2 } + 0 x y + ( - 4 ) y ^ { 2 } + 100 x + 16 y + 20 &= 0 \end{align*}$$ avec$A=−25$ et$C=−4$. Parce que$AC>0$ et$A≠C$, le graphique de cette équation est une ellipse.

Exercice$\PageIndex{1}$

Identifiez le graphe de chacune des sections coniques non dégénérées suivantes.

1. $16y^2−x^2+x−4y−9=0$
2. $16x^2+4y^2+16x+49y−81=0$

Répondez à une

hyperbole

Réponse b

ellipse

Trouver une nouvelle représentation de l'équation donnée après une rotation selon un angle donné

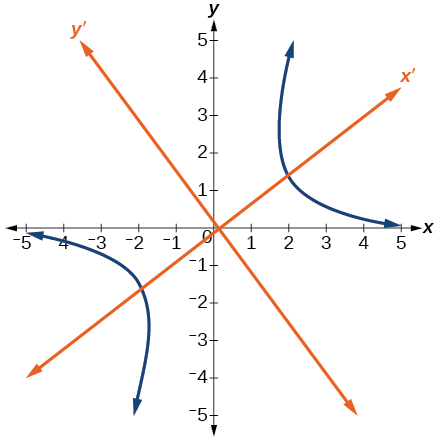
Jusqu'à présent, nous avons examiné les équations de sections coniques sans$xy$ terme, qui alignent les graphes sur les axes x et y. Lorsque nous ajoutons un$xy$ terme, nous faisons pivoter la conique autour de l'origine. Si les axes x et y sont pivotés d'un angle, par exemple$\theta$, chaque point du plan peut être considéré comme ayant deux représentations :$(x,y)$ sur le plan cartésien avec les axes x et y d'origine, et$(x^\prime ,y^\prime )$ sur le nouveau plan défini par les nouveaux axes pivotés, appelés axe x' et axe y' (Figure$\PageIndex{3}$).

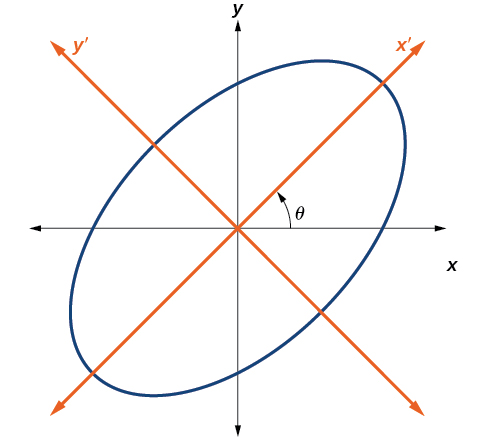
Figure$\PageIndex{3}$ : Le graphique de l'ellipse pivotée$x^2+y^2–xy–15=0$

Nous trouverons les relations entre$x$ et$y$ sur le plan cartésien avec$x^\prime$ et$y^\prime$ sur le nouveau plan pivoté (Figure$\PageIndex{4}$).

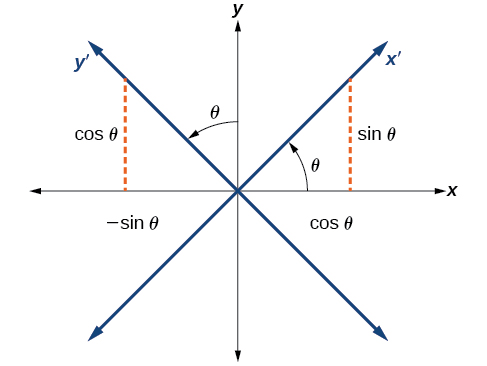
Figure$\PageIndex{4}$ : Le plan cartésien avec les axes$x$ - et$y$ - et les$y^\prime$ axes$x^\prime$ − et - qui en résultent, formés par une rotation d'un angle$\theta$.

Les axes x et y des coordonnées d'origine ont des vecteurs unitaires$\hat{i}$ et$\hat{j}$. Les axes de coordonnées pivotés ont des vecteurs unitaires$\hat{i}^\prime$ et$\hat{j}^\prime$. L'angle$\theta$ est connu sous le nom d'angle de rotation (Figure$\PageIndex{5}$). Nous pouvons écrire les nouveaux vecteurs unitaires en fonction des vecteurs d'origine.

$$\hat{i}′=\cos \theta \hat{i}+\sin \theta \hat{j}$$

$$\hat{j}′=−\sin \theta \hat{i}+\cos \theta \hat{j}$$

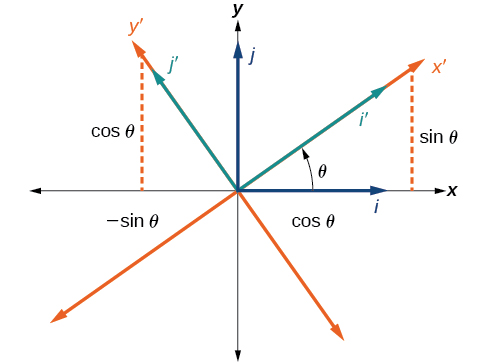
Figure$\PageIndex{5}$ : Relation entre l'ancien et le nouveau plan de coordonnées.

Considérez un vecteur$\vec{u}$ dans le nouveau plan de coordonnées. Il peut être représenté par ses axes de coordonnées.

$$\begin{align*} \vec{u}&=x^\prime i′+y^\prime j′ \\[4pt] &=x^\prime (i \cos \theta+j \sin \theta)+y^\prime (−i \sin \theta+j \cos \theta) & \text{Substitute.} \\[4pt] &=ix' \cos \theta+jx' \sin \theta−iy' \sin \theta+jy' \cos \theta & \text{Distribute.} \\[4pt] &=ix' \cos \theta−iy' \sin \theta+jx' \sin \theta+jy' \cos \theta & \text{Apply commutative property.} \\[4pt] &=(x' \cos \theta−y' \sin \theta)i+(x' \sin \theta+y' \cos \theta)j & \text{Factor by grouping.} \end{align*}$$

Parce que$\vec{u}=x^\prime i′+y^\prime j′$ nous avons des représentations du nouveau système de coordonnées$x$ et$y$ en termes de celui-ci.

$x=x^\prime \cos \theta−y^\prime \sin \theta$

et

$y=x^\prime \sin \theta+y^\prime \cos \theta$

ÉQUATIONS DE ROTATION

Si un point$(x,y)$ du plan cartésien est représenté sur un nouveau plan de coordonnées où les axes de rotation sont formés en faisant pivoter un angle par rapport$\theta$ à l'axe x positif, les coordonnées du point par rapport aux nouveaux axes sont$(x^\prime ,y^\prime )$. Nous pouvons utiliser les équations de rotation suivantes pour définir la relation entre$(x,y)$ et$(x^\prime , y^\prime )$ :

$$x=x^\prime \cos \theta−y^\prime \sin \theta$$

et

$$y=x^\prime \sin \theta+y^\prime \cos \theta$$

Comment : à partir de l'équation d'une conique, trouver une nouvelle représentation après avoir fait pivoter un angle

1. Trouvez$x$ et$y$ où$x=x^\prime \cos \theta−y^\prime \sin \theta$ et$y=x^\prime \sin \theta+y^\prime \cos \theta$.
2. Remplacez l'expression par$x$ et par$y$ dans l'équation donnée, puis simplifiez.
3. Écrivez les équations avec$x^\prime$ et$y^\prime$ sous une forme standard.

Exemple$\PageIndex{2}$: Finding a New Representation of an Equation after Rotating through a Given Angle

Trouvez une nouvelle représentation de l'équation$2x^2−xy+2y^2−30=0$ après une rotation d'un angle de$\theta=45°$.

Solution

Trouvez$x$ et$y$, où$x=x^\prime \cos \theta−y^\prime \sin \theta$ et$y=x^\prime \sin \theta+y^\prime \cos \theta$.

Parce que$\theta=45°$,

$$\begin{align*} x &= x^\prime \cos(45°)−y^\prime \sin(45°) \\[4pt] x &= x^\prime \left(\dfrac{1}{\sqrt{2}}\right)−y^\prime \left(\dfrac{1}{\sqrt{2}}\right) \\[4pt] x &=\dfrac{x^\prime −y^\prime }{\sqrt{2}} \end{align*}$$

et

$$\begin{align*} y &= x^\prime \sin(45°)+y^\prime \cos(45°) \\[4pt] y &= x^\prime \left(\dfrac{1}{\sqrt{2}}\right) + y^\prime \left(\dfrac{1}{\sqrt{2}}\right) \\[4pt] y &= \dfrac{x^\prime +y^\prime }{\sqrt{2}} \end{align*}$$

Substituer$x=x^\prime \cos\theta−y^\prime \sin\theta$ et$y=x^\prime \sin \theta+y^\prime \cos \theta$ introduire$2x^2−xy+2y^2−30=0$.

$2{\left(\dfrac{x^\prime −y^\prime }{\sqrt{2}}\right)}^2−\left(\dfrac{x^\prime −y^\prime }{\sqrt{2}}\right)\left(\dfrac{x^\prime +y^\prime }{\sqrt{2}}\right)+2{\left(\dfrac{x^\prime +y^\prime }{\sqrt{2}}\right)}^2−30=0$

Simplifiez.

$\begin{array}{rl} 2\dfrac{(x^\prime−y^\prime )(x^\prime −y^\prime )}{2}−\dfrac{(x^\prime −y^\prime )(x^\prime +y^\prime )}{2}+2\dfrac{(x^\prime +y^\prime )(x^\prime +y^\prime )}{2}−30=0 & \text{FOIL method} \\[4pt] {x^\prime }^2−2x^\prime y^\prime +{y^\prime }^2−\dfrac{({x^\prime }^2−{y^\prime }^2)}{2}+{x^\prime }^2+2x^\prime y^\prime +{y^\prime }^2−30=0 & \text{Combine like terms.} \\[4pt] 2{x^\prime }^2+2{y^\prime }^2−\dfrac{({x^\prime }^2−{y^\prime }^2)}{2}=30 & \text{Combine like terms.} \\[4pt] 2(2{x^\prime }^2+2{y^\prime }^2−\dfrac{({x^\prime }^2−{y^\prime }^2)}{2})=2(30) & \text{Multiply both sides by 2.} \\[4pt] 4{x^\prime }^2+4{y^\prime }^2−({x^\prime }^2−{y^\prime }^2)=60 & \text{Simplify. } \\[4pt] 4{x^\prime }^2+4{y^\prime }^2−{x^\prime }^2+{y^\prime }2=60 & \text{Distribute.} \\[4pt] \dfrac{3{x^\prime }^2}{60}+\dfrac{5{y^\prime }^2}{60}=\dfrac{60}{60} & \text{Set equal to 1.} \end{array}$

Écrivez les équations avec$x^\prime$ et$y^\prime$ sous la forme standard.

$$\dfrac{{x^\prime }^2}{20}+\dfrac{{y^\prime}^2}{12}=1 \nonumber$$

Cette équation est une ellipse. La figure$\PageIndex{6}$ montre le graphique.

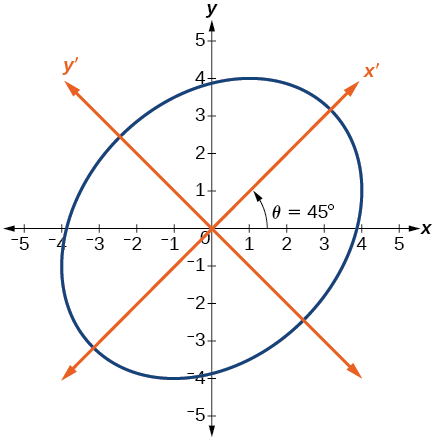
Figurine$\PageIndex{6}$

Ecriture d'équations de coniques pivotées sous forme standard

Maintenant que nous pouvons trouver la forme standard d'une conique lorsqu'on nous donne un angle de rotation, nous allons apprendre à transformer l'équation d'une conique donnée dans la forme$Ax^2+Bxy+Cy^2+Dx+Ey+F=0$ en forme standard en faisant tourner les axes. Pour ce faire, nous allons réécrire la forme générale sous forme d'équation dans le système de$y^\prime$ coordonnées$x^\prime$ et sans le$x^\prime y^\prime$ terme, en faisant pivoter les axes d'une mesure$\theta$ qui satisfait

$$\cot(2\theta)=\dfrac{A−C}{B}$$

Nous avons déjà appris que n'importe quelle conique peut être représentée par l'équation du second degré

$Ax^2+Bxy+Cy^2+Dx+Ey+F=0$

où$A$$B$, et ne$C$ sont pas tous nuls. Cependant, si$B≠0$, alors nous avons un$xy$ terme qui nous empêche de réécrire l'équation sous une forme standard. Pour l'éliminer, nous pouvons faire pivoter les axes d'un angle aigu$\theta$ où$\cot(2\theta)=\dfrac{A−C}{B}$.

• Si$\cot(2\theta)>0$, alors$2\theta$ se trouve dans le premier quadrant, et$\theta$ se situe entre$(0°,45°)$.
• Si$\cot(2\theta)<0$, alors$2\theta$ se trouve dans le deuxième quadrant, et$\theta$ se situe entre$(45°,90°)$.
• Si$A=C$, alors$\theta=45°$.

Comment faire : étant donné une équation pour une conique dans$x^\prime y^\prime$ system, rewrite the equation without the $x^\prime y^\prime$ term in terms of $x^\prime$ and $y^\prime$,where the $x^\prime$ and $y^\prime$ axes are rotations of the standard axes by $\theta$ degrees

1. Trouvez$\cot(2\theta)$.
2. Trouvez$\sin \theta$ et$\cos \theta$.
3. Substituer$\sin \theta$ et$\cos \theta$ insérer dans$x=x^\prime \cos \theta−y^\prime \sin \theta$ et$y=x^\prime \sin \theta+y^\prime \cos \theta$.
4. Remplacez l'expression par$x$ et par$y$ dans l'équation donnée, puis simplifiez.
5. Écrivez les équations avec$x^\prime$ et$y^\prime$ sous la forme standard par rapport aux axes pivotés.

Exemple$\PageIndex{3}$: Rewriting an Equation with respect to the $x^\prime$ and $y^\prime$ axes without the $x^\prime y^\prime$ Term

Réécrivez l'équation$8x^2−12xy+17y^2=20$ dans le$x^\prime y^\prime$ système sans$x^\prime y^\prime$ terme.

Solution

Tout d'abord, nous trouvons$\cot(2\theta)$.

$8x^2−12xy+17y^2=20\rightarrow A=8$,$B=−12$ et$C=17$

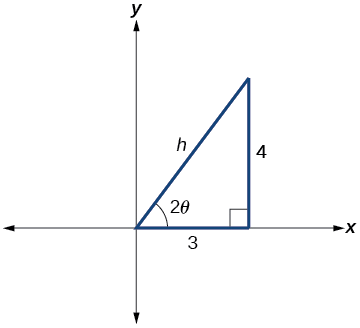
Figurine$\PageIndex{7}$

De la figure$\PageIndex{7}$ :

$$\begin{align*} \cot(2\theta) &=\dfrac{A−C}{B}=\dfrac{8−17}{−12} \\[4pt] & =\dfrac{−9}{−12}=\dfrac{3}{4} \end{align*}$$

$\cot(2\theta)=\dfrac{3}{4}=\dfrac{\text{adjacent}}{\text{opposite}}$

Donc, l'hypoténuse est

$$\begin{align*} 3^2+4^2 &=h^2 \\[4pt] 9+16 &=h^2 \\[4pt] 25&=h^2 \\[4pt] h&=5 \end{align*}$$

Ensuite, nous trouvons$\sin \theta$ et$\cos \theta$.

$$\begin{align*} \sin \theta &=\sqrt{\dfrac{1−\cos(2\theta)}{2}}=\sqrt{\dfrac{1−\dfrac{3}{5}}{2}}=\sqrt{\dfrac{\dfrac{5}{5}−\dfrac{3}{5}}{2}}=\sqrt{\dfrac{5−3}{5}⋅\dfrac{1}{2}}=\sqrt{\dfrac{2}{10}}=\sqrt{\dfrac{1}{5}} \\ \sin \theta &= \dfrac{1}{\sqrt{5}} \\ \cos \theta &= \sqrt{\dfrac{1+\cos(2\theta)}{2}}=\sqrt{\dfrac{1+\dfrac{3}{5}}{2}}=\sqrt{\dfrac{\dfrac{5}{5}+\dfrac{3}{5}}{2}}=\sqrt{\dfrac{5+3}{5}⋅\dfrac{1}{2}}=\sqrt{\dfrac{8}{10}}=\sqrt{\dfrac{4}{5}} \\ \cos \theta &= \dfrac{2}{\sqrt{5}} \end{align*}$$

Remplacez les valeurs de$\sin \theta$ et$\cos \theta$ dans$x=x^\prime \cos \theta−y^\prime \sin \theta$ et$y=x^\prime \sin \theta+y^\prime \cos \theta$.

$$\begin{align*} x &=x'\cos \theta−y^\prime \sin \theta \\[4pt] &=x^\prime \left(\dfrac{2}{\sqrt{5}}\right)−y^\prime \left(\dfrac{1}{\sqrt{5}}\right) \\[4pt] &=\dfrac{2x^\prime −y^\prime }{\sqrt{5}} \end{align*}$$

et

$$\begin{align*} y&=x^\prime \sin \theta+y^\prime \cos \theta \\[4pt] &=x^\prime \left(\dfrac{1}{\sqrt{5}}\right)+y^\prime \left(\dfrac{2}{\sqrt{5}}\right) \\[4pt] &=\dfrac{x^\prime +2y^\prime }{\sqrt{5}} \end{align*}$$

Remplacez les expressions par$x$ et par$y$ dans l'équation donnée, puis simplifiez.

$$\begin{align*} 8{\left(\dfrac{2x^\prime −y^\prime }{\sqrt{5}}\right)}^2−12\left(\dfrac{2x^\prime −y^\prime }{\sqrt{5}}\right)\left(\dfrac{x^\prime +2y^\prime }{\sqrt{5}}\right)+17{\left(\dfrac{x^\prime +2y^\prime }{\sqrt{5}}\right)}^2&=20 \\[4pt] 8\left(\dfrac{(2x^\prime −y^\prime )(2x^\prime −y^\prime )}{5}\right)−12\left(\dfrac{(2x^\prime −y^\prime )(x^\prime +2y^\prime )}{5}\right)+17\left(\dfrac{(x^\prime +2y^\prime )(x^\prime +2y^\prime )}{5}\right)&=20 \\[4pt] 8(4{x^\prime }^2−4x^\prime y^\prime +{y^\prime }^2)−12(2{x^\prime }^2+3x^\prime y^\prime −2{y^\prime }^2)+17({x^\prime }^2+4x^\prime y^\prime +4{y^\prime }^2)&=100 \\[4pt] 32{x^\prime }^2−32x^\prime y^\prime +8{y^\prime }^2−24{x^\prime }^2−36x^\prime y^\prime +24{y^\prime }^2+17{x^\prime }^2+68x^\prime y^\prime +68{y^\prime }^2&=100 \\[4pt] 25{x^\prime }^2+100{y^\prime }^2&=100 \\[4pt] \dfrac{25}{100}{x^\prime }^2+\dfrac{100}{100}{y^\prime }^2&=\dfrac{100}{100} \end{align*}$$

Écrivez les équations avec$x^\prime$ et$y^\prime$ dans le formulaire standard par rapport au nouveau système de coordonnées.

$$\dfrac{{x^\prime }^2}{4}+\dfrac{{y^\prime }^2}{1}=1 \nonumber$$

La figure$\PageIndex{8}$ montre le graphique de l'ellipse.

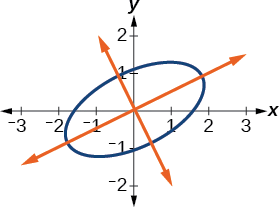
Figurine$\PageIndex{8}$

Exercice$\PageIndex{2}$

Réécrivez le$13x^2−6\sqrt{3}xy+7y^2=16$ dans le$x^\prime y^\prime$ système sans le$x^\prime y^\prime$ terme.

Réponse

$\dfrac{{x^\prime }^2}{4}+\dfrac{{y^\prime }^2}{1}=1$

Exemple$\PageIndex{4}$ :Graphing an Equation That Has No $x^\prime y^\prime$ Terms

Représentez graphiquement l'équation suivante par rapport au$x^\prime y^\prime$ système :

$x^2+12xy−4y^2=30$

Solution

Tout d'abord, nous trouvons$\cot(2\theta)$.

$x^2+12xy−4y^2=20\rightarrow A=1$$B=12$, et$C=−4$

$$\begin{align*} \cot(2\theta) &= \dfrac{A−C}{B} \\ \cot(2\theta) &= \dfrac{1−(−4)}{12} \\ \cot(2\theta) &= \dfrac{5}{12} \end{align*}$$

Parce que$\cot(2\theta)=\dfrac{5}{12}$ nous pouvons dessiner un triangle de référence comme dans la figure$\PageIndex{9}$.

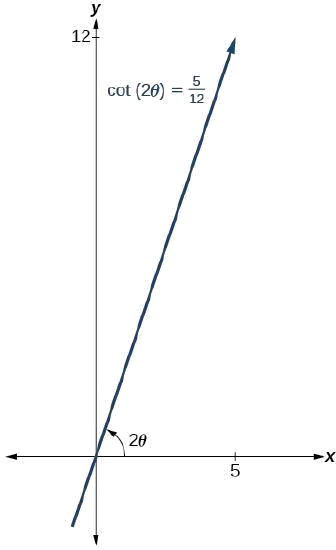
Figurine$\PageIndex{9}$

$\cot(2\theta)=\dfrac{5}{12}=\dfrac{adjacent}{opposite}$

Ainsi, l'hypoténuse est

$$\begin{align*} 5^2+{12}^2&=h^2 \\[4pt] 25+144 &=h^2 \\[4pt] 169 &=h^2 \\[4pt] h&=13 \end{align*}$$

Ensuite, nous trouvons$\sin \theta$ et$\cos \theta$. Nous utiliserons des identités en demi-angle.

$\sin \theta=\sqrt{\dfrac{1−\cos(2\theta)}{2}}=\sqrt{\dfrac{1−\dfrac{5}{13}}{2}}=\sqrt{\dfrac{\dfrac{13}{13}−\dfrac{5}{13}}{2}}=\sqrt{\dfrac{8}{13}⋅\dfrac{1}{2}}=\dfrac{2}{\sqrt{13}}$

$\cos \theta=\sqrt{\dfrac{1+\cos(2\theta)}{2}}=\sqrt{\dfrac{1+\dfrac{5}{13}}{2}}=\sqrt{\dfrac{\dfrac{13}{13}+\dfrac{5}{13}}{2}}=\sqrt{\dfrac{18}{13}⋅\dfrac{1}{2}}=\dfrac{3}{\sqrt{13}}$

Maintenant, nous trouvons$x$ et$y$.

$x=x^\prime \cos \theta−y^\prime \sin \theta$

$x=x^\prime \left(\dfrac{3}{\sqrt{13}}\right)−y^\prime \left(\dfrac{2}{\sqrt{13}}\right)$

$x=\dfrac{3x^\prime −2y^\prime }{\sqrt{13}}$

et

$y=x^\prime \sin \theta+y^\prime \cos \theta$

$y=x^\prime \left(\dfrac{2}{\sqrt{13}}\right)+y^\prime \left(\dfrac{3}{\sqrt{13}}\right)$

$y=\dfrac{2x^\prime +3y^\prime }{\sqrt{13}}$

Maintenant, nous$x=\dfrac{3x^\prime −2y^\prime }{\sqrt{13}}$ remplaçons et$y=\dfrac{2x^\prime +3y^\prime }{\sqrt{13}}$ introduisons$x^2+12xy−4y^2=30$.

$\begin{array}{rl} {\left(\dfrac{3x^\prime −2y^\prime }{\sqrt{13}}\right)}^2+12\left(\dfrac{3x^\prime −2y^\prime }{\sqrt{13}}\right)\left(\dfrac{2x^\prime +3y^\prime }{\sqrt{13}}\right)−4{\left(\dfrac{2x^\prime +3y^\prime }{\sqrt{13}}\right)}^2=30 \\ \left(\dfrac{1}{13}\right)[ {(3x^\prime −2y^\prime )}^2+12(3x^\prime −2y^\prime )(2x^\prime +3y^\prime )−4{(2x^\prime +3y^\prime )}^2 ]=30 & \text{Factor.} \\ \left(\dfrac{1}{13}\right)[ 9{x^\prime }^2−12x^\prime y^\prime +4{y^\prime }^2+12(6{x^\prime }^2+5x^\prime y^\prime −6{y^\prime }^2)−4(4{x^\prime }^2+12x^\prime y^\prime +9{y^\prime }^2) ]=30 & \text{Multiply.} \\ \left(\dfrac{1}{13}\right)[ 9{x^\prime }^2−12x^\prime y^\prime +4{y^\prime }^2+72{x^\prime }^2+60x^\prime y^\prime −72{y^\prime }^2−16{x^\prime }^2−48x^\prime y^\prime −36{y^\prime }^2 ]=30 & \text{Distribute.} \\ \left(\dfrac{1}{13}\right)[ 65{x^\prime }^2−104{y^\prime }^2 ]=30 & \text{Combine like terms.} \\ 65{x^\prime }^2−104{y^\prime }^2=390 & \text{Multiply.} \\ \dfrac{{x^\prime }^2}{6}−\dfrac{4{y^\prime }^2}{15}=1 & \text{Divide by 390.} \end{array}$

La figure$\PageIndex{10}$ montre le graphique de l'hyperbole$\dfrac{{x^\prime }^2}{6}−\dfrac{4{y^\prime }^2}{15}=1$

Figurine$\PageIndex{10}$

Identification des coniques sans axes rotatifs

Maintenant, la boucle est bouclée. Comment identifier le type de conique décrit par une équation ? Que se passe-t-il lorsque les axes pivotent ? Rappelons que la forme générale d'une conique est

$Ax^2+Bxy+Cy^2+Dx+Ey+F=0$

Si nous appliquons les formules de rotation à cette équation, nous obtenons la forme

$A′{x^\prime }^2+B′x^\prime y^\prime +C′{y^\prime }^2+D′x^\prime +E′y^\prime +F′=0$

On peut montrer que

$B^2−4AC={B′}^2−4A′C′$

L'expression ne varie pas après la rotation, c'est pourquoi nous l'appelons invariante. Le discriminant,$B^2−4AC$, est invariant et reste inchangé après la rotation. Comme le discriminant reste inchangé, l'observation du discriminant permet d'identifier la section conique.

HOWTO : UTILISER LE DISCRIMINANT POUR IDENTIFIER UNE CONIQUE

Si l'équation

$$Ax^2+Bxy+Cy^2+Dx+Ey+F=0$$

est transformé par la rotation des axes dans l'équation

$$A′{x^\prime }^2+B′x^\prime y^\prime +C′{y^\prime }^2+D′x^\prime +E′y^\prime +F′=0$$

alors $$B^2−4AC={B′}^2−4A′C′$$

L'équation$Ax^2+Bxy+Cy^2+Dx+Ey+F=0$ est une ellipse, une parabole ou une hyperbole, ou un cas dégénéré de l'une d'entre elles. Si le discriminant$B^2−4AC$, est

• $<0$, la section conique est une ellipse
• $=0$, la section conique est une parabole
• $>0$, la section conique est une hyperbole

Exemple$\PageIndex{5}$: Identifying the Conic without Rotating Axes

Identifiez la conique pour chacun des éléments suivants sans les axes de rotation.

1. $5x^2+2\sqrt{3}xy+2y^2−5=0$
2. $5x^2+2\sqrt{3}xy+12y^2−5=0$

Solution

a. Commençons par déterminer$A$$B$, et$C$.

$\underbrace{5}_{A}x^2+\underbrace{2\sqrt{3}}_{B}xy+\underbrace{2}_{C}y^2−5=0$

Maintenant, nous trouvons le discriminant.

$$\begin{align*} B^2−4AC &= {(2\sqrt{3})}^2−4(5)(2) \\ &=4(3)−40 \\ &=12−40 \\ &=−28<0 \end{align*}$$

$5x^2+2\sqrt{3}xy+2y^2−5=0$Représente donc une ellipse.

b. Encore une fois, commençons par déterminer$A$$B$, et$C$.

$\underbrace{5}_{A}x^2+\underbrace{2\sqrt{3}}_{B}xy+\underbrace{12}_{C}y^2−5=0 \nonumber$

Maintenant, nous trouvons le discriminant.

$$\begin{align*} B^2−4AC &= {(2\sqrt{3})}^2−4(5)(12) \\ &= 4(3)−240 \\ &= 12−240 \\ &=−228<0 \end{align*}$$

$5x^2+2\sqrt{3}xy+12y^2−5=0$Représente donc une ellipse.

Exercice$\PageIndex{3}$

Identifiez la conique pour chacun des éléments suivants sans les axes de rotation.

1. $x^2−9xy+3y^2−12=0$
2. $10x^2−9xy+4y^2−4=0$

Répondez à une

hyperbole

Réponse b

ellipse

Équations clés

Équation de forme générale d'une section conique	$Ax^2+Bxy+Cy^2+Dx+Ey+F=0$
Rotation d'une section conique	$x=x^\prime \cos \theta−y^\prime \sin \theta$ $y=x^\prime \sin \theta+y^\prime \cos \theta$
Angle de rotation	$\theta$, où$\cot(2\theta)=\dfrac{A−C}{B}$

Concepts clés

• Quatre formes de base peuvent résulter de l'intersection d'un plan avec une paire de cônes circulaires droits reliés queue à queue. Ils comprennent une ellipse, un cercle, une hyperbole et une parabole.
• Une section conique non dégénérée a la forme générale$Ax^2+Bxy+Cy^2+Dx+Ey+F=0$ où$A$,$B$ et ne$C$ sont pas toutes nulles. Les valeurs de$A$$B$, et$C$ déterminent le type de conique. Voir l'exemple$\PageIndex{1}$.
• Les équations des sections coniques comportant un$xy$ terme ont été pivotées autour de l'origine. Voir l'exemple$\PageIndex{2}$.
• La forme générale peut être transformée en équation dans le système de$y^\prime$ coordonnées$x^\prime$ et sans le$x^\prime y^\prime$ terme. Voir Exemple$\PageIndex{3}$ et Exemple$\PageIndex{4}$.
• Une expression est qualifiée d'invariante si elle reste inchangée après la rotation. Comme le discriminant est invariant, son observation permet d'identifier la section conique. Voir l'exemple$\PageIndex{5}$.