12.3 : La parabole

Objectifs d'apprentissage

• Tracez des paraboles avec des sommets à l'origine.
• Écrivez des équations de paraboles sous une forme standard.
• Tracez des paraboles dont les sommets ne se trouvent pas à l'origine.
• Résolvez des problèmes appliqués impliquant des paraboles.

Saviez-vous que la torche olympique est allumée plusieurs mois avant le début des Jeux ? La méthode cérémonielle pour allumer la flamme est la même que dans les temps anciens. La cérémonie a lieu au temple d'Héra à Olympie, en Grèce, et est ancrée dans la mythologie grecque et rend hommage à Prométhée, qui a volé le feu à Zeus pour le donner à tous les humains. L'une des onze prêtresses par intérim place la torche au centre d'un miroir parabolique (Figure$\PageIndex{1}$), qui focalise les rayons lumineux du soleil pour allumer la flamme.

Figure$\PageIndex{1}$ : La torche olympique conclut son voyage autour du monde lorsqu'elle est utilisée pour allumer le chaudron olympique lors de la cérémonie d'ouverture. (crédit : Ken Hackman, armée de l'air américaine)

Les miroirs paraboliques (ou réflecteurs) sont capables de capter l'énergie et de la concentrer sur un point unique. Les avantages de cette propriété sont mis en évidence par la vaste liste d'objets paraboliques que nous utilisons au quotidien : antennes paraboliques, ponts suspendus, télescopes, microphones, projecteurs et phares de voiture, pour n'en nommer que quelques-uns. Les réflecteurs paraboliques sont également utilisés dans les dispositifs à énergie alternative, tels que les cuisinières solaires et les chauffe-eau, car leur fabrication est peu coûteuse et nécessite peu d'entretien. Dans cette section, nous allons explorer la parabole et ses utilisations, y compris les conceptions solaires à faible coût et économes en énergie.

Représentation graphique de paraboles avec des sommets à l'origine

Nous avons vu précédemment qu'une ellipse se forme lorsqu'un plan traverse un cône circulaire droit. Si le plan est parallèle à l'arête du cône, une courbe illimitée est formée. Cette courbe est une parabole (Figure$\PageIndex{2}$).

Figure$\PageIndex{2}$ : Parabole

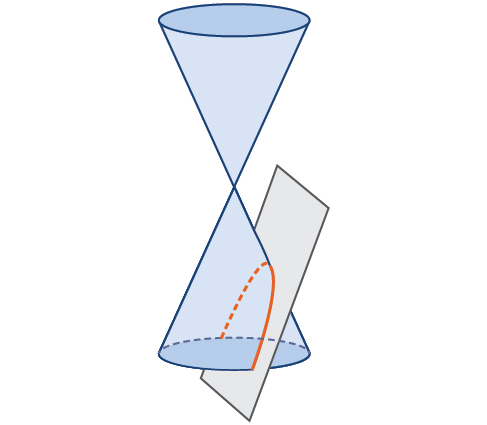
Comme l'ellipse et l'hyperbole, la parabole peut également être définie par un ensemble de points dans le plan de coordonnées. Une parabole est l'ensemble de tous les points d'un plan qui se trouvent$(x,y)$ à la même distance d'une ligne fixe, appelée directrice, et d'un point fixe (le point focal) qui ne se trouve pas sur la directrice.

Nous avons déjà découvert le sommet et l'axe de symétrie d'une parabole. Nous étendons maintenant la discussion pour inclure d'autres caractéristiques clés de la parabole (Figure$\PageIndex{3}$). Notez que l'axe de symétrie passe par le foyer et le sommet et est perpendiculaire à la directrice. Le sommet est le point médian entre la directrice et le foyer. Le segment de ligne qui passe par le foyer et qui est parallèle à la directrice est appelé latus rectum. Les extrémités du latus rectal se situent sur la courbe. Par définition, la distance d entre le foyer et tout point de la$P$ parabole est égale à la distance$P$ entre le foyer et la directrice.

Figure$\PageIndex{3}$ : Caractéristiques principales de la parabole

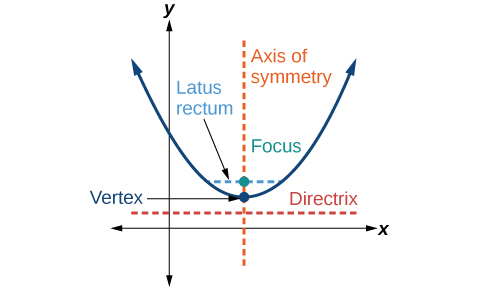
Pour travailler avec des paraboles dans le plan de coordonnées, nous considérons deux cas : ceux avec un sommet à l'origine et ceux avec un sommet situé à un point autre que l'origine. Nous commençons par le premier.

Figurine$\PageIndex{4}$

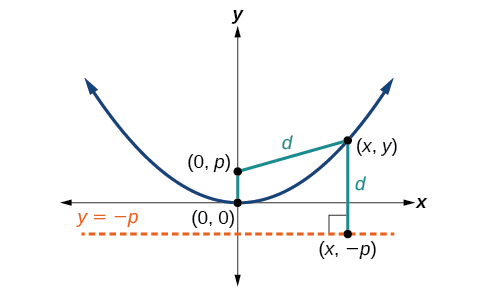
$(x,y)$Soit un point sur la parabole avec un sommet$(0,0)$, un foyer et une directrice$(0,p)$,$y=−p$ comme indiqué sur la figure$\PageIndex{4}$. La distance d d'un point$(x,y)$ à l'autre$(x,−p)$ sur la directrice est la différence des valeurs y :$d=y+p$. La distance entre le point focal$(0,p)$ et le point$(x,y)$ est également égale à$d$ et peut être exprimée à l'aide de la formule de distance.

$$\begin{align*} d &=\sqrt{{(x−0)}^2+{(y−p)}^2} \\[4pt] &=\sqrt{x^2+{(y−p)}^2} \end{align*}$$

Définissez les deux expressions pour qu'elles$d$ soient égales l'une à l'autre et résolvez$y$ pour obtenir l'équation de la parabole. Nous faisons cela parce que la distance de$(x,y)$ à$(0,p)$ est égale à la distance de$(x,y)$ à$(x,−p)$.

$$\sqrt{x^2+{(y−p)}^2}=y+p$$

Nous mettons ensuite au carré les deux côtés de l'équation, élargissons les termes au carré et simplifions en combinant des termes similaires.

$$\begin{align*} x^2+{(y−p)}^2 &={(y+p)}^2 \\[4pt] x^2+y^2−2py+p^2 &=y^2+2py+p^2 \\[4pt] x^2−2py &=2py \\[4pt] x^2 &=4py \end{align*}$$

Les équations des paraboles avec sommet$(0,0)$ sont$y^2=4px$ lorsque l'axe x est l'axe de symétrie et$x^2=4py$ lorsque l'axe y est l'axe de symétrie. Ces formulaires standard sont présentés ci-dessous, avec leurs graphiques généraux et leurs principales caractéristiques.

FORMES STANDARD DE PARABOLES AVEC VERTEX$(0,0)$

Le tableau$\PageIndex{1}$ et la figure$\PageIndex{5}$ résument les caractéristiques standard des paraboles ayant un sommet à l'origine.

Tableau$\PageIndex{1}$

Axe de symétrie	équation	Se concentrer	Directrix	Paramètres du latus rectal
axe x	$y^2=4px$	$(p, 0)$	$x=−p$	$(p, \pm 2p)$
axe Y	$x^2=4py$	$(0, p)$	$y=−p$	$(\pm 2p, p)$

Figure$\PageIndex{5}$ : (a) Lorsque$p>0$ et que l'axe de symétrie est l'axe X, la parabole s'ouvre vers la droite. (b) Lorsque$p<0$ et que l'axe de symétrie est l'axe X, la parabole s'ouvre vers la gauche. (c) Lorsque$p<0$ et que l'axe de symétrie est l'axe Y, la parabole s'ouvre. (d) Lorsque$p<0$ et que l'axe de symétrie est l'axe Y, la parabole s'ouvre vers le bas.

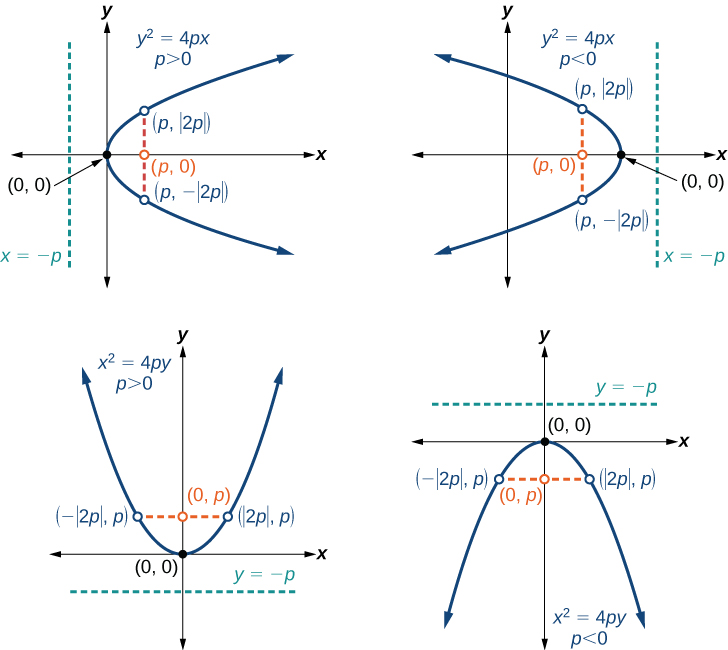
Les principales caractéristiques d'une parabole sont son sommet, son axe de symétrie, son foyer, sa directrice et son latus rectal (Figure$\PageIndex{5}$). Lorsque l'on donne une équation standard pour une parabole centrée à l'origine, on peut facilement identifier les principales caractéristiques pour représenter graphiquement la parabole. Une droite est dite tangente à une courbe si elle coupe la courbe en un point précis. Si nous esquissons des lignes tangentes à la parabole aux extrémités du latus rectum, ces lignes se croisent sur l'axe de symétrie, comme le montre la figure$\PageIndex{6}$.

Figurine$\PageIndex{6}$

Comment faire : Avec une équation de forme standard pour une parabole centrée sur$(0,0)$, sketch the graph

1. Déterminez lequel des formulaires standard s'applique à l'équation donnée :$y^2=4px$ ou$x^2=4py$.
2. Utilisez le formulaire standard identifié à l'étape 1 pour déterminer l'axe de symétrie, la focalisation, l'équation de la directrice et les extrémités du latus rectal.
   • Si l'équation se trouve dans la forme$y^2=4px$, alors
     • l'axe de symétrie est l'$x$axe -,$y=0$
     • défini$4p$ égal au coefficient de$x$ dans l'équation donnée à résoudre$p$. Si$p>0$, la parabole s'ouvre à droite. Si$p<0$, la parabole s'ouvre vers la gauche.
     • utiliser$p$ pour trouver les coordonnées du focus,$(p,0)$
     • utiliser$p$ pour trouver l'équation de la directrice,$x=−p$
     • utiliser$p$ pour trouver les terminaisons du latus rectal,$(p,\pm 2p)$. Vous pouvez également la remplacer$x=p$ dans l'équation d'origine.
   • Si l'équation se trouve dans la forme$x^2=4py$, alors
     • l'axe de symétrie est l'$y$axe -,$x=0$
     • défini$4p$ égal au coefficient de$y$ dans l'équation donnée à résoudre$p$. Si$p>0$, la parabole s'ouvre. Si$p<0$, la parabole s'ouvre.
     • utiliser$p$ pour trouver les coordonnées du focus,$(0,p)$
     • utiliser$p$ pour trouver l'équation de la directrice,$y=−p$
     • utiliser$p$ pour trouver les terminaisons du latus rectal,$(\pm 2p,p)$
3. Tracez le foyer, la directrice et le latus rectal et tracez une courbe lisse pour former la parabole.

-axe comme axe de symétrie

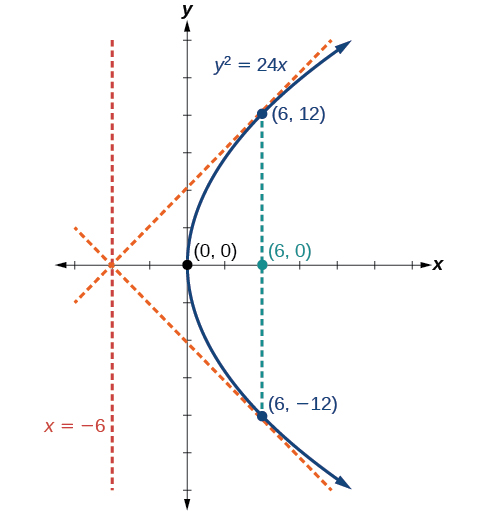
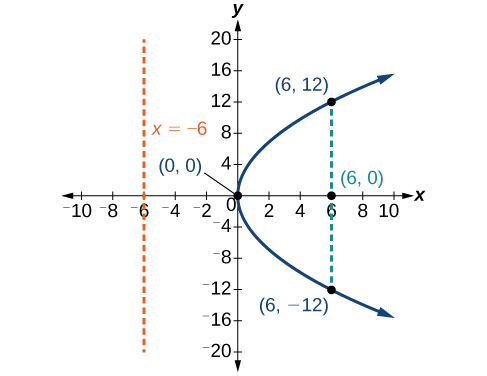
Graphe$y^2=24x$. Identifiez et étiquetez le foyer, les directeurs et les points d'extrémité du latus rectal.

Solution

La forme standard qui s'applique à l'équation donnée est$y^2=4px$. Ainsi, l'axe de symétrie est l'axe x. Il s'ensuit que :

• $24=4p$, donc$p=6$. Depuis$p>0$, la parabole s'ouvre à droite
• les coordonnées du focus sont$(p,0)=(6,0)$
• l'équation de la directrice est$x=−p=−6$
• les extrémités du latus rectal ont la même coordonnée x au niveau du foyer. Pour trouver les points finaux,$x=6$ remplacez-les par l'équation d'origine :$(6,\pm 12)$

Ensuite, nous tracons le foyer, la directrice et le rectum latus, et dessinons une courbe lisse pour former la parabole (Figure$\PageIndex{7}$).

Figurine$\PageIndex{7}$

Exercice$\PageIndex{1}$

Graphe$y^2=−16x$. Identifiez et étiquetez le foyer, les directeurs et les points d'extrémité du latus rectal.

Réponse

• Mettre l'accent :$(−4,0)$
• Directrice :$x=4$
• Terminaux du latus rectal :$(−4,\pm 8)$

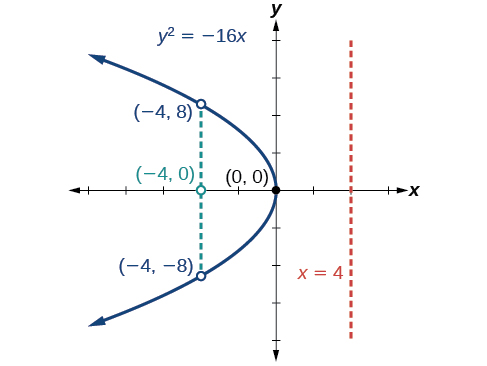
Figurine$\PageIndex{8}$

-axe comme axe de symétrie

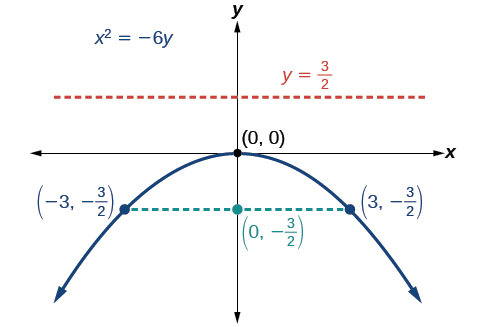
Graphe$x^2=−6y$. Identifiez et étiquetez le foyer, les directeurs et les points d'extrémité du latus rectal.

Solution

La forme standard qui s'applique à l'équation donnée est$x^2=4py$. Ainsi, l'axe de symétrie est l'$y$axe. Il s'ensuit que :

• $−6=4p$, donc$p=−\dfrac{3}{2}$. Depuis$p<0$, la parabole s'ouvre.
• les coordonnées du focus sont$(0,p)=(0,−\dfrac{3}{2})$
• l'équation de la directrice est$y=−p=\dfrac{3}{2}$
• les paramètres du latus rectum peuvent être déterminés en les remplaçant$y=\dfrac{3}{2}$ dans l'équation d'origine,$(\pm 3,−\dfrac{3}{2})$

Ensuite, nous tracons le foyer, la directrice et le rectum latus, et dessinons une courbe lisse pour former la parabole.

Figurine$\PageIndex{9}$

Exercice$\PageIndex{2}$

Graphe$x^2=8y$. Identifiez et étiquetez le foyer, les directeurs et les points d'extrémité du latus rectal.

Réponse

• Mettre l'accent :$(0,2)$
• Directrice :$y=−2$
• Terminaux du latus rectal :$(\pm 4,2)$.

Figurine$\PageIndex{10}$

Écrire des équations de paraboles sous forme standard

Dans les exemples précédents, nous avons utilisé l'équation de forme standard d'une parabole pour calculer l'emplacement de ses principales caractéristiques. Nous pouvons également utiliser les calculs inverses pour écrire une équation pour une parabole lorsque ses principales caractéristiques sont prises en compte.

Comment : compte tenu de son objectif et de sa directrice, écrire l'équation d'une parabole sous forme standard

1. Déterminez si l'axe de symétrie est l'$y$axe$x$ - ou l'axe.
   1. Si les coordonnées données du foyer ont la forme$(p,0)$, alors l'axe de symétrie est l'$x$axe. Utilisez le formulaire standard$y^2=4px$.
   2. Si les coordonnées données du foyer ont la forme$(0,p)$, alors l'axe de symétrie est l'$y$axe. Utilisez le formulaire standard$x^2=4py$.
2. Multipliez$4p$.
3. Remplacez la valeur de l'étape 2 par l'équation déterminée à l'étape 1.

Exemple$\PageIndex{3}$: Writing the Equation of a Parabola in Standard Form Given its Focus and Directrix

Quelle est l'équation de la parabole avec foyer$(−\dfrac{1}{2},0)$ et directrice$x=\dfrac{1}{2}$ ?

Solution

Le focus a la forme$(p,0)$, donc l'équation aura la forme$y^2=4px$.

• En multipliant$4p$, nous l'avons fait$4p=4(−\dfrac{1}{2})=−2$.
• En remplacement de$4p$, nous avons$y^2=4px=−2x$. =

Par conséquent, l'équation de la parabole est$y^2=−2x$.

Exercice$\PageIndex{3}$

Quelle est l'équation de la parabole avec foyer$\left(0,\dfrac{7}{2}\right)$ et directrice$y=−\dfrac{7}{2}$ ?

Réponse

$x^2=14y$.

Représentation graphique de paraboles dont les sommets ne se trouvent pas à l'origine

Comme les autres graphes avec lesquels nous avons travaillé, le graphe d'une parabole peut être traduit. Si une parabole est$h$ translatée en$k$ unités horizontalement et en unités verticalement, le sommet sera$(h,k)$. Cette traduction donne la forme standard de l'équation que nous avons vue précédemment, à savoir «$x$ remplacé par »$(x−h)$ et «$y$ remplacé par »$(y−k)$.

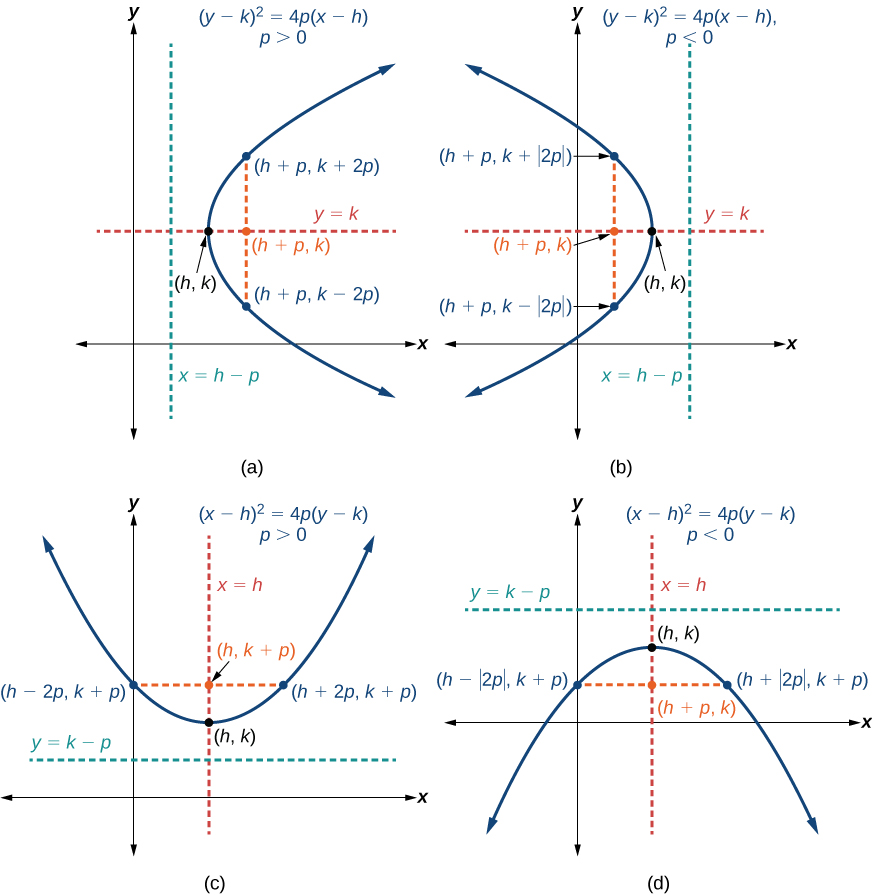
Pour représenter graphiquement des paraboles dont le sommet est$(h,k)$ différent de l'origine, nous utilisons la forme standard${(y−k)}^2=4p(x−h)$ pour les paraboles dont l'axe de symétrie est parallèle à l'$x$axe -et${(x−h)}^2=4p(y−k)$ pour les paraboles dont l'axe de symétrie est parallèle à l'$y$axe des. Ces formulaires standard sont présentés ci-dessous, avec leurs graphiques généraux et leurs principales caractéristiques.

FORMES STANDARD DE PARABOLES AVEC VERTEX$(H, K)$

Le tableau$\PageIndex{2}$ et la figure$\PageIndex{11}$ résument les caractéristiques standard des paraboles avec un sommet en un point$(h,k)$.

Tableau$\PageIndex{2}$

Axe de symétrie	équation	Se concentrer	Directrix	Paramètres du latus rectal
$y=k$	${(y−k)}^2=4p(x−h)$	$(h+p, k)$	$x=h−p$	$(h+p, k\pm 2p)$
$x=h$	${(x−h)}^2=4p(y−k)$	$(h, k+p)$	$y=k−p$	$(h\pm 2p, k+p)$

Figure$\PageIndex{11}$ : (a) Quand$p>0$, la parabole s'ouvre vers la droite. (b) Quand$p<0$, la parabole s'ouvre vers la gauche. (c) Quand$p>0$, la parabole s'ouvre. (d) Quand$p<0$, la parabole s'ouvre.

Comment faire : Avec une équation de forme standard pour une parabole centrée sur$(h,k)$, sketch the graph

1. Déterminez lequel des formulaires standard s'applique à l'équation donnée :${(y−k)}^2=4p(x−h)$ ou${(x−h)}^2=4p(y−k)$.
2. Utilisez le formulaire standard identifié à l'étape 1 pour déterminer le sommet, l'axe de symétrie, le foyer, l'équation de la directrice et les extrémités du latus rectal.
   • Si l'équation se présente sous la forme${(y−k)}^2=4p(x−h)$, alors :
     • utiliser l'équation donnée pour identifier$h$ et$k$ pour le sommet,$(h,k)$
     • utiliser la valeur de$k$ pour déterminer l'axe de symétrie,$y=k$
     • défini$4p$ égal au coefficient de$(x−h)$ dans l'équation donnée à résoudre$p$. Si$p>0$, la parabole s'ouvre à droite. Si$p<0$, la parabole s'ouvre vers la gauche.
     • utilisez$h$$k$, et$p$ pour trouver les coordonnées du focus,$(h+p, k)$
     • utilisez$h$ andp p pour trouver l'équation de la directrice,$x=h−p$
     • utiliser$h$$k$, et$p$ pour trouver les terminaisons du latus rectal,$(h+p,k\pm 2p)$
   • Si l'équation se présente sous la forme${(x−h)}^2=4p(y−k)$, alors :
     • utiliser l'équation donnée pour identifier$h$ et$k$ pour le sommet,$(h,k)$
     • utiliser la valeur de$h$ pour déterminer l'axe de symétrie,$x=h$
     • défini$4p$ égal au coefficient de$(y−k)$ dans l'équation donnée à résoudre$p$. Si$p>0$, la parabole s'ouvre. Si$p<0$, la parabole s'ouvre.
     • utilisez$h$$k$, et$p$ pour trouver les coordonnées du focus,$(h, k+p)$
     • utilisez$k$ et$p$ pour trouver l'équation de la directrice,$y=k−p$
     • utiliser$h$$k$, et$p$ pour trouver les terminaisons du latus rectal,$(h\pm 2p, k+p)$
3. Tracez le sommet, l'axe de symétrie, le foyer, la directrice et le latus rectum, puis tracez une courbe lisse pour former la parabole.

Exemple$\PageIndex{4}$: Graphing a Parabola with Vertex $(h, k)$ and Axis of Symmetry Parallel to the $x$-axis

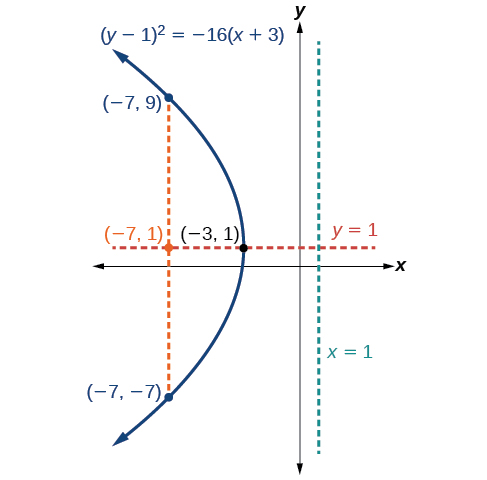
Graphe${(y−1)}^2=−16(x+3)$. Identifiez et étiquetez le sommet, l'axe de symétrie, le foyer, la directrice et les extrémités du latus rectal.

Solution

La forme standard qui s'applique à l'équation donnée est${(y−k)}^2=4p(x−h)$. Ainsi, l'axe de symétrie est parallèle à l'$x$axe. Il s'ensuit que :

• le sommet est$(h,k)=(−3,1)$
• l'axe de symétrie est$y=k=1$
• $−16=4p$, donc$p=−4$. Depuis$p<0$, la parabole s'ouvre vers la gauche.
• les coordonnées du focus sont$(h+p,k)=(−3+(−4),1)=(−7,1)$
• l'équation de la directrice est$x=h−p=−3−(−4)=1$
• les points d'extrémité du latus rectal sont$(h+p,k\pm 2p)=(−3+(−4),1\pm 2(−4))$, ou$(−7,−7)$$(−7,9)$

Ensuite, nous tracons le sommet, l'axe de symétrie, le foyer, la directrice et le latus rectum, et dessinons une courbe lisse pour former la parabole (Figure$\PageIndex{10}$).

Figurine$\PageIndex{12}$

Exercice$\PageIndex{4}$

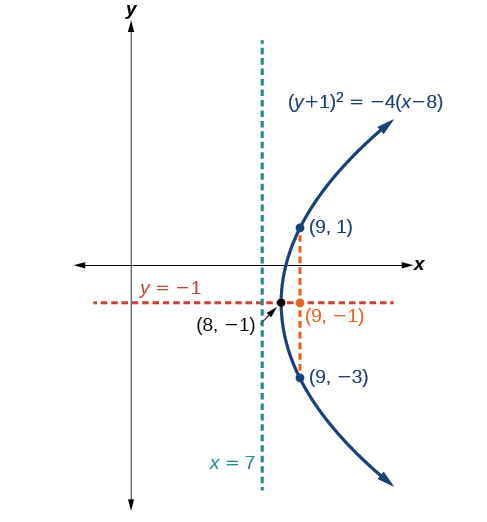
Graphe${(y+1)}^2=4(x−8)$. Identifiez et étiquetez le sommet, l'axe de symétrie, le foyer, la directrice et les extrémités du latus rectal.

Réponse

• Sommet :$(8,−1)$
• Axe de symétrie :$y=−1$
• Mettre l'accent :$(9,−1)$
• Directrice :$x=7$
• Terminaux du latus rectal :$(9,−3)$ et$(9,1)$.

Figurine$\PageIndex{13}$

Exemple$\PageIndex{5}$: Graphing a Parabola from an Equation Given in General Form

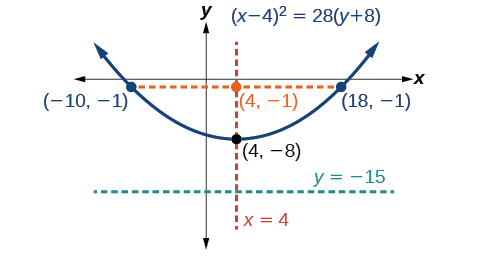
Graphe$x^2−8x−28y−208=0$. Identifiez et étiquetez le sommet, l'axe de symétrie, le foyer, la directrice et les extrémités du latus rectal.

Solution

Commencez par écrire l'équation de la parabole sous forme standard. La forme standard qui s'applique à l'équation donnée est${(x−h)}^2=4p(y−k)$. Ainsi, l'axe de symétrie est parallèle à l'$y$axe. Pour exprimer l'équation de la parabole sous cette forme, nous commençons par isoler les termes qui contiennent la variable$x$ afin de compléter le carré.

$$\begin{align*} x^2−8x−28y−208&=0 \\[4pt] x^2−8x &=28y+208 \\[4pt] x^2−8x+16 &=28y+208+16 \\[4pt] (x−4)^2 &=28y+224 \\[4pt] (x−4)^2 &=28(y+8) \\[4pt] (x−4)^2&= 4⋅7⋅(y+8) \end{align*}$$

Il s'ensuit que :

• le sommet est$(h,k)=(4,−8)$
• l'axe de symétrie est$x=h=4$
• depuis$p=7$,$p>0$ et donc la parabole s'ouvre
• les coordonnées du focus sont$(h,k+p)=(4,−8+7)=(4,−1)$
• l'équation de la directrice est$y=k−p=−8−7=−15$
• les points d'extrémité du latus rectal sont$(h\pm 2p,k+p)=(4\pm 2(7),−8+7)$, ou$(−10,−1)$$(18,−1)$

Ensuite, nous tracons le sommet, l'axe de symétrie, le foyer, la directrice et le latus rectum, et dessinons une courbe lisse pour former la parabole (Figure$\PageIndex{14}$).

Figurine$\PageIndex{14}$

Exercice$\PageIndex{5}$

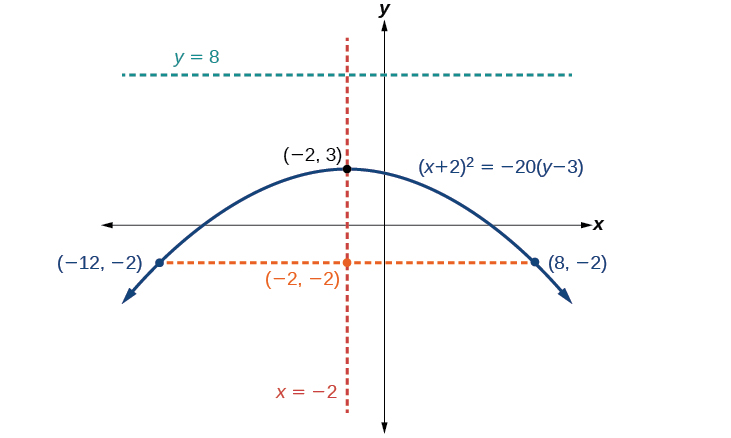
Graphe${(x+2)}^2=−20(y−3)$. Identifiez et étiquetez le sommet, l'axe de symétrie, le foyer, la directrice et les extrémités du latus rectal.

Réponse

• Sommet :$(−2,3)$
• Axe de symétrie :$x=−2$
• Mettre l'accent :$(−2,−2)$
• Directrice :$y=8$
• Terminaux du latus rectal :$(−12,−2)$ et$(8,−2)$.

Figurine$\PageIndex{15}$

Résolution de problèmes appliqués impliquant des paraboles

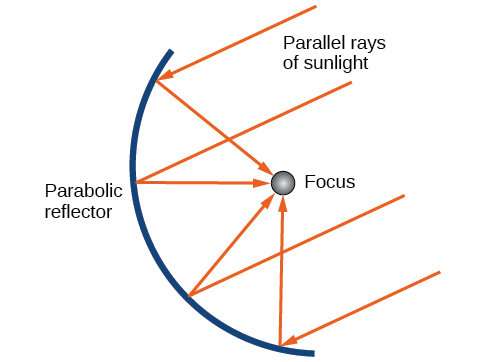
Comme nous l'avons mentionné au début de la section, les paraboles sont utilisées pour concevoir de nombreux objets que nous utilisons tous les jours, tels que des télescopes, des ponts suspendus, des microphones et des équipements radar. Les miroirs paraboliques, tels que celui utilisé pour allumer la torche olympique, possèdent une propriété réfléchissante tout à fait unique. Lorsque des rayons de lumière parallèles à l'axe de symétrie de la parabole sont dirigés vers n'importe quelle surface du miroir, la lumière est réfléchie directement vers le foyer (Figure$\PageIndex{16}$). C'est pourquoi la torche olympique s'allume lorsqu'elle est maintenue au centre du miroir parabolique.

Figure$\PageIndex{16}$ : Propriété réfléchissante des paraboles

Les miroirs paraboliques ont la capacité de concentrer l'énergie du soleil sur un seul point, élevant la température de centaines de degrés en quelques secondes. Ainsi, les miroirs paraboliques sont intégrés à de nombreux produits solaires peu coûteux et économes en énergie, tels que les cuiseurs solaires, les radiateurs solaires et même les allume-feu de format voyage.

Exemple$\PageIndex{6}$: Solving Applied Problems Involving Parabolas

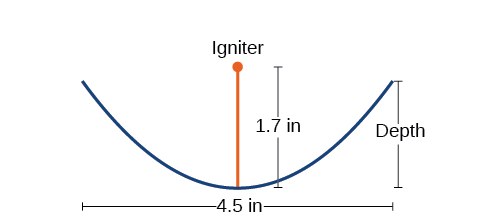
Une coupe transversale d'une conception d'un allume-feu solaire de format voyage est illustrée à la figure$\PageIndex{17}$. Les rayons du soleil sont réfléchis par le miroir parabolique en direction d'un objet fixé à l'allumeur. Comme l'allumeur est situé au centre de la parabole, les rayons réfléchis font brûler l'objet en quelques secondes seulement.

1. Trouvez l'équation de la parabole qui modélise l'allume-feu. Supposons que le sommet du miroir parabolique soit l'origine du plan de coordonnées.
2. Utilisez l'équation de la partie (a) pour déterminer la profondeur de l'allume-feu.

Figure$\PageIndex{17}$ Coupe transversale d'un allume-feu solaire de format voyage

Solution

1. Le sommet de la cuvette est l'origine du plan de coordonnées, de sorte que la parabole prendra la forme standard$x^2=4py$, où$p>0$. L'allumeur, qui est au centre, se trouve à$1.7$ quelques centimètres au-dessus du sommet de la coupelle. C'est ainsi que nous avons$p=1.7$.

$$\begin{align*} x^2&=4py\qquad \text{Standard form of upward-facing parabola with vertex } (0,0)\\ x^2&=4(1.7)y\qquad \text{Substitute } 1.7 \text{ for } p\\ x^2&=6.8y\qquad \text{Multiply.} \end{align*}$$

2. Le plat s'étend$\dfrac{4.5}{2}=2.25$ en pouces de chaque côté de l'origine. Nous pouvons remplacer$x$ dans$2.25$ l'équation de la partie (a) la profondeur du plat.

$$\begin{align*} x^2&=6.8y\qquad \text{ Equation found in part } (a)\\ {(2.25)}^2&=6.8y\qquad \text{Substitute } 2.25 \text{ for } x\\ y&\approx 0.74\qquad \text{Solve for } y \end{align*}$$

Le plat mesure environ$0.74$ pouces de profondeur.

Exercice$\PageIndex{6}$

Des cuisinières solaires de la taille d'un balcon ont été conçues pour les familles vivant en Inde. Le dessus d'un plat a un diamètre de$1600$ mm. Les rayons du soleil se reflètent sur le miroir parabolique en direction de la « cuisinière », qui est placée à$320$ mm de la base.

1. Trouvez une équation qui modélise une coupe transversale du cuiseur solaire. Supposons que le sommet du miroir parabolique soit l'origine du plan de coordonnées et que la parabole s'ouvre vers la droite (c'est-à-dire qu'elle ait l'axe x comme axe de symétrie).
2. Utilisez l'équation de la partie (a) pour déterminer la profondeur de la cuisinière.

Répondez à une

$y^2=1280x$

Réponse b

La profondeur de la cuisinière est de$500$ mm

Équations clés

Parabole, sommet à l'origine, axe de symétrie sur l'axe x	$y^2=4px$
Parabole, sommet à l'origine, axe de symétrie sur l'axe y	$x^2=4py$
Parabole, sommet à$(h,k)$, axe de symétrie sur l'axe x	${(y−k)}^2=4p(x−h)$
Parabole, sommet à$(h,k)$, axe de symétrie sur l'axe y	${(x−h)}^2=4p(y−k)$

Concepts clés

• Une parabole est l'ensemble de tous les points d'un plan qui se trouvent$(x,y)$ à la même distance d'une ligne fixe, appelée directrice, et d'un point fixe (le point focal) qui ne se trouve pas sur la directrice.
• La forme standard d'une parabole avec un sommet$(0,0)$ et l'axe x comme axe de symétrie peut être utilisée pour représenter graphiquement la parabole. Si$p>0$, la parabole s'ouvre à droite. Si$p<0$, la parabole s'ouvre vers la gauche. Voir l'exemple$\PageIndex{1}$.
• La forme standard d'une parabole avec un sommet$(0,0)$ et l'axe y comme axe de symétrie peut être utilisée pour représenter graphiquement la parabole. Si$p>0$, la parabole s'ouvre. Si$p<0$, la parabole s'ouvre. Voir l'exemple$\PageIndex{2}$.
• Lorsque l'on donne le foyer et la directrice d'une parabole, on peut écrire son équation sous forme standard. Voir l'exemple$\PageIndex{3}$.
• La forme standard d'une parabole avec un sommet$(h,k)$ et un axe de symétrie parallèles à l'$x$axe -peut être utilisée pour représenter graphiquement la parabole. Si$p>0$, la parabole s'ouvre à droite. Si$p<0$, la parabole s'ouvre vers la gauche. Voir l'exemple$\PageIndex{4}$.
• La forme standard d'une parabole avec un sommet$(h,k)$ et un axe de symétrie parallèles à l'$y$axe -peut être utilisée pour représenter graphiquement la parabole. Si$p>0$, la parabole s'ouvre. Si$p<0$, la parabole s'ouvre. Voir l'exemple$\PageIndex{5}$.
• Les situations du monde réel peuvent être modélisées à l'aide des équations standard des paraboles. Par exemple, étant donné le diamètre et la focalisation d'une section transversale d'un réflecteur parabolique, nous pouvons trouver une équation qui modélise ses côtés. Voir l'exemple$\PageIndex{6}$.