12.2 : L'hyperbole

Objectifs d'apprentissage

• Localisez les sommets et les foyers d'une hyperbole.
• Écrivez les équations des hyperboles sous une forme standard.
• Tracez les hyperboles centrées à l'origine.
• Les hyperboles du graphe ne sont pas centrées à l'origine.
• Résolvez des problèmes appliqués impliquant des hyperboles.

Qu'ont en commun les trajectoires des comètes, des estacades supersoniques, des anciens piliers grecs et des tours de refroidissement à tirage naturel ? Ils peuvent tous être modélisés par le même type de conique. Par exemple, lorsque quelque chose se déplace plus vite que la vitesse du son, une onde de choc sous la forme d'un cône est créée. Une partie d'une conique se forme lorsque l'onde croise le sol, ce qui donne lieu à un boom sonique (Figure\(\PageIndex{1}\)).

Figure\(\PageIndex{1}\) : Une onde de choc traversant le sol forme une portion de cône et produit un boom sonique.

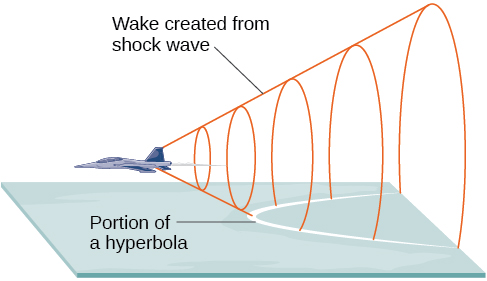
La plupart des gens connaissent le boom sonore créé par les avions supersoniques, mais les humains franchissaient le mur du son bien avant le premier vol supersonique. La fissure d'un fouet se produit parce que la pointe dépasse la vitesse du son. Les balles tirées par de nombreuses armes à feu franchissent également le mur du son, bien que le bruit du pistolet remplace généralement celui du boom sonique.

Localisation des sommets et des foyers d'une hyperbole

En géométrie analytique, une hyperbole est une section conique formée en croisant un cône circulaire droit avec un plan formant un angle tel que les deux moitiés du cône se croisent. Cette intersection produit deux courbes indépendantes distinctes qui sont des images miroir l'une de l'autre (Figure\(\PageIndex{2}\)).

Figure\(\PageIndex{2}\) : Une hyperbole

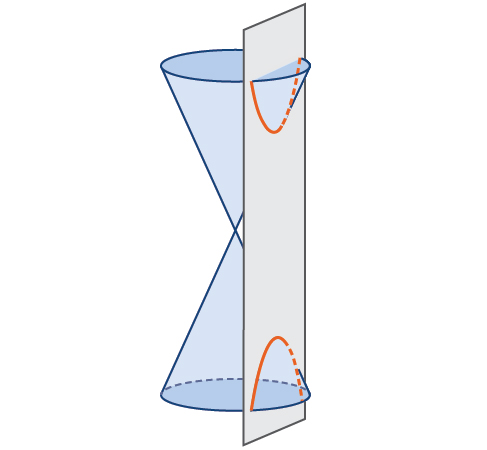
Comme l'ellipse, l'hyperbole peut également être définie comme un ensemble de points dans le plan de coordonnées. Une hyperbole est l'ensemble de tous\((x,y)\) les points d'un plan tel que la différence entre les distances\((x,y)\) et les foyers soit une constante positive.

Notez que la définition d'une hyperbole est très similaire à celle d'une ellipse. La différence est que l'hyperbole est définie en termes de différence de deux distances, tandis que l'ellipse est définie en termes de somme de deux distances.

Comme pour l'ellipse, chaque hyperbole possède deux axes de symétrie. L'axe transversal est un segment de ligne qui passe par le centre de l'hyperbole et dont les extrémités sont des sommets. Les foyers se situent sur la ligne qui contient l'axe transversal. L'axe conjugué est perpendiculaire à l'axe transversal et ses extrémités sont les co-sommets. Le centre d'une hyperbole est le point médian des axes transversal et conjugué, où ils se croisent. Chaque hyperbole possède également deux asymptotes qui passent par son centre. Lorsqu'une hyperbole s'éloigne du centre, ses branches se rapprochent de ces asymptotes. Le rectangle central de l'hyperbole est centré à l'origine avec des côtés passant par chaque sommet et co-sommet ; c'est un outil utile pour représenter graphiquement l'hyperbole et ses asymptotes. Pour esquisser les asymptotes de l'hyperbole, il suffit d'esquisser et d'étendre les diagonales du rectangle central (Figure\(\PageIndex{3}\)).

Figure\(\PageIndex{3}\) : Principales caractéristiques de l'hyperbole

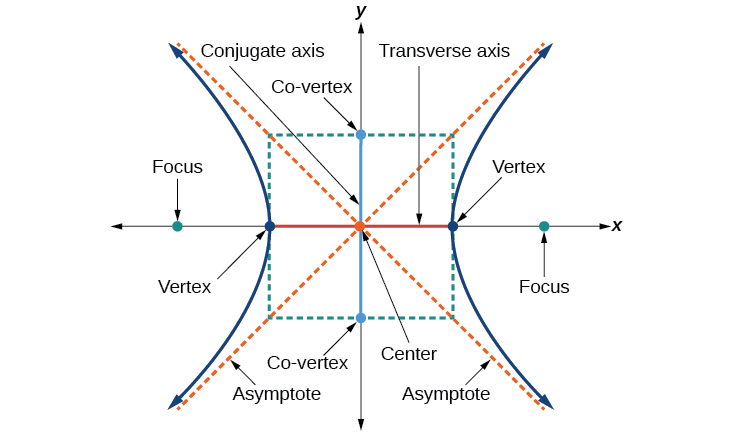
Dans cette section, nous allons limiter notre discussion aux hyperboles positionnées verticalement ou horizontalement dans le plan de coordonnées ; les axes seront situés sur les axes\(x\) - et\(y\) - ou seront parallèles à ceux-ci. Nous examinerons deux cas : ceux qui sont centrés sur l'origine et ceux qui sont centrés sur un point autre que l'origine.

Dériver l'équation d'une ellipse centrée à l'origine

\((c,0)\)Soyons\((−c,0)\) les foyers d'une hyperbole centrée sur l'origine. L'hyperbole est l'ensemble de tous les points\((x,y)\) tels que la différence des distances entre\((x,y)\) les foyers et les foyers est constante. Voir la figure\(\PageIndex{4}\).

Figurine\(\PageIndex{4}\)

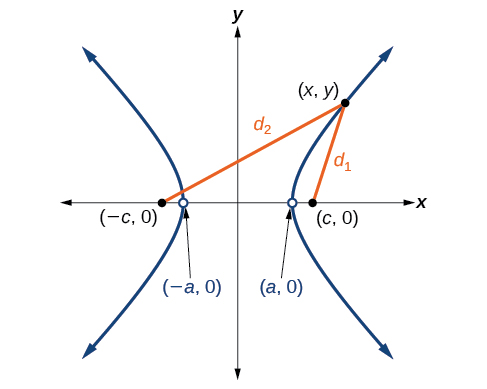
Si\((a,0)\) est un sommet de l'hyperbole, la distance\((−c,0)\) entre et\((a,0)\) est\(a−(−c)=a+c\). La distance entre\((c,0)\) et\((a,0)\) est\(c−a\). La somme des distances entre les foyers et le sommet est

\((a+c)−(c−a)=2a\)

S'il s'\((x,y)\)agit d'un point de l'hyperbole, nous pouvons définir les variables suivantes :

\(d_2=\)la distance entre\((−c,0)\) et\((x,y)\)

\(d_1=\)la distance entre\((c,0)\) et\((x,y)\)

Par définition d'une hyperbole,\(d_2−d_1\) est constant pour n'importe quel point\((x,y)\) de l'hyperbole. Nous savons que la différence de ces distances\(2a\) concerne le sommet\((a,0)\). Il s'ensuit que\(d_2−d_1=2a\) pour tout point de l'hyperbole. Comme pour la dérivation de l'équation d'une ellipse, nous allons commencer par appliquer la formule de distance. Le reste de la dérivation est algébrique. Comparez cette dérivation avec celle de la section précédente pour les ellipses.

\[\begin{align*} d_2-d_1&=2a\\ \sqrt{{(x-(-c))}^2+{(y-0)}^2}-\sqrt{{(x-c)}^2+{(y-0)}^2}&=2a\qquad \text{Distance Formula}\\ \sqrt{{(x+c)}^2+y^2}-\sqrt{{(x-c)}^2+y^2}&=2a\qquad \text{Simplify expressions.}\\ \sqrt{{(x+c)}^2+y^2}&=2a+\sqrt{{(x-c)}^2+y^2}\qquad \text{Move radical to opposite side.}\\ {(x+c)}^2+y^2&={(2a+\sqrt{{(x-c)}^2+y^2})}^2\qquad \text{Square both sides.}\\ x^2+2cx+c^2+y^2&=4a^2+4a\sqrt{{(x-c)}^2+y^2}+{(x-c)}^2+y^2\qquad \text{Expand the squares.}\\ x^2+2cx+c^2+y^2&=4a^2+4a\sqrt{{(x-c)}^2+y^2}+x^2-2cx+c^2+y^2\qquad \text{Expand remaining square.}\\ 2cx&=4a^2+4a\sqrt{{(x-c)}^2+y^2}-2cx\qquad \text{Combine like terms.}\\ 4cx-4a^2&=4a\sqrt{{(x-c)}^2+y^2}\qquad \text{Isolate the radical.}\\ cx-a^2&=a\sqrt{{(x-c)}^2+y^2}\qquad \text{Divide by 4.}\\ {(cx-a^2)}^2&=a^2{\left[\sqrt{{(x-c)}^2+y^2}\right]}^2\qquad \text{Square both sides.}\\ c^2x^2-2a^2cx+a^4&=a^2(x^2-2cx+c^2+y^2)\qquad \text{Expand the squares.}\\ c^2x^2-2a^2cx+a^4&=a^2x^2-2a^2cx+a^2c^2+a^2y^2\qquad \text{Distribute } a^2\\ a^4+c^2x^2&=a^2x^2+a^2c^2+a^2y^2\qquad \text{Combine like terms.}\\ c^2x^2-a^2x^2-a^2y^2&=a^2c^2-a^4\qquad \text{Rearrange terms.}\\ x^2(c^2-a^2)-a^2y^2&=a^2(c^2-a^2)\qquad \text{Factor common terms.}\\ x^2b^2-a^2y^2&=a^2b^2\qquad \text{Set } b^2=c^2−a^2\\. \dfrac{x^2b^2}{a^2b^2}-\dfrac{a^2y^2}{a^2b^2}&=\dfrac{a^2b^2}{a^2b^2}\qquad \text{Divide both sides by } a^2b^2\\ \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}&=1\\ \end{align*}\]

Cette équation définit une hyperbole centrée à l'origine avec des sommets\((\pm a,0)\) et des co-sommets\((0,\pm b)\).

FORMES STANDARD DE L'ÉQUATION D'UNE HYPERBOLE AVEC CENTRE\((0,0)\)

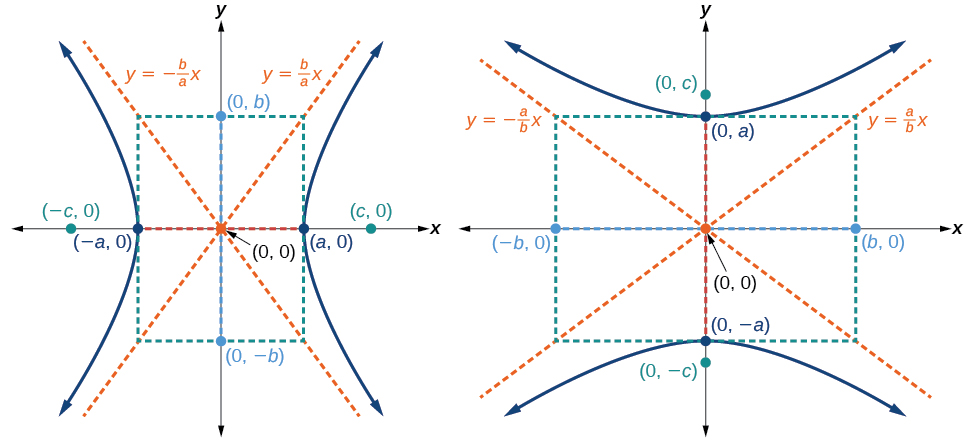
La forme standard de l'équation d'une hyperbole avec un centre\((0,0)\) et un axe transversal sur l'\(x\)axe -est

\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\)

où

• la longueur de l'axe transversal est\(2a\)
• les coordonnées des sommets sont\((\pm a,0)\)
• la longueur de l'axe conjugué est\(2b\)
• les coordonnées des co-sommets sont\((0,\pm b)\)
• la distance entre les foyers est\(2c\), où\(c^2=a^2+b^2\)
• les coordonnées des foyers sont\((\pm c,0)\)
• les équations des asymptotes sont\(y=\pm \dfrac{b}{a}x\)

Voir la figure\(\PageIndex{5a}\).

La forme standard de l'équation d'une hyperbole avec un centre\((0,0)\) et un axe transversal sur l'\(y\)axe -est

\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\)

où

• la longueur de l'axe transversal est\(2a\)
• les coordonnées des sommets sont\((0,\pm a)\)
• la longueur de l'axe conjugué est\(2b\)
• les coordonnées des co-sommets sont\((\pm b,0)\)
• la distance entre les foyers est\(2c\), où\(c^2=a^2+b^2\)
• les coordonnées des foyers sont\((0,\pm c)\)
• les équations des asymptotes sont\(y=\pm \dfrac{a}{b}x\)

Voir la figure\(\PageIndex{5b}\).

Notez que les sommets, les co-sommets et les foyers sont liés par l'équation\(c^2=a^2+b^2\). Lorsque l'on nous donne l'équation d'une hyperbole, nous pouvons utiliser cette relation pour identifier ses sommets et ses foyers.

Figure\(\PageIndex{5}\) : (a) Hyperbole horizontale avec centre\((0,0)\) (b) Hyperbole verticale avec centre\((0,0)\)

Comment : À partir de l'équation d'une hyperbole sous forme standard, localiser ses sommets et ses foyers

1. Déterminez si l'axe transversal se trouve sur l'\(y\)axe\(x\) - ou sur l'axe. Notez que\(a^2\) c'est toujours sous la variable avec le coefficient positif. Ainsi, si vous définissez l'autre variable sur zéro, vous pouvez facilement trouver les interceptions. Dans le cas où l'hyperbole est centrée à l'origine, les points d'intersection coïncident avec les sommets.
   • Si l'équation a la forme\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\), l'axe transversal se trouve sur l'\(x\)axe des. Les sommets sont situés à\((\pm a,0)\), et les foyers sont situés à\((\pm c,0)\).
   • Si l'équation a la forme\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\), l'axe transversal se trouve sur l'\(y\)axe des. Les sommets sont situés à\((0,\pm a)\), et les foyers sont situés à\((0,\pm c)\).
2. Résolvez pour\(a\) utiliser l'équation\(a=\sqrt{a^2}\).
3. Résolvez pour\(c\) utiliser l'équation\(c=\sqrt{a^2+b^2}\).

Exemple\(\PageIndex{1}\): Locating a Hyperbola’s Vertices and Foci

Identifiez les sommets et les foyers de l'hyperbole à l'aide d'une équation\(\dfrac{y^2}{49}−\dfrac{x^2}{32}=1\).

Solution

L'équation a la forme\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\), de sorte que l'axe transversal se trouve sur l'\(y\)axe des. L'hyperbole est centrée sur l'origine, de sorte que les sommets servent d'intercepts y du graphe. Pour trouver les sommets\(x=0\), définissez et résolvez pour\(y\).

\[\begin{align*} 1&=\dfrac{y^2}{49}-\dfrac{x^2}{32}\\ 1&=\dfrac{y^2}{49}-\dfrac{0^2}{32}\\ 1&=\dfrac{y^2}{49}\\ y^2&=49\\ y&=\pm \sqrt{49}\\ &=\pm 7 \end{align*}\]

Les foyers sont situés à\((0,\pm c)\). Résoudre pour\(c\),

\[\begin{align*} c&=\sqrt{a^2+b^2}\\ &=\sqrt{49+32}\\ &=\sqrt{81}\\ &=9 \end{align*}\]

Par conséquent, les sommets sont situés à\((0,\pm 7)\), et les foyers sont situés à\((0,9)\).

Exercice\(\PageIndex{1}\)

Identifiez les sommets et les foyers de l'hyperbole à l'aide d'une équation\(\dfrac{x^2}{9}−\dfrac{y^2}{25}=1\).

Réponse

Sommets :\((\pm 3,0)\) ; Points focaux :\((\pm \sqrt{34},0)\)

Écrire des équations d'hyperboles sous forme standard

Tout comme pour les ellipses, l'écriture de l'équation d'une hyperbole sous forme standard nous permet de calculer les principales caractéristiques : son centre, ses sommets, ses co-sommets, ses foyers, ses asymptotes, ainsi que les longueurs et positions des axes transversal et conjugué. À l'inverse, une équation pour une hyperbole peut être trouvée compte tenu de ses principales caractéristiques. Nous commençons par trouver des équations standard pour les hyperboles centrées à l'origine. Nous allons ensuite nous concentrer sur la recherche d'équations standard pour les hyperboles centrées à un point autre que l'origine.

Hyperboles centrées sur l'origine

En examinant les formes standard données pour les hyperboles centrées sur\((0,0)\), nous constatons que les sommets, les co-sommets et les foyers sont liés par l'équation\(c^2=a^2+b^2\). Notez que cette équation peut également être réécrite sous la forme\(b^2=c^2−a^2\). Cette relation est utilisée pour écrire l'équation d'une hyperbole lorsque l'on lui donne les coordonnées de ses foyers et de ses sommets.

Comment faire : Compte tenu des sommets et des foyers d'une hyperbole centrée sur\((0,0)\), write its equation in standard form

1. Déterminez si l'axe transversal se trouve sur l'\(y\)axe\(x\) - ou sur l'axe.
   • Si les coordonnées données des sommets et des foyers ont la forme\((\pm a,0)\) et\((\pm c,0)\), respectivement, l'axe transversal est l'\(x\)axe. Utilisez le formulaire standard\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\).
   • Si les coordonnées données des sommets et des foyers ont la forme\((0,\pm a)\) et\((0,\pm c)\), respectivement, l'axe transversal est l'\(y\)axe. Utilisez le formulaire standard\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\).
2. Trouvez\(b^2\) à l'aide de l'équation\(b^2=c^2−a^2\).
3. Remplacez les valeurs par\(a^2\) et\(b^2\) dans la forme standard de l'équation déterminée à l'étape 1.

Exemple\(\PageIndex{2}\): Finding the Equation of a Hyperbola Centered at \((0,0)\) Given its Foci and Vertices

Quelle est l'équation de forme standard de l'hyperbole qui comporte des sommets\((\pm 6,0)\) et des foyers\((\pm 2\sqrt{10},0)\) ?

Solution

Les sommets et les foyers se trouvent sur l'\(x\)axe. Ainsi, l'équation de l'hyperbole aura la forme\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\).

Les sommets sont\((\pm 6,0)\), ainsi\(a=6\) et\(a^2=36\).

Les points d'intérêt sont\((\pm 2\sqrt{10},0)\), ainsi\(c=2\sqrt{10}\) et\(c^2=40\).

Pour résoudre ce problème\(b^2\), nous avons

\[\begin{align*} b^2&=c^2-a^2\\ b^2&=40-36\qquad \text{Substitute for } c^2 \text{ and } a^2\\ b^2&=4\qquad \text{Subtract.} \end{align*}\]

Enfin, nous substituons\(a^2=36\) et\(b^2=4\) dans la forme standard de l'équation,\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\). L'équation de l'hyperbole est\(\dfrac{x^2}{36}−\dfrac{y^2}{4}=1\), comme le montre la figure\(\PageIndex{6}\).

Figurine\(\PageIndex{6}\)

Exercice\(\PageIndex{2}\)

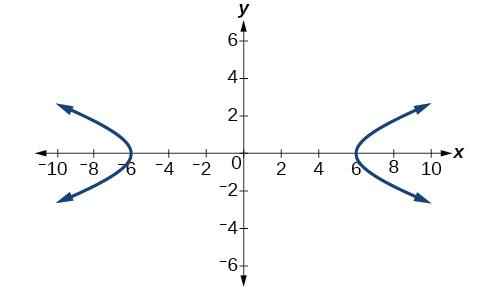
Quelle est l'équation de forme standard de l'hyperbole qui comporte des sommets\((0,\pm 2)\) et des foyers\((0,\pm 2\sqrt{5})\) ?

Réponse

\(\dfrac{y^2}{4}−\dfrac{x^2}{16}=1\)

Hyperboles non centrées à l'origine

Comme les graphes d'autres équations, le graphe d'une hyperbole peut être traduit. Si une hyperbole est traduite en\(h\) unités horizontalement et en\(k\) unités verticalement, le centre de l'hyperbole sera\((h,k)\). Cette traduction donne la forme standard de l'équation que nous avons vue précédemment,\(x\) remplacée par\((x−h)\) et\(y\) remplacée par\((y−k)\).

FORMES STANDARD DE L'ÉQUATION D'UNE HYPERBOLE AVEC CENTRE\((H, K)\)

La forme standard de l'équation d'une hyperbole dont le centre\((h,k)\) et l'axe transversal sont parallèles à l'\(x\)axe -est

\[\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\]

où

• la longueur de l'axe transversal est\(2a\)
• les coordonnées des sommets sont\((h\pm a,k)\)
• la longueur de l'axe conjugué est\(2b\)
• les coordonnées des co-sommets sont\((h,k\pm b)\)
• la distance entre les foyers est\(2c\), où\(c^2=a^2+b^2\)
• les coordonnées des foyers sont\((h\pm c,k)\)

Les asymptotes de l'hyperbole coïncident avec les diagonales du rectangle central. La longueur du rectangle est\(2a\) et sa largeur est\(2b\). Les pentes des diagonales sont\(\pm \dfrac{b}{a}\), et chaque diagonale passe par le centre\((h,k)\). À l'aide de la formule de pente ponctuelle, il est simple de montrer que les équations des asymptotes sont\(y=\pm \dfrac{b}{a}(x−h)+k\). Voir la figure\(\PageIndex{7a}\).

La forme standard de l'équation d'une hyperbole dont le centre\((h,k)\) et l'axe transversal sont parallèles à l'\(y\)axe -est

\[\dfrac{{(y−k)}^2}{a^2}−\dfrac{{(x−h)}^2}{b^2}=1\]

où

• la longueur de l'axe transversal est\(2a\)
• les coordonnées des sommets sont\((h,k\pm a)\)
• la longueur de l'axe conjugué est\(2b\)
• les coordonnées des co-sommets sont\((h\pm b,k)\)
• la distance entre les foyers est\(2c\), où\(c^2=a^2+b^2\)
• les coordonnées des foyers sont\((h,k\pm c)\)

En utilisant le raisonnement ci-dessus, les équations des asymptotes sont\(y=\pm \dfrac{a}{b}(x−h)+k\). Voir la figure\(\PageIndex{7b}\).

Figure\(\PageIndex{7}\) : (a) Hyperbole horizontale avec centre\((h,k)\) (b) Hyperbole verticale avec centre\((h,k)\)

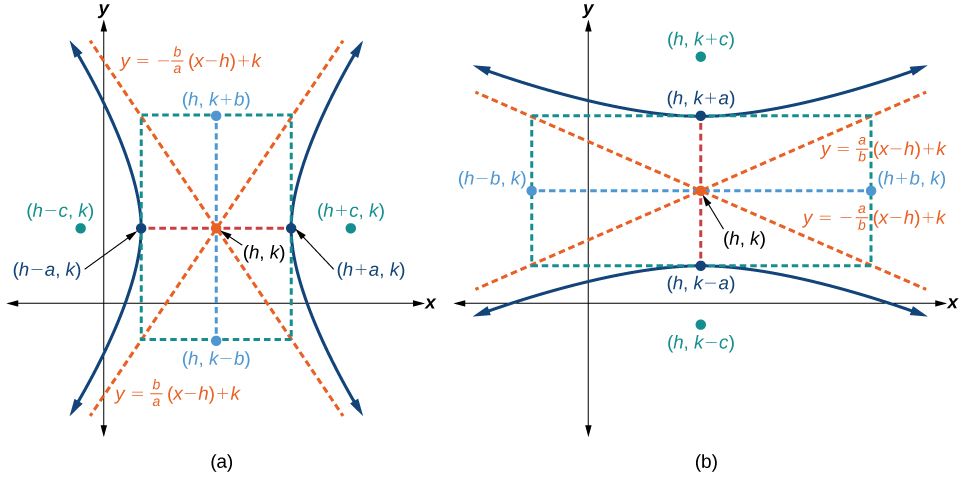
Comme les hyperboles centrées sur l'origine, les hyperboles centrées sur un point\((h,k)\) ont des sommets, des co-sommets et des foyers liés par l'équation\(c^2=a^2+b^2\). Nous pouvons utiliser cette relation ainsi que les formules de point médian et de distance pour trouver l'équation standard d'une hyperbole lorsque les sommets et les foyers sont donnés.

Comment faire : Compte tenu des sommets et des foyers d'une hyperbole centrée sur\((h,k)\),write its equation in standard form

1. Déterminez si l'axe transversal est parallèle à l'\(y\)axe\(x\) - ou à l'axe.
   • Si les\(y\) coordonnées des sommets et des foyers donnés sont identiques, alors l'axe transversal est parallèle à l'\(x\)axe. Utilisez le formulaire standard\(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\).
   • Si les\(x\) coordonnées des sommets et des foyers donnés sont identiques, alors l'axe transversal est parallèle à l'\(y\)axe. Utilisez le formulaire standard\(\dfrac{{(y−k)}^2}{a^2}−\dfrac{{(x−h)}^2}{b^2}=1\).
2. Identifiez le centre de l'hyperbole en utilisant la formule du point médian et les coordonnées données pour les sommets.\((h,k)\)
3. Trouvez\(a^2\) en résolvant la longueur de l'axe transversal\(2a\), qui est la distance entre les sommets donnés.
4. Trouvez\(c^2\) en utilisant\(h\) et\(k\) trouvé à l'étape 2 avec les coordonnées données pour les foyers.
5. Résolvez pour\(b^2\) utiliser l'équation\(b^2=c^2−a^2\).
6. Remplacez les valeurs par\(h\)\(k\),\(a^2\), et\(b^2\) dans la forme standard de l'équation déterminée à l'étape 1.

Exemple\(\PageIndex{3}\): Finding the Equation of a Hyperbola Centered at \((h, k)\) Given its Foci and Vertices

Quelle est l'équation de forme standard de l'hyperbole qui a des sommets à\((0,−2)\) et\((6,−2)\) et des foyers à\((−2,−2)\) et\((8,−2)\) ?

Solution

Les\(y\) coordonnées des sommets et des foyers sont les mêmes, de sorte que l'axe transversal est parallèle à l'\(x\)axe. Ainsi, l'équation de l'hyperbole aura la forme

\(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\)

Tout d'abord, nous identifions le centre,\((h,k)\). Le centre se trouve à mi-chemin entre les sommets\((0,−2)\) et\((6,−2)\). En appliquant la formule du point médian, nous avons

\((h,k)=(\dfrac{0+6}{2},\dfrac{−2+(−2)}{2})=(3,−2)\)

Ensuite, nous trouvons\(a^2\). La longueur de l'axe transversal\(2a\),, est limitée par les sommets. Nous pouvons donc le trouver\(a^2\) en trouvant la distance entre\(x\) les coordonnées des sommets.

\[\begin{align*} 2a&=| 0-6 |\\ 2a&=6\\ a&=3\\ a^2&=9 \end{align*}\]

Maintenant, nous devons trouver\(c^2\). Les coordonnées des foyers sont\((h\pm c,k)\). Donc\((h−c,k)=(−2,−2)\) et\((h+c,k)=(8,−2)\). Nous pouvons utiliser la\(x\) coordonnée -de l'un ou l'autre de ces points pour résoudre\(c\). En utilisant le point\((8,−2)\) et en le remplaçant\(h=3\),

\[\begin{align*} h+c&=8\\ 3+c&=8\\ c&=5\\ c^2&=25 \end{align*}\]

Ensuite, résolvez\(b^2\) l'équation suivante\(b^2=c^2−a^2\) :

\[\begin{align*} b^2&=c^2-a^2\\ &=25-9\\ &=16 \end{align*}\]

Enfin, remplacez les valeurs trouvées pour\(h\),\(k\)\(a^2\), et\(b^2\) dans la forme standard de l'équation.

\(\dfrac{{(x−3)}^2}{9}−\dfrac{{(y+2)}^2}{16}=1\)

Exercice\(\PageIndex{3}\)

Quelle est l'équation de forme standard de l'hyperbole qui a des sommets\((1,−2)\)\((1,8)\) et des foyers\((1,−10)\) et\((1,16)\) ?

Réponse

\(\dfrac{{(y−3)}^2}{25}+\dfrac{{(x−1)}^2}{144}=1\)

Représentation graphique d'hyperboles centrées à l'origine

Lorsque nous avons une équation sous forme standard pour une hyperbole centrée sur l'origine, nous pouvons interpréter ses parties pour identifier les principales caractéristiques de son graphe : le centre, les sommets, les co-sommets, les asymptotes, les foyers, les longueurs et les positions des axes transversal et conjugué. Pour représenter graphiquement les hyperboles centrées à l'origine, nous utilisons la forme standard\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\) pour les hyperboles horizontales et la forme standard\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\) pour les hyperboles verticales.

Comment faire : à partir d'une équation de forme standard pour une hyperbole centrée sur\((0,0)\), sketch the graph

1. Déterminez lequel des formulaires standard s'applique à l'équation donnée.
2. Utilisez le formulaire standard identifié à l'étape 1 pour déterminer la position de l'axe transversal, les coordonnées des sommets, des co-sommets et des foyers, ainsi que les équations des asymptotes.
   • Si l'équation se trouve dans la forme\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\), alors
     • l'axe transversal est sur l'\(x\)axe -
     • les coordonnées des sommets sont \ ((\ pm a,0) \ 0
     • les coordonnées des co-sommets sont\((0,\pm b)\)
     • les coordonnées des foyers sont\((\pm c,0)\)
     • les équations des asymptotes sont\(y=\pm \dfrac{b}{a}x\)
   • Si l'équation se trouve dans la forme\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\), alors
     • l'axe transversal est sur l'\(y\)axe -
     • les coordonnées des sommets sont\((0,\pm a)\)
     • les coordonnées des co-sommets sont\((\pm b,0)\)
     • les coordonnées des foyers sont\((0,\pm c)\)
     • les équations des asymptotes sont\(y=\pm \dfrac{a}{b}x\)
3. Déterminez les coordonnées des foyers à l'aide de l'équation\(c=\pm \sqrt{a^2+b^2}\).
4. Tracez les sommets, les co-sommets, les foyers et les asymptotes dans le plan de coordonnées et tracez une courbe lisse pour former l'hyperbole.

Exemple\(\PageIndex{4}\): Graphing a Hyperbola Centered at \((0,0)\) Given an Equation in Standard Form

Représentez graphiquement l'hyperbole donnée par l'équation\(\dfrac{y^2}{64}−\dfrac{x^2}{36}=1\). Identifiez et étiquetez les sommets, les co-sommets, les foyers et les asymptotes.

Solution

La forme standard qui s'applique à l'équation donnée est\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\). Ainsi, l'axe transversal se trouve sur l'\(y\)axe

Les coordonnées des sommets sont\((0,\pm a)=(0,\pm \sqrt{64})=(0,\pm 8)\)

Les coordonnées des co-sommets sont\((\pm b,0)=(\pm \sqrt{36}, 0)=(\pm 6,0)\)

Les coordonnées des foyers sont\((0,\pm c)\), où\(c=\pm \sqrt{a^2+b^2}\). Pour résoudre ce problème\(c\), nous avons

\(c=\pm \sqrt{a^2+b^2}=\pm \sqrt{64+36}=\pm \sqrt{100}=\pm 10\)

Par conséquent, les coordonnées des foyers sont\((0,\pm 10)\)

Les équations des asymptotes sont\(y=\pm \dfrac{a}{b}x=\pm \dfrac{8}{6}x=\pm \dfrac{4}{3}x\)

Tracez et étiquetez les sommets et les co-sommets, puis esquissez le rectangle central. Les côtés du rectangle sont parallèles aux axes et passent par les sommets et les co-sommets. Esquissez et étendez les diagonales du rectangle central pour montrer les asymptotes. Le rectangle central et les asymptotes fournissent le cadre nécessaire pour esquisser un graphique précis de l'hyperbole. Étiquetez les foyers et les asymptotes, et tracez une courbe lisse pour former l'hyperbole, comme indiqué sur la figure\(\PageIndex{8}\).

Figurine\(\PageIndex{8}\)

Exercice\(\PageIndex{4}\)

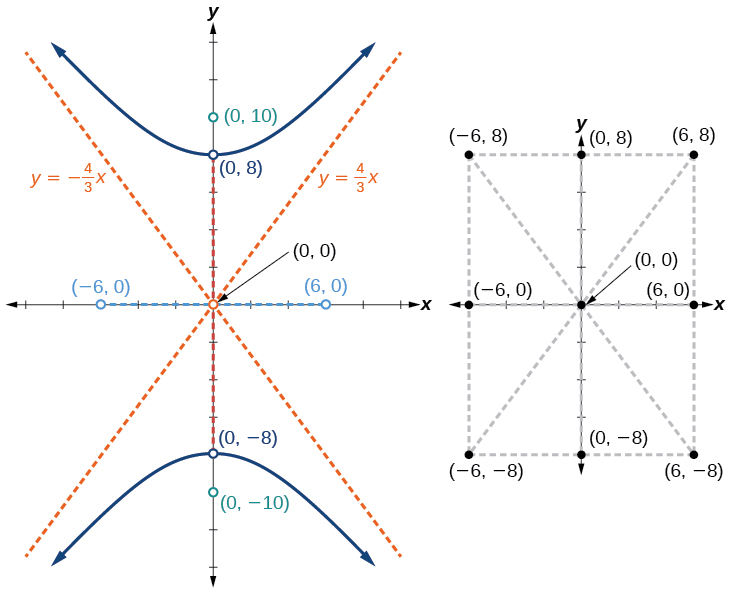
Représentez graphiquement l'hyperbole donnée par l'équation\(\dfrac{x^2}{144}−\dfrac{y^2}{81}=1\). Identifiez et étiquetez les sommets, les co-sommets, les foyers et les asymptotes.

Réponse

sommets :\((\pm 12,0)\) ; co-sommets :\((0,\pm 9)\) ; foyers :\((\pm 15,0)\) ; asymptotes :\(y=\pm \dfrac{3}{4}x\) ;

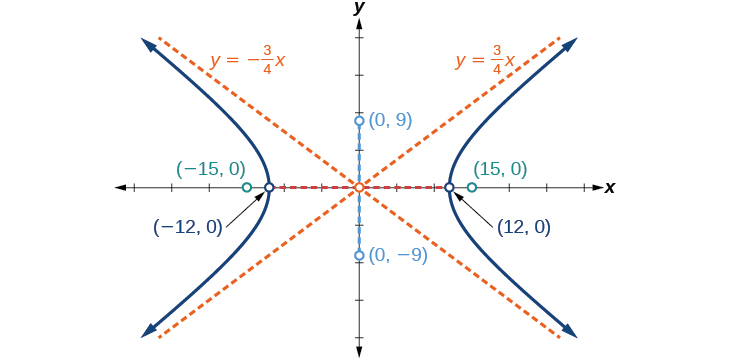
Figurine\(\PageIndex{9}\)

Représentation graphique d'hyperboles non centrées à l'origine

La représentation graphique d'hyperboles centrées sur un point\((h,k)\) autre que l'origine est similaire à la représentation graphique d'ellipses centrées sur un point autre que l'origine. Nous utilisons les formulaires standard\(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\) pour les hyperboles horizontales et\(\dfrac{{(y−k)}^2}{a^2}−\dfrac{{(x−h)}^2}{b^2}=1\) pour les hyperboles verticales. À partir de ces équations de forme standard, nous pouvons facilement calculer et tracer les principales caractéristiques du graphe : les coordonnées de son centre, de ses sommets, de ses co-sommets et de ses foyers ; les équations de ses asymptotes ; et les positions des axes transversal et conjugué.

Mode d'emploi : Avec une forme générale pour une hyperbole centrée sur\((h, k)\), sketch the graph

1. Convertissez le formulaire général en formulaire standard. Déterminez lequel des formulaires standard s'applique à l'équation donnée.
2. Utilisez le formulaire standard identifié à l'étape 1 pour déterminer la position de l'axe transversal, les coordonnées du centre, les sommets, les co-sommets, les foyers et les équations pour les asymptotes.
   1. Si l'équation se trouve dans la forme\(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\), alors
      • l'axe transversal est parallèle à l'\(x\)axe
      • le centre est\((h,k)\)
      • les coordonnées des sommets sont\((h\pm a,k)\)
      • les coordonnées des co-sommets sont\((h,k\pm b)\)
      • les coordonnées des foyers sont\((h\pm c,k)\)
      • les équations des asymptotes sont\(y=\pm \dfrac{b}{a}(x−h)+k\)
   2. Si l'équation se trouve dans la forme\(\dfrac{{(y−k)}^2}{a^2}−\dfrac{{(x−h)}^2}{b^2}=1\), alors
      • l'axe transversal est parallèle à l'\(y\)axe
      • le centre est\((h,k)\)
      • les coordonnées des sommets sont\((h,k\pm a)\)
      • les coordonnées des co-sommets sont\((h\pm b,k)\)
      • les coordonnées des foyers sont\((h,k\pm c)\)
      • les équations des asymptotes sont\(y=\pm \dfrac{a}{b}(x−h)+k\)
3. Déterminez les coordonnées des foyers à l'aide de l'équation\(c=\pm \sqrt{a^2+b^2}\).
4. Tracez le centre, les sommets, les co-sommets, les foyers et les asymptotes dans le plan de coordonnées et tracez une courbe lisse pour former l'hyperbole.

Exemple\(\PageIndex{5}\): Graphing a Hyperbola Centered at \((h, k)\) Given an Equation in General Form

Représentez graphiquement l'hyperbole donnée par l'équation\(9x^2−4y^2−36x−40y−388=0\). Identifiez et étiquetez le centre, les sommets, les co-sommets, les foyers et les asymptotes.

Solution

Commencez par exprimer l'équation sous forme standard. Regroupez les termes qui contiennent la même variable et déplacez la constante vers le côté opposé de l'équation.

\((9x^2−36x)−(4y^2+40y)=388\)

Facturez le coefficient principal de chaque expression.

\(9(x^2−4x)−4(y^2+10y)=388\)

Complétez le carré deux fois. N'oubliez pas d'équilibrer l'équation en ajoutant les mêmes constantes de chaque côté.

\(9(x^2−4x+4)−4(y^2+10y+25)=388+36−100\)

Réécrivez en carrés parfaits.

\(9{(x−2)}^2−4{(y+5)}^2=324\)

Divisez les deux côtés par le terme constant pour placer l'équation sous forme standard.

\(\dfrac{{(x−2)}^2}{36}−\dfrac{{(y+5)}^2}{81}=1\)

La forme standard qui s'applique à l'équation donnée est\(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\), où\(a^2=36\) et\(b^2=81\), ou\(a=6\) et\(b=9\). Ainsi, l'axe transversal est parallèle à l'\(x\)axe. Il s'ensuit que :

le centre de l'ellipse est\((h,k)=(2,−5)\)

les coordonnées des sommets sont\((h\pm a,k)=(2\pm 6,−5)\), ou\((−4,−5)\)\((8,−5)\)

les coordonnées des co-sommets sont\((h,k\pm b)=(2,−5\pm 9)\), ou\((2,−14)\)\((2,4)\)

les coordonnées des foyers sont\((h\pm c,k)\), où\(c=\pm \sqrt{a^2+b^2}\). Pour résoudre ce problème\(c\), nous avons

\(c=\pm \sqrt{36+81}=\pm \sqrt{117}=\pm 3\sqrt{13}\)

Par conséquent, les coordonnées des foyers sont\((2−3\sqrt{13},−5)\) et\((2+3\sqrt{13},−5)\).

Les équations des asymptotes sont\(y=\pm \dfrac{b}{a}(x−h)+k=\pm \dfrac{3}{2}(x−2)−5\).

Ensuite, nous tracons et étiquetons le centre, les sommets, les co-sommets, les foyers et les asymptotes, puis nous dessinons des courbes lisses pour former l'hyperbole, comme indiqué sur la figure\(\PageIndex{10}\).

Figurine\(\PageIndex{10}\)

Exercice\(\PageIndex{5}\)

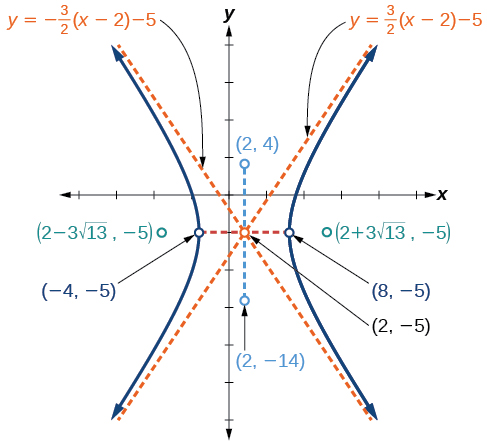
Représentez graphiquement l'hyperbole donnée par la forme standard d'une équation\(\dfrac{{(y+4)}^2}{100}−\dfrac{{(x−3)}^2}{64}=1\). Identifiez et étiquetez le centre, les sommets, les co-sommets, les foyers et les asymptotes.

Réponse

centre :\((3,−4)\) ; sommets :\((3,−14)\) et\((3,6)\) ; co-sommets :\((−5,−4)\) ; et\((11,−4)\) ; foyers :\((3,−4−2\sqrt{41})\) et\((3,−4+2\sqrt{41})\) ; asymptotes :\(y=\pm \dfrac{5}{4}(x−3)−4\)

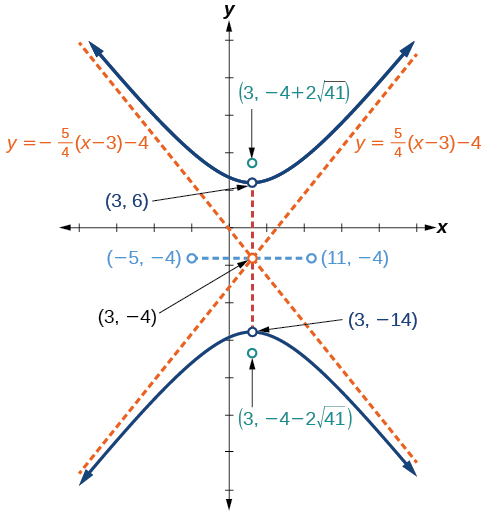
Figurine\(\PageIndex{11}\)

Résolution de problèmes appliqués impliquant des hyperboles

Comme nous l'avons vu au début de cette section, les hyperboles ont des applications concrètes dans de nombreux domaines, tels que l'astronomie, la physique, l'ingénierie et l'architecture. L'efficacité de conception des tours de refroidissement hyperboliques est particulièrement intéressante. Les tours de refroidissement sont utilisées pour transférer la chaleur perdue vers l'atmosphère et sont souvent vantées pour leur capacité à générer de l'énergie de manière efficace. En raison de leur forme hyperbolique, ces structures sont capables de résister à des vents extrêmes tout en nécessitant moins de matériaux que toute autre forme de taille et de résistance (Figure\(\PageIndex{12}\)). Par exemple, une tour\(500\) d'un pied peut être faite d'une coque en béton armé uniquement\(6\) ou d'une largeur de\(8\) quelques centimètres !

Figure\(\PageIndex{12}\) : Tours de refroidissement de la centrale de Drax dans le Yorkshire du Nord, au Royaume-Uni (crédit : Les Haines, Flickr)

Les premières tours hyperboliques ont été conçues en 1914 et mesuraient des\(35\) mètres de haut. Aujourd'hui, les plus hautes tours de refroidissement se trouvent en France, avec une hauteur remarquable de\(170\) plusieurs mètres. Dans Exemple,\(\PageIndex{6}\) nous utiliserons le plan de conception d'une tour de refroidissement pour trouver une équation hyperbolique qui modélise ses côtés.

Exemple\(\PageIndex{6}\): Solving Applied Problems Involving Hyperbolas

Le schéma de conception d'une tour de refroidissement est illustré sur la figure\(\PageIndex{13}\). La tour mesure quelques\(179.6\) mètres de haut. Le diamètre du sommet est de\(72\) mètres. Au plus près, les côtés de la tour sont distants de\(60\) quelques mètres.

Figure\(\PageIndex{13}\) : Conception du projet d'une tour de refroidissement à tirage naturel

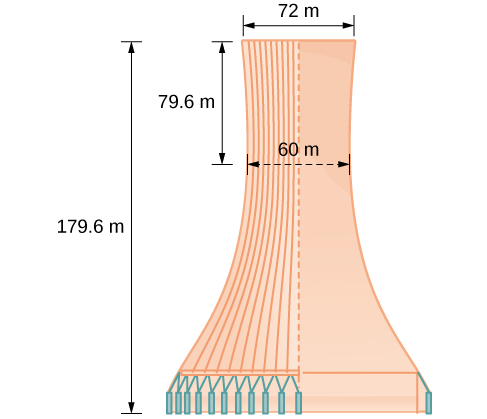
Trouvez l'équation de l'hyperbole qui modélise les côtés de la tour de refroidissement. Supposons que le centre de l'hyperbole, indiqué par l'intersection de lignes perpendiculaires en pointillés sur la figure, soit l'origine du plan de coordonnées. Arrondissez les valeurs finales à quatre décimales.

Solution

Nous supposons que le centre de la tour se trouve à l'origine. Nous pouvons donc utiliser la forme standard d'une hyperbole horizontale centrée sur l'origine :\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\), où les branches de l'hyperbole forment les côtés de la tour de refroidissement. Nous devons trouver les valeurs du modèle\(a^2\) et\(b^2\) le compléter.

Tout d'abord, nous trouvons\(a^2\). Rappelons que la longueur de l'axe transversal d'une hyperbole est de\(2a\). Cette longueur est représentée par la distance à laquelle les côtés sont les plus proches, exprimée en\(65.3\) mètres. Donc,\(2a=60\). Par conséquent,\(a=30\) et\(a^2=900\).

Pour résoudre ce problème\(b^2\), nous devons remplacer\(x\) et\(y\) dans notre équation en utilisant un point connu. Pour ce faire, nous pouvons utiliser les dimensions de la tour pour trouver un point\((x,y)\) situé sur l'hyperbole. Nous utiliserons le coin supérieur droit de la tour pour représenter ce point. Puisque l'\(y\)axe -coupe la tour en deux, notre\(x\) valeur -peut être représentée par le rayon du sommet, ou par des\(36\) mètres. La valeur y est représentée par la distance entre l'origine et le sommet, exprimée en\(79.6\) mètres. Par conséquent,

\[\begin{align*} \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}&=1\qquad \text{Standard form of horizontal hyperbola.}\\ b^2&=\dfrac{y^2}{\dfrac{x^2}{a^2}-1}\qquad \text{Isolate } b^2\\ &=\dfrac{{(79.6)}^2}{\dfrac{{(36)}^2}{900}-1}\qquad \text{Substitute for } a^2,\: x, \text{ and } y\\ &\approx 14400.3636\qquad \text{Round to four decimal places} \end{align*}\]

Les côtés de la tour peuvent être modélisés par l'équation hyperbolique

\(\dfrac{x^2}{900}−\dfrac{y^2}{14400.3636}=1\), ou\(\dfrac{x^2}{{30}^2}−\dfrac{y^2}{{120.0015}^2}=1\)

Exercice\(\PageIndex{6}\)

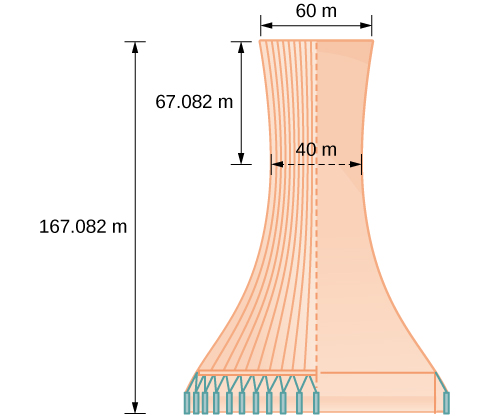
La conception d'un projet de tour de refroidissement est illustrée à la figure\(\PageIndex{14}\). Trouvez l'équation de l'hyperbole qui modélise les côtés de la tour de refroidissement. Supposons que le centre de l'hyperbole, indiqué par l'intersection de lignes perpendiculaires en pointillés sur la figure, soit l'origine du plan de coordonnées. Arrondissez les valeurs finales à quatre décimales.

Figurine\(\PageIndex{14}\)

Réponse

Les côtés de la tour peuvent être modélisés par l'équation hyperbolique. \(\dfrac{x^2}{400}−\dfrac{y^2}{3600}=1\)ou\(\dfrac{x^2}{{20}^2}−\dfrac{y^2}{{60}^2}=1\).

Médias

Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner à utiliser les hyperboles.

• Sections coniques : L'hyperbole, partie 1 de 2
• Sections coniques : L'hyperbole, partie 2 de 2
• Tracez une hyperbole avec le centre à l'origine
• Tracez une hyperbole avec le centre non à l'origine

Équations clés

Hyperbole, centre à l'origine, axe transversal sur l'axe x	\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\)
Hyperbole, centre à l'origine, axe transversal sur l'axe y	\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\)
Hyperbole, centre en\((h,k)\), axe transversal parallèle à l'axe x	\(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\)
Hyperbole, centre en\((h,k)\), axe transversal parallèle à l'axe y	\(\dfrac{{(y−k)}^2}{a^2}−\dfrac{{(x−h)}^2}{b^2}=1\)

Concepts clés

• Une hyperbole est l'ensemble de tous\((x,y)\) les points d'un plan tel que la différence entre les distances\((x,y)\) et les foyers soit une constante positive.
• La forme standard d'une hyperbole peut être utilisée pour localiser ses sommets et ses foyers. Voir l'exemple\(\PageIndex{1}\).
• Lorsque l'on donne les coordonnées des foyers et des sommets d'une hyperbole, on peut écrire l'équation de l'hyperbole sous forme standard. Voir Exemple\(\PageIndex{2}\) et Exemple\(\PageIndex{3}\).
• Lorsque l'on donne une équation pour une hyperbole, on peut identifier ses sommets, ses co-sommets, ses foyers, ses asymptotes, ainsi que les longueurs et les positions des axes transversal et conjugué afin de représenter graphiquement l'hyperbole. Voir Exemple\(\PageIndex{4}\) et Exemple\(\PageIndex{5}\).
• Les situations du monde réel peuvent être modélisées à l'aide des équations standard des hyperboles. Par exemple, étant donné les dimensions d'une tour de refroidissement à tirage naturel, nous pouvons trouver une équation hyperbolique qui modélise ses côtés. Voir l'exemple\(\PageIndex{6}\).