12.1 : L'Ellipse

Objectifs d'apprentissage

• Écrivez les équations des ellipses sous une forme standard.
• Tracez des ellipses centrées à l'origine.
• Les ellipses du graphe ne sont pas centrées à l'origine.
• Résolvez des problèmes appliqués impliquant des ellipses.

Vous imaginez-vous debout à une extrémité d'une grande pièce tout en étant capable d'entendre le murmure d'une personne debout à l'autre bout ? Le National Statuary Hall de Washington, D.C., illustré sur la figure$\PageIndex{1}$, est une telle pièce. Il s'agit d'une pièce de forme ovale appelée chambre à chuchotement parce que sa forme permet au son de se déplacer le long des murs. Dans cette section, nous étudierons la forme de cette pièce et ses applications réelles, y compris la distance à laquelle deux personnes peuvent se tenir debout dans la salle statuaire tout en s'entendant chuchoter.

Figure$\PageIndex{1}$ : Le National Statuary Hall de Washington, D.C. (crédit : Greg Palmer, Flickr)

Écrire des équations d'ellipses sous forme standard

Une section conique, ou conique, est une forme résultant de l'intersection d'un cône circulaire droit avec un plan. L'angle auquel le plan croise le cône détermine la forme, comme le montre la figure$\PageIndex{2}$.

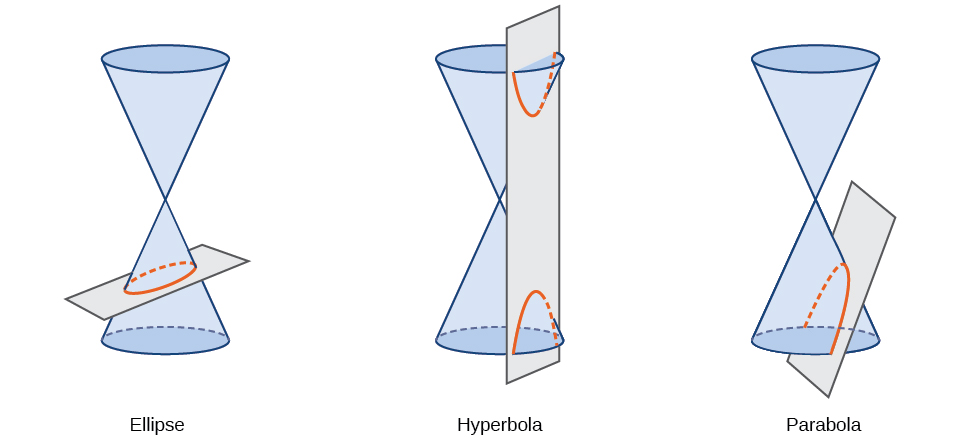
Figurine$\PageIndex{2}$

Les sections coniques peuvent également être décrites par un ensemble de points dans le plan de coordonnées. Plus loin dans ce chapitre, nous verrons que le graphique de toute équation quadratique à deux variables est une section conique. Les signes des équations et les coefficients des termes variables déterminent la forme. Cette section se concentre sur les quatre variantes de la forme standard de l'équation pour l'ellipse. Une ellipse est l'ensemble de tous les points$(x,y)$ d'un plan de telle sorte que la somme de leurs distances par rapport à deux points fixes est une constante. Chaque point fixe est appelé foyer (pluriel : foyer).

Nous pouvons dessiner une ellipse à l'aide d'un morceau de carton, de deux punaises, d'un crayon et d'une ficelle. Placez les punaises dans le carton pour former les foyers de l'ellipse. Coupez un morceau de ficelle plus long que la distance entre les deux punaises (la longueur de la chaîne représente la constante de la définition). Collez chaque extrémité de la ficelle au carton et tracez une courbe à l'aide d'un crayon tendu contre la ficelle. Le résultat est une ellipse. Voir la figure$\PageIndex{3}$.

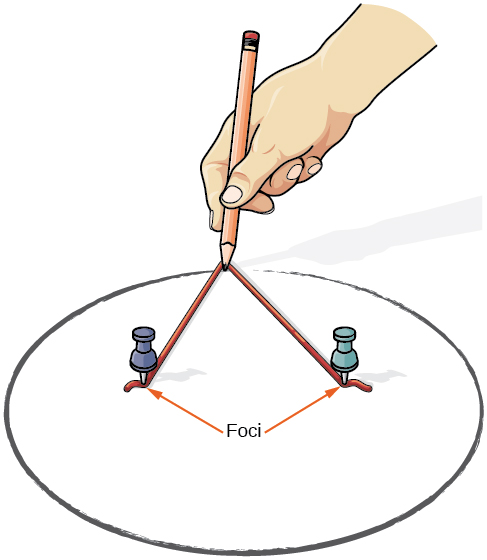
Figurine$\PageIndex{3}$

Chaque ellipse possède deux axes de symétrie. L'axe le plus long est appelé axe principal et l'axe le plus court est appelé axe mineur. Chaque extrémité de l'axe principal est le sommet de l'ellipse (au pluriel : sommets), et chaque extrémité de l'axe secondaire est un co-sommet de l'ellipse. Le centre d'une ellipse est le point médian de l'axe principal et de l'axe secondaire. Les axes sont perpendiculaires au centre. Les foyers se situent toujours sur l'axe principal et la somme des distances entre les foyers et tout point de l'ellipse (la somme constante) est supérieure à la distance entre les foyers (Figure$\PageIndex{4}$).

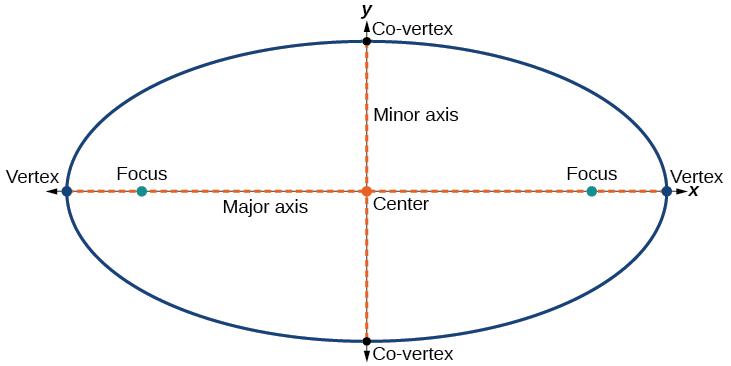
Figurine$\PageIndex{4}$

Dans cette section, nous limitons les ellipses à celles qui sont positionnées verticalement ou horizontalement dans le plan de coordonnées. En d'autres termes, les axes seront situés sur les axes$x$ - et$y$ - ou seront parallèles à ceux-ci. Plus loin dans le chapitre, nous verrons des ellipses pivotées dans le plan de coordonnées.

Pour travailler avec des ellipses horizontales et verticales dans le plan de coordonnées, nous considérons deux cas : celles qui sont centrées sur l'origine et celles qui sont centrées sur un point autre que l'origine. Nous allons d'abord apprendre à dériver les équations des ellipses, puis nous apprendrons à écrire les équations des ellipses sous forme standard. Plus tard, nous utiliserons ce que nous avons appris pour dessiner les graphiques.

Dériver l'équation d'une ellipse centrée à l'origine

Pour dériver l'équation d'une ellipse centrée à l'origine, nous commençons par les foyers$(−c,0)$ et$(c,0)$. L'ellipse est l'ensemble de tous les points de$(x,y)$ telle sorte que la somme des distances entre$(x,y)$ les foyers et les foyers soit constante, comme le montre la figure$\PageIndex{5}$.

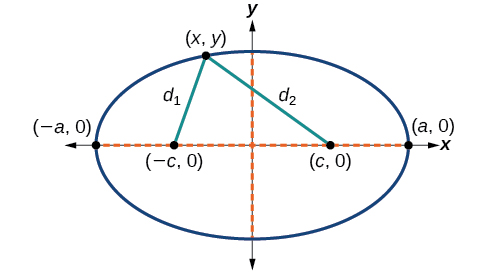
Figurine$\PageIndex{5}$

S'il s'$(a,0)$agit d'un sommet de l'ellipse, la distance$(−c,0)$ entre et$(a,0)$ est$a−(−c)=a+c$. La distance entre$(c,0)$ et$(a,0)$ est$a−c$. La somme des distances entre les foyers et le sommet est

$(a+c)+(a−c)=2a$

S'il s'$(x,y)$agit d'un point sur l'ellipse, nous pouvons définir les variables suivantes :

• $d_1=$la distance entre$(−c,0)$ et$(x,y)$
• $d_2=$la distance entre$(c,0)$ et$(x,y)$

Selon la définition d'une ellipse,$d_1+d_2$ est constante pour n'importe quel point$(x,y)$ de l'ellipse. Nous savons que la somme de ces distances correspond$2a$ au sommet$(a,0)$. Cela s'ensuit$d_1+d_2=2a$ pour n'importe quel point de l'ellipse. Nous allons commencer la dérivation en appliquant la formule de distance. Le reste de la dérivation est algébrique.

$$\begin{align*} d_1+d_2&= 2a\\ \sqrt{{(x-(-c))}^2+{(y-0)}^2}+\sqrt{{(x-c)}^2+{(y-0)}^2}&=2a\qquad \text{Distance formula}\\ \sqrt{{(x+c)}^2+y^2}+\sqrt{{(x-c)}^2+y^2}&=2a\qquad \text{Simplify expressions.}\\ \sqrt{{(x+c)}^2+y^2}&=2a-\sqrt{{(x-c)}^2+y^2}\qquad \text{Move radical to opposite side.}\\ {(x+c)}^2+y^2&={\left[2a-\sqrt{{(x-c)}^2+y^2}\right]}^2\qquad \text{Square both sides.}\\ x^2+2cx+c^2+y^2&=4a^2-4a\sqrt{{(x-c)}^2+y^2}+{(x-c)}^2+y^2\qquad \text{Expand the squares.}\\ x^2+2cx+c^2+y^2&=4a^2-4a\sqrt{{(x-c)}^2+y^2}+x^2-2cx+c^2+y^2\qquad \text{Expand remaining squares.}\\ 2cx&=4a^2-4a\sqrt{{(x-c)}^2+y^2}-2cx\qquad \text{Combine like terms.}\\ 4cx-4a^2&=-4a\sqrt{{(x-c)}^2+y^2}\qquad \text{Isolate the radical.}\\ cx-a^2&=-a\sqrt{{(x-c)}^2+y^2}\qquad \text{Divide by 4.}\\ {\left[ cx-a^2\right]}^2&=a^2{\left[ \sqrt{{(x-c)}^2+y^2}\right] }^2\qquad \text{Square both sides.}\\ c^2x^2-2a^2cx+a^4&=a^2(x^2-2cx+c^2+y^2)\qquad \text{Expand the squares.}\\ c^2x^2-2a^2cx+a^4&=a^2x^2-2a^2cx+a^2c^2+a^2y^2\qquad \text{Distribute } a^2\\ a^2x^2-c^2x^2+a^2y^2&=a^4-a^2c^2\qquad \text{Rewrite.}\\ x^2(a^2-c^2)+a^2y^2&=a^2(a^2-c^2)\qquad \text{Factor common terms.}\\ x^2b^2+a^2y^2&=a^2b^2\qquad \text{Set } b^2=a^2-c^2\\ \dfrac{x^2b^2}{a^2b^2}+\dfrac{a^2y^2}{a^2b^2}&=\dfrac{a^2b^2}{a^2b^2}\qquad \text{Divide both sides by } a^2b^2\\ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}&=1\qquad \text{Simplify} \end{align*}$$

Ainsi, l'équation standard d'une ellipse est la suivante :$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ cette équation définit une ellipse centrée à l'origine. Si$a>b$, l'ellipse est étirée davantage dans la direction horizontale, et si$b>a$, l'ellipse est étirée davantage dans la direction verticale.

Écrire des équations d'ellipses centrées à l'origine sous forme standard

Les formes standard d'équations nous renseignent sur les principales caractéristiques des graphes. Prenez un moment pour vous rappeler certaines des formes standard d'équations que nous avons utilisées dans le passé : linéaire, quadratique, cubique, exponentielle, logarithmique, etc. En apprenant à interpréter des formes standard d'équations, nous établissons un pont entre les représentations algébriques et géométriques des phénomènes mathématiques.

Les principales caractéristiques de l'ellipse sont son centre, ses sommets, ses co-sommets, ses foyers, ainsi que la longueur et la position des axes principaux et secondaires. Comme pour les autres équations, nous pouvons identifier toutes ces caractéristiques simplement en examinant la forme standard de l'équation. Il existe quatre variantes de la forme standard de l'ellipse. Ces variations sont classées d'abord en fonction de l'emplacement du centre (origine ou non), puis en fonction de la position (horizontale ou verticale). Chacune est présentée avec une description de la façon dont les parties de l'équation sont liées au graphique. L'interprétation de ces parties permet de se faire une image mentale de l'ellipse.

FORMES STANDARD DE L'ÉQUATION D'UNE ELLIPSE AVEC CENTRE$(0,0)$

La forme standard de l'équation d'une ellipse dont le centre$(0,0)$ et l'axe principal sont situés sur l'$x$axe -est

$$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$$

où

• $a>b$
• la longueur de l'axe principal est$2a$
• les coordonnées des sommets sont$(\pm a,0)$
• la longueur du petit axe est$2b$
• les coordonnées des co-sommets sont$(0,\pm b)$
• les coordonnées des foyers sont$(\pm c,0)$, où$c^2=a^2−b^2$. Voir la figure$\PageIndex{6a}$.

La forme standard de l'équation d'une ellipse dont le centre$(0,0)$ et l'axe principal sont situés sur l'$y$axe -est

$$\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1$$

où

• $a>b$
• la longueur de l'axe principal est$2a$
• les coordonnées des sommets sont$(0,\pm a)$
• la longueur du petit axe est$2b$
• les coordonnées des co-sommets sont$(\pm b,0)$
• les coordonnées des foyers sont$(0,\pm c)$, où$c^2=a^2−b^2$. Voir la figure$\PageIndex{6b}$.

Notez que les sommets, les co-sommets et les foyers sont liés par l'équation$c^2=a^2−b^2$. Lorsque l'on nous donne les coordonnées des foyers et des sommets d'une ellipse, nous pouvons utiliser cette relation pour trouver l'équation de l'ellipse sous forme standard.

Figure$\PageIndex{6}$ : (a) Ellipse horizontale avec centre$(0,0)$ (b) Ellipse verticale avec centre$(0,0)$

Comment : étant donné les sommets et les foyers d'une ellipse centrée sur l'origine, écrire son équation sous une forme standard

1. Déterminez si l'axe principal se trouve sur l'axe x ou l'axe y.
   • Si les coordonnées données des sommets et des foyers ont la forme$(\pm a,0)$ et$(\pm c,0)$ respectivement, alors l'axe principal est l'axe X. Utilisez le formulaire standard$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$
   • Si les coordonnées données des sommets et des foyers ont la forme$(0,\pm a)$ et$(\pm c,0)$, respectivement, l'axe principal est l'axe y. Utilisez le formulaire standard$\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1$
2. Utilisez l'équation$c^2=a^2−b^2$, ainsi que les coordonnées données des sommets et des foyers, pour résoudre$b^2$.
3. Remplacez les valeurs par$a^2$ et$b^2$ dans la forme standard de l'équation déterminée à l'étape 1.

Exemple$\PageIndex{1}$: Writing the Equation of an Ellipse Centered at the Origin in Standard Form

Quelle est l'équation de forme standard de l'ellipse qui possède des sommets$(\pm 8,0)$ et des foyers$(\pm 5,0)$ ?

Solution

Les foyers se trouvent sur l'$x$axe -, de sorte que l'axe principal est l'$x$axe X. Ainsi, l'équation aura la forme$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$

Les sommets sont$(\pm 8,0)$, ainsi$a=8$ et$a^2=64$.

Les points d'intérêt sont$(\pm 5,0)$, ainsi$c=5$ et$c^2=25$.

Nous savons que les sommets et les foyers sont liés par l'équation$c^2=a^2−b^2$. Pour résoudre ce problème$b^2$, nous avons :

$$\begin{align*} c^2&=a^2-b^2\\ 25&=64-b^2\qquad \text{Substitute for } c^2 \text{ and } a^2\\ b^2&=39\qquad \text{Solve for } b^2 \end{align*}$$

Il ne nous reste plus qu'à remplacer$a^2=64$ et$b^2=39$ à adopter la forme standard de l'équation. L'équation de l'ellipse est$\dfrac{x^2}{64}+\dfrac{y^2}{39}=1$.

Exercice$\PageIndex{1}$

Quelle est l'équation de forme standard de l'ellipse qui possède des sommets$(0,\pm 4)$ et des foyers$(0,\pm \sqrt{15})$ ?

Réponse

$x^2+\dfrac{y^2}{16}=1$

QUESTIONS-RÉPONSES

Pouvons-nous écrire l'équation d'une ellipse centrée à l'origine à partir des coordonnées d'un seul foyer et d'un seul sommet ?

Oui. Les ellipses étant symétriques, les coordonnées des sommets d'une ellipse centrée autour de l'origine auront toujours la forme$(\pm a,0)$ ou$(0, \pm a)$. De même, les coordonnées des foyers auront toujours la forme$(\pm c,0)$ ou$(0, \pm c)$. Sachant cela, nous pouvons utiliser$a$ et$c$ à partir des points donnés, ainsi que l'équation$c^2=a^2−b^2$, pour trouver$b^2$.

Écrire des équations d'ellipses non centrées à l'origine

Comme les graphes d'autres équations, le graphe d'une ellipse peut être traduit. Si une ellipse est$h$ translatée en unités horizontalement et en$k$ unités verticalement, le centre de l'ellipse sera$(h,k)$. Cette traduction donne la forme standard de l'équation que nous avons vue précédemment, avec$x$ remplacé par$(x−h)$ et y remplacé par$(y−k)$.

FORMES STANDARD DE L'ÉQUATION D'UNE ELLIPSE AVEC CENTRE$(H, K)$

La forme standard de l'équation d'une ellipse dont le centre$(h, k)$ et l'axe principal sont parallèles à l'$x$axe y est

$$\dfrac{{(x−h)}^2}{a^2}+\dfrac{{(y−k)}^2}{b^2}=1$$

où

• $a>b$
• la longueur de l'axe principal est$2a$
• les coordonnées des sommets sont$(h\pm a,k)$
• la longueur du petit axe est$2b$
• les coordonnées des co-sommets sont$(h,k\pm b)$
• les coordonnées des foyers sont$(h\pm c,k)$, où$c^2=a^2−b^2$. Voir la figure$\PageIndex{7a}$.

La forme standard de l'équation d'une ellipse dont le centre$(h,k)$ et l'axe principal sont parallèles à l'$y$axe y est

$$\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1$$

où

• $a>b$
• la longueur de l'axe principal est$2a$
• les coordonnées des sommets sont$(h,k\pm a)$
• la longueur du petit axe est$2b$
• les coordonnées des co-sommets sont$(h\pm b,k)$
• les coordonnées des foyers sont$(h,k\pm c)$, où$c^2=a^2−b^2$. Voir la figure$\PageIndex{7b}$.

Tout comme les ellipses centrées à l'origine, les ellipses centrées sur un point$(h,k)$ ont des sommets, des co-sommets et des foyers liés par l'équation$c^2=a^2−b^2$. Nous pouvons utiliser cette relation ainsi que les formules de point médian et de distance pour trouver l'équation de l'ellipse sous forme standard lorsque les sommets et les foyers sont donnés.

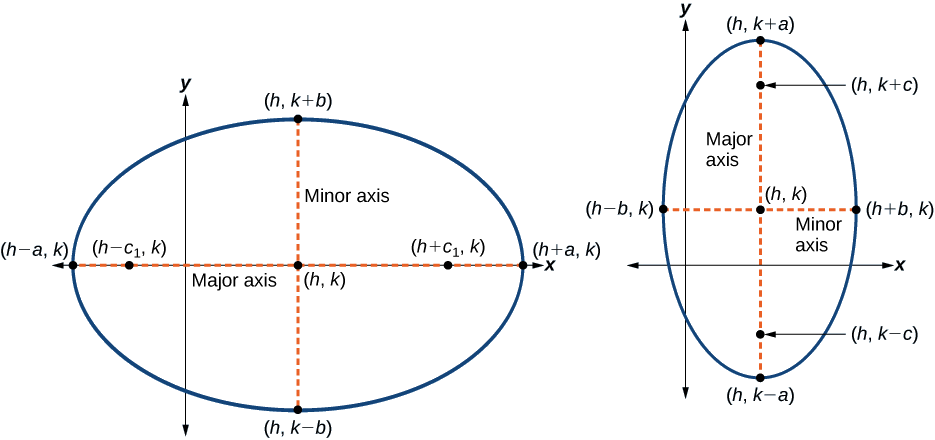
Figure$\PageIndex{7}$ : (a) Ellipse horizontale avec centre$(h,k)$ (b) Ellipse verticale avec centre$(h,k)$

Comment : étant donné les sommets et les foyers d'une ellipse qui ne sont pas centrés à l'origine, écrire son équation sous une forme standard

1. Déterminez si l'axe principal est parallèle à l'$y$axe$x$ - ou à l'axe.
   • Si les coordonnées y des sommets et des foyers donnés sont identiques, alors l'axe principal est parallèle à l'$x$axe. Utilisez le formulaire standard$\dfrac{{(x−h)}^2}{a^2}+\dfrac{{(y−k)}^2}{b^2}=1$
   • Si les coordonnées x des sommets et des foyers donnés sont identiques, alors l'axe principal est parallèle à l'axe y. Utilisez le formulaire standard$\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1$
2. Identifiez le centre de l'ellipse$(h,k)$ à l'aide de la formule du point médian et des coordonnées données pour les sommets.
3. Trouvez$a^2$ en résolvant la longueur de l'axe principal$2a$, qui est la distance entre les sommets donnés.
4. Recherchez$c^2$ en utilisant$h$ et$k$, trouvé à l'étape 2, avec les coordonnées données pour les foyers.
5. Résolvez pour$b^2$ utiliser l'équation$c^2=a^2−b^2$.
6. Remplacez les valeurs par$h$$k$,$a^2$, et$b^2$ dans la forme standard de l'équation déterminée à l'étape 1.

Exemple$\PageIndex{2}$: Writing the Equation of an Ellipse Centered at a Point Other Than the Origin

Quelle est l'équation de forme standard de l'ellipse qui a des sommets$(−2,−8)$$(−2,2)$ et des foyers$(−2,−7)$ et$(−2,1)$ ?

Solution

Les$x$ coordonnées des sommets et des foyers sont les mêmes, de sorte que l'axe principal est parallèle à l'$y$axe. Ainsi, l'équation de l'ellipse aura la forme

$\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1 \nonumber$

Tout d'abord, nous identifions le centre,$(h,k)$. Le centre se trouve à mi-chemin entre les sommets,$(−2,−8)$ et$(−2,2)$. En appliquant la formule du point médian, nous avons :

$$\begin{align} (h,k) &=\left(\dfrac{−2+(−2)}{2},\dfrac{−8+2}{2}\right) \nonumber \\ &=(−2,−3) \nonumber \end{align} \nonumber$$

Ensuite, nous trouvons$a^2$. La longueur de l'axe principal$2a$,, est limitée par les sommets. Nous résolvons le problème$a$ en trouvant la distance entre les coordonnées y des sommets.

$$\begin{align} 2a &=2−(−8) \nonumber \\ 2a &=10 \nonumber\\ a&=5 \nonumber \end{align} \nonumber$$

Donc$a^2=25$.

Maintenant on trouve$c^2$. Les foyers sont donnés par$(h,k\pm c)$. Donc,$(h,k−c)=(−2,−7)$ et$(h,k+c)=(−2,1)$. Nous substituons$k=−3$ l'utilisation de l'un ou l'autre de ces points pour résoudre$c$.

$$\begin{align} k+c &=1 \nonumber \\ −3+c&=1 \nonumber \\ c&=4 \nonumber \end{align} \nonumber$$

Donc$c^2=16$.

Ensuite, nous résolvons l'$b^2$utilisation de l'équation$c^2=a^2−b^2$.

$$\begin{align} c^2&=a^2−b^2 \nonumber \\ 16&=25−b^2 \nonumber \\ b^2&=9 \nonumber \end{align} \nonumber$$

Enfin, nous remplaçons les valeurs trouvées pour$h$$k$,$a^2$, et$b^2$ dans l'équation de forme standard par une ellipse :

$$\dfrac{{(x+2)}^2}{9}+\dfrac{{(y+3)}^2}{25}=1 \nonumber$$

Exercice$\PageIndex{2}$

Quelle est l'équation de forme standard de l'ellipse qui a des sommets$(−3,3)$$(5,3)$ et des foyers$(1−2\sqrt{3},3)$ et$(1+2\sqrt{3},3)$ ?

Réponse

$\dfrac{{(x−1)}^2}{16}+\dfrac{{(y−3)}^2}{4}=1 \nonumber$

Représentation graphique d'ellipses centrées à l'origine

Tout comme nous pouvons écrire l'équation d'une ellipse en fonction de son graphe, nous pouvons représenter graphiquement une ellipse en fonction de son équation. Pour représenter graphiquement des ellipses centrées à l'origine, nous utilisons le formulaire standard

$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1, a>b$pour ellipses horizontales

et

$\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1, a>b$pour ellipses verticales

Procédure : étant donné la forme standard d'une équation pour une ellipse centrée sur$(0, 0)$, sketch the graph.

1. Utilisez les formes standard des équations d'une ellipse pour déterminer l'axe principal, les sommets, les co-sommets et les foyers.
   • Si l'équation est sous la forme$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$, où$a>b$, alors
     • l'axe principal est l'$x$axe -
     • les coordonnées des sommets sont$(\pm a,0)$
     • les coordonnées des co-sommets sont$(0,\pm b)$
     • les coordonnées des foyers sont$(\pm c,0)$
   • Si l'équation est sous la forme$x^2b^2+y^2a^2=1$, où$a>b$, alors
     • l'axe principal est l'$y$axe -
     • les coordonnées des sommets sont$(0,\pm a)$
     • les coordonnées des co-sommets sont$(\pm b,0)$
     • les coordonnées des foyers sont$(0,\pm c)$
2. Résolvez pour$c$ utiliser l'équation$c^2=a^2−b^2$.
3. Tracez le centre, les sommets, les co-sommets et les foyers dans le plan de coordonnées, puis tracez une courbe lisse pour former l'ellipse.

Exemple$\PageIndex{3}$: Graphing an Ellipse Centered at the Origin

Tracez l'ellipse donnée par l'équation,$\dfrac{x^2}{9}+\dfrac{y^2}{25}=1$. Identifiez et étiquetez le centre, les sommets, les co-sommets et les foyers.

Solution

Nous déterminons d'abord la position de l'axe principal. Parce$25>9$ que l'axe principal se trouve sur l'$y$axe. Par conséquent, l'équation se présente sous la forme$\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1$, où$b^2=9$ et$a^2=25$. Il s'ensuit que :

• le centre de l'ellipse est$(0,0)$
• les coordonnées des sommets sont$(0,\pm a)=(0,\pm \sqrt{25})=(0,\pm 5)$
• les coordonnées des co-sommets sont$(\pm b,0)=(\pm 9,0)=(\pm 3,0)$
• les coordonnées des foyers sont$(0,\pm c)$, où$c^2=a^2−b^2$ Solving for$c$, nous avons :

$$\begin{align} c&=\pm \sqrt{a^2−b^2} \nonumber \\ &=\pm \sqrt{25−9} \nonumber\\ &=\pm \sqrt{16} \nonumber\\ &=\pm 4 \nonumber \end{align} \nonumber$$

Par conséquent, les coordonnées des foyers sont$(0,\pm 4)$.

Ensuite, nous tracons et étiquetons le centre, les sommets, les co-sommets et les foyers, puis nous dessinons une courbe lisse pour former l'ellipse. Voir la figure$\PageIndex{8}$.

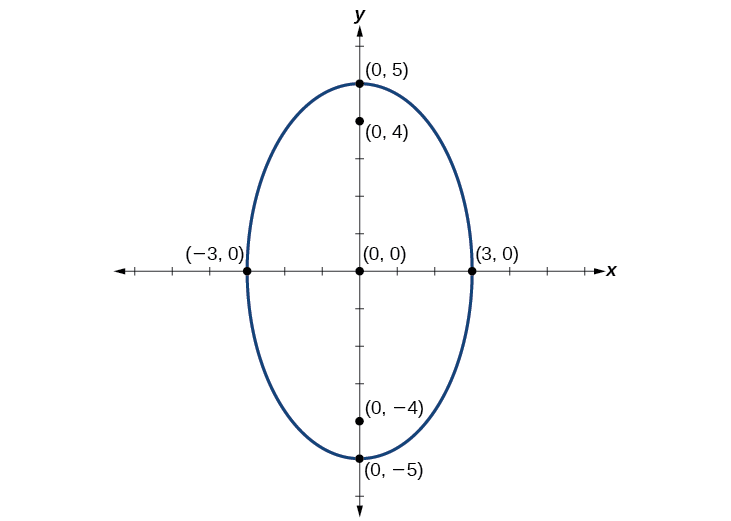
Figurine$\PageIndex{8}$

Exercice$\PageIndex{3}$

Tracez l'ellipse donnée par l'équation$\dfrac{x^2}{36}+\dfrac{y^2}{4}=1$. Identifiez et étiquetez le centre, les sommets, les co-sommets et les foyers.

Réponse

centre :$(0,0)$ ; sommets :$(\pm 6,0)$ ; co-sommets :$(0,\pm 2)$ ; foyers :$(\pm 4\sqrt{2},0)$

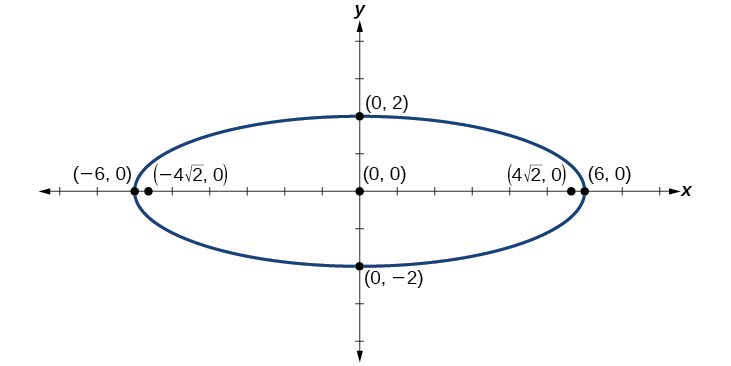
Figurine$\PageIndex{9}$

Exemple$\PageIndex{4}$: Graphing an Ellipse Centered at the Origin from an Equation Not in Standard Form

Tracez l'ellipse donnée par l'équation$4x^2+25y^2=100$. Réécrivez l'équation sous forme standard. Identifiez et étiquetez ensuite le centre, les sommets, les co-sommets et les foyers.

Solution

Tout d'abord, utilisez l'algèbre pour réécrire l'équation sous forme standard.

$$\begin{align} 4x^2+25y^2&=100 \nonumber \\ \dfrac{4x^2}{100}+\dfrac{25y^2}{100}&=\dfrac{100}{100} \nonumber \\ \dfrac{x^2}{25}+\dfrac{y^2}{4}&=1 \nonumber \end{align} \nonumber$$

Ensuite, nous déterminons la position de l'axe principal. Parce$25>4$ que l'axe principal se trouve sur l'$x$axe. Par conséquent, l'équation se présente sous la forme$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$, où$a^2=25$ et$b^2=4$. Il s'ensuit que :

• le centre de l'ellipse est$(0,0)$
• les coordonnées des sommets sont$(\pm a,0)=(\pm \sqrt{25},0)=(\pm 5,0)$
• les coordonnées des co-sommets sont$(0,\pm b)=(0,\pm \sqrt{4})=(0,\pm 2)$
• les coordonnées des foyers sont$(\pm c,0)$, où$c^2=a^2−b^2$. Pour résoudre ce problème$c$, nous avons :

$$\begin{align} c&=\pm \sqrt{a^2−b^2} \nonumber \\ &=\pm \sqrt{25−4} \nonumber \\ &=\pm \sqrt{21} \nonumber \end{align} \nonumber$$

Les coordonnées des foyers sont donc$(\pm \sqrt{21},0)$.

Ensuite, nous tracons et étiquetons le centre, les sommets, les co-sommets et les foyers, puis nous dessinons une courbe lisse pour former l'ellipse.

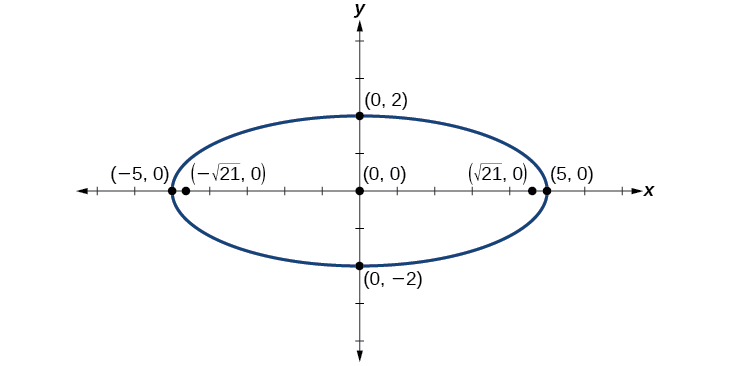
Figurine$\PageIndex{10}$

Exercice$\PageIndex{4}$

Tracez l'ellipse donnée par l'équation$49x^2+16y^2=784$. Réécrivez l'équation sous forme standard. Identifiez et étiquetez ensuite le centre, les sommets, les co-sommets et les foyers.

Réponse

Forme standard :$\dfrac{x^2}{16}+\dfrac{y^2}{49}=1$ ; centre :$(0,0)$ ; sommets :$(0,\pm 7)$ ; co-sommets :$(\pm 4,0)$ ; foyers :$(0,\pm \sqrt{33})$

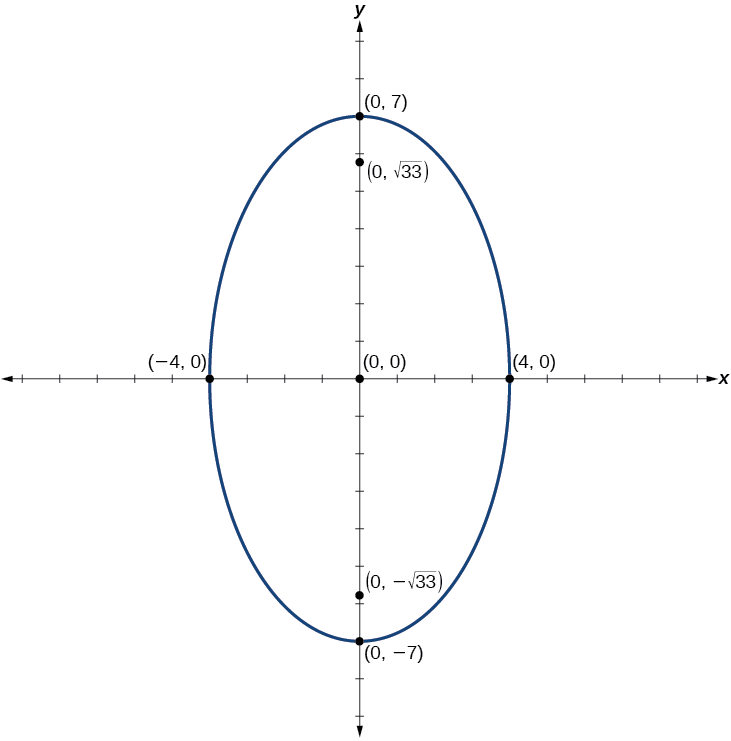
Figurine$\PageIndex{11}$

Représentation graphique d'ellipses non centrées à l'origine

Lorsqu'une ellipse n'est pas centrée sur l'origine, nous pouvons toujours utiliser les formulaires standard pour trouver les principales caractéristiques du graphique. Lorsque l'ellipse est centrée à un moment donné$(h,k)$, nous utilisons les formes standard$\dfrac{{(x−h)}^2}{a^2}+\dfrac{{(y−k)}^2}{b^2}=1$,$a>b$ pour les ellipses horizontales et$\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1$$a>b$ pour les ellipses verticales. À partir de ces équations standard, nous pouvons facilement déterminer le centre, les sommets, les co-sommets, les foyers et les positions des axes majeurs et mineurs.

Procédure : étant donné la forme standard d'une équation pour une ellipse centrée sur$(h, k)$, sketch the graph.

1. Utilisez les formes standard des équations d'une ellipse pour déterminer le centre, la position de l'axe principal, les sommets, les co-sommets et les foyers.
   • Si l'équation est sous la forme$\dfrac{{(x−h)}^2}{a^2}+\dfrac{{(y−k)}^2}{b^2}=1$, où$a>b$, alors
     • le centre est$(h,k)$
     • l'axe principal est parallèle à l'$x$axe -
     • les coordonnées des sommets sont$(h\pm a,k)$
     • les coordonnées des co-sommets sont$(h,k\pm b)$
     • les coordonnées des foyers sont$(h\pm c,k)$
   • Si l'équation est sous la forme$\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1$, où$a>b$, alors
     • le centre est$(h,k)$
     • l'axe principal est parallèle à l'$y$axe -
     • les coordonnées des sommets sont$(h,k\pm a)$
     • les coordonnées des co-sommets sont$(h\pm b,k)$
     • les coordonnées des foyers sont$(h,k\pm c)$
2. Résolvez pour$c$ utiliser l'équation$c^2=a^2−b^2$.
3. Tracez le centre, les sommets, les co-sommets et les foyers dans le plan de coordonnées, puis tracez une courbe lisse pour former l'ellipse.

Exemple$\PageIndex{5}$: Graphing an Ellipse Centered at $(h, k)$

Tracez l'ellipse donnée par l'équation,$\dfrac{{(x+2)}^2}{4}+\dfrac{{(y−5)}^2}{9}=1$. Identifiez et étiquetez le centre, les sommets, les co-sommets et les foyers.

Solution

Nous déterminons d'abord la position de l'axe principal. Parce$9>4$ que l'axe principal est parallèle à l'$y$axe. Par conséquent, l'équation se présente sous la forme$\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1$, où$b^2=4$ et$a^2=9$. Il s'ensuit que :

• le centre de l'ellipse est$(h,k)=(−2,5)$
• les coordonnées des sommets sont$(h,k\pm a)=(−2,5\pm \sqrt{9})=(−2,5\pm 3)$, ou$(−2,2)$$(−2,8)$
• les coordonnées des co-sommets sont$(h\pm b,k)=(−2\pm \sqrt{4},5)=(−2\pm 2,5)$, ou$(−4,5)$$(0,5)$
• les coordonnées des foyers sont$(h,k\pm c)$, où$c^2=a^2−b^2$. Pour résoudre ce problème$c$, nous avons :

$$\begin{align} c&=\pm \sqrt{a^2−b^2} \nonumber \\[4pt] &=\pm \sqrt{9−4} \nonumber \\[4pt] &=\pm \sqrt{5} \nonumber \end{align} \nonumber$$

Par conséquent, les coordonnées des foyers sont$(−2,5−\sqrt{5})$ et$(−2,5+\sqrt{5})$.

Ensuite, nous tracons et étiquetons le centre, les sommets, les co-sommets et les foyers, puis nous dessinons une courbe lisse pour former l'ellipse.

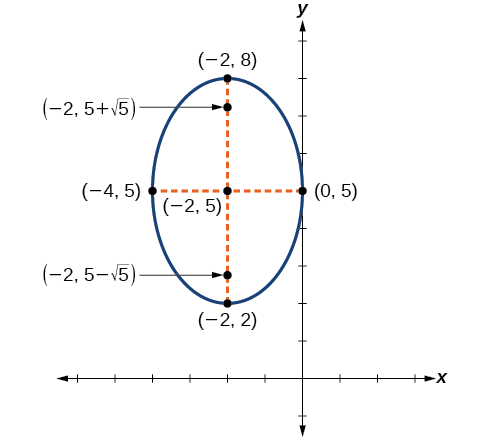
Figurine$\PageIndex{12}$

Exercice$\PageIndex{5}$

Tracez l'ellipse donnée par l'équation$\dfrac{{(x−4)}^2}{36}+\dfrac{{(y−2)}^2}{20}=1$. Identifiez et étiquetez le centre, les sommets, les co-sommets et les foyers.

Réponse

Centre :$(4,2)$ ; sommets :$(−2,2)$ et$(10,2)$ ; co-sommets :$(4,2−2\sqrt{5})$ et$(4,2+2\sqrt{5})$ ; foyers :$(0,2)$ et$(8,2)$

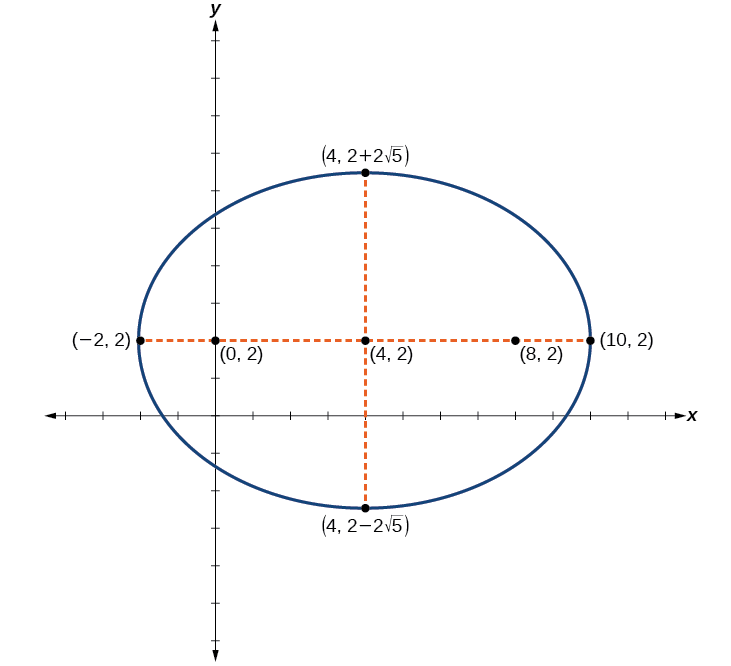
Figurine$\PageIndex{13}$

Comment faire : Compte tenu de la forme générale d'une équation pour une ellipse centrée sur$(h, k)$, express the equation in standard form.

1. Reconnaissez qu'une ellipse décrite par une équation du formulaire$ax^2+by^2+cx+dy+e=0$ est de forme générale.
2. Réorganisez l'équation en regroupant les termes qui contiennent la même variable. Déplace le terme constant vers le côté opposé de l'équation.
3. Tenez compte des coefficients des$y^2$ termes$x^2$ et pour vous préparer à compléter le carré.
4. Complétez le carré de chaque variable pour réécrire l'équation sous la forme de la somme des multiples de deux binômes au carré égaux à une constante$m_1{(x−h)}^2+m_2{(y−k)}^2=m_3$, où$m_1$$m_2$, et$m_3$ sont des constantes.
5. Divisez les deux côtés de l'équation par le terme constant pour exprimer l'équation sous forme standard.

Exemple$\PageIndex{6}$: Graphing an Ellipse Centered at $(h, k)$ by First Writing It in Standard Form

Tracez l'ellipse donnée par l'équation$4x^2+9y^2−40x+36y+100=0$. Identifiez et étiquetez le centre, les sommets, les co-sommets et les foyers.

Solution

Nous devons commencer par réécrire l'équation sous une forme standard.

$4x^2+9y^2−40x+36y+100=0$

Regroupez les termes qui contiennent la même variable et déplacez la constante vers le côté opposé de l'équation.

$(4x^2−40x)+(9y^2+36y)=−100$

Facturez les coefficients des termes au carré.

$4(x^2−10x)+9(y^2+4y)=−100$

Complétez le carré deux fois. N'oubliez pas d'équilibrer l'équation en ajoutant les mêmes constantes de chaque côté.

$4(x^2−10x+25)+9(y^2+4y+4)=−100+100+36$

Réécrivez en carrés parfaits.

$4{(x−5)}^2+9{(y+2)}^2=36$

Divisez les deux côtés par le terme constant pour placer l'équation sous forme standard.

$\dfrac{{(x−5)}^2}{9}+\dfrac{{(y+2)}^2}{4}=1$

Maintenant que l'équation est sous forme standard, nous pouvons déterminer la position du grand axe. Parce$9>4$ que l'axe principal est parallèle à l'$x$axe. Par conséquent, l'équation se présente sous la forme$\dfrac{{(x−h)}^2}{a^2}+\dfrac{{(y−k)}^2}{b^2}=1$, où$a^2=9$ et$b^2=4$. Il s'ensuit que :

• le centre de l'ellipse est$(h,k)=(5,−2)$
• les coordonnées des sommets sont$(h\pm a,k)=(5\pm \sqrt{9},−2)=(5\pm 3,−2)$, ou$(2,−2)$$(8,−2)$
• les coordonnées des co-sommets sont$(h,k\pm b)=(5,−2\pm \sqrt{4})=(5,−2\pm 2)$, ou$(5,−4)$$(5,0)$
• les coordonnées des foyers sont$(h\pm c,k)$, où$c^2=a^2−b^2$. Pour résoudre ce problème$c$, nous avons :

$$\begin{align*} c&=\pm \sqrt{a^2-b^2}\\ &=\pm \sqrt{9-4}\\ &=\pm \sqrt{5} \end{align*}$$

Par conséquent, les coordonnées des foyers sont$(5−\sqrt{5},−2)$ et$(5+\sqrt{5},−2)$.

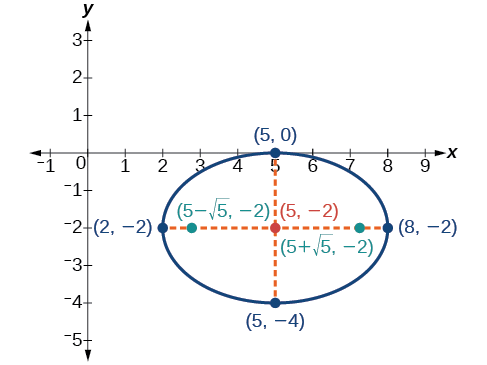
Ensuite, nous tracons et étiquetons le centre, les sommets, les co-sommets et les foyers, puis nous dessinons une courbe lisse pour former l'ellipse, comme indiqué sur la figure$\PageIndex{14}$.

Figurine$\PageIndex{14}$

Exercice$\PageIndex{6}$

Exprime l'équation de l'ellipse donnée sous forme standard. Identifiez le centre, les sommets, les co-sommets et les foyers de l'ellipse.

$4x^2+y^2−24x+2y+21=0$

Réponse

$\dfrac{{(x−3)}^2}{4}+\dfrac{{(y+1)}^2}{16}=1$; centre :$(3,−1)$ ; sommets :$(3,−5)$ et$(3,3)$ ; co-sommets :$(1,−1)$ et$(5,−1)$ ; foyers :$(3,−1−2\sqrt{3})$ et$(3,−1+2\sqrt{3})$

Résolution de problèmes appliqués impliquant des ellipses

De nombreuses situations du monde réel peuvent être représentées par des ellipses, notamment des orbites de planètes, de satellites, de lunes et de comètes, ainsi que des formes de quilles de bateaux, de gouvernails et de certaines ailes d'avion. Un dispositif médical appelé lithotripteur utilise des réflecteurs elliptiques pour décomposer les calculs rénaux en générant des ondes sonores. Certains bâtiments, appelés chambres à chuchoter, sont conçus avec des dômes elliptiques de sorte qu'une personne chuchotant sur un foyer puisse facilement être entendue par quelqu'un qui se tient debout sur l'autre foyer. Cela se produit en raison des propriétés acoustiques d'une ellipse. Lorsqu'une onde sonore provient d'un foyer d'une chambre de chuchotement, elle est réfléchie par le dôme elliptique et renvoyée vers l'autre foyer (Figure$\PageIndex{15}$). Dans la chambre à chuchotement du Musée des sciences et de l'industrie de Chicago, deux personnes debout au foyer, à environ un$43$ mètre l'une de l'autre, peuvent s'entendre chuchoter.

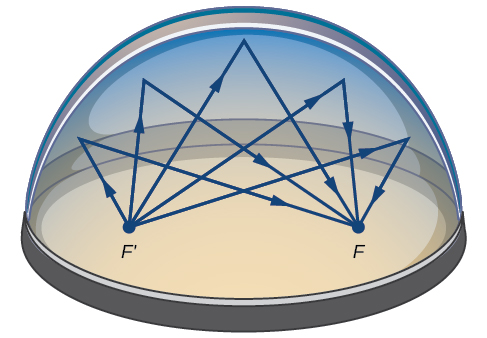
Figure$\PageIndex{15}$ : Les ondes sonores sont réfléchies entre les foyers d'une pièce elliptique, appelée chambre de chuchotement.

Exemple$\PageIndex{7}$: Locating the Foci of a Whispering Chamber

La salle statuaire du Capitole à Washington D.C. est une chambre à chuchoter. Ses dimensions sont des$46$ pieds de large sur des$96$ pieds de long, comme indiqué sur la figure$\PageIndex{16}$.

1. Quelle est la forme standard de l'équation de l'ellipse représentant le contour de la pièce ? Conseil : supposons une ellipse horizontale et que le centre de la pièce soit le point$(0,0)$.
2. Si deux sénateurs qui se tiennent au centre de cette pièce peuvent s'entendre chuchoter, à quelle distance se trouvent les sénateurs ? Arrondir au pied le plus proche.

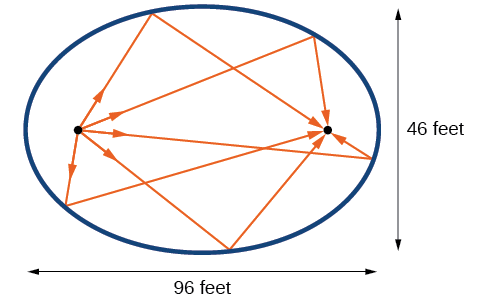
Figurine$\PageIndex{16}$

Solution

1. Nous supposons une ellipse horizontale avec un centre$(0,0)$, nous devons donc trouver une équation de la forme$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$, où$a>b$. Nous savons que la longueur du grand axe,$2a$, est plus longue que la longueur du petit axe,$2b$. Ainsi, la longueur de la pièce, 96, est représentée par l'axe principal, et la largeur de la pièce, 46, est représentée par le petit axe.

   Par conséquent, l'équation de l'ellipse est \ [(dfrac {x^2} {2304} + \ dfrac {y^2} {529} =1 \)

   • Résoudre pour$a$, nous avons$2a=96$, donc$a=48$, et$a^2=2304$.
   • Résoudre pour$b$, nous avons$2b=46$, donc$b=23$, et$b^2=529$.
2. Pour trouver la distance entre les sénateurs, il faut trouver la distance entre les foyers$(\pm c,0)$, où$c^2=a^2−b^2$. Pour résoudre ce problème$c$, nous avons :

$$\begin{align*} c^2&=a^2-b^2\\ c^2&=2304-529\qquad \text{Substitute using the values found in part } (a)\\ c&=\pm \sqrt{2304-529}\qquad \text{Take the square root of both sides.}\\ c&=\pm \sqrt{1775}\qquad \text{Subtract.}\\ c&\approx \pm 42\qquad \text{Round to the nearest foot.} \end{align*}$$

Les points$(\pm 42,0)$ représentent les points focaux. Ainsi, la distance entre les sénateurs est de$2(42)=84$ pieds.

Exercice$\PageIndex{7}$

Supposons qu'une chambre à murmure mesure des$480$ pieds de long et des$320$ pieds de large.

1. Quelle est la forme standard de l'équation de l'ellipse représentant la pièce ? Conseil : supposons une ellipse horizontale et que le centre de la pièce soit le point$(0,0)$.
2. Si deux personnes se tiennent au foyer de cette pièce et peuvent s'entendre chuchoter, à quelle distance se trouvent les personnes ? Arrondir au pied le plus proche.

Répondez à une

$\dfrac{x^2}{57,600}+\dfrac{y^2}{25,600}=1$

Réponse b

Les gens se tiennent les$358$ pieds à l'écart.

Médias

Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner avec des ellipses.

• Sections coniques : l'ellipse
• Tracez une ellipse dont le centre est à l'origine
• Tracez une ellipse dont le centre n'est pas à l'origine

Équations clés

Ellipse horizontale, centre à l'origine	$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$,$a>b$
Ellipse verticale, centre à l'origine	$\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1$,$a>b$
Ellipse horizontale, centre$(h,k)$	$\dfrac{{(x−h)}^2}{a^2}+\dfrac{{(y−k)}^2}{b^2}=1$,$a>b$
Ellipse verticale, centre$(h,k)$	$\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1$,$a>b$

Key Concepts

• An ellipse is the set of all points $(x,y)$ in a plane such that the sum of their distances from two fixed points is a constant. Each fixed point is called a focus (plural: foci).
• When given the coordinates of the foci and vertices of an ellipse, we can write the equation of the ellipse in standard form. See Example $\PageIndex{1}$ and Example $\PageIndex{2}$.
• When given an equation for an ellipse centered at the origin in standard form, we can identify its vertices, co-vertices, foci, and the lengths and positions of the major and minor axes in order to graph the ellipse. See Example $\PageIndex{3}$ and Example $\PageIndex{4}$.
• When given the equation for an ellipse centered at some point other than the origin, we can identify its key features and graph the ellipse. See Example $\PageIndex{5}$ and Example $\PageIndex{6}$.
• Real-world situations can be modeled using the standard equations of ellipses and then evaluated to find key features, such as lengths of axes and distance between foci. See Example $\PageIndex{7}$.

Contributors and Attributions

• Template:ContribOpenStaxPreCalc