9.2 : Identités de somme et de différence
- Page ID
- 195329
- Utilisez des formules de somme et de différence pour le cosinus.
- Utilisez des formules de somme et de différence pour le sinus.
- Utilisez des formules de somme et de différence pour la tangente.
- Utilisez des formules de somme et de différence pour les cofonctions.
- Utilisez des formules de somme et de différence pour vérifier les identités.
Comment mesurer la hauteur d'une montagne ? Qu'en est-il de la distance entre la Terre et le soleil ? Comme de nombreux problèmes apparemment impossibles, nous nous appuyons sur des formules mathématiques pour trouver des réponses. Les identités trigonométriques, couramment utilisées dans les preuves mathématiques, ont des applications dans le monde réel depuis des siècles, notamment pour le calcul de longues distances.
Les identités trigonométriques que nous allons examiner dans cette section remontent à un astronome persan qui a vécu vers 950 après JC, mais les Grecs de l'Antiquité ont découvert ces mêmes formules bien plus tôt et les ont énoncées en termes d'accords. Il s'agit d'équations ou de postulats spéciaux, valables pour toutes les valeurs entrées dans les équations, et avec d'innombrables applications.

Dans cette section, nous allons apprendre des techniques qui nous permettront de résoudre des problèmes tels que ceux présentés ci-dessus. Les formules qui suivent simplifieront de nombreuses expressions et équations trigonométriques. N'oubliez pas que, dans cette section, le terme formule est utilisé comme synonyme du mot identité.
Utilisation des formules de somme et de différence pour le cosinus
Il est souvent plus facile de trouver la valeur exacte du sinus, du cosinus ou de la tangente d'un angle si l'on peut réécrire l'angle donné en termes de deux angles dont les valeurs trigonométriques sont connues. Nous pouvons utiliser les angles spéciaux, que nous pouvons consulter dans le cercle unitaire illustré sur la figure\(\PageIndex{2}\).
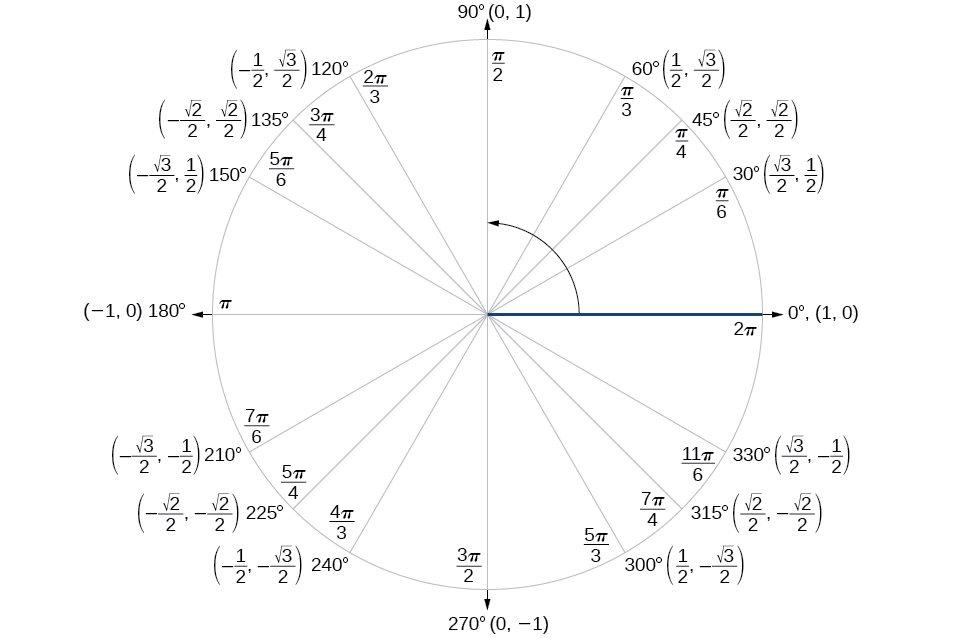
Nous allons commencer par les formules de somme et de différence pour le cosinus, afin de pouvoir trouver le cosinus d'un angle donné si nous pouvons le diviser en somme ou différence de deux des angles spéciaux (Tableau\(\PageIndex{1}\)).
| Formule de somme pour le cosinus | \(\cos(\alpha+\beta)=\cos \alpha \cos \beta−\sin \alpha \sin \beta\) |
| Formule de différence pour le cosinus | \(\cos(\alpha−\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta\) |
Tout d'abord, nous allons prouver la formule de différence pour les cosinus. Considérons deux points sur le cercle unitaire (Figure\(\PageIndex{3}\)). \(P\)Le point fait un angle\(\alpha\) par rapport à l'axe positif\(x\) avec des coordonnées\((\cos \alpha,\sin \alpha)\) et le point\(Q\) fait un angle par rapport\(\beta\) à l'axe positif\(x\) avec des coordonnées\((\cos \beta,\sin \beta)\). Notez que la mesure de l'angle\(POQ\) est de\(\alpha−\beta\).
Étiquetez deux points supplémentaires :\(A\) à un angle par rapport\((\alpha−\beta)\) à l'axe positif\(x\) avec des coordonnées\((\cos(\alpha−\beta),\sin(\alpha−\beta))\) ; et un point\(B\) avec des coordonnées\((1,0)\). \(POQ\)Le triangle est une rotation du triangle\(AOB\) et donc la distance\(P\) entre et\(Q\) est la même que la distance\(A\) entre et\(B\).
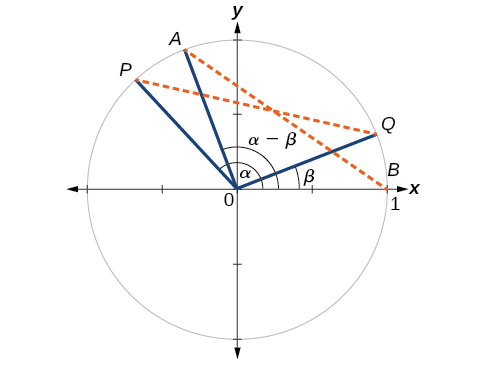
Nous pouvons trouver la distance entre et\(P\) en\(Q\) utilisant la formule de distance.
\ [\ begin {align*}
d_ {PQ} &= \ sqrt {(\ cos \ alpha - \ cos \ bêta)} ^2+ {(péché \ alpha - péché \ bêta)} ^2} \ \ [4pt]
&= \ sqrt {{\ cos} ^2 \ alpha-2 \ cos \ alpha \ cos \ beta+ {\ cos} ^2 \ bêta+ {\ sin} ^2 \ bêta+ {\ sin} ^2 \ alpha-2 \ cos \ alpha \ cos} 2 \ alpha-2 \ sin \ alpha \ sin \ beta+ {\ sin} ^2 \ beta} & \ text {Appliquez l'identité pythagoricienne et simplifier.} \ \ [4 points]
&= \ sqrt {({\ cos} ^2 \ alpha+ {\ sin} ^2 \ alpha) + ({\ cos} ^2 \ bêta+ {\ sin} ^2 \ bêta) -2 \ cos \ alpha \ cos \ bêta-2 \ sin \ alpha \ sin \ bêta} \ \ [4 points]
&= \ sqrt {1+1-2 \ cos \ alpha \ cos \ bêta-2 \ sin \ alpha \ sin \ bêta} \ \ [4 points]
&= \ sqrt {2-2 \ cos \ alpha \ cos \ bêta-2 \ sin \ alpha \ sin \ bêta} \ end {align*} \]
De même, en utilisant la formule de distance, nous pouvons trouver la distance entre\(A\) et\(B\).
\ [\ begin {align*}
d_ {AB} &= \ sqrt {(\ cos (\ alpha- \ beta) -1)} ^2+ {(\ sin (\ alpha- \ bêta) -0)} ^2} \ \ [4pt]
&= \ sqrt {{\ cos} ^2 (\ alpha- \ bêta) -2 \ cos (\ alpha- \ bêta) +1+ {\ sin} ^2 (\ alpha- \ beta)} & & \ text {Appliquez l'identité pythagoricienne et simplifiez} \ \ [4pt]
&= \ sqrt {({\ cos} ^2 (\ alpha- \ beta) + {\ sin} ^2 (\ alpha- \ beta)) -2 \ cos (\ alpha- \ beta) +1} \ \ [4pt]
&= \ sqrt {1-2 \ cos (\ alpha- \ beta) +1} \ \ [4pt]
&= \ sqrt {2-2 \ cos (\ alpha- \ beta)} & & \ text {Soustrayez 2 des deux côtés et divisez les deux côte à côte −2.} \ \ [4pt]
\ cos \ alpha \ cos \ beta+ \ sin \ alpha \ sin \ beta&= \ cos (\ alpha- \ bêta)
\ end {align*} \]
Ainsi, nous avons la formule de différence pour le cosinus. Nous pouvons utiliser des méthodes similaires pour dériver le cosinus de la somme de deux angles.
Ces formules peuvent être utilisées pour calculer le cosinus des sommes et des différences d'angles.
\[\cos(\alpha+\beta)=\cos \alpha \cos \beta−\sin \alpha \sin \beta\]
\[\cos(\alpha−\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta\]
- Écrivez la formule de différence pour le cosinus.
- Remplacez les valeurs des angles donnés dans la formule.
- Simplifiez.
À l'aide de la formule du cosinus de la différence de deux angles, déterminez la valeur exacte de\(\cos\left(\dfrac{5\pi}{4}−\dfrac{\pi}{6}\right)\).
Solution
Commencez par écrire la formule du cosinus de la différence de deux angles. Remplacez ensuite les valeurs données.
\[\begin{align*} \cos(\alpha-\beta)&= \cos \alpha \cos \beta+\sin \alpha \sin \beta\\[4pt] \cos\left(\dfrac{5\pi}{4}-\dfrac{\pi}{6}\right)&= \cos\left(\dfrac{5\pi}{4}\right)\cos\left(\dfrac{\pi}{6}\right)+\sin\left(\dfrac{5\pi}{4}\right)\sin\left(\dfrac{\pi}{6}\right)\\[4pt] &= \left(-\dfrac{\sqrt{2}}{2}\right)\left(\dfrac{\sqrt{3}}{2}\right)-\left(\dfrac{\sqrt{2}}{2}\right )\left(\dfrac{1}{2}\right)\\[4pt] &= -\dfrac{\sqrt{6}}{4}-\dfrac{\sqrt{2}}{4}\\[4pt] &= \dfrac{-\sqrt{6}-\sqrt{2}}{4} \end{align*}\]
N'oubliez pas que nous pouvons toujours vérifier la réponse à l'aide d'une calculatrice graphique en mode radian.
Trouvez la valeur exacte de\(\cos\left(\dfrac{\pi}{3}−\dfrac{\pi}{4}\right)\).
- Réponse
-
\(\dfrac{\sqrt{2}+\sqrt{6}}{4}\)
Trouvez la valeur exacte de\(\cos(75°)\).
Solution
Comme\(75°=45°+30°\), nous pouvons évaluer\(\cos(75°)\) comme\(\cos(45°+30°)\).
\[\begin{align*} \cos(\alpha+\beta)&= \cos \alpha \cos \beta -\sin \alpha \sin \beta\\[4pt] \cos(45^{\circ}+30^{\circ})&= \cos(45^{\circ})\cos(30^{\circ})-\sin(45^{\circ})\sin(30^{\circ})\\[4pt] &= \dfrac{\sqrt{2}}{2}\left(\dfrac{\sqrt{3}}{2}\right)-\dfrac{\sqrt{2}}{2}\left(\dfrac{1}{2}\right)\\[4pt] &= \dfrac{\sqrt{6}}{4}-\dfrac{\sqrt{2}}{4}\\[4pt] &= \dfrac{\sqrt{6}-\sqrt{2}}{4} \end{align*}\]
N'oubliez pas que nous pouvons toujours vérifier la réponse à l'aide d'une calculatrice graphique en mode degrés.
Analyse
Notez que nous aurions également pu résoudre ce problème en utilisant le fait que\( 75°=135°−60°\).
\[\begin{align*} \cos(\alpha-\beta)&= \cos \alpha \cos \beta+\sin \alpha \sin \beta\\[4pt] \cos(135^{\circ}-60^{\circ})&= \cos(135^{\circ})\cos(60^{\circ})+\sin(135^{\circ})\sin(60^{\circ})\\[4pt] &= \left(-\dfrac{\sqrt{2}}{2}\right)\left(\dfrac{1}{2}\right)+\left(\dfrac{\sqrt{2}}{2}\right )\left(\dfrac{\sqrt{3}}{2}\right)\\[4pt] &= -\dfrac{\sqrt{2}}{4}+\dfrac{\sqrt{6}}{4}\\[4pt] &= \dfrac{\sqrt{6}-\sqrt{2}}{4} \end{align*}\]
Trouvez la valeur exacte de\(\cos(105°)\).
- Réponse
-
\(\dfrac{\sqrt{2}-\sqrt{6}}{4}\)
Utilisation des formules de somme et de différence pour le sinus
Les formules de somme et de différence pour le sinus peuvent être dérivées de la même manière que celles pour le cosinus, et elles ressemblent aux formules du cosinus.
Ces formules peuvent être utilisées pour calculer les sinus des sommes et les différences d'angles.
\[\sin(\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta\]
\[\sin(\alpha−\beta)=\sin \alpha \cos \beta−\cos \alpha \sin \beta\]
- Écrivez la formule de différence pour le sinus.
- Remplacez les angles donnés dans la formule.
- Simplifiez.
Utilisez les identités de somme et de différence pour évaluer la différence des angles et montrer que la partie a est égale à la partie b.
- \(\sin(45°−30°)\)
- \(\sin(135°−120°)\)
Solution
- Commençons par écrire la formule et substituons les angles donnés.
\[\begin{align*} \sin(\alpha-\beta)&= \sin \alpha \cos \beta-\cos \alpha \sin \beta\\[4pt] \sin(45^{\circ}-30^{\circ})&= \sin(45^{\circ})\cos(30^{\circ})-\cos(45^{\circ})\sin(30^{\circ}) \end{align*}\]
Ensuite, nous devons trouver les valeurs des expressions trigonométriques.
\(\sin(45°)=\frac{\sqrt{2}}{2}, \qquad \cos(30°)=\frac{\sqrt{3}}{2}, \qquad \cos(45°)=\frac{\sqrt{2}}{2}, \qquad \sin(30°)=\frac{1}{2}\)
Nous pouvons maintenant remplacer ces valeurs dans l'équation et simplifier.
\[\begin{align*} \sin(45°-30°)&= \dfrac{\sqrt{2}}{2}\left(\dfrac{\sqrt{3}}{2}\right)-\dfrac{\sqrt{2}}{2}\left(\dfrac{1}{2}\right)\\[4pt] &= \dfrac{\sqrt{6}-\sqrt{2}}{4} \end{align*}\]
- Encore une fois, nous écrivons la formule et remplaçons les angles donnés.
\[\begin{align*} \sin(\alpha-\beta)&= \sin \alpha \cos \beta-\cos \alpha \sin \beta\\[4pt] \sin(135^{\circ}-120^{\circ})&= \sin(135^{\circ})\cos(120^{\circ})-\cos(135^{\circ})\sin(120^{\circ}) \end{align*}\]
Ensuite, nous trouvons les valeurs des expressions trigonométriques.
\(\sin(135°)=\frac{\sqrt{2}}{2}, \qquad \cos(120°)=-\frac{1}{2}, \qquad \cos(135°)=\frac{\sqrt{2}}{2}, \qquad \sin(120°)=\frac{\sqrt{3}}{2}\)
Nous pouvons maintenant remplacer ces valeurs dans l'équation et simplifier.
\[\begin{align*} \sin(135^{\circ}-120^{\circ})&= \dfrac{\sqrt{2}}{2}\left(-\dfrac{1}{2}\right)-\left(-\dfrac{\sqrt{2}}{2}\right)\left (\dfrac{\sqrt{3}}{2}\right)\\[4pt] &= \dfrac{\sqrt{6}-\sqrt{2}}{4} \end{align*}\]
Trouvez la valeur exacte de\(\sin\left ({\cos}^{−1}\frac{1}{2}+{\sin}^{−1}\frac{3}{5}\right)\). Vérifiez ensuite la réponse à l'aide d'une calculatrice graphique.
Solution
Le schéma affiché dans ce problème est\(\sin(\alpha+\beta)\). Laissez\(\alpha={\cos}^{−1}\frac{1}{2}\) et\(\beta={\sin}^{−1}\frac{3}{5}\). Ensuite, nous pouvons écrire
\ [\ begin {align*}
\ cos \ alpha&= \ dfrac {1} {2}, \ quad 0 \ leq \ alpha \ leq \ pi \ \ [4 points]
\ sin \ beta&= \ dfrac {3} {5}, \ quad - \ dfrac {\ pi} {2} \ leq \ bêta \ leq \ dfrac {\ pi} {2} \\[4pt]\end{align*}\]
Nous utiliserons les identités pythagoriciennes pour trouver\(\sin \alpha\) et\(\cos \beta\)
\ [\ begin {align*}
\ sin \ alpha&= \ sqrt {1- {\ cos} ^2 \ alpha} \ \ [4 points]
&= \ sqrt {1- \ dfrac {1} {4}} \ \ [4 points]
&= \ sqrt {\ dfrac {3} {4}} \ \ [4 points] &= \ dfrac {\ sqrt {3} {4}} \ \ [4 points]
&= \ dfrac {\ sqrt {3}} {2}
\ \ [4 points] \ cos \ beta&= \ sqrt {1- {\ sin} ^2 \ bêta} \ \ [4 points]
& = \ sqrt {1- \ dfrac {9} {25}} \ \ [4 points]
&= \ sqrt {\ dfrac {16} {25}} \ \ [4 points]
&= \ dfrac {4} {5}
\ end {align*} \]
En utilisant la formule de somme pour le sinus,
\[\begin{align*} \sin \left({\cos}^{-1}\tfrac{1}{2}+{\sin}^{-1}\tfrac{3}{5}\right)&= \sin(\alpha+\beta)\\[4pt] &= \sin \alpha \cos \beta+\cos \alpha \sin \beta\\[4pt] &= \dfrac{\sqrt{3}}{2}\cdot \dfrac{4}{5}+\dfrac{1}{2}\cdot \dfrac{3}{5}\\[4pt] &= \dfrac{4\sqrt{3}+3}{10} \end{align*}\]
Utilisation des formules de somme et de différence pour la tangente
Trouver des valeurs exactes pour la tangente de la somme ou de la différence de deux angles est un peu plus compliqué, mais là encore, il s'agit de reconnaître le motif.
Pour trouver la formule de la somme de deux angles pour la tangente, il faut prendre le quotient des formules de somme pour le sinus et le cosinus et les simplifier. Rappelez-vous\(\tan x=\dfrac{\sin x}{\cos x}\), quand\(\cos x≠0\).
Déterminons la formule de somme pour la tangente.
\ [\ begin {align*}
\ tan \ left (\ alpha+ \ beta \ right) &= \ dfrac {\ sin \ left (\ alpha+ \ beta \ right)} {\ cos (\ alpha+ \ beta)} \ \ [6pt]
&= \ dfrac {\ sin \ alpha \ cos \ beta+ \ cos \ alpha \ sin \ bêta} {\ cos \ alpha \ cos \ alpha \ cos \ beta- \ sin \ alpha \ sin \ bêta} \ \ [6 points]
&= \ dfrac {\ dfrac {\ sin \ alpha \ cos \ beta+ \ cos \ alpha \ sin \ bêta} {\ cos \ alpha \ cos \ bêta}} {\ dfrac {\ cos \ alpha \ cos \ bêta- \ sin \ alpha \ sin \ sin \ bêta} {\ cos \ alpha \ cos \ bêta}} \ \ [6pt]
&= \ dfrac {\ dfrac {\ sin \ alpha \ cos \ bêta} {\ cos \ alpha \ cos \ beta} {\ cos \ alpha \ cos \ bêta} + \ dfrac {\ cos \ alpha \ sin \ bêta} {\ cos \ alpha \ cos \ bêta}} {\ dfrac {\ cos \ alpha \ cos \ cos \ bêta} {\ cos \ alpha \ cos \ bêta} - \ dfrac {\ sin \ alpha \ sin \ bêta} {\ cos \ alpha \ cos \ bêta}} \ \ [6pt]
&= \ dfrac {\ dfrac {\ sin \ alpha} {\ cos \ alpha} + \ dfrac {\ sin \ beta} {\ cos \ beta}} {1- \ dfrac {\ sin \ sin \ alpha \ sin \ bêta} {\ cos \ alpha \ cos \ bêta}} \ \ [6 points]
&= \ dfrac {\ tan \ alpha+ \ tan \ bêta} {1- \ tan \ bêta} {1- \ tan \ alpha \ tan \ bêta}
\ end {align*} \]
Nous pouvons obtenir la formule de différence pour la tangente de la même manière.
Les formules de somme et de différence pour la tangente sont les suivantes :
\[\tan(\alpha+\beta)=\dfrac{\tan \alpha+\tan \beta}{1−\tan \alpha \tan \beta}\]
\[\tan(\alpha-\beta)=\dfrac{\tan \alpha-\tan \beta}{1+\tan \alpha \tan \beta}\]
- Ecrivez la formule de somme pour la tangente.
- Remplacez les angles donnés dans la formule.
- Simplifiez.
Trouvez la valeur exacte de\(\tan\left(\dfrac{\pi}{6}+\dfrac{\pi}{4}\right)\).
Solution
Écrivons d'abord la formule de somme pour la tangente, puis substituons les angles donnés dans la formule.
\ [\ begin {align*}
\ tan (\ alpha+ \ bêta) &= \ dfrac {\ tan \ alpha+ \ tan \ beta} {1- \ tan \ alpha \ tan \ bêta} \ \ [4 points]
\ tan \ left (\ dfrac {\ pi} {6} + \ dfrac {\ pi} {4} \ right) &= \ dfrac {\ tan left (\ dfrac {\ pi} {6} \ right) + \ tan \ left (\ dfrac {\ pi} {4} \ right)} {1- \ left (\ tan \ left (\ dfrac {\ pi} {6} \ right) \ right) \ right ) \ left (\ tan \ left (\ dfrac {\ pi} {4} \ right) \ right)} \ end {align*} \]
Ensuite, nous déterminons les valeurs de chaque fonction dans la formule :
\[\tan\left (\dfrac{\pi}{6}\right )= \dfrac{1}{\sqrt{3}}, \quad \text{and} \quad \tan\left (\dfrac{\pi}{4}\right) = 1\]
Nous avons donc,
\ [\ begin {align*} \ tan \ left (\ dfrac {\ pi} {6} + \ dfrac {\ pi} {4} \ right) &= \ dfrac {\ dfrac {1} {\ sqrt {3}} +1} {1- \ left (\ dfrac {1} {\ sqrt {3}} \ right) (1)} \ \ [6 points]
&= \ dfrac {\ dfrac {1+ \ sqrt {3}} {\ sqrt {3}}} {\ dfrac {\ sqrt {3} -1} {\ sqrt {3}}} \ \ [6 points]
& amp ; = \ dfrac {1+ \ sqrt {3}} {\ sqrt {3}} \ cdot \ dfrac {\ sqrt {3}} {\ sqrt {3} -1} \ \ [6pt]
&= \ dfrac {\ sqrt {3} +1} {\ sqrt {3} -1}
\ end {align*} \]
Trouvez la valeur exacte de\(\tan\left (\dfrac{2\pi}{3}+\dfrac{\pi}{4}\right )\).
- Réponse
-
\(\dfrac{1-\sqrt{3}}{1+\sqrt{3}}\)
Étant donné\(\sin \alpha=\frac{3}{5}, \quad 0<\alpha<\frac{\pi}{2},\) et\(\cos \beta=−\frac{5}{13}, \quad \pi<\beta<\frac{3\pi}{2}\),
trouver
- \(\sin(\alpha+\beta)\)
- \(\cos(\alpha+\beta)\)
- \(\tan(\alpha+\beta)\)
- \(\tan(\alpha−\beta)\)
Solution
Nous pouvons utiliser les formules de somme et de différence pour identifier la somme ou la différence des angles lorsque le rapport du sinus, du cosinus ou de la tangente est fourni pour chacun des angles individuels. Pour ce faire, nous construisons ce que l'on appelle un triangle de référence pour aider à trouver chaque composante des formules de somme et de différence.
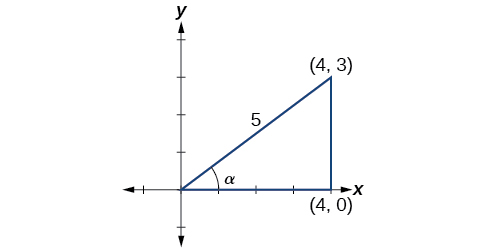
- Pour trouver\(\sin(\alpha+\beta)\), on commence par\(\sin \alpha=\dfrac{3}{5}\) et\(0<\alpha<\dfrac{\pi}{2}\). Le côté opposé\(\alpha\) a une longueur 3, l'hypoténuse a une longueur de 5 et\(\alpha\) se trouve dans le premier quadrant. Voir la figure\(\PageIndex{4}\). En utilisant le théorème de Pythagore, nous pouvons trouver la longueur du côté\(a\) :
\[\begin{align*} a^2+3^2&= 5^2\\[4pt] a^2&= 16\\[4pt] a&= 4 \end{align*}\]
Depuis\(\cos \beta=−\dfrac{5}{13}\) et\(\pi<\beta<\dfrac{3\pi}{2}\), le côté adjacent à\(\beta\) est\(−5\), l'hypoténuse se trouve\(13\) et\(\beta\) se trouve dans le troisième quadrant. Voir la figure\(\PageIndex{5}\). Encore une fois, en utilisant le théorème de Pythagore, nous avons
\[\begin{align*} {(-5)}^2+a^2&= {13}^2\\[4pt] 25+a^2&= 169\\[4pt] a^2&= 144\\[4pt] a&= \pm 12 \end{align*}\]
Puisque\(\beta\) c'est dans le troisième quadrant,\(a=–12\).
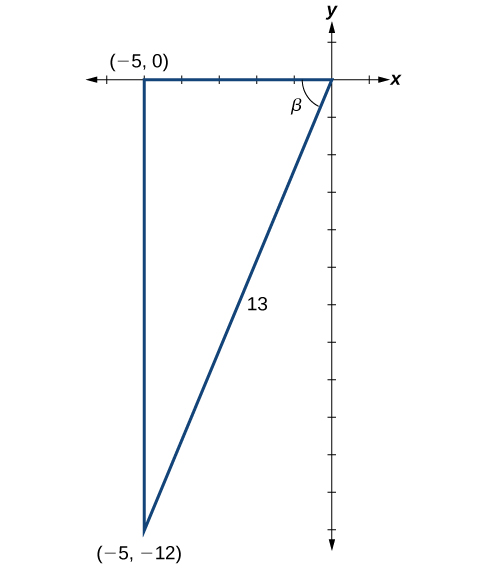
L'étape suivante consiste à trouver le cosinus\(\alpha\) et le sinus de\(\beta\). Le cosinus de α α est le côté adjacent au-dessus de l'hypoténuse. Nous pouvons le trouver à partir du triangle de la figure\(\PageIndex{5}\) :\(\cos \alpha=\dfrac{4}{5}\). Nous pouvons également trouver le sinus\(\beta\) du triangle sur la figure\(\PageIndex{5}\), en face de l'hypoténuse :\(\sin \beta=−\dfrac{12}{13}\). Nous sommes maintenant prêts à évaluer\(\sin(\alpha+\beta)\).
\[\begin{align*} \sin(\alpha+\beta)&= \sin \alpha \cos \beta+\cos \alpha \sin \beta\\[4pt] &= \left(\dfrac{3}{5}\right)\left(-\dfrac{5}{13}\right )+\left (\dfrac{4}{5}\right )\left(-\dfrac{12}{13}\right )\\[4pt] &= -\dfrac{15}{65}-\dfrac{48}{65}\\[4pt] &= -\dfrac{63}{65} \end{align*}\]
- Nous pouvons trouver\(\cos(\alpha+\beta)\) de la même manière. Nous substituons les valeurs selon la formule.
\[\begin{align*} \cos(\alpha+\beta)&= \cos \alpha \cos \beta-\sin \alpha \sin \beta\\[4pt] &= \left(\dfrac{4}{5}\right)\left(-\dfrac{5}{13}\right)-\left(\dfrac{3}{5}\right )\left(-\dfrac{12}{13}\right)\\[4pt] &= -\dfrac{20}{65}+\dfrac{36}{65}\\[4pt] &= \dfrac{16}{65} \end{align*}\]
- Pour\(\tan(\alpha+\beta)\), si\(\sin \alpha=\dfrac{3}{5}\) et\(\cos \alpha=\dfrac{4}{5}\), alors
\(\tan \alpha=\dfrac{\dfrac{3}{5}}{\dfrac{4}{5}}=\dfrac{3}{4}\)
Si\(\sin \beta=−\dfrac{12}{13}\) et\(\cos \beta=−\dfrac{5}{13}\), alors
\(\tan \beta=\dfrac{−\dfrac{12}{13}}{−\dfrac{5}{13}}=\dfrac{12}{5}\)
Ensuite,
\ [\ begin {align*}
\ tan (\ alpha+ \ bêta) &= \ dfrac {\ tan \ alpha+ \ tan \ bêta} {1- \ tan \ alpha \ tan \ bêta} \ \ [6 points]
&= \ dfrac {\ dfrac {3} {4} + \ dfrac {12} {5}} {1- \ dfrac {3} {4}} \ left (\ dfrac {12} {5} \ right)} \ \ [6 points]
&= \ dfrac {\ dfrac {63} {20}} {- \ dfrac {16} {20}} \ \ [6 points]
& amp ; = - \ dfrac {63} {16}
\ end {align*} \]
- Pour trouver\(\tan(\alpha−\beta)\), nous avons les valeurs dont nous avons besoin. Nous pouvons les remplacer et les évaluer.
\ [\ begin {align*}
\ tan (\ alpha- \ bêta) &= \ dfrac {\ tan \ alpha- \ tan \ bêta} {1+ \ tan \ alpha \ tan \ bêta} \ \ [6 points]
&= \ dfrac {\ dfrac {3} {4} - \ dfrac {12} {5}} {1+ \ dfrac {3} {4}} - \ dfrac {12} {5}} {1+ \ dfrac {3} {4}} left (\ dfrac {12} {5} \ right)} \ \ [6 points]
&= \ dfrac {- \ dfrac {33} {20}} {\ dfrac {56} {20}} \ \ [6 points]
& amp ; = - \ dfrac {33} {56}
\ end {align*} \]
Analyse
Une erreur courante lorsqu'on aborde des problèmes comme celui-ci est que nous pouvons être tentés de penser cela\(\alpha\) et d'être\(\beta\) des angles dans le même triangle, ce qui n'est évidemment pas le cas. Notez également que
\(\tan(\alpha+\beta)=\sin(\alpha+\beta)\cos(\alpha+\beta)\)
Utilisation de formules de somme et de différence pour les cofonctions
Maintenant que nous pouvons trouver les fonctions sinus, cosinus et tangente pour les sommes et les différences d'angles, nous pouvons les utiliser pour faire de même pour leurs cofonctions. Vous vous souvenez peut-être de la trigonométrie du triangle droit que, si la somme de deux angles positifs est\(\frac{\pi}{2}\), ces deux angles sont des compléments, et que la somme des deux angles aigus d'un triangle droit l'est\(\frac{\pi}{2}\), ils sont donc également des compléments. Dans la figure\(\PageIndex{6}\), notez que si l'un des angles aigus est étiqueté comme\(\theta\), alors l'autre angle aigu doit être étiqueté\(\frac{\pi}{2}−\theta\).
Remarquez également cela\(\sin \theta=\cos\left(\frac{\pi}{2}−\theta\right)\), ce qui est opposé à l'hypoténuse. Ainsi, lorsque deux angles sont complémentaires, on peut dire que le sinus de\(\theta\) est égal à la cofonction du complément de\(\theta\). De même, la tangente et la cotangente sont des cofonctions, et la sécante et la cosécante sont des cofonctions.
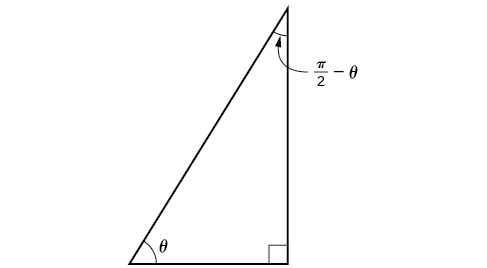
À partir de ces relations, les identités de cofonctions sont formées. Rappelez-vous que vous avez rencontré ces identités pour la première fois dans The Unit Circle : Sine and Cosine Functions.
Les identités des cofonctions sont résumées dans le tableau\(\PageIndex{2}\).
| \(\sin \theta=\cos\left(\dfrac{\pi}{2}−\theta\right)\) | \(\cos \theta=\sin\left(\dfrac{\pi}{2}−\theta\right)\) |
| \(\tan \theta=\cot\left(\dfrac{\pi}{2}−\theta\right)\) | \(\cot \theta=\tan\left(\dfrac{\pi}{2}−\theta\right )\) |
| \(\sec \theta=\csc\left (\dfrac{\pi}{2}−\theta\right )\) | \(\csc \theta=\sec\left (\dfrac{\pi}{2}−\theta\right )\) |
Notez que les formules du tableau peuvent également être justifiées algébriquement à l'aide des formules de somme et de différence. Par exemple, en utilisant
\(\cos(\alpha-\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta\)
Nous pouvons écrire
\[\begin{align*} \cos\left (\dfrac{\pi}{2}-\theta \right )&= \cos \dfrac{\pi}{2} \cos \theta+\sin \dfrac{\pi}{2} \sin \theta \\[4pt] &=(0)\cos \theta+(1)\sin \theta \\[4pt] &=\sin \theta \end{align*}\]
Écrivez\(\tan \dfrac{\pi}{9}\) en fonction de sa cofonction.
Solution
La cofonction de\(\tan \theta=\cot\left (\dfrac{\pi}{2}−\theta\right )\). Ainsi,
\[\begin{align*} \tan\left (\dfrac{\pi}{9}\right )&= \cot\left (\dfrac{\pi}{2}-\dfrac{\pi}{9}\right )\\[4pt] &= \cot\left (\dfrac{9\pi}{18}-\dfrac{2\pi}{18}\right )\\[4pt] &= \cot\left (\dfrac{7\pi}{18}\right ) \end{align*}\]
\(\sin \dfrac{\pi}{7}\) in terms of its Cofonction d'écriture.
- Réponse
-
\(\cos\left (\dfrac{5\pi}{14}\right )\)
Utilisation des formules de somme et de différence pour vérifier les identités
Vérifier une identité signifie démontrer que l'équation est valable pour toutes les valeurs de la variable. Il est utile de bien connaître les identités ou d'en avoir une liste accessible tout en résolvant les problèmes. La révision des règles générales présentées précédemment peut contribuer à simplifier le processus de vérification d'une identité.
- Commencez par l'expression située sur le côté du signe égal qui semble la plus complexe. Réécrivez cette expression jusqu'à ce qu'elle corresponde à l'autre côté du signe égal. De temps en temps, il se peut que nous devions modifier les deux côtés, mais travailler sur un seul côté est la solution la plus efficace.
- Recherchez des opportunités d'utiliser les formules de somme et de différence.
- Réécrivez les sommes ou les différences de quotients sous forme de quotients uniques.
- Si le processus devient fastidieux, réécrivez l'expression en termes de sinus et de cosinus.
Vérifiez l'identité\(\sin(\alpha+\beta)+\sin(\alpha−\beta)=2\sin \alpha \cos \beta\).
Solution
Nous voyons que le côté gauche de l'équation inclut les sinus de la somme et la différence des angles.
\(\sin(\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta\)
\(\sin(\alpha-\beta)=\sin \alpha \cos \beta-\cos \alpha \sin \beta\)
Nous pouvons les réécrire à l'aide des formules de somme et de différence.
\[\begin{align*} \sin(\alpha+\beta)+\sin(\alpha-\beta)&= \sin \alpha \cos \beta+\cos \alpha \sin \beta+\sin \alpha \cos \beta-\cos \alpha \sin \beta\\[4pt] &= 2\sin \alpha \cos \beta \end{align*}\]
Nous voyons que l'identité est vérifiée.
Vérifiez l'identité suivante.
\(\dfrac{\sin(\alpha−\beta)}{\cos \alpha \cos \beta}=\tan \alpha−\tan \beta\)
Solution
Nous pouvons commencer par réécrire le numérateur sur le côté gauche de l'équation.
\[\begin{align*} \dfrac{\sin(\alpha-\beta)}{\cos \alpha \cos \beta}&= \dfrac{\sin \alpha \cos \beta-\cos \alpha \sin \beta}{\cos \alpha \cos \beta}\\[4pt] &= \dfrac{\sin \alpha \cos \beta}{\cos \alpha \cos \beta}-\dfrac{\cos \alpha \sin \beta}{\cos \alpha \cos \beta} & & \text{Rewrite using a common denominator}\\[4pt] &= \dfrac{\sin \alpha}{\cos \alpha}-\dfrac{\sin \beta}{\cos \beta} & & \text{Cancel}\\[4pt] &= \tan \alpha-\tan \beta & & \text{Rewrite in terms of tangent} \end{align*}\]
Vérifiez l'identité :\(\tan(\pi−\theta)=−\tan \theta\).
- Réponse
-
\[\begin{align*} \tan(\pi-\theta)&= \dfrac{\tan(\pi)-\tan \theta}{1+\tan(\pi)\tan \theta}\\[4pt] &= \dfrac{0-\tan \theta}{1+0\cdot \tan \theta}\\[4pt] &= -\tan \theta \end{align*}\]
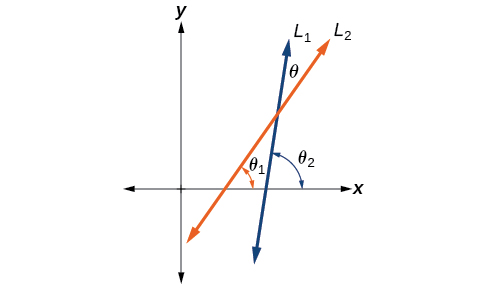
Soient\(L_1\) et\(L_2\) désignent deux lignes qui se croisent non verticales, et\(θ\) notons l'angle aigu entre\(L_1\) et\(L_2\). Voir la figure\(\PageIndex{7}\). Montrez que
\(\tan \theta=\dfrac{m_2-m_1}{1+m_1m_2}\)
où\(m_1\) et\(m_2\) sont\(L_2\) respectivement les pentes de\(L_1\) et. (Conseil : utilisez le fait que\(\tan \theta_1=m_1\) et\(\tan \theta_2=m_2\).)
Solution
En utilisant la formule de différence pour la tangente, ce problème ne semble pas aussi intimidant qu'il le pourrait.
\[\begin{align*} \tan \theta&= \tan(\theta_2-\theta_1)\\[4pt] &= \dfrac{\tan \theta_2-\tan \theta_1}{1+\tan \theta_1 \tan \theta_2}\\[4pt] &= \dfrac{m_2-m_1}{1+m_1m_2} \end{align*}\]
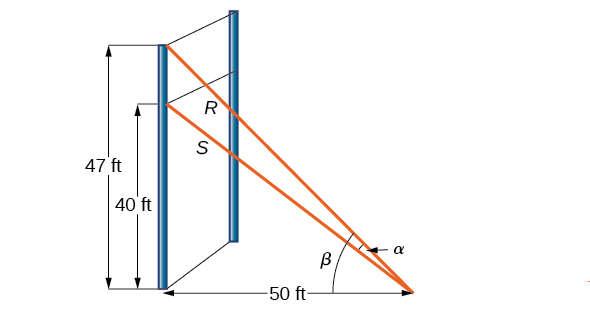
Pour un mur d'escalade, un hauban\(R\) est fixé\(47\) pieds haut sur un poteau vertical. Un autre support supplémentaire est fourni par un autre hauban\(S\) fixé à\(40\) pieds au-dessus du sol sur le même poteau. Si les fils sont fixés aux\(50\) pieds du sol à partir du poteau, trouvez l'angle\(\alpha\) entre les fils. Voir la figure\(\PageIndex{8}\).
Solution
Résumons d'abord les informations que nous pouvons recueillir à partir du diagramme. Comme seuls les côtés adjacents à l'angle droit sont connus, nous pouvons utiliser la fonction tangente. Remarquez que\(\tan \beta=\frac{47}{50}\), et\(\tan(\beta−\alpha)=\frac{40}{50}=\frac{4}{5}\). Nous pouvons ensuite utiliser la formule de différence pour la tangente.
\[\tan(\beta-\alpha) = \dfrac{\tan \beta-\tan \alpha}{1+\tan \beta \tan \alpha}\]
Maintenant, en substituant les valeurs que nous connaissons dans la formule, nous avons :
\ [\ begin {align*} \ dfrac {4} {5} &= \ dfrac {\ tfrac {47} {50} - \ tan \ alpha} {1+ \ tfrac {47} {50} \ tan \ alpha} \ \ [4pt]
4 \ left (1+ \ tfrac {47} {50}} \ tan \ alpha \ right) &= 5 \ left (\ tfrac {47} {50} - \ tan \ alpha \ right) \ end {align*} \]
Utilisez la propriété distributive, puis simplifiez les fonctions.
\ [\ begin {align*} 4 (1) +4 \ gauche (\ tfrac {47} {50} \ droite) \ tan \ alpha &= 5 \ left (\ tfrac {47} {50} \ droite) -5 \ tan \ alpha \ \ [4 points]
4+3,76 \ tan \ alpha&= 4,7-5 \ tan \ alpha \ [4 points]
5 \ tan \ alpha+3,76 \ tan \ alpha&= 0,7 \ \ [4 points]
8,76 \ tan \ alpha&= 0,7 \ \ [4 points]
\ tan \ alpha& \ approx 0,07991 \ \ [4pt]
\ tan^ {-1} (0,07991) & \ approx .079741 \ end {align*} \] Nous pouvons
maintenant calculer l'angle en degrés.
\ [\ begin {align*} \ alpha et \ environ 0,079741 \ left (\ dfrac {180} {\ pi} \ right) \ \ [4 points]
& \ environ 4,57^ {\ circ}
\ end {align*} \]
Analyse
Parfois, lorsqu'une application incluant un triangle droit apparaît, nous pouvons penser que la résolution consiste à appliquer le théorème de Pythagore. C'est peut-être partiellement vrai, mais cela dépend de la nature du problème et des informations fournies.
Accédez à ces ressources en ligne pour obtenir des instructions et des exercices supplémentaires sur les identités de somme et de différence.
- Identités de somme et de différence pour les cosinus
- Identités de somme et de différence pour le sinus
- Identités de somme et de différence pour Tangent
Équations clés
| Formule de somme pour le cosinus | \(\cos(\alpha+\beta)=\cos \alpha \cos \beta−\sin \alpha \sin \beta\) |
| Formule de différence pour le cosinus | \(\cos(\alpha-\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta\) |
| Formule de somme pour le sinus | \(\sin(\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta\) |
| Formule de différence pour le sinus | \(\sin(\alpha-\beta)=\sin \alpha \cos \beta-\cos \alpha \sin \beta\) |
| Formule de somme pour la tangente | \(\tan(\alpha+\beta)=\dfrac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta}\) |
| Formule de différence pour la tangente | \(\cos(\alpha−\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta\) |
| Identités de cofonctions |
\(\sin \theta=\cos\left(\dfrac{\pi}{2}-\theta\right)\) \(\cos \theta=\sin\left(\dfrac{\pi}{2}-\theta\right)\) \(\tan \theta=\cot\left(\dfrac{\pi}{2}-\theta\right)\) \(\cot \theta=\tan\left(\dfrac{\pi}{2}-\theta\right)\) \(\sec \theta=\csc\left(\dfrac{\pi}{2}-\theta\right)\) \(\csc \theta=\sec\left(\dfrac{\pi}{2}-\theta\right)\) |
Concepts clés
- La formule de somme des cosinus indique que le cosinus de la somme de deux angles est égal au produit des cosinus des angles moins le produit des sinus des angles. La formule de différence pour les cosinus indique que le cosinus de la différence de deux angles est égal au produit des cosinus des angles plus le produit des sinus des angles.
- Les formules de somme et de différence peuvent être utilisées pour déterminer les valeurs exactes du sinus, du cosinus ou de la tangente d'un angle. Voir Exemple\(\PageIndex{1}\) et Exemple\(\PageIndex{2}\).
- La formule de somme des sinus indique que le sinus de la somme de deux angles est égal au produit du sinus du premier angle et du cosinus du second angle plus le produit du cosinus du premier angle et du sinus du second angle. La formule de différence pour les sinus indique que le sinus de la différence de deux angles est égal au produit du sinus du premier angle et du cosinus du second angle moins le produit du cosinus du premier angle et du sinus du second angle. Voir l'exemple\(\PageIndex{3}\).
- Les formules de somme et de différence pour le sinus et le cosinus peuvent également être utilisées pour les fonctions trigonométriques inverses. Voir l'exemple\(\PageIndex{4}\).
- La formule de somme de la tangente indique que la tangente de la somme de deux angles est égale à la somme des tangentes des angles divisée par\(1\) moins le produit des tangentes des angles. La formule de différence pour la tangente indique que la tangente de la différence de deux angles est égale à la différence des tangentes des angles divisée par\(1\) plus le produit des tangentes des angles. Voir l'exemple\(\PageIndex{5}\).
- Le théorème de Pythagore ainsi que les formules de somme et de différence peuvent être utilisés pour trouver plusieurs sommes et différences d'angles. Voir l'exemple\(\PageIndex{6}\).
- Les identités de cofonctions s'appliquent à des angles complémentaires et à des paires de fonctions réciproques. Voir l'exemple\(\PageIndex{7}\).
- Les formules de somme et de différence sont utiles pour vérifier les identités. Voir Exemple\(\PageIndex{8}\) et Exemple\(\PageIndex{9}\).
- Les problèmes d'application sont souvent plus faciles à résoudre à l'aide de formules de somme et de différence. Voir Exemple\(\PageIndex{10}\) et Exemple\(\PageIndex{11}\).


