8.2 : Graphiques des autres fonctions trigonométriques

Objectifs d'apprentissage

• Analysez le graphique de\(y=\tan x\).
• Variations graphiques de\(y=\tan x\).
• Analysez les graphes de\(y=\sec x\) et\(y=\csc x\).
• Diagramme des variations de\(y=\sec x\) et\(y=\csc x\).
• Analysez le graphique de\(y=\cot x\).
• Variations graphiques de\(y=\cot x\).

Nous savons que la fonction tangente peut être utilisée pour déterminer des distances, telles que la hauteur d'un bâtiment, d'une montagne ou d'un mât de drapeau. Mais que se passe-t-il si nous voulons mesurer des occurrences répétées de distance ? Imaginez, par exemple, une voiture de police garée à côté d'un entrepôt. La lumière rotative de la voiture de police traversait le mur de l'entrepôt à intervalles réguliers. Si l'entrée est le temps, la sortie serait la distance parcourue par le faisceau de lumière. Le faisceau lumineux répéterait la distance à intervalles réguliers. La fonction tangente peut être utilisée pour approximer cette distance. Des asymptotes seraient nécessaires pour illustrer les cycles répétés lorsque le faisceau est parallèle au mur car, apparemment, le faisceau de lumière pourrait sembler s'étendre à jamais. Le graphique de la fonction tangente illustrerait clairement les intervalles répétés. Dans cette section, nous allons explorer les graphes de la tangente et d'autres fonctions trigonométriques.

Analyse du graphique de\(y =\tan x\)

Nous allons commencer par le graphique de la fonction tangente, en traçant les points comme nous l'avons fait pour les fonctions sinus et cosinus. Rappelons que

\[\tan \, x=\dfrac{\sin \, x}{\cos \, x}\]

La période de la fonction tangente est\(\pi\) due au fait que le graphe se répète à des intervalles\(k\pi\) où\(k\) est une constante. Si nous tracons la fonction tangente sur\(−\frac{\pi}{2}\)\(\frac{\pi}{2}\), nous pouvons voir le comportement du graphe sur un cycle complet. Si nous examinons un intervalle plus grand, nous verrons que les caractéristiques du graphique se répètent.

Nous pouvons déterminer si la tangente est une fonction paire ou impaire en utilisant la définition de tangente.

\[\begin{align*} \tan(-x)&= \dfrac{\sin(-x)}{\cos(-x)} \qquad \text{Definition of tangent}\\ &= \dfrac{-\sin \, x}{\cos \, x} \qquad \text{Sine is an odd function, cosine is even}\\ &= -\dfrac{\sin \, x}{\cos \, x} \qquad \text{The quotient of an odd and an even function is odd}\\ &= -\tan \, x \qquad \text{Definition of tangent} \end{align*}\]

Par conséquent, la tangente est une fonction étrange. Nous pouvons analyser plus en détail le comportement graphique de la fonction tangente en examinant les valeurs de certains angles spéciaux, comme indiqué dans le tableau\(\PageIndex{1}\).

Tableau\(\PageIndex{1}\)

\(x\)	\(−\dfrac{\pi}{2}\)	\(−\dfrac{\pi}{3}\)	\(−\dfrac{\pi}{4}\)	\(−\dfrac{\pi}{6}\)	0	\(\dfrac{\pi}{6}\)	\(\dfrac{\pi}{4}\)	\(\dfrac{\pi}{3}\)	\(\dfrac{\pi}{2}\)
\(\tan x\)	indéfini	\(-\sqrt{3}\)	\(–1\)	\(-\dfrac{\sqrt{3}}{3}\)	0	\(\dfrac{\sqrt{3}}{3}\)	1	\(\sqrt{3}\)	indéfini

Ces points nous aideront à dessiner notre graphe, mais nous devons déterminer comment le graphe se comporte lorsqu'il n'est pas défini. Si nous examinons de plus près les valeurs à\(\frac{\pi}{3}<x<\frac{\pi}{2}\) quel moment, nous pouvons utiliser un tableau pour rechercher une tendance. Parce que\(\frac{\pi}{3}≈1.05\) et\(\frac{\pi}{2}≈1.57\), nous évaluerons les mesures\(x\) en radian\(1.05<x<1.57\) comme indiqué dans le tableau\(\PageIndex{2}\).

Tableau\(\PageIndex{2}\)

\(x\)	1.3	1,5	1,55	1,56
\(\tan x\)	3.6	14.1	48,1	92,6

À mesure que l'on\(x\) approche\(\dfrac{\pi}{2}\), les sorties de la fonction s'agrandissent de plus en plus. Comme\(y=\tan \, x\) il s'agit d'une fonction étrange, nous voyons la table correspondante de valeurs négatives dans la table\(\PageIndex{3}\).

Tableau\(\PageIndex{3}\)

\(x\)	−1,3	−1,5	−1,55	−1,56
\(\tan x\)	−3,6	−14,1	−48,1	−92,6

Nous pouvons constater qu'à mesure que l'on\(x\) approche\(−\frac{\pi}{2}\), les résultats diminuent de plus en plus. N'oubliez pas qu'il existe certaines valeurs\(x\) pour lesquelles\(\cos \, x=0\). Par exemple,\(\cos \left (\frac{\pi}{2} \right)=0\) et\(\cos \left (\frac{3\pi}{2} \right )=0\). À ces valeurs, la fonction tangente n'est pas définie, de sorte que le graphe de\(y=\tan \, x\) présente des discontinuités à\(x=\frac{\pi}{2}\) et\(\frac{3\pi}{2}\). À ces valeurs, le graphe de la tangente présente des asymptotes verticales. La figure\(\PageIndex{1}\) représente le graphique de\(y=\tan \, x\). La tangente est positive de\(0\) à\(\frac{\pi}{2}\) et de\(\pi\) à\(\frac{3\pi}{2}\), correspondant aux quadrants I et III du cercle unitaire.

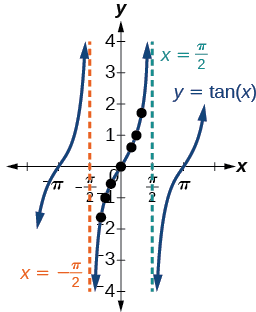
Figure\(\PageIndex{1}\) : Graphique de la fonction tangente

Représentation graphique des variations de\(y = \tan \, x\)

Comme pour les fonctions sinus et cosinus, la fonction tangente peut être décrite par une équation générale.

\[y=A\tan(Bx) \nonumber\]

Nous pouvons identifier les étirements et les compressions horizontaux et verticaux à l'aide des valeurs de\(A\) et\(B\). L'étirement horizontal peut généralement être déterminé à partir de la période du graphique. Dans le cas des graphes tangents, il est souvent nécessaire de déterminer un étirement vertical à l'aide d'un point du graphique.

Comme il n'existe aucune valeur maximale ou minimale pour une fonction tangente, le terme amplitude ne peut pas être interprété comme il l'est pour les fonctions sinus et cosinus. Nous utiliserons plutôt l'expression « facteur d'étirement/de compression » pour faire référence à la constante\(A\).

CARACTÉRISTIQUES DU GRAPHIQUE DE\(Y = A \tan(Bx)\)

• Le facteur d'étirement est\(|A|\).
• La période est\(P=\dfrac{\pi}{|B|}\).
• Le domaine est composé uniquement de nombres réels\(x\),\(x≠\dfrac{\pi}{2| B |}+\dfrac{π}{| B |}k\) tels qu'ils\(k\) sont des nombres entiers.
• La gamme est\((−\infty,\infty)\).
• Les asymptotes apparaissent à l'\(x=\dfrac{\pi}{2| B |}+\dfrac{π}{| B |}k\)endroit où\(k\) est un entier.
• \(y=A\tan(Bx)\)est une fonction étrange.

Représentation graphique d'une période d'une fonction tangente étirée ou compressée

Nous pouvons utiliser ce que nous savons sur les propriétés de la fonction tangente pour esquisser rapidement un graphique de toute fonction tangente étirée et/ou compressée de la forme\(f(x)=A\tan(Bx)\). Nous nous concentrons sur une seule période de la fonction, y compris l'origine, car la propriété périodique nous permet d'étendre le graphe au reste du domaine de la fonction si nous le souhaitons. Notre domaine limité est alors l'intervalle\(\left (−\dfrac{P}{2},\dfrac{P}{2} \right )\) et le graphe présente des asymptotes verticales à l'\(\pm \dfrac{P}{2}\)endroit où\(P=\dfrac{\pi}{B}\). Sur\(\left (−\dfrac{\pi}{2},\dfrac{\pi}{2} \right )\), le graphique remontera de l'asymptote gauche à\(x=−\dfrac{\pi}{2}\), traversera l'origine et continuera à augmenter à mesure qu'il s'approche de l'asymptote droite à\(x=\dfrac{\pi}{2}\). Pour que la fonction s'approche des asymptotes au bon rythme, nous devons également définir l'échelle verticale en évaluant réellement la fonction pour au moins un point que le graphe traversera. Par exemple, nous pouvons utiliser

\[f \left (\dfrac{P}{4} \right )=A\tan \left (B\dfrac{P}{4} \right )=A\tan \left (B\dfrac{\pi}{4B} \right )=A \nonumber\]

parce que\(\tan \left (\dfrac{\pi}{4} \right )=1\).

Comment : étant donné la fonction\(f(x)=A \tan(Bx)\), graph one period.

1. Identifiez le facteur d'étirement,\(| A |\).
2. Identifiez B et déterminez la période,\(P=\dfrac{\pi}{| B |}\).
3. Dessinez des asymptotes verticales à\(x=−\dfrac{P}{2}\) et\(x=\dfrac{P}{2}\).
4. Pour\(A>0\), le graphique se rapproche de l'asymptote gauche à des valeurs de sortie négatives et de l'asymptote droite à des valeurs de sortie positives (inverse pour\(A<0\)).
5. Tracez les points de référence aux points\(\left (\dfrac{P}{4},A \right )\)\((0,0)\)\(\left (−\dfrac{P}{4},−A \right )\), et et dessinez le graphique à travers ces points.

Exemple\(\PageIndex{1}\): Sketching a Compressed Tangent

Esquissez un graphique d'une période de la fonction\(y=0.5\tan \left (\dfrac{\pi}{2}x \right )\).

Solution

Tout d'abord, nous identifions\(A\) et\(B\).

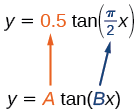
Figurine\(\PageIndex{2}\)

Parce que\(A=0.5\) et\(B=\dfrac{\pi}{2}\), nous pouvons trouver le facteur d'étirement/compression et la période. La période est\(\dfrac{\pi}{\dfrac{\pi}{2}}=2\), donc les asymptotes sont à\(x=±1\). À un quart de la période d'origine, nous avons

\[\begin{align*} f(0.5)&= 0.5\tan \left (\dfrac{0.5\pi}{2} \right )\\ &= 0.5\tan \left (\dfrac{\pi}{4} \right )\\ &= 0.5 \end{align*}\]

Cela signifie que la courbe doit passer par les points\((0.5,0.5)\)\((0,0)\), et\((−0.5,−0.5)\). Le seul point d'inflexion se trouve à l'origine. La figure\(\PageIndex{3}\) montre le graphique d'une période de la fonction.

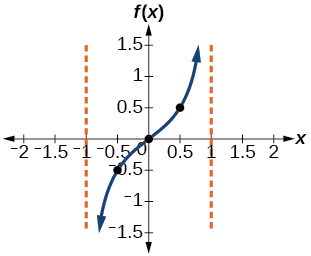
Figurine\(\PageIndex{3}\)

Exercice\(\PageIndex{1}\)

Esquissez un graphique de\(f(x)=3\tan \left (\dfrac{\pi}{6}x \right )\).

Réponse

Figurine\(\PageIndex{4}\)

Représentation graphique d'une période d'une fonction tangente décalée

Maintenant que nous pouvons représenter graphiquement une fonction tangente étirée ou compressée, nous allons ajouter un décalage vertical et/ou horizontal (ou de phase). Dans ce cas, on ajoute\(C\) et\(D\) à la forme générale de la fonction tangente.

\[f(x)=A\tan(Bx−C)+D \nonumber\]

Le graphe d'une fonction tangente transformée est différent de la fonction tangente de base\(\tan x\) à plusieurs égards :

CARACTÉRISTIQUES DU GRAPHIQUE DE\(Y = A\tan(Bx−C)+D\)

• Le facteur d'étirement est\(| A |\).
• La période est\(\dfrac{\pi}{| B |}\).
• Le domaine est\(x≠\dfrac{C}{B}+\dfrac{\pi}{| B |}k\), où\(k\) est un entier.
• La gamme est\((−∞,−| A |]∪[| A |,∞)\).
• Les asymptotes verticales apparaissent à\(x=\dfrac{C}{B}+\dfrac{\pi}{| B |}k\), où\(k\) est un entier impair.
• Il n'y a pas d'amplitude.
• \(y=A \tan(Bx)\)est une fonction impaire car c'est le quotient de fonctions paires et impaires (sin et cosinus en perspective).

Comment : Compte tenu de la fonction\(y=A\tan(Bx−C)+D\), sketch the graph of one period.

1. Exprime la fonction donnée dans le formulaire\(y=A\tan(Bx−C)+D\).
2. Identifiez le facteur d'étirement/de compression,\(| A |\).
3. Identifiez\(B\) et déterminez la période,\(P=\dfrac{\pi}{|B|}\).
4. Identifier\(C\) et déterminer le décalage de phase,\(\dfrac{C}{B}\).
5. Tracez le graphique des\(y=A\tan(Bx)\) décalages vers la droite\(\dfrac{C}{B}\) et de haut en haut\(D\).
6. Esquissez les asymptotes verticales qui se produisent à\(x=\dfrac{C}{B}+\dfrac{\pi}{2| B |}k\), où\(k\) est un entier impair.
7. Tracez trois points de référence et tracez le graphique à travers ces points.

Exemple\(\PageIndex{2}\): Graphing One Period of a Shifted Tangent Function

Tracez une période de la fonction\(y=−2\tan(\pi x+\pi)−1\).

Solution

• Étape 1. La fonction est déjà écrite dans le formulaire\(y=A\tan(Bx−C)+D\).
• Étape 2. \(A=−2 \), donc le facteur d'étirement est\(|A|=2\).
• Étape 3. \(B= \ pi \), donc la période est\(P=\dfrac{\pi}{| B |}=\dfrac{\pi}{pi}=1\).
• Étape 4. \(C=− \ pi \), donc le décalage de phase est\(CB=\dfrac{−\pi}{\pi}=−1\).
• Étape 5 à 7. Les asymptotes sont à\(x=−\dfrac{3}{2}\) et\(x=−\dfrac{1}{2}\) et les trois points de référence recommandés sont\((−1.25,1)\)\((−1,−1)\), et\((−0.75,−3)\). Le graphique est illustré dans la figure\(\PageIndex{5}\).

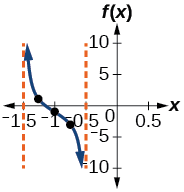
Figurine\(\PageIndex{5}\)

Analyse

Notez qu'il s'agit d'une fonction décroissante car\(A<0\).

Exercice\(\PageIndex{2}\)

En quoi le graphique de l'exemple serait-il\(\PageIndex{2}\) différent si nous le faisions à la\(A=2\) place de\(−2\) ?

Réponse

Elle se refléterait à travers la ligne de\(y=−1\) démarcation et deviendrait une fonction croissante.

Mode d'emploi : À partir du graphe d'une fonction tangente, identifiez les étirements horizontaux et verticaux.

1. Détermine la période\(P\) à partir de l'espacement entre les asymptotes verticales ou les interceptions en x successives.
2. Écrivez\(f(x)=A\tan \left (\dfrac{\pi}{P}x \right )\).
3. Déterminez un point approprié\((x,f(x))\) sur le graphique donné et utilisez-le pour le déterminer\(A\).

Exemple\(\PageIndex{3}\): Identifying the Graph of a Stretched Tangent

Trouvez une formule pour la fonction illustrée dans la figure\(\PageIndex{6}\).

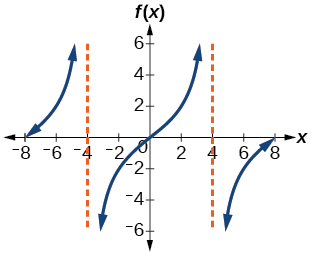
Figure\(\PageIndex{6}\) : Une fonction tangente étirée

Solution

Le graphe a la forme d'une fonction tangente.

• Étape 1. Un cycle s'étend de\(–4\) à\(4\), donc la période est\(P=8\). Depuis\(P=\dfrac{\pi}{| B |}\), nous l'avons fait\(B=\dfrac{π}{P}=\dfrac{\pi}{8}\).
• Étape 2. L'équation doit avoir la forme\(f(x)=A\tan \left (\dfrac{\pi}{8}x \right )\).
• Étape 3. Pour trouver l'étirement vertical\(A\), on peut utiliser le point\((2,2)\). \[\begin{align*} 2&=A\tan \left (\dfrac{\pi}{8}\cdot 2 \right )\\ &=A\tan \left (\dfrac{\pi}{4} \right ) \end{align*}\]

Parce que\(\tan \left (\dfrac{\pi}{4} \right )=1\),\(A=2\).

Cette fonction aurait une formule\(f(x)=2\tan \left (\dfrac{\pi}{8}x \right )\).

Exercice\(\PageIndex{3}\)

Trouvez une formule pour la fonction dans la figure\(\PageIndex{7}\).

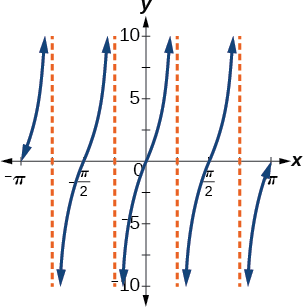
Figurine\(\PageIndex{7}\)

Réponse

\(g(x)=4\tan(2x)\)

Analyse des graphes de\(y = \sec x\) et\(y = \csc x\)

La sécante était définie par l'identité réciproque\(sec \, x=\dfrac{1}{\cos x}\). Notez que la fonction n'est pas définie lorsque le cosinus est\(0\), ce qui entraîne des asymptotes verticales à\(\dfrac{\pi}{2}\),\(\dfrac{3\pi}{2}\) etc. Comme le cosinus n'est jamais supérieur\(1\) à la valeur absolue, la sécante, étant l'inverse, ne sera jamais inférieure\(1\) à la valeur absolue.

Nous pouvons représenter graphiquement en\(y=\sec x\) observant le graphe de la fonction cosinus, car ces deux fonctions sont réciproques. Voir la figure\(\PageIndex{8}\). Le graphique du cosinus est représenté par une onde orange pointillée afin que nous puissions voir la relation. Lorsque le graphe de la fonction cosinus diminue, le graphe de la fonction sécante augmente. Lorsque le graphe de la fonction cosinus augmente, le graphe de la fonction sécante diminue. Lorsque la fonction cosinus est nulle, la sécante n'est pas définie.

Le graphe sécant possède des asymptotes verticales à chaque valeur\(x\) où le graphe en cosinus croise l'\(x\)axe ; nous les montrons dans le graphique ci-dessous avec des lignes verticales pointillées, mais nous n'afficherons pas toutes les asymptotes de manière explicite sur tous les graphes ultérieurs impliquant la sécante et la cosécante.

Notez que, comme le cosinus est une fonction paire, la sécante est également une fonction paire. C'est-à-dire,\(\sec(−x)=\sec x\).

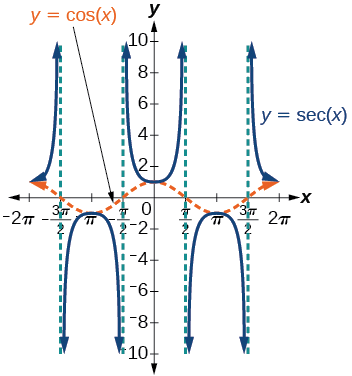
Figure\(\PageIndex{8}\) : Graphique de la fonction sécante,\(f(x)=\sec x=\dfrac{1}{\cos x}\)

Comme nous l'avons fait pour la fonction tangente, nous appellerons à nouveau la constante\(| A |\) le facteur d'étirement, et non l'amplitude.

CARACTÉRISTIQUES DU GRAPHIQUE DE\(Y = A \sec(Bx)\)

• Le facteur d'étirement est\(| A |\).
• La période est\(\dfrac{2\pi}{| B |}\).
• Le domaine est\(x≠\dfrac{\pi}{2| B |}k\), où\(k\) est un entier impair.
• La gamme est\((−∞,−|A|]∪[|A|,∞)\).
• Les asymptotes verticales apparaissent à\(x=\dfrac{\pi}{2| B |}k\), où\(k\) est un entier impair.
• Il n'y a pas d'amplitude.
• \(y=A\sec(Bx)\)est une fonction paire car le cosinus est une fonction paire.

Comme la sécante, la cosécante est définie par l'identité réciproque\(\csc x=\dfrac{1}{\sin x}\). Notez que la fonction n'est pas définie lorsque le sinus est\(0\), ce qui conduit à une asymptote verticale sur le graphe à\(0\)\(\pi\), etc. Comme le sinus n'est jamais supérieur\(1\) à la valeur absolue, la cosécante, étant l'inverse, ne sera jamais inférieure\(1\) à la valeur absolue.

Nous pouvons représenter graphiquement\(y=\csc x\) en observant le graphe de la fonction sinusoïdale, car ces deux fonctions sont réciproques l'une de l'autre. Voir la figure\(\PageIndex{7}\). Le graphique du sinus est représenté par une onde orange pointillée afin que nous puissions voir la relation. Lorsque le graphe de la fonction sinusoïdale diminue, le graphe de la fonction cosécante augmente. Lorsque le graphe de la fonction sinusoïdale augmente, le graphe de la fonction cosécante diminue.

Le graphe cosécant présente des asymptotes verticales à chaque valeur de l'\(x\)intersection du graphe sinusoïdal avec l'\(x\)axe des -; nous les montrons dans le graphique ci-dessous avec des lignes verticales pointillées.

Notez que, puisque le sinus est une fonction impaire, la fonction cosécante est également une fonction impaire. C'est-à-dire,\(\csc(−x)=−\csc x\).

Le graphique de la cosécante, qui est illustré à la figure\(\PageIndex{9}\), est similaire au graphique de la sécante.

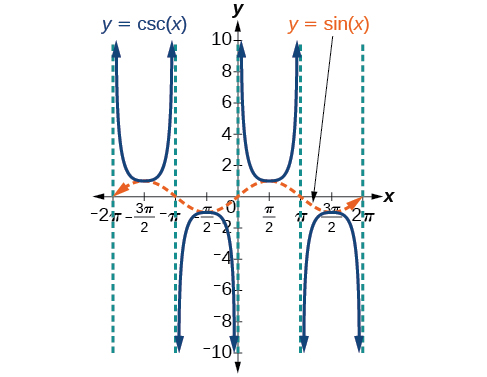
Figure\(\PageIndex{9}\) : Le graphique de la fonction cosécante,\(f(x)=\csc x=\frac{1}{\sin x}\)

CARACTÉRISTIQUES DU GRAPHIQUE DE\(Y = A \csc(Bx)\)

• Le facteur d'étirement est\(| A |\).
• La période est\(\dfrac{2\pi}{|B|}\).
• Le domaine est\(x≠\dfrac{\pi}{|B|}k\), où\(k\) est un entier.
• La gamme est\((−∞,−|A|]∪[|A|,∞)\).
• Les asymptotes apparaissent à\(x=\dfrac{\pi}{| B |}k\), où\(k\) est un entier.
• \(y=A\csc(Bx)\)est une fonction étrange car le sinus est une fonction étrange.

Représentation graphique des variations de\(y = \sec x\) et\(y= \csc x\)

Pour les versions décalées, compressées et/ou étirées des fonctions sécantes et cosécantes, nous pouvons suivre des méthodes similaires à celles que nous avons utilisées pour la tangente et la cotangente. C'est-à-dire que nous localisons les asymptotes verticales et évaluons également les fonctions de quelques points (en particulier les extrêmes locaux). Si nous voulons représenter graphiquement une seule période, nous pouvons choisir l'intervalle de la période de plusieurs manières. La procédure pour la sécante est très similaire, car l'identité de la cofonction signifie que le graphe sécant est le même que le graphe cosécant décalé d'une demi-période vers la gauche. Les décalages verticaux et de phase peuvent être appliqués à la fonction cosécante de la même manière que pour la fonction sécante et les autres fonctions. Les équations deviennent les suivantes.

\[y=A\sec(Bx−C)+D\]

\[y=A\csc(Bx−C)+D\]

CARACTÉRISTIQUES DU GRAPHIQUE DE\(Y = A\sec(Bx−C)+D\)

• Le facteur d'étirement est\(|A|\).
• La période est\(\dfrac{2\pi}{|B|}\).
• Le domaine est\(x≠\dfrac{C}{B}+\dfrac{\pi}{2| B |}k\), où\(k\) est un entier impair.
• La gamme est\((−∞,−|A|]∪[|A|,∞)\).
• Les asymptotes verticales apparaissent à\(x=\dfrac{C}{B}+\dfrac{π}{2| B |}k\), où\(k\) est un entier impair.
• Il n'y a pas d'amplitude.
• \(y=A\sec(Bx)\)est une fonction paire car le cosinus est une fonction paire.

CARACTÉRISTIQUES DU GRAPHIQUE DE\(Y = A\csc(Bx−C)+D\)

1. Le facteur d'étirement est\(|A|\).
2. La période est\(\dfrac{2\pi}{|B|}\).
3. Le domaine est\(x≠\dfrac{C}{B}+\dfrac{\pi}{2| B |}k\), où\(k\) est un entier.
4. La gamme est\((−∞,−|A|]∪[|A|,∞)\).
5. Les asymptotes verticales apparaissent à\(x=\dfrac{C}{B}+\dfrac{\pi}{|B|}k\), où\(k\) est un entier.
6. Il n'y a pas d'amplitude.
7. \(y=A\csc(Bx)\)est une fonction étrange car le sinus est une fonction étrange.

HOWTO : Compte tenu d'une fonction du formulaire\(y=A\sec(Bx)\), graph one period

1. Exprime la fonction donnée dans le formulaire\(y=A\sec(Bx)\).
2. Identifiez le facteur d'étirement/de compression,\(|A|\).
3. Identifiez\(B\) et déterminez la période,\(P=\dfrac{2\pi}{| B |}\).
4. Esquissez le graphique de\(y=A\cos(Bx)\).
5. Utilisez la relation réciproque entre\(y=\cos \, x\) et\(y=\sec \, x\) pour dessiner le graphique de\(y=A\sec(Bx)\).
6. Esquissez les asymptotes.
7. Tracez deux points de référence quelconques et tracez le graphique à travers ces points.

Exemple\(\PageIndex{4}\): Graphing a Variation of the Secant Function

Tracez une période de\(f(x)=2.5\sec(0.4x)\).

Solution

• Étape 1. La fonction donnée est déjà écrite sous la forme générale,\(y=A\sec(Bx)\).
• Étape 2. \(A=2.5\)donc le facteur d'étirement est\(2.5\).
• Étape 3. \(B=0.4\)donc\(P=\dfrac{2\pi}{0.4}=5\pi\). La période est exprimée en\(5\pi\) unités.
• Étape 4. Esquissez le graphe de la fonction\(g(x)=2.5\cos(0.4x)\).
• Étape 5. Utilisez la relation réciproque entre les fonctions cosinus et sécante pour dessiner la fonction cosécante.
• Étapes 6 à 7. Esquissez deux asymptotes à\(x=1.25\pi\) et\(x=3.75\pi\). Nous pouvons utiliser deux points de référence, le minimum local à\((0,2.5)\) et le maximum local à\((2.5\pi,−2.5)\). La figure\(\PageIndex{10}\) montre le graphique.

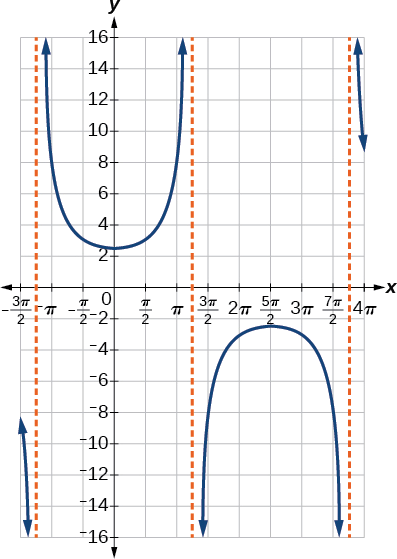
Figurine\(\PageIndex{10}\)

Exercice\(\PageIndex{4}\)

Tracez une période de\(f(x)=−2.5\sec(0.4x)\).

Réponse

Il s'agit d'un reflet vertical du graphique précédent car il\(A\) est négatif.

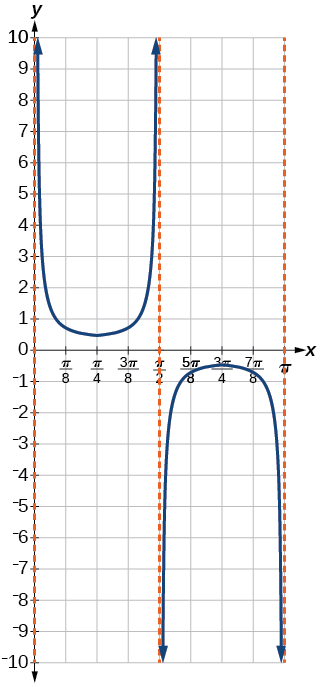
Figurine\(\PageIndex{11}\)

Q&R : Le décalage vertical et l'étirement/la compression affectent-ils l'amplitude de la sécante ?

Oui. La gamme de\(f(x)=A\sec(Bx−C)+D\) est\((−∞,−|A|+D]∪[|A|+D,∞)\).

Comment : Compte tenu d'une fonction du formulaire\(f(x)=A\sec(Bx−C)+D\), graph one period.

1. Exprime la fonction donnée dans le formulaire\(y=A \sec(Bx−C)+D\).
2. Identifiez le facteur d'étirement/de compression,\(| A |\).
3. Identifiez\(B\) et déterminez la période,\(\dfrac{2\pi}{|B|}\).
4. Identifier\(C\) et déterminer le décalage de phase,\(\dfrac{C}{B}\).
5. Tracez le graphique de\(y=A \sec(Bx)\). mais déplacez-le vers la droite de plus en\(\dfrac{C}{B}\) plus vers le haut\(D\).
6. Esquissez les asymptotes verticales qui se produisent à\(x=\dfrac{C}{B}+\dfrac{\pi}{2| B |}k\), où\(k\) est un entier impair.

Exemple\(\PageIndex{5}\): Graphing a Variation of the Secant Function

Tracez une période de\(y=4\sec \left (\dfrac{\pi}{3x}−\dfrac{\pi}{2} \right )+1\).

Solution

• Étape 1. Exprime la fonction donnée dans le formulaire\(y=4\sec \left (\dfrac{\pi}{3x}−\dfrac{\pi}{2} \right )+1\).
• Étape 2. Le facteur d'étirement/compression est de\(| A |=4\).
• Étape 3. La période est

\[\begin{align*} \dfrac{2\pi}{|B|}&= \dfrac{2\pi}{\dfrac{\pi}{3}}\\ &= 2\pi \cdot \dfrac{3}{\pi}\\ &= 6 \end{align*}\]

• Étape 4. Le décalage de phase est

\[\begin{align*} \dfrac{C}{B}&= \dfrac{\dfrac{\pi}{2}}{\dfrac{\pi}{3}}\\ &= \dfrac{\pi}{2}\cdot \dfrac{3}{\pi}\\ &= 1.5 \end{align*}\]

• Étape 5. Dessinez le graphique de\(y=A\sec(Bx)\), mais déplacez-le vers la droite\(\dfrac{C}{B}=1.5\) de plus en plus\(D=6\).
• Étape 6. Esquissez les asymptotes verticales, qui se produisent à\(x=0\)\(x=3\), et\(x=6\). Il y a un minimum local\((1.5,5)\) et un maximum local à\((4.5,−3)\). La figure\(\PageIndex{12}\) montre le graphique.

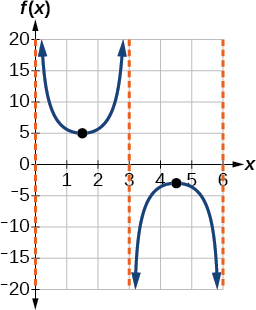
Figurine\(\PageIndex{12}\)

Exercice\(\PageIndex{5}\)

Tracez une période de\(f(x)=−6\sec(4x+2)−8\).

Réponse

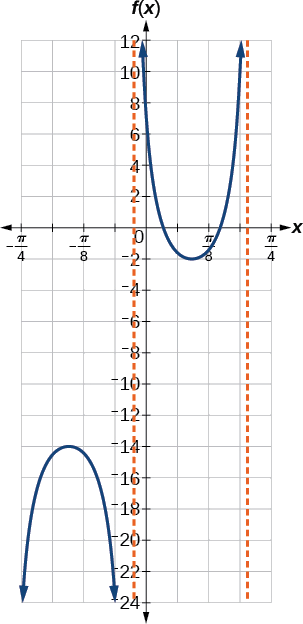
Figurine\(\PageIndex{13}\)

Q&R : Le domaine de\(\csc \, x\) was given to be all \(x\) such that \(x≠k\pi\) for any integer \(k\). Would the domain of \(y=A\csc(Bx−C)+D\) be \(x≠\dfrac{C+k\pi}{B}\)?

Oui. Les points exclus du domaine suivent les asymptotes verticales. Leurs emplacements indiquent le décalage horizontal et la compression ou l'expansion qu'implique la transformation vers l'entrée de la fonction d'origine.

Comment : Compte tenu d'une fonction du formulaire\(y=A\csc(Bx)\), graph one period.

1. Exprime la fonction donnée dans le formulaire\(y=A\csc(Bx)\).
2. \(|A|\).
3. Identifiez\(B\) et déterminez la période,\(P=\dfrac{2\pi}{| B |}\).
4. Dessine le graphique de\(y=A\sin(Bx)\).
5. Utilisez la relation réciproque entre\(y=sin \, x\) et\(y=\csc \, x\) pour dessiner le graphique de\(y=A\csc(Bx)\).
6. Esquissez les asymptotes.
7. Tracez deux points de référence quelconques et tracez le graphique à travers ces points.

Exemple\(\PageIndex{6}\): Graphing a Variation of the Cosecant Function

Tracez une période de\(f(x)=−3\csc(4x)\).

Solution

• Étape 1. La fonction donnée est déjà écrite sous la forme générale,\(y=A\csc(Bx)\).
• Étape 2. \(| A |=| −3 |=3\), donc le facteur d'étirement est\(3\).
• Étape 3. \(B=4\), donc\(P=\dfrac{2\pi}{4}=\dfrac{\pi}{2}\). La période est exprimée en\(\dfrac{\pi}{2}\) unités.
• Étape 4. Esquissez le graphe de la fonction\(g(x)=−3\sin(4x)\).
• Étape 5. Utilisez la relation réciproque entre les fonctions sinusoïdale et cosécante pour dessiner la fonction cosécante.
• Étapes 6 à 7. Esquissez trois asymptotes à\(x=0\)\(x=\dfrac{\pi}{4}\), et\(x=\dfrac{\pi}{2}\). Nous pouvons utiliser deux points de référence, le maximum local à\(\left (\dfrac{\pi}{8},−3 \right )\) et le minimum local à\(\left (\dfrac{3\pi}{8},3 \right )\). La figure\(\PageIndex{14}\) montre le graphique.

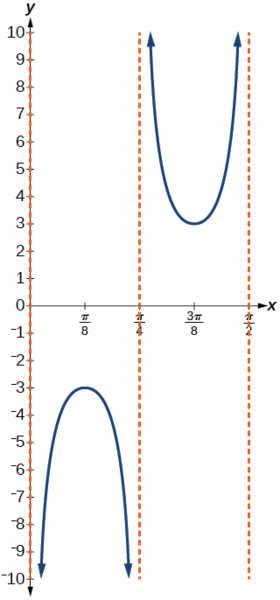
Figurine\(\PageIndex{14}\)

Exercice\(\PageIndex{6}\)

Tracez une période de\(f(x)=0.5\csc(2x)\).

Réponse

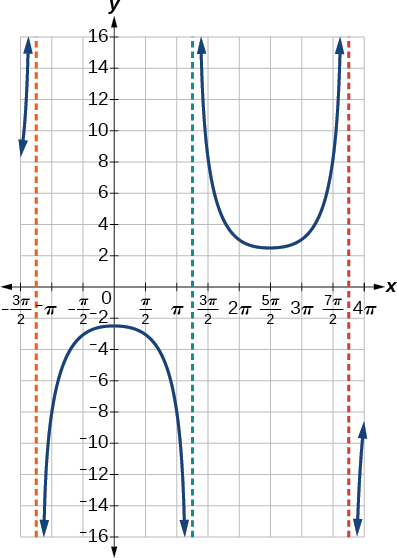
Figurine\(\PageIndex{15}\)

Comment : Compte tenu d'une fonction du formulaire\(f(x)=A \csc(Bx−C)+D\), graph one period

1. Exprime la fonction donnée dans le formulaire\(y=A\csc(Bx−C)+D\).
2. Identifiez le facteur d'étirement/de compression,\(|A|\).
3. Identifiez\(B\) et déterminez la période,\(\dfrac{2\pi}{| B |}\).
4. Identifier\(C\) et déterminer le décalage de phase,\(\dfrac{C}{B}\).
5. Dessinez le graphique de\(y=A\csc(Bx)\) mais déplacez-le vers la droite de plus en plus vers le haut\(D\).
6. Esquissez les asymptotes verticales qui se produisent à\(x=\dfrac{C}{B}+\dfrac{\pi}{| B |}k\), où\(k\) est un entier.

Exemple\(\PageIndex{7}\): Graphing a Vertically Stretched, Horizontally Compressed, and Vertically Shifted Cosecant

Esquissez un graphique de\(y=2\csc \left (\dfrac{\pi}{2}x \right )+1\). Quels sont le domaine et l'étendue de cette fonction ?

Solution

• Étape 1. Exprime la fonction donnée dans le formulaire\(y=2\csc \left (\dfrac{\pi}{2}x \right )+1\).
• Étape 2. Identifiez le facteur d'étirement/de compression,\(| A |=2\).
• Étape 3. La période est\(\dfrac{2\pi}{| B |}=\dfrac{2\pi}{\dfrac{\pi}{2}}=2\pi⋅\dfrac{2}{\pi}=4\).
• Étape 4. Le décalage de phase est\(\dfrac{0}{\dfrac{\pi}{2}}=0\).
• Étape 5. Dessinez le graphique de\(y=A\csc(Bx)\) mais déplacez-le vers le haut\(D=1\).
• Étape 6. Esquissez les asymptotes verticales qui se produisent à\(x=0\),\(x=2\),\(x=4\).

Le graphique de cette fonction est illustré dans la figure\(\PageIndex{16}\).

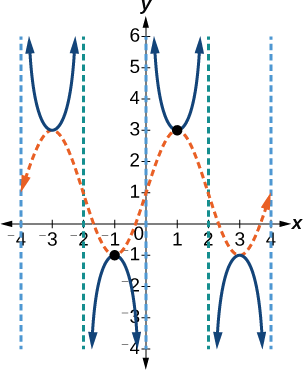
Figure\(\PageIndex{16}\) : Une fonction cosécante transformée

Analyse

Les asymptotes verticales affichées sur le graphique marquent une période de la fonction, et les extrêmes locaux de cet intervalle sont représentés par des points. Remarquez comment le graphe de la cosécante transformée est lié au graphe de\(f(x)=2\sin \left (\frac{\pi}{2}x \right )+1\), représenté par l'onde pointillée orange.

Exercice\(\PageIndex{7}\)

Sur la base du graphique\(f(x)=2\cos \left (\frac{\pi}{2}x \right )+1\) illustré à la figure\(\PageIndex{17}\), esquissez le graphique\(g(x)=2\sec \left (\dfrac{\pi}{2}x \right )+1\) sur les mêmes axes.

Figurine\(\PageIndex{17}\)

Réponse

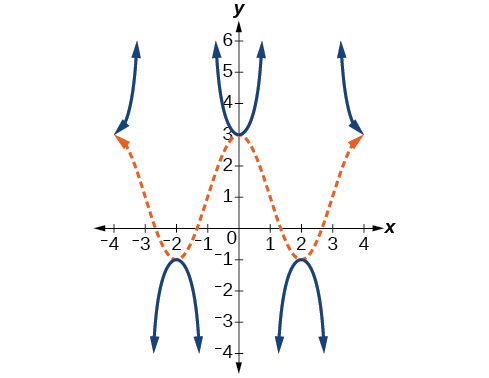
Figurine\(\PageIndex{18}\)

Analyse du graphique de\(y = \cot x\)

La dernière fonction trigonométrique que nous devons explorer est la cotangente. La cotangente est définie par l'identité réciproque\(cot \, x=\dfrac{1}{\tan x}\). Notez que la fonction n'est pas définie lorsque la fonction tangente l'est\(0\), ce qui entraîne une asymptote verticale dans le graphe à\(0\)\(\pi\), etc. Comme la sortie de la fonction tangente est constituée uniquement de nombres réels, la sortie de la fonction cotangente est également constituée de nombres réels.

Nous pouvons représenter graphiquement en\(y=\cot x\) observant le graphe de la fonction tangente, car ces deux fonctions sont réciproques l'une de l'autre. Voir la figure\(\PageIndex{19}\). Lorsque le graphe de la fonction tangente diminue, le graphe de la fonction cotangente augmente. Lorsque le graphe de la fonction tangente augmente, le graphe de la fonction cotangente diminue.

Le graphe cotangent présente des asymptotes verticales à chaque valeur d'\(x\)où\(\tan x=0\) ; nous les montrons dans le graphique ci-dessous avec des lignes pointillées. Puisque la cotangente est l'inverse de la tangente,\(\cot x\) possède des asymptotes verticales à toutes les valeurs d'\(x\)où\(\tan x=0\), et\(\cot x=0\) à toutes les valeurs\(x\) où\(\tan x\) a ses asymptotes verticales.

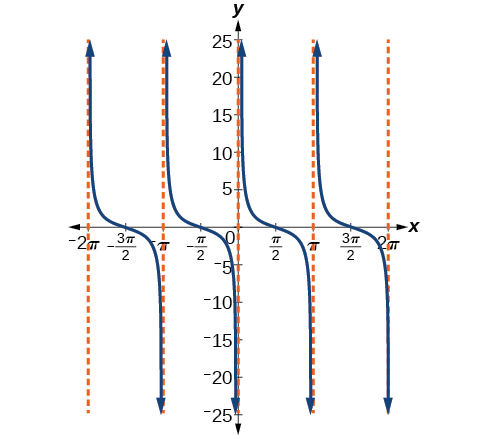
Figure\(\PageIndex{19}\) : La fonction cotangente

CARACTÉRISTIQUES DU GRAPHIQUE DE\(Y = A \cot(BX)\)

• Le facteur d'étirement est\(|A|\).
• La période est\(P=\dfrac{\pi}{|B|}\).
• Le domaine est\(x≠\dfrac{\pi}{|B|}k\), où\(k\) est un entier.
• La gamme est\((−∞,∞)\).
• Les asymptotes apparaissent à\(x=\dfrac{\pi}{| B |}k\), où\(k\) est un entier.
• \(y=A\cot(Bx)\)est une fonction étrange.

Représentation graphique des variations de\(y =\cot x\)

Nous pouvons transformer le graphe de la cotangente de la même manière que nous l'avons fait pour la tangente. L'équation devient la suivante.

\[y=A\cot(Bx−C)+D\]

PROPRIÉTÉS DU GRAPHE DE\(Y = A \cot(Bx-c)+D\)

• Le facteur d'étirement est\(| A |\).
• La période est\(\dfrac{\pi}{|B|}\)
• Le domaine est\(x≠\dfrac{C}{B}+\dfrac{\pi}{| B |}k\), où\(k\) est un entier.
• La gamme est\((−∞,−|A|]∪[|A|,∞)\).
• Les asymptotes verticales apparaissent à\(x=\dfrac{C}{B}+\dfrac{\pi}{| B |}k\), où\(k\) est un entier.
• Il n'y a pas d'amplitude.
• \(y=A\cot(Bx)\)est une fonction impaire car c'est le quotient des fonctions paires et impaires (cosinus et sinus, respectivement)

Comment : étant donné une fonction cotangente modifiée de la forme\(f(x)=A\cot(Bx)\),graph one period.

1. Exprimez la fonction dans le formulaire\(f(x)=A\cot(Bx)\).
2. Identifiez le facteur d'étirement,\(|A|\).
3. Identifiez la période,\(P=\dfrac{\pi}{|B|}\).
4. Dessine le graphique de\(y=A\tan(Bx)\).
5. Tracez deux points de référence.
6. Utilisez la relation réciproque entre la tangente et la cotangente pour dessiner le graphe de\(y=Acot(Bx)\).
7. Esquissez les asymptotes.

Exemple\(\PageIndex{8}\): Graphing Variations of the Cotangent Function

Déterminez le facteur d'étirement, la période et le décalage de phase de\(y=3\cot(4x)\), puis esquissez un graphique.

Solution

• Étape 1. Exprimer la fonction sous la forme\(f(x)=A\cot(Bx)\) donne\(f(x)=3\cot(4x)\).
• Étape 2. Le facteur d'étirement est\(|A|=3\).
• Étape 3. La période est\(P=\dfrac{\pi}{4}\).
• Étape 4. Esquissez le graphique de\(y=3\tan(4x)\).
• Étape 5. Tracez deux points de référence. Deux de ces points sont\(\left (\dfrac{\pi}{16},3 \right )\) et\(\left (\dfrac{3\pi}{16},−3 \right )\).
• Étape 6. Utilisez la relation réciproque pour dessiner\(y=3\cot(4x)\).
• Étape 7. Esquissez les asymptotes,\(x=0\),\(x=\dfrac{\pi}{4}\).

Le graphique orange de la figure le\(\PageIndex{20}\) montre\(y=3\tan(4x)\) et le graphique bleu le montre\(y=3\cot(4x)\).

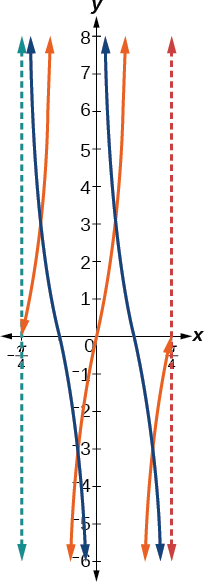
Figurine\(\PageIndex{20}\)

Comment : étant donné une fonction cotangente modifiée de la forme\(f(x)=A\cot(Bx−C)+D\), graph one period.

1. Exprimez la fonction dans le formulaire\(f(x)=A\cot(Bx−C)+D\).
2. Identifiez le facteur d'étirement,\(| A |\).
3. Identifiez la période,\(P=\dfrac{\pi}{|B|}\).
4. Identifiez le décalage de phase,\(\dfrac{C}{B}\).
5. Tracez le graphique des\(y=A\tan(Bx)\) décalages vers la droite\(\dfrac{C}{B}\) et de haut en haut\(D\).
6. Esquissez les asymptotes\(x=\dfrac{C}{B}+\dfrac{\pi}{| B |}k\), où\(k\) est un entier.
7. Tracez trois points de référence et tracez le graphique à travers ces points.

Exemple\(\PageIndex{9}\): Graphing a Modified Cotangent

Esquissez un graphique d'une période de la fonction\(f(x)=4\cot \left (\dfrac{\pi}{8}x−\dfrac{\pi}{2} \right )−2\).

Solution

• Étape 1 La fonction est déjà écrite sous la forme générale\(f(x)=A\cot(Bx−C)+D\).
• Étape 2 \(A=4\), donc le facteur d'étirement est\(4\).
• Étape 3 \(B=\dfrac{\pi}{8}\), donc la période est\(P=\dfrac{\pi}{| B |}=\dfrac{\pi}{\dfrac{\pi}{8}}=8\).
• Étape 4. \(C=\dfrac{\pi}{2}\), donc le décalage de phase est\(CB=\dfrac{\dfrac{\pi}{2}}{\dfrac{\pi}{8}}=4\).
• Étape 5. Nous dessinons\(f(x)=4\tan \left (\dfrac{\pi}{8}x−\dfrac{\pi}{2} \right )−2\).
• Étape 6-7. Trois points que nous pouvons utiliser pour guider le graphique sont\((6,2)\)\((8,−2)\), et\((10,−6)\). Nous utilisons la relation réciproque de tangente et de cotangente pour dessiner\(f(x)=4\cot \left (\dfrac{\pi}{8}x−\dfrac{\pi}{2} \right )−2\).
• Étape 8. Les asymptotes verticales sont\(x=4\) et\(x=12\).

Le graphique est illustré dans la figure\(\PageIndex{21}\).

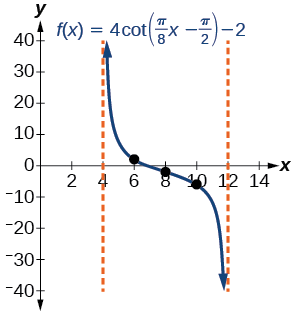
Figure\(\PageIndex{21}\) : Une période d'une fonction cotangente modifiée

Utiliser les graphes des fonctions trigonométriques pour résoudre des problèmes du monde réel

De nombreux scénarios du monde réel représentent des fonctions périodiques et peuvent être modélisés par des fonctions trigonométriques. À titre d'exemple, revenons au scénario de l'ouverture de section. Avez-vous déjà observé le faisceau formé par la lumière rotative d'une voiture de police et vous êtes-vous déjà posé des questions sur le mouvement du faisceau lumineux lui-même à travers le mur ? Le comportement périodique de la distance à laquelle la lumière brille en fonction du temps est évident, mais comment déterminer la distance ? Nous pouvons utiliser la fonction tangente.

Exemple\(\PageIndex{10}\): Using Trigonometric Functions to Solve Real-World Scenarios

Supposons que\(y=5\tan(\dfrac{\pi}{4}t)\) la fonction indique la distance parcourue par un faisceau lumineux entre le haut d'une voiture de police et un mur, où\(t\) est le temps en secondes et\(y\) la distance en pieds par rapport à un point du mur situé directement en face de la voiture de police.

1. Trouvez et interprétez le facteur et la période d'étirement.
2. Graphique de l'intervalle\([0,5]\).
3. Évaluez\(f(1)\) et discutez de la valeur de la fonction à cette entrée.

Solution

1. Nous savons, d'après sa forme générale,\(y=A\tan(Bt)\) qu'il s'\(| A |\)agit du facteur d'étirement et\(\dfrac{\pi}{B}\) de la période.

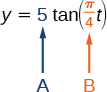
Figurine\(\PageIndex{22}\)

Nous voyons que le facteur d'étirement est\(5\). Cela signifie que le faisceau de lumière se sera déplacé de\(5\) pieds après la moitié de la période.

La période est\(\dfrac{\pi}{\tfrac{\pi}{4}}=\dfrac{\pi}{1}⋅\dfrac{4}{\pi}=4\). Cela signifie que toutes les\(4\) secondes, le faisceau de lumière balaie le mur. La distance entre l'endroit situé en face de la voiture de police augmente à mesure que la voiture de police approche.

2. Pour représenter graphiquement la fonction, nous dessinons une asymptote à\(t=2\) et utilisons le facteur d'étirement et la période. Voir la figure\(\PageIndex{23}\)

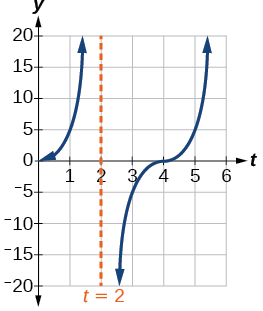
Figurine\(\PageIndex{23}\)

3. point :\(f(1)=5\tan(\frac{\pi}{4}(1))=5(1)=5\) ; au bout de\(1\) quelques secondes, le faisceau de s'est déplacé à\(5\) un pied de l'endroit situé en face de la voiture de police.

Médias

Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner à utiliser des graphiques d'autres fonctions trigonométriques.

• Représentation graphique de la tangente
• Représentation graphique du cosécant et du sécant
• Représentation graphique de la cotangente

Équations clés

Fonction tangente décalée, compressée et/ou étirée	\(y=A \tan(Bx−C)+D\)
Fonction sécante décalée, comprimée et/ou étirée	\(y=A \sec(Bx−C)+D\)
Fonction cosécante décalée, comprimée et/ou étirée	\(y=A \csc(Bx−C)+D\)
Fonction cotangente décalée, comprimée et/ou étirée	\(y=A \cot(Bx−C)+D\)

Concepts clés

• La fonction tangente possède une période\(π\).
• \(f( x )=A\tan( Bx−C )+D\)est une tangente avec étirement/compression et décalage verticaux et/ou horizontaux. Voir Exemple\(\PageIndex{1}\)\(\PageIndex{2}\), Exemple et Exemple\(\PageIndex{3}\).
• La sécante et la cosécante sont toutes deux des fonctions périodiques avec une période de\(2\pi\). \(f( x )=A\sec( Bx−C )+D\)donne un graphe de fonction sécante décalé, compressé et/ou étiré. Voir Exemple\(\PageIndex{4}\) et Exemple\(\PageIndex{5}\).
• \(f( x )=A\csc( Bx−C )+D\)donne un graphe de fonctions cosécantes décalées, compressées et/ou étirées. Voir Exemple\(\PageIndex{6}\) et Exemple\(\PageIndex{7}\).
• La fonction cotangente possède des asymptotes périodiques\(\pi\) et verticales à\(0,±\pi,±2\pi\),...
• La plage de cotangente est\(( −∞,∞ )\), et la fonction diminue à chaque point de sa plage.
• La cotangente est nulle à\(±\dfrac{\pi}{2},±\dfrac{3\pi}{2}\),...
• \(f(x)=A\cot(Bx−C)+D\)est une cotangente avec étirement/compression et décalage verticaux et/ou horizontaux. Voir Exemple\(\PageIndex{8}\) et Exemple\(\PageIndex{9}\).
• Les scénarios du monde réel peuvent être résolus à l'aide de graphes de fonctions trigonométriques. Voir l'exemple\(\PageIndex{10}\).