7.4 : Les autres fonctions trigonométriques

Objectifs d'apprentissage

• Trouvez les valeurs exactes des fonctions trigonométriques sécante, cosécante, tangente et cotangente de\(\frac{\pi}{3}\)\(\frac{\pi}{4}\), et\(\frac{\pi}{6}\).
• Utilisez les angles de référence pour évaluer les fonctions trigonométriques sécante, tangente et cotangente.
• Utilisez les propriétés des fonctions trigonométriques paires et impaires.
• Reconnaissez et utilisez les identités fondamentales.
• Évaluez les fonctions trigonométriques à l'aide d'un calculateur.

Une rampe pour fauteuils roulants conforme aux normes de l'Americans with Disabilities Act doit former un angle avec le sol dont la tangente est égale\(\frac{1}{12}\) ou inférieure, quelle que soit sa longueur. Une tangente représente un ratio, ce qui signifie que pour chaque pouce de montée, la rampe doit avoir 12 pouces de course. Les fonctions trigonométriques nous permettent de spécifier les formes et les proportions des objets indépendamment de leurs dimensions exactes. Nous avons déjà défini les fonctions sinus et cosinus d'un angle. Bien que le sinus et le cosinus soient les fonctions trigonométriques les plus utilisées, il en existe quatre autres. Ensemble, ils constituent l'ensemble des six fonctions trigonométriques. Dans cette section, nous allons étudier les fonctions restantes.

Trouver les valeurs exactes des fonctions trigonométriques sécante, cosécante, tangente et cotangente

Pour définir les fonctions restantes, nous allons à nouveau dessiner un cercle unitaire avec un point\((x,y)\) correspondant à un angle de\(t\), comme indiqué sur la figure\(\PageIndex{1}\). Comme pour le sinus et le cosinus, nous pouvons utiliser les\((x,y)\) coordonnées pour trouver les autres fonctions.

Figurine\(\PageIndex{1}\)

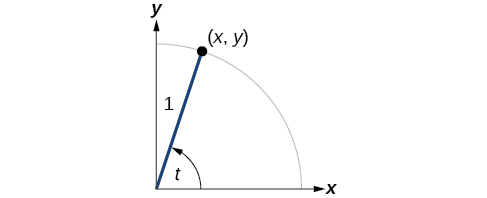
La première fonction que nous allons définir est la tangente. La tangente d'un angle est le rapport entre la valeur y et la valeur x du point correspondant sur le cercle unitaire. Sur la figure\(\PageIndex{1}\), la tangente de l'angle\(t\) est égale à\(\frac{y}{x},x≠0 \). Comme la valeur y est égale au sinus de\(t\) et que la valeur x est égale au cosinus de\(t\), la tangente de l'angle\(t\) peut également être définie comme suit :\( \frac{ \sin t}{ \cos t}, \cos t≠0.\) La fonction tangente est abrégée en\( \tan.\) Les trois fonctions restantes peuvent toutes être exprimées comme des fonctions réciproques que nous avons déjà définies.

• La fonction sécante est l'inverse de la fonction cosinus. Dans la figure\(\PageIndex{1}\), la sécante de l'angle\(t\) est égale à\(\frac{1}{ \cos t} = \frac{1}{x},x≠0\). La fonction sécante est abrégée en\( \sec \).
• La fonction cotangente est l'inverse de la fonction tangente. Dans la figure\(\PageIndex{1}\), la cotangente de l'angle\(t\) est égale à\( \frac{ \cos t}{ \sin t}= \frac{x}{y}, y≠0.\) La fonction cotangente est abrégée comme\( \cot.\)
• La fonction cosécante est l'inverse de la fonction sinusoïdale. Dans la figure\(\PageIndex{1}\), la cosécante de l'angle\(t\) est égale à\(\frac{1}{ \sin t}= \frac{1}{y},y≠0.\) La fonction cosécante est abrégée comme\( \csc.\)

FONCTIONS TANGENTES, SÉCANTES, COSÉCANTES ET COTANGENTES

S'il s'\(t\)agit d'un nombre réel et\((x,y)\) d'un point où le côté terminal d'un angle de\(t\) radians intercepte le cercle unitaire, alors

\[\begin{align} \tan t &= \frac{y}{x},x≠0 \\ \sec t & =\frac{1}{x},x≠0 \\ \csc t &=\frac{1}{y},y≠0 \\ \cot t &= \frac{x}{y},y≠0 \end{align}\]

Exemple\(\PageIndex{1}\): Finding Trigonometric Functions from a Point on the Unit Circle

Le point\((−\frac{\sqrt{3}}{2},\frac{1}{2})\) se trouve sur le cercle unitaire, comme indiqué sur la figure\(\PageIndex{2}\). Trouvez\( \sin t, \cos t, \tan t, \sec t, \csc t,\) et\( \cot t\).

Figurine\(\PageIndex{2}\)

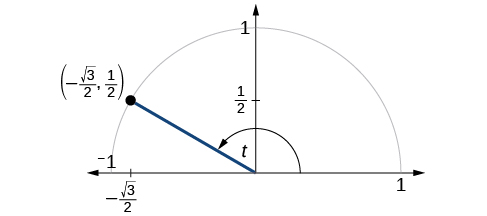
Solution

Comme nous connaissons les\((x,y)\) coordonnées du point du cercle unitaire indiqué par l'angle\(t\), nous pouvons utiliser ces coordonnées pour trouver les six fonctions :

\[\begin{align*} \sin t &=y=\dfrac{1}{2} \\ \cos t &=x= −\dfrac{\sqrt{3}}{2} \\ \tan t &= \dfrac{y}{x}= \dfrac{\frac{1}{2}}{−\frac{\sqrt{3}}{2}}=\dfrac{1}{2}(−\dfrac{2}{\sqrt{3}})=−\dfrac{1}{\sqrt{3}}=−\dfrac{\sqrt{3}}{3} \\ \sec t &= \dfrac{1}{x}=\dfrac{1}{−\frac{\sqrt{3}}{2}}=−\dfrac{2}{\sqrt{3}}=−\dfrac{2\sqrt{3}}{3} \\ \csc t &= \dfrac{1}{y}=\dfrac{1}{\frac{1}{2}}=2 \\ \cot t &= \dfrac{x}{y}=\dfrac{−\frac{\sqrt{3}}{2}}{\frac{1}{2}}=−\dfrac{\sqrt{3}}{2}(\dfrac{2}{1})=−\sqrt{3} \end{align*}\]

Exercice\(\PageIndex{1}\):

Le point\((\frac{\sqrt{2}}{2},−\frac{\sqrt{2}}{2})\) se trouve sur le cercle unitaire, comme indiqué sur la figure\(\PageIndex{3}\). Trouvez\( \sin t, \cos t, \tan t, \sec t, \csc t,\) et\( \cot t\).

Figurine\(\PageIndex{3}\)

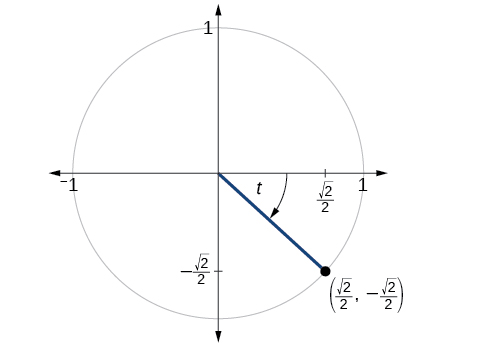
Solution

\( \sin t=−\frac{\sqrt{2}}{2}, \cos t= \frac{\sqrt{2}}{2}, \tan t=−1, \sec t=\sqrt{2}, \csc t=−\sqrt{2}, \cot t=−1\)

Exemple\(\PageIndex{2}\): Finding the Trigonometric Functions of an Angle

Trouvez\( \sin t, \cos t, \tan t, \sec t, \csc t, \) et\( \cot t\) quand\(t=\frac{π}{6}\).

Solution

Nous avons déjà utilisé les propriétés des triangles équilatéraux pour démontrer que\( \sin \frac{π}{6}=\frac{1}{2}\) et\( \cos \frac{π}{6}=\frac{\sqrt{3}}{2} \). Nous pouvons utiliser ces valeurs et les définitions de tangente, sécante, cosécante et cotangente en tant que fonctions du sinus et du cosinus pour trouver les valeurs de fonction restantes.

\[ \begin{align*} \tan \dfrac{π}{6} & = \dfrac{ \sin \frac{π}{6}}{\cos \frac{π}{6}} \\ & = \dfrac{\frac{1}{2} }{\frac{\sqrt{3}}{2}}=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3} \\ \sec \dfrac{π}{6} &= \dfrac{1}{ \cos \frac{π}{6}} \\ & = \dfrac{1}{\frac{\sqrt{3}}{2}} = \dfrac{2}{\sqrt{3}}= \dfrac{2\sqrt{3}}{3} \\ \csc \dfrac{π}{6} &= \dfrac{1}{ \sin \frac{π}{6}}= \dfrac{1}{\frac{1}{2}}=2 \\ \cot \dfrac{π}{6} & = \dfrac{ \cos \frac{π}{6}}{ \sin \frac{π}{6}} \\ &= \dfrac{\frac{\sqrt{3}}{2}}{\frac{1}{2}} =\sqrt{3} \end{align*}\]

Exercice\(\PageIndex{2}\):

Trouvez\( \sin t, \cos t, \tan t, \sec t, \csc t,\) et\( \cot t\) quand\(t=\frac{π}{3}.\)

Solution

\(\begin{align} \sin \frac{π}{3} & = \frac{\sqrt{3}}{2} \\ \cos \frac{π}{3} &=\frac{1}{2} \\ \tan \frac{π}{3} &= \sqrt{3} \\ \sec \frac{π}{3} &= 2 \\ \csc \frac{π}{3} &= \frac{2\sqrt{3}}{3} \\ \cot \frac{π}{3} &= \frac{\sqrt{3}}{3} \end{align}\)

Comme nous connaissons les valeurs du sinus et du cosinus pour les angles communs du premier quadrant, nous pouvons également trouver les autres valeurs de fonction pour ces angles en définissant x x égal au cosinus et y y égal au sinus, puis en utilisant les définitions de tangente, sécante, cosécante et cotangente. Les résultats sont présentés dans le tableau\(\PageIndex{1}\).

Tableau\(\PageIndex{1}\)

Angle	\(0\)	\(\frac{π}{6}, \text{ or } 30°\)	\(\frac{π}{4}, \text{ or } 45°\)	\(\frac{π}{3},\text{ or }60°\)	\(\frac{π}{2},\text{ or }90°\)
Cosinus	\ (0 \) » style="vertical-align:middle ; « >1	\ (\ frac {π} {6}, \ text {ou} 30° \) » style="vertical-align:middle ; « >\(\frac{\sqrt{3}}{2}\)	\ (\ frac {π} {4}, \ text {ou} 45° \) » style="vertical-align:middle ; « >\(\frac{\sqrt{2}}{2}\)	\ (\ frac {π} {3}, \ text {ou} 60° \) » style="vertical-align:middle ; « >\(\frac{1}{2}\)	\ (\ frac {π} {2}, \ text {ou} 90° \) » style="vertical-align:middle ; « >0
Sinus	\ (0 \) » style="vertical-align:middle ; « >0	\ (\ frac {π} {6}, \ text {ou} 30° \) » style="vertical-align:middle ; « >\(\frac{1}{2}\)	\ (\ frac {π} {4}, \ text {ou} 45° \) » style="vertical-align:middle ; « >\(\frac{\sqrt{2}}{2}\)	\ (\ frac {π} {3}, \ text {ou} 60° \) » style="vertical-align:middle ; « >\(\frac{\sqrt{3}}{2}\)	\ (\ frac {π} {2}, \ text {ou} 90° \) » style="vertical-align:middle ; « >1
Tangente	\ (0 \) » style="vertical-align:middle ; « >0	\ (\ frac {π} {6}, \ text {ou} 30° \) » style="vertical-align:middle ; « >\(\frac{\sqrt{3}}{3}\)	\ (\ frac {π} {4}, \ text {ou} 45° \) » style="vertical-align:middle ; « >1	\ (\ frac {π} {3}, \ text {ou} 60° \) » style="vertical-align:middle ; « >\(\sqrt{3}\)	\ (\ frac {π} {2}, \ text {ou} 90° \) » style="vertical-align:middle ; « >Non défini
Sécant	\ (0 \) » style="vertical-align:middle ; « >1	\ (\ frac {π} {6}, \ text {ou} 30° \) » style="vertical-align:middle ; « >\(\frac{2\sqrt{3}}{3}\)	\ (\ frac {π} {4}, \ text {ou} 45° \) » style="vertical-align:middle ; « >\(\sqrt{2}\)	\ (\ frac {π} {3}, \ text {ou} 60° \) » style="vertical-align:middle ; « >2	\ (\ frac {π} {2}, \ text {ou} 90° \) » style="vertical-align:middle ; « >Non défini
Cosécant	\ (0 \) » style="vertical-align:middle ; ">Non défini	\ (\ frac {π} {6}, \ text {ou} 30° \) » style="vertical-align:middle ; « >2	\ (\ frac {π} {4}, \ text {ou} 45° \) » style="vertical-align:middle ; « >\(\sqrt{2}\)	\ (\ frac {π} {3}, \ text {ou} 60° \) » style="vertical-align:middle ; « >\(\frac{2\sqrt{3}}{3}\)	\ (\ frac {π} {2}, \ text {ou} 90° \) » style="vertical-align:middle ; « >1
Cotangente	\ (0 \) » style="vertical-align:middle ; ">Non défini	\ (\ frac {π} {6}, \ text {ou} 30° \) » style="vertical-align:middle ; « >\(\sqrt{3}\)	\ (\ frac {π} {4}, \ text {ou} 45° \) » style="vertical-align:middle ; « >1	\ (\ frac {π} {3}, \ text {ou} 60° \) » style="vertical-align:middle ; « >\(\frac{\sqrt{3}}{3}\)	\ (\ frac {π} {2}, \ text {ou} 90° \) » style="vertical-align:middle ; « >0

Utilisation d'angles de référence pour évaluer la tangente, la sécante, la cosécante et la cotangente

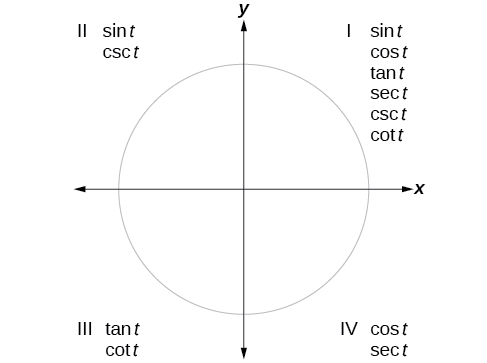
Nous pouvons évaluer les fonctions trigonométriques des angles situés en dehors du premier quadrant à l'aide d'angles de référence, comme nous l'avons déjà fait avec les fonctions sinus et cosinus. La procédure est la même : Trouvez l'angle de référence formé par le côté terminal de l'angle donné avec l'axe horizontal. Les valeurs de la fonction trigonométrique pour l'angle d'origine seront les mêmes que celles de l'angle de référence, à l'exception du signe positif ou négatif, qui est déterminé par les valeurs x et y dans le quadrant d'origine. La figure\(\PageIndex{4}\) montre quelles fonctions sont positives dans quel quadrant.

Pour nous aider à nous souvenir laquelle des six fonctions trigonométriques est positive dans chaque quadrant, nous pouvons utiliser l'expression mnémotechnique « Une classe de trig intelligente ». Chacun des quatre mots de la phrase correspond à l'un des quatre quadrants, en commençant par le quadrant I et en tournant dans le sens antihoraire. Dans le quadrant I, qui est « A », toutes les six fonctions trigonométriques sont positives. Dans le quadrant II, « Si intelligent », seule la ligne et sa fonction réciproque, la cosécante, sont positives. Dans le quadrant III, « anneau en T », seules l'angente et sa fonction réciproque, la cotangente, sont positives. Enfin, dans le quadrant IV, « Classe C », seules la c osine et sa fonction réciproque, sécante, sont positives.

Figurine\(\PageIndex{4}\)

COMMENT : À partir d'un angle ne se trouvant pas dans le premier quadrant, utilisez des angles de référence pour trouver les six fonctions trigonométriques

1. Mesurez l'angle formé par le côté terminal de l'angle donné et de l'axe horizontal. Il s'agit de l'angle de référence.
2. Evaluez la fonction à l'angle de référence.
3. Observez le quadrant où se trouve le côté terminal de l'angle d'origine. Sur la base du quadrant, déterminez si la sortie est positive ou négative.

Exemple\(\PageIndex{3}\): Using Reference Angles to Find Trigonometric Functions

Utilisez les angles de référence pour trouver les six fonctions trigonométriques de\(−\frac{5π}{6}\).

Solution

L'angle entre le côté terminal de cet angle et l'axe x est de\(\frac{π}{6}\), donc c'est l'angle de référence. Puisque\(−\frac{5π}{6}\) se trouve dans le troisième quadrant, où\(x\) les deux\(y\) sont négatifs, le cosinus, le sinus, la sécante et la cosécante seront négatifs, tandis que la tangente et la cotangente seront positifs.

\[ \begin{align} \cos (−\dfrac{5π}{6}) &=−\dfrac{\sqrt{3}}{2}, \sin (−\dfrac{5π}{6})=−\dfrac{1}{2}, \tan (−\dfrac{5π}{6}) = \dfrac{\sqrt{3}}{3} \\ \sec (−\dfrac{5π}{6}) &=−\dfrac{2\sqrt{3}}{3}, \csc (−\dfrac{5π}{6})=−2, \cot (−\dfrac{5π}{6})=\sqrt{3} \end{align} \]

Exercice\(\PageIndex{3}\)

Utilisez les angles de référence pour trouver les six fonctions trigonométriques de\(−\frac{7π}{4}\).

Solution

\( \sin (−\frac{7π}{4})= \frac{\sqrt{2}}{2}, \cos(\frac{−7π}{4})=\frac{\sqrt{2}}{2}, \tan (\frac{−7π}{4})=1,\)

\( \sec (\frac{−7π}{4})= \sqrt{2}, \csc (\frac{−7π}{4})= \sqrt{2}, \cot (\frac{−7π}{4})=1 \)

Utilisation de fonctions trigonométriques paires et impaires

Pour pouvoir utiliser librement nos six fonctions trigonométriques avec des entrées angulaires positives et négatives, nous devons examiner comment chaque fonction traite une entrée négative. Il s'avère qu'il existe une différence importante entre les fonctions à cet égard.

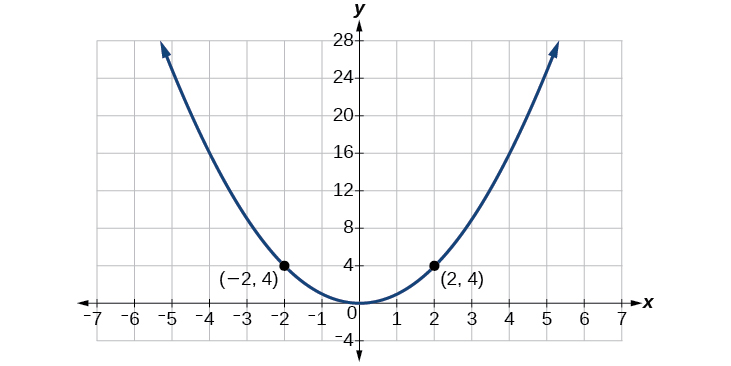
Considérez la fonction\(f(x)=x^2\), illustrée dans la figure\(\PageIndex{5}\). Le graphe de la fonction est symétrique par rapport à l'axe y. Tout au long de la courbe, deux points ayant des valeurs x opposées ont la même valeur de fonction. Cela correspond au résultat du calcul :\((4)^2=(−4)^2,(−5)^2=(5)^2\), et ainsi de suite. \(f(x)=x^2\)Il en va de même pour une fonction paire, une fonction telle que deux entrées opposées ont la même sortie. Ça veut dire\(f(−x)=f(x)\).

Figure\(\PageIndex{5}\) : La fonction\(f(x)=x^2\) est une fonction paire.

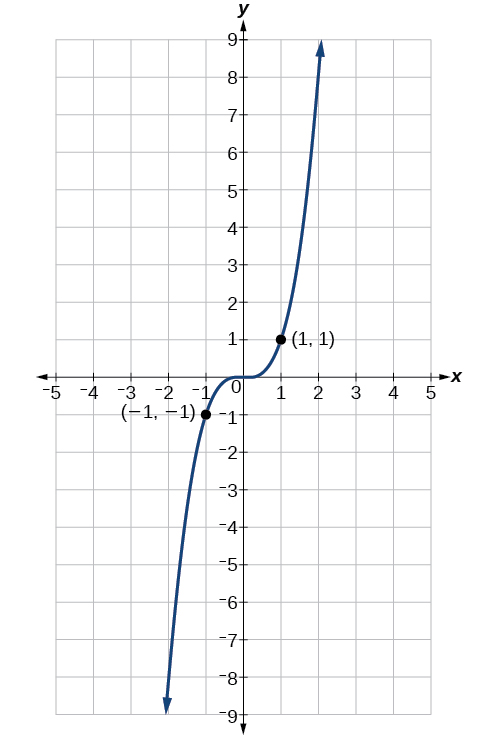
Maintenant, considérez la fonction\(f(x)=x^3\), illustrée dans la figure\(\PageIndex{6}\). Le graphique n'est pas symétrique par rapport à l'axe y. Tout au long du graphique, deux points ayant des valeurs x opposées ont également des valeurs y opposées. \(f(x)=x^3\)Il en va de même pour une fonction étrange, telle que deux entrées opposées ont des sorties également opposées. Ça veut dire\(f(−x)=−f(x)\).

Figure\(\PageIndex{6}\) : La fonction\(f(x)=x^3\) est une fonction étrange.

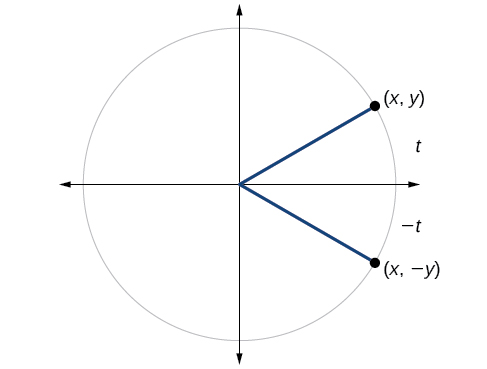
Nous pouvons tester si une fonction trigonométrique est paire ou impaire en traçant un cercle unitaire avec un angle positif et un angle négatif, comme dans la Figure\(\PageIndex{7}\). Le sinus de l'angle positif est\(y\). Le sinus de l'angle négatif est − y. La fonction sinusoïdale est donc une fonction étrange. Nous pouvons tester chacune des six fonctions trigonométriques de cette manière. Les résultats sont présentés dans le tableau\(\PageIndex{2}\).

Figurine\(\PageIndex{7}\)

Tableau\(\PageIndex{2}\)

\(\begin{align} \sin t &=y \\ \sin (−t) &=−y \\ \sin t &≠sin(−t) \end{align}\)	\( \begin{align} \cos t &=x \\ \cos (−t)=x \\ \cos t &= \cos (−t) \end{align}\)	\(\begin{align} \tan (t) &= \frac{y}{x} \\ \tan (−t) &=−\frac{y}{x} \\ \tan t &≠ \tan (−t) \end{align}\)
\(\begin{align} \sec t &= \frac{1}{x} \\ \sec (−t) &= \frac{1}{x} \\ \sec t &= \sec (−t) \end{align}\)	\( \begin{align} \csc t &= \frac{1}{y} \\ \csc (−t) &= \frac{1}{−y} \\ \csc t &≠ \csc (−t) \end{align}\)	\( \begin{align} \cot t &= \frac{x}{y} \\ \cot (−t) &= \frac{x}{−y} \\ \cot t & ≠ \cot (−t) \end{align}\)

FONCTIONS TRIGONOMÉTRIQUES PAIRES ET IMPAIRES

• Une fonction paire est une fonction dans laquelle\(f(−x)=f(x)\).
• Une fonction étrange est une fonction dans laquelle\(f(−x)=−f(x)\).

Le cosinus et la sécante sont pairs :

\[ \begin{align} \cos (−t) &= \cos t \\ \sec (−t) &= \sec t \end{align}\]

Le sinus, la tangente, la cosécante et la cotangente sont impairs :

\[\begin{align} \sin (−t) &=− \sin t \\ \tan (−t) &=−\tan t \\ \csc (−t) &=−\csc t \\ \cot (−t) &=−\cot t \end{align}\]

Exemple\(\PageIndex{4}\): Using Even and Odd Properties of Trigonometric Functions

Si la sécante de l'angle t est égale à 2, quelle est la sécante de\(−t\) ?

Solution

La sécante est une fonction uniforme. La sécante d'un angle est la même que la sécante de son opposé. Donc, si la sécante de l'angle t est égale à 2, la sécante de\(−t\) est également égale à 2.

Exercice\(\PageIndex{4}\):

Si la cotangente de l'angle\(t\) est\(\sqrt{3}\), quelle est la cotangente de\(−t?\)

Solution

\(−\sqrt{3}\)

Reconnaître et utiliser les identités fondamentales

Nous avons exploré un certain nombre de propriétés des fonctions trigonométriques. Maintenant, nous pouvons aller plus loin dans les relations et en dériver certaines identités fondamentales. Les identités sont des déclarations qui sont vraies pour toutes les valeurs de l'entrée sur laquelle elles sont définies. Habituellement, les identités peuvent être dérivées de définitions et de relations que nous connaissons déjà. Par exemple, l'identité pythagoricienne que nous avons apprise plus tôt est dérivée du théorème de Pythagore et des définitions du sinus et du cosinus.

IDENTITÉS FONDAMENTALES

Nous pouvons déduire des identités utiles à partir des six fonctions trigonométriques. Les quatre autres fonctions trigonométriques peuvent être reliées aux fonctions sinus et cosinus à l'aide des relations de base suivantes :

\[ \tan t= \dfrac{ \sin t}{ \cos t} \]

\[ \sec t= \dfrac{1}{\cos t}\]

\[ \csc t= \dfrac{1}{\sin t}\]

\[ \cot t= \dfrac{1}{ \tan t}= \dfrac{ \cos t}{ \sin t} \]

Exemple\(\PageIndex{5}\): Using Identities to Evaluate Trigonometric Functions

1. Étant donné\( \sin (45°)= \frac{\sqrt{2}}{2}, \cos (45°)= \frac{\sqrt{2}}{2}\), évaluez\( \tan(45°).\)
2. \( \sin (\frac{5π}{6})= \frac{1}{2}, \cos( \frac{5π}{6})=−\frac{\sqrt{3}}{2},\)Évaluer\(\sec (\frac{5π}{6})\).

Solution

Comme nous connaissons les valeurs du sinus et du cosinus de ces angles, nous pouvons utiliser des identités pour évaluer les autres fonctions.

1. \[ \begin{align*} \tan(45°) &=\dfrac{ \sin(45°)}{ \cos (45°)} \\ &= \dfrac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} \\ & =1 \end{align*} \]
2. \[\begin{align*} \sec (\dfrac{5π}{6}) &= \dfrac{1}{ \cos (\frac{5π}{6})} \\ &= \dfrac{1}{−\frac{\sqrt{3}}{2}} \\ &= \dfrac{−2\sqrt{3}}{1} \\ &=\dfrac{−2}{\sqrt{3}} \\ &=−\dfrac{2\sqrt{3}}{3} \end{align*}\]

Exercice\(\PageIndex{5}\)

Évaluer\(\csc (\frac{7π}{6}).\)

Solution

\(−2\)

Exemple\(\PageIndex{6}\): Using Identities to Simplify Trigonometric Expressions

SIMPLIFIER\(\frac{ \sec t}{ \tan t}.\)

Solution

Nous pouvons simplifier cela en réécrivant les deux fonctions en termes de sinus et de cosinus.

\[\begin{array}{lll} \dfrac{\sec t}{\tan t} & =\dfrac{1 / \cos t}{ \sin t / \cos t} & \text{To divide the functions, we multiply by the reciprocal.} \\ \text{} &= \dfrac{1}{\cos t} \dfrac{ \cos t}{\sin t} & \text{Divide out the cosines.} \\ \text{} & =\dfrac{1}{\sin t} & \text{Simplify and use the identity.} \\ \text{} & = \csc t \end{array}\]

En montrant que cela\(\frac{ \sec t}{ \tan t}\) peut être simplifié\( \csc t\), nous avons en fait établi une nouvelle identité.

\[ \dfrac{ \sec t}{ \tan t}= \csc t \nonumber \]

Exercice\(\PageIndex{6}\)

SIMPLIFIER\(( \tan t)( \cos t).\)

Solution

\( \sin t \)

Formes alternatives de l'identité pythagoricienne

Nous pouvons utiliser ces identités fondamentales pour dériver des formes alternatives de l'identité pythagoricienne,\( \cos ^2 t+ \sin ^2 t=1\). Une forme est obtenue en divisant les deux côtés par\( \cos ^2 t:\)

\[ \begin{align} \dfrac{ \cos ^2 t}{ \cos ^2 t} + \dfrac{ \sin ^2 t}{ \cos ^2 t} & = \dfrac{1}{ \cos ^2 t} \\ 1+ \tan ^2 t & = \sec ^2 t \end{align}\]

L'autre forme est obtenue en divisant les deux côtés par\( \sin ^2 t\) :

\[ \begin{align} \dfrac{ \cos ^2 t}{ \sin ^2 t}+ \dfrac{ \sin ^2 t}{ \sin ^2 t} &= \dfrac{1}{ \sin ^2 t} \\ \cot ^2 t+1 &= \csc ^2 t \end{align}\]

FORMES ALTERNATIVES DE L'IDENTITÉ PYTHAGORICIENNE

\[1+ \tan ^2 t= \sec ^2 t \]

\[ \cot ^2 t+1= \csc ^2 t\]

Exemple\(\PageIndex{7}\): Using Identities to Relate Trigonometric Functions

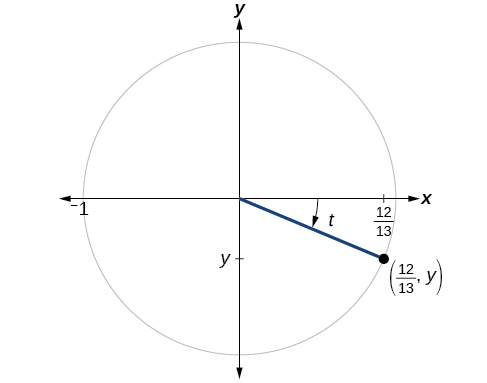
Si cos (t) =1213 cos (t) =1213 et que t t se trouve dans le quadrant IV, comme indiqué sur la figure\(\PageIndex{8}\), trouvez les valeurs des cinq autres fonctions trigonométriques.

Figurine\(\PageIndex{8}\)

Solution

Nous pouvons trouver le sinus en utilisant l'identité de Pythagore\( \cos ^2 t+ \sin ^2t=1 \), et les fonctions restantes en les reliant au sinus et au cosinus.

\[ \begin{align} (\dfrac{12}{13})^2+ \sin ^2 t &= 1 \\ \sin ^2 t &=1−(\dfrac{12}{13})^2 \\ \sin ^2 t &=1− \dfrac{144}{169} \\ \sin ^2 t &= \dfrac{25}{169} \\ \sin t &=±\sqrt{\dfrac{25}{169}} \\ \sin t &=±\dfrac{\sqrt{25}}{\sqrt{169}} \\ \sin t &=± \dfrac{5}{13} \end{align} \]

Le signe du sinus dépend des valeurs y dans le quadrant où se situe l'angle. Puisque l'angle se trouve dans le quadrant IV, où les valeurs y sont négatives, son sinus est négatif,\(−\frac{5}{13}\).

Les fonctions restantes peuvent être calculées à l'aide d'identités les reliant au sinus et au cosinus.

\[ \begin{align} \tan t &= \dfrac{\sin t}{ \cos t}=\dfrac{−\frac{5}{13}}{\frac{12}{13}}=−\dfrac{5}{12} \\ \sec t &= \dfrac{1}{ \cos t}=\dfrac{1}{\frac{12}{13}}=\dfrac{13}{12} \\ \csc t &= \dfrac{1}{\sin t}=\dfrac{1}{−\frac{5}{13}} =−\dfrac{13}{5} \\ \cot t &= \dfrac{1}{ \tan t}=\dfrac{1}{−\frac{5}{12}}=−\dfrac{12}{5} \end{align} \]

Exercice\(\PageIndex{7}\):

Si\( \sec (t)=− \frac{17}{8}\) et\(0<t<π,\) trouvez les valeurs des cinq autres fonctions.

Solution

\( \cos t=−\frac{8}{17}, \sin t=\frac{15}{17}, \tan t=−\frac{15}{8}\)

\( \csc t= \frac{17}{15}, \cot t=−\frac{8}{15} \)

Comme nous l'avons vu dans l'ouverture du chapitre, une fonction qui répète ses valeurs à intervalles réguliers est connue sous le nom de fonction périodique. Les fonctions trigonométriques sont périodiques. Pour les quatre fonctions trigonométriques (sinus, cosinus, cosécante et sécante), une révolution d'un cercle\(2π\), ou, donnera les mêmes résultats pour ces fonctions. Et pour la tangente et la cotangente, une demi-révolution seulement produira les mêmes sorties.

D'autres fonctions peuvent également être périodiques. Par exemple, la durée des mois se répète tous les quatre ans. Si x x représente la durée, mesurée en années, et\(f(x)\) le nombre de jours en février, alors\(f(x+4)=f(x)\). Ce schéma se répète encore et encore dans le temps. En d'autres termes, tous les quatre ans, le mois de février aura le même nombre de jours que 4 ans plus tôt. Le nombre positif 4 est le plus petit nombre positif qui satisfait cette condition et s'appelle la période. Une période est l'intervalle le plus court au cours duquel une fonction effectue un cycle complet. Dans cet exemple, la période est de 4 et représente le temps qu'il nous faut pour être certains que le mois de février comporte le même nombre de jours.

DURÉE D'UNE FONCTION

La période\(P\) d'une fonction récurrente f f est le nombre représentant l'intervalle tel que\(f(x+P)=f(x)\) pour n'importe quelle valeur de\(x\).

La période des fonctions cosinus, sinus, sécante et cosécante est\(2π\).

La période des fonctions tangente et cotangente est\(π\).

Exemple\(\PageIndex{8}\): Finding the Values of Trigonometric Functions

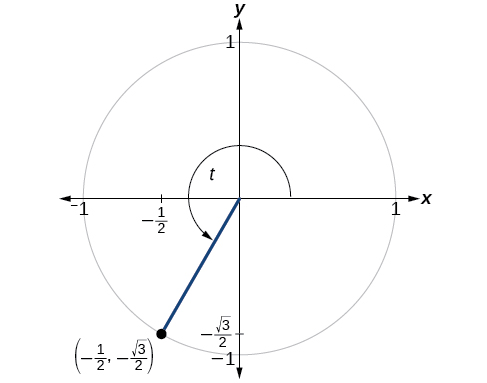
Trouvez les valeurs des six fonctions trigonométriques de l'angle en\(t\) fonction de la figure\(\PageIndex{9}\).

Figurine\(\PageIndex{9}\)

Solution

\[\begin{align*} \sin t &= y=−\dfrac{\sqrt{3}}{2} \\ \cos t &=x =−\dfrac{1}{2} \\ \tan t &= \dfrac{ \sin t}{ \cos t}=\dfrac{−\frac{\sqrt{3}}{2}}{−\frac{1}{2}}= \sqrt{3} \\ \sec t &= \dfrac{1}{\cos t} = \dfrac{1}{−\frac{1}{2}}=−2 \\ \csc t &= \dfrac{1}{\sin t}= \dfrac{1}{−\frac{\sqrt{3}}{2}}=−\dfrac{2\sqrt{3}}{3} \\ \cot t &= \dfrac{1}{ \tan t}=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3} \end{align*}\]

Exercice\(\PageIndex{8}\)

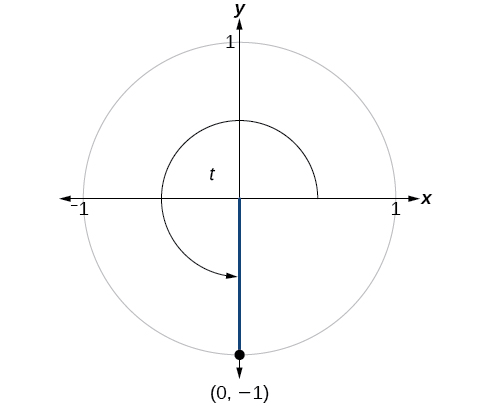
Trouvez les valeurs des six fonctions trigonométriques de l'angle en\(t\) fonction de la figure\(\PageIndex{10}\).

Figurine\(\PageIndex{10}\)

Solution

\(\begin{align} \sin t &=−1, \cos t=0, \tan t= \text{Undefined} \\ \\sec t &= \text{Undefined}, \csc t=−1, \cot t=0 \end{align}\)

Exemple\(\PageIndex{9}\): Finding the Value of Trigonometric Functions

Si\( \sin(t)=−\frac{\sqrt{3}}{2}\) et\( \cos (t)=\frac{1}{2}\), trouvez\( \sec (t),\csc (t),\tan (t), \cot (t).\)

Solution

\[ \begin{align} \sec t &= \dfrac{1}{ \cos t}= \dfrac{1}{\frac{1}{2}}=2 \\ \csc t &= \dfrac{1}{ \sin t}= \dfrac{1}{−\frac{\sqrt{3}}{2}}−\dfrac{2\sqrt{3}}{3} \\ \tan t &= \dfrac{\sin t}{\cos t}=\dfrac{−\frac{\sqrt{3}}{2}}{\frac{1}{2}}=−\sqrt{3} \\ \cot t &= \dfrac{1}{ \tan t}= \dfrac{1}{−\sqrt{3}}=−\dfrac{\sqrt{3}}{3} \end{align}\]

Exercice\(\PageIndex{9}\):

Si\(\sin (t)= \frac{\sqrt{2}}{2}\) et\(\cos (t)=\frac{\sqrt{2}}{2},\) trouvez\( \sec (t), \csc (t),\tan (t),\) et\( \cot (t)\).

Solution

\( \sec t= \sqrt{2},\csc t=\sqrt{2}, \tan t=1, \cot t=1\)

Évaluation des fonctions trigonométriques à l'aide d'une calculatrice

Nous avons appris à évaluer les six fonctions trigonométriques pour les angles communs du premier quadrant et à les utiliser comme angles de référence pour les angles situés dans d'autres quadrants. Pour évaluer les fonctions trigonométriques d'autres angles, nous utilisons une calculatrice scientifique ou graphique ou un logiciel informatique. Si la calculatrice possède un mode degrés et un mode radian, vérifiez que le mode correct est choisi avant d'effectuer un calcul.

L'évaluation d'une fonction tangente à l'aide d'une calculatrice scientifique par opposition à une calculatrice graphique ou à un système d'algèbre informatique revient à évaluer un sinus ou un cosinus : entrez la valeur et appuyez sur la touche TAN. Pour les fonctions réciproques, il se peut qu'il n'y ait aucune clé dédiée indiquant CSC, SEC ou COT. Dans ce cas, la fonction doit être évaluée comme l'inverse d'un sinus, d'un cosinus ou d'une tangente.

Si nous devons travailler avec des degrés et que notre calculatrice ou notre logiciel ne dispose pas de mode degrés, nous pouvons saisir les degrés multipliés par le facteur de conversion\(\frac{π}{180}\) pour convertir les degrés en radians. Pour trouver la sécante de\( 30°\), nous pourrions appuyer sur

\[\mathrm{(for \; a \; scientific \; calculator):\dfrac{1}{30×\frac{π}{180}}COS }\]

ou

\[ \mathrm{(for \; a \; graphing \; calculator): \dfrac{1}{cos(\frac{30π}{180})} }\]

Comment : À partir d'une mesure d'angle en radians, utiliser une calculatrice scientifique pour trouver la cosécante

1. Si la calculatrice possède le mode degrés et le mode radian, réglez-le sur le mode radian.
2. Entrez :\(1 \; / \)
3. Entrez la valeur de l'angle entre parenthèses.
4. Appuyez sur la touche SIN.
5. Appuyez sur la touche =.

Comment : À partir d'une mesure d'angle en radians, utiliser un utilitaire/une calculatrice graphique pour trouver la cosécante

1. Si l'utilitaire de création graphique possède le mode degrés et le mode radian, réglez-le sur le mode radian.
2. Entrez :\(1 \; /\)
3. Appuyez sur la touche SIN.
4. Entrez la valeur de l'angle entre parenthèses.
5. Appuyez sur la touche ENTER.

Exemple\(\PageIndex{10}\): Evaluating the Cosecant Using Technology

Évaluez la cosécante de\(\frac{5π}{7}\).

Solution

Pour une calculatrice scientifique, entrez les informations comme suit :

\[ \mathrm{1 / ( 5 × π / 7 ) SIN =}\]

\[ \mathrm{ \csc (\dfrac{5π}{7})≈1.279} \]

Exercice\(\PageIndex{10}\):

Évaluez la cotangente de\(−\frac{π}{8}\).

\(≈−2.414\)

médias

Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner à utiliser d'autres fonctions trigonométriques.

• Déterminer les valeurs de la fonction Trig
• Autres exemples de détermination des fonctions de déclenchement
• Identités pythagoriciennes
• Fonctions de déclenchement sur une calculatrice

Équations clés

Fonction tangente	\( \tan t= \frac{ \sin t}{\cos t}\)
Fonction sécante	\( \sec t= \frac{1}{ \cos t}\)
Fonction cosécante	\( \csc t= \frac{1}{ \sin t}\)
Fonction cotangente	\( \cot t= \frac{1}{\tan t}= \frac{\cos t}{ \sin t}\)

Concepts clés

• La tangente d'un angle est le rapport entre la valeur y et la valeur x du point correspondant sur le cercle unitaire.
• La sécante, la cotangente et la cosécante sont toutes réciproques des autres fonctions. La sécante est l'inverse de la fonction cosinus, la cotangente est l'inverse de la fonction tangente et la cosécante est l'inverse de la fonction sinusoïdale.
• Les six fonctions trigonométriques peuvent être trouvées à partir d'un point du cercle unitaire. Voir l'exemple.
• Les fonctions trigonométriques peuvent également être trouvées sous un angle. Voir l'exemple.
• Les fonctions trigonométriques des angles situés à l'extérieur du premier quadrant peuvent être déterminées à l'aide d'angles de référence. Voir l'exemple.
• Une fonction est dite paire si\(f(−x)=f(x)\) et impaire si\(f(−x)=−f(x)\).
• Le cosinus et la sécante sont pairs ; le sinus, la tangente, la cosécante et la cotangente sont impairs.
• Les propriétés paires et impaires peuvent être utilisées pour évaluer les fonctions trigonométriques. Voir l'exemple.
• L'identité pythagoricienne permet de trouver un cosinus à partir d'un sinus ou un sinus à partir d'un cosinus.
• Les identités peuvent être utilisées pour évaluer les fonctions trigonométriques. Voir Exemple et Exemple.
• Les identités fondamentales telles que l'identité pythagoricienne peuvent être manipulées algébriquement pour produire de nouvelles identités. Voir l'exemple.
• Les fonctions trigonométriques se répètent à intervalles réguliers.
• La période\(P\) d'une fonction récurrente f f est le plus petit intervalle tel que\(f(x+P)=f(x)\) pour toute valeur de\(x\).
• Les valeurs des fonctions trigonométriques des angles spéciaux peuvent être trouvées par analyse mathématique.
• Pour évaluer les fonctions trigonométriques d'autres angles, nous pouvons utiliser une calculatrice ou un logiciel informatique. Voir l'exemple.

Lexique

cosécant

l'inverse de la fonction sinus : sur le cercle unitaire,\( \csc t=\frac{1}{y},y≠0\)

cotangente

l'inverse de la fonction tangente : sur le cercle unitaire,\( \cot t= \frac{x}{y},y≠0\)

identités

des déclarations qui sont vraies pour toutes les valeurs de l'entrée sur laquelle elles sont définies

période

le plus petit intervalle\(P\) d'une fonction répétitive\(f\) tel que\(f(x+P)=f(x)\)

sécant

l'inverse de la fonction cosinus : sur le cercle unitaire,\( \sec t= \frac{1}{x},x≠0 \)

tangente

le quotient du sinus et du cosinus : sur le cercle unitaire,\( \tan t= \frac{y}{x},x≠0\)