6.4 : Graphiques des fonctions logarithmiques
- Page ID
- 195648
- Identifiez le domaine d'une fonction logarithmique.
- Fonctions logarithmiques du graphe.
Dans la section sur les graphes des fonctions exponentielles, nous avons vu comment la création d'une représentation graphique d'un modèle exponentiel nous donne une autre couche de connaissances pour prédire les événements futurs. Comment les graphes logarithmiques nous donnent-ils un aperçu des situations ? Comme chaque fonction logarithmique est la fonction inverse d'une fonction exponentielle, nous pouvons considérer chaque sortie d'un graphe logarithmique comme l'entrée de l'équation exponentielle inverse correspondante. En d'autres termes, les logarithmes indiquent la cause d'un effet.
À titre d'exemple, supposons que nous investissions\($2500\) dans un compte qui offre un taux d'intérêt annuel de 5 %, composé en continu. Nous savons déjà que le solde de notre compte pour chaque année\(t\) peut être trouvé à l'aide de l'équation\(A=2500e^{0.05t}\).
Et si nous voulions connaître l'année pour trouver un équilibre ? Nous aurions besoin de créer une nouvelle fonction correspondante en échangeant l'entrée et la sortie ; nous aurions donc besoin de créer un modèle logarithmique pour cette situation. En dessinant le modèle, nous pouvons voir la production (année) pour n'importe quelle entrée (solde du compte). Et si nous voulions savoir combien d'années il faudrait pour que notre investissement initial double ? La figure\(\PageIndex{1}\) montre ce point sur le graphique logarithmique.
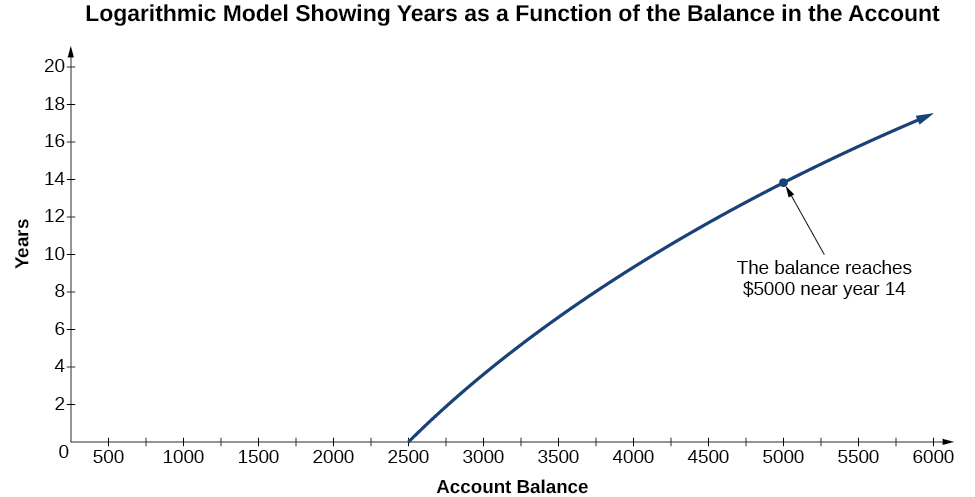
Dans cette section, nous allons discuter des valeurs pour lesquelles une fonction logarithmique est définie, puis nous allons nous concentrer sur la représentation graphique de la famille de fonctions logarithmiques.
Trouver le domaine d'une fonction logarithmique
Avant de travailler avec des graphes, nous allons examiner le domaine (l'ensemble des valeurs d'entrée) pour lequel la fonction logarithmique est définie.
Rappelons que la fonction exponentielle est définie comme\(y=b^x\) pour tout nombre réel\(x\) et constante\(b>0\),\(b≠1\), où
- Le domaine de\(y\) est\((−\infty,\infty)\).
- La gamme de\(y\) est\((0,\infty)\).
Dans la dernière section, nous avons appris que la fonction logarithmique\(y={\log}_b(x)\) est l'inverse de la fonction exponentielle\(y=b^x\). Donc, en tant que fonctions inverses :
- Le domaine de\(y={\log}_b(x)\) est la gamme de\(y=b^x\) :\((0,\infty)\).
- La gamme de\(y={\log}_b(x)\) est le domaine de\(y=b^x\) :\((−\infty,\infty)\).
Les transformations de la fonction parent\(y={\log}_b(x)\) se comportent de la même manière que celles des autres fonctions. Comme pour les autres fonctions parents, nous pouvons appliquer les quatre types de transformations (décalages, étirements, compressions et réflexions) à la fonction parent sans perte de forme.
Dans Graphs of Exponential Functions, nous avons vu que certaines transformations peuvent modifier la plage de\(y=b^x\). De même, l'application de transformations à la fonction parent\(y={\log}_b(x)\) peut modifier le domaine. Lors de la recherche du domaine d'une fonction logarithmique, il est donc important de se rappeler que le domaine ne comprend que des nombres réels positifs. C'est-à-dire que l'argument de la fonction logarithmique doit être supérieur à zéro.
Par exemple, considérez\(f(x)={\log}_4(2x−3)\). Cette fonction est définie pour toutes les valeurs\(x\) telles que l'argument, dans ce cas\(2x−3\), soit supérieur à zéro. Pour trouver le domaine, nous établissons une inégalité et résolvons les problèmes\(x\) suivants :
\[\begin{align*} 2x-3&> 0 \qquad \text {Show the argument greater than zero}\\ 2x&> 3 \qquad \text{Add 3} \\ x&> 1.5 \qquad \text{Divide by 2} \\ \end{align*}\]
En notation par intervalles, le domaine de\(f(x)={\log}_4(2x−3)\) est\((1.5,\infty)\).
- Définissez une inégalité avec un argument supérieur à zéro.
- Résolvez pour\(x\).
- Écrivez le domaine en notation par intervalles.
Quel est le domaine de\(f(x)={\log}_2(x+3)\) ?
Solution
La fonction logarithmique est définie uniquement lorsque l'entrée est positive, donc cette fonction est définie quand\(x+3>0\). Résoudre cette inégalité,
\[\begin{align*} x+3&> 0 \qquad \text{The input must be positive}\\ x&> -3 \qquad \text{Subtract 3} \end{align*}\]
Le domaine de\(f(x)={\log}_2(x+3)\) est\((−3,\infty)\).
Quel est le domaine de\(f(x)={\log}_5(x−2)+1\) ?
- Réponse
-
\((2,\infty)\)
Quel est le domaine de\(f(x)=\log(5−2x)\) ?
Solution
La fonction logarithmique est définie uniquement lorsque l'entrée est positive, donc cette fonction est définie quand\(5–2x>0\). Résoudre cette inégalité,
\[\begin{align*} 5-2x&> 0 \qquad \text{The input must be positive}\\ -2x&> -5 \qquad \text{Subtract 5}\\ x&< \dfrac{5}{2} \qquad \text{Divide by -2 and switch the inequality} \end{align*}\]
Le domaine de\(f(x)=\log(5−2x)\) est\(\left(–\infty,\dfrac{5}{2}\right)\).
Quel est le domaine de\(f(x)=\log(x−5)+2\) ?
- Réponse
-
\((5,\infty)\)
Représentation graphique de fonctions logarithmiques
Maintenant que nous avons une idée de l'ensemble de valeurs pour lesquelles une fonction logarithmique est définie, nous passons à la représentation graphique des fonctions logarithmiques. La famille des fonctions logarithmiques inclut la fonction parent\(y={\log}_b(x)\) ainsi que toutes ses transformations : déplacements, étirements, compressions et réflexions.
Nous commençons par la fonction parent\(y={\log}_b(x)\). Comme chaque fonction logarithmique de cette forme est l'inverse d'une fonction exponentielle associée à la forme\(y=b^x\), leurs graphes seront des reflets les uns des autres sur la ligne\(y=x\). Pour illustrer cela, nous pouvons observer la relation entre les valeurs d'entrée et de sortie de\(y=2^x\) et leur équivalent\(x={\log}_2(y)\) dans le tableau\(\PageIndex{1}\).
| \(x\) | \(−3\) | \(−2\) | \(−1\) | \(0\) | \(1\) | \(2\) | \(3\) |
|---|---|---|---|---|---|---|---|
| \(2^x=y\) | \(\dfrac{1}{8}\) | \(\dfrac{1}{4}\) | \(\dfrac{1}{2}\) | \(1\) | \(2\) | \(4\) | \(8\) |
| \({\log}_2(y)=x\) | \(−3\) | \(−2\) | \(−1\) | \(0\) | \(1\) | \(2\) | \(3\) |
En utilisant les entrées et les sorties de Table\(\PageIndex{1}\), nous pouvons créer un autre tableau pour observer la relation entre les points sur les graphes des fonctions inverses\(f(x)=2^x\) et\(g(x)={\log}_2(x)\). Voir le tableau\(\PageIndex{2}\).
| \(f(x)=2^x\) | \(\left(−3,\dfrac{1}{8}\right)\) | \(\left(−2,\dfrac{1}{4}\right)\) | \(\left(−1,\dfrac{1}{2}\right)\) | \((0,1)\) | \((1,2)\) | \((2,4)\) | \((3,8)\) |
|---|---|---|---|---|---|---|---|
| \(g(x)={\log}_2(x)\) | \(\left(\dfrac{1}{8},−3\right)\) | \(\left(\dfrac{1}{4},−2\right)\) | \(\left(\dfrac{1}{2},−1\right)\) | \((1,0)\) | \((2,1)\) | \((4,2)\) | \((8,3)\) |
Comme on pouvait s'y attendre, les\(y\) coordonnées\(x\) - et - sont inversées pour les fonctions inverses. La figure\(\PageIndex{2}\) montre le graphique de\(f\) et\(g\).
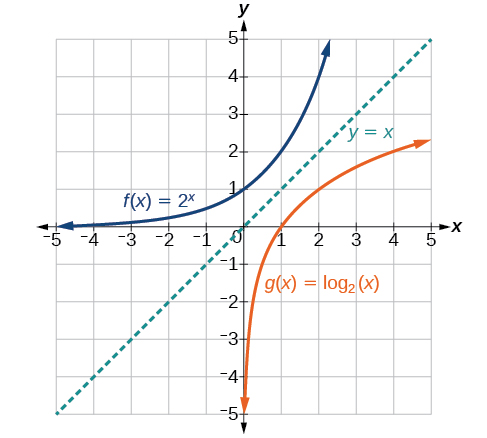
Observez ce qui suit sur le graphique :
- \(f(x)=2^x\)possède un\(y\) -intercept à\((0,1)\) et\(g(x)={\log}_2(x)\) possède un\(x\) - intercept à\((1,0)\).
- Le domaine de\(f(x)=2^x\)\((−\infty,\infty)\), est identique à la plage de\(g(x)={\log}_2(x)\).
- La plage de\(f(x)=2^x\)\((0,\infty)\), est identique au domaine de\(g(x)={\log}_2(x)\).
Pour tout nombre réel\(x\) et constant\(b>0\)\(b≠1\), nous pouvons voir les caractéristiques suivantes dans le graphique de\(f(x)={\log}_b(x)\) :
- fonction un à un
- asymptote verticale :\(x=0\)
- domaine :\((0,\infty)\)
- gamme :\((−\infty,\infty)\)
- \(x\)- interception :\((1,0)\) et point clé\((b,1)\)
- \(y\)-interception : aucune
- augmentant si\(b>1\)
- décroissant si\(0<b<1\)
Voir la figure\(\PageIndex{3}\).
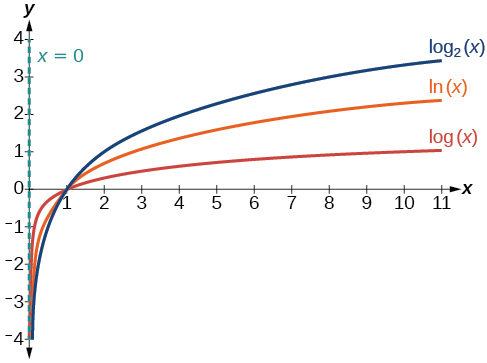
La figure\(\PageIndex{4}\) montre comment la modification de la base\(b\) dans\(f(x)={\log}_b(x)\) peut affecter les graphiques. Observez que les graphes se compriment verticalement lorsque la valeur de la base augmente. (Remarque : rappelez-vous que la fonction\(\ln(x)\) a une base\(e≈2.718\).)
- Dessinez et étiquetez l'asymptote verticale,\(x=0\).
- Tracez l'intersection X,\((1,0)\).
- Tracez le point clé\((b,1)\).
- Tracez une courbe lisse à travers les points.
- Indiquez le domaine\((0,\infty)\), la plage et l'asymptote verticale,\(x=0\).\((−\infty,\infty)\)
Graphe\(f(x)={\log}_5(x)\). Indiquez le domaine, la plage et l'asymptote.
Solution
Avant de créer un graphique, identifiez le comportement et les points clés du graphique.
- Puisque\(b=5\) c'est supérieur à un, nous savons que la fonction augmente. La queue gauche du graphique se rapprochera de l'asymptote verticale\(x=0\), et la queue droite augmentera lentement sans limite.
- Le\(x\) -intercept est\((1,0)\).
- Le point clé\((5,1)\) se trouve sur le graphique.
- Nous dessinons et étiquetons l'asymptote, traçons et étiquetons les points et dessinons une courbe lisse à travers les points (voir Figure\(\PageIndex{5}\)).
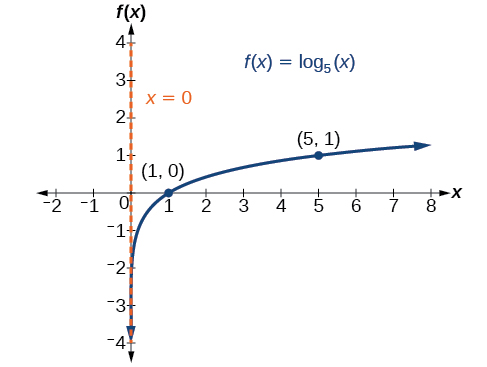
Le domaine est\((0,\infty)\), la plage est\((−\infty,\infty)\) et l'asymptote verticale est\(x=0\).
Graphe\(f(x)={\log}_{\tfrac{1}{5}}(x)\). Indiquez le domaine, la plage et l'asymptote.
- Réponse
-
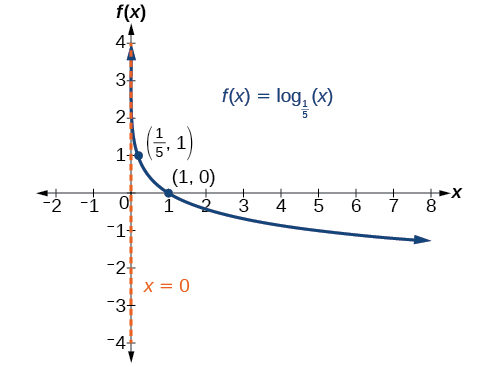
Figurine\(\PageIndex{6}\) Le domaine est\((0,\infty)\), la plage est\((−\infty,\infty)\) et l'asymptote verticale est\(x=0\).
Représentation graphique des transformations de fonctions logarithmiques
Comme nous l'avons mentionné au début de la section, les transformations des graphes logarithmiques se comportent de la même manière que celles des autres fonctions mères. Nous pouvons déplacer, étirer, comprimer et refléter la fonction mère\(y={\log}_b(x)\) sans perte de forme.
Représentation graphique d'un décalage horizontal de\(f(x) = log_b(x)\)
Lorsqu'une constante\(c\) est ajoutée à l'entrée de la fonction parent\(f(x)={\log}_b(x)\), le résultat est un décalage horizontal des\(c\) unités dans la direction opposée à celle du signe\(c\). Pour visualiser les décalages horizontaux, nous pouvons observer le graphique général de la fonction parent\(f(x)={\log}_b(x)\) et du décalage à\(c>0\) côté du décalage vers la gauche et du décalage vers la droite\(h(x)={\log}_b(x−c)\).\(g(x)={\log}_b(x+c)\) Voir la figure\(\PageIndex{7}\).
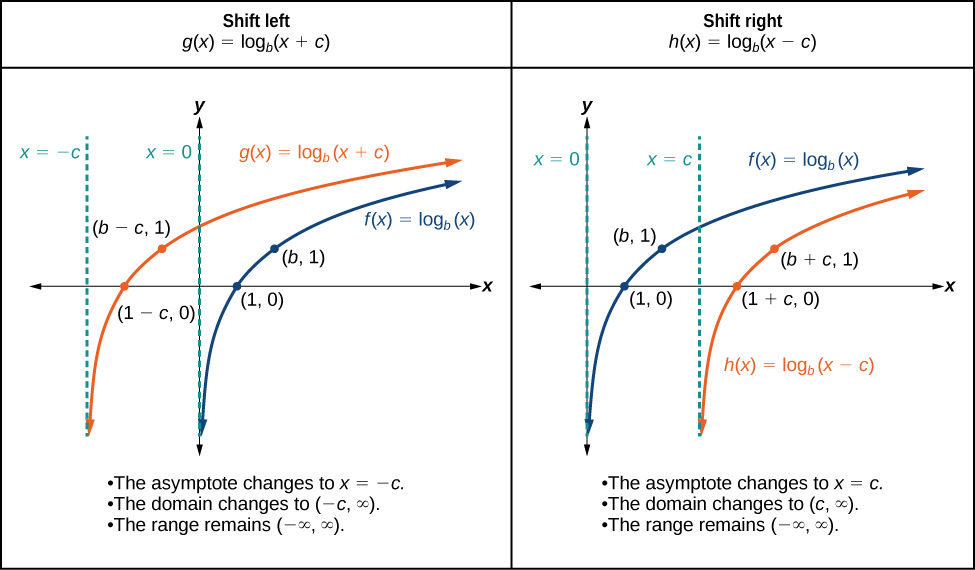
Pour toute constante\(c\), la fonction\(f(x)={\log}_b(x+c)\)
- déplace la fonction parent\(y={\log}_b(x)\) vers la gauche\(c\) des unités si\(c>0\).
- décale la fonction parent d'\(c\)unités\(y={\log}_b(x)\) droites si\(c<0\).
- possède l'asymptote verticale\(x=−c\).
- possède un domaine\((−c,\infty)\).
- a de la portée\((−\infty,\infty)\).
- Identifiez le décalage horizontal :
- Si\(c>0\), décalez le graphique des\(c\) unités de\(f(x)={\log}_b(x)\) gauche.
- Si\(c<0\), déplacez le graphique des\(c\) unités\(f(x)={\log}_b(x)\) droites.
- Dessine l'asymptote verticale\(x=−c\).
- Identifiez trois points clés de la fonction parent. Trouvez de nouvelles coordonnées pour les fonctions décalées en les soustrayant\(c\) de la\(x\) coordonnée.
- Étiquetez les trois points.
- Le domaine est\((−c,\infty)\), la plage est\((−\infty,\infty)\) et l'asymptote verticale est\(x=−c\).
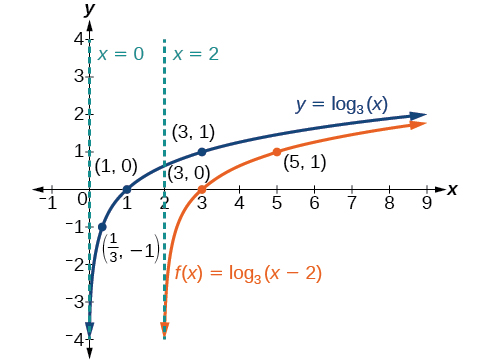
Esquissez le décalage horizontal\(f(x)={\log}_3(x−2)\) à côté de sa fonction parent. Incluez les points clés et les asymptotes sur le graphique. Indiquez le domaine, la plage et l'asymptote.
Solution
Puisque la fonction est\(f(x)={\log}_3(x−2)\), on le remarque\(x+(−2)=x–2\).
Donc\(c=−2\), donc\(c<0\). Cela signifie que nous allons déplacer la fonction de 2 unités vers la\(f(x)={\log}_3(x)\) droite.
L'asymptote verticale est\(x=−(−2)\) ou\(x=2\).
Tenez compte des trois points clés de la fonction parent\(\left(\dfrac{1}{3},−1\right)\),\((1,0)\), et\((3,1)\).
Les nouvelles coordonnées sont trouvées en\(2\) les ajoutant aux\(x\) coordonnées.
Étiquetez les points\(\left(\dfrac{7}{3},−1\right)\)\((3,0)\), et\((5,1)\).
Le domaine est\((2,\infty)\), la plage est\((−\infty,\infty)\) et l'asymptote verticale est\(x=2\).
Esquissez un graphique à\(f(x)={\log}_3(x+4)\) côté de sa fonction parent. Incluez les points clés et les asymptotes sur le graphique. Indiquez le domaine, la plage et l'asymptote.
- Réponse
-
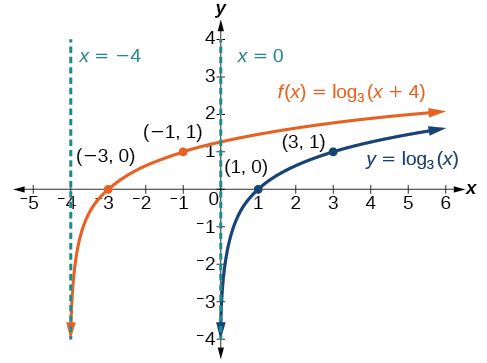
Figurine\(\PageIndex{9}\) Le domaine est\((−4,\infty)\), la plage\((−\infty,\infty)\) et l'asymptote\(x=–4\).
Représentation graphique d'un décalage vertical de\(y = log_b(x)\)
Lorsqu'une constante\(d\) est ajoutée à la fonction parent\(f(x)={\log}_b(x)\), le résultat est un décalage vertical\(d\) d'unités dans la direction du signe\(d\). Pour visualiser les décalages verticaux, nous pouvons observer le graphique général de la fonction parent à\(f(x)={\log}_b(x)\) côté du décalage vers le haut\(g(x)={\log}_b(x)+d\) et du décalage vers le bas,\(h(x)={\log}_b(x)−d\) voir Figure\(\PageIndex{10}\).
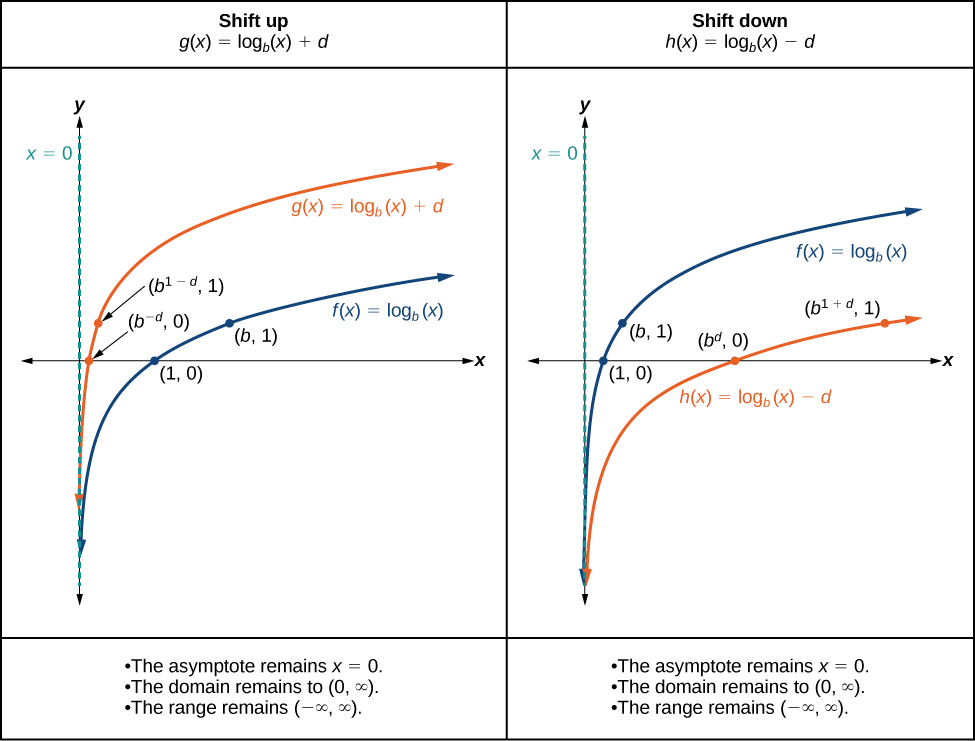
Pour toute constante\(d\), la fonction\(f(x)={\log}_b(x)+d\)
- déplace la fonction parent vers le\(y={\log}_b(x)\) haut\(d\) d'unités si\(d>0\).
- déplace la fonction parent\(y={\log}_b(x)\) vers le bas\(d\) d'unités si\(d<0\).
- possède l'asymptote verticale\(x=0\).
- possède un domaine\((0,\infty)\).
- a de la portée\((−\infty,\infty)\).
- Identifiez le décalage vertical :
- Si\(d>0\), décalez le graphique des\(d\) unités\(f(x)={\log}_b(x)\) vers le haut.
- Si\(d<0\), décalez le graphique des\(d\) unités\(f(x)={\log}_b(x)\) vers le bas.
- Dessine l'asymptote verticale\(x=0\).
- Identifiez trois points clés de la fonction parent. Trouvez de nouvelles coordonnées pour les fonctions décalées en les ajoutant\(d\) aux\(y\) coordonnées.
- Étiquetez les trois points.
- Le domaine est\((0,\infty)\), la plage est\((−\infty,\infty)\) et l'asymptote verticale est\(x=0\).
Esquissez un graphique à\(f(x)={\log}_3(x)−2\) côté de sa fonction parent. Incluez les points clés et l'asymptote sur le graphique. Indiquez le domaine, la plage et l'asymptote.
Solution
Puisque la fonction est\(f(x)={\log}_3(x)−2\), nous le remarquerons\(d=–2\). Ainsi\(d<0\).
Cela signifie que nous allons déplacer la fonction\(f(x)={\log}_3(x)\) vers le\(2\) bas.
L'asymptote verticale est\(x=0\).
Tenez compte des trois points clés de la fonction parent\(\left(\dfrac{1}{3},−1\right)\),\((1,0)\), et\((3,1)\).
Les nouvelles coordonnées sont trouvées en les\(2\) soustrayant des coordonnées y.
Étiquetez les points\(\left(\dfrac{1}{3},−3\right)\)\((1,−2)\), et\((3,−1)\).
Le domaine est\((0,\infty)\), la plage est\((−\infty,\infty)\) et l'asymptote verticale est\(x=0\).
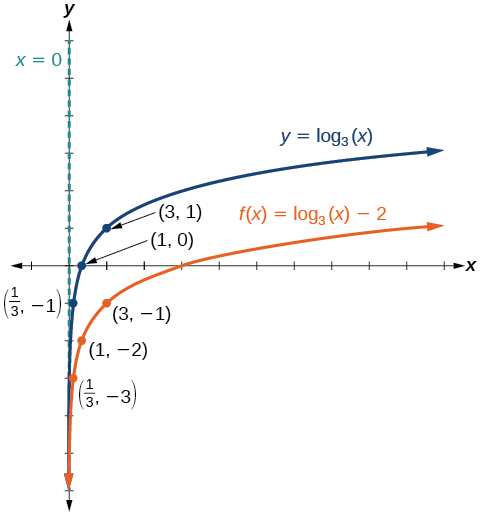
Le domaine est\((0,\infty)\), la plage est\((−\infty,\infty)\) et l'asymptote verticale est\(x=0\).
Esquissez un graphique à\(f(x)={\log}_2(x)+2\) côté de sa fonction parent. Incluez les points clés et l'asymptote sur le graphique. Indiquez le domaine, la plage et l'asymptote.
- Réponse
-
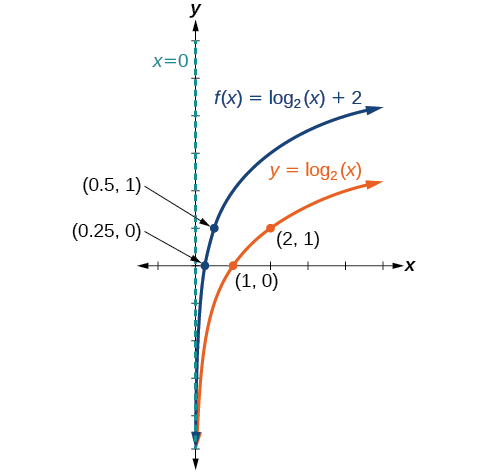
Figurine\(\PageIndex{12}\) Le domaine est\((0,\infty)\), la plage est\((−\infty,\infty)\) et l'asymptote verticale est\(x=0\).
Représentation graphique des étirements et des compressions de\(y = log_b(x)\)
Lorsque la fonction parent\(f(x)={\log}_b(x)\) est multipliée par une constante\(a>0\), le résultat est un étirement vertical ou une compression du graphe d'origine. Pour visualiser les étirements et les compressions, nous définissons\(a>1\) et observons le graphique général de la fonction parent à\(f(x)={\log}_b(x)\) côté de l'étirement vertical\(g(x)=a{\log}_b(x)\) et de la compression verticale,\(h(x)=\dfrac{1}{a}{\log}_b(x)\) voir Figure\(\PageIndex{13}\).
Pour toute constante\(a>1\), la fonction\(f(x)=a{\log}_b(x)\)
- étend la fonction parent\(y={\log}_b(x)\) verticalement d'un facteur\(a\) if\(a>1\).
- comprime la fonction parent\(y={\log}_b(x)\) verticalement d'un facteur\(a\) if\(0<a<1\).
- possède l'asymptote verticale\(x=0\).
- possède l'\(x\)option -intercept\((1,0)\).
- possède un domaine\((0,\infty)\).
- a de la portée\((−\infty,\infty)\).
- Identifiez l'étirement vertical ou les compressions :
- Si\(|a|>1\), le graphique de\(f(x)={\log}_b(x)\) est étiré par un facteur d'\(a\)unités.
- Si\(|a|<1\), le graphe de\(f(x)={\log}_b(x)\) est compressé par un facteur d'\(a\)unités.
- Dessine l'asymptote verticale\(x=0\).
- Identifiez trois points clés de la fonction parent. Trouvez de nouvelles coordonnées pour les fonctions décalées en multipliant leurs coordonnées y par\(a\).
- Étiquetez les trois points.
- Le domaine est\((0,\infty)\), la plage est\((−\infty,\infty)\) et l'asymptote verticale est\(x=0\).
Esquissez un graphique à\(f(x)=2{\log}_4(x)\) côté de sa fonction parent. Incluez les points clés et l'asymptote sur le graphique. Indiquez le domaine, la plage et l'asymptote.
Solution
Puisque la fonction est\(f(x)=2{\log}_4(x)\), nous le remarquerons\(a=2\).
Cela signifie que nous allons étirer la fonction\(f(x)={\log}_4(x)\) d'un facteur de\(2\).
L'asymptote verticale est\(x=0\).
Tenez compte des trois points clés de la fonction parent\(\left(\dfrac{1}{4},−1\right)\),\((1,0)\), et\((4,1)\).
Les nouvelles coordonnées sont trouvées en multipliant les\(y\) coordonnées par\(2\).
Étiquetez les points\(\left(\dfrac{1}{4},−2\right)\)\((1,0)\), et\((4,2)\).
Le domaine est\((0, \infty)\), la plage est\((−\infty,\infty)\) et l'asymptote verticale est\(x=0\). Voir la figure\(\PageIndex{14}\).
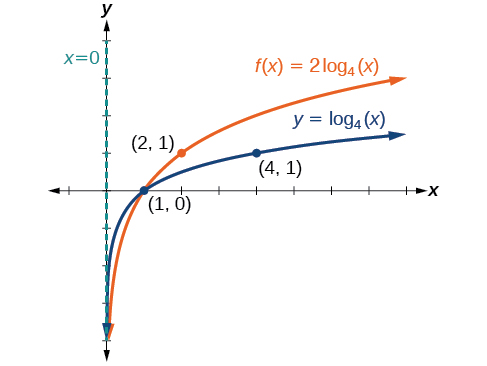
Le domaine est\((0,\infty)\), la plage est\((−\infty,\infty)\) et l'asymptote verticale est\(x=0\).
Esquissez un graphique à\(f(x)=\dfrac{1}{2}{\log}_4(x)\) côté de sa fonction parent. Incluez les points clés et l'asymptote sur le graphique. Indiquez le domaine, la plage et l'asymptote.
- Réponse
-
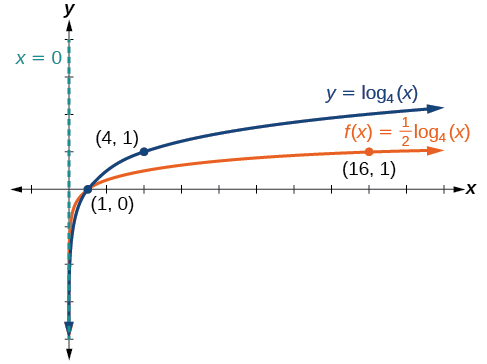
Figurine\(\PageIndex{15}\) Le domaine est\((0,\infty)\), la plage est\((−\infty,\infty)\) et l'asymptote verticale est\(x=0\).
Esquissez un graphique de\(f(x)=5{\log}(x+2)\). Indiquez le domaine, la plage et l'asymptote.
Solution
N'oubliez pas que ce qui se passe entre parenthèses se produit en premier. Tout d'abord, nous déplaçons le graphe\(2\) d'unités vers la gauche, puis nous étendons la fonction verticalement d'un facteur de\(5\), comme dans la Figure\(\PageIndex{16}\). L'asymptote verticale sera déplacée vers\(x=−2\). Le\(x\) -intercept sera\((−1,0)\). Le domaine sera\((−2,\infty)\). Deux points aideront à donner la forme du graphique :\((−1,0)\) et\((8,5)\). Nous avons choisi\(x=8\) comme coordonnée x d'un point à tracer car quand\(x=8\)\(x+2=10\), la base du logarithme commun.
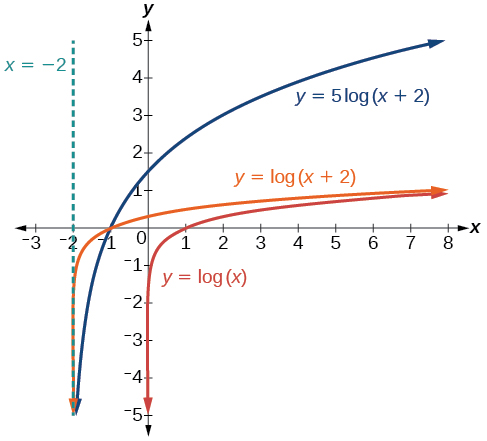
Le domaine est\((−2,\infty)\), la plage est\((−\infty,\infty)\) et l'asymptote verticale est\(x=−2\).
Esquissez un graphique de la fonction\(f(x)=3{\log}(x−2)+1\). Indiquez le domaine, la plage et l'asymptote.
- Réponse
-
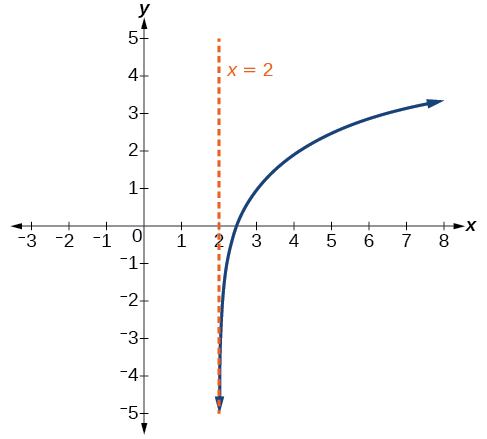
Figurine\(\PageIndex{17}\) Le domaine est\((2,\infty)\), la plage est\((−\infty,\infty)\) et l'asymptote verticale est\(x=2\).
Reflections graphiques de\(f(x) = log_b(x)\)
Lorsque la fonction parent\(f(x)={\log}_b(x)\) est multipliée par\(−1\), le résultat est une réflexion autour de l'\(x\)axe. Lorsque l'entrée est multipliée par\(−1\), le résultat est une réflexion autour de l'\(y\)axe. Pour visualiser les réflexions, nous\(b>1\) limitons et observons le graphe général de la fonction parent à\(f(x)={\log}_b(x)\) côté de la réflexion sur\(x\) l'axe\(g(x)=−{\log}_b(x)\) -et de la réflexion sur l'\(y\)axe\(h(x)={\log}_b(−x)\) -.
La fonction\(f(x)=−{\log}_b(x)\)
- reflète la fonction parent\(y={\log}_b(x)\) concernant l'\(x\)axe.
- possède un domaine\((0,\infty)\)\((−\infty,\infty)\), une plage et une asymptote verticale\(x=0\), qui sont inchangés par rapport à la fonction parent.
La fonction\(f(x)={\log}_b(−x)\)
- reflète la fonction parent\(y={\log}_b(x)\) concernant l'\(y\)axe.
- possède un domaine\((−\infty,0)\).
- possède une plage et une asymptote verticale\(x=0\), qui sont inchangées par rapport à la fonction parent.\((−\infty,\infty)\)
| Si\(f(x)=−{\log}_b(x)\) | Si\(f(x)={\log}_b(−x)\) |
|---|---|
\ (f (x) =− {\ log} _b (x) \) « >
|
\ (f (x) = {\ log} _b (−x) \) « >
|
\ (f (x) =− {\ log} _b (x) \) « >
|
\ (f (x) = {\ log} _b (−x) \) « >
|
\ (f (x) =− {\ log} _b (x) \) « >
|
\ (f (x) = {\ log} _b (−x) \) « >
|
\ (f (x) =− {\ log} _b (x) \) « >
|
\ (f (x) = {\ log} _b (−x) \) « >
|
\ (f (x) =− {\ log} _b (x) \) « >
|
\ (f (x) = {\ log} _b (−x) \) « >
|
Esquissez un graphique à\(f(x)=\log(−x)\) côté de sa fonction parent. Incluez les points clés et l'asymptote sur le graphique. Indiquez le domaine, la plage et l'asymptote.
Solution
Avant de créer un graphique\(f(x)=log(−x)\)\(f(x)=log(−x)\), identifiez le comportement et les points clés du graphique.
- Puisque\(b=10\) est supérieur à un, nous savons que la fonction parentale augmente. Puisque la valeur d'entrée est multipliée par\(−1\),\(f(x)\) reflète le graphe parent autour de l'axe\(y\) -. Ainsi, il\(f(x)=\log(−x)\) diminuera au fur et à mesure que l'on\(x\) passe de l'infini négatif à zéro, et la fin droite du graphique se rapprochera de l'asymptote verticale\(x=0\).
- Le\(x\) -intercept est\((−1,0)\).
- Nous dessinons et étiquetons l'asymptote, traçons et étiquetons les points et dessinons une courbe lisse à travers les points.
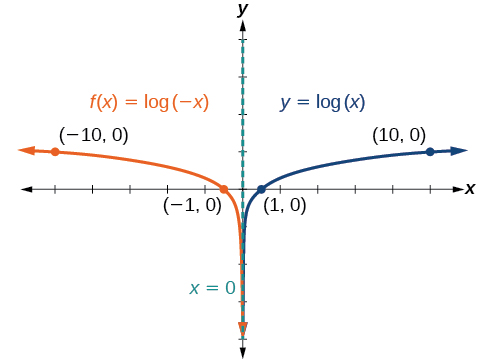
Le domaine est\((−\infty,0)\), la plage est\((−\infty,\infty)\) et l'asymptote verticale est\(x=0\).
Graphe\(f(x)=−\log(−x)\). Indiquez le domaine, la plage et l'asymptote.
- Réponse
-
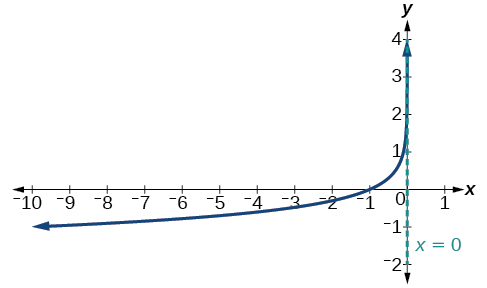
Figurine\(\PageIndex{20}\) Le domaine est\((−\infty,0)\), la plage est\((−\infty,\infty)\) et l'asymptote verticale est\(x=0\).
À
- Appuyez sur [Y=]. Entrez la ou les équations logarithmiques données sous la forme Y 1 = et, si nécessaire, Y 2 =.
- Appuyez sur [GRAPHIQUE] pour observer les graphes des courbes et utilisez [FENÊTRE] pour obtenir une vue appropriée des graphes, y compris leurs points d'intersection.
- Pour trouver la valeur de\(x\), nous calculons le point d'intersection. Appuyez sur [2ND] puis sur [CALC]. Sélectionnez « Intersecter » et appuyez trois fois sur [ENTER]. Le point d'intersection donne la valeur de\(x\), pour le ou les points d'intersection.
Résolvez\(4\ln(x)+1=−2\ln(x−1)\) graphiquement Arrondir au millième le plus proche.
Solution
Appuyez sur [Y=] et entrez à\(4\ln(x)+1\) côté de Y 1 =. Entrez ensuite à\(−2\ln(x−1)\) côté de Y 2 =. Pour une fenêtre, utilisez les valeurs\(0\) de\(5\) forme\(x\0 and \(–10\) à\(10\) pour\(y\). Appuyez sur [GRAPH]. Les graphes doivent se croiser quelque part un peu plus à droite\(x=1\).
Pour une meilleure approximation, appuyez sur [2ND] puis sur [CALC]. Sélectionnez [5 : intersection] et appuyez trois fois sur [ENTER]. La coordonnée x du point d'intersection s'affiche sous la forme\(1.3385297\). (Votre réponse peut être différente si vous utilisez une fenêtre différente ou si vous utilisez une valeur différente pour Guess ? ) Donc, au millième le plus proche,\(x≈1.339\).
Résolvez\(5\log(x+2)=4−\log(x)\) graphiquement Arrondir au millième le plus proche.
- Réponse
-
\(x≈3.049\)
Synthèse des traductions de la fonction logarithmique
Maintenant que nous avons travaillé sur chaque type de translation pour la fonction logarithmique, nous pouvons les résumer dans le tableau\(\PageIndex{4}\) pour obtenir l'équation générale permettant de traduire les fonctions exponentielles.
| Traductions de la fonction parent\(y={\log}_b(x)\) | |
|---|---|
| Traduction | Formulaire |
| \ (y= {\ log} _b (x) \) Traduction">
Shift \(c\)Unités horizontales vers la gauche \(d\)Unités verticales |
\ (y= {\ log} _b (x) \) Formulaire » style="vertical-align:middle ; « >\(y={\log}_b(x+c)+d\) |
| \ (y= {\ log} _b (x) \) Traduction">
Étirer et compresser S'étirer\(|a|>1\) Compression si\(|a|<1\) |
\ (y= {\ log} _b (x) \) Formulaire » style="vertical-align:middle ; « >\(y=a{\log}_b(x)\) |
| \ (y= {\ log} _b (x) \) Translation">Réfléchir sur l'axe des abscisses | \ (y= {\ log} _b (x) \) Formulaire">\(y=−{\log}_b(x)\) |
| \ (y= {\ log} _b (x) \) Translation">Réfléchir à propos de l'axe y | \ (y= {\ log} _b (x) \) Formulaire">\(y={\log}_b(−x)\) |
| \ (y= {\ log} _b (x) \) Translation">Équation générale pour toutes les traductions | \ (y= {\ log} _b (x) \) Formulaire">\(y=a{\log}_b(x+c)+d\) |
Toutes les traductions de la fonction logarithmique parent,\(y={\log}_b(x)\), ont la forme
\(f(x)=a{\log}_b(x+c)+d\)
où la fonction parent,\(y={\log}_b(x)\),\(b>1\), est
- \(d\)unités décalées verticalement vers le haut.
- déplacé horizontalement vers les\(c\) unités de gauche.
- étiré verticalement d'un facteur\(|a|\) if\(|a|>0\).
- compressé verticalement par un facteur\(|a|\) if\(0<|a|<1\).
- reflété autour de l'axe X lorsque\(a<0\).
Pour\(f(x)=\log(−x)\), le graphe de la fonction parent est reflété autour de l'axe y.
De quoi est l'asymptote verticale\(f(x)=−2{\log}_3(x+4)+5\) ?
Solution
L'asymptote verticale est à\(x=−4\).
Analyse
Le coefficient, la base et la translation vers le haut n'affectent pas l'asymptote. Le décalage des\(4\) unités de la courbe vers la gauche déplace l'asymptote verticale vers\(x=−4\).
De quoi est l'asymptote verticale\(f(x)=3+\ln(x−1)\) ?
- Réponse
-
\(x=1\)
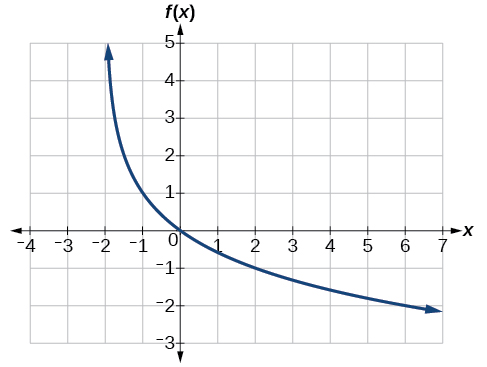
Trouvez une équation possible pour la fonction logarithmique commune représentée sur la figure\(\PageIndex{21}\).
Solution
Ce graphique présente une asymptote verticale à\(x=–2\) et a été réfléchi verticalement. Nous ne connaissons pas encore le décalage vertical ou l'étirement vertical. Nous savons jusqu'à présent que l'équation aura la forme suivante :
\(f(x)=−a\log(x+2)+k\)
Il semble que le graphique passe par les points\((–1,1)\) et\((2,–1)\). Substituant\((–1,1)\),
\[\begin{align*} 1&= -a\log(-1+2)+k \qquad \text{Substitute} (-1,1)\\ 1&= -a\log(1)+k \qquad \text{Arithmetic}\\ 1&= k\log(1)\\ &= 0 \end{align*}\]
Ensuite, en le remplaçant par\((2,–1)\),
\[\begin{align*} -1&= -a\log(2+2)+1 \qquad \text{Substitute} (2,-1)\\ -2&= -a\log(4) \qquad \text{Arithmetic}\\ a&= \dfrac{2}{\log(4)} \qquad \text{Solve for a} \end{align*}\]
Cela nous donne l'équation\(f(x)=–\dfrac{2}{\log(4)}\log(x+2)+1\).
Analyse
Nous pouvons vérifier cette réponse en comparant les valeurs des fonctions dans le tableau\(\PageIndex{5}\) avec les points du graphique de la figure\(\PageIndex{21}\).
| \(x\) | −1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|
| \(f(x)\) | 1 | 0 | −0,58496 | −1 | −1,3219 |
| \(x\) | 4 | 5 | 6 | 7 | 8 |
| \(f(x)\) | −1,5850 | −1 8074 | −2 | −2,1699 | −2,3219 |
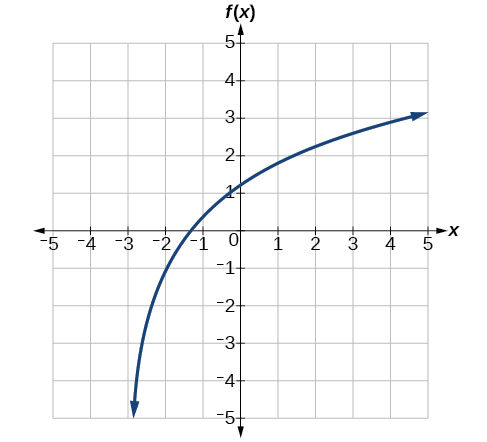
Donnez l'équation du logarithme naturel représentée dans la figure\(\PageIndex{22}\).
- Réponse
-
\(f(x)=2\ln(x+3)−1\)
Oui, si nous savons que la fonction est une fonction logarithmique générale. Par exemple, regardez le graphique de la figure\(\PageIndex{22}\). Le graphe s'approche\(x=−3\) (ou à peu près) de plus en plus près, de même que\(x=−3\) l'asymptote verticale, ou est très proche de celle-ci. Il s'approche par la droite, donc le domaine est composé de tous les points vers la droite,\({x|x>−3}\). La plage, comme toutes les fonctions logarithmiques générales, est composée uniquement de nombres réels. Et nous pouvons voir le comportement final parce que le graphique descend à gauche et monte à droite. Le comportement final est celui en tant que\(x\rightarrow −3^+\),\(f(x)\rightarrow −\infty\) et en tant que\(x\rightarrow \infty\),\(f(x)\rightarrow \infty\).
Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner à utiliser les logarithmes graphiques.
- Représenter graphiquement une fonction exponentielle et une fonction logarithmique
- Associer des graphes à des fonctions exponentielles et logarithmiques
- Trouvez le domaine des fonctions logarithmiques
Équations clés
| Formulaire général pour la traduction de la fonction logarithmique mère\(f(x)={\log}_b(x)\) | \(f(x)=a{\log}_b(x+c)+d\) |
Concepts clés
- Pour trouver le domaine d'une fonction logarithmique, définissez une inégalité indiquant que l'argument est supérieur à zéro et résolvez pour\(x\). Voir Exemple\(\PageIndex{1}\) et Exemple\(\PageIndex{2}\)
- Le graphe de la fonction parent\(f(x)={\log}_b(x)\) possède une intersection X au niveau\((1,0)\), au domaine\((0,\infty)\), à la plage\((−\infty,\infty)\), à l'asymptote\(x=0\) verticale et
-
- si\(b>1\), la fonction augmente.
- si\(0<b<1\), la fonction est décroissante.
- L'équation\(f(x)={\log}_b(x+c)\) déplace la fonction parent\(y={\log}_b(x)\) horizontalement
- \(c\)unités laissées si\(c>0\).
- bonnes\(c\) unités si\(c<0\).
- L'équation\(f(x)={\log}_b(x)+d\) déplace la fonction parent\(y={\log}_b(x)\) verticalement
- \(d\)unités supérieures si\(d>0\).
- \(d\)unités de réduction si\(d<0\).
- Pour toute constante\(a>0\), l'équation\(f(x)=a{\log}_b(x)\)
- étend la fonction parent\(y={\log}_b(x)\) verticalement d'un facteur\(a\) if\(|a|>1\).
- comprime la fonction parent\(y={\log}_b(x)\) verticalement d'un facteur\(a\) if\(|a|<\) 1.
- Lorsque la fonction parent\(y={\log}_b(x)\) est multipliée par\(−1\), le résultat est une réflexion autour de l'axe X. Lorsque l'entrée est multipliée par\(−1\), le résultat est une réflexion autour de l'axe y.
- L'équation\(f(x)=−{\log}_b(x)\) représente le reflet de la fonction parent autour de l'axe X.
- L'équation\(f(x)={\log}_b(−x)\) représente le reflet de la fonction parent par rapport à l'axe y.
- Un calculateur graphique peut être utilisé pour approximer les solutions de certaines équations logarithmiques. Voir Exemple\(\PageIndex{9}\).
- Toutes les traductions de la fonction logarithmique peuvent être résumées par l'équation générale\(f(x)=a{\log}_b(x+c)+d\). Voir le tableau\(\PageIndex{4}\).
- À partir d'une équation de forme générale\(f(x)=a{\log}_b(x+c)+d\), nous pouvons identifier l'asymptote verticale\(x=−c\) de la transformation. Voir l'exemple\(\PageIndex{10}\).
- À l'aide de l'équation générale\(f(x)=a{\log}_b(x+c)+d\), nous pouvons écrire l'équation d'une fonction logarithmique en fonction de son graphe. Voir l'exemple\(\PageIndex{11}\).


