6.3 : Fonctions logarithmiques
- Page ID
- 195684
- Passez de la forme logarithmique à la forme exponentielle.
- Passez de la forme exponentielle à la forme logarithmique.
- Évaluez les logarithmes.
- Utilisez des logarithmes courants.
- Utilisez des logarithmes naturels.
En 2010, un tremblement de terre majeur a frappé Haïti, détruisant ou endommageant plus de 285 000 maisons. Un an plus tard, un autre tremblement de terre plus violent a dévasté Honshu, au Japon, détruisant ou endommageant plus de 332 000 bâtiments, comme ceux illustrés sur la figure\(\PageIndex{1}\). Même si les deux ont causé des dégâts considérables, le tremblement de terre de 2011 a été 100 fois plus violent que celui d'Haïti. Comment le savons-nous ? Les magnitudes des tremblements de terre sont mesurées sur une échelle connue sous le nom d'échelle de Richter. Le tremblement de terre en Haïti a enregistré une valeur de 7,0 sur l'échelle de Richter alors que le tremblement de terre japonais a enregistré une

Figure\(\PageIndex{1}\) : Dévastation causée par le tremblement de terre du 11 mars 2011 à Honshu, au Japon. (crédit : Daniel Pierce).
L'échelle de Richter est une échelle logarithmique de base 10. En d'autres termes, un séisme de magnitude n'\(8\)est pas deux fois plus important qu'un tremblement de terre de magnitude\(4\). C'est
\[10^{8−4}=10^4=10,000 \nonumber\]
fois aussi génial ! Dans cette leçon, nous étudierons la nature de l'échelle de Richter et la fonction de base dix dont elle dépend.
Conversion d'une forme logarithmique à une forme exponentielle
Afin d'analyser l'ampleur des tremblements de terre ou de comparer les magnitudes de deux séismes différents, nous devons être capables de passer de la forme logarithmique à la forme exponentielle. Supposons, par exemple, que la quantité d'énergie libérée par un tremblement de terre soit 500 fois supérieure à la quantité d'énergie libérée par un autre. Nous voulons calculer la différence de magnitude. L'équation qui représente ce problème est\(10^x=500\), où\(x\) représente la différence de magnitudes sur l'échelle de Richter. Comment pourrions-nous résoudre ce problème\(x\) ?
Nous n'avons pas encore appris de méthode pour résoudre des équations exponentielles. Aucun des outils algébriques discutés jusqu'à présent n'est suffisant pour le résoudre\(10^x=500\). Nous le savons\({10}^2=100\) et\({10}^3=1000\) il est donc clair qu'il\(x\) doit y avoir une valeur comprise entre 2 et 3, car elle\(y={10}^x\) augmente. Nous pouvons examiner un graphique, comme dans la figure\(\PageIndex{1}\), pour mieux estimer la solution.
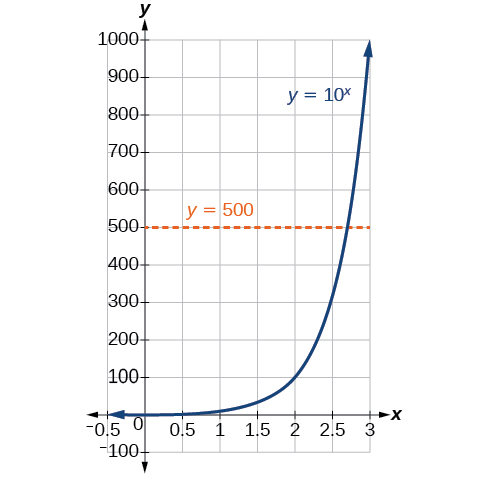
Figurine\(\PageIndex{2}\)
L'estimation à partir d'un graphique est toutefois imprécise. Pour trouver une solution algébrique, il faut introduire une nouvelle fonction. Observez que le graphique de la figure\(\PageIndex{2}\) passe le test de la ligne horizontale. La fonction exponentielle\(y=b^x\) est univoque, donc son inverse\(x=b^y\) est également une fonction. Comme c'est le cas pour toutes les fonctions inverses, nous échangeons simplement\(x\)\(y\) et résolvons\(y\) pour trouver la fonction inverse. Pour représenter\(y\) en fonction de\(x\), nous utilisons une fonction logarithmique de la forme\(y={\log}_b(x)\). Le\(b\) logarithme de base d'un nombre est l'exposant par lequel nous devons augmenter\(b\) pour obtenir ce nombre.
Nous lisons une expression logarithmique comme suit : « Le logarithme avec base\(b\) de\(x\) est égal à » ou\(y\), de manière simplifiée, « base logarithmique\(b\) de\(x\) est »\(y\). On peut aussi dire «\(b\) élevé au pouvoir de l'\(y\)est »\(x\), car les rondins sont des exposants. Par exemple, le\(2\) logarithme de base de\(32\) est\(5\), parce que\(5\) c'est l'exposant auquel nous devons nous appliquer\(2\) pour obtenir\(32\). Depuis\(2^5=32\), on peut écrire\({\log}_232=5\). Nous lisons cela comme « base\(2\)\(32\) logarithmique »\(5\).
Nous pouvons exprimer la relation entre la forme logarithmique et sa forme exponentielle correspondante comme suit :
\[\begin{align} \log_b(x)=y\Leftrightarrow b^y=x, b> 0, b\neq 1 \end{align}\]
Notez que la base\(b\) est toujours positive.
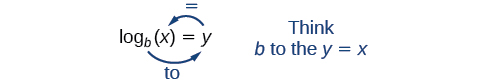
Le logarithme étant une fonction, il est très correctement écrit en utilisant des parenthèses pour indiquer l'évaluation de la fonction, comme nous le ferions avec\(f(x)\).\(\log_b(x)\) Toutefois, lorsque l'entrée est une variable ou un nombre unique, il est courant de voir les parenthèses supprimées et l'expression écrite sans parenthèses, comme\(\log_bx\). Notez que de nombreuses calculatrices nécessitent des parenthèses autour du\(x\).
Nous pouvons illustrer la notation des logarithmes comme suit :

Notez qu'en comparant la fonction logarithme et la fonction exponentielle, l'entrée et la sortie sont commutées. Cela signifie\(y={\log}^b(x)\) et\(y=b^x\) sont des fonctions inverses.
Une base logarithmique\(b\) d'un nombre positif\(x\) répond à la définition suivante.
Pour\(x>0\),\(b>0\),\(b≠1\),
\[\begin{align} y={\log}_b(x)\text{ is equivalent to } b^y=x \end{align}\]
où,
- nous nous lisons\({\log}_b(x)\) comme « le logarithme avec base\(b\) de\(x\) » ou « base logarithmique\(b\) de »\(x\).
- le logarithme\(y\) est l'exposant auquel\(b\) il faut augmenter pour obtenir\(x\).
De plus, étant donné que les fonctions logarithmique et exponentielle\(x\) modifient\(y\) les valeurs et, le domaine et la plage de la fonction exponentielle sont échangés contre la fonction logarithmique. Par conséquent,
- le domaine de la fonction logarithme avec base\(b\) est\((0,\infty)\).
- la plage de la fonction logarithme avec base\(b\) est\((−\infty,\infty)\).
Non. Comme la base d'une fonction exponentielle est toujours positive, aucune puissance de cette base ne peut jamais être négative. On ne peut jamais prendre le logarithme d'un nombre négatif. De plus, nous ne pouvons pas prendre le logarithme de zéro. Les calculateurs peuvent générer un log d'un nombre négatif en mode complexe, mais le log d'un nombre négatif n'est pas un nombre réel.
- Examinez l'équation\(y={\log}_bx\) et identifiez\(b\)\(y\), et\(x\).
- Réécrivez\({\log}_bx=y\) en tant que\(b^y=x\).
Écrivez les équations logarithmiques suivantes sous forme exponentielle.
- \({\log}_6(\sqrt{6})=\dfrac{1}{2}\)
- \({\log}_3(9)=2\)
Solution
Tout d'abord, identifiez les valeurs de\(b\)\(y\), et\(x\). Ensuite, écrivez l'équation dans le formulaire\(b^y=x\).
- \({\log}_6(\sqrt{6})=\dfrac{1}{2}\)
Ici\(b=6\),\(y=\dfrac{1}{2}\), et\(x=\sqrt{6}\). Par conséquent, l'équation\({\log}_6(\sqrt{6})=\dfrac{1}{2}\) est équivalente à
\(6^{\tfrac{1}{2}}=\sqrt{6}\)
- \({\log}_3(9)=2\)
Ici\(b=3\),\(y=2\), et\(x=9\). Par conséquent, l'équation\({\log}_3(9)=2\) est équivalente à
\(3^2=9\)
Écrivez les équations logarithmiques suivantes sous forme exponentielle.
- \({\log}_{10}(1,000,000)=6\)
- \({\log}_5(25)=2\)
- Répondez à une
-
\({\log}_{10}(1,000,000)=6\)est équivalent à\({10}^6=1,000,000\)
- Réponse b
-
\({\log}_5(25)=2\)est équivalent à\(5^2=25\)
Conversion d'une forme exponentielle à une forme logarithmique
Pour convertir des exposants en logarithmes, nous suivons les mêmes étapes en sens inverse. Nous identifions la base\(b\)\(x\), l'exposant et la sortie\(y\). Ensuite, nous écrivons\(x={\log}_b(y)\).
Écrivez les équations exponentielles suivantes sous forme logarithmique.
- \(2^3=8\)
- \(5^2=25\)
- \({10}^{−4}=\dfrac{1}{10,000}\)
Solution
Tout d'abord, identifiez les valeurs de\(b\)\(y\), et\(x\). Ensuite, écrivez l'équation dans le formulaire\(x={\log}_b(y)\).
- \(2^3=8\)
Ici\(b=2\),\(x=3\), et\(y=8\). Par conséquent, l'équation\(2^3=8\) est équivalente à\({\log}_2(8)=3\).
- \(5^2=25\)
Ici\(b=5\),\(x=2\), et\(y=25\). Par conséquent, l'équation\(5^2=25\) est équivalente à\({\log}_5(25)=2\).
- \({10}^{−4}=\dfrac{1}{10,000}\)
Ici\(b=10\),\(x=−4\), et\(y=\dfrac{1}{10,000}\). Par conséquent, l'équation\({10}^{−4}=\dfrac{1}{10,000}\) est équivalente à\({\log}_{10} \left (\dfrac{1}{10,000} \right )=−4\).
Écrivez les équations exponentielles suivantes sous forme logarithmique.
- \(3^2=9\)
- \(5^3=125\)
- \(2^{−1}=\dfrac{1}{2}\)
- Répondez à une
-
\(3^2=9\)est équivalent à\({\log}_3(9)=2\)
- Réponse b
-
\(5^3=125\)est équivalent à\({\log}_5(125)=3\)
- Réponse c
-
\(2^{−1}=\dfrac{1}{2}\)est équivalent à\({\log}_2 \left (\dfrac{1}{2} \right )=−1\)
Évaluation des logarithmes
La connaissance des carrés, des cubes et des racines des nombres nous permet d'évaluer mentalement de nombreux logarithmes. Par exemple, considérez\({\log}_28\). Nous demandons : « À quel exposant\(2\) faut-il augmenter pour obtenir 8 ? » Parce que nous le savons déjà\(2^3=8\), cela s'ensuit\({\log}_28=3\).
Maintenant, pensez à résoudre\({\log}_749\) et\({\log}_327\) mentalement.
- Nous demandons : « À quel exposant\(7\) faut-il augmenter pour obtenir\(49\) ? » Nous le savons\(7^2=49\). Par conséquent,\({\log}_749=2\)
- Nous demandons : « À quel exposant\(3\) faut-il augmenter pour obtenir\(27\) ? » Nous le savons\(3^3=27\). Par conséquent,\(\log_{3}27=3\)
Même certains logarithmes apparemment plus complexes peuvent être évalués sans calculatrice. Par exemple, évaluons\(\log_{\ce{2/3}} \frac{4}{9}\) mentalement.
- Nous nous demandons : « À quel exposant\(\ce{2/3}\) faut-il augmenter pour obtenir\(\ce{4/9}\) ? » Nous savons\(2^2=4\)\(3^2=9\) et\[{\left(\dfrac{2}{3} \right )}^2=\dfrac{4}{9}. \nonumber\] donc,\[{\log}_{\ce{2/3}} \left (\dfrac{4}{9} \right )=2. \nonumber\]
- Réécrivez l'argument\(x\) comme une puissance de\(b\) :\(b^y=x\).
- Utilisez vos connaissances antérieures sur les pouvoirs de l'\(b\)identité\(y\) en vous demandant : « À quel exposant\(b\) faut-il augmenter pour obtenir\(x\) ? »
Résolvez\(y={\log}_4(64)\) sans utiliser de calculatrice.
Solution
Nous réécrivons d'abord le logarithme sous forme exponentielle :\(4^y=64\). Ensuite, nous demandons : « À quel exposant\(4\) faut-il augmenter pour obtenir\(64\) ? »
Nous savons
\(4^3=64\)
Par conséquent,
\({\log}_4(64)=3\)
Résolvez\(y={\log}_{121}(11)\) sans utiliser de calculatrice.
- Réponse
-
\({\log}_{121}(11)=\dfrac{1}{2}\)(rappelant que\(\sqrt{121}={(121)}^{\tfrac{1}{2}}=11)\)
Évaluez\(y={\log}_3 \left (\dfrac{1}{27} \right )\) sans utiliser de calculatrice.
Solution
Nous réécrivons d'abord le logarithme sous forme exponentielle :\(3^y=\dfrac{1}{27}\). Ensuite, nous demandons : « À quel exposant\(3\) faut-il augmenter pour obtenir\(\dfrac{1}{27}\) ? »
Nous le savons\(3^3=27\), mais que devons-nous faire pour obtenir la réciprocité\(\dfrac{1}{27}\) ? N'oubliez pas de travailler avec des exposants qui\(b^{−a}=\dfrac{1}{b^a}\). Nous utilisons ces informations pour écrire
\[\begin{align*} 3^{-3}&= \dfrac{1}{3^3}\\ &= \dfrac{1}{27} \end{align*}\]
Par conséquent,\({\log}_3 \left (\dfrac{1}{27} \right )=−3\).
Évaluez\(y={\log}_2 \left (\dfrac{1}{32} \right )\) sans utiliser de calculatrice.
- Réponse
-
\({\log}_2 \left (\dfrac{1}{32} \right )=−5\)
Utilisation de logarithmes courants
Parfois, nous pouvons voir un logarithme écrit sans base. Dans ce cas, nous supposons que la base est\(10\). En d'autres termes, l'expression\(\log(x)\) signifie\({\log}_{10}(x)\). Nous appelons\(-10\) logarithme de base logarithme commun. Des logarithmes courants sont utilisés pour mesurer l'échelle de Richter mentionnée au début de la section. Les échelles de mesure de la luminosité des étoiles et du pH des acides et des bases utilisent également des logarithmes courants.
Un logarithme courant est un logarithme avec base\(10\). Nous écrivons\({\log}_{10}(x)\) simplement comme\(\log(x)\). Le logarithme commun d'un nombre positif\(x\) répond à la définition suivante.
Pour\(x>0\),
\[\begin{align} y={\log}(x)\text{ is equivalent to } {10}^y=x \end{align}\]
Nous nous lisons\(\log(x)\) comme « le logarithme avec base\(10\) de\(x\) » ou « base logarithmique\(10\) de »\(x\).
Le logarithme\(y\) est l'exposant auquel\(10\) il faut augmenter pour obtenir\(x\).
- Réécrivez l'argument\(x\) comme une puissance de\(10\) :\({10}^y=x\).
- Utilisez vos connaissances antérieures sur\(10\) les pouvoirs d'identification\(y\) en vous demandant : « À quel exposant\(10\) faut-il augmenter pour obtenir\(x\) ? »
Évaluez\(y=\log(1000)\) sans utiliser de calculatrice.
Solution
Nous réécrivons d'abord le logarithme sous forme exponentielle :\({10}^y=1000\). Ensuite, nous demandons : « À quel exposant\(10\) faut-il augmenter pour obtenir\(1000\) ? » Nous savons
\({10}^3=1000\)
Par conséquent,\(\log(1000)=3\).
Évaluer\(y=\log(1,000,000)\).
- Réponse
-
\(\log(1,000,000)=6\)
- Appuyez sur [LOG].
- Entrez la valeur donnée pour\(x\), suivie de [)].
- Appuyez sur [ENTER].
Évaluez\(y=\log(321)\) à quatre décimales à l'aide d'une calculatrice.
Solution
- Appuyez sur [LOG].
- Entrez 321, suivi de [)].
- Appuyez sur [ENTER].
En arrondissant à quatre décimales,\(\log(321)≈2.5065\).
Analyse
Notez cela\({10}^2=100\) et cela\({10}^3=1000\). Puisque\(321\) c'est entre\(100\) et\(1000\), nous savons que cela\(\log(321)\) doit être entre\(\log(100)\) et\(\log(1000)\). Cela nous donne ce qui suit :
\(100<321<1000\)
\(2<2.5065<3\)
Évaluez\(y=\log(123)\) à quatre décimales à l'aide d'une calculatrice.
- Réponse
-
\(\log(123)≈2.0899\)
La quantité d'énergie libérée par un tremblement de terre était\(500\) plusieurs fois supérieure à la quantité d'énergie libérée par un autre. L'équation\({10}^x=500\) représente cette situation, où se\(x\) trouve la différence de magnitudes sur l'échelle de Richter. Au millième près, quelle était la différence de magnitudes ?
Solution
Nous commençons par réécrire l'équation exponentielle sous forme logarithmique.
\({10}^x=500\)
\(\log(500)=x\)Utilisez la définition du journal commun.
Ensuite, nous évaluons le logarithme à l'aide d'une calculatrice :
- Appuyez sur [LOG].
- Entrez\(500\), suivi de [)].
- Appuyez sur [ENTER].
- Au millième le plus proche,\(\log(500)≈2.699\).
La différence de magnitudes était d'environ\(2.699\).
La quantité d'énergie libérée par un tremblement de terre était\(8,500\) plusieurs fois supérieure à la quantité d'énergie libérée par un autre. L'équation\({10}^x=8500\) représente cette situation, où se\(x\) trouve la différence de magnitudes sur l'échelle de Richter. Au millième près, quelle était la différence de magnitudes ?
- Réponse
-
La différence de magnitudes était d'environ\(3.929\).
Utilisation de logarithmes naturels
La base la plus fréquemment utilisée pour les logarithmes est\(e\). Les\(e\) logarithmes de base sont importants en calcul et dans certaines applications scientifiques ; ils sont appelés logarithmes naturels. Le\(e\) logarithme de base\({\log}_e(x)\), possède sa propre notation,\(\ln(x)\). La plupart des valeurs de\(\ln(x)\) peuvent être trouvées uniquement à l'aide d'une calculatrice. La principale exception est que, parce que le logarithme de\(1\) est toujours\(0\) dans n'importe quelle base,\(\ln1=0\). Pour les autres logarithmes naturels, nous pouvons utiliser la\(\ln\) clé que l'on trouve sur la plupart des calculateurs scientifiques. Nous pouvons également trouver le logarithme naturel de toute puissance d'\(e\)utilisation de la propriété inverse des logarithmes.
Un logarithme naturel est un logarithme avec base\(e\). Nous écrivons\({\log}_e(x)\) simplement comme\(\ln(x)\). Le logarithme naturel d'un nombre positif\(x\) répond à la définition suivante.
Pour\(x>0\),
\(y=\ln(x)\)est équivalent à\(e^y=x\)
Nous nous lisons\(\ln(x)\) comme « le logarithme avec base\(e\) de\(x\) » ou « le logarithme naturel de »\(x\).
Le logarithme\(y\) est l'exposant auquel\(e\) il faut augmenter pour obtenir\(x\).
Puisque les fonctions\(y=e^x\) et\(y=\ln(x)\) sont des fonctions inverses,\(\ln(e^x)=x\) pour tous\(x\) et\(e^{\ln (x)}=x\) pour\(x>0\).
- Appuyez sur [LN].
- Entrez la valeur donnée pour\(x\), suivie de [)].
- Appuyez sur [ENTER].
Évaluez\(y=\ln(500)\) à quatre décimales à l'aide d'une calculatrice.
Solution
- Appuyez sur [LN].
- Entrez\(500\), suivi de [)].
- Appuyez sur [ENTER].
En arrondissant à quatre décimales,\(\ln(500)≈6.2146\)
Évaluer\(\ln(−500)\).
- Réponse
-
Il n'est pas possible de prendre le logarithme d'un nombre négatif dans l'ensemble des nombres réels.
Accédez à cette ressource en ligne pour obtenir des instructions et des exercices supplémentaires avec les logarithmes.
Équations clés
| Définition de la fonction logarithmique | Pour\(x>0\),\(b>0\)\(b≠1\),\(y={\log}_b(x)\) si et seulement si\(b^y=x\). |
| Définition du logarithme commun | Pour\(x>0\),\(y=\log(x)\) si et seulement si\({10}^y=x\). |
| Définition du logarithme naturel | Pour\(x>0\),\(y=\ln(x)\) si et seulement si\(e^y=x\). |
Key Concepts
- The inverse of an exponential function is a logarithmic function, and the inverse of a logarithmic function is an exponential function.
- Logarithmic equations can be written in an equivalent exponential form, using the definition of a logarithm. See Example \(\PageIndex{1}\).
- Exponential equations can be written in their equivalent logarithmic form using the definition of a logarithm See Example \(\PageIndex{2}\).
- Logarithmic functions with base \(b\) can be evaluated mentally using previous knowledge of powers of \(b\). See Example \(\PageIndex{3}\) and Example \(\PageIndex{4}\).
- Common logarithms can be evaluated mentally using previous knowledge of powers of \(10\). See Example \(\PageIndex{5}\).
- When common logarithms cannot be evaluated mentally, a calculator can be used. See Example \(\PageIndex{6}\).
- Real-world exponential problems with base \(10\) can be rewritten as a common logarithm and then evaluated using a calculator. See Example \(\PageIndex{7}\).
- Natural logarithms can be evaluated using a calculator Example \(\PageIndex{8}\).


