5.7 : Inverses et fonctions radicales
- Page ID
- 195563
Objectifs d'apprentissage
Dans cette section, vous allez :
- Détermine l'inverse d'une fonction polynomiale inversible.
- Limitez le domaine pour trouver l'inverse d'une fonction polynomiale.
Un monticule de gravier a la forme d'un cône dont la hauteur est égale au double du rayon.
Le volume est déterminé à l'aide d'une formule issue de la géométrie élémentaire.
\[ \begin{align*} V&=\dfrac{1}{3}\pi r^2h \\[4pt] &=\dfrac{1}{3}\pi r^2(2r)\\[4pt] &=\dfrac{2}{3}\pi r^3 \end{align*}\]
Nous avons écrit le volume\(V\) en termes de rayon\(r\). Cependant, dans certains cas, nous pouvons commencer par le volume et vouloir trouver le rayon. Par exemple : un client achète 100 pieds cubes de gravier pour construire un monticule en forme de cône dont la hauteur est le double du rayon. Quels sont le rayon et la hauteur du nouveau cône ? Pour répondre à cette question, nous utilisons la formule
\[r=\sqrt[3]{\dfrac{3V}{2\pi}} \nonumber\]
Cette fonction est l'inverse de la formule pour\(V\) en termes de\(r\).
Dans cette section, nous allons explorer les inverses des fonctions polynomiales et rationnelles, et en particulier les fonctions radicales que nous rencontrons au cours du processus.
Trouver l'inverse d'une fonction polynomiale
Deux fonctions\(f\) et\(g\) sont des fonctions inverses si pour chaque paire de coordonnées dans\(f\)\((a,b)\),, il existe une paire de coordonnées correspondante dans la fonction inverse,\(g\),\((b, a)\). En d'autres termes, les paires de coordonnées des fonctions inverses ont l'entrée et la sortie interchangées. Seules les fonctions un-à-une ont des inverses. Rappelez-vous qu'une fonction biunivoque possède une valeur de sortie unique pour chaque valeur d'entrée et passe le test de la ligne horizontale.
Par exemple, supposons qu'un collecteur d'eau de ruissellement soit construit sous la forme d'une cuvette parabolique, comme le montre la figure\(\PageIndex{2}\). Nous pouvons utiliser les informations de la figure pour déterminer la surface de l'eau dans la cuvette en fonction de la profondeur de l'eau.
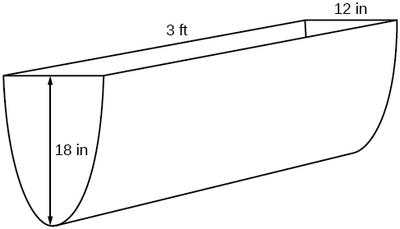
Comme il sera utile de disposer d'une équation pour la forme de la coupe parabolique, nous imposerons un système de coordonnées au niveau de la section transversale, avec une\(x\)\(y\) mesure horizontale et une mesure verticale, avec l'origine au sommet de la parabole (Figure\(\PageIndex{3}\)).
À partir de là, nous trouvons une équation pour la forme parabolique. Nous avons placé l'origine au sommet de la parabole, afin de savoir que l'équation aura une forme\(y(x)=ax^2\). Notre équation devra passer par le point\((6, 18)\) à partir duquel nous pouvons résoudre le facteur d'étirement\(a\).
\[ \begin{align*} 18&=a6^2 \\[4pt] a &=\dfrac{18}{36} \\[4pt] &=\dfrac{1}{2} \end{align*}\]
Notre section parabolique a l'équation
\(y(x)=\dfrac{1}{2}x^2\)
Nous nous intéressons à la surface de l'eau, nous devons donc déterminer la largeur au sommet de l'eau en fonction de la profondeur de l'eau. Pour toute profondeur\(y\), la largeur sera donnée par\(2x\), nous devons donc résoudre l'équation ci-dessus pour\(x\) et trouver la fonction inverse. Cependant, notez que la fonction d'origine n'est pas biunivoque et qu'en effet, quelle que soit la sortie, deux entrées produisent la même sortie, une positive et une négative.
Pour trouver l'inverse, nous pouvons restreindre notre fonction d'origine à un domaine limité sur lequel elle est biunivoque. Dans ce cas, il est logique de se limiter à des\(x\) valeurs positives. Sur ce domaine, nous pouvons trouver un inverse en résolvant la variable d'entrée :
\[ \begin{align*} y&=\dfrac{1}{2}x^2 \\[4pt] 2y&=x^2 \\[4pt] x&=\pm \sqrt{2y} \end{align*}\]
Ce n'est pas une fonction telle qu'elle est écrite. Nous nous limitons aux\(x\) valeurs positives, donc nous éliminons la solution négative, nous donnant la fonction inverse que nous recherchons.
\(y=\dfrac{x^2}{2}\),\(x>0\)
En raison\(x\) de la distance entre le centre de la parabole et les deux côtés, toute la largeur de l'eau au sommet sera égale à\(2x\). La cuvette mesure 3 pieds (36 pouces) de long, de sorte que la surface sera alors de :
\[ \begin{align*} \text{Area} &=l⋅w \\[4pt] &=36⋅2x \\[4pt] &=72x \\[4pt] &=72\sqrt{2y} \end{align*}\]
Cet exemple illustre deux points importants :
- Pour trouver l'inverse d'une quadratique, nous devons nous limiter à un domaine dans lequel la fonction est biunivoque.
- L'inverse d'une fonction quadratique est une fonction de racine carrée. Les deux sont des fonctions de boîte à outils et différents types de fonctions d'alimentation.
Les fonctions impliquant les racines sont souvent appelées fonctions radicales. Bien qu'il ne soit pas possible de trouver l'inverse de la plupart des fonctions polynomiales, certains polynômes de base ont des inverses. Ces fonctions sont appelées fonctions inversibles, et nous utilisons la notation\(f^{−1}(x)\).
Attention :\(f^{−1}(x)\) ce n'est pas la même chose que l'inverse de la fonction\(f(x)\). Cette utilisation de « —1 » est réservée aux fonctions inverses. Pour indiquer l'inverse d'une fonction\(f(x)\), il faudrait écrire :
\[ (f(x))^{−1}=\frac{1}{f(x)}.\]
Une relation importante entre les fonctions inverses est qu'elles « s'annulent » mutuellement. Si\(f^{−1}\) est l'inverse d'une fonction\(f\), alors\(f\) est l'inverse de la fonction\(f^{−1}\). En d'autres termes, quelle que soit l'action de la fonction\(f\)\(x\), elle l'\(f^{−1}\)annule, et vice-versa.
\(f^{−1}(f(x))=x\), pour tous ceux\(x\) qui travaillent dans le domaine de\(f\)
et
\(f(f^{−1}(x))=x\), pour tous ceux\(x\) qui travaillent dans le domaine de\(f^{−1}\)
Notez que l'inverse change le domaine et la plage de la fonction d'origine.
VÉRIFIER QUE DEUX FONCTIONS SONT INVERSES L'UNE DE L'AUTRE
Deux fonctions,\(f\) et\(g\), sont inverses l'une de l'autre si elles se situent toutes\(x\) dans le domaine de\(f\) et\(g\),
\(g(f(x))=f(g(x))=x\)
Comment : À partir d'une fonction polynomiale, trouvez l'inverse de la fonction en limitant le domaine de telle sorte que la nouvelle fonction soit biunivoque
- Remplacez\(f(x)\) par\(y\).
- Échange\(x\) et\(y\).
- Recherchez\(y\) et renommez la fonction\(f^{−1}(x)\).
Exemple\(\PageIndex{1}\): Verifying Inverse Functions
Montrez cela\(f(x)=\frac{1}{x+1}\) et\(f^{−1}(x)=\frac{1}{x}−1\) sont inverses, pour\(x≠0,−1\).
Solution
Nous devons le montrer\(f^{−1}(f(x))=x\) et\(f(f^{−1}(x))=x\).
\[ \begin{align*} f^{−1}(f(x)) &=f^{−1}\left(\dfrac{1}{x+1}\right)\\[4pt] &=\dfrac{1}{\dfrac{1}{x+1}}−1\\[4pt] &=(x+1)−1\\[4pt] &=x\end{align*}\]
et
\[ \begin{align*} f(f^{−1}(x)) &=f(\dfrac{1}{x−1})\\[4pt] &=\dfrac{1}{\left(\dfrac{1}{x−1}\right)+1}\\[4pt] &=\dfrac{1}{\dfrac{1}{x}}\\[4pt] &=x\end{align*}\]
Par conséquent,\(f(x)=\dfrac{1}{x+1}\) et\(f^{−1}(x)=\dfrac{1}{x}−1\) sont des inverses.
Exercice\(\PageIndex{1}\)
Montrez cela\(f(x)=\frac{x+5}{3}\) et ce\(f^{−1}(x)=3x−5\) sont des inverses.
- Répondez à une
-
\(f^{−1}(f(x))=f^{−1}(\frac{x+5}{3})=3(\frac{x+5}{3})−5=(x−5)+5=x\)
- Réponse b
-
\(f(f^{−1}(x))=f(3x−5)=\frac{(3x−5)+5}{3}=\frac{3x}{3}=x\)
Exemple\(\PageIndex{2}\): Finding the Inverse of a Cubic Function
Détermine l'inverse de la fonction\(f(x)=5x^3+1\).
Solution
Il s'agit d'une transformation de la fonction de base de la boîte à outils cubique, et sur la base de notre connaissance de cette fonction, nous savons qu'elle est individuelle. Résoudre l'inverse en résolvant pour\(x\).
\(y=5x^3+1\)
\(x=5y^3+1\)
\(x−1=5y^3\)
\(\dfrac{x−1}{5}=y^3\)
\(f^{−1}(x)=\sqrt[3]{\dfrac{x−1}{5}}\)
Analyse
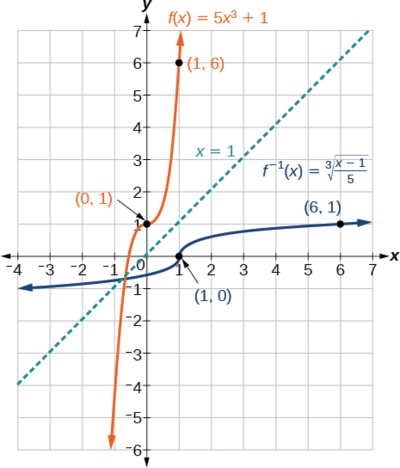
Regardez le graphique de\(f\) et\(f^{–1}\). Notez qu'un graphique est le reflet de l'autre autour de la ligne\(y=x\). C'est toujours le cas lors de la représentation graphique d'une fonction et de sa fonction inverse.
De plus, étant donné que la méthode impliquait d'\(x\)échanger et\(y\) de noter les points correspondants. Si\((a,b)\) se trouve sur le graphique de\(f\), alors\((b,a)\) se trouve sur le graphique de\(f^{–1}\). Puisque\((0,1)\) se trouve sur le graphique de\(f\), alors\((1,0)\) se trouve sur le graphique de\(f^{–1}\). De même, puisque\((1,6)\) se trouve sur le graphique de\(f\), alors\((6,1)\) se trouve sur le graphique de\(f^{–1}\) (Figure\(\PageIndex{9}\)).
Exercice\(\PageIndex{2}\)
Détermine la fonction inverse de\(f(x)=\sqrt[3]{x+4}\).
- Réponse
-
\(f^{−1}(x)=x^3−4\)
Restreindre le domaine pour trouver l'inverse d'une fonction polynomiale
Jusqu'à présent, nous avons pu trouver les fonctions inverses des fonctions cubiques sans avoir à restreindre leurs domaines. Cependant, comme nous le savons, tous les polynômes cubiques ne sont pas un-à-un. Certaines fonctions qui ne sont pas individuelles peuvent voir leur domaine restreint de manière à ce qu'elles soient individuelles, mais uniquement sur ce domaine. La fonction sur le domaine restreint aurait alors une fonction inverse. Comme les fonctions quadratiques ne sont pas univoques, nous devons restreindre leur domaine afin de trouver leurs inverses.
RESTREINDRE LE DOMAINE
Si une fonction n'est pas biunivoque, elle ne peut pas avoir d'inverse. Si nous restreignons le domaine de la fonction pour qu'elle devienne biunivoque, créant ainsi une nouvelle fonction, cette nouvelle fonction aura un inverse.
Comment : à partir d'une fonction polynomiale, restreindre le domaine d'une fonction qui n'est pas biunivoque, puis trouver l'inverse
- Limitez le domaine en déterminant un domaine sur lequel la fonction d'origine est biunivoque.
- Remplacez\(f(x)\) par\(y\).
- Échange\(x\) et\(y\).
- Recherchez\(y\) et renommez la fonction ou la paire de fonctions\(f^{−1}(x)\).
- Révisez la formule pour\(f^{−1}(x)\) en vous assurant que les sorties de la fonction inverse correspondent au domaine restreint de la fonction d'origine.
Exemple\(\PageIndex{3}\): Restricting the Domain to Find the Inverse of a Polynomial Function
Trouvez la fonction inverse de\(f\) :
- \(f(x)={(x−4)}^2\),\(x≥4\)
- \(f(x)={(x−4)}^2\),\(x≤4\)
Solution
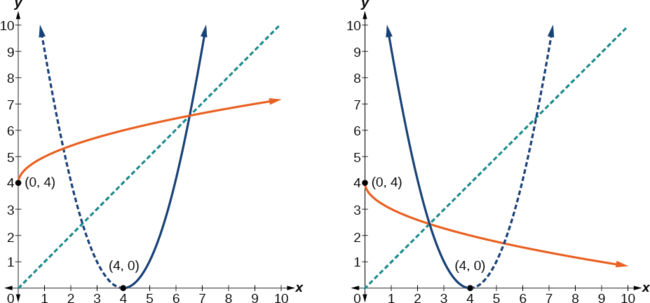
La fonction d'origine n'\(f(x)={(x−4)}^2\)est pas biunivoque, mais elle est limitée à un domaine\(x≤4\) de\(x≥4\) ou dans lequel elle est individuelle (Figure\(\PageIndex{6}\)).
Pour trouver l'inverse, commencez par le\(f(x)\) remplacer par la variable simple\(y\).
\(y={(x−4)}^2\)Échange\(x\) et\(y\).
\(x={(y−4)}^2\)Prenez la racine carrée.
\(\pm \sqrt{x}=y−4\)Ajouter\(4\) des deux côtés.
\(4\pm \sqrt{x} =y\)
Ce n'est pas une fonction telle qu'elle est écrite. Nous devons examiner les restrictions sur le domaine de la fonction d'origine pour déterminer l'inverse. Puisque nous avons inversé les rôles de\(x\) et\(y\) pour l'original\(f(x)\), nous avons examiné le domaine : les valeurs\(x\) pouvaient être assumées. Lorsque nous avons inversé les rôles de\(x\) et\(y\), cela nous a donné les valeurs que nous\(y\) pouvions assumer. Pour cette fonction\(x≥4\), donc pour l'inverse, nous devrions avoir\(y≥4\), et c'est ce que donne notre fonction inverse.
- Le domaine de la fonction d'origine était limité à\(x≥4\), donc les sorties de l'inverse doivent être les mêmes\(f(x)≥4\), et nous devons utiliser le cas + :
\(f^{−1}(x)=4+\sqrt{x}\)
- Le domaine de la fonction d'origine était limité à\(x≤4\), donc les sorties de l'inverse doivent être les mêmes\(f(x)≤4\), et nous devons utiliser le cas — :
\(f^{−1}(x)=4−\sqrt{x}\)
Analyse
Sur les graphiques de la figure\(\PageIndex{6}\), nous voyons la fonction d'origine représentée sur le même ensemble d'axes que sa fonction inverse. Notez que l'ensemble des graphiques montre une symétrie par rapport à la droite\(y=x\). La paire de coordonnées\((4,0)\) se trouve sur le graphe de f et la paire de coordonnées\((0, 4)\) se trouve sur le graphique de\(f^{−1}\). Pour toute paire de coordonnées, elle\((a, b)\) se trouve sur le graphe de\(f\), alors\((b, a)\) sur le graphique de\(f^{−1}\). Enfin, observez que le graphe de\(f\) croise le graphe de\(f^{−1}\) sur la droite\(y=x\). Les points d'intersection des graphes de\(f\) et se\(f^{−1}\) situeront toujours sur la ligne\(y=x\).
Exemple\(\PageIndex{4}\): Finding the Inverse of a Quadratic Function When the Restriction Is Not Specified
Restreignez le domaine, puis trouvez l'inverse de
\(f(x)={(x−2)}^2−3\).
Solution
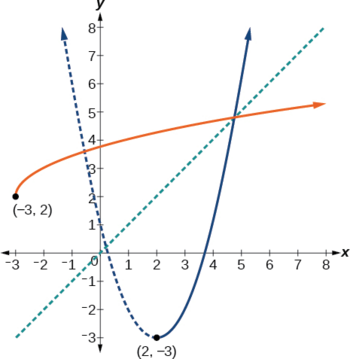
Nous pouvons voir qu'il s'agit d'une parabole dont le sommet\((2,–3)\) s'ouvre vers le haut. Comme le graphe diminuera d'un côté du sommet et augmentera de l'autre côté, nous pouvons restreindre cette fonction à un domaine sur lequel elle sera biunivoque en limitant le domaine à\(x≥2\).
Pour trouver l'inverse, nous utiliserons la forme du sommet du quadratique. Nous commençons par la\(f(x)\) remplacer par une variable simple\(y\), puis nous résolvons pour\(x\).
\(y={(x−2)}^2−3\)Échange\(x\) et\(y\).
\(x={(y−2)}^2−3\)Ajoutez-en 3 des deux côtés.
\(x+3={(y−2)}^2\)Prenez la racine carrée.
\(\pm \sqrt{x+3}=y−2\)Ajoutez-en 2 des deux côtés.
\(2\pm \sqrt{x+3}=y\)Renommez la fonction.
\(f^{−1}(x)=2\pm \sqrt{x+3}\)
Nous devons maintenant déterminer quel boîtier utiliser. Comme nous avons limité notre fonction d'origine à un domaine de\(x≥2\), les sorties de l'inverse devraient être les mêmes, ce qui nous indique d'utiliser le cas +
\(f^{−1}(x)=2+\sqrt{x+3}\)
Si le quadratique n'avait pas été donné sous forme de sommet, la réécrire sous forme de sommet serait la première étape. De cette façon, nous pouvons facilement observer les coordonnées du sommet pour nous aider à restreindre le domaine.
Analyse
Notez que nous avons décidé arbitrairement de restreindre le domaine sur\(x≥2\). Nous aurions tout aussi bien pu choisir de restreindre le domaine à\(x≤2\), auquel cas\(f^{−1}(x)=2−\sqrt{x+3}\). Observez la fonction d'origine représentée sur le même ensemble d'axes que sa fonction inverse sur la figure\(\PageIndex{7}\). Notez que les deux graphes présentent une symétrie par rapport à la droite\(y=x\). La paire de coordonnées\((2, −3)\) se trouve sur le graphique de\(f\) et la paire de coordonnées\((−3, 2)\) se trouve sur le graphique de\(f^{−1}\). Observez à partir du graphique des deux fonctions sur le même ensemble d'axes que
domaine de\(f=\) gamme de\(f^{–1}=[2,\infty)\)
et
domaine de\(f^{–1}=\) gamme de\(f=[–3,\infty)\).
Enfin, observez que le graphe de\(f\) croise le graphe du\(f^{−1}\) long de la ligne\(y=x\).
Exercice\(\PageIndex{4}\)
Trouvez l'inverse de la fonction\(f(x)=x^2+1\), sur le domaine\(x≥0\).
- Réponse
-
\(f^{−1}(x)=\sqrt{x−1}\)
Trouver les inverses
Notez que les fonctions des exemples précédents étaient toutes des polynômes et que leurs inverses étaient des fonctions radicales. Si nous voulons trouver l'inverse d'une fonction radicale, nous devrons restreindre le domaine de la réponse car la plage de la fonction d'origine est limitée.
Comment : à partir d'une fonction radicale, trouver l'inverse
- Déterminez la plage de la fonction d'origine.
- Remplacez\(f(x)\) par\(y\), puis résolvez pour\(x\).
- Si nécessaire, limitez le domaine de la fonction inverse à la plage de la fonction d'origine.
Exemple\(\PageIndex{5}\): Finding the Inverse of a Radical Function
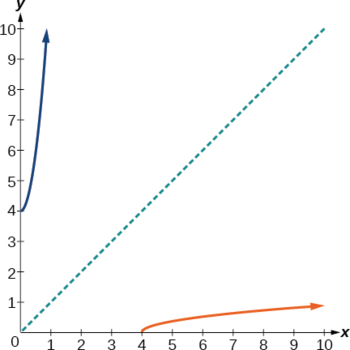
Restreignez le domaine de la fonction,\(f(x)=\sqrt{x−4}\) puis trouvez l'inverse.
Solution
Notez que la fonction d'origine possède une plage\(f(x)≥0\). Remplacez\(f(x)\) par\(y\), puis résolvez pour\(x\).
\(y=\sqrt{x−4}\)Remplacez\(f(x)\) par\(y\).
\(x=\sqrt{y−4}\)Échange\(x\) et\(y\).
\(x=\sqrt{y−4}\)Mettre chaque côté au carré.
\(x^2=y−4\)Ajoutez 4.
\(x^2+4=y\)Renommez la fonction\(f^{−1}(x)\).
\(f^{−1}(x)=x^2+4\)
Rappelez-vous que le domaine de cette fonction doit être limité à la plage de la fonction d'origine.
\(f^{−1}(x)=x^2+4\),\(x≥0\)
Analyse
Remarquez dans la figure\(\PageIndex{8}\) que l'inverse est le reflet de la fonction d'origine sur la ligne\(y=x\). Comme la fonction d'origine n'a que des sorties positives, la fonction inverse n'a que des entrées non négatives.
Exercice\(\PageIndex{5}\)
Restreignez le domaine, puis trouvez l'inverse de la fonction\(f(x)=\sqrt{2x+3}\).
- Réponse
-
\(f^{−1}(x)=\frac{x^2−3}{2}\),\(x≥0\)
Résolution d'applications de fonctions radicales
Les fonctions radicales sont courantes dans les modèles physiques, comme nous l'avons vu dans l'ouverture de la section. Nous disposons désormais de suffisamment d'outils pour pouvoir résoudre le problème posé au début de la section.
Exemple\(\PageIndex{6}\): Solving an Application with a Cubic Function
Un monticule de gravier a la forme d'un cône dont la hauteur est égale au double du rayon. Le volume du cône en termes de rayon est donné par
\[V=\dfrac{2}{3}\pi r^3 \nonumber\]
Détermine l'inverse de la fonction\(V=\frac{2}{3}\pi r^3\) qui détermine le volume\(V\) d'un cône et qui est fonction du rayon\(r\). Utilisez ensuite la fonction inverse pour calculer le rayon d'un tel monticule de gravier de 100 pieds cubes. Utiliser\(\pi=3.14\).
Solution
Commencez par la fonction donnée pour\(V\). Notez que le domaine significatif de la fonction est que\(r>0\) des rayons négatifs n'auraient aucun sens dans ce contexte, pas plus qu'un rayon de\(0\). Notez également que la plage de la fonction (d'où le domaine de la fonction inverse) est\(V>0\). Résolvez\(r\) en termes de\(V\), en utilisant la méthode décrite précédemment. Notez que dans les applications du monde réel, nous n'échangeons pas les variables lors de la recherche d'inverses. Au lieu de cela, nous changeons quelle variable est considérée comme la variable indépendante.
\[ V =\dfrac{2}{3}\pi r^3\nonumber \]
Résolvez pour\(r^3\).
\[r^3 =\dfrac{3V}{2\pi} \nonumber\]
Résolvez pour\(r\).
\[ r=\sqrt[3]{\dfrac{3V}{2\pi}} \nonumber \]
C'est le résultat indiqué dans l'ouvre-section. Maintenant, évaluez cela pour\(V=100\) et\(\pi=3.14\).
\[ \begin{align*} r&=\sqrt[3]{\dfrac{3V}{2\pi}} \\[4pt] &=\sqrt[3]{\dfrac{3⋅100}{2⋅3.14}} \\[4pt] &≈\sqrt[3]{47.7707} \\[4pt] &≈3.63 \end{align*}\]
Par conséquent, le rayon est d'environ 3,63 pieds.
Déterminer le domaine d'une fonction radicale composée d'autres fonctions
Lorsque des fonctions radicales sont composées avec d'autres fonctions, la détermination du domaine peut devenir plus complexe.
Exemple\(\PageIndex{7}\): Finding the Domain of a Radical Function Composed with a Rational Function
Trouvez le domaine de la fonction :
\[f(x)=\sqrt{\frac{(x+2)(x−3)}{(x−1)}}. \nonumber\]
Solution
Comme une racine carrée n'est définie que lorsque la quantité sous le radical n'est pas négative, nous devons déterminer où
\[\frac{(x+2)(x−3)}{(x−1)}≥0. \nonumber\]
La sortie d'une fonction rationnelle peut changer de signe (passage du positif au négatif ou vice versa) aux interceptions x et aux asymptotes verticales. Pour cette équation, le graphique peut changer de signe à\(x=–2\)\(1\), et\(3\).
Pour déterminer les intervalles sur lesquels l'expression rationnelle est positive, nous pouvons tester certaines valeurs de l'expression ou dessiner un graphique. Bien que les deux approches fonctionnent aussi bien, pour cet exemple, nous utiliserons un graphique comme le montre la figure\(\PageIndex{9}\).
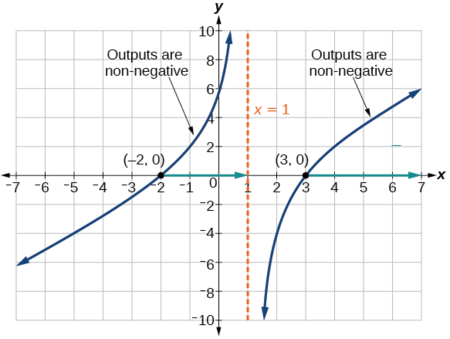
Cette fonction possède deux interceptions x, qui présentent toutes deux un comportement linéaire à proximité des interceptions X. Il existe une asymptote verticale, correspondant à un facteur linéaire ; ce comportement est similaire à la fonction réciproque de base de la boîte à outils, et il n'y a pas d'asymptote horizontale car le degré du numérateur est supérieur au degré du dénominateur. Il existe un at y -intercept\((0,\sqrt{6})\).
À partir des valeurs y -intercept et x -intercept at\(x=−2\), nous pouvons esquisser le côté gauche du graphique. À partir du comportement au niveau de l'asymptote, nous pouvons esquisser le côté droit du graphique.
À partir du graphique, nous pouvons maintenant déterminer à quels intervalles les sorties seront non négatives, afin d'être sûrs que la fonction d'origine\(f(x)\) sera définie. \(f(x)\)possède un domaine\(−2≤x<1\) ou\(x≥3\), ou en notation par intervalles,\([−2,1)∪[3,\infty)\).
Trouver les inverses des fonctions rationnelles
Comme pour trouver les inverses de fonctions quadratiques, il est parfois souhaitable de trouver l'inverse d'une fonction rationnelle, en particulier des fonctions rationnelles qui sont le ratio de fonctions linéaires, comme dans les applications de concentration.
Exemple\(\PageIndex{8}\): Finding the Inverse of a Rational Function
La fonction
\[\displaystyle C=\frac{20+0.4n}{100+n}\]
représente la concentration\(C\) d'une solution acide après ajout d'un\(n\) mL de solution à 40 % à 100 mL d'une solution à 20 %. Tout d'abord, trouvez l'inverse de la fonction, c'est-à-dire recherchez une expression pour\(n\) en termes de\(C\). Utilisez ensuite votre résultat pour déterminer la quantité de solution à 40 % à ajouter afin que le mélange final soit une solution à 35 %.
Solution
Nous voulons d'abord l'inverse de la fonction afin de déterminer le nombre de ml dont nous avons besoin pour une concentration donnée. Nous allons résoudre\(n\) en termes de\(C\).
\[ \begin{align*} C&=\dfrac{20+0.4n}{100+n} \\[4pt] C(100+n)&=20+0.4n\\[4pt] 100C+Cn&=20+0.4n\\[4pt] 100C−20&=0.4n−Cn\\[4pt] 100C−20&=(0.4−C)n\\[4pt] n&=\dfrac{100C−20}{0.4−C}\end{align*}\]
Évaluez maintenant cette fonction à 35%, ce qui est\(C=0.35\).
\[ \begin{align*} n&=\dfrac{100(0.35)−20}{0.4−0.35}\\[4pt] &=\dfrac{15}{0.05}\\[4pt] &=300\end{align*}\]
Nous pouvons conclure que 300 ml de la solution à 40 % doivent être ajoutés.
Exercice\(\PageIndex{8}\)
Détermine l'inverse de la fonction\(f(x)=\frac{x+3}{x−2}\).
- Réponse
-
\(f^{−1}(x)=\frac{2x+3}{x−1}\)
Médias
Accédez à ces ressources en ligne pour des instructions et des exercices supplémentaires avec des fonctions inverses et radicales.
Concepts clés
- L'inverse d'une fonction quadratique est une fonction de racine carrée.
- Si\(f^{−1}\) est l'inverse d'une fonction\(f\), alors\(f\) est l'inverse de la fonction\(f^{−1}\). Voir l'exemple\(\PageIndex{1}\).
- Bien qu'il ne soit pas possible de trouver l'inverse de la plupart des fonctions polynomiales, certains polynômes de base sont inversibles. Voir l'exemple\(\PageIndex{2}\).
- Pour trouver l'inverse de certaines fonctions, il faut restreindre la fonction à un domaine sur lequel elle sera biunivoque. Voir les exemples\(\PageIndex{3}\) et\(\PageIndex{4}\)
- Pour trouver l'inverse d'une fonction radicale, nous avons besoin d'une restriction sur le domaine de la réponse. Voir Exemple\(\PageIndex{5}\) et\(\PageIndex{7}\).
- Les fonctions et inverses et radicales peuvent être utilisées pour résoudre des problèmes d'application. Voir les exemples\(\PageIndex{6}\) et\(\PageIndex{8}\).


