5.6 : Fonctions rationnelles

Objectifs d'apprentissage

• Utilisez la notation par flèche.
• Résoudre des problèmes appliqués impliquant des fonctions rationnelles.
• Trouvez les domaines des fonctions rationnelles.
• Identifiez les asymptotes verticales.
• Identifiez les asymptotes horizontales.
• Représenter les fonctions rationnelles.

Supposons que nous sachions que le coût de fabrication d'un produit dépend du nombre d'\(x\)articles produits. Ceci est donné par l'équation\(C (x)=15,000x−0.1x^2+1000.\) Si nous voulons connaître le coût moyen de production d'\(x\)articles, nous diviserions la fonction de coût par le nombre d'articles,\(x\). La fonction de coût moyen, qui donne le coût moyen par article pour les\(x\) articles produits, est

\[f(x)=\dfrac{15,000x−0.1x^2+1000}{x} \nonumber\]

De nombreux autres problèmes d'application nécessitent de trouver une valeur moyenne de la même manière, en nous donnant des variables dans le dénominateur. Écrite sans variable dans le dénominateur, cette fonction contiendra une puissance entière négative.

Dans les dernières sections, nous avons travaillé avec des fonctions polynomiales, qui sont des fonctions avec des entiers non négatifs pour les exposants. Dans cette section, nous explorons les fonctions rationnelles, dont le dénominateur comporte des variables.

Utiliser la notation fléchée

Nous avons examiné les graphes de la fonction réciproque de base et de la fonction réciproque carrée dans le cadre de notre étude des fonctions de la boîte à outils. Examinez ces graphiques, comme le montre la figure\(\PageIndex{1}\), et remarquez certaines de leurs caractéristiques.

Figurine\(\PageIndex{1}\)

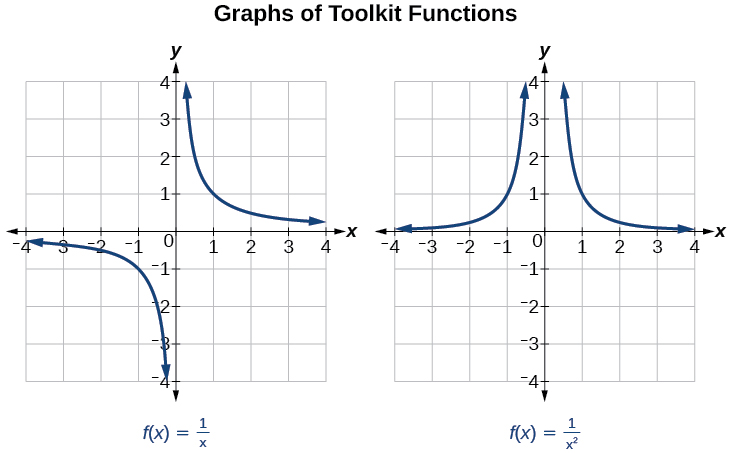
Plusieurs choses apparaissent si nous examinons le graphique de\(f(x)=\frac{1}{x}\).

• Sur la branche gauche du graphique, la courbe s'approche de l'\(x\)axe\((y=0)\) des\(x\rightarrow -\infty\).
• Lorsque le graphique s'approche\(x = 0\) par la gauche, la courbe baisse, mais lorsque nous approchons de zéro depuis la droite, la courbe augmente.
• Enfin, sur la branche droite du graphique, les courbes se rapprochent de l'\(x\)axe\((y=0) \) des\(x\rightarrow \infty\).

Pour résumer, nous utilisons la notation fléchée pour montrer que\(x\) ou\(f (x)\) s'approche d'une valeur particulière (Tableau\(\PageIndex{1}\)).

Tableau\(\PageIndex{1}\)

symbole	Sens
\(x\rightarrow a^-\)	\(x\)s'approche de a depuis la gauche (\(x<a\)mais près de\(a\))
\(x\rightarrow a^+\)	\(x\)s'approche de a depuis la droite (\(x>a\)mais près de\(a\))
\(x\rightarrow \infty\)	\(x\)approche de l'infini (\(x\)augmente sans limite)
\(x\rightarrow −\infty\)	\(x\)approche l'infini négatif (\(x\)diminue sans limite)
\(f(x)\rightarrow \infty\)	la sortie se rapproche de l'infini (la sortie augmente sans limite)
\(f(x)\rightarrow −\infty\)	la sortie se rapproche de l'infini négatif (la sortie diminue sans limite)
\(f(x)\rightarrow a\)	les approches de sortie\(a\)

Comportement local de\(f(x)=\frac{1}{x}\)

Commençons par examiner la fonction réciproque,\(f(x)=\frac{1}{x}\). Nous ne pouvons pas diviser par zéro, ce qui signifie que la fonction n'est pas définie à\(x=0\) ; zéro n'est donc pas dans le domaine. Lorsque les valeurs d'entrée s'approchent de zéro depuis la gauche (devenant de très petites valeurs négatives), les valeurs de la fonction diminuent sans limite (en d'autres termes, elles se rapprochent de l'infini négatif). Nous pouvons voir ce comportement dans le tableau\(\PageIndex{2}\).

Tableau\(\PageIndex{2}\)

\(x\)	—0,1	—0,01	—0,001	—0,0001
\(f(x)=\frac{1}{x}\)	—10	—100	—100	—10 000

Nous écrivons en notation flèche

comme\(x\rightarrow 0^−,f(x)\rightarrow −\infty\)

Lorsque les valeurs d'entrée s'approchent de zéro depuis le côté droit (devenant de très petites valeurs positives), les valeurs de la fonction augmentent sans limite (proche de l'infini). Nous pouvons voir ce comportement dans le tableau\(\PageIndex{3}\).

Tableau\(\PageIndex{3}\)

\(x\)	0,1	0,01	0,001	0,0001
\(f(x)=\frac{1}{x}\)	10	100	1000	10 000

Nous écrivons en notation flèche

Comme\(x\rightarrow 0^+, f(x)\rightarrow \infty\).

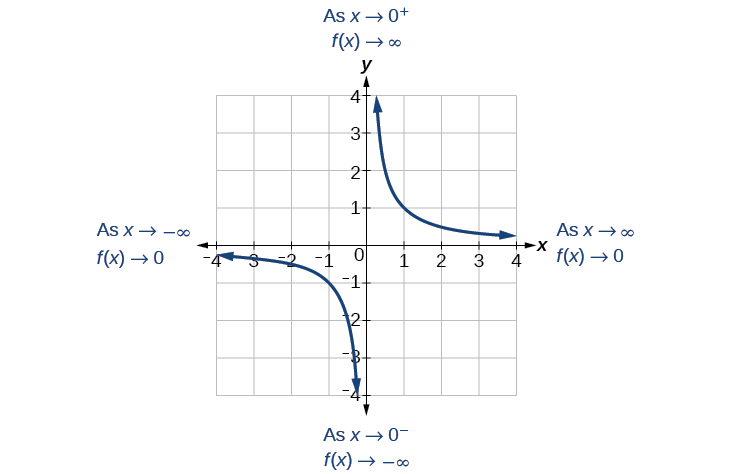
Voir la figure\(\PageIndex{2}\).

Chiffre\(\PageIndex{2}\).

Ce comportement crée une asymptote verticale, c'est-à-dire une ligne verticale que le graphe approche mais ne franchit jamais. Dans ce cas, le graphique se rapproche de la ligne\(x=0\) verticale lorsque l'entrée est proche de zéro (Figure\(\PageIndex{3}\)).

Chiffre\(\PageIndex{3}\).

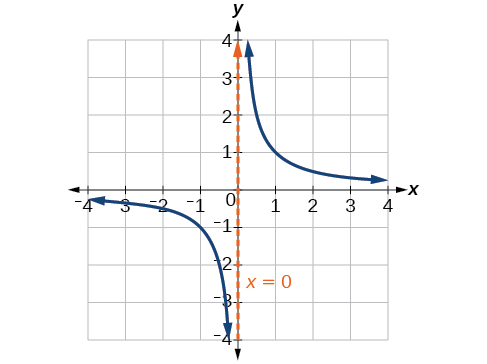
Définition : ASYMPTOTE VERTICALE

Une asymptote verticale d'un graphe est une ligne verticale\(x=a\) où le graphe tend vers l'infini positif ou négatif à l'approche des entrées\(a\). Nous écrivons

En tant que\(x\rightarrow a\)\(f(x)\rightarrow \infty\), ou en tant que\(x\rightarrow a\),\(f(x)\rightarrow −\infty\).

Comportement final de\(f(x)=\frac{1}{x}\)

Lorsque les valeurs de l'\(x\)approche de l'infini, les valeurs de la fonction s'approchent\(0\). Lorsque les valeurs de l'infini\(x\) s'approchent de l'infini négatif, les valeurs de la fonction approchent\(0\) (Figure\(\PageIndex{4}\)). Symboliquement, en utilisant la notation des flèches

En tant que\(x\rightarrow \infty\)\(f(x)\rightarrow 0\), et en tant que\(x\rightarrow −\infty\),\(f(x)\rightarrow 0\).

Chiffre\(\PageIndex{4}\).

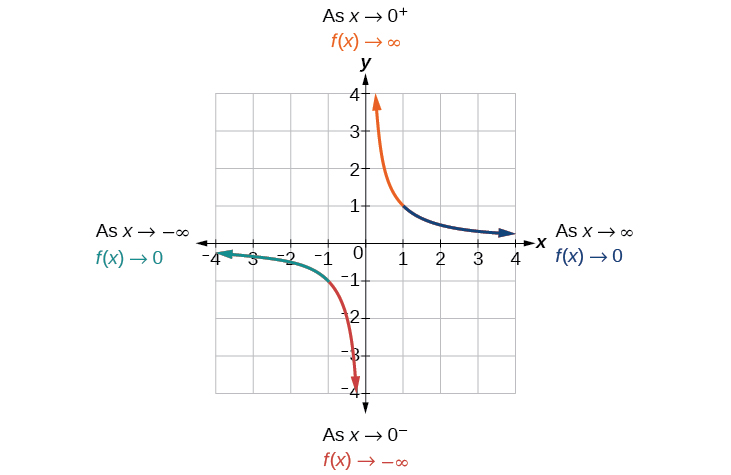
Sur la base de ce comportement global et du graphique, nous pouvons voir que la fonction approche 0 mais n'atteint jamais réellement 0 ; elle semble se stabiliser à mesure que les entrées deviennent volumineuses. Ce comportement crée une asymptote horizontale, une ligne horizontale que le graphe approche lorsque l'entrée augmente ou diminue sans limite. Dans ce cas, le graphique se rapproche de la ligne horizontale\(y=0\). Voir la figure\(\PageIndex{5}\).

Chiffre\(\PageIndex{5}\).

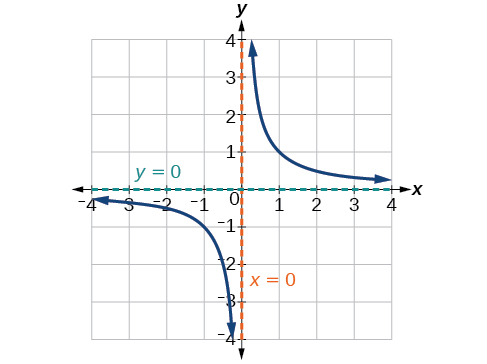
Définition : ASYMPTOTE HORIZONTALE

Une asymptote horizontale d'un graphe est une ligne horizontale\(y=b\) où le graphe s'approche de la droite lorsque les entrées augmentent ou diminuent sans limite. Nous écrivons

Comme\(x\rightarrow \infty \text{ or } x\rightarrow −\infty\),\(f(x)\rightarrow b\).

 

Exemple\(\PageIndex{1}\): Using Arrow Notation.

Utilisez la notation fléchée pour décrire le comportement final et le comportement local de la fonction illustrée dans la figure\(\PageIndex{6}\).

Chiffre\(\PageIndex{6}\).

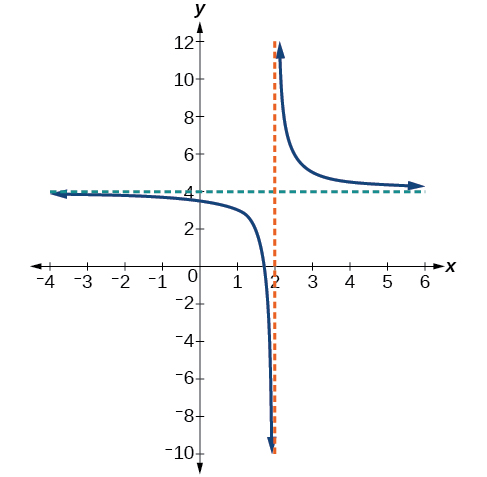
Solution

Notez que le graphique montre une asymptote verticale à\(x=2\), ce qui nous indique que la fonction n'est pas définie à\(x=2\).

En tant que\(x\rightarrow 2^−\),\(f(x)\rightarrow −\infty,\) et en tant que\(x\rightarrow 2^+\),\(f(x)\rightarrow \infty\).

Et à mesure que les entrées diminuent sans limite, le graphique semble se stabiliser à des valeurs de sortie de\(4\), indiquant une asymptote horizontale à\(y=4\). Lorsque les entrées augmentent sans limite, le graphique se stabilise à\(4\).

En tant que\(x\rightarrow \infty\),\(f(x)\rightarrow 4\) et en tant que\(x\rightarrow −\infty\),\(f(x)\rightarrow 4\).

 

Exercices\(\PageIndex{1}\)

Utilisez la notation fléchée pour décrire le comportement final et le comportement local de la fonction quadratique réciproque.

Réponse

Comportement final : comme\(x\rightarrow \pm \infty\),\(f(x)\rightarrow 0\) ;

Comportement local : as\(x\rightarrow 0\),\(f(x)\rightarrow \infty\) (il n'y a pas d'interception x ou y)

Exemple\(\PageIndex{2}\): Using Transformations to Graph a Rational Function.

Esquissez un graphique de la fonction réciproque décalée de deux unités vers la gauche et de trois unités vers le haut. Identifiez les asymptotes horizontales et verticales du graphique, le cas échéant.

Solution

Déplacer le graphique vers la gauche (2) et vers le haut (3) entraînerait la fonction

\[f(x)=\dfrac{1}{x+2}+3\]

ou de manière équivalente, en donnant aux termes un dénominateur commun,

\[f(x)=\dfrac{3x+7}{x+2}\]

Le graphique de la fonction décalée est affiché sur la figure\(\PageIndex{7}\).

Chiffre\(\PageIndex{7}\).

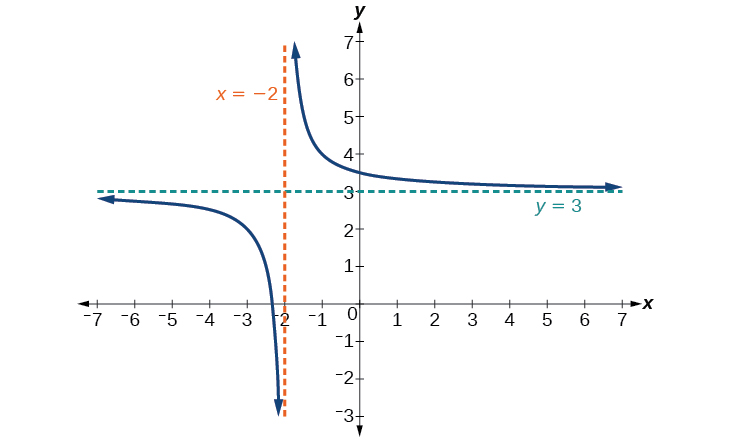
Notez que cette fonction n'est pas définie à\(x=−2\) et que le graphique montre également une asymptote verticale à\(x=−2\).

En tant que\(x\rightarrow −2^−\)\(f(x)\rightarrow −\infty\), et en tant que\(x\rightarrow −2^+\),\(f(x)\rightarrow \infty\).

À mesure que les entrées augmentent et diminuent sans limite, le graphique semble se stabiliser à des valeurs de sortie de 3, indiquant une asymptote horizontale à\(y=3\).

Comme\(x\rightarrow \pm \infty\),\(f(x)\rightarrow 3\).

Analyse

Notez que les asymptotes horizontales et verticales sont décalées de 2 vers la gauche et de 3 vers le haut en même temps que la fonction.

Exercice\(\PageIndex{2}\)

Esquissez le graphique et trouvez les asymptotes horizontales et verticales de la fonction quadratique réciproque qui a été décalée de 3 unités vers la droite et de 4 unités vers le bas.

Solution

Chiffre\(\PageIndex{8}\).

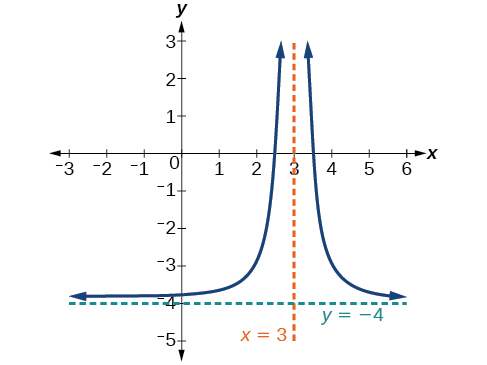
La fonction et les asymptotes sont décalées de 3 unités vers la droite et de 4 unités vers le bas. Comme\(x\rightarrow 3\), \(f(x)\rightarrow \infty\), and as \(x\rightarrow \pm \infty\), \(f(x)\rightarrow −4\).

La fonction est\(f(x)=\frac{1}{{(x−3)}^2}−4\).

Résolution de problèmes appliqués impliquant des fonctions rationnelles

Dans Exemple\(\PageIndex{2}\), nous avons déplacé une fonction de boîte à outils de manière à obtenir la fonction\(f(x)=\frac{3x+7}{x+2}\). Il s'agit d'un exemple de fonction rationnelle. Une fonction rationnelle est une fonction qui peut être écrite comme le quotient de deux fonctions polynomiales. De nombreux problèmes du monde réel nous obligent à trouver le rapport entre deux fonctions polynomiales. Les problèmes liés aux taux et aux concentrations font souvent intervenir des fonctions rationnelles.

Définition : FONCTION RATIONNELLE

Une fonction rationnelle est une fonction qui peut être écrite comme le quotient de deux fonctions polynomiales\(P(x)\) et\(Q(x)\).

\[f(x)=\dfrac{P(x)}{Q(x)}=\dfrac{a_px^p+a_{p−1}x^{p−1}+...+a_1x+a_0}{b_qx^q+b_{q−1}x^{q−1}+...+b_1x+b_0},\space Q(x)≠0\]

Exemple\(\PageIndex{3}\): Solving an Applied Problem Involving a Rational Function

Un grand réservoir de mélange contient actuellement 100 gallons d'eau dans lesquels 5 livres de sucre ont été mélangées. Un robinet s'ouvre pour verser 10 gallons d'eau par minute dans le réservoir en même temps que du sucre est versé dans le réservoir à raison de 1 livre par minute. Déterminez la concentration (livres par gallon) de sucre dans le réservoir après 12 minutes. Est-ce une plus grande concentration qu'au début ?

Solution

Soit le nombre de minutes écoulées depuis l'ouverture du robinet. Comme l'eau augmente de 10 gallons par minute et que le sucre augmente de 1 livre par minute, il s'agit de taux de variation constants. Cela nous indique que la quantité d'eau dans le réservoir change de façon linéaire, tout comme la quantité de sucre dans le réservoir. Nous pouvons écrire une équation indépendamment pour chacun :

eau :\(W(t)=100+10t\) en gallons

sucre :\(S(t)=5+1t\) en livres

La concentration,\(C\), sera le rapport entre les livres de sucre et les gallons d'eau

\[C(t)=\dfrac{5+t}{100+10t}\]

La concentration après 12 minutes est donnée en évaluant\(C(t)\) à\(t= 12\).

\[\begin{align} C(12) & =\dfrac{5+12}{100+10(12)} \\ &= \dfrac{17}{220} \end{align} \]

Cela signifie que la concentration est de 17 livres de sucre pour 220 gallons d'eau.

Au début, la concentration est

\[\begin{align} C(0) & =\dfrac{5+0}{100+10(0)} \\ & =\dfrac{1}{20} \end{align} \]

Depuis\(\frac{17}{220}≈0.08>\frac{1}{20}=0.05\), la concentration est plus élevée au bout de 12 minutes qu'au début.

Analyse

Pour trouver l'asymptote horizontale, divisez le coefficient principal du numérateur par le coefficient principal du dénominateur :

\[\dfrac{1}{10}=0.1\]

Remarquez que l'asymptote horizontale est\(y= 0.1.\) Cela signifie que la concentration,\(C,\) le rapport entre les livres de sucre et les gallons d'eau, approchera 0,1 à long terme.

Exercice\(\PageIndex{3}\)

Il y a 1 200 étudiants de première année et 1 500 étudiants de deuxième année à un rassemblement préparatoire à midi. Après 12 heures, 20 étudiants de première année arrivent au rallye toutes les cinq minutes tandis que 15 étudiants de deuxième année quittent le rallye. Trouvez le ratio entre étudiants de première année et étudiants de deuxième année à 13 heures.

Réponse

\(\frac{12}{11}\)

Trouver les domaines des fonctions rationnelles

Une asymptote verticale représente une valeur pour laquelle une fonction rationnelle n'est pas définie, de sorte que la valeur ne se trouve pas dans le domaine de la fonction. Une fonction réciproque ne peut pas avoir de valeurs dans son domaine qui font que le dénominateur est égal à zéro. En général, pour trouver le domaine d'une fonction rationnelle, nous devons déterminer quelles entrées entraîneraient une division par zéro.

Définition : DOMAINE D'UNE FONCTION RATIONNELLE

Le domaine d'une fonction rationnelle inclut tous les nombres réels à l'exception de ceux qui font que le dénominateur est égal à zéro.

Mode d'emploi : À partir d'une fonction rationnelle, trouvez le domaine.

1. Réglez le dénominateur à zéro.
2. Résolvez pour trouver les valeurs x qui font que le dénominateur est égal à zéro.
3. Le domaine est composé uniquement de nombres réels, sauf ceux trouvés à l'étape 2.

Exemple\(\PageIndex{4}\): Finding the Domain of a Rational Function

Trouvez le domaine de\(f(x)=\dfrac{x+3}{x^2−9}\).

Solution

Commencez par définir le dénominateur égal à zéro et résolvez.

\[x^2-9=0 \nonumber \]

\[x^2=9 \nonumber \]\[x=\pm 3 \nonumber \]

Le dénominateur est égal à zéro lorsque\(x=\pm 3\). Le domaine de la fonction comprend tous les nombres réels sauf\(x=\pm 3\).

Analyse

Un graphique de cette fonction, comme le montre la figure\(\PageIndex{9}\), confirme que la fonction n'est pas définie quand\(x=\pm 3\).

Chiffre\(\PageIndex{9}\).

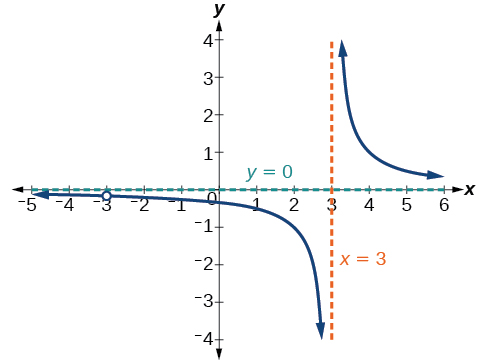
Il y a une asymptote verticale\(x=3\) et un trou dans le graphique à\(x=−3\). Nous aborderons ces types de trous plus en détail plus loin dans cette section.

Exercice\(\PageIndex{4}\)

Trouvez le domaine de\(f(x)=\dfrac{4x}{5(x−1)(x−5)}\).

Réponse

Le domaine est composé uniquement de nombres réels, sauf\(x=1\) et\(x=5\).

Identification des asymptotes verticales des fonctions rationnelles

En regardant le graphique d'une fonction rationnelle, nous pouvons étudier son comportement local et voir facilement s'il existe des asymptotes. Nous pourrions même être en mesure de les localiser de manière approximative. Même sans le graphique, nous pouvons toujours déterminer si une fonction rationnelle donnée comporte des asymptotes et calculer leur localisation.

Asymptomtotes verticales

Les asymptotes verticales d'une fonction rationnelle peuvent être trouvées en examinant les facteurs du dénominateur qui ne sont pas communs aux facteurs du numérateur. Les asymptotes verticales apparaissent aux zéros de ces facteurs.

Mode d'emploi : À partir d'une fonction rationnelle, identifiez toutes les asymptotes verticales de son graphe

1. Facturez le numérateur et le dénominateur.
2. Notez toutes les restrictions dans le domaine de la fonction.
3. Réduisez l'expression en annulant les facteurs communs au numérateur et au dénominateur.
4. Notez toutes les valeurs qui font que le dénominateur est nul dans cette version simplifiée. C'est là que se produisent les asymptotes verticales.
5. Notez toutes les restrictions dans le domaine où aucune asymptote ne se produit. Il s'agit de discontinuités ou de « trous » amovibles.

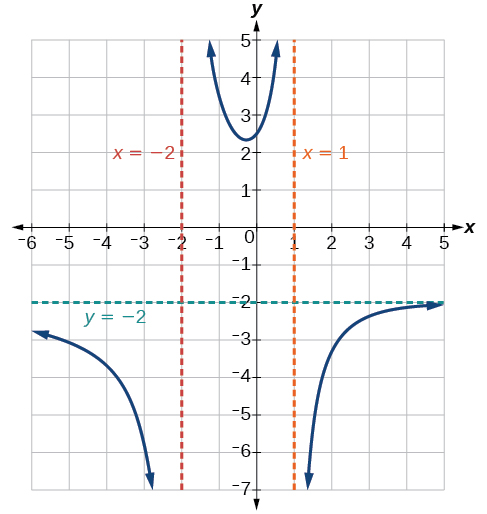
Exemple\(\PageIndex{5}\): Identifying Vertical Asymptotes

Détermine les asymptotes verticales du graphe de\(k(x)=\dfrac{5+2x^2}{2−x−x^2}\).

Solution

Tout d'abord, factorisez le numérateur et le dénominateur.

\[k(x)=\dfrac{5+2x^2}{2−x−x^2}  \nonumber \]

\[=\dfrac{5+2x^2}{(2+x)(1-x)} \nonumber \]

Pour trouver les asymptotes verticales, nous déterminons où cette fonction ne sera pas définie en définissant le dénominateur égal à zéro :

\[(2+x)(1−x)=0 \nonumber \]

\[x=−2, \; x=1 \nonumber \]

\(x=1\)Les zéros du numérateur\(x=–2\) ne sont pas non plus, de sorte que les deux valeurs indiquent deux asymptotes verticales. Le graphique de la figure\(\PageIndex{10}\) confirme l'emplacement des deux asymptotes verticales.

 

Chiffre\(\PageIndex{10}\).

Discontinuités amovibles

Parfois, un graphique contient un trou : un point unique où le graphe n'est pas défini, indiqué par un cercle ouvert. Nous appelons un tel trou une discontinuité amovible. Par exemple, la fonction\(f(x)=\dfrac{x^2−1}{x^2−2x−3}\) peut être réécrite en factorisant le numérateur et le dénominateur.

\[f(x)=\dfrac{(x+1)(x−1)}{(x+1)(x−3)} \nonumber \]

Notez que\(x+1\) c'est un facteur commun au numérateur et au dénominateur. Le zéro de ce facteur,\(x=−1\), est l'emplacement de la discontinuité amovible. Notez également que ce n'\( (x–3) \)est pas un facteur à la fois dans le numérateur et le dénominateur. Le zéro de ce facteur,\(x=3\), est l'asymptote verticale. Voir la figure\(\PageIndex{11}\). [Notez que les discontinuités amovibles peuvent ne pas être visibles lorsque nous utilisons une calculatrice graphique, en fonction de la fenêtre sélectionnée.]

Chiffre\(\PageIndex{11}\).

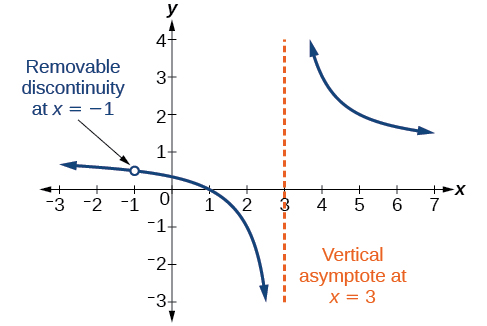
DISCONTINUITÉS SUPPRIMABLES DES FONCTIONS RATIONNELLES

Une discontinuité amovible se produit dans le graphe d'une fonction rationnelle\(x=a\) lorsque si\(a\) est un zéro pour un facteur du dénominateur commun à un facteur du numérateur. Nous prenons en compte le numérateur et le dénominateur et recherchons des facteurs communs. Si nous en trouvons, nous définissons le facteur commun égal à 0 et résolvons. Il s'agit de l'emplacement de la discontinuité amovible. Cela est vrai si la multiplicité de ce facteur est supérieure ou égale à celle du dénominateur. Si la multiplicité de ce facteur est plus grande au dénominateur, il existe toujours une asymptote à cette valeur.

Exemple\(\PageIndex{6}\): Identifying Vertical Asymptotes and Removable Discontinuities for a Graph

Trouvez les asymptotes verticales et les discontinuités amovibles du graphe de\(k(x)=\dfrac{x−2}{x^2−4}\).

Solution

Facturez le numérateur et le dénominateur.

\[k(x)=\dfrac{x−2}{(x−2)(x+2)} \nonumber \]

Notez qu'il existe un facteur commun entre le numérateur et le dénominateur,\(x–2\). Le zéro pour ce facteur est\(x=2\). Il s'agit de l'emplacement de la discontinuité amovible.

Notez qu'il y a un facteur dans le dénominateur qui ne se trouve pas dans le numérateur,\(x+2\). Le zéro pour ce facteur est\(x=−2\). L'asymptote verticale est\(x=−2\). Voir la figure\(\PageIndex{12}\).

Chiffre\(\PageIndex{12}\).

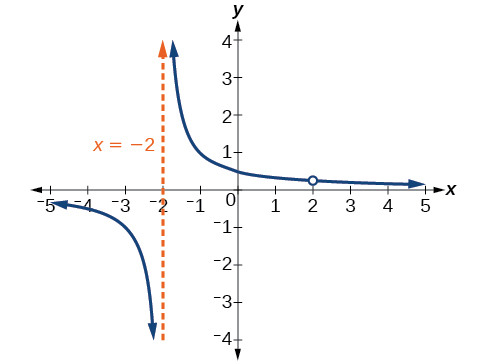
Le graphe de cette fonction aura l'asymptote verticale à\(x=−2\), mais il y aura un trou\(x=2\) au niveau du graphe.

Exercice\(\PageIndex{5}\)

Trouvez les asymptotes verticales et les discontinuités amovibles du graphe de\(f(x)=\dfrac{x^2−25}{x^3−6x^2+5x}\).

Réponse

Discontinuité amovible à\(x=5\).

Asymptotes verticales :\(x=0\),\(x=1\).

Identification des asymptotes horizontales des fonctions rationnelles

Alors que les asymptotes verticales décrivent le comportement d'un graphe lorsque la sortie devient très grande ou très petite, les asymptotes horizontales aident à décrire le comportement d'un graphe lorsque l'entrée devient très grande ou très petite. Rappelez-vous que le comportement final d'un polynôme reflétera celui du terme principal. De même, le comportement final d'une fonction rationnelle reflétera celui du ratio de la fonction qui est le ratio des termes principaux.

Il existe trois résultats distincts lors de la vérification des asymptotes horizontales :

Cas 1 : Si le degré du dénominateur > le degré du numérateur, il existe une asymptote horizontale à\(y=0\).

Exemple :\(f(x)=\dfrac{4x+2}{x^2+4x−5}\)

Dans ce cas, le comportement final est\(f(x)≈\dfrac{4x}{x^2}=\dfrac{4}{x}\). Cela nous indique que, lorsque les entrées augmentent ou diminuent sans limite, cette fonction se comportera de la même manière que la fonction\(g(x)=\dfrac{4}{x}\), et les sorties approcheront de zéro, ce qui se traduira par une asymptote horizontale à\(y=0\). Voir la figure\(\PageIndex{13}\). Notez que ce graphique traverse l'asymptote horizontale.

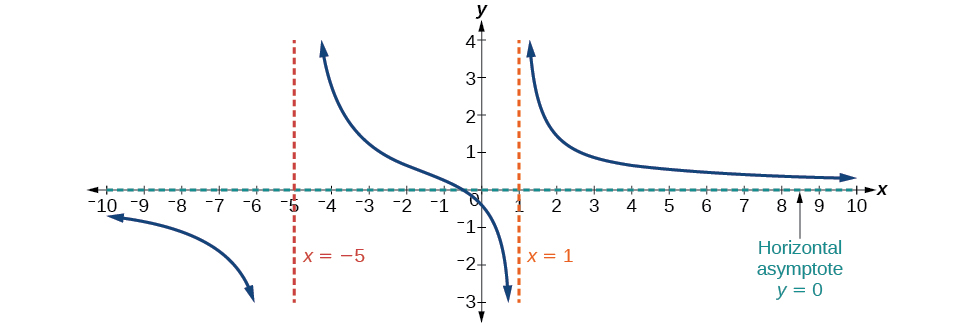
Figure\(\PageIndex{13}\) : Asymptote horizontale\(y=0\) lorsque\(f(x)=\dfrac{p(x)}{q(x)}\),\(q(x)≠0\) où degré\(p\) < degré de\(q\).

Cas 2 : Si le degré du dénominateur est inférieur de un au degré du numérateur, on obtient une asymptote oblique.

Exemple :\(f(x)=\dfrac{3x^2−2x+1}{x−1}\)

Dans ce cas, le comportement final est\(f(x)≈\dfrac{3x^2}{x}=3x\). Cela nous indique que lorsque les entrées augmentent ou diminuent sans limite, cette fonction se comportera de la même manière que la fonction\(g(x)=3x\). Au fur et à mesure que les entrées augmentent, les sorties augmentent et ne se stabilisent pas. Ce graphique ne présente donc aucune asymptote horizontale. Cependant, le graphe de\(g(x)=3x\) ressemble à une ligne diagonale et, comme il se\(f\) comportera de la même manière\(g\), il s'approchera d'une ligne proche de\(y=3x\). Cette ligne est une asymptote oblique.

Pour trouver l'équation de l'asymptote oblique, divisez\(\dfrac{3x^2−2x+1}{x−1}\). Le quotient est\(3x+1\) de 2 et le reste est de 2. L'asymptote oblique est le graphique de la droite\(g(x)=3x+1\). Voir la figure\(\PageIndex{14}\).

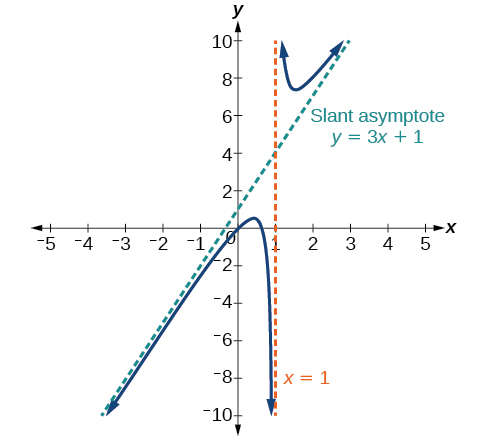
Figure\(\PageIndex{14}\) : Asymptote oblique quand\(f(x)=\dfrac{p(x)}{q(x)}\),\(q(x)≠0\) où degré\(p\) > degré\(q\) de 1.

Cas 3 : Si le degré du dénominateur = degré du numérateur, il existe une asymptote horizontale à\(y=\dfrac{a_n}{b_n}\), où\(a_n\) et\(b_n\) sont respectivement les principaux coefficients de\(p(x)\) et\(q(x)\) pour\(f(x)=\dfrac{p(x)}{q(x)}\),\(q(x)≠0\).

Exemple :\(f(x)=\dfrac{3x^2+2}{x^2+4x−5}\)

Dans ce cas, le comportement final est\(f(x)≈\dfrac{3x^2}{x^2}=3\). Cela nous indique qu'à mesure que les entrées deviennent volumineuses, cette fonction se comportera comme la fonction\(g(x)=3\), qui est une ligne horizontale. Comme\(x\rightarrow \pm \infty\)\(f(x)\rightarrow 3\), résultant en une asymptote horizontale à\(y=3\). Voir la figure\(\PageIndex{15}\). Notez que ce graphique traverse l'asymptote horizontale.

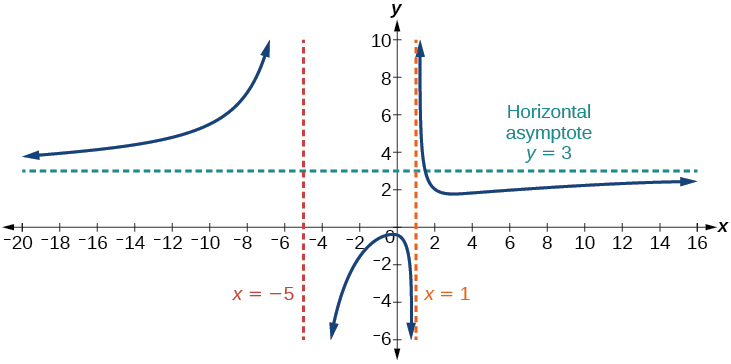
Figure\(\PageIndex{15}\) : Asymptote horizontale lorsque\(f(x)=\dfrac{p(x)}{q(x)}\),\(q(x)≠0\) où degré de\(p\) = degré de\(q\).

Notez que, bien que le graphe d'une fonction rationnelle ne croise jamais une asymptote verticale, il peut ou non croiser une asymptote horizontale ou oblique. De plus, bien que le graphe d'une fonction rationnelle puisse comporter de nombreuses asymptotes verticales, le graphe comportera au plus une asymptote horizontale (ou oblique).

Il convient de noter que, si le degré du numérateur est supérieur de plus d'un au degré du dénominateur, le comportement final du graphe imitera le comportement de la fraction de comportement final réduite. Par exemple, si nous avions la fonction

\[f(x)=\dfrac{3x^5−x^2}{x+3} \nonumber \]

avec comportement final

\[f(x)≈\dfrac{3x^5}{x}=3x^4 \nonumber \]

le comportement final du graphe serait similaire à celui d'un polynôme pair avec un coefficient principal positif.

\(x\rightarrow \pm \infty, f(x)\rightarrow \infty\)

ASYMPTOTES HORIZONTALES DE FONCTIONS RATIONN

L'asymptote horizontale d'une fonction rationnelle peut être déterminée en examinant les degrés du numérateur et du dénominateur.

• Le degré du numérateur est inférieur au degré du dénominateur : asymptote horizontale à\(y=0\).
• Le degré du numérateur est supérieur au degré du dénominateur par un : aucune asymptote horizontale ; asymptote oblique.
• Le degré du numérateur est égal au degré du dénominateur : asymptote horizontale au ratio des principaux coefficients.

Exemple\(\PageIndex{7}\): Identifying Horizontal and Slant Asymptotes

Pour les fonctions répertoriées, identifiez l'asymptote horizontale ou oblique.

1. \(g(x)=\dfrac{6x^3−10x}{2x^3+5x^2}\)
2. \(h(x)=\dfrac{x^2−4x+1}{x+2}\)
3. \(k(x)=\dfrac{x^2+4x}{x^3−8}\)

Solution

Pour ces solutions, nous utiliserons\(f(x)=\dfrac{p(x)}{q(x)},\space q(x)≠0\).

1. \(g(x)=\dfrac{6x^3−10x}{2x^3+5x^2}\): Le\(p = \) degré de\(q=3\), nous pouvons donc trouver l'asymptote horizontale en prenant le ratio des principaux termes. Il existe une asymptote horizontale à\(y =\frac{6}{2}\) ou\(y=3\).
2. \(h(x)=\dfrac{x^2−4x+1}{x+2}\): Le degré\(p=2\) et le degré de\(q=1\). Puisque\(p>q\) par 1, il y a une asymptote oblique trouvée à\(\dfrac{x^2−4x+1}{x+2}\).
   
3. \(k(x)=\dfrac{x^2+4x}{x^3−8}\): Le degré\(p=2\) < degré de\(q=3\), donc il y a une asymptote horizontale\(y=0\).

Exemple\(\PageIndex{8}\) Identifying Horizontal Asymptotes

 

Dans le cas du problème de concentration en sucre plus tôt, nous avons créé l'équation\(C(t)=\dfrac{5+t}{100+10t}\).

Trouvez l'asymptote horizontale et interprétez-la dans le contexte du problème.

Solution

Le numérateur et le dénominateur sont linéaires (degré 1). Comme les degrés sont égaux, il y aura une asymptote horizontale au ratio des principaux coefficients. Dans le numérateur, le terme principal est\(t\), avec le coefficient 1. Au dénominateur, le terme principal est 10t, avec un coefficient 10. L'asymptote horizontale sera au ratio de ces valeurs :

\(t\rightarrow \infty,\space C(t)\rightarrow \frac{1}{10}\)

Cette fonction aura une asymptote horizontale à\(y=\frac{1}{10}\).

Cela nous indique qu'à mesure que les valeurs de volonté\(t\) augmentent, les valeurs de\(C\) volonté s'approchent\(\frac{1}{10}\). Dans le contexte, cela signifie qu'au fil du temps, la concentration de sucre dans le réservoir approchera un dixième de livre de sucre par gallon d'eau ou des\(\frac{1}{10}\) livres par gallon.

Exemple\(\PageIndex{9}\): Identifying Horizontal and Vertical Asymptotes

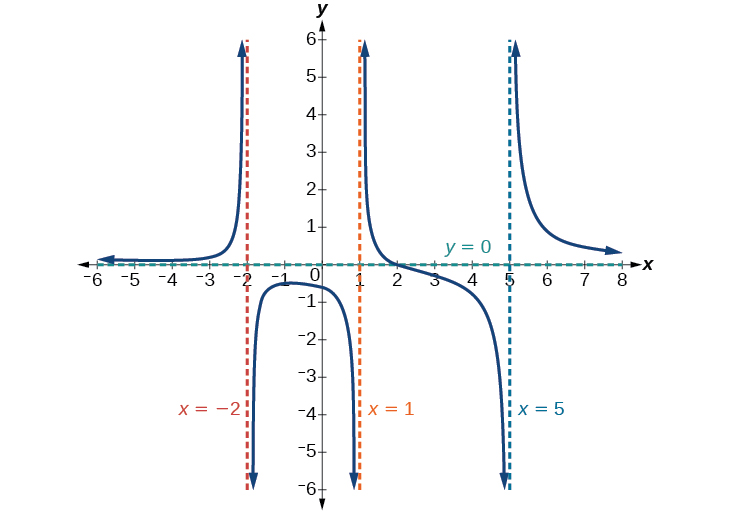
Trouvez les asymptotes horizontales et verticales de la fonction\(f(x)=\dfrac{(x−2)(x+3)}{(x−1)(x+2)(x−5)}\)

 

Solution

Tout d'abord, notez que cette fonction n'a pas de facteurs communs, il n'y a donc pas de discontinuités amovibles potentielles.

La fonction aura des asymptotes verticales lorsque le dénominateur est nul, ce qui la rend indéfinie. Le dénominateur sera zéro à\(x=1,–2,\) et\(5\), indiquant des asymptotes verticales à ces valeurs.

Le numérateur a le degré\(2\), tandis que le dénominateur a le degré 3. Puisque le degré du dénominateur est supérieur au degré du numérateur, le dénominateur augmentera plus rapidement que le numérateur, ce qui entraînera une tendance des sorties vers zéro à mesure que les entrées deviennent grandes, et ainsi\(x\rightarrow \pm \infty\) de suite\(f(x)\rightarrow 0\). Cette fonction aura une asymptote horizontale sur\(y =0.\) Voir la figure\(\PageIndex{16}\).

Chiffre\(\PageIndex{16}\).

Exercice\(\PageIndex{6}\)

Trouvez les asymptotes verticales et horizontales de la fonction :

\(f(x)=\dfrac{(2x−1)(2x+1)}{(x−2)(x+3)}\)

Réponse

Asymptotes verticales à\(x=2\) et\(x=–3\)

asymptote horizontale à\(y =4\).

INTERCEPTIONS DE FONCTIONS RATIONNELLES

Une fonction rationnelle aura une valeur\(y\) -intercept à\(f(0),\) si elle est définie à zéro. Une fonction rationnelle n'aura pas de\(y\) -intercept si elle n'est pas définie à zéro.

De même, une fonction rationnelle aura des\(x\) -intercepts sur les entrées qui font que la sortie est nulle. Comme une fraction n'est égale à zéro que lorsque le numérateur est nul, les interceptions X ne peuvent se produire que lorsque le numérateur de la fonction rationnelle est égal à zéro.

Exemple\(\PageIndex{10}\): Finding the Intercepts of a Rational Function

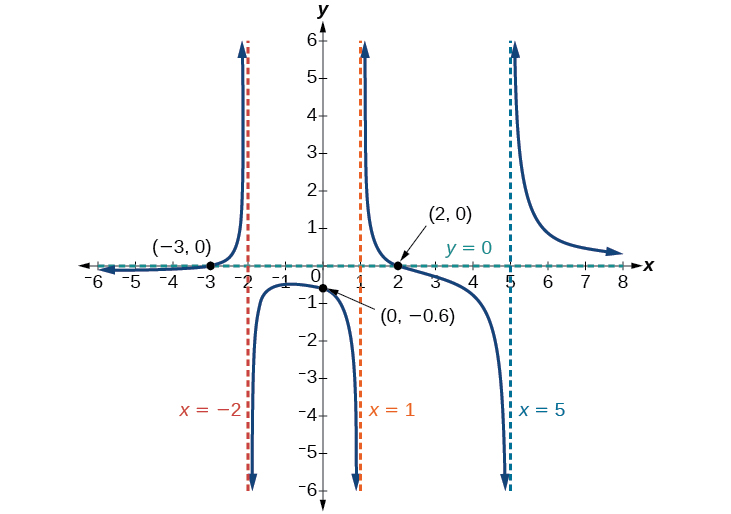
Trouvez les interceptions de \(f(x)=\dfrac{(x−2)(x+3)}{(x−1)(x+2)(x−5)}\).

Solution

Nous pouvons trouver l'intersection y en évaluant la fonction à zéro

\(f(0)=\dfrac{(0−2)(0+3)}{(0−1)(0+2)(0−5)}\)

\(=−\dfrac{6}{10}\)

\(=−\dfrac{3}{5}\)

\(=−0.6\)

Les interceptions X se produisent lorsque la fonction est égale à zéro :

\[ 0=\dfrac{(x−2)(x+3)}{(x−1)(x+2)(x−5)}  \text{   This is zero when the numerator is zero.} \nonumber \]

\[  0=(x−2)(x+3) \qquad \qquad \qquad \qquad \qquad \nonumber \]

\[  x=2, x=−3  \qquad \qquad \qquad \qquad \qquad \nonumber \]

L'intersection Y est\((0,–0.6)\), les interceptions X sont\((2,0)\) et\((–3,0)\). Voir la figure\(\PageIndex{17}\).

Chiffre\(\PageIndex{17}\).

Exercice\(\PageIndex{7}\)

Étant donné la fonction carrée réciproque qui est décalée de 3 unités vers la droite et de 4 unités vers le bas, écrivez-la comme une fonction rationnelle. Ensuite, trouvez les interceptions x et y ainsi que les asymptotes horizontales et verticales.

Réponse

Pour la fonction quadratique réciproque transformée, nous trouvons la forme rationnelle.

\(f(x)=\dfrac{1}{{(x−3)}^2}−4=\dfrac{1−4{(x−3)}^2}{{(x−3)}^2}=\dfrac{1−4(x^2−6x+9)}{(x−3)(x−3)}=\dfrac{−4x^2+24x−35}{x^2−6x+9}\)

Comme le numérateur est le même degré que le dénominateur, nous le connaissons sous le nom de\(x\rightarrow \pm \infty\),\(f(x)\rightarrow −4\) ; il en va\(y=–4\) de même pour l'asymptote horizontale. Ensuite, nous définissons le dénominateur égal à zéro et trouvons que l'asymptote verticale est\(x=3\), car comme\(x\rightarrow 3\),\(f(x)\rightarrow \infty\). Nous mettons ensuite le numérateur à la valeur\(0\) et trouvons que les interceptions X sont à\((2.5,0)\) et\((3.5,0)\). Enfin, nous évaluons la fonction à 0 et trouvons que l'intersection y est égale à\((0,−\frac{35}{9})\).

Représentation graphique de fonctions rationnelles

Dans l'exemple\(\PageIndex{10}\), nous voyons que le numérateur d'une fonction rationnelle révèle les interceptions x du graphe, tandis que le dénominateur révèle les asymptotes verticales du graphe. Comme pour les polynômes, les facteurs du numérateur peuvent avoir des puissances entières supérieures à un. Heureusement, l'effet sur la forme du graphe à ces points d'intersection est le même que celui observé avec les polynômes.

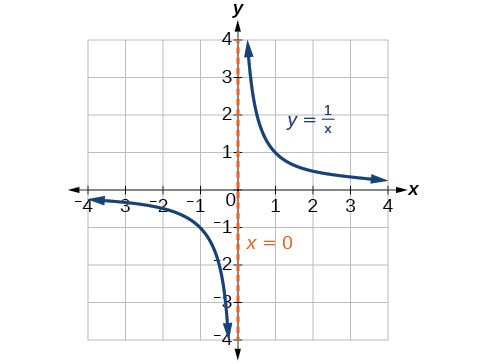
Les asymptotes verticales associées aux facteurs du dénominateur refléteront l'une des deux fonctions réciproques de la boîte à outils. Lorsque le degré du facteur au dénominateur est impair, la caractéristique distinctive est que, d'un côté de l'asymptote verticale, le graphe se dirige vers l'infini positif, et de l'autre côté, le graphe se dirige vers l'infini négatif. Voir la figure\(\PageIndex{18}\).

Chiffre\(\PageIndex{18}\).

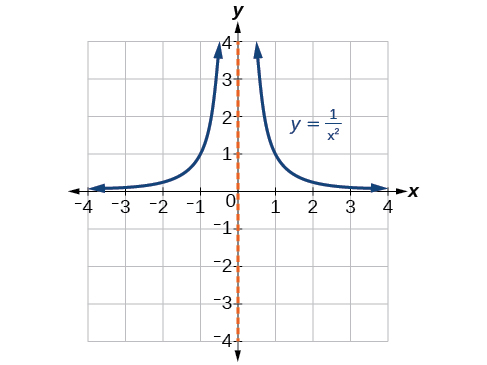
Lorsque le degré du facteur au dénominateur est pair, la caractéristique distinctive est que le graphe se dirige soit vers l'infini positif des deux côtés de l'asymptote verticale, soit vers l'infini négatif des deux côtés. Voir la figure\(\PageIndex{19}\).

Chiffre\(\PageIndex{19}\).

Par exemple, le graphique de \(f(x)=\dfrac{{(x+1)}^2(x−3)}{{(x+3)}^2(x−2)}\)est illustré sur la figure\(\PageIndex{20}\).

Chiffre\(\PageIndex{20}\).

• À l'intersection X\(x=−1\) correspondant au\({(x+1)}^2\) facteur du numérateur, le graphe « rebondit », conformément à la nature quadratique du facteur.
• À l'intersection X\(x=3\) correspondant au\((x−3)\) facteur du numérateur, le graphe passe par l'axe comme on peut s'y attendre avec un facteur linéaire.
• Au niveau de l'asymptote verticale\(x=−3\) correspondant au\({(x+3)}^2\) facteur du dénominateur, le graphe se dirige vers l'infini positif des deux côtés de l'asymptote, conformément au comportement de la fonction\(f(x)=\dfrac{1}{x^2}\).
• Au niveau de l'asymptote verticale\(x=2\), correspondant au\((x−2)\) facteur du dénominateur, le graphe se dirige vers l'infini positif sur le côté gauche de l'asymptote et vers l'infini négatif sur le côté droit, conformément au comportement de la fonction\(f(x)=\dfrac{1}{x}\).

Comment : à partir d'une fonction rationnelle, esquissez un graphique.

1. Évaluez la fonction à 0 pour trouver l'intersection Y.
2. Facturez le numérateur et le dénominateur.
3. Pour les facteurs du numérateur qui ne sont pas communs au dénominateur, déterminez où chaque facteur du numérateur est égal à zéro pour trouver les points d'intersection X.
4. Trouvez les multiplicités des points d'intersection X pour déterminer le comportement du graphe à ces points.
5. Pour les facteurs du dénominateur, notez les multiplicités des zéros afin de déterminer le comportement local. Pour les facteurs qui ne sont pas communs au numérateur, trouvez les asymptotes verticales en mettant ces facteurs à zéro, puis résolvez.
6. Pour les facteurs du dénominateur commun aux facteurs du numérateur, trouvez les discontinuités amovibles en définissant ces facteurs sur 0, puis résolvez.
7. Comparez les degrés du numérateur et du dénominateur pour déterminer les asymptotes horizontales ou obliques.
8. Esquissez le graphique.

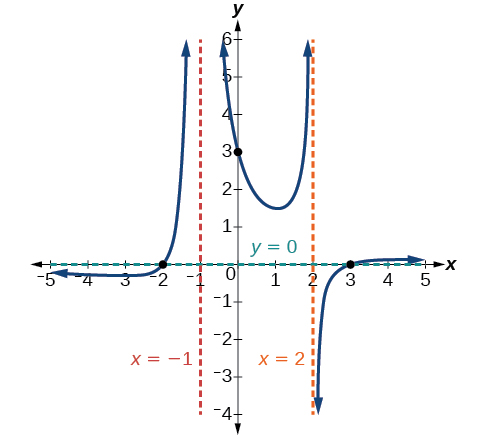
Exemple\(\PageIndex{11}\): Graphing a Rational Function

Esquissez un graphique de\(f(x)=\frac{(x+2)(x−3)}{{(x+1)}^2(x−2)}\).

Solution

Nous pouvons commencer par constater que la fonction est déjà prise en compte, ce qui nous évite une étape.

Ensuite, nous trouverons les interceptions. L'évaluation de la fonction à zéro donne l'intersection y :

\(f(0)=\dfrac{(0+2)(0−3)}{{(0+1)}^2(0−2)}=3\)

 

Pour trouver les interceptions X, nous déterminons quand le numérateur de la fonction est zéro. En mettant chaque facteur égal à zéro, nous trouvons les interceptions x à\(x=–2\) et\(x=3\). À chaque fois, le comportement sera linéaire (multiplicité 1), le graphe passant par l'intersection.

Nous avons une intersection Y à\((0,3)\) et des interceptions X à\((–2,0)\) et\((3,0)\).

Pour trouver les asymptotes verticales, on détermine quand le dénominateur est égal à zéro. Cela se produit quand\(x+1=0\) et quand\(x–2=0\), nous donnant des asymptotes verticales à\(x=–1\) et\(x=2\).

Le numérateur et le dénominateur ne présentent aucun facteur commun. Cela signifie qu'il n'y a pas de discontinuités amovibles.

Enfin, le degré du dénominateur est plus grand que le degré du numérateur, ce qui nous indique que ce graphique possède une asymptote horizontale à\(y =0\).

Pour esquisser le graphique, nous pouvons commencer par tracer les trois points d'intersection. Comme le graphique n'a pas d'intersection X entre les asymptotes verticales et que l'intersection y est positive, nous savons que la fonction doit rester positive entre les asymptotes, ce qui nous permet de remplir la partie centrale du graphique comme indiqué sur la figure\(\PageIndex{21}\).

Chiffre\(\PageIndex{21}\).

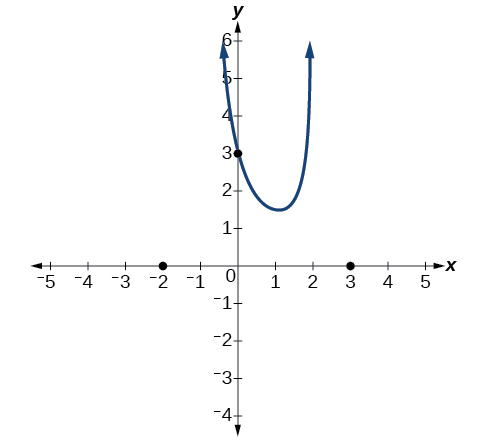
Le facteur associé à l'asymptote verticale à\(x=−1\) était au carré, donc nous savons que le comportement sera le même des deux côtés de l'asymptote. Le graphique se dirige vers l'infini positif lorsque les entrées se rapprochent de l'asymptote de droite, de sorte que le graphique se dirige également vers l'infini positif sur la gauche.

Pour l'asymptote verticale à\(x=2\), le facteur n'était pas au carré, de sorte que le graphique aura un comportement opposé de chaque côté de l'asymptote. Voir la figure\(\PageIndex{22}\). Après avoir franchi les points d'intersection X, le graphique se stabilise vers une sortie de zéro, comme l'indique l'asymptote horizontale.

Chiffre\(\PageIndex{22}\).

 

Exercice\(\PageIndex{8}\)

Compte tenu de la fonction\(f(x)=\frac{{(x+2)}^2(x−2)}{2{(x−1)}^2(x−3)}\), utilisez les caractéristiques des polynômes et des fonctions rationnelles pour décrire son comportement et esquisser la fonction.

Réponse

Asymptote horizontale à\(y=\frac{1}{2}\). Asymptotes verticales à\(x=1\) et\(x=3\). Y intercepte à\((0,\frac{4}{3})\).

X intercepte à\((2,0)\) et\((–2,0)\). \((–2,0)\)est un zéro avec multiplicité\(2\), et le graphe rebondit sur l'axe des abscisses à ce point. \((2,0)\)est un zéro unique et le graphique croise l'axe à ce point.

Chiffre\(\PageIndex{23}\).

Écrire des fonctions rationnelles

Maintenant que nous avons analysé les équations des fonctions rationnelles et leur relation avec un graphe de la fonction, nous pouvons utiliser les informations fournies par un graphe pour écrire la fonction. Une fonction rationnelle écrite sous forme factorielle aura une intersection x où chaque facteur du numérateur est égal à zéro. (Une exception se produit en cas de discontinuité amovible.) Par conséquent, nous pouvons former un numérateur d'une fonction dont le graphe passera par un ensemble d'interceptions x en introduisant un ensemble de facteurs correspondants. De même, étant donné que la fonction aura une asymptote verticale où chaque facteur du dénominateur est égal à zéro, nous pouvons former un dénominateur qui produira les asymptotes verticales en introduisant un ensemble de facteurs correspondant.

ECRIRE DES FONCTIONS RATIONNELLES À PARTIR D'INTERCEPTES ET D'AS

Si une fonction rationnelle a des interceptions X à\(x=x_1,x_2,...,x_n\), des asymptotes verticales à\(x=v_1,v_2,…,v_m\) et\(x_i=\) aucune\(v_j\), alors la fonction peut être écrite sous la forme suivante :

\(f(x)=a\dfrac{ {(x−x_1)}^{p_1} {(x−x_2)}^{p_2}⋯{(x−x_n)}^{p_n} }{ {(x−v_1)}^{q_1} {(x−v_2)}^{q_2}⋯{(x−v_m)}^{q_n}}\)

où les puissances\(p_i\) ou\(q_i\) sur chaque facteur peuvent être déterminées par le comportement du graphe à l'intersection ou à l'asymptote correspondante, et le facteur d'étirement\(a\) peut être déterminé en fonction d'une valeur de la fonction autre que l'intersection x ou par l'asymptote horizontale s'il est différent de zéro.

À partir du graphe d'une fonction rationnelle, écrivez la fonction.

1. Déterminez les facteurs du numérateur. Examinez le comportement du graphe aux points d'intersection x pour déterminer les zéros et leurs multiplicités. (Cela est facile lorsque vous recherchez la fonction « la plus simple » avec de petites multiplicités, telles que 1 ou 3, mais cela peut s'avérer difficile pour des multiplicités plus importantes, telles que 5 ou 7, par exemple.)
2. Déterminez les facteurs du dénominateur. Examinez le comportement des deux côtés de chaque asymptote verticale pour déterminer les facteurs et leurs pouvoirs.
3. Utilisez n'importe quel point clair du graphique pour trouver le facteur d'étirement.

Exemple\(\PageIndex{12}\): Writing a Rational Function from Intercepts and Asymptotes

Écrivez une équation pour la fonction rationnelle illustrée à la figure\(\PageIndex{24}\).

Chiffre\(\PageIndex{24}\).

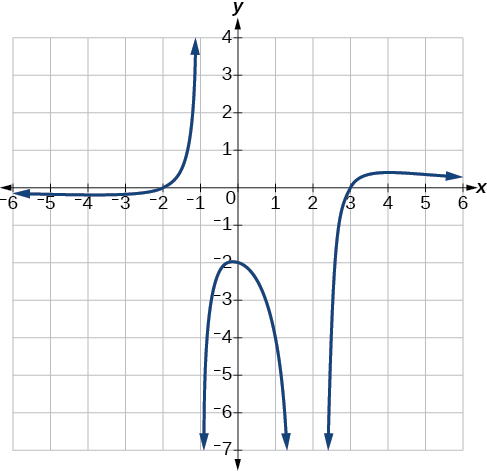
Solution

Le graphique semble avoir des interceptions X à\(x=–2\) et\(x=3\). Dans les deux cas, le graphique passe par l'intersection, suggérant des facteurs linéaires. Le graphique comporte deux asymptotes verticales. Celui à\(x=–1\) semble présenter un comportement de base similaire à celui de\(\dfrac{1}{x}\), avec le graphe se dirigeant vers l'infini positif d'un côté et se dirigeant vers l'infini négatif de l'autre. L'asymptote at\(x=2\) présente un comportement similaire à\(\dfrac{1}{x^2}\), le graphe se dirigeant vers l'infini négatif des deux côtés de l'asymptote. Voir la figure\(\PageIndex{25}\).

Chiffre\(\PageIndex{25}\).

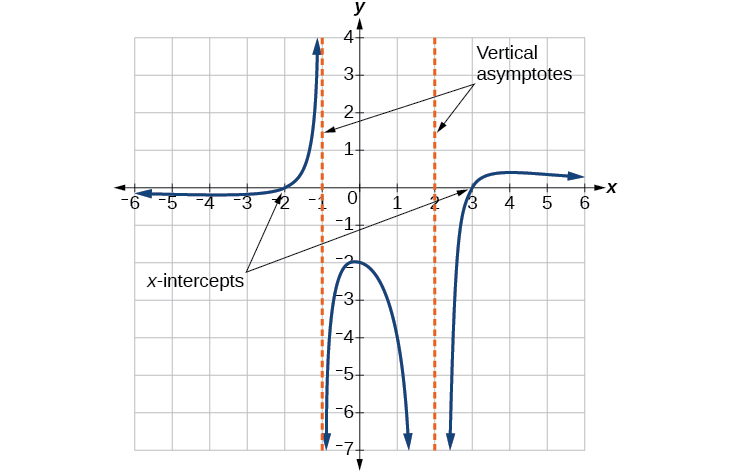
Nous pouvons utiliser ces informations pour écrire une fonction du formulaire

\(f(x)=a\dfrac{(x+2)(x−3)}{(x+1){(x−2)}^2}\)

 

Pour trouver le facteur d'étirement, nous pouvons utiliser un autre point clair du graphique, tel que l'intersection \((0,–2)\)y.

\(−2=a\dfrac{(0+2)(0−3)}{(0+1){(0−2)}^2}\)

\(-2=a\dfrac{−6}{4}\)

\(a=\dfrac{−8}{−6}=\dfrac{4}{3}\)

Cela nous donne une fonction finale de\(f(x)=\dfrac{4(x+2)(x−3)}{3(x+1){(x−2)}^2}\).

 

Médias

Accédez à ces ressources en ligne pour des instructions et des exercices supplémentaires grâce à des fonctions rationnelles.

• Représentation graphique de fonctions rationnelles
• Trouver l'équation d'une fonction rationnelle
• Déterminer les asymptotes verticales et horizontales
• Trouvez les interceptions, les asymptotes et le trou d'une fonction rationnelle

Équations clés

Fonction rationnelle\( \qquad \)\(f(x)=\dfrac{P(x)}{Q(x)}=\dfrac{a_px^p+a_{p−1}x^{p−1}+...+a_1x+a_0}{b_qx^q+b_{q−1}x^{q−1}+...+b_1x+b_0},\space Q(x)≠0\)

Concepts clés

• Nous pouvons utiliser la notation flèche pour décrire le comportement local et le comportement final des fonctions de la boîte à outils\(f(x)=\frac{1}{x}\) et\(f(x)=\frac{1}{x^2}\). Voir l'exemple\(\PageIndex{1}\).
• Une fonction qui se stabilise à une valeur horizontale possède une asymptote horizontale. Une fonction peut avoir plusieurs asymptotes verticales. Voir l'exemple.
• Les problèmes d'application concernant les taux et les concentrations impliquent souvent des fonctions rationnelles. Voir l'exemple.
• Le domaine d'une fonction rationnelle inclut tous les nombres réels à l'exception de ceux qui font que le dénominateur est égal à zéro. Voir l'exemple.
• Les asymptotes verticales d'une fonction rationnelle apparaîtront lorsque le dénominateur de la fonction est égal à zéro et que le numérateur n'est pas nul. Voir l'exemple.
• Une discontinuité amovible peut apparaître dans le graphe d'une fonction rationnelle si une entrée fait en sorte que le numérateur et le dénominateur soient nuls. Voir l'exemple.
• Le comportement final d'une fonction rationnelle reflétera celui du ratio des principaux termes des fonctions numérateur et dénominateur. Voir Exemple, Exemple, Exemple et Exemple.
• Représentez graphiquement les fonctions rationnelles en recherchant les interceptions, le comportement au niveau des interceptions et des asymptotes et le comportement final. Voir l'exemple.
• Si une fonction rationnelle a des interceptions X à\(x=x_1,x_2,…,x_n\), des asymptotes verticales à\(x=v_1,v_2,…,v_m\) et\(x_i=\) aucune\(v_j\), alors la fonction peut être écrite sous la forme