5.5 : Zéros des fonctions polynomiales

Last updated
Save as PDF

Page ID: 195599

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

Evaluez un polynôme à l'aide du théorème du reste.
Utilisez le théorème des facteurs pour résoudre une équation polynomiale.
Utilisez le théorème du zéro rationnel pour trouver des zéros rationnels.
Trouve les zéros d'une fonction polynomiale.
Utilisez le théorème de factorisation linéaire pour trouver des polynômes avec des zéros donnés.
Utilisez la règle des signes de Descartes.
Résolvez des applications réelles d'équations polynomiales

Une nouvelle boulangerie propose des gâteaux en feuille décorés pour les fêtes d'anniversaire d'enfants et autres occasions spéciales. La boulangerie souhaite que le volume d'un petit gâteau soit de 351 pouces cubes. Le gâteau a la forme d'un solide rectangulaire. Ils veulent que la longueur du gâteau soit supérieure de quatre pouces à la largeur du gâteau et que la hauteur du gâteau soit un tiers de la largeur. Quelles devraient être les dimensions du moule à gâteau ?

Ce problème peut être résolu en écrivant une fonction cubique et en résolvant une équation cubique pour le volume du gâteau. Dans cette section, nous aborderons divers outils permettant d'écrire des fonctions polynomiales et de résoudre des équations polynomiales.

Évaluation d'un polynôme à l'aide du théorème du reste

Dans la dernière section, nous avons appris à diviser les polynômes. Nous pouvons désormais utiliser la division polynomiale pour évaluer les polynômes à l'aide du théorème du reste. Si le polynôme est divisé par$x–k$, le reste peut être trouvé rapidement en évaluant la fonction polynomiale à$k$, c'est-à-dire,$f(k)$. Passons en revue la preuve du théorème.

Rappelons que l'algorithme de division indique que, étant donné un dividende polynomial$f(x)$ et un diviseur polynomial non nul$d(x)$ où le degré de$d(x)$ est inférieur ou égal au degré de$f(x)$, il existe des polynômes uniques$q(x)$ et$r(x)$ tels que

\[f(x)=d(x)q(x)+r(x) \nonumber\]

Si le diviseur est$d(x)$,$x−k$,, cela prend la forme

\[f(x)=(x−k)q(x)+r \nonumber\]

Depuis le diviseur$x−k$

est linéaire, le reste sera une constante,$r$. Et, si nous évaluons cela pour$x=k$, nous avons

\[\begin{align*} f(k)&=(k−k)q(k)+r \\[4pt] &=0{\cdot}q(k)+r \\[4pt] &=r \end{align*}\]

En d'autres termes,$f(k)$ le reste est-il obtenu en divisant$f(x)$ par$x−k$.

Le théorème du reste

Si un polynôme$f(x)$ est divisé par$x−k$, le reste est la valeur$f(k)$.

$alt$ Étant donné une fonction polynomiale$f$, évaluez$f(x)$ à$x=k$ l'aide du théorème du reste.

Utilisez la division synthétique pour diviser le polynôme par$x−k$.
Le reste est la valeur$f(k)$.

Exemple$\PageIndex{1}$: Using the Remainder Theorem to Evaluate a Polynomial

Utilisez le théorème du reste pour évaluer$f(x)=6x^4−x^3−15x^2+2x−7$ à$x=2$.

Solution

Pour trouver le reste à l'aide du théorème du reste, utilisez la division synthétique pour diviser le polynôme par$x−2$.

\[ 2 \begin{array}{|ccccc} \; 6 & −1 & −15 & 2 & −7 \\ \text{} & 12 & 22 & 14 & 32 \\ \hline \end{array} \\ \begin{array}{ccccc} 6 & 11 & \; 7 & \;\;16 & \;\; 25 \end{array} \]

Le reste est de 25. Par conséquent,$f(2)=25$.

Analyse

Nous pouvons vérifier notre réponse en évaluant$f(2)$.

\[\begin{align*} f(x)&=6x^4−x^3−15x^2+2x−7 \\ f(2)&=6(2)^4−(2)^3−15(2)^2+2(2)−7 \\ &=25 \end{align*}\]

Exercice$\PageIndex{1}$

Utilisez le théorème du reste pour évaluer$f(x)=2x^5−3x^4−9x^3+8x^2+2$ l'art$x=−3$.

Réponse: $f(−3)=−412$

Utilisation du théorème des facteurs pour résoudre une équation polynomiale

Le théorème des facteurs est un autre théorème qui nous aide à analyser les équations polynomiales. Il nous indique comment les zéros d'un polynôme sont liés aux facteurs. Rappelons que l'algorithme de division.

\[f(x)=(x−k)q(x)+r\]

Si$k$ vaut zéro, alors le reste$r$ est$f(k)=0$ et$f (x)=(x−k)q(x)+0$ ou$f(x)=(x−k)q(x)$.

L'avis, écrit sous cette forme,$x−k$ est un facteur de$f(x)$. Nous pouvons conclure que si$k$ est un zéro de$f(x)$, alors$x−k$ est un facteur de$f(x)$.

De même, si$x−k$ est un facteur de$f(x)$, alors le reste de l'algorithme de division l'$f(x)=(x−k)q(x)+r$est$0$. Cela nous indique que$k$ c'est un zéro.

Cette paire d'implications constitue le théorème des facteurs. Comme nous le verrons bientôt, un polynôme de degré$n$ dans le système numérique complexe aura des$n$ zéros. Nous pouvons utiliser le théorème des facteurs pour factoriser complètement un polynôme dans le produit des$n$ facteurs. Une fois que le polynôme a été complètement factorisé, nous pouvons facilement déterminer les zéros du polynôme.

LE THÉORÈME DES FACTEURS

Selon le théorème des facteurs,$k$ est un zéro de$f(x)$ si et seulement si$(x−k)$ est un facteur de$f(x)$.

Comment : à partir d'un facteur et d'un polynôme du troisième degré, utiliser le théorème des facteurs pour factoriser le polynôme

Utilisez la division synthétique pour diviser le polynôme par$(x−k)$.
Confirmez que le reste l'est$0$.
Écrivez le polynôme comme le produit de$(x−k)$ et le quotient quadratique.
Si possible, factorisez le quadratique.
Écrivez le polynôme comme le produit de facteurs.

Exemple$\PageIndex{2}$: Using the Factor Theorem to Solve a Polynomial Equation

Montrez que$(x+2)$ c'est un facteur de$x^3−6x^2−x+30$. Trouvez les autres facteurs. Utilisez les facteurs pour déterminer les zéros du polynôme.

Solution

Nous pouvons utiliser la division synthétique pour montrer qu'il$(x+2)$ s'agit d'un facteur du polynôme.

\[ -2 \begin{array}{|cccc} \; 1 & −6 & −1 & 30 \\ \text{} & -2 & 16 & -30 \\ \hline \end{array} \\ \begin{array}{cccc} 1 & -8 & \; 15 & \;\;0 \end{array} \]

Le reste est nul, de$(x+2)$ même qu'un facteur du polynôme. Nous pouvons utiliser l'algorithme de division pour écrire le polynôme comme le produit du diviseur et du quotient :

\[(x+2)(x^2−8x+15)\]

Nous pouvons factoriser le facteur quadratique pour écrire le polynôme comme

\[(x+2)(x−3)(x−5)\]

Selon le théorème des facteurs, les zéros de$x^3−6x^2−x+30$ sont —2, 3 et 5.

Exercice$\PageIndex{2}$

Utilisez le théorème des facteurs pour trouver les zéros d'une$f(x)=x^3+4x^2−4x−16$ donnée qui$(x−2)$ est un facteur du polynôme.

Réponse: Les zéros sont 2, —2 et —4.

Utiliser le théorème du zéro rationnel pour trouver des zéros rationnels

Une autre utilisation du théorème du reste est de tester si un nombre rationnel est nul pour un polynôme donné. Mais nous avons d'abord besoin d'un ensemble de nombres rationnels à tester. Le théorème du zéro rationnel nous aide à réduire le nombre de zéros rationnels possibles en utilisant le rapport entre les facteurs du terme constant et les facteurs du coefficient principal du polynôme

Considérons une fonction quadratique avec deux zéros,$x=\frac{2}{5}$ et$x=\frac{3}{4}$. Selon le théorème des facteurs, ces zéros sont associés à des facteurs. Mettons chaque facteur égal à 0, puis construisons la fonction quadratique d'origine en l'absence de son facteur d'étirement.

$alt$

Notez que deux des facteurs du terme constant, 6, sont les deux numérateurs des racines rationnelles d'origine : 2 et 3. De même, deux des facteurs du coefficient principal, 20, sont les deux dénominateurs des racines rationnelles initiales : 5 et 4.

Nous pouvons en déduire que les numérateurs des racines rationnelles seront toujours des facteurs du terme constant et que les dénominateurs seront des facteurs du coefficient principal. C'est l'essence du théorème du zéro rationnel ; c'est un moyen de nous donner un ensemble de zéros rationnels possibles.

LE THÉORÈME DU ZÉRO RATIONAL

Le théorème du zéro rationnel indique que, si le polynôme$f(x)=a_nx^n+a_{n−1}x^{n−1}+...+a_1x+a_0$ a des coefficients entiers, alors chaque zéro rationnel de$f(x)$ a la forme$\frac{p}{q}$ où$p$ est un facteur du terme constant$a_0$ et$q$ un facteur du coefficient principal$a_n$.

Lorsque le coefficient principal est 1, les zéros rationnels possibles sont les facteurs du terme constant.

Procédure : étant donné une fonction polynomiale$f(x)$, use the Rational Zero Theorem to find rational zeros.

Déterminez tous les facteurs du terme constant et tous les facteurs du coefficient principal.
Déterminez toutes les valeurs possibles de$\dfrac{p}{q}$, où$p$ est un facteur du terme constant et$q$ un facteur du coefficient principal. Assurez-vous d'inclure à la fois des candidats positifs et négatifs.
Déterminez quels zéros possibles sont des zéros réels en évaluant chaque cas de$f(\frac{p}{q})$.

Exemple$\PageIndex{3}$: Listing All Possible Rational Zeros

Énumérez tous les zéros rationnels possibles de$f(x)=2x^4−5x^3+x^2−4$.

Solution

Les seuls zéros rationnels possibles de$f(x)$ sont les quotients des facteurs du dernier terme, —4, et les facteurs du coefficient principal, 2.

Le terme constant est —4 ; les facteurs de —4 le sont$p=±1,±2,±4$.

Le coefficient principal est de 2 ; les facteurs de 2 sont$q=±1,±2$.

Si l'un des quatre zéros réels est un zéro rationnel, il correspondra à l'un des facteurs suivants de —4 divisé par l'un des facteurs de 2.

\[\dfrac{p}{q}=±\dfrac{1}{1},±\dfrac{1}{2} \; \; \; \; \; \; \frac{p}{q}=±\dfrac{2}{1},±\dfrac{2}{2} \; \; \; \; \; \; \dfrac{p}{q}=±\dfrac{4}{1},±\dfrac{4}{2} \nonumber\]

Notez que$\frac{2}{2}=1$ et$\frac{4}{2}=2$, qui ont déjà été listés. Nous pouvons donc raccourcir notre liste.

\[\dfrac{p}{q} = \dfrac{\text{Factors of the last}}{\text{Factors of the first}}=±1,±2,±4,±\dfrac{1}{2}\nonumber \]

Exemple$\PageIndex{4}$: Using the Rational Zero Theorem to Find Rational Zeros

Utilisez le théorème du zéro rationnel pour trouver les zéros rationnels de$f(x)=2x^3+x^2−4x+1$.

Solution

Le théorème du zéro rationnel nous indique que si$\frac{p}{q}$ est un zéro de$f(x)$, alors$p$ est un facteur de 1 et$q$ est un facteur de 2.

\[ \begin{align*} \dfrac{p}{q}=\dfrac{factor\space of\space constant\space term}{factor\space of\space leading\space coefficient} \\[4pt] &=\dfrac{factor\space of\space 1}{factor\space of\space 2} \end{align*}\]

Les facteurs de 1 sont de ±1 et les facteurs de 2 sont de ±1 et ±2. Les valeurs possibles pour$\frac{p}{q}$ sont ±1 et$±\frac{1}{2}$. Il s'agit des zéros rationnels possibles pour la fonction. Nous pouvons déterminer quels zéros possibles sont des zéros réels en remplaçant ces valeurs par$x$ in$f(x)$.

\[f(−1)=2{(−1)}^3+{(−1)}^2−4(−1)+1=4\]

\[f(1)=1{(1)}^3+{(1)}^2−4(1)+1=0\]

\[f(−\dfrac{1}{2})=2{(−\dfrac{1}{2})}^3+{(−\dfrac{1}{2})}^2−4(−\dfrac{1}{2})+1=3\]

\[f(\dfrac{1}{2})=2{(\dfrac{1}{2})}^3+{(\dfrac{1}{2})}^2−4(\dfrac{1}{2})+1=−\dfrac{1}{2}\]

Parmi ceux-ci,$−1$$−\dfrac{1}{2}$, et ne$\dfrac{1}{2}$ sont pas des zéros de$f(x)$. 1 est le seul zéro rationnel de$f(x)$.

Exercice$\PageIndex{3}$

Utilisez le théorème du zéro rationnel pour trouver les zéros rationnels de$f(x)=x^3−5x^2+2x+1$.

Réponse: Il n'y a pas de zéros rationnels.

Trouver les zéros des fonctions polynomiales

Le théorème du zéro rationnel nous aide à affiner la liste des zéros rationnels possibles pour une fonction polynomiale. Une fois cela fait, nous pouvons utiliser la division synthétique à plusieurs reprises pour déterminer tous les zéros d'une fonction polynomiale.

Procédure : étant donné une fonction polynomiale$f$, use synthetic division to find its zeros.

Utilisez le théorème du zéro rationnel pour répertorier tous les zéros rationnels possibles de la fonction.
Utilisez la division synthétique pour évaluer un zéro possible donné en divisant synthétiquement le candidat dans le polynôme. Si le reste est égal à 0, le candidat est égal à zéro. Si le reste n'est pas nul, éliminez le candidat.
Répétez la deuxième étape en utilisant le quotient obtenu avec la division synthétique. Si possible, continuez jusqu'à ce que le quotient soit quadratique.
Trouvez les zéros de la fonction quadratique. Deux méthodes possibles pour résoudre les quadratiques sont la factorisation et l'utilisation de la formule quadratique.

Exemple$\PageIndex{5}$: Finding the Zeros of a Polynomial Function with Repeated Real Zeros

Trouvez les zéros de$f(x)=4x^3−3x−1$.

Solution

Le théorème du zéro rationnel nous indique que si$\dfrac{p}{q}$ est un zéro de$f(x)$, alors$p$ est un facteur de -1 et$q$ est un facteur de 4.

\[\begin{align*}\dfrac{p}{q}=\dfrac{factor\space of\space constant\space term}{factor\space of\space leading\space coefficient} \\[4pt] =\dfrac{factor\space of\space -1}{factor\space of\space 4} \end{align*}\]

Les facteurs de —1 sont ±1 et les facteurs de 4 sont ±1, ±2 et ±4. Les valeurs possibles pour$\dfrac{p}{q}$ sont$±1$$±\dfrac{1}{2}$, et$±\dfrac{1}{4}$. Il s'agit des zéros rationnels possibles pour la fonction. Nous utiliserons une division synthétique pour évaluer chaque zéro possible jusqu'à ce que nous en trouvions un qui donne un reste de 0. Commençons par 1.

La division par$(x−1)$ donne un reste de 0, donc 1 est un zéro de la fonction. Le polynôme peut être écrit comme

\[(x−1)(4x^2+4x+1) \nonumber\]

Le quadratique est un carré parfait. $f(x)$peut être écrit comme

\[(x−1){(2x+1)}^2\nonumber\]

Nous savons déjà que 1 est un zéro. L'autre zéro aura une multiplicité de 2 car le facteur est au carré. Pour trouver l'autre zéro, nous pouvons définir un facteur égal à 0.

\[ \begin{align*} 2x+1=0 \\[4pt] x &=−\dfrac{1}{2} \end{align*}\]

Les zéros de la fonction sont 1 et$−\frac{1}{2}$ avec une multiplicité de 2.

Analyse

Regardez le graphique de la fonction$f$ dans la figure$\PageIndex{1}$. Remarquez qu'à$x =−0.5$, le graphe rebondit sur l'axe des abscisses, indiquant la multiplicité paire (2,4,6...) pour le zéro −0,5. À$x=1$, le graphique croise l'axe des abscisses, indiquant la multiplicité impaire (1,3,5...) pour le zéro$x=1$.

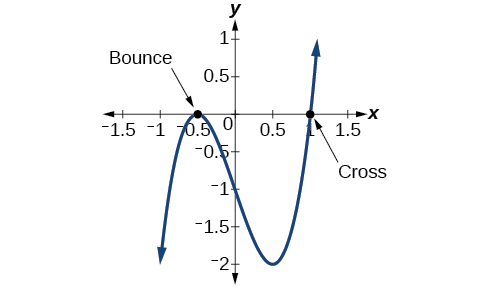
Utilisation du théorème fondamental de l'algèbre

Maintenant que nous pouvons trouver des zéros rationnels pour une fonction polynomiale, nous allons examiner un théorème qui traite du nombre de zéros complexes d'une fonction polynomiale. Le théorème fondamental de l'algèbre nous indique que chaque fonction polynomiale possède au moins un zéro complexe. Ce théorème constitue la base de la résolution d'équations polynomiales.

Supposons qu'$f$il s'agisse d'une fonction polynomiale de degré quatre, et$f (x)=0$. Le théorème fondamental de l'algèbre indique qu'il existe au moins une solution complexe, appelez-la$c_1$. Selon le théorème des facteurs, nous pouvons écrire$f(x)$ comme un produit$x−c_1$ et un quotient polynomial. Comme$x−c_1$ il est linéaire, le quotient polynomial sera de degré trois. Nous appliquons maintenant le théorème fondamental de l'algèbre au quotient polynomial du troisième degré. Il aura au moins un zéro complexe, appelez-le$c_2$. Nous pouvons donc écrire le quotient polynomial comme un produit de$x−c_2$ et un nouveau quotient polynomial de degré deux. Continuez à appliquer le théorème fondamental de l'algèbre jusqu'à ce que tous les zéros soient trouvés. Il y en aura quatre et chacune donnera un facteur de$f(x)$.

LE THÉORÈME FONDAMENTAL DE L'ALGÈBRE

Le théorème fondamental de l'algèbre indique que, s'il s'$f(x)$agit d'un polynôme de degré$n > 0$, il$f(x)$ possède alors au moins un zéro complexe.

Nous pouvons utiliser ce théorème pour soutenir que, si$f(x)$ est un polynôme de degré$n >0$ et a est un nombre réel non nul, alors$f(x)$ a exactement des facteurs$n$ linéaires

\[f(x)=a(x−c_1)(x−c_2)...(x−c_n)\]

où$c_1,c_2$,... ,$c_n$ sont des nombres complexes. Par conséquent,$f(x)$ a$n$ des racines si l'on tient compte des multiplicités.

Q&R : Chaque polynôme possède-t-il au moins un zéro imaginaire ?

Non. Les nombres réels sont un sous-ensemble de nombres complexes, mais pas l'inverse. Un nombre complexe n'est pas nécessairement imaginaire. Les nombres réels sont également des nombres complexes.

Exemple$\PageIndex{6}$: Finding the Zeros of a Polynomial Function with Complex Zeros

Trouvez les zéros de$f(x)=3x^3+9x^2+x+3$.

Solution

Le théorème du zéro rationnel nous indique que si$\frac{p}{q}$ est un zéro de$f(x)$, alors$p$ est un facteur de 3 et$q$ est un facteur de 3.

Les facteurs de 3 sont ±1 et ±3. Les valeurs possibles pour$\dfrac{p}{q}$, et donc les zéros rationnels possibles pour la fonction, sont ±3, ±1 et$±\dfrac{1}{3}$. Nous utiliserons une division synthétique pour évaluer chaque zéro possible jusqu'à ce que nous en trouvions un qui donne un reste de 0. Commençons par —3.

La division par$(x+3)$ donne un reste de 0, donc —3 est un zéro de la fonction. Le polynôme peut être écrit comme

\[(x+3)(3x^2+1) \nonumber\]

Nous pouvons ensuite définir le quadratique égal à 0 et résoudre pour trouver les autres zéros de la fonction.

\[ \begin{align*} 3x^2+1=0 \\[4pt] x^2 &=−\dfrac{1}{3} \\[4pt] x&=±−\sqrt{\dfrac{1}{3}} \\[4pt] &=±\dfrac{i\sqrt{3}}{3} \end{align*}\]

Les zéros de$f(x)$ sont$–3$ et$±\dfrac{i\sqrt{3}}{3}$.

Analyse

Regardez le graphique de la fonction$f$ dans la figure$\PageIndex{2}$. Notez que, à$x =−3$, le graphique croise l'axe des abscisses, indiquant une multiplicité impaire (1) pour le zéro$x=–3$. Notez également la présence des deux points tournants. Cela signifie que, comme il existe un polynôme de$3^{rd}$ degrés, nous examinons le nombre maximum de points de retournement. Ainsi, le comportement final consistant à augmenter sans limite vers la droite et à diminuer sans limite vers la gauche se poursuivra. Ainsi, toutes les interceptions X de la fonction sont affichées. Donc, soit la multiplicité de$x=−3$ est 1 et il y a deux solutions complexes, ce que nous avons constaté, soit la multiplicité de$x =−3$ est de trois. Quoi qu'il en soit, notre résultat est correct.

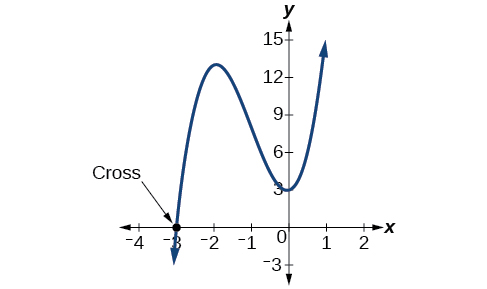
$\PageIndex{4}$

Trouvez les zéros de$f(x)=2x^3+5x^2−11x+4$.

Solution

Les zéros sont$–4$$\frac{1}{2}$, et$1$.

Utilisation du théorème de factorisation linéaire pour trouver des polynômes avec des zéros donnés

Une implication vitale du théorème fondamental de l'algèbre, comme nous l'avons indiqué ci-dessus, est qu'une fonction polynomiale de degré n aura des$n$ zéros dans l'ensemble des nombres complexes, si nous prenons en compte les multiplicités. Cela signifie que nous pouvons fractionner la fonction polynomiale en$n$ facteurs. Le théorème de factorisation linéaire nous indique qu'une fonction polynomiale aura le même nombre de facteurs que son degré, et que chaque facteur sera sous la forme$(x−c)$, où c est un nombre complexe.

$f$Soit une fonction polynomiale avec des coefficients réels, et supposons que$a +bi$$b≠0$, est un zéro de$f(x)$. Ensuite, selon le théorème des facteurs,$x−(a+bi)$ est un facteur de$f(x)$. $f$Pour avoir des coefficients réels,$x−(a−bi)$ il faut également être un facteur de$f(x)$. Cela est vrai parce que tout facteur autre que$x−(a−bi)$, lorsqu'il est multiplié par$x−(a+bi)$, laissera des composants imaginaires dans le produit. Seule la multiplication avec des paires conjuguées éliminera les parties imaginaires et produira des coefficients réels. En d'autres termes, si une fonction polynomiale$f$ avec des coefficients réels possède un zéro complexe$a +bi$, le conjugué complexe$a−bi$ doit également être un zéro de$f(x)$. C'est ce que l'on appelle le théorème conjugué complexe.

THÉORÈME CONJUGUÉ COMPLEXE

Selon le théorème de factorisation linéaire, une fonction polynomiale aura le même nombre de facteurs que son degré, et chaque facteur se présentera sous la forme$(x−c)$ d'un nombre complexe.$c$

Si la fonction polynomiale$f$ possède des coefficients réels et un zéro complexe dans la forme$a+bi$, alors le conjugué complexe du zéro est également un zéro.$a−bi$

Comment

Étant donné les zéros d'une fonction polynomiale$f$ et un point$(c, f(c))$ sur le graphique de$f$, utilisez le théorème de factorisation linéaire pour trouver la fonction polynomiale.

Utilisez les zéros pour construire les facteurs linéaires du polynôme.
Multipliez les facteurs linéaires pour étendre le polynôme.
$(c,f(c))$Substituez-le dans la fonction pour déterminer le coefficient principal.
Simplifiez.

Exemple$\PageIndex{7}$: Using the Linear Factorization Theorem to Find a Polynomial with Given Zeros

Trouvez un polynôme du quatrième degré avec des coefficients réels dont les zéros sont de$–3$$2$,$i$,, tels que$f(−2)=100$.

Solution

Parce que$x =i$ c'est un zéro, selon le théorème des conjugués complexes,$x =–i$ il y a également un zéro. Le polynôme doit avoir des facteurs de$(x+3),(x−2),(x−i)$, et$(x+i)$. Puisque nous recherchons un polynôme de degré 4 et que nous avons maintenant quatre zéros, nous avons les quatre facteurs. Commençons par multiplier ces facteurs.

\[\begin{align} f(x) & =a(x+3)(x−2)(x−i)(x+i) \\ f(x) & =a(x^2+x−6)(x^2+1) \\ f(x) & =a(x^4+x^3−5x^2+x−6) \end{align} \]

Nous devons trouver pour nous$a$ en assurer$f(–2)=100$. Substituer$x=–2$ et$f (-2)=100$ introduire$f (x)$.

\[\begin{align} 100=a({(−2)}^4+{(−2)}^3−5{(−2)}^2+(−2)−6) \\ 100=a(−20) \\ −5=a \end{align} \]

Donc, la fonction polynomiale est

\[f(x)=−5(x^4+x^3−5x^2+x−6)\]

\[f(x)=−5x^4−5x^3+25x^2−5x+30\] Analyse

Nous avons constaté que les deux$i$ et$−i$ étaient des zéros, mais qu'un seul de ces zéros devait être indiqué. Si$i$ est le zéro d'un polynôme avec des coefficients réels, alors$−i$ doit également être un zéro du polynôme car$−i$ c'est le conjugué complexe de$i$.

QUESTIONS-RÉPONSES

S'$2+3i$ils étaient donnés sous la forme du zéro d'un polynôme avec des coefficients réels, devrait-il$2−3i$ également être un zéro ?

Oui. Lorsqu'un nombre complexe avec une composante imaginaire est donné sous la forme du zéro d'un polynôme avec des coefficients réels, le conjugué doit également être un zéro du polynôme.

$\PageIndex{5}$

Trouvez un polynôme du troisième degré avec des coefficients réels dont les zéros sont de$5$ et$−2i$ tels que$f (1)=10$.

Solution

$f(x)=−\frac{1}{2}x^3+\frac{5}{2}x^2−2x+10$

Utiliser la règle des signes de Descartes

Il existe un moyen simple de déterminer le nombre possible de zéros réels positifs et négatifs pour n'importe quelle fonction polynomiale. Si le polynôme est écrit par ordre décroissant, la Règle des signes de Descartes nous indique une relation entre le nombre de changements de signes$f(x)$ et le nombre de zéros réels positifs. Par exemple, la fonction polynomiale ci-dessous présente un changement de signe.

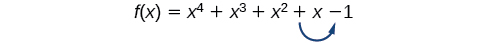
$CNX_Precalc_Figure_03_06_003.jpg$

Cela nous indique que la fonction doit avoir 1 zéro réel positif.

Il existe une relation similaire entre le nombre de changements de signes$f(−x)$ et le nombre de zéros réels négatifs.

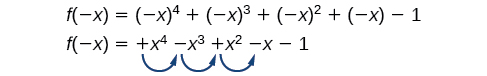
$CNX_Precalc_Figure_03_06_004.jpg$

Dans ce cas,$f(−x)$ a 3 changements de signe. Cela nous indique qu'il$f(x)$ pourrait y avoir 3 ou 1 zéros réels négatifs.

LA RÈGLE DES SIGNES DE DESCARTES

Selon la Règle des signes de Descartes, si l'on considère une$f(x)=a_nx^n+a_{n−1}x^{n−1}+...+a_1x+a_0$ fonction polynomiale avec des coefficients réels :

Le nombre de zéros réels positifs est soit égal au nombre de changements de signe,$f(x)$ soit inférieur au nombre de changements de signe d'un entier pair.
Le nombre de zéros réels négatifs est soit égal au nombre de changements de signe,$f(−x)$ soit inférieur au nombre de changements de signe d'un entier pair.

Exemple$\PageIndex{8}$: Using Descartes’ Rule of Signs

Utilisez la règle des signes de Descartes pour déterminer le nombre possible de zéros réels positifs et négatifs pour$f(x)=−x^4−3x^3+6x^2−4x−12$.

Solution

Commencez par déterminer le nombre de changements de signes.

Il y a deux changements de signes, donc il y a 2 ou 0 racines réelles positives. Ensuite, nous examinons$f(−x)$ pour déterminer le nombre de racines réelles négatives.

\[ \begin{align} f(−x) & =−{(−x)}^4−3{(−x)}^3+6{(−x)}^2−4(−x)−12 \\ f(−x) & =−x^4+3x^3+6x^2+4x−12 \end{align} \]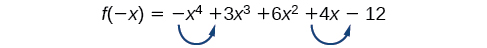

$La fonction, f (-x) =-x^4+3x^3+6x^2+4x-12, présente deux changements de signes entre -x^4 et 3x^3, et 4x et -12. `$

Encore une fois, il y a deux changements de signes, donc il y a 2 ou 0 racines réelles négatives.

Il existe quatre possibilités, comme nous pouvons le voir dans le tableau$\PageIndex{1}$.

Tableau$\PageIndex{1}$
Zéros réels positifs	Zéros réels négatifs	Zéros complexes	Zéros totaux
2	2	0	4
2	0	2	4
0	2	2	4
0	0	4	4

Analyse

Nous pouvons confirmer le nombre de racines réelles positives et négatives en examinant un graphique de la fonction. Voir la figure$\PageIndex{3}$. Nous pouvons voir sur le graphique que la fonction a 0 racines réelles positives et 2 racines réelles négatives.

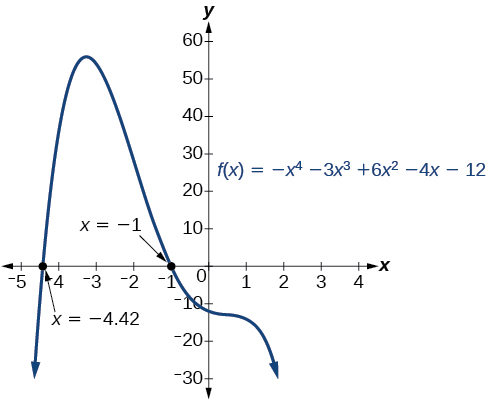
Graphique de f (x) =-x^4-3x^3+6x^2-4x-12 avec des interceptions x à -4,42 et -1. — Chiffre$\PageIndex{3}$.

$\PageIndex{6}$

Utilisez la règle des signes de Descartes pour déterminer le nombre maximum possible de zéros réels positifs et négatifs pour$f(x)=2x^4−10x^3+11x^2−15x+12$. Utilisez un graphique pour vérifier le nombre de zéros réels positifs et négatifs pour la fonction.

Solution

Il doit y avoir 4, 2 ou 0 racines réelles positives et 0 racines réelles négatives. Le graphique montre qu'il y a 2 zéros réels positifs et 0 zéros réels négatifs.

Résoudre des applications du monde réel

Nous avons maintenant introduit divers outils pour résoudre des équations polynomiales. Utilisons ces outils pour résoudre le problème de la boulangerie dès le début de la section.

Exemple$\PageIndex{9}$

Résolution d'équations polynomiales

Solution

Commencez par écrire une équation pour le volume du gâteau. Le volume d'un solide rectangulaire est donné par$V=lwh$. On nous a donné que la longueur devait être supérieure de quatre pouces à la largeur, afin que nous puissions exprimer la longueur du gâteau sous la forme$l=w+4$. On nous a indiqué que la hauteur du gâteau est le tiers de la largeur, de sorte que nous pouvons exprimer la hauteur du gâteau sous la forme$h=\dfrac{1}{3}w$. Ecrivons le volume du gâteau en termes de largeur du gâteau.

\[V=(w+4)(w)(\dfrac{1}{3}w)\] \[V=\dfrac{1}{3}w^3+\dfrac{4}{3}w^2\]

Substituez le volume donné dans cette équation.

$351=13w^3+43w^2$Remplacez 351 par V. $1053=w^3+4w^2$ Multipliez les deux côtés par 3. $0=w^3+7w^2−1053$Soustrayez 1053 des deux côtés.

La règle des signes de Descartes nous indique qu'il existe une solution positive. Le théorème du zéro rationnel nous indique que les zéros rationnels possibles sont$\pm 1,±3,±9,±13,±27,±39,±81,±117,±351,$ et$±1053$. Nous pouvons utiliser la division synthétique pour tester ces zéros possibles. Seuls les nombres positifs ont du sens en tant que dimensions d'un gâteau, nous n'avons donc pas besoin de tester des valeurs négatives. Commençons par tester les valeurs les plus pertinentes en tant que dimensions pour un petit gâteau en feuille. Utilisez une division synthétique pour vérifier$x=1$.

$alt$

Puisque 1 n'est pas une solution, nous allons vérifier$x=3$.

$alt$

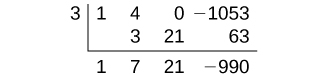
Puisque 3 n'est pas non plus une solution, nous allons le tester$x=9$.

$alt$

La division synthétique donne un reste de 0, donc 9 est une solution à l'équation. Nous pouvons utiliser les relations entre la largeur et les autres dimensions pour déterminer la longueur et la hauteur de la plaque à gâteau.

$l=w+4=9+4=13$et$h=\dfrac{1}{3}w=\dfrac{1}{3}(9)=3$

Le moule à gâteau doit avoir des dimensions de 13 pouces par 9 pouces par 3 pouces

$\PageIndex{7}$

Un conteneur d'expédition en forme de solide rectangulaire doit avoir un volume de 84 mètres cubes. Le client indique au fabricant qu'en raison du contenu, la longueur du contenant doit être supérieure d'un mètre à la largeur et que la hauteur doit être supérieure d'un mètre au double de la largeur. Quelles doivent être les dimensions du contenant ?

Solution

3 mètres par 4 mètres par 7 mètres

Médias

Accédez à ces ressources en ligne pour des instructions et des exercices supplémentaires avec des zéros de fonctions polynomiales.

Concepts clés

Pour trouver$f(k)$, déterminez le reste du polynôme$f(x)$ lorsqu'il est divisé par$x−k$. C'est ce que l'on appelle le théorème du reste. Voir l'exemple$\PageIndex{1}$.
Selon le théorème des facteurs,$k$ est un zéro de$f(x)$ si et seulement si$(x−k)$ est un facteur de$f(x)$. Voir l'exemple$\PageIndex{2}$.
Selon le théorème du zéro rationnel, chaque zéro rationnel d'une fonction polynomiale à coefficients entiers sera égal à un facteur du terme constant divisé par un facteur du coefficient principal. Voir Exemple$\PageIndex{3}$ et Exemple$\PageIndex{4}$.
Lorsque le coefficient principal est 1, les zéros rationnels possibles sont les facteurs du terme constant.
La division synthétique peut être utilisée pour trouver les zéros d'une fonction polynomiale. Voir l'exemple$\PageIndex{5}$.
Selon le théorème fondamental, chaque fonction polynomiale de degré supérieur à 0 possède au moins un zéro complexe. Voir l'exemple$\PageIndex{6}$.
Si l'on tient compte des multiplicités, une fonction polynomiale aura le même nombre de facteurs que son degré. Chaque facteur sera présenté sous la forme$(x−c)$, où se$c$ trouve un nombre complexe. Voir l'exemple$\PageIndex{7}$.
Le nombre de zéros réels positifs d'une fonction polynomiale est soit le nombre de changements de signes de la fonction, soit inférieur au nombre de changements de signes d'un entier pair.
Le nombre de zéros réels négatifs d'une fonction polynomiale est soit le nombre de changements de signe égal$f(−x)$ ou inférieur au nombre de changements de signe d'un entier pair. Voir l'exemple$\PageIndex{8}$.
Les équations polynomiales modélisent de nombreux scénarios du monde réel. La résolution des équations est plus facile par division synthétique. Voir l'exemple$\PageIndex{9}$.

Lexique

La règle des signes de Descartes

une règle qui détermine le nombre maximum possible de zéros réels positifs et négatifs en fonction du nombre de changements de signes de$f(x)$ et$f(−x)$

Théorème des facteurs

$k$est un zéro d'une fonction polynomiale$f(x)$ si et seulement si$(x−k)$ est un facteur de$f(x)$

Théorème fondamental de l'algèbre

une fonction polynomiale de degré supérieur à 0 possède au moins un zéro complexe

Théorème de factorisation linéaire

si l'on tient compte des multiplicités, une fonction polynomiale aura le même nombre de facteurs que son degré, et chaque facteur se présentera sous la forme$(x−c)$, où$c$ est un nombre complexe

Théorème du zéro rationnel

les zéros rationnels possibles d'une fonction polynomiale ont la forme$\frac{p}{q}$ où$p$ est un facteur du terme constant et$q$ un facteur du coefficient principal.

Théorème du reste

si un polynôme$f(x)$ est divisé par$x−k$, alors le reste est égal à la valeur$f(k)$