3.6 : Fonctions de valeurs absolues
- Page ID
- 195521
Objectifs d'apprentissage
- Tracez une fonction de valeur absolue.
- Résolvez une équation de valeur absolue.
Jusqu'aux années 1920, les nébuleuses dites spirales étaient considérées comme des nuages de poussière et de gaz dans notre propre galaxie, située à des dizaines de milliers d'années-lumière. Ensuite, l'astronome Edwin Hubble a prouvé que ces objets sont des galaxies à part entière, à des distances de millions d'années-lumière. Aujourd'hui, les astronomes peuvent détecter des galaxies situées à des milliards d'années-lumière. Les distances dans l'univers peuvent être mesurées dans toutes les directions. Il est donc utile de considérer la distance comme une fonction de valeur absolue. Dans cette section, nous allons étudier les fonctions des valeurs absolues.

Comprendre la valeur absolue
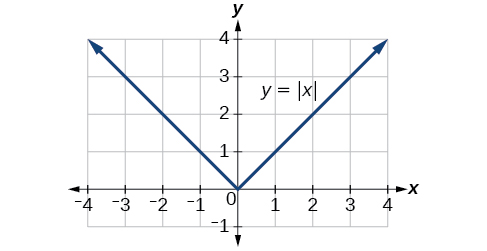
Rappelons que dans sa forme de base\(f(x)=|x|\), la fonction de valeur absolue, est l'une des fonctions de notre boîte à outils. La fonction de valeur absolue est généralement considérée comme fournissant la distance entre le nombre et zéro sur une ligne numérique. Algébriquement, quelle que soit la valeur d'entrée, la sortie est la valeur sans égard au signe.
Fonction de valeur absolue
La fonction de valeur absolue peut être définie comme une fonction par morceaux
\[f(x)=|x|= \begin{cases} x & \text{ if }x{\geq}0 \\ -x & \text{ if } x<0 \end{cases}\]
Exemple\(\PageIndex{1}\): Determine a Number within a Prescribed Distance
Décrivez toutes les valeurs\(x\) situées à une distance comprise entre 4 et le chiffre 5.
Solution
Nous voulons que la distance entre\(x\) et 5 soit inférieure ou égale à 4. Nous pouvons tracer une ligne numérique, telle que celle qui entre, pour représenter la condition à remplir.

La distance de\(x\) 0 à 5 peut être représentée en utilisant la valeur absolue comme\(|x−5|\). Nous voulons que les valeurs de\(x\) cette valeur satisfassent à la condition\(| x−5 |\leq4\).
Analyse
Notez que
\[\begin{align*} -4&{\leq}x-5 & x-5&\leq4 \\[4pt] 1&{\leq}x & x&{\leq}9 \end{align*}\]
Donc,\(|x−5|\leq4\) c'est équivalent à\(1{\leq}x\leq9\).
Cependant, les mathématiciens préfèrent généralement la notation des valeurs absolues.
Exercice\(\PageIndex{1}\)
Décrivez toutes les valeurs à une\(x\) distance de 3 du chiffre 2.
- Réponse
-
\(|x−2|\leq3\)
Exemple\(\PageIndex{2}\): Resistance of a Resistor
Les composants électriques, tels que les résistances et les condensateurs, présentent des valeurs spécifiques de leurs paramètres de fonctionnement : résistance, capacité, etc. Cependant, en raison de l'imprécision de fabrication, les valeurs réelles de ces paramètres varient quelque peu d'une pièce à l'autre, même lorsqu'elles sont censées être les mêmes. Le mieux que les fabricants puissent faire est d'essayer de garantir que les variations se maintiendront dans une fourchette spécifiée, souvent ± 1 %, ± 5 % ou ± 10 %.
Supposons que nous ayons une résistance nominale de 680 ohms, ± 5 %. Utilisez la fonction de valeur absolue pour exprimer la plage de valeurs possibles de la résistance réelle.
Solution
5 % des 680 ohms correspondent à 34 ohms. La valeur absolue de la différence entre la résistance réelle et la résistance nominale ne doit pas dépasser la variabilité indiquée, donc, avec la résistance\(R\) en ohms,
\[|R−680|\leq34 \nonumber\]
Exercice\(\PageIndex{2}\)
Les étudiants qui obtiennent un score de moins de 20 points sur 80 passeront un test. Écrivez ceci comme une distance de 80 en utilisant la notation des valeurs absolues.
- Réponse
-
En utilisant la variable\(p\) pour passer,\(| p−80 |\leq20\)
Représentation graphique d'une fonction de valeur absolue
La caractéristique la plus significative du graphique des valeurs absolues est le point d'angle auquel le graphique change de direction. Ce point est indiqué à l'origine sur la figure\(\PageIndex{3}\).
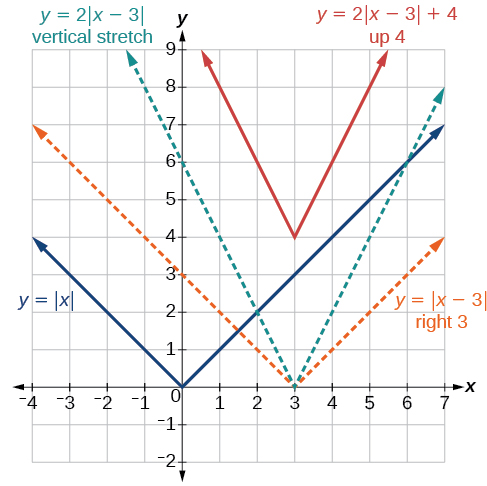
La figure\(\PageIndex{3}\) montre le graphique de\(y=2|x–3|+4\). Le graphique de\(y=|x|\) a été décalé vers la droite de 3 unités, étiré verticalement d'un facteur 2 et décalé vers le haut de 4 unités. Cela signifie que le point d'angle est situé au niveau\((3,4)\) de cette fonction transformée.
Exemple\(\PageIndex{3}\): Writing an Equation for an Absolute Value Function
Écrivez une équation pour la fonction illustrée dans la figure\(\PageIndex{5}\).
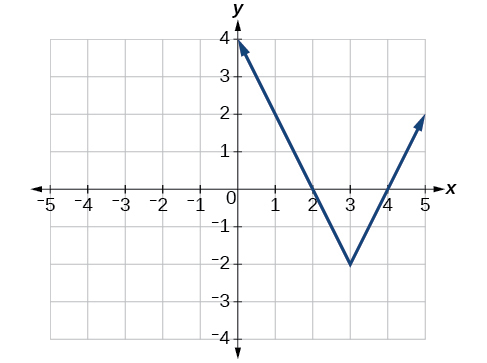
Solution
La fonction de valeur absolue de base change de direction à l'origine. Ce graphique a donc été déplacé vers la droite de 3 unités et vers le bas de 2 unités par rapport à la fonction de base de la boîte à outils. Voir la figure\(\PageIndex{6}\).
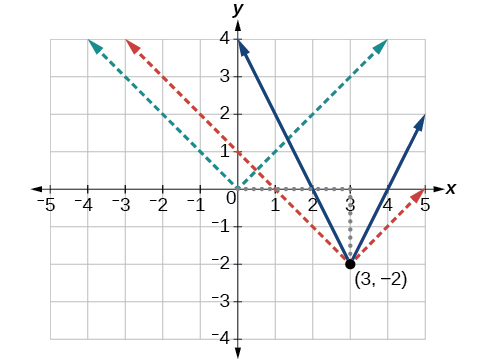
Nous remarquons également que le graphe semble étiré verticalement, car la largeur du graphe final sur une ligne horizontale n'est pas égale à 2 fois la distance verticale entre le coin et cette ligne, comme ce serait le cas pour une fonction de valeur absolue non étirée. Au lieu de cela, la largeur est égale à 1 fois la distance verticale, comme indiqué sur la figure\(\PageIndex{7}\).
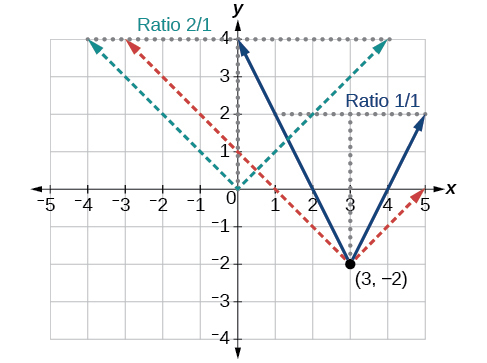
À partir de ces informations, nous pouvons écrire l'équation
\[\begin{align*} f(x)&=2|x-3|-2, \;\;\;\;\;\; \text{treating the stretch as a vertial stretch, or} \\ f(x)&=|2(x-3)|-2, \;\;\; \text{treating the stretch as a horizontal compression.} \end{align*}\]
Analyse
Notez que ces équations sont algébriquement équivalentes : l'étirement d'une fonction de valeur absolue peut être écrit de manière interchangeable sous la forme d'un étirement ou d'une compression vertical ou horizontal.
Q & R
Si nous ne pouvions pas observer l'étendue de la fonction à partir des graphes, pourrions-nous la déterminer algébriquement ?
- Réponse
-
Oui. Si nous ne sommes pas en mesure de déterminer l'étirement en fonction de la largeur du graphique, nous pouvons résoudre le facteur d'étirement en saisissant une paire connue de valeurs pour\(x\) et\(f(x)\).
\[f(x)=a|x−3|−2 \nonumber\]
Maintenant, en remplaçant par le point\((1, 2)\)
\[\begin{align*} 2&=a|1-3|-2 \\ 4&=2a \\ a&=2 \end{align*}\]
Exercice\(\PageIndex{3}\)
Écrivez l'équation de la fonction de valeur absolue qui est décalée horizontalement de 2 unités vers la gauche, inversée verticalement et décalée verticalement vers le haut de 3 unités.
- Réponse
-
\(f(x)=−| x+2 |+3\)
Q & R
Les graphes des fonctions de valeurs absolues croisent-ils toujours l'axe vertical ? L'axe horizontal ?
- Réponse
-
Oui, ils croisent toujours l'axe vertical. Le graphique d'une fonction de valeur absolue croise l'axe vertical lorsque l'entrée est nulle.
Non, ils ne coupent pas toujours l'axe horizontal. Le graphique peut ou non croiser l'axe horizontal, en fonction de la façon dont il a été déplacé et réfléchi. Il est possible que la fonction de valeur absolue coupe l'axe horizontal à zéro, à un ou deux points (Figure\(\PageIndex{8}\)).
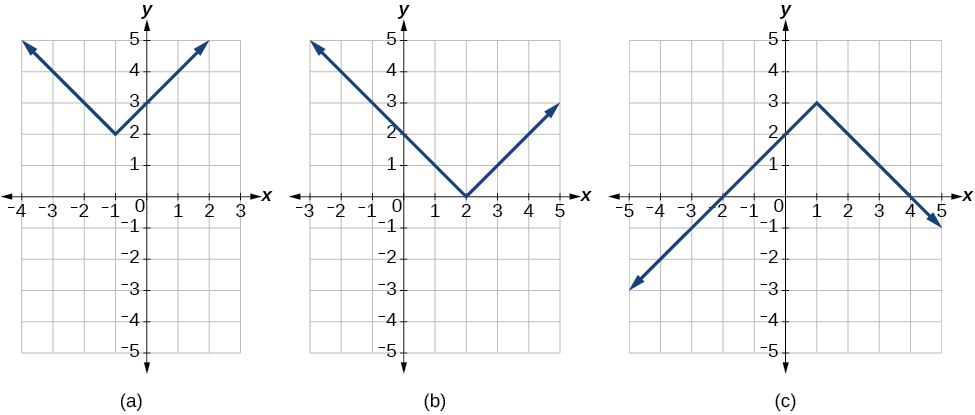
Figure\(\PageIndex{8}\) : (a) La fonction de valeur absolue ne coupe pas l'axe horizontal. (b) La fonction de valeur absolue coupe l'axe horizontal en un point. (c) La fonction de valeur absolue coupe l'axe horizontal en deux points.
Résolution d'une équation de valeur absolue
Maintenant que nous pouvons représenter graphiquement une fonction de valeur absolue, nous allons apprendre à résoudre une équation de valeur absolue. Pour résoudre une équation telle que\(8=|2x−6|\), nous remarquons que la valeur absolue sera égale à 8 si la quantité à l'intérieur de la valeur absolue est 8 ou -8. Cela conduit à deux équations différentes que nous pouvons résoudre indépendamment.
\[2x-6=8 \quad \text{ or } \quad 2x-6=-8 \nonumber\]
\[\begin{align*} 2x &= 14 & 2x &= -2 \\ x&=7 & x&=-1 \end{align*}\]
Il est utile de savoir comment résoudre des problèmes impliquant des fonctions de valeurs absolues. Par exemple, nous pouvons avoir besoin d'identifier des nombres ou des points sur une ligne situés à une distance spécifiée d'un point de référence donné.
Une équation de valeur absolue est une équation dans laquelle la variable inconnue apparaît dans des barres de valeurs absolues. Par exemple,
\[\begin{align*}|x|&=4, \nonumber \\[4pt] |2x−1| &=3, \\[4pt] |5x+2|−4 &=9. \end{align*}\]
Solutions aux équations de valeurs absolues
Pour les nombres réels\(A\) et\(B\), une équation de la forme\(|A|=B\), avec\(B\geq0\), aura des solutions quand\(A=B\) ou\(A=−B\). Si\(B<0\), l'équation n'\(|A|=B\)a pas de solution.
Comment...
À partir de la formule d'une fonction de valeur absolue, trouvez les intersections horizontales de son graphe.
- Isolez le terme de valeur absolue.
- \(|A|=B\)À utiliser pour écrire\(A=B\) ou\(−A=B\), en supposant\(B>0\).
- Résolvez pour\(x\).
Exemple\(\PageIndex{4}\): Finding the Zeros of an Absolute Value Function
Pour la fonction\(f(x)=|4x+1|−7\), trouvez les valeurs de\(x\) telles que\(f(x)=0\).
Solution
\[\begin{align*} 0&=|4x+1|-7 & & &\text{Substitute 0 for f(x).} \\ 7&=|4x+1| & & &\text{Isolate the absolute value on one side of the equation.} \\ 7&=4x+1 &\text{or} -7&=4x+1 &\text{Break into two separate equations and solve.} \\ 6&=4x & -8&=4x & \\ x&=\frac{6}{4}=1.5 & x&=\frac{-8}{4}=-2 \end{align*}\]
La fonction affiche 0 lorsque\(x=1.5\) ou\(x=−2\) (Figure\(\PageIndex{9}\)).
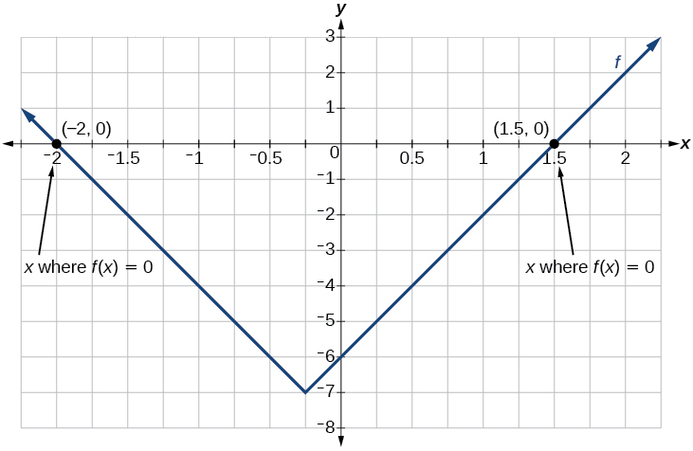
Exercice\(\PageIndex{4}\)
Pour la fonction\(f(x)=|2x−1|−3\), trouvez les valeurs de\(x\) telles que\(f(x)=0\).
Solution
\(x=−1\)ou\(x=2\)
Q & R
Faut-il toujours s'attendre à deux réponses lors de la résolution\(|A|=B\) ?
Réponse
Non Il se peut que nous trouvions une, deux ou même aucune réponse. Par exemple, il n'existe pas de solution à\(2+|3x−5|=1\).
Comment...
À partir d'une équation de valeur absolue, résolvez-la.
- Isolez le terme de valeur absolue.
- \(|A|=B\)À utiliser pour écrire\(A=B\) ou\(A=−B\).
- Résolvez pour\(x\).
Exemple\(\PageIndex{5}\): Solving an Absolute Value Equation
Résoudre\(1=4|x−2|+2\).
Solution
En isolant la valeur absolue d'un côté de l'équation, on obtient ce qui suit.
\[\begin{align*} 1&=4|x-2|+2 \\ -1&=4|x-2| \\ -\frac{1}{4}&=|x-2| \end{align*}\]
La valeur absolue renvoie toujours une valeur positive, il est donc impossible que la valeur absolue soit égale à une valeur négative. À ce stade, nous remarquons que cette équation n'a pas de solution.
Q & R
Dans l'exemple\(\PageIndex{5}\), si\(f(x)=1\) et\(g(x)=4|x−2|+2\) étaient représentés sur le même ensemble d'axes, les graphes se croiseraient-ils ?
Réponse
Non Les graphes de\(f\) et ne se\(g\) croiseraient pas, comme le montre la figure\(\PageIndex{10}\). Cela confirme graphiquement que l'équation n'\(1=4|x−2|+2\)a pas de solution.
Déterminez où le graphe de la fonction\(f(x)=−| x+2 |+3\) croise les axes horizontal et vertical.
\(f(0)=1\), de sorte que le graphique coupe l'axe vertical en\((0,1)\). \(f(x)=0\)quand\(x=−5\) et\(x=1\) ainsi le graphe coupe l'axe horizontal à\((−5,0)\) et\((1,0)\).
Résoudre une inégalité de valeur absolue
Les équations de valeurs absolues n'impliquent pas toujours des égalités. Au lieu de cela, il se peut que nous devions résoudre une équation dans une plage de valeurs. Nous utiliserions une inégalité de valeur absolue pour résoudre une telle équation. Une inégalité en valeur absolue est une équation de la forme
\[|A|<B,\;|A|{\leq}B,|A|>B, \nonumber\]
ou
\[ |A|{\geq}B, \nonumber\]
où une expression\(A\) (et peut-être mais pas généralement\(B\)) dépend d'une variable\(x\). Résoudre l'inégalité, c'est trouver l'ensemble de tous\(x\) ceux qui répondent à l'inégalité. Habituellement, cet ensemble sera un intervalle ou l'union de deux intervalles.
Il existe deux approches de base pour résoudre les inégalités de valeurs absolues : graphique et algébrique. L'avantage de l'approche graphique est que nous pouvons lire la solution en interprétant les graphes de deux fonctions. L'avantage de l'approche algébrique est qu'elle fournit des solutions qui peuvent être difficiles à lire à partir du graphique.
Par exemple, nous savons que tous les nombres situés à moins de 200 unités de 0 peuvent être exprimés comme
\[|x|<200 \nonumber\]
ou
\[ −200<x<200 \nonumber\]
Supposons que nous souhaitions connaître tous les rendements possibles d'un investissement si nous pouvions gagner une certaine somme d'argent entre 200 et 600 dollars. Nous pouvons résoudre algébriquement l'ensemble de valeurs de\(x\) telle sorte que la distance entre\(x\) et 600 soit inférieure à 200. Nous représentons la distance entre\(x\) 0 et 600 as\(|x−600|\).
\[|x−600|<200\]
ou
\[−200<x−600<200\]
\[\begin{align*} −200+600< &x−600+600<200+600 \\[4pt] 400< &x<800 \end{align*}\]
Cela signifie que nos rendements se situeraient entre 400$ et 800$.
Parfois, un problème d'inégalité des valeurs absolues nous sera présenté sous la forme d'une fonction de valeur absolue décalée et/ou étirée ou compressée, où nous devons déterminer pour quelles valeurs de l'entrée la sortie de la fonction sera négative ou positive.
Comment...
Étant donné une inégalité de valeur absolue de la forme\(|x−A|{\leq}B\) pour les nombres réels\(a\) et\(b\) où\(b\) est positive, résolvez l'inégalité de valeur absolue de manière algébrique.
- Trouvez des points limites en résolvant\(|x−A|=B\).
- Testez les intervalles créés par les points limites pour déterminer où\(|x−A|{\leq}B\).
- Écrivez l'intervalle ou l'union d'intervalles satisfaisant l'inégalité en notation d'intervalle, d'inégalité ou de setbuilder.
Exemple\(\PageIndex{6}\): Solving an Absolute Value Inequality
Résoudre\(|x −5|{\leq}4\).
Solution
Avec les deux approches, nous devrons d'abord savoir où se trouve l'égalité correspondante. Dans ce cas, nous allons d'abord trouver où\(|x−5|=4\). Nous faisons cela parce que la valeur absolue est une fonction sans interruption. Par conséquent, la seule façon pour les valeurs de la fonction de passer d'une valeur inférieure à 4 à une valeur supérieure à 4 est de passer par là où les valeurs sont égales à 4. Résoudre\(|x−5|=4\).
\[\begin{align*} x−5&=4 &\text{ or }\;\;\;\;\;\;\;\; x&=9 \\ x−5&=−4 & x&=1\end{align*}\]
Après avoir déterminé que la valeur absolue est égale à 4 à\(x=1\) et\(x=9\), nous savons que le graphique ne peut changer que d'une valeur inférieure à 4 à une valeur supérieure à 4 à ces valeurs. Cela divise la ligne de numéros en trois intervalles :
\[x<1,\; 1<x<9, \text{ and } x>9. \nonumber\]
Pour déterminer si la fonction est inférieure à 4, nous pouvons choisir une valeur dans chaque intervalle et voir si la sortie est inférieure ou supérieure à 4, comme indiqué dans le tableau\(\PageIndex{1}\).
| Test par intervalles\(x\) | \(f(x)\) | \(<4\)ou\(>4\) | |
|---|---|---|---|
| \ (x \) » style="vertical-align:middle ; « >\(x<1\) | \ (f (x) \) » style="vertical-align:middle ; « >0 | \ (<4 \) ou\(>4\) « style="vertical-align:middle ; « >\(|0-5|=5\) | Supérieur à |
| \ (x \) » style="vertical-align:middle ; « >\(1<x<9\) | \ (f (x) \) » style="vertical-align:middle ; ">6 | \ (<4 \) ou\(>4\) « style="vertical-align:middle ; « >\(|6-5|=1\) | Inférieur à |
| \ (x \) » style="vertical-align:middle ; « >\(x>9\) | \ (f (x) \) » style="vertical-align:middle ; ">11 | \ (<4 \) ou\(>4\) « style="vertical-align:middle ; « >\(|11-5|=6\) | Supérieur à |
Comme\(1{\leq}x{\leq}9\) c'est le seul intervalle dans lequel la sortie à la valeur de test est inférieure à 4, nous pouvons en conclure que la solution à\(|x−5|{\leq}4\) est\(1{\leq}x{\leq}9\), ou\([1,9]\).
Pour utiliser un graphique, nous pouvons esquisser la fonction\(f(x)=|x−5|\). Pour nous aider à voir où se situent les sorties 4, la ligne\(g(x)=4\) peut également être esquissée comme sur la figure\(\PageIndex{11}\).
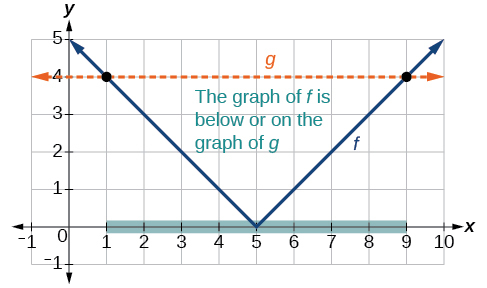
Nous pouvons voir ce qui suit :
- Les valeurs de sortie de la valeur absolue sont égales à 4 à\(x=1\) et\(x=9\).
- Le graphique de\(f\) est en dessous du graphique\(g\) de\(1<x<9\). Cela signifie que les valeurs de sortie de\(f(x)\) sont inférieures aux valeurs de sortie de\(g(x)\).
- La valeur absolue est inférieure ou égale à 4 entre ces deux points, quand\(1{\leq}x\leq9\). En notation par intervalles, il s'agirait de l'intervalle\([1,9]\).
Analyse
Pour les inégalités de valeur absolue,
\[|x−A|<C,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; |x−A|>C, \\−C<x−A<C,\;\;\;\; x−A<−C \text{ or } x−A>C. \nonumber\]
Le\(>\) symbole\(<\) ou peut être remplacé par\(\leq\) ou\(\geq\).
Donc, pour cet exemple, nous pourrions utiliser cette approche alternative.
\[\begin{align*} |x−5|&{\leq}4 \\ −4&{\leq}x−5{\leq}4 &\text{Rewrite by removing the absolute value bars.} \\ −4+5&{\leq}x−5+5{\leq}4+5 &\text{Isolate the x.} \\ 1&{\leq}x\leq9 \end{align*}\]
Exercice\(\PageIndex{5}\)
Résoudre\(|x+2| \leq 6\).
- Réponse
-
\(-8 \leq x \leq 4\)
Comment...
À partir d'une fonction de valeur absolue, déterminez l'ensemble des entrées dont la sortie est positive (ou négative).
- Définissez la fonction sur zéro et résolvez les points limites de l'ensemble de solutions.
- Utilisez des points de test ou un graphique pour déterminer où la sortie de la fonction est positive ou négative.
Exemple\(\PageIndex{7}\): Using a Graphical Approach to Solve Absolute Value Inequalities
\(f(x)=−\frac{1}{2}|4x−5|+3\)En fonction de la fonction, déterminez les\(x\) valeurs pour lesquelles les valeurs de la fonction sont négatives.
Solution
Nous essayons de déterminer où\(f(x)<0\) et quand\(−\frac{1}{2}|4x−5|+3<0\). Nous commençons par isoler la valeur absolue.
\[ \begin{align*} -\frac{1}{2}|4x−5|&<−3 \;\;\; \text{Multiply both sides by –2, and reverse the inequality.} \\ |4x−5|&>6\end{align*}\]
Ensuite, nous résolvons pour l'égalité\(|4x−5|=6\).
\[\begin{align*} 4x-5&=6 & 4x-5&=-6 \\ 4x-6&=6 \end{align*}\]
ou
\[\begin{align*} 4x&=-1 \\ x&=\frac{11}{4} & x&=-\frac{1}{4} \end{align*}\]
Maintenant, nous pouvons examiner le graphique de\(f\) pour observer où la sortie est négative. Nous allons observer où se situent les branches en dessous de l'\(x\)axe. Notez que l'apparence exacte du graphique n'a même pas d'importance, tant que nous savons qu'il traverse l'axe horizontal à\(x=−\frac{1}{4}\)\(x=\frac{11}{4}\) et que le graphique a été réfléchi verticalement. Voir la figure\(\PageIndex{12}\).
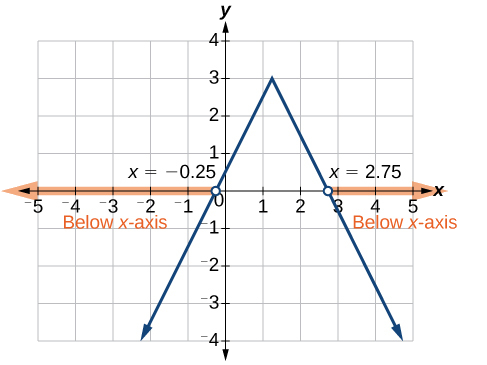
Nous observons que le graphe de la fonction se trouve en dessous de l'\(x\)axe -à gauche\(x=−\frac{1}{4}\) et à droite de\(x=\frac{11}{4}\). Cela signifie que les valeurs de la fonction sont négatives à gauche de la première intersection\(x=−\frac{1}{4}\) horizontale à et négatives à droite de la deuxième intersection à\(x=\frac{11}{4} \). Cela nous donne la solution à l'inégalité.
\[x<−\frac{1}{4} \text{ or } x>1\frac{1}{4} \nonumber\]
En notation par intervalles, ce serait\(( −\infty,−0.25 )\cup( 2.75,\infty)\).
Exercice\(\PageIndex{6}\)
Résoudre\(−2|k−4|\leq−6\).
- Réponse
-
\(k\leq1\)ou\(k\geq7\) ; en notation par intervalles, ce serait\(\left(−\infty,1\right]\cup\left[7,\infty\right)\)
Concepts clés
- La fonction de valeur absolue est couramment utilisée pour mesurer les distances entre des points.
- Les problèmes appliqués, tels que les plages de valeurs possibles, peuvent également être résolus à l'aide de la fonction de valeur absolue.
- Le graphique de la fonction des valeurs absolues ressemble à la lettre V. Il comporte un point d'angle auquel le graphe change de direction.
- Dans une équation de valeur absolue, une variable inconnue est l'entrée d'une fonction de valeur absolue.
- Si la valeur absolue d'une expression est définie comme étant un nombre positif, attendez-vous à deux solutions pour la variable inconnue.
- Une équation de valeur absolue peut avoir une solution, deux solutions ou aucune solution.
- Une inégalité en valeur absolue est similaire à une équation de valeurs absolues mais prend la forme | A |B<B, | A |≤B, | A |> ou | A |≥B.Elle peut être résolue en déterminant les limites de l'ensemble de solutions, puis en testant quels segments se trouvent dans l'ensemble.
- Les inégalités de valeurs absolues peuvent également être résolues graphiquement.
Lexique
équation de valeur absolue
une équation de la forme\(|A|=B\), avec\(B\geq0\) ; elle aura des solutions lorsque\(A=B\) ou\(A=−B\)
inégalité en valeur absolue,
une relation sous la forme\(|A|<B\)\(|A|{\leq}B\),\(|A|>B\), ou\(|A|{\geq}B\)


