3.5 : Transformation des fonctions

Last updated
Save as PDF

Page ID: 195527

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

Fonctions graphiques utilisant des décalages verticaux et horizontaux.
Fonctions graphiques utilisant des réflexions autour de l'axe X et de l'axe Y.
Déterminez si une fonction est paire, impaire ou aucune des deux à partir de son graphe.
Fonctions graphiques à l'aide de compressions et d'étirements.
Combinez les transformations.

Nous savons tous qu'un miroir plat nous permet de voir une image précise de nous-mêmes et de ce qui se trouve derrière nous. Lorsque nous inclinons le miroir, les images que nous voyons peuvent se déplacer horizontalement ou verticalement. Mais que se passe-t-il lorsque nous plions un miroir flexible ? Comme un miroir de carnaval, il nous présente une image déformée de nous-mêmes, étirée ou comprimée horizontalement ou verticalement. De la même manière, nous pouvons déformer ou transformer des fonctions mathématiques pour mieux les adapter à la description d'objets ou de processus dans le monde réel. Dans cette section, nous allons examiner plusieurs types de transformations.

alt — Figure$\PageIndex{1}$ : (crédit : « Misko » /Flickr)

Souvent, lorsque nous sommes confrontés à un problème, nous essayons de modéliser le scénario en utilisant les mathématiques sous forme de mots, de tableaux, de graphiques et d'équations. L'une des méthodes que nous pouvons utiliser consiste à adapter les graphiques de base des fonctions de la boîte à outils afin de créer de nouveaux modèles pour un scénario donné. Il existe des moyens systématiques de modifier les fonctions afin de construire des modèles appropriés aux problèmes que nous essayons de résoudre.

Identifier les décalages verticaux

Un type de transformation simple consiste à déplacer l'ensemble du graphe d'une fonction vers le haut, le bas, la droite ou la gauche. Le décalage le plus simple est un décalage vertical, déplaçant le graphique vers le haut ou vers le bas, car cette transformation implique l'ajout d'une constante positive ou négative à la fonction. En d'autres termes, nous ajoutons la même constante à la valeur de sortie de la fonction, quelle que soit l'entrée. Pour une fonction$g(x)=f(x)+k$, la fonction$f(x)$ est décalée verticalement$k$ d'unités. Voir la figure$\PageIndex{2}$ pour un exemple.

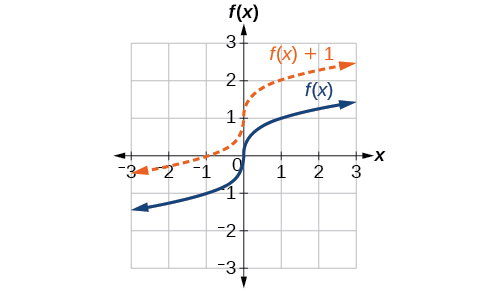
Déplacement vertical de k=1 de la fonction racine cubique f (x) =3√ x. — Figure$\PageIndex{2}$ : Déplacement vertical par rapport à$k=1$ la fonction racine du cube$f(x)=\sqrt[3]{x}$.

Pour vous aider à visualiser le concept d'un décalage vertical, considérez cela$y=f(x)$. Par conséquent,$f(x)+k$ est équivalent à$y+k$. Chaque unité de$y$ est remplacée par$y+k$, de sorte que la$y$ valeur -augmente ou diminue en fonction de la valeur de$k$. Il en résulte un déplacement vers le haut ou vers le bas.

Définition : décalage vertical

Étant donné une fonction$f(x)$, une nouvelle fonction$g(x)=f(x)+k$, où$k$ est une constante, est un décalage vertical de la fonction$f(x)$. Toutes les valeurs de sortie changent par$k$ unités. Si la$k$ valeur est positive, le graphique se déplacera vers le haut. Si la$k$ valeur est négative, le graphique sera décalé vers le bas.

Exemple$\PageIndex{1}$: Adding a Constant to a Function

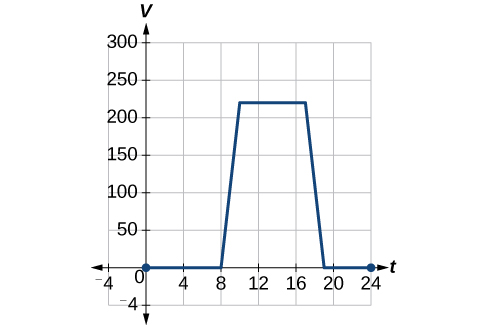
Pour réguler la température dans un bâtiment écologique, les bouches d'aération situées près du toit s'ouvrent et se ferment tout au long de la journée. La figure$\PageIndex{3}$ montre la surface des évents ouverts$V$ (en pieds carrés) tout au long de la journée en heures après minuit$t$. Au cours de l'été, le responsable des installations décide d'essayer de mieux réguler la température en augmentant le nombre d'évents ouverts de 20 pieds carrés tout au long de la journée et de la nuit. Esquissez un graphique de cette nouvelle fonction.

Solution

Nous pouvons esquisser un graphique de cette nouvelle fonction en ajoutant 20 à chacune des valeurs de sortie de la fonction d'origine. Cela aura pour effet de déplacer le graphique verticalement vers le haut, comme le montre la figure$\PageIndex{4}$.

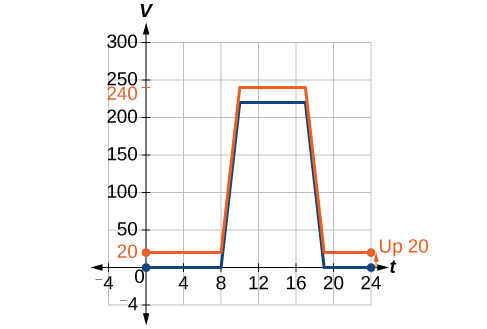
Notez que dans la figure$\PageIndex{4}$, pour chaque valeur d'entrée, la valeur de sortie a augmenté de 20, donc si nous appelons la nouvelle fonction$S(t)$, nous pourrions écrire

\[S(t)=V(t)+20\]

Cette notation nous indique que, pour n'importe quelle valeur de$t$,$S(t)$ peut être trouvée en évaluant la fonction sur la$V$ même entrée, puis en ajoutant 20 au résultat. Cela se définit$S$ comme une transformation de la fonction$V$, dans ce cas un décalage vertical de 20 unités. Notez qu'avec un décalage vertical, les valeurs d'entrée restent les mêmes et seules les valeurs de sortie changent. Voir le tableau$\PageIndex{1}$.

Tableau$\PageIndex{1}$
$t$	0	8	10	17	19	24
$V(t)$	0	0	220	220	0	0
$S(t)$	20	20	240	240	20	20

Comment...

À partir d'une fonction tabulaire, créez une nouvelle ligne pour représenter un décalage vertical.

Identifiez la ligne ou la colonne de sortie.
Déterminez l'ampleur du décalage.
Ajoutez le décalage à la valeur de chaque cellule de sortie. Ajoutez une valeur positive pour le haut ou une valeur négative pour le bas.

Exemple$\PageIndex{2}$: Shifting a Tabular Function Vertically

Une fonction$f(x)$ est donnée dans le tableau$\PageIndex{2}$. Créez un tableau pour la fonction$g(x)=f(x)−3$.

Tableau$\PageIndex{2}$
$x$	2	4	6	8
$f(x)$	1	3	7	11

Solution

La formule nous$g(x)=f(x)−3$ indique que nous pouvons trouver les valeurs de sortie de$g$ en soustrayant 3 des valeurs de sortie de$f$. Par exemple :

\[\begin{align*} f(x)&=1 &\text{Given} \\[4pt] g(x)&=f(x)-3 &\text{Given Transformation} \\[4pt] g(2) & =f(2)−3 \\ &=1-3\\ &=-2\end{align*}\]

En soustrayant 3 de chaque$f(x)$ valeur, nous pouvons compléter un tableau de valeurs$g(x)$ comme indiqué dans le tableau$\PageIndex{3}$.

Tableau$\PageIndex{3}$
$x$	2	4	6	8
$f(x)$	1	3	7	11
$g(x)$	-2	0	4	8

Analyse

Comme pour le décalage vertical précédent, notez que les valeurs d'entrée restent les mêmes et que seules les valeurs de sortie changent.

Exercice$\PageIndex{1}$

La fonction$h(t)=−4.9t^2+30t$ donne la hauteur$h$ d'une balle (en mètres) lancée vers le haut depuis le sol après$t$ quelques secondes. Supposons que la balle ait été lancée depuis le haut d'un bâtiment de 10 mètres. Associez cette nouvelle fonction$b(t)$ de hauteur à$h(t)$, puis trouvez une formule pour$b(t)$.

Réponse: $b(t)=h(t)+10=−4.9t^2+30t+10$

Identifier les déplacements horizontaux

Nous venons de voir que le décalage vertical est une modification de la sortie, ou de l'extérieur, de la fonction. Nous allons maintenant voir comment les modifications apportées à l'entrée, à l'intérieur de la fonction, modifient son graphe et sa signification. Un décalage de l'entrée entraîne un mouvement du graphe de la fonction vers la gauche ou vers la droite selon ce que l'on appelle un décalage horizontal, illustré sur la figure$\PageIndex{4}$.

alt — Figure$\PageIndex{4}$ : Déplacement horizontal de la fonction$f(x)=\sqrt[3]{x}$. Notez que cela$h=-1$ déplace le graphique vers la gauche, c'est-à-dire vers des valeurs négatives de$x$.

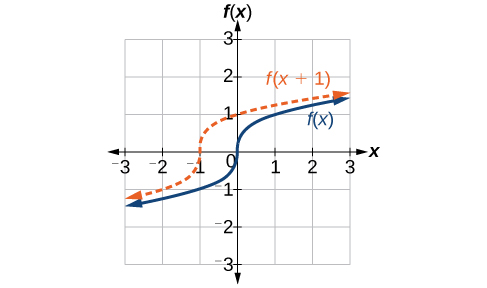
Par exemple, si$f(x)=x^2$, alors$g(x)=(x−2)^2$ est une nouvelle fonction. Chaque entrée est réduite de 2 avant la mise au carré de la fonction. Le résultat est que le graphique est décalé de 2 unités vers la droite, car il faudrait augmenter l'entrée précédente de 2 unités pour obtenir la même valeur de sortie que celle indiquée dans$f$.

Définition : Déplacement horizontal

Étant donné une fonction$f$, une nouvelle fonction$g(x)=f(x−h)$, où$h$ est une constante, est un décalage horizontal de la fonction$f$. Si la$h$ valeur est positive, le graphique se déplacera vers la droite. Si la$h$ valeur est négative, le graphique se déplacera vers la gauche.

Exemple$\PageIndex{4}$: Adding a Constant to an Input

Pour en revenir à notre exemple de flux d'air de bâtiment tiré de la Figure$\PageIndex{2}$, supposons qu'à l'automne, le responsable des installations décide que le plan de ventilation initial commence trop tard et souhaite commencer l'ensemble du programme de ventilation 2 heures plus tôt. Esquissez un graphique de la nouvelle fonction.

Solution

Nous pouvons$V(t)$ définir qu'il s'agit du programme original et$F(t)$ du programme révisé.

\[V(t)= \text{ the original venting plan} \nonumber\]

\[F(t)= \text{ starting 2 hrs sooner} \nonumber\]

Dans le nouveau graphique, à chaque fois, le débit d'air est le même que celui de la fonction$V$ initiale 2 heures plus tard. Par exemple, dans la fonction d'origine$V$, le débit d'air commence à changer à 8 heures du matin, alors que pour la fonction$F$, le débit d'air commence à changer à 6 heures du matin. Les valeurs de fonction comparables sont$V(8)=F(6)$. Voir la figure$\PageIndex{5}$. Notez également que les évents s'ouvraient pour la première fois$220 \text{ft}^2$ à 10 heures du matin selon le plan initial, tandis que selon le nouveau plan, les évents atteignent$220 \text{ft}^2$ 8 heures du matin, donc$V(10)=F(8)$.

Dans les deux cas, on voit que, car$F(t)$ commence 2 heures plus tôt,$h=−2$. Cela signifie que les mêmes valeurs de sortie sont atteintes lorsque$F(t)=V(t−(−2))=V(t+2)$.

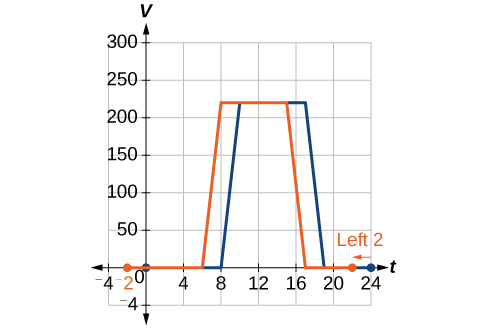
Analyse

Notez que cela$V(t+2)$ a pour effet de déplacer le graphique vers la gauche.

Les modifications horizontales ou « modifications internes » affectent le domaine d'une fonction (l'entrée) plutôt que la plage et semblent souvent contre-intuitives. La nouvelle fonction$F(t)$ utilise les mêmes sorties que$V(t)$, mais fait correspondre ces sorties à des entrées 2 heures plus tôt que celles de$V(t)$. Autrement dit, nous devons ajouter 2 heures à l'entrée de$V$ pour trouver la sortie correspondante pour$F:F(t)=V(t+2)$.

Comment...

À partir d'une fonction tabulaire, créez une nouvelle ligne pour représenter un décalage horizontal.

Identifiez la ligne ou la colonne d'entrée.
Déterminez l'ampleur du décalage.
Ajoutez le décalage à la valeur de chaque cellule en entrée.

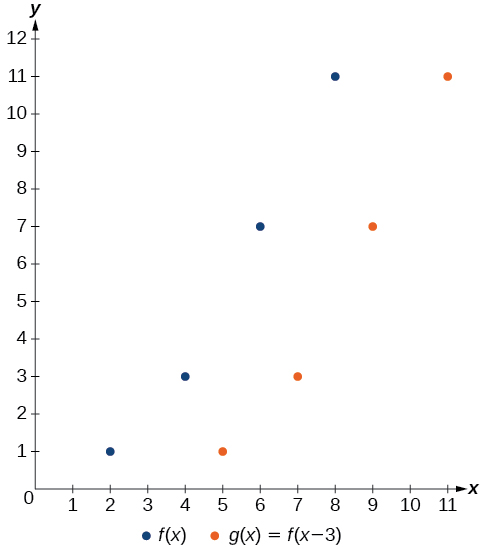
Exemple$\PageIndex{5}$: Shifting a Tabular Function Horizontally

Une fonction$f(x)$ est donnée dans le tableau$\PageIndex{4}$. Créez un tableau pour la fonction$g(x)=f(x−3)$.

Tableau$\PageIndex{4}$
$x$	2	4	6	8
$f(x)$	1	3	7	11

Solution

La formule nous$g(x)=f(x−3)$ indique que les valeurs de sortie de$g$ sont identiques à la valeur de sortie$f$ lorsque la valeur d'entrée est inférieure de 3 à la valeur d'origine. Par exemple, nous le savons$f(2)=1$. Pour obtenir la même sortie de la fonction$g$, nous aurons besoin d'une valeur d'entrée 3 plus grande. Nous entrons une valeur 3 plus grande$g(x)$ car la fonction en retire 3 avant d'évaluer la fonction$f$.

\[\begin{align*} g(5)&=f(5-3) \\ &=f(2) \\ &=1 \end{align*}\]

Nous continuons avec les autres valeurs pour créer une table$\PageIndex{5}$.

Tableau$\PageIndex{5}$
$x$	5	7	9	11
$x-3$	2	4	6	8
$f(x)$	1	3	7	11
$g(x)$	1	3	7	11

Le résultat est que la fonction$g(x)$ a été décalée de 3 vers la droite. Notez que les valeurs de sortie pour$g(x)$ restent identiques aux valeurs de sortie pour$f(x)$, mais que les valeurs d'entrée correspondantes,$x$, ont été décalées de 3 vers la droite. Plus précisément, 2 sont passés à 5, 4 sont passés à 7, 6 sont passés à 9 et 8 sont passés à 11.

Analyse

La figure$\PageIndex{6}$ représente les deux fonctions. Nous pouvons voir le décalage horizontal dans chaque point.

Graphique des points du tableau précédent pour f (x) et g (x) =f (x-3) — Figure$\PageIndex{6}$ : Graphique des points du tableau précédent pour$f(x)$ et$g(x)=f(x-3)$

Exemple$\PageIndex{6}$: Identifying a Horizontal Shift of a Toolkit Function

La figure$\PageIndex{7}$ représente une transformation de la fonction de la boîte à outils$f(x)=x^2$. Associez cette nouvelle fonction$g(x)$ à$f(x)$, puis trouvez une formule pour$g(x)$.

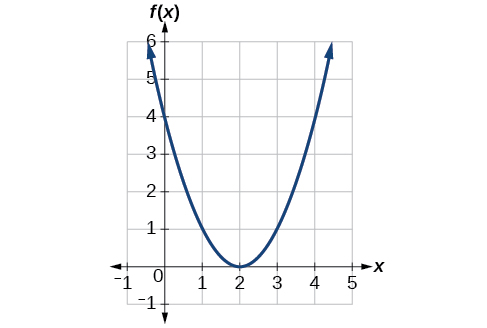
Graphe d'une parabole — Figure$\PageIndex{7}$ : Graphique d'une parabole

Solution

Notez que la forme du graphique est identique à celle de la$f(x)=x^2$ fonction, mais que les$x$ valeurs -sont décalées de 2 unités vers la droite. Le sommet était situé à$(0,0)$, mais maintenant le sommet est à$(2,0)$. Le graphique est la fonction quadratique de base décalée de 2 unités vers la droite, donc

\[g(x)=f(x−2) \nonumber\]

Remarquez comment nous devons saisir la valeur$x=2$ pour obtenir la valeur de sortie$y=0$ ; les$x$ valeurs -doivent être plus grandes de 2 unités en raison du décalage de 2 unités vers la droite. Nous pouvons ensuite utiliser la définition de la$f(x)$ fonction pour écrire une formule$g(x)$ en évaluant$f(x−2)$.

\[\begin{align*} f(x)&=x^2 \\ g(x)&=f(x-2) \\ g(x)&=f(x-2)=(x-2)^2 \end{align*}\]

Analyse

Pour déterminer si le décalage est$+2$ ou$−2$, considérez un point de référence unique sur le graphique. Pour un quadratique, il est pratique de regarder le point du sommet. Dans la fonction d'origine,$f(0)=0$. Dans notre fonction modifiée,$g(2)=0$. Pour obtenir la valeur de sortie de 0 à partir de la fonction$f$, nous devons décider si un signe plus ou moins fonctionnera pour satisfaire$g(2)=f(x−2)=f(0)=0$. Pour que cela fonctionne, nous devrons soustraire 2 unités de nos valeurs d'entrée.

Exemple$\PageIndex{7}$: Interpreting Horizontal versus Vertical Shifts

La fonction$G(m)$ indique le nombre de gallons d'essence nécessaires pour parcourir des$m$ kilomètres. Interpréter$G(m)+10$ et$G(m+10)$

Solution

$G(m)+10$peut être interprété comme ajoutant 10 à la sortie, gallons. Il s'agit de l'essence nécessaire pour parcourir des$m$ kilomètres, plus 10 gallons d'essence supplémentaires. Le graphique indiquerait un décalage vertical.

$G(m+10)$peut être interprété comme ajoutant 10 miles à l'entrée. C'est donc le nombre de gallons d'essence nécessaires pour parcourir 10 miles de plus que des$m$ miles. Le graphique indiquerait un décalage horizontal.

Exercice$\PageIndex{7}$

Compte tenu de la fonction$f(x)=\sqrt{x}$, tracez la fonction d'origine$f(x)$ et la transformation$g(x)=f(x+2)$ sur les mêmes axes. S'agit-il d'un décalage horizontal ou vertical ? De quelle manière le graphique est-il décalé et de combien d'unités ?

Réponse: Les graphiques de$f(x)$ et$g(x)$ sont présentés ci-dessous. La transformation est un déplacement horizontal. La fonction est décalée de 2 unités vers la gauche.

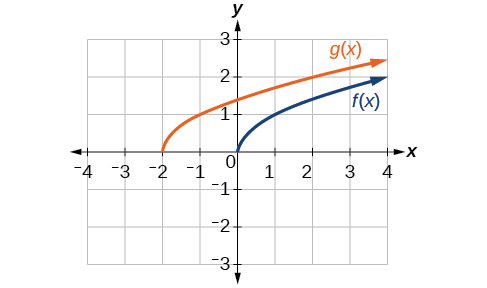
$Représentation graphique d'une fonction de racine carrée et d'une fonction de décalage horizontal du pied carré.$
Figurine$\PageIndex{8}$

Combinaison de déplacements verticaux et horizontaux

Maintenant que nous avons deux transformations, nous pouvons les combiner. Les décalages verticaux sont des modifications extérieures qui affectent les valeurs de l'$(y-)$axe de sortie et déplacent la fonction vers le haut ou vers le bas. Les décalages horizontaux sont des modifications internes qui affectent les valeurs des$(x-)$ axes d'entrée et déplacent la fonction vers la gauche ou la droite. La combinaison des deux types de décalages entraîne le décalage du graphique d'une fonction vers le haut ou vers le bas et vers la droite ou la gauche.

Comment...

En fonction d'une fonction et d'un décalage vertical et horizontal, esquissez le graphique.

Identifiez les décalages verticaux et horizontaux par rapport à la formule.
Le décalage vertical résulte d'une constante ajoutée à la sortie. Déplace le graphique vers le haut pour une constante positive et vers le bas pour une constante négative.
Le décalage horizontal résulte d'une constante ajoutée à l'entrée. Déplacez le graphique vers la gauche pour une constante positive et vers la droite pour une constante négative.
Appliquez les décalages au graphique dans l'un ou l'autre ordre.

Exemple$\PageIndex{8}$: Graphing Combined Vertical and Horizontal Shifts

Étant donné$f(x)=|x|$, esquissez un graphique de$h(x)=f(x+1)−3$.

Solution

La fonction$f$ est la fonction à valeur absolue de notre boîte à outils. Nous savons que ce graphe a la forme d'un V, avec le point à l'origine. Le graphe de$h$ s'est transformé de deux$f$ manières :$f(x+1)$ est un changement à l'intérieur de la fonction, donnant un décalage horizontal vers la gauche de 1, et la soustraction de 3 pouces$f(x+1)−3$ est un changement vers l'extérieur de la fonction, donnant un décalage vertical vers le bas de 3. La transformation du graphique est illustrée dans la figure$\PageIndex{9}$.

Suivons un point du graphique de$f(x)=|x|$.

Le point$(0,0)$ est d'abord transformé en décalant d'une unité vers la gauche :$(0,0)\rightarrow(−1,0)$
Le point$(−1,0)$ est ensuite transformé en décalant 3 unités vers le bas :$(−1,0)\rightarrow(−1,−3)$

Graphe d'une fonction absolue, <span translate= — Figure$\PageIndex{9}$ : Graphique d'une fonction absolue et de$y=|x|$ la façon dont elle a été transformée en$y=|x+1|-3$

La figure$\PageIndex{10}$ montre le graphique de$h$.

La fonction finale <span translate= — Figure$\PageIndex{10}$ : La fonction finale$y=|x+1|-3$.

Exercice$\PageIndex{8}$

Étant donné$f(x)=|x|$, esquissez un graphique de$h(x)=f(x−2)+4$.

Réponse: $alt$
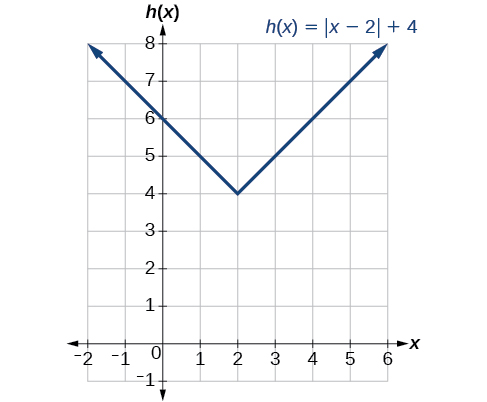
Figurine$\PageIndex{11}$

Exemple$\PageIndex{9}$: Identifying Combined Vertical and Horizontal Shifts

Écrivez une formule pour le graphique illustré à la figure$\PageIndex{12}$, qui est une transformation de la fonction de racine carrée de la boîte à outils.

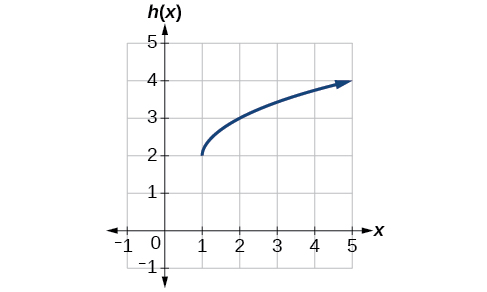
Graphe d'une fonction de racine carrée transposée à droite d'une unité et vers le haut 2. — Figure$\PageIndex{12}$ : Graphique d'une fonction de racine carrée transposée à droite d'une unité et vers le haut de 2.

Solution

Le graphique de la fonction de la boîte à outils commence à l'origine. Ce graphique a donc été décalé de 1 vers la droite et de 2 vers le haut. En notation fonctionnelle, nous pourrions écrire cela comme

\[h(x)=f(x−1)+2 \nonumber\]

En utilisant la formule de la fonction de racine carrée, nous pouvons écrire

\[h(x)=\sqrt{x−1}+2 \nonumber\]

Analyse

Notez que cette transformation a modifié le domaine et la plage de la fonction. Ce nouveau graphique possède un domaine$\left[1,\infty\right)$ et une plage$\left[2,\infty\right)$.

Exercice$\PageIndex{9}$

Écrivez une formule pour une transformation de la fonction réciproque de la boîte à outils$f(x)=\frac{1}{x}$ qui déplace le graphe de la fonction d'une unité vers la droite et d'une unité vers le haut.

Réponse: \[g(x)=\dfrac{1}{x-1}+1 \nonumber \]

Fonctions graphiques à l'aide de réflexions sur les axes

Une autre transformation qui peut être appliquée à une fonction est la réflexion sur l'axe X ou Y. Une réflexion verticale reflète un graphique verticalement sur l'axe X, tandis qu'une réflexion horizontale reflète un graphique horizontalement sur l'axe Y. Les reflets sont illustrés sur la figure$\PageIndex{13}$.

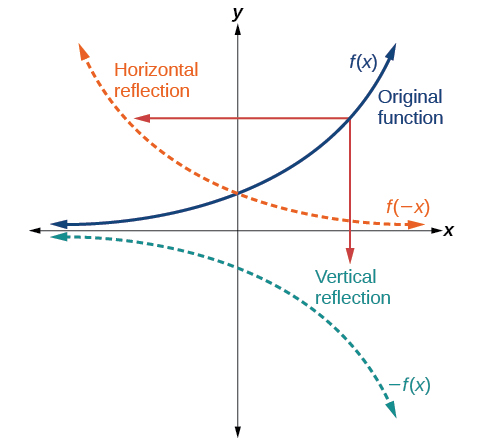Graphe de la réflexion verticale et horizontale d'une fonction. — Figure$\PageIndex{13}$ : Graphique de la réflexion verticale et horizontale d'une fonction.

Notez que la réflexion verticale produit un nouveau graphique qui est une image miroir du graphe de base ou d'origine autour de l'axe X. La réflexion horizontale produit un nouveau graphique qui est une image miroir du graphe de base ou d'origine autour de l'axe Y.

Définitions : réflexions

Étant donné une fonction$f(x)$, une nouvelle fonction$g(x)=−f(x)$ est une réflexion verticale de la fonction$f(x)$, parfois appelée réflexion autour de (ou au-dessus ou à travers) l'axe X.

Étant donné une fonction$f(x)$, une nouvelle fonction$g(x)=f(−x)$ est une réflexion horizontale de la fonction$f(x)$, parfois appelée réflexion sur l'axe y.

Comment...

En fonction d'une fonction, reflétez le graphique à la fois verticalement et horizontalement.

Multipliez toutes les sorties par —1 pour obtenir une réflexion verticale. Le nouveau graphique reflète le graphe d'origine sur l'axe X.
Multipliez toutes les entrées par —1 pour obtenir une réflexion horizontale. Le nouveau graphique reflète le graphe d'origine autour de l'axe Y.

Exemple$\PageIndex{10}$: Reflecting a Graph Horizontally and Vertically

Reflète le graphique de$s(t)=\sqrt{t}$ (a) verticalement et (b) horizontalement.

Solution

a. Le fait de refléter le graphique verticalement signifie que chaque valeur de sortie sera reflétée sur l'axe horizontal en T, comme indiqué sur la figure$\PageIndex{14}$.

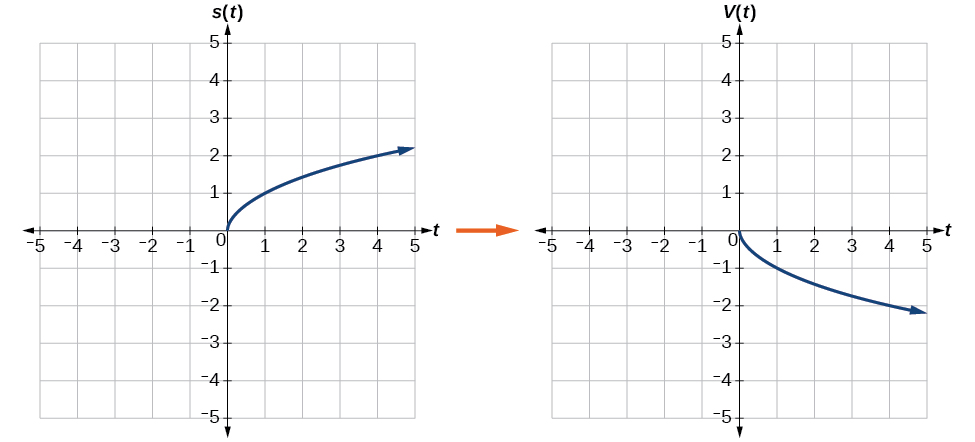
Figure$\PageIndex{14}$ : Graphique de la réflexion verticale de la fonction de racine carrée.

Comme chaque valeur de sortie est l'opposé de la valeur de sortie d'origine, nous pouvons écrire

\[V(t)=−s(t) \text{ or } V(t)=−\sqrt{t} \nonumber\]

Notez qu'il s'agit d'une modification extérieure, ou d'un décalage vertical, qui affecte les$s(t)$ valeurs de sortie, de sorte que le signe négatif appartient à l'extérieur de la fonction.

b. Réfléchir horizontalement signifie que chaque valeur d'entrée sera reflétée sur l'axe vertical, comme indiqué sur la figure$\PageIndex{15}$.

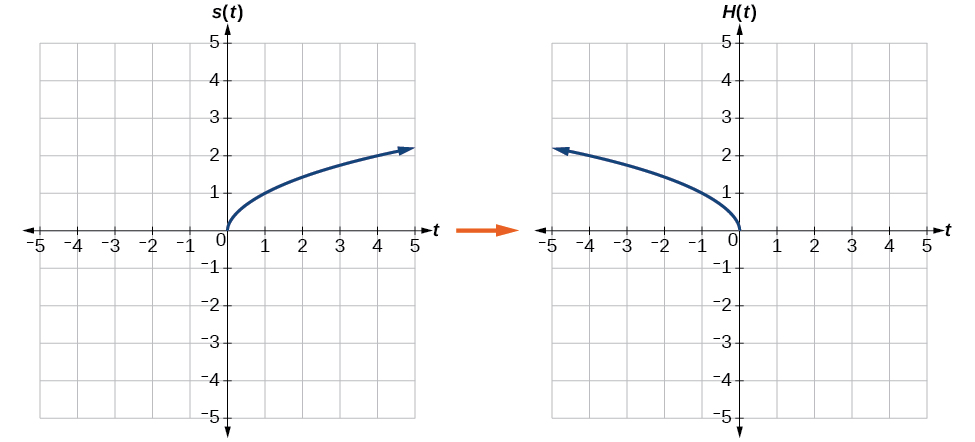
Graphique de la réflexion horizontale de la fonction de racine carrée. — Figure$\PageIndex{15}$ : Reflet horizontal de la fonction de racine carrée

Comme chaque valeur d'entrée est l'opposé de la valeur d'entrée d'origine, nous pouvons écrire

\[H(t)=s(−t) \text{ or } H(t)=\sqrt{−t} \nonumber\]

Notez qu'il s'agit d'une modification interne ou horizontale qui affecte les valeurs d'entrée, de sorte que le signe négatif se trouve à l'intérieur de la fonction.

Notez que ces transformations peuvent affecter le domaine et l'étendue des fonctions. Alors que la fonction de racine carrée d'origine possède un domaine$\left[0,\infty\right)$ et une plage$\left[0,\infty\right)$, la réflexion verticale donne à la$V(t)$ fonction la plage$\left(−\infty,0\right]$ et la réflexion horizontale donne à la$H(t)$ fonction le domaine$\left(−\infty, 0\right]$.

Exercice$\PageIndex{5}$

Reflète le graphique de$f(x)=|x−1|$ (a) verticalement et (b) horizontalement.

Réponse

un.

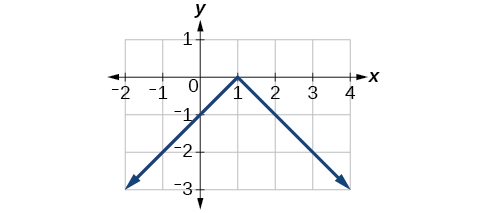
Graphe d'une fonction absolue réfléchie verticalement. — Figure$\PageIndex{16}$ : Graphique d'une fonction absolue réfléchie verticalement.

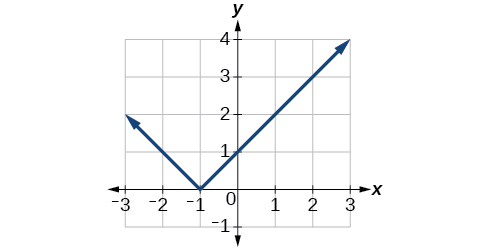
Figure$\PageIndex{17}$ : Graphique d'une fonction absolue traduite d'une unité à gauche.

Exemple$\PageIndex{11}$: Reflecting a Tabular Function Horizontally and Vertically

Une fonction$f(x)$ est donnée sous la forme Table$\PageIndex{6}$. Créez un tableau pour les fonctions ci-dessous.

a.$g(x)=−f(x)$
b.$h(x)=f(−x)$

Tableau$\PageIndex{6}$
$x$	2	4	6	8
$f(x)$	1	3	7	11

a. En effet$g(x)$, le signe négatif situé à l'extérieur de la fonction indique une réflexion verticale, de sorte que les valeurs X restent les mêmes et que chaque valeur de sortie sera opposée à la valeur de sortie d'origine. Voir le tableau$\PageIndex{7}$.

Tableau$\PageIndex{7}$
$x$	2	4	6	8
$g(x)$	-1	-3	-7	-11

b. En effet$h(x)$, le signe négatif à l'intérieur de la fonction indique une réflexion horizontale, de sorte que chaque valeur d'entrée sera opposée à la valeur d'entrée d'origine et les$h(x)$ valeurs resteront les mêmes que les$f(x)$ valeurs. Voir le tableau$\PageIndex{8}$.

Tableau$\PageIndex{8}$
$x$	-2	-4	-6	-8
$h(x)$	1	3	7	11

Exercice$\PageIndex{6}$

Une fonction$f(x)$ est donnée sous la forme Table$\PageIndex{9}$. Créez un tableau pour les fonctions ci-dessous.

a.$g(x)=−f(x)$
b.$h(x)=f(−x)$

Tableau$\PageIndex{9}$
$x$	-2	0	2	4
$f(x)$	5	10	15	20

Réponse

un.$g(x)=−f(x)$

Tableau$\PageIndex{10}$
$x$	-2	0	2	4
$g(x)$	-5	-10	-15	-20

b.$h(x)=f(−x)$

Tableau$\PageIndex{11}$
$x$	-2	0	2	-4
$h(x)$	15	10	5	20

Exemple$\PageIndex{12}$: Applying a Learning Model Equation

Un modèle d'apprentissage courant a une équation similaire à$k(t)=−2^{−t}+1$, où$k$ est le pourcentage de maîtrise qui peut être atteint après des séances d'$t$entraînement. Il s'agit d'une transformation de la fonction$f(t)=2^t$ illustrée à la figure$\PageIndex{18}$. Esquissez un graphique de$k(t)$.

Graphe de <span translate= — Figure$\PageIndex{18}$ : Graphique de$k(t)$

Solution

Cette équation combine trois transformations en une seule équation.

Un reflet horizontal :$f(−t)=2^{−t}$
Une réflexion verticale :$−f(−t)=−2^{−t}$
Un décalage vertical :$−f(−t)+1=−2^{−t}+1$

Nous pouvons esquisser un graphe en appliquant ces transformations une par une à la fonction d'origine. Suivons deux points à travers chacune des trois transformations. Nous choisirons les points$(0, 1)$ et$(1, 2)$.

Tout d'abord, nous appliquons une réflexion horizontale :$(0, 1) \; (–1, 2)$.
Ensuite, nous appliquons une réflexion verticale :$(0, −1) \; (-1, –2)$.
Enfin, nous appliquons un décalage vertical :$(0, 0) \; (-1, -1)$.

Cela signifie que les points d'origine,$(0,1)$ et$(1,2)$ deviennent$(0,0)$ et$(-1,-1)$ après avoir appliqué les transformations.

Dans la figure$\PageIndex{19}$, le premier graphe résulte d'une réflexion horizontale. La seconde résulte d'une réflexion verticale. La troisième résulte d'un décalage vertical d'une unité vers le haut.

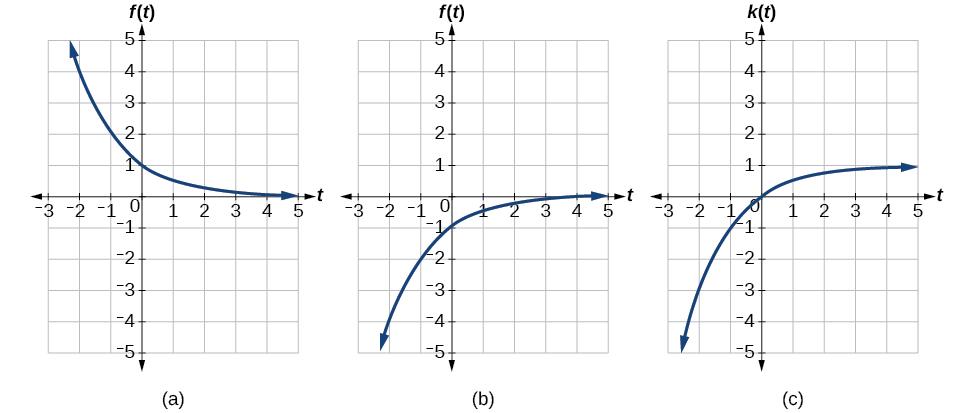
Figure$\PageIndex{19}$ : Graphiques de toutes les transformations.

Analyse

En tant que modèle d'apprentissage, cette fonction serait limitée à un domaine de$t\geq0$, avec une plage correspondante$\left[0,1\right)$.

Exercice$\PageIndex{7}$

Étant donné la fonction de la boîte à outils$f(x)=x^2$, graphique$g(x)=−f(x)$ et$h(x)=f(−x)$. Prenez note de tout comportement surprenant associé à ces fonctions.

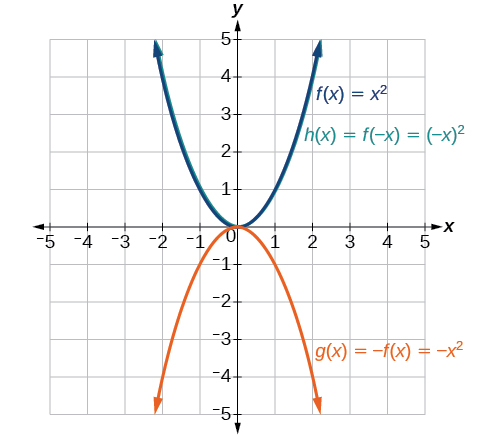
Réponse: $Graphe de x^2 et de ses réflexions.$
Figure$\PageIndex{20}$ : Graphique de$x^2$ et de ses reflets.

Remarque :$g(x)=f(−x)$ ressemble à$f(x)$.

Déterminer les fonctions paires et impaires

Certaines fonctions présentent une symétrie, de sorte que les réflexions donnent le graphe d'origine. Par exemple, refléter horizontalement les fonctions de la boîte à outils$f(x)=x^2$ ou$f(x)=|x|$ aboutira au graphique original. Nous disons que ces types de graphes sont symétriques par rapport à l'axe Y. Les fonctions dont les graphes sont symétriques par rapport à l'axe Y sont appelées fonctions paires.

Si les graphes de$f(x)=x^3$ ou$f(x)=\frac{1}{x}$ étaient réfléchis sur les deux axes, le résultat serait le graphique d'origine, comme le montre la figure$\PageIndex{21}$.

Nous disons que ces graphes sont symétriques par rapport à l'origine. Une fonction dont le graphe est symétrique par rapport à l'origine est appelée fonction impaire.

Remarque : Une fonction ne peut être ni paire ni impaire si elle ne présente aucune symétrie. Par exemple, n'$f(x)=2^x$est ni pair ni étrange. De plus, la seule fonction à la fois paire et impaire est la fonction constante$f(x)=0$.

Définitions : fonctions paires et impaires

Une fonction est appelée fonction paire si pour chaque entrée$x$

$f(x)=f(−x)$

Le graphe d'une fonction paire est symétrique par rapport à l'axe Y.

Une fonction est appelée fonction impaire si pour chaque entrée$x$

$f(x)=−f(−x)$

Le graphe d'une fonction impaire est symétrique par rapport à l'origine.

Comment...

À partir de la formule d'une fonction, déterminez si la fonction est paire, impaire ou aucune des deux.

Déterminez si la fonction est satisfaisante$f(x)=f(−x)$. Si c'est le cas, c'est égal.
Déterminez si la fonction est satisfaisante$f(x)=−f(−x)$. Si c'est le cas, c'est étrange.
Si la fonction ne satisfait à aucune des deux règles, elle n'est ni paire ni impaire.

Exemple$\PageIndex{13}$: Determining whether a Function Is Even, Odd, or Neither

La fonction est-elle$f(x)=x^3+2x$ paire, étrange ou aucune des deux ?

Solution

Sans regarder un graphique, nous pouvons déterminer si la fonction est paire ou impaire en trouvant des formules pour les réflexions et en déterminant si elles nous ramènent à la fonction d'origine. Commençons par la règle des fonctions paires.

\[f(−x)=(−x)^3+2(−x)=−x^3−2x \nonumber\]

Cela ne nous ramène pas à la fonction d'origine, donc cette fonction n'est pas uniforme. Nous pouvons maintenant tester la règle pour les fonctions impaires.

\[−f(−x)=−(−x^3−2x)=x^3+2x \nonumber\]

Parce$−f(−x)=f(x)$ que c'est une fonction étrange.

Analyse

Considérez le graphique de$f$ la figure$\PageIndex{22}$. Notez que le graphique est symétrique par rapport à l'origine. Pour chaque point$(x,y)$ du graphique, le point correspondant$(−x,−y)$ figure également sur le graphique. Par exemple,$(1, 3)$ se trouve sur le graphique de$f$, et le point correspondant$(−1,−3)$ se trouve également sur le graphique.

Exercice$\PageIndex{8}$

La fonction est-elle$f(s)=s^4+3s^2+7$ paire, étrange ou aucune des deux ?

Réponse: même

Fonctions graphiques à l'aide d'étirements et de compressions

L'ajout d'une constante aux entrées ou aux sorties d'une fonction modifiait la position d'un graphe par rapport aux axes, mais cela n'affectait pas la forme du graphe. Nous explorons maintenant les effets de la multiplication des entrées ou des sorties par une certaine quantité.

Nous pouvons transformer l'intérieur (valeurs d'entrée) d'une fonction ou l'extérieur (valeurs de sortie) d'une fonction. Chaque modification a un effet spécifique qui peut être vu graphiquement.

Étirements et compressions verticaux

Lorsque nous multiplions une fonction par une constante positive, nous obtenons une fonction dont le graphe est étiré ou compressé verticalement par rapport au graphe de la fonction d'origine. Si la constante est supérieure à 1, on obtient un étirement vertical ; si la constante est comprise entre 0 et 1, on obtient une compression verticale. La figure$\PageIndex{23}$ montre une fonction multipliée par des facteurs constants 2 et 0,5 et l'étirement vertical et la compression qui en résultent.

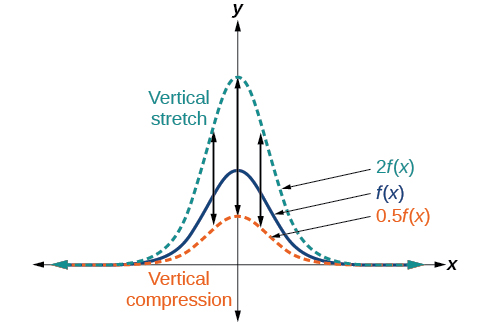
Graphique d'une fonction qui montre l'étirement et la compression verticaux. — Figure$\PageIndex{23}$ : Extraction et compression verticales

Définitions : étirements et compressions verticaux

Étant donné une fonction$f(x)$, une nouvelle fonction$g(x)=af(x)$, où$a$ est une constante, est un étirement vertical ou une compression verticale de la fonction$f(x)$.

Si$a>1$, alors le graphique sera étiré.
Si$0<a<1$, alors le graphique sera compressé.
Si tel est le cas$a<0$, il y aura une combinaison d'un étirement vertical ou d'une compression avec une réflexion verticale.

Comment...

À partir d'une fonction, tracez son étirement vertical.

Identifiez la valeur de$a$.
Multiplier toutes les valeurs de plage par$a$
Si$a>1$, le graphique est étiré d'un facteur de$a$.
Si$0<a<1$, le graphique est compressé par un facteur de$a$.
Si$a<0$, le graphique est étiré ou compressé et est également reflété autour de l'axe X.

Exemple 1.5.14 : Représentation graphique d'un étirement vertical

Une fonction$P(t)$ modélise la population de mouches des fruits. Le graphique est illustré dans la figure$\PageIndex{24}$.

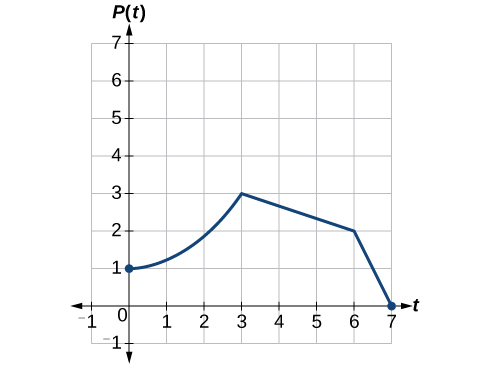
Figure$\PageIndex{24}$ : Graphique représentant la croissance de la population de mouches des fruits.

Un scientifique compare cette population à une autre population$Q$, dont la croissance suit le même schéma, mais qui est deux fois plus importante. Esquissez un graphique de cette population.

Solution

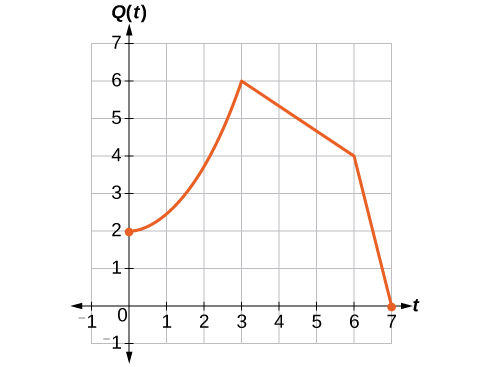
Comme la population est toujours deux fois plus grande, les valeurs en sortie de la nouvelle population sont toujours deux fois supérieures aux valeurs en sortie de la fonction d'origine. Cela est illustré graphiquement sur la figure$\PageIndex{25}$.

Si nous choisissons quatre points de référence$(0, 1)$$(3, 3)$,,$(6, 2)$ et$(7, 0)$ nous multiplierons toutes les sorties par 2.

Ce qui suit indique où seront situés les nouveaux points du nouveau graphique.

\[(0, 1)\rightarrow(0, 2)\]

\[(3, 3)\rightarrow(3, 6)\]

\[(6, 2)\rightarrow(6, 4)\]

\[(7, 0)\rightarrow(7, 0)\]

Le graphique de la fonction de population a été doublé. — Figure$\PageIndex{25}$ : Graphique de la fonction de population doublé.

Symboliquement, la relation s'écrit comme suit :

\[Q(t)=2P(t) \nonumber\]

Cela signifie que pour toute entrée$t$, la valeur de la fonction$Q$ est le double de la valeur de la fonction$P$. Notez que l'effet sur le graphique est un étirement vertical du graphique, où chaque point double sa distance par rapport à l'axe horizontal. Les valeurs en entrée$t$, restent les mêmes tandis que les valeurs en sortie sont deux fois plus grandes qu'auparavant.

Comment...

À partir d'une fonction tabulaire et en supposant que la transformation est un étirement ou une compression verticale, créez un tableau pour une compression verticale.

Déterminez la valeur de$a$.
Multipliez toutes les valeurs de sortie par$a$.

Exemple$\PageIndex{15}$: Finding a Vertical Compression of a Tabular Function

Une fonction$f$ est donnée sous la forme Table$\PageIndex{12}$. Créez un tableau pour la fonction$g(x)=\frac{1}{2}f(x)$.

Tableau$\PageIndex{12}$
$x$	2	4	6	8
$f(x)$	1	3	7	11

Solution

La formule nous$g(x)=\frac{1}{2}f(x)$ indique que les valeurs de sortie de$g$ sont la moitié des valeurs de sortie de$f$ avec les mêmes entrées. Par exemple, nous le savons$f(4)=3$. Alors

\[g(4)=\frac{1}{2}f(4)=\frac{1}{2}(3)=\frac{3}{2} \nonumber\]

Nous faisons de même pour les autres valeurs afin de produire une table$\PageIndex{13}$.

Tableau$\PageIndex{13}$
$x$	2	4	6	8
$g(x)$	$\dfrac{1}{2}$	$\dfrac{3}{2}$	$\dfrac{7}{2}$	$\dfrac{11}{2}$

Analyse

Il en résulte que la fonction$g(x)$ a été compressée verticalement par$\frac{1}{2}$. Chaque valeur de sortie est divisée en deux, de sorte que le graphique correspond à la moitié de la hauteur d'origine.

Exercice$\PageIndex{9}$

Une fonction$f$ est donnée sous la forme Table$\PageIndex{14}$. Créez un tableau pour la fonction$g(x)=\frac{3}{4}f(x)$.

Tableau$\PageIndex{14}$
$x$	2	4	6	8
$f(x)$	12	16	20	0

Réponse

Tableau$\PageIndex{15}$
$x$	2	4	6	8
$g(x)$	9	12	15	0

Exemple$\PageIndex{16}$: Recognizing a Vertical Stretch

Le graphique de la figure$\PageIndex{26}$ est une transformation de la fonction de la boîte à outils$f(x)=x^3$. Associez cette nouvelle fonction$g(x)$ à$f(x)$, puis trouvez une formule pour$g(x)$.

[Graphique d'une transformation de <span translate= — Figure$\PageIndex{26}$ : Graphique d'une transformation de$f(x)=x^3$

Lorsque vous essayez de déterminer un étirement ou un décalage vertical, il est utile de rechercher un point relativement clair sur le graphique. Sur ce graphique, il apparaît que$g(2)=2$. Avec la fonction cubique de base sur la même entrée,$f(2)=2^3=8$. Sur cette base, il apparaît que les sorties de$g$ sont$\frac{1}{4}$ les sorties de la fonction$f$ car$g(2)=\frac{1}{4}f(2)$. De cela, nous pouvons en conclure de manière assez sûre$g(x)=\frac{1}{4}f(x)$.

Nous pouvons écrire une formule pour$g$ en utilisant la définition de la fonction$f$.

\[g(x)=\frac{1}{4} f(x)=\frac{1}{4}x^3.\]

Exercice$\PageIndex{1}$

Écrivez la formule de la fonction que nous obtenons lorsque nous étendons la fonction de la boîte à outils d'identité d'un facteur 3, puis que nous la décalons de 2 unités vers le bas.

Réponse: $g(x)=3x-2$

Étirements et compressions horizontaux

Nous examinons maintenant les modifications apportées à l'intérieur d'une fonction. Lorsque nous multiplions l'entrée d'une fonction par une constante positive, nous obtenons une fonction dont le graphe est étiré ou compressé horizontalement par rapport au graphe de la fonction d'origine. Si la constante est comprise entre 0 et 1, on obtient un étirement horizontal ; si la constante est supérieure à 1, on obtient une compression horizontale de la fonction.

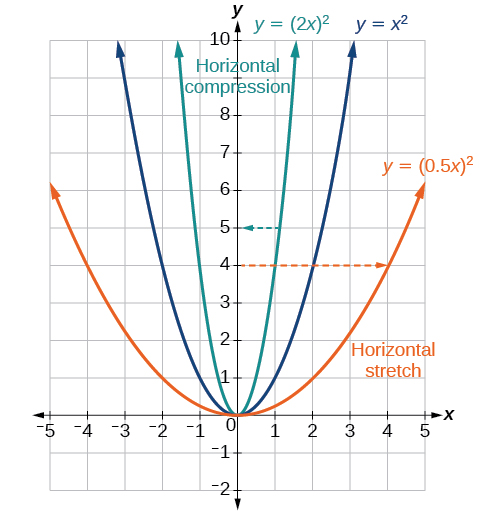
Graphique de l'étirement vertical et de la compression de x^2. — Figure$\PageIndex{27}$ : Graphique de l'étirement vertical et de la compression de$x^2$.

En fonction d'une fonction$y=f(x)$, la forme$y=f(bx)$ entraîne un étirement ou une compression horizontale. Réfléchissez à la fonction$y=x^2$. Observez la figure$\PageIndex{27}$. Le graphe de$y=(0.5x)^2$ est un étirement horizontal du graphe de la fonction$y=x^2$ par un facteur 2. Le graphe de$y=(2x)^2$ est une compression horizontale du graphe de la fonction$y=x^2$ par un facteur 2.

Définitions : étirements et compressions horizontaux

Étant donné une fonction$f(x)$, une nouvelle fonction$g(x)=f(bx)$, où$b$ est une constante, est un étirement horizontal ou une compression horizontale de la fonction$f(x)$.

Si$b>1$, alors le graphique sera compressé par$\frac{1}{b}$.
Si$0<b<1$, alors le graphique sera étiré de$\frac{1}{b}$.
Si tel est le cas$b<0$, il y aura une combinaison d'un étirement horizontal ou d'une compression avec une réflexion horizontale.

Comment...

À partir de la description d'une fonction, esquissez une compression ou un étirement horizontal.

Écrivez une formule pour représenter la fonction.
Définissez l'$g(x)=f(bx)$endroit où$b>1$ vous souhaitez effectuer une compression ou$0<b<1$ un étirement.

Exemple$\PageIndex{17}$: Graphing a Horizontal Compression

Supposons qu'un scientifique compare une population de mouches des fruits à une population dont la durée de vie progresse deux fois plus vite que la population d'origine. En d'autres termes, cette nouvelle population progressera en 1 heure de la même manière que la population d'origine en 2 heures, et en 2 heures, elle progressera autant que la population d'origine en 4 heures.$R$ Esquissez un graphique de cette population.

Solution

Symboliquement, nous pourrions écrire

$\begin{align} R(1)&=P(2), \\ R(2)&=P(4), &\text{and in general,} \\ R(t)&=P(2t).\end{align}$

Voir la figure$\PageIndex{28}$ pour une comparaison graphique de la population d'origine et de la population compressée.

Deux graphiques côte à côte. Le premier graphique a une fonction pour la population d'origine dont le domaine est [0,7] et l'intervalle est [0,3]. La valeur maximale se trouve à (3,3). Le deuxième graphique a la même forme que le premier, sauf qu'il est deux fois moins large. Il s'agit d'un graphique de la population transformée, avec un domaine de [0, 3,5] et une fourchette de [0,3]. Le maximum se produit à (1,5, 3). — Figure$\PageIndex{28}$ : (a) Graphique de population original (b) Graphique de population compressé

Analyse

Notez que l'effet sur le graphique est une compression horizontale dans laquelle toutes les valeurs en entrée sont égales à la moitié de leur distance initiale par rapport à l'axe vertical.

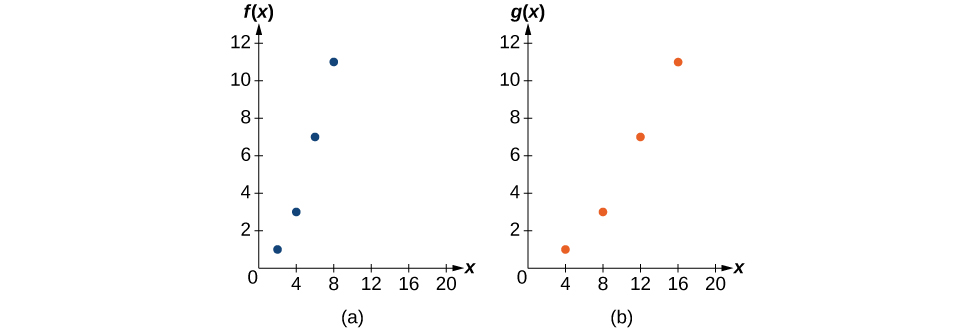
Exemple$\PageIndex{18}$: Finding a Horizontal Stretch for a Tabular Function

Une fonction$f(x)$ est donnée sous la forme Table$\PageIndex{16}$. Créez un tableau pour la fonction$g(x)=f(\frac{1}{2}x)$.

Tableau$\PageIndex{16}$
$x$	2	4	6	8
$f(x)$	1	3	7	11

La formule nous$g(x)=f(\frac{1}{2}x)$ indique que les valeurs de sortie pour$g$ sont identiques aux valeurs de sortie de la fonction sur une entrée dont la taille est égale$f$ à la moitié. Notez que nous ne disposons pas de suffisamment d'informations pour déterminer$g(2)$ car$g(2)=f(\frac{1}{2}⋅2)=f(1)$, et nous n'avons pas de valeur pour$f(1)$ dans notre tableau. Nos valeurs d'entrée$g$ devront être deux fois plus grandes pour obtenir des entrées$f$ que nous puissions évaluer. Par exemple, nous pouvons déterminer$g(4)$.

\[g(4)=f(\dfrac{1}{2}⋅4)=f(2)=1\]

Nous faisons de même pour les autres valeurs afin de produire une table$\PageIndex{17}$.

Tableau$\PageIndex{17}$
$x$	4	8	12	16
$g(x)$	1	3	7	11

La figure$\PageIndex{29}$ montre les graphes de ces deux ensembles de points.

Figure$\PageIndex{29}$ : Graphique du tableau précédent.

Analyse

Comme chaque valeur d'entrée a été doublée, la fonction$g(x)$ a été étirée horizontalement d'un facteur 2.

Exemple$\PageIndex{19}$: Recognizing a Horizontal Compression on a Graph

Reliez la fonction$g(x)$ à celle$f(x)$ de la figure$\PageIndex{30}$.

Solution

Le graphique de$g(x)$ ressemble au graphique de compressé$f(x)$ horizontalement. Comme$f(x)$ se termine à (6,4) et$g(x)$ se termine à (2,4), nous pouvons voir que les valeurs x ont été compressées par$\frac{1}{3}$, car$6(\frac{1}{3})=2$. Nous pouvons également remarquer que$g(2)=f(6)$ et$g(1)=f(3)$. Quoi qu'il en soit, nous pouvons décrire cette relation comme$g(x)=f(3x)$. Il s'agit d'une compression horizontale par$\frac{1}{3}$.

Analyse

Notez que le coefficient requis pour un étirement ou une compression horizontale est l'inverse de l'étirement ou de la compression. Donc, pour étirer le graphique horizontalement d'un facteur d'échelle de 4, nous avons besoin d'un coefficient de$\frac{1}{4}$ dans notre fonction :$f(\frac{1}{4}x)$. Cela signifie que les valeurs d'entrée doivent être quatre fois plus grandes pour produire le même résultat, ce qui nécessite que l'entrée soit plus grande, ce qui provoque l'étirement horizontal.

Exercice$\PageIndex{11}$

Écrivez une formule pour la fonction de racine carrée de la boîte à outils, étirée horizontalement d'un facteur 3.

Réponse: $g(x)=f(\frac{1}{3}x)$, donc en utilisant la fonction de racine carrée, nous obtenons$g(x)=\sqrt{\frac{1}{3}x}$

Exécution d'une séquence de transformations

Lorsque vous combinez des transformations, il est très important de prendre en compte l'ordre des transformations. Par exemple, le décalage vertical de 3 puis l'étirement vertical de 2 ne créent pas le même graphique que l'étirement vertical de 2 puis le décalage vertical de 3, car lorsque nous décalons en premier, la fonction d'origine et le décalage s'étirent, alors que seule la fonction d'origine est étirée lorsque nous étirez-vous d'abord.

Lorsque nous voyons une expression telle que$2f(x)+3$, par quelle transformation devons-nous commencer ? La réponse ici découle bien de l'ordre des opérations. Étant donné la valeur de sortie de$f(x)$, nous multiplions d'abord par 2, ce qui provoque l'étirement vertical, puis nous ajoutons 3, provoquant le décalage vertical. En d'autres termes, multiplication avant addition.

Les transformations horizontales sont un peu plus délicates à envisager. Lorsque nous écrivons$g(x)=f(2x+3)$, par exemple, nous devons réfléchir à la manière dont les entrées de la fonction$g$ sont liées aux entrées de la fonction$f$. Supposons qu'on le sache$f(7)=12$. Quelle entrée$g$ produirait cette sortie ? En d'autres termes, de quelle valeur de$x$ volonté nous le permettrait$g(x)=f(2x+3)=12?$ Nous aurions besoin$2x+3=7$. Pour résoudre ce problème$x$, nous devons d'abord soustraire 3, ce qui entraîne un décalage horizontal, puis le diviser par 2, ce qui provoque une compression horizontale.

Ce format s'avère très difficile à utiliser, car il est généralement beaucoup plus facile d'étirer un graphique horizontalement avant de le déplacer. Nous pouvons contourner ce problème en prenant en compte la fonction.

\[f(bx+p)=f(b(x+\frac{p}{b})) \nonumber\]

Examinons un exemple.

\[f(x)=(2x+4)^2 \nonumber\]

Nous pouvons prendre en compte un 2.

\[f(x)=(2(x+2))^2 \nonumber\]

Nous pouvons maintenant observer plus clairement un décalage horizontal vers la gauche de 2 unités et une compression horizontale. La prise en compte de cette manière nous permet de nous étirer d'abord horizontalement, puis de nous déplacer horizontalement.

Combiner des transformations

Lorsque vous combinez des transformations verticales écrites dans le formulaire$af(x)+k$, commencez par les étirer verticalement,$a$ puis déplacez-les verticalement$k$.
Lorsque vous combinez des transformations horizontales écrites dans le formulaire$f(bx+h)$, commencez par décaler horizontalement,$h$ puis étirez horizontalement$\frac{1}{b}$.
Lorsque vous combinez des transformations horizontales écrites dans le formulaire$f(b(x+h))$, commencez par les étirer horizontalement,$\frac{1}{b}$ puis déplacez-les horizontalement$h$.
Les transformations horizontales et verticales sont indépendantes. Peu importe que les transformations horizontales ou verticales soient effectuées en premier.

Exemple$\PageIndex{20}$: Finding a Triple Transformation of a Tabular Function

Dans la table spécifiée$\PageIndex{18}$ pour la fonction$f(x)$, créez une table de valeurs pour la fonction$g(x)=2f(3x)+1$.

Tableau$\PageIndex{18}$
$x$	6	12	18	24
$f(x)$	10	14	15	17

Solution

Cette transformation comporte trois étapes, et nous travaillerons de l'intérieur vers l'extérieur. En commençant par les transformations horizontales,$f(3x)$ on obtient une compression horizontale par$\frac{1}{3}$, ce qui signifie que nous multiplions chaque$x$ valeur par$\frac{1}{3}$ .Voir le tableau$\PageIndex{19}$.

Tableau$\PageIndex{19}$
$x$	2	4	6	8
$f(3x)$	10	14	15	17

En ce qui concerne les transformations verticales, nous commençons par l'étirement vertical, qui multipliera les valeurs de sortie par 2. Nous appliquons cela à la transformation précédente. Voir le tableau$\PageIndex{20}$.

Tableau$\PageIndex{20}$
$x$	2	4	6	8
$2f(3x)$	20	28	30	34

Enfin, nous pouvons appliquer le décalage vertical, qui ajoutera 1 à toutes les valeurs de sortie. Voir le tableau$\PageIndex{21}$.

Tableau$\PageIndex{21}$
$x$	2	4	6	8
$g(x)=2f(3x)+1+1$	21	29	31	35

Exemple$\PageIndex{21}$: Finding a Triple Transformation of a Graph

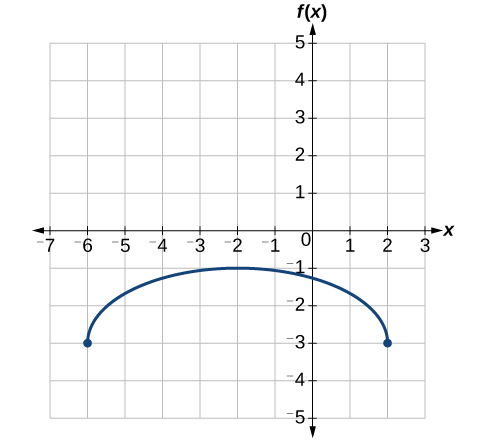
Utilisez le graphique de$f(x)$ la figure$\PageIndex{31}$ pour esquisser un graphique de$k(x)=f\Big(\frac{1}{2}x+1\Big)−3$.

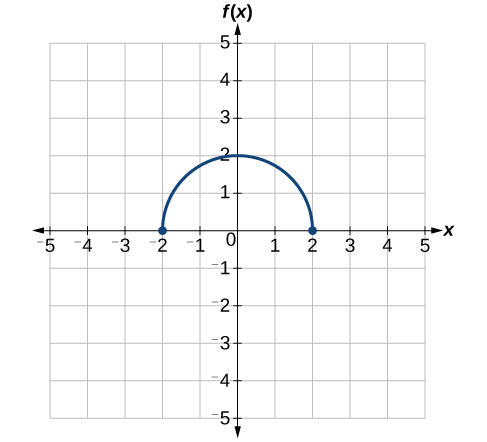
Graphe d'un demi-cercle. — Figure$\PageIndex{31}$ : Diagramme d'un demi-cercle.

Pour simplifier, commençons par factoriser l'intérieur de la fonction.

\[f\Big(\dfrac{1}{2}x+1\Big)−3=f\Big(\dfrac{1}{2}(x+2)\Big)−3\]

En factorisant l'intérieur, nous pouvons d'abord nous étirer horizontalement de 2, comme indiqué par l'$\frac{1}{2}$élément situé à l'intérieur de la fonction. N'oubliez pas que deux fois la taille de 0 est toujours égale à 0, donc le point$(0,2)$ reste à zéro tant$(0,2)$ que le point$(2,0)$ s'étire jusqu'à$(4,0)$. Voir la figure$\PageIndex{32}$.

alt — Figure$\PageIndex{32}$ : Diagramme d'un demi-cercle étiré verticalement.

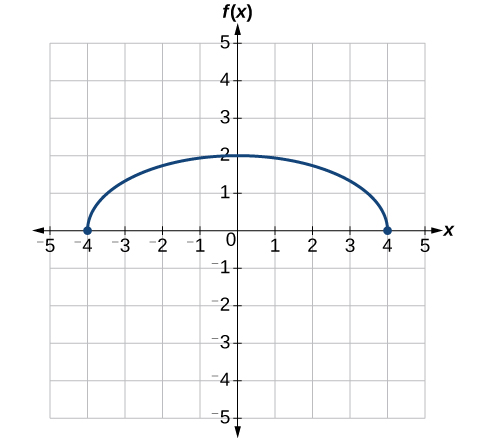
Ensuite, nous décalons horizontalement vers la gauche de 2 unités, comme indiqué par$x+2$. Voir la figure$\PageIndex{33}$.

alt — Figure$\PageIndex{33}$ : Diagramme d'un demi-cercle étiré verticalement et traduit.

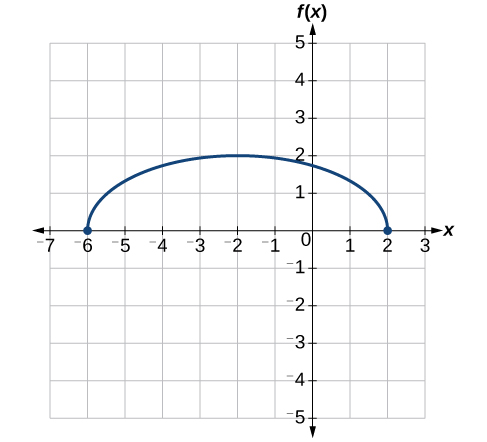
Enfin, nous décalons verticalement de 3 vers le bas pour terminer notre esquisse, comme indiqué par le −3 à l'extérieur de la fonction. Voir la figure$\PageIndex{34}$.

alt — Figure$\PageIndex{34}$ : Diagramme d'un demi-cercle étiré verticalement et traduit.

Équations clés

Déplacement vertical$g(x)=f(x)+k$ (vers le haut$k>0$)
Déplacement horizontal$g(x)=f(x−h)$ (droite) pour$h>0$
Réflexion verticale$g(x)=−f(x)$
Réflexion horizontale$g(x)=f(−x)$
Étirement vertical$g(x)=af(x)$ (a>0)
Compression verticale$g(x)=af(x)$ (0<a<1)
Étirement horizontal$g(x)=f(bx)(0<b<1)$
Compression horizontale$g(x)=f(bx)$ (b>1)

Concepts clés

Une fonction peut être déplacée verticalement en ajoutant une constante à la sortie.
Une fonction peut être déplacée horizontalement en ajoutant une constante à l'entrée.
Relier le décalage au contexte d'un problème permet de comparer et d'interpréter les décalages verticaux et horizontaux.
Les décalages verticaux et horizontaux sont souvent combinés.
Une réflexion verticale reflète un graphique autour de l'axe X. Un graphique peut être reflété verticalement en multipliant la sortie par —1.
Une réflexion horizontale reflète un graphique autour de l'axe Y. Un graphique peut être reflété horizontalement en multipliant l'entrée par —1.
Un graphique peut être reflété à la fois verticalement et horizontalement. L'ordre dans lequel les réflexions sont appliquées n'affecte pas le graphique final.
Une fonction présentée sous forme de tableau peut également être reflétée en multipliant les valeurs dans les lignes ou les colonnes d'entrée et de sortie en conséquence.
Une fonction présentée sous forme d'équation peut être reflétée en appliquant les transformations une par une.
Les fonctions paires sont symétriques par rapport à l'axe Y, tandis que les fonctions impaires sont symétriques par rapport à l'origine.
Même les fonctions répondent à cette condition$f(x)=f(−x)$.
Des fonctions impaires satisfont à la condition$f(x)=−f(−x)$.
Une fonction peut être impaire, paire ou aucune des deux.
Une fonction peut être compressée ou étirée verticalement en multipliant la sortie par une constante.
Une fonction peut être compressée ou étirée horizontalement en multipliant l'entrée par une constante.
L'ordre dans lequel les différentes transformations sont appliquées affecte la fonction finale. Les transformations verticales et horizontales doivent être appliquées dans l'ordre indiqué. Cependant, une transformation verticale peut être combinée à une transformation horizontale dans n'importe quel ordre.

Lexique

fonction uniforme

fonction dont le graphe est inchangé par réflexion horizontale et est symétrique par rapport à l'axe y$f(x)=f(−x)$

compression
horizontale : transformation qui comprime le graphe d'une fonction horizontalement, en multipliant l'entrée par une constante b>1

réflexion
horizontale : transformation qui reflète le graphe d'une fonction sur l'axe y en multipliant l'entrée par −1

décalage
horizontal : transformation qui déplace le graphe d'une fonction vers la gauche ou la droite en ajoutant une constante positive ou négative à l'entrée

étirement
horizontal : transformation qui étire le graphe d'une fonction horizontalement en multipliant l'entrée par une constante 0<b<1

fonction impaire : fonction dont le graphe est inchangé par
une réflexion horizontale et verticale combinée$f(x)=−f(−x)$, et qui est symétrique par rapport à l'origine

compression
verticale : transformation de fonction qui comprime le graphe de la fonction verticalement en multipliant la sortie par une constante 0<a<1

réflexion
verticale : transformation qui reflète le graphe d'une fonction sur l'axe X en multipliant la sortie par −1

décalage
vertical : transformation qui déplace le graphe d'une fonction vers le haut ou vers le bas en ajoutant une constante positive ou négative à la sortie

étirement
vertical : transformation qui étire verticalement le graphe d'une fonction en multipliant la sortie par une constante a>1

\(x\)	2	4	6	8
\(f(x)\)	1	3	7	11
\(g(x)\)	-2	0	4	8

\(x\)	5	7	9	11
\(x-3\)	2	4	6	8
\(f(x)\)	1	3	7	11
\(g(x)\)	1	3	7	11

\(x\)	2	4	6	8
\(g(x)\)	\(\dfrac{1}{2}\)	\(\dfrac{3}{2}\)	\(\dfrac{7}{2}\)	\(\dfrac{11}{2}\)

Tableau\(\PageIndex{8}\)
\(x\)	-2	-4	-6	-8
\(h(x)\)	1	3	7	11

Tableau\(\PageIndex{11}\)
\(x\)	-2	0	2	-4
\(h(x)\)	15	10	5	20

Tableau\(\PageIndex{19}\)
\(x\)	2	4	6	8
\(f(3x)\)	10	14	15	17

Tableau\(\PageIndex{20}\)
\(x\)	2	4	6	8
\(2f(3x)\)	20	28	30	34