3.2 : Domaine et gamme

Objectifs d'apprentissage

• Détermine le domaine d'une fonction définie par une équation.
• Représentez graphiquement des fonctions définies par morceaux.

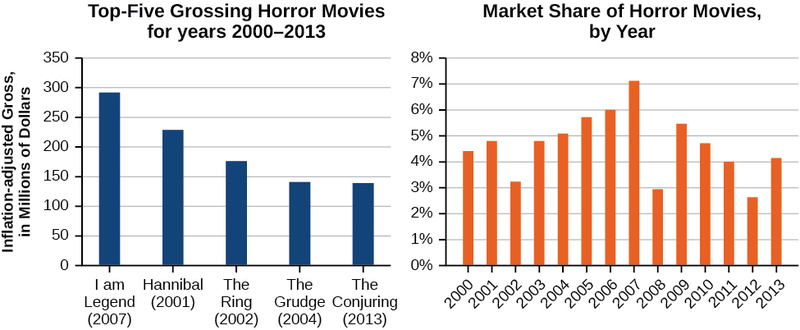
Si vous avez envie d'un film d'horreur, vous pouvez regarder l'un des cinq films d'horreur les plus populaires de tous les temps : I am Legend, Hannibal, The Ring, The Grudge et The Conjuring. La figure\(\PageIndex{1}\) montre le montant, en dollars, des recettes de chacun de ces films lors de leur sortie ainsi que les ventes de billets pour les films d'horreur en général par année. Notez que nous pouvons utiliser les données pour créer une fonction du montant gagné par chaque film ou du total des ventes de billets pour tous les films d'horreur par année. En créant diverses fonctions à l'aide des données, nous pouvons identifier différentes variables indépendantes et dépendantes, et nous pouvons analyser les données et les fonctions pour déterminer le domaine et la plage. Dans cette section, nous étudierons des méthodes permettant de déterminer le domaine et la gamme de telles fonctions.

Figure\(\PageIndex{1}\) : Graphique des cinq films d'horreur les plus rentables pour les années 2000 à 2003 et graphique de la part de marché des films d'horreur par année. Sur la base de données compilées par www.the-numbers.com.

Trouver le domaine d'une fonction définie par une équation

Dans Fonctions et notation des fonctions, nous avons été initiés aux concepts de domaine et de plage. Dans cette section, nous nous entraînerons à déterminer des domaines et des plages pour des fonctions spécifiques. N'oubliez pas que, pour déterminer les domaines et les plages, nous devons prendre en compte ce qui est physiquement possible ou significatif dans des exemples concrets, tels que la vente de billets et l'année dans l'exemple de film d'horreur ci-dessus. Nous devons également considérer ce qui est mathématiquement autorisé. Par exemple, nous ne pouvons inclure aucune valeur d'entrée qui nous amène à prendre la racine paire d'un nombre négatif si le domaine et la plage sont constitués de nombres réels. Ou dans une fonction exprimée sous forme de formule, nous ne pouvons inclure aucune valeur d'entrée dans le domaine qui nous conduirait à diviser par 0.

Nous pouvons visualiser le domaine comme une « zone de stockage » contenant des « matières premières » pour une « machine fonctionnelle » et la gamme comme une autre « zone de stockage » pour les produits de la machine (Figure\(\PageIndex{2}\)).

Figure\(\PageIndex{2}\) : Schéma de la façon dont une fonction relie deux relations

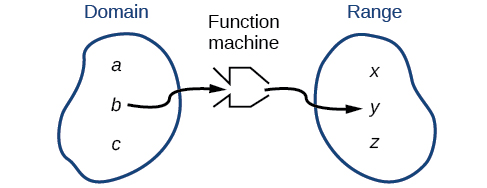
Nous pouvons écrire le domaine et la plage en notation par intervalles, qui utilise des valeurs entre parenthèses pour décrire un ensemble de nombres. Dans la notation par intervalles, nous utilisons un crochet [lorsque l'ensemble inclut le point final] et une parenthèse () pour indiquer que le point de terminaison n'est pas inclus ou que l'intervalle est illimité. Par exemple, si une personne a 100$ à dépenser, elle devra exprimer l'intervalle supérieur à 0 et inférieur ou égal à 100 et écrire\(\left(0, 100\right]\). Nous aborderons la notation par intervalles plus en détail ultérieurement.

Passons maintenant à la recherche du domaine d'une fonction dont l'équation est fournie. Souvent, pour trouver le domaine de telles fonctions, il faut se souvenir de trois formes différentes. Tout d'abord, si la fonction n'a pas de dénominateur ou de racine paire, demandez-vous si le domaine peut être composé uniquement de nombres réels. Ensuite, s'il existe un dénominateur dans l'équation de la fonction, excluez les valeurs du domaine qui obligent le dénominateur à être nul. Troisièmement, s'il existe une racine paire, pensez à exclure les valeurs qui rendraient le radical et négatif.

Avant de commencer, passons en revue les conventions de notation par intervalles :

• Le plus petit terme de l'intervalle est écrit en premier.
• Le terme le plus long de l'intervalle s'écrit en second, après une virgule.
• Les parenthèses,\((\) ou\()\), sont utilisées pour indiquer qu'un point final n'est pas inclus, ce que l'on appelle exclusif.
• Les crochets,\([\) ou\(]\), sont utilisés pour indiquer qu'un point de terminaison est inclus, appelé inclusif.

Voir la figure\(\PageIndex{3}\) pour un résumé de la notation par intervalles.

Figure\(\PageIndex{3}\) : Résumé de la notation par intervalles.

Exemple\(\PageIndex{1}\): Finding the Domain of a Function as a Set of Ordered Pairs

Trouvez le domaine de la fonction suivante :\(\{(2, 10),(3, 10),(4, 20),(5, 30),(6, 40)\}\).

Solution

Identifiez d'abord les valeurs d'entrée. La valeur d'entrée est la première coordonnée d'une paire ordonnée. Il n'y a aucune restriction, car les paires commandées sont simplement répertoriées. Le domaine est l'ensemble des premières coordonnées des paires ordonnées.

\[\{2,3,4,5,6\} \nonumber\]

Exercice\(\PageIndex{1}\)

Trouvez le domaine de la fonction :

\[\{(−5,4),(0,0),(5,−4),(10,−8),(15,−12)\} \nonumber\]

Réponse

\(\{−5, 0, 5, 10, 15\}\)

Procédure : à partir d'une fonction écrite sous forme d'équation, trouvez le domaine.

1. Identifiez les valeurs d'entrée.
2. Identifiez toutes les restrictions sur l'entrée et excluez ces valeurs du domaine.
3. Écrivez le domaine sous forme d'intervalles, si possible.

Exemple\(\PageIndex{2}\): Finding the Domain of a Function

Trouvez le domaine de la fonction\(f(x)=x^2−1\).

Solution

La valeur d'entrée, indiquée par la variable x dans l'équation, est mise au carré, puis le résultat est abaissé d'une unité. Tout nombre réel peut être mis au carré puis abaissé d'un, de sorte qu'il n'y a aucune restriction quant au domaine de cette fonction. Le domaine est l'ensemble des nombres réels.

Sous forme d'intervalle, le domaine de f est\((−\infty,\infty)\).

Exercice\(\PageIndex{2}\)

Trouvez le domaine de la fonction :

\[f(x)=5−x+x^3 \nonumber\]

Réponse

\((−\infty,\infty)\)

Comment : à partir d'une fonction écrite sous forme d'équation qui inclut une fraction, trouvez le domaine

1. Identifiez les valeurs d'entrée.
2. Identifiez toutes les restrictions relatives à l'entrée. S'il existe un dénominateur dans la formule de la fonction, définissez-le à zéro et résolvez pour x. Si la formule de la fonction contient une racine paire, définissez un radical supérieur ou égal à 0, puis résolvez.
3. Écrivez le domaine sous forme d'intervalles, en veillant à exclure toutes les valeurs restreintes du domaine.

Exemple\(\PageIndex{3}\): Finding the Domain of a Function Involving a Denominator

Trouvez le domaine de la fonction\(f(x)=\dfrac{x+1}{2−x}\).

Solution

Lorsqu'il existe un dénominateur, nous voulons inclure uniquement les valeurs de l'entrée qui ne forcent pas le dénominateur à être nul. Nous allons donc définir le dénominateur égal à 0 et résoudre pour x.

\[ \begin{align*} 2−x=0 \\[4pt] −x &=−2 \\[4pt] x&=2 \end{align*}\]

Maintenant, nous allons exclure 2 du domaine. Les réponses sont toutes des nombres réels où\(x<2\) ou\(x>2\). Nous pouvons utiliser un symbole appelé union\(\cup\), pour combiner les deux ensembles. En notation par intervalles, nous écrivons la solution :\((−\infty,2)∪(2,\infty)\).

Sous forme d'intervalle, le domaine de f est\((−\infty,2)\cup(2,\infty)\).

Exercice\(\PageIndex{3}\)

Trouvez le domaine de la fonction :

\[f(x)=\dfrac{1+4x}{2x−1} \nonumber\]

Réponse

\[(−\infty,\dfrac{1}{2})\cup(\dfrac{1}{2},\infty) \nonumber\]

Mode d'emploi : À partir d'une fonction écrite sous forme d'équation incluant une racine paire, trouvez le domaine.

1. Identifiez les valeurs d'entrée.
2. Comme il existe une racine paire, excluez tous les nombres réels qui se traduisent par un nombre négatif dans le radicand. Définissez le radical et supérieur ou égal à zéro et résolvez pour x.
3. La ou les solutions sont le domaine de la fonction. Si possible, écrivez la réponse sous forme d'intervalles.

Exemple\(\PageIndex{4}\): Finding the Domain of a Function with an Even Root

Trouvez le domaine de la fonction :

\[f(x)=\sqrt{7-x} \nonumber .\]

Solution

Lorsqu'il y a une racine paire dans la formule, nous excluons tous les nombres réels qui se traduisent par un nombre négatif dans le radicand.

Définissez le radical et supérieur ou égal à zéro et résolvez pour x.

\[ \begin{align*} 7−x&≥0 \\[4pt] −x&≥−7\\[4pt] x&≤7 \end{align*}\]

Maintenant, nous allons exclure tout nombre supérieur à 7 du domaine. Les réponses sont toutes des nombres réels inférieurs ou égaux à 7, ou\(\left(−\infty,7\right]\).

Exercice\(\PageIndex{4}\)

Trouvez le domaine de la fonction

\[f(x)=\sqrt{5+2x}. \nonumber\]

Réponse

\[\left[−2.5,\infty\right) \nonumber\]

Q&R : Peut-il y avoir des fonctions dans lesquelles le domaine et la plage ne se croisent pas du tout ?

Oui. Par exemple, la fonction\(f(x)=-\dfrac{1}{\sqrt{x}}\) possède l'ensemble de tous les nombres réels positifs comme domaine, mais l'ensemble de tous les nombres réels négatifs comme plage. À titre d'exemple plus extrême, les entrées et les sorties d'une fonction peuvent appartenir à des catégories complètement différentes (par exemple, les noms des jours de la semaine comme entrées et les nombres comme sorties, comme sur un graphique de présence). Dans de tels cas, le domaine et la plage n'ont aucun élément en commun.

Utiliser des notations pour spécifier le domaine et la plage

Dans les exemples précédents, nous avons utilisé des inégalités et des listes pour décrire le domaine des fonctions. Nous pouvons également utiliser des inégalités, ou d'autres instructions susceptibles de définir des ensembles de valeurs ou de données, pour décrire le comportement de la variable en notation setbuilder. Par exemple,\(\{x|10≤x<30\}\) décrit le comportement de x dans la notation set-builder. \(\{\}\)Les accolades sont lues comme « l'ensemble de » et la barre\(|\) verticale comme « telle que ». Nous\( \{x|10≤x<30\}\) lirons donc « l'ensemble de valeurs x tel que 10 est inférieur ou égal à x, et x est inférieur à 30 ».

La figure\(\PageIndex{4}\) compare la notation des inégalités, la notation setbuilder et la notation par intervalles.

Figure\(\PageIndex{4}\) : Résumé des notations pour les inégalités, le générateur de sets et l'intervalle.

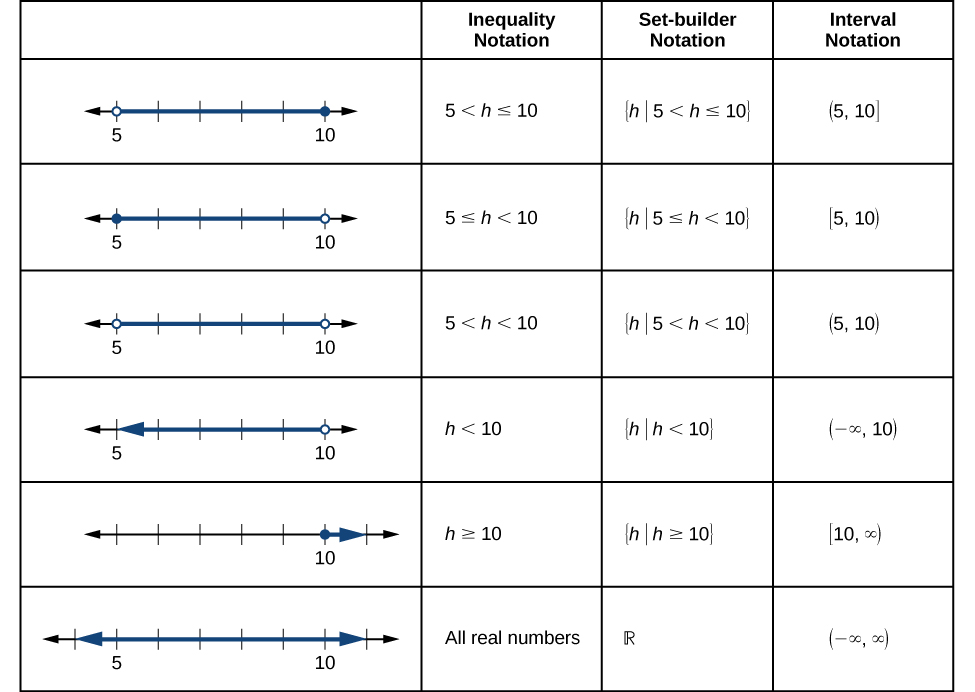
Pour combiner deux intervalles à l'aide de la notation d'inégalité ou de la notation Set-Builder, nous utilisons le mot « ou ». Comme nous l'avons vu dans les exemples précédents, nous utilisons le symbole de l'union\(\cup\), pour combiner deux intervalles non connectés. Par exemple, l'union des ensembles\(\{2,3,5\}\) et\(\{4,6\}\) est l'ensemble\(\{2,3,4,5,6\}\). Il s'agit de l'ensemble de tous les éléments qui appartiennent à l'un ou à l'autre (ou aux deux) des deux ensembles d'origine. Pour les ensembles comportant un nombre fini d'éléments tels que ceux-ci, les éléments n'ont pas besoin d'être listés par ordre croissant de valeur numérique. Si les deux ensembles d'origine ont des éléments en commun, ces éléments ne doivent être listés qu'une seule fois dans l'ensemble d'union. Pour les ensembles de nombres réels sur des intervalles, un autre exemple d'union est

\[\{x| |x|≥3\}=\left(−\infty,−3\right]\cup\left[3,\infty\right)\]

Notation Set-Builder et notation par intervalles

La notation Set-Builder est une méthode qui permet de spécifier un ensemble d'éléments qui répondent à une certaine condition. Il prend la forme\(\{x|\text{ statement about x}\}\) suivante : « l'ensemble de tous les x tels que l'affirmation concernant x est vraie ». Par exemple,

\[\{x|4<x≤12\} \nonumber\]

La notation par intervalles est un moyen de décrire des ensembles qui incluent tous les nombres réels entre une limite inférieure qui peut être incluse ou non et une limite supérieure qui peut ou non être incluse. Les valeurs de point final sont répertoriées entre crochets ou parenthèses. Un crochet indique l'inclusion dans l'ensemble et une parenthèse indique l'exclusion de l'ensemble. Par exemple,

\[\left(4,12\right] \nonumber\]

À partir d'un graphique linéaire, décrivez l'ensemble de valeurs en utilisant la notation par intervalles.

1. Identifiez les intervalles à inclure dans l'ensemble en déterminant où la ligne lourde recouvre la ligne réelle.
2. À l'extrémité gauche de chaque intervalle, utilisez [avec chaque valeur finale à inclure dans l'ensemble (point plein) ou (pour chaque valeur finale exclue) (point ouvert).
3. À l'extrémité droite de chaque intervalle, utilisez] avec chaque valeur finale à inclure dans l'ensemble (point plein) ou) pour chaque valeur finale exclue (point ouvert).
4. Utilisez le symbole de l'union\(\cup\) pour combiner tous les intervalles en un seul ensemble.

Exemple\(\PageIndex{5}\): Describing Sets on the Real-Number Line

Décrivez les intervalles de valeurs illustrés dans la figure en\(\PageIndex{5}\) utilisant la notation d'inégalité, la notation setbuilder et la notation par intervalles.

\ (1<=x<=3 \) et\(5\)] « src= » https://math.libretexts.org/@api/dek..._01_02_004.jpg « fileid="867" />

Figure\(\PageIndex{5}\) : Diagramme linéaire de\(1≤x≤3 \text{ or }x>5\).

Solution

Pour décrire les valeurs\(x\), incluses dans les intervalles indiqués, nous dirions : «\(x\) est un nombre réel supérieur ou égal à 1 et inférieur ou égal à 3, ou un nombre réel supérieur à 5 ».

Inégalité

\[1≤x≤3 \text{ or }x>5 \nonumber\]

Notation Set-builder

\[\{x|1≤x≤3 \text{ or } x>5\}\nonumber\]

Notation par intervalles

\[[1,3]\cup(5,\infty)\nonumber\]

N'oubliez pas que, lors de l'écriture ou de la lecture de la notation par intervalles, l'utilisation d'un crochet signifie que la limite est incluse dans l'ensemble. L'utilisation d'une parenthèse signifie que la limite n'est pas incluse dans l'ensemble.

Exercice\(\PageIndex{5}\)

Figure donnée\(\PageIndex{6}\), spécifiez l'ensemble graphique dans

1. mots
2. notation Set-Builder
3. notation par intervalles

Figure\(\PageIndex{6}\) : graphique linéaire de\(-2{\leq}x\),\(-1{\leq}x<3\) .leq} x \),\(-1{\leq}x<3\).

Répondez à une

Des valeurs inférieures ou égales à -2, ou des valeurs supérieures ou égales à -1 et inférieures à 3 ;

Réponse b

\(\{x|x≤−2 or −1≤x<3\}\)

Réponse c

\(\left(−∞,−2\right]\cup\left[−1,3\right)\)

Trouver un domaine et une plage à partir de graphes

Un autre moyen d'identifier le domaine et la gamme de fonctions consiste à utiliser des graphiques. Comme le domaine fait référence à l'ensemble des valeurs d'entrée possibles, le domaine d'un graphe comprend toutes les valeurs d'entrée affichées sur l'axe des abscisses. La plage est l'ensemble des valeurs de sortie possibles, qui sont affichées sur l'axe Y. N'oubliez pas que si le graphique continue au-delà de la partie visible du graphique, le domaine et la plage peuvent être supérieurs aux valeurs visibles. Voir la figure\(\PageIndex{7}\).

Figure\(\PageIndex{7}\) : Diagramme d'un polynôme qui montre que l'axe X est le domaine et l'axe y est la plage

Nous pouvons observer que le graphe s'étend horizontalement de −5 vers la droite sans limite, donc le domaine est\(\left[−5,∞\right)\). L'étendue verticale du graphique correspond à toutes les valeurs de plage inférieures ou égales à 5, donc la plage est\(\left(−∞,5\right]\). Notez que le domaine et la plage sont toujours écrits à partir de valeurs plus petites ou plus grandes, ou de gauche à droite pour le domaine, et du bas du graphique vers le haut du graphique pour la plage.

Exemple\(\PageIndex{6A}\): Finding Domain and Range from a Graph

Déterminez le domaine et la plage de la fonction f dont le graphe est illustré à la Figure 1.2.8.

Figure\(\PageIndex{8}\) : Graphique d'une fonction à partir de (-3, 1].

Solution

Nous pouvons observer que l'étendue horizontale du graphe est de -3 pour 1, donc le domaine de f est\(\left(−3,1\right]\).

L'étendue verticale du graphique est comprise entre 0 et —4, donc la plage est\(\left[−4,0\right)\). Voir la figure\(\PageIndex{9}\).

Figure\(\PageIndex{9}\) : Le graphique de la fonction précédente montre le domaine et la plage

Exemple\(\PageIndex{6B}\): Finding Domain and Range from a Graph of Oil Production

Déterminez le domaine et la plage de la fonction f dont le graphe est illustré sur la figure\(\PageIndex{10}\).

Figure\(\PageIndex{10}\) : Graphique de la production de pétrole brut de l'Alaska où l'axe Y représente les milliers de barils par jour et l'axe -les années (crédit : modification des travaux de l'Energy Information Administration des États-Unis)

Solution

La quantité d'entrée le long de l'axe horizontal est « années », que nous représentons avec la variable t pour le temps. La quantité produite est de « milliers de barils de pétrole par jour », que nous représentons avec la variable b pour les barils. Le graphique peut continuer vers la gauche et la droite au-delà de ce qui est affiché, mais en fonction de la partie du graphique visible, nous pouvons déterminer le domaine\(1973≤t≤2008\) et la plage de manière approximative\(180≤b≤2010\).

En notation par intervalles, le domaine est\([1973, 2008]\) et la plage est d'environ\([180, 2010]\). Pour le domaine et la plage, nous approximons les valeurs les plus petites et les plus grandes car elles ne se situent pas exactement sur les lignes de la grille.

Exercice\(\PageIndex{6}\)

Sur la figure donnée\(\PageIndex{11}\), identifiez le domaine et la plage en utilisant la notation par intervalles.

Figure\(\PageIndex{11}\) : Graphique de l'augmentation de la population mondiale où l'axe des ordonnées représente des millions de personnes et l'axe des abscisses représente l'année.

Réponse

domaine =\([1950,2002]\)

gamme =\([47,000,000,89,000,000]\)

Le domaine et la plage d'une fonction peuvent-ils être identiques ?

Oui. Par exemple, le domaine et la plage de la fonction racine cubique constituent tous deux l'ensemble de tous les nombres réels.

Recherche de domaines et de plages de fonctions de la boîte à outils

Nous allons maintenant revenir à notre ensemble de fonctions de la boîte à outils pour déterminer le domaine et la portée de chacune d'elles.

Figure\(\PageIndex{12}\) : Fonction constante\(f(x)=c\).

Pour la fonction constante\( f(x)=c\), le domaine est composé de tous les nombres réels ; il n'y a aucune restriction quant à l'entrée. La seule valeur de sortie est la constante\(c\), de sorte que la plage est l'ensemble\(\{c\}\) qui contient cet élément unique. En notation par intervalles, cela s'écrit comme\([c,c]\) l'intervalle qui commence et se termine par\(c\).

Figure\(\PageIndex{13}\) : Fonction d'identité f (x) =x.

Pour la fonction d'identité\(f(x)=x\), il n'y a aucune restriction sur\(x\). Le domaine et la plage constituent l'ensemble de tous les nombres réels.

Figure\(\PageIndex{14}\) : Fonction absolue\(f(x)=|x|\).

Pour la fonction de valeur absolue\(f(x)=|x|\), il n'y a aucune restriction sur\(x\). Toutefois, étant donné que la valeur absolue est définie comme une distance par rapport à 0, la sortie ne peut être que supérieure ou égale à 0.

Figure\(\PageIndex{15}\) : Fonction quadratique\(f(x)=x^2\).

Pour la fonction quadratique\(f(x)=x^2\), le domaine est composé uniquement de nombres réels puisque l'étendue horizontale du graphique est la totalité de la ligne des nombres réels. Comme le graphique n'inclut aucune valeur négative pour la plage, celle-ci ne contient que des nombres réels non négatifs.

Figure\(\PageIndex{16}\) : Fonction cubique\(f(x)-x^3\).

Pour la fonction cubique\(f(x)=x^3\), le domaine est composé uniquement de nombres réels, car l'étendue horizontale du graphique est la totalité de la ligne des nombres réels. Il en va de même pour l'étendue verticale du graphique, de sorte que le domaine et la plage incluent tous les nombres réels.

Figure\(\PageIndex{17}\) : Fonction réciproque\(f(x)=\dfrac{1}{x}\).

Pour la fonction réciproque\(f(x)=\dfrac{1}{x}\), nous ne pouvons pas diviser par 0, nous devons donc exclure 0 du domaine. De plus, 1 divisé par une valeur quelconque ne peut jamais être égal à 0, de sorte que la plage n'inclura pas non plus 0. En notation setbuilder, nous pourrions également écrire\(\{x| x≠0\}\) l'ensemble de tous les nombres réels qui ne sont pas nuls.

Figure\(\PageIndex{18}\) : Fonction quadratique réciproque\(f(x)=\dfrac{1}{x^2}\)

Pour la fonction quadratique réciproque\(f(x)=\dfrac{1}{x^2}\), nous ne pouvons pas diviser par 0, nous devons donc exclure 0 du domaine. Il n'y a pas non plus de x qui peut donner une sortie de 0, donc 0 est également exclu de la plage. Notez que la sortie de cette fonction est toujours positive en raison du carré du dénominateur, de sorte que la plage ne comprend que des nombres positifs.

Figure\(\PageIndex{19}\) : fonction de racine carrée\(f(x)=\sqrt{(x)}\).

Pour la fonction de racine carrée\(f(x)=\sqrt{x}\), nous ne pouvons pas prendre la racine carrée d'un nombre réel négatif. Le domaine doit donc être égal ou supérieur à 0. La plage exclut également les nombres négatifs car la racine carrée d'un nombre positif\(x\) est définie comme étant positive, même si le carré du nombre négatif nous donne\(−\sqrt{x}\) également\(x\).

Figure\(\PageIndex{20}\) : fonction racine cubique\(f(x)=\sqrt[3]{x}\).

Pour la fonction racine cubique\(f(x)=\sqrt[3]{x}\), le domaine et la plage incluent tous les nombres réels. Notez qu'il n'y a aucun problème à prendre une racine cubique, ou toute racine entière impaire, d'un nombre négatif, et que le résultat obtenu est négatif (c'est une fonction impaire).

À partir de la formule d'une fonction, déterminez le domaine et la plage.

1. Excluez du domaine toutes les valeurs en entrée qui entraînent une division par zéro.
2. Excluez du domaine toutes les valeurs d'entrée qui ont des sorties numériques non réelles (ou non définies).
3. Utilisez les valeurs d'entrée valides pour déterminer la plage des valeurs de sortie.
4. Examinez le graphique des fonctions et les valeurs du tableau pour confirmer le comportement réel de la fonction.

Trouver le domaine et la plage à l'aide des fonctions du kit

Trouvez le domaine et la gamme de\(f(x)=2x^3−x\).

Solution

Il n'y a aucune restriction sur le domaine, car tout nombre réel peut être coupé en cubes puis soustrait du résultat.

Le domaine est\((−\infty,\infty)\) et la gamme l'est également\((−\infty,\infty)\).

Exemple\(\PageIndex{7B}\): Finding the Domain and Range

Trouvez le domaine et la gamme de\(f(x)=\frac{2}{x+1}\).

Solution

Nous ne pouvons pas évaluer la fonction à −1 car la division par zéro n'est pas définie. Le domaine est\((−\infty,−1)\cup(−1,\infty)\). Comme la fonction n'est jamais nulle, nous excluons 0 de la plage. La gamme est\((−\infty,0)\cup(0,\infty)\).

Exemple\(\PageIndex{7C}\): Finding the Domain and Range

Trouvez le domaine et la gamme de\(f(x)=2 \sqrt{x+4}\).

Solution

Nous ne pouvons pas prendre la racine carrée d'un nombre négatif, donc la valeur à l'intérieur du radical doit être non négative.

\(x+4≥0\)quand\(x≥−4\)

Le domaine de\(f(x)\) est\([−4,\infty)\).

On trouve ensuite la gamme. Nous le savons\(f(−4)=0\), et la valeur de la fonction augmente au fur et à\(x\) mesure sans limite supérieure. Nous concluons que la plage de f est\(\left[0,\infty\right)\).

Analyse

La figure\(\PageIndex{19}\) représente la fonction\(f\).

" src="https://math.libretexts.org/@api/dek..._01_02_020.jpg">

Figure\(\PageIndex{19}\) : Graphique d'une fonction de racine carrée à\((-4, 0)\).

Exercice\(\PageIndex{7}\)

Trouvez le domaine et la gamme de

\(f(x)=\sqrt{−2−x}\).

Réponse

domaine :\(\left(−\infty,-2\right]\)

gamme :\(\left[0,\infty\right)\)

Représentation graphique de fonctions définies par morceaux

Parfois, nous rencontrons une fonction qui nécessite plus d'une formule pour obtenir la sortie donnée. Par exemple, dans les fonctions de la boîte à outils, nous avons introduit la fonction de valeur absolue\(f(x)=|x|\). Avec un domaine de tous les nombres réels et une plage de valeurs supérieures ou égales à 0, la valeur absolue peut être définie comme l'amplitude, ou le module, d'une valeur numérique réelle quel que soit son signe. Il s'agit de la distance par rapport à 0 sur la ligne numérique. Toutes ces définitions nécessitent que la sortie soit supérieure ou égale à 0.

Si nous saisissons 0, ou une valeur positive, la sortie est la même que l'entrée.

\[ f(x)=x \; \text{ if } \; x≥0 \nonumber \]

Si nous saisissons une valeur négative, la sortie est l'opposé de l'entrée.

\[ f(x) = -x \; \text { if } \; x < 0 \nonumber \]

Comme cela nécessite deux processus ou éléments différents, la fonction de valeur absolue est un exemple de fonction par morceaux. Une fonction par morceaux est une fonction dans laquelle plusieurs formules sont utilisées pour définir la sortie sur différentes parties du domaine.

Nous utilisons des fonctions par morceaux pour décrire les situations dans lesquelles une règle ou une relation change lorsque la valeur d'entrée franchit certaines « limites ». Par exemple, nous sommes souvent confrontés à des situations commerciales dans lesquelles le coût par pièce d'un certain article est réduit une fois que le nombre commandé dépasse une certaine valeur. Les tranches d'imposition sont un autre exemple concret de fonctions fragmentaires. Prenons l'exemple d'un système fiscal simple dans lequel les revenus jusqu'à 10 000$ sont imposés à 10 % et tout revenu supplémentaire à 20 %. L'impôt sur un revenu total S serait\(0.1S\) si\(S≤$10,000\) et\($1000+0.2(S−$10,000)\) si\(S>$10,000\).

Fonction par morceaux

Une fonction par morceaux est une fonction dans laquelle plusieurs formules sont utilisées pour définir la sortie. Chaque formule possède son propre domaine, et le domaine de la fonction est l'union de tous ces domaines plus petits. Nous notons cette idée comme suit :

\[f(x)= \begin{cases} \text{formula 1} & \text{if x is in domain 1} \\ \text{formula 2} &\text{if x is in domain 2} \\ \text{formula 3} &\text{if x is in domain 3}\end{cases} \nonumber \]

En notation par morceaux, la fonction de valeur absolue est

\[|x|= \begin{cases} x & \text{if $x \geq 0$} \\ -x &\text{if $x<0$} \end{cases} \nonumber \]

À partir d'une fonction par morceaux, écrivez la formule et identifiez le domaine pour chaque intervalle.

1. Identifiez les intervalles auxquels les différentes règles s'appliquent.
2. Déterminez les formules qui décrivent comment calculer une sortie à partir d'une entrée dans chaque intervalle.
3. Utilisez des accolades et des instructions if pour écrire la fonction.

Exemple\(\PageIndex{8A}\): Writing a Piecewise Function

Un musée facture 5$ par personne pour une visite guidée avec un groupe de 1 à 9 personnes ou un tarif fixe de 50$ pour un groupe de 10 personnes ou plus. Écrivez une fonction reliant le nombre de personnes\(n\), au coût,\(C\).

Solution

Deux formules différentes seront nécessaires. Pour les\(n\) valeurs -inférieures à 10,\(C=5n\). Pour les valeurs de n supérieures ou égales à 10,\(C=50\).

\[C(n)= \begin{cases} 5n & \text{if $n < 10$} \\ 50 &\text{if $n\geq10$} \end{cases} \nonumber \]

Analyse

La fonction est représentée sur la figure\(\PageIndex{20}\). Le graphique est une ligne diagonale allant de\(n=0\) à\(n=10\) et suivie d'une constante. Dans cet exemple, les deux formules s'accordent au point de rencontre où\(n=10\), mais pas toutes les fonctions fragmentées, possèdent cette propriété.

Figurine\(\PageIndex{20}\)

Exemple\(\PageIndex{8B}\): Working with a Piecewise Function

Une entreprise de téléphonie mobile utilise la fonction ci-dessous pour déterminer le coût, C, en dollars pour g gigaoctets de transfert de données.

\[C(g)= \begin{cases} 25 & \text{if $0<g<2$} \\ 25+10(g-2) &\text{if $g\geq2$} \end{cases} \nonumber \]

Déterminez le coût d'utilisation de 1,5 gigaoctet de données et le coût d'utilisation de 4 gigaoctets de données.

Solution

Pour déterminer le coût d'utilisation de 1,5 gigaoctet de données\(C(1.5)\), nous cherchons d'abord à déterminer la partie du domaine dans laquelle se situent nos entrées. Comme 1,5 est inférieur à 2, nous utilisons la première formule.

\[C(1.5)=$25 \nonumber \]

Pour déterminer le coût d'utilisation de 4 gigaoctets de données, C (4), nous voyons que notre entrée de 4 est supérieure à 2. Nous utilisons donc la deuxième formule.

\[C(4)=25+10(4−2)=$45 \nonumber \]

Analyse

La fonction est représentée sur la figure\(\PageIndex{21}\). Nous pouvons voir où la fonction passe d'une identité constante à une identité décalée et étendue\(g=2\). Nous traçons les graphiques des différentes formules sur un ensemble d'axes communs, en nous assurant que chaque formule est appliquée sur son domaine approprié.

Figurine\(\PageIndex{21}\)

Si vous utilisez une fonction par morceaux, esquissez un graphique.

1. Indiquez sur l'axe X les limites définies par les intervalles sur chaque partie du domaine.
2. Pour chaque élément du domaine, tracez un graphique sur cet intervalle à l'aide de l'équation correspondante se rapportant à cette pièce. Ne tracez pas deux fonctions sur un intervalle, car cela violerait les critères d'une fonction.

Exemple\(\PageIndex{8C}\): Graphing a Piecewise Function

Esquissez un graphique de la fonction.

\[f(x)= \begin{cases} x^2 & \text{if $x \leq 1$} \\ 3 &\text{if $1<x\leq2$} \\ x &\text{if $x>2$} \end{cases} \nonumber \]

Solution

Chacune des fonctions des composants provient de notre bibliothèque de fonctions de la boîte à outils, ce qui nous permet de connaître leurs formes. Nous pouvons imaginer de représenter graphiquement chaque fonction, puis de limiter le graphe au domaine indiqué. Aux extrémités du domaine, nous dessinons des cercles ouverts pour indiquer où le point final n'est pas inclus en raison d'une inégalité inférieure ou supérieure à ; nous dessinons un cercle fermé où le point final est inclus en raison d'une inégalité inférieure ou égale ou supérieure ou égale à.

La figure\(\PageIndex{20}\) montre les trois composants de la fonction par morceaux représentés sur des systèmes de coordonnées distincts.

Figure\(\PageIndex{20}\) : Graphique de chaque partie de la fonction par morceaux f (x)

a)\( f(x)=x^2\) si\(x≤1\) ; b)\(f(x)=3\) si\(1< x≤2\) ; c)\(f(x)=x\) si\(x>2\)

Maintenant que nous avons esquissé chaque pièce individuellement, nous les combinons dans le même plan de coordonnées. Voir la figure\(\PageIndex{21}\).

Figure\(\PageIndex{21}\) : graphique de l'ensemble de la fonction.

Analyse

Notez que le graphique passe le test de la ligne verticale même à\(x=1\) et\(x=2\) parce que les points\((1,3)\) et ne\((2,2)\) font pas partie du graphe de la fonction, mais qu'\((1,1)\)ils le\((2, 3)\) sont.

Exercice\(\PageIndex{8}\)

Représentez graphiquement la fonction suivante par morceaux.

\[f(x)= \begin{cases} x^3 & \text{if $x < -1$} \\ -2 &\text{if $-1<x<4$} \\ \sqrt{x} &\text{if $x>4$} \end{cases} \nonumber \]

Réponse

Figurine\(\PageIndex{22}\)

Est-ce que plusieurs formules d'une fonction par morceaux peuvent être appliquées à une valeur du domaine ?

Non Chaque valeur correspond à une équation dans une formule par morceaux.

Concepts clés

• Le domaine d'une fonction inclut toutes les valeurs d'entrée réelles qui ne nous obligeraient pas à tenter une opération mathématique non définie, telle que la division par zéro ou la prise de la racine carrée d'un nombre négatif.
• Le domaine d'une fonction peut être déterminé en listant les valeurs d'entrée d'un ensemble de paires ordonnées.
• Le domaine d'une fonction peut également être déterminé en identifiant les valeurs d'entrée d'une fonction écrite sous forme d'équation.
• Les valeurs d'intervalle représentées sur une ligne numérique peuvent être décrites à l'aide de la notation d'inégalité, de la notation setbuilder et de la notation par intervalles.
• Pour de nombreuses fonctions, le domaine et la plage peuvent être déterminés à partir d'un graphique.
• Une compréhension des fonctions de la boîte à outils peut être utilisée pour trouver le domaine et la gamme de fonctions connexes.
• Une fonction par morceaux est décrite par plusieurs formules.
• Une fonction par morceaux peut être représentée graphiquement à l'aide de chaque formule algébrique du sous-domaine qui lui est attribué.

Notes

1 Les chiffres : là où les données et le secteur du cinéma se rencontrent. « Histoire du box office pour les films d'horreur ». http://www.the-numbers.com/market/genre/Horror. Consulté le 24 mars 2014
2 www.eia.gov/DNAV/PET/Hist/Lea... s=MCRFPak2&f=A.

Lexique

notation par intervalles

méthode de description d'un ensemble qui inclut tous les nombres compris entre une limite inférieure et une limite supérieure ; les valeurs inférieure et supérieure sont répertoriées entre crochets ou parenthèses, un crochet indiquant l'inclusion dans l'ensemble et une parenthèse indiquant l'exclusion

fonction par morceaux

une fonction dans laquelle plusieurs formules sont utilisées pour définir la sortie

notation Set-Builder

une méthode pour décrire un ensemble par une règle à laquelle tous ses membres obéissent ; elle prend la forme {x| statement about x}