2.4 : Nombres complexes

Last updated
Save as PDF

Page ID: 195226

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

Additionnez et soustrayez des nombres complexes.
Multipliez et divisez des nombres complexes.
Résoudre des équations quadratiques avec des nombres complexes

Découvert par Benoit Mandelbrot vers 1980, l'ensemble Mandelbrot est l'une des images fractales les plus reconnaissables. L'image est construite sur la théorie de l'auto-similitude et sur le fonctionnement de l'itération. Zoomer sur une image fractale réserve de nombreuses surprises, notamment en raison du niveau élevé de répétition des détails qui apparaît lorsque le grossissement augmente. L'équation qui génère cette image s'avère assez simple.

Une représentation visuelle de l'ensemble de Mandelbrot — Figure$\PageIndex{1}$ : L'ensemble de Mandelbrot présente des similitudes, ce qui est mieux illustré dans une animation.

Pour mieux le comprendre, nous devons nous familiariser avec un nouvel ensemble de chiffres. Gardez à l'esprit que l'étude des mathématiques s'appuie continuellement sur elle-même. Les entiers négatifs, par exemple, comblent un vide laissé par l'ensemble d'entiers positifs. L'ensemble des nombres rationnels, à son tour, comble un vide laissé par l'ensemble des nombres entiers. L'ensemble des nombres réels comble un vide laissé par l'ensemble des nombres rationnels. Il n'est pas surprenant que l'ensemble des nombres réels comporte également des vides. Dans cette section, nous allons explorer un ensemble de nombres qui comble les vides de l'ensemble des nombres réels et découvrir comment y travailler.

Expression des racines carrées de nombres négatifs sous forme de multiples de$i$

Nous savons comment trouver la racine carrée de tout nombre réel positif. De la même manière, nous pouvons trouver la racine carrée de n'importe quel nombre négatif. La différence est que la racine n'est pas réelle. Si la valeur du radicand est négative, la racine est dite être un nombre imaginaire. Le nombre imaginaire$i$ est défini comme la racine carrée de$−1$.

\[\sqrt{-1}=i\]

Donc, en utilisant les propriétés des radicaux,

\[i^2=(\sqrt{-1})^2=-1\]

Nous pouvons écrire la racine carrée de n'importe quel nombre négatif comme un multiple de$i$. Considérez la racine carrée de$−49$.

\[\begin{align*} \sqrt{-49}&= \sqrt{49\times(-1)}\\[4pt] &= \sqrt{49}\sqrt{-1}\\[4pt] &= 7i \end{align*}\]

Nous utilisons$7i$ et non$−7i$ parce que la racine principale de$49$ est la racine positive.

Un nombre complexe est la somme d'un nombre réel et d'un nombre imaginaire. Un nombre complexe est exprimé sous une forme standard lorsqu'il$a$ est écrit$a+bi$ où se trouvent la partie réelle et$b$ la partie imaginaire. Par exemple,$5+2i$ est un nombre complexe. Donc, aussi, c'est le cas$3+4i\sqrt{3}$.

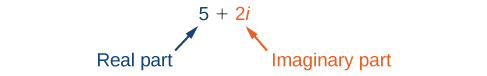
$Le nombre complexe 5 + 2i s'affiche. Le 5 est étiqueté comme : Partie réelle et le 2i est étiqueté comme : Partie imaginaire$

Les nombres imaginaires diffèrent des nombres réels en ce sens qu'un nombre imaginaire au carré produit un nombre réel négatif. Rappelez-vous que lorsqu'un nombre réel positif est au carré, le résultat est un nombre réel positif et qu'un nombre réel négatif est au carré, le résultat est également un nombre réel positif. Les nombres complexes se composent de nombres réels et imaginaires.

Définition : NOMBRES IMAGINAIRES ET COMPLEXES

Un nombre complexe est un numéro de la forme$a+bi$ où

$a$est la partie réelle du nombre complexe.
$b$est la partie imaginaire du nombre complexe.

Si$b=0$, alors$a+bi$ c'est un vrai nombre. Si$a=0$ et n'$b$est pas égal à$0$, le nombre complexe est appelé un nombre imaginaire pur. Un nombre imaginaire est la racine paire d'un nombre négatif.

Comment : À partir d'un nombre imaginaire, exprimez-le sous la forme standard d'un nombre complexe

Écrivez$\sqrt{-a}$ comme$\sqrt{a}\sqrt{-1}$.
Exprimez$\sqrt{-1}$ comme$i$.
Écrivez$\sqrt{a}\times i$ sous la forme la plus simple

Exemple$\PageIndex{1}$: Expressing an Imaginary Number in Standard Form

Exprimez$\sqrt{-9}$ sous forme standard.

Solution

\[\begin{align*} \sqrt{-9}&= \sqrt{9}\sqrt{-1)}\\[4pt] &= 3i\\[4pt] \end{align*}\]

Dans la forme standard, c'est$0+3i$.

Exercice$\PageIndex{1}$

Exprimez$\sqrt{-24}$ sous forme standard.

Réponse: $\sqrt{-24}=0+2i\sqrt{6}$

Tracé d'un nombre complexe sur le plan complexe

Nous ne pouvons pas tracer des nombres complexes sur une ligne numérique comme nous le ferions avec des nombres réels. Cependant, nous pouvons toujours les représenter graphiquement. Pour représenter un nombre complexe, nous devons aborder les deux composantes du nombre. Nous utilisons le plan complexe, qui est un système de coordonnées dans lequel l'axe horizontal représente le composant réel et l'axe vertical représente le composant imaginaire. Les nombres complexes sont les points du plan, exprimés sous forme de paires ordonnées$(a,b)$, où$a$ représentent les coordonnées de l'axe horizontal et$b$ les coordonnées de l'axe vertical.

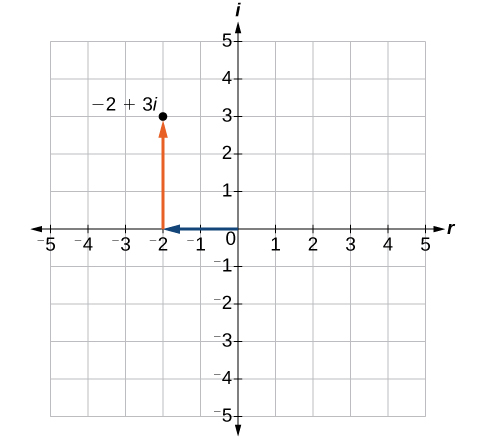
Regardons le nombre$−2+3i$. La partie réelle du nombre complexe est$−2$ et la partie imaginaire l'est$3$. Nous tracons la paire ordonnée$(−2,3)$ pour représenter le nombre complexe$−2+3i$, comme indiqué sur la figure$\PageIndex{2}$.

Plan de coordonnées dont les axes x et y sont compris entre moins 5 et 5. Le point négatif 2 plus 3i est représenté sur le graphique. Une flèche s'étend vers la gauche à partir de deux unités d'origine, puis une flèche s'étend vers le haut de trois unités à partir de la fin de la flèche précédente. — Figurine$\PageIndex{2}$

AVION COMPLEXE

Dans le plan complexe, l'axe horizontal est l'axe réel et l'axe vertical est l'axe imaginaire, comme le montre la figure$\PageIndex{3}$.

Un plan de coordonnées vide dont l'axe X est étiqueté : réel et l'axe y est étiqueté : imaginaire. — Figurine$\PageIndex{3}$

Comment : à partir d'un nombre complexe, représenter ses composants sur le plan complexe

Déterminez la partie réelle et la partie imaginaire du nombre complexe.
Déplacez-vous le long de l'axe horizontal pour afficher la partie réelle du nombre.
Déplacez-vous parallèlement à l'axe vertical pour afficher la partie imaginaire du nombre.
Tracez le point.

Exemple$\PageIndex{2}$: Plotting a Complex Number on the Complex Plane

Tracez le nombre complexe$3−4i$ sur le plan complexe.

Solution

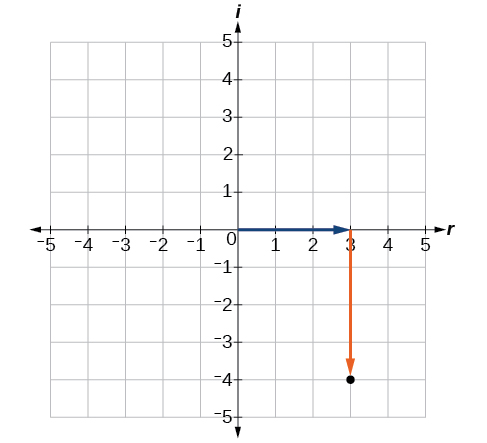
La partie réelle du nombre complexe est$3$, et la partie imaginaire l'est$–4$. Nous tracons la paire ordonnée$(3,−4)$ comme indiqué sur la figure$\PageIndex{4}$.

Plan de coordonnées dont les axes x et y sont compris entre -5 et 5. Le point 3 — 4i est tracé, avec une flèche s'étendant vers la droite à partir de l'origine (3 unités) et une flèche s'étendant vers le bas (4 unités) à partir de la fin de la flèche précédente. — Figurine$\PageIndex{4}$

Exercice$\PageIndex{2}$

Tracez le nombre complexe$−4−i$ sur le plan complexe.

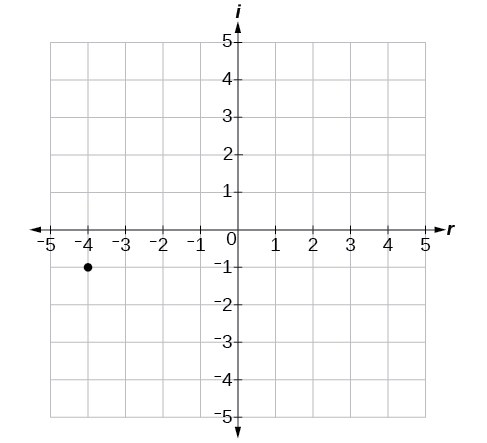
Réponse: $Plan de coordonnées dont les axes x et y sont compris entre moins 5 et 5. Le point -4 i est tracé.$
Figurine$\PageIndex{5}$

Ajouter et soustraire des nombres complexes

Tout comme pour les nombres réels, nous pouvons effectuer des opérations arithmétiques sur des nombres complexes. Pour ajouter ou soustraire des nombres complexes, nous combinons les parties réelles, puis les parties imaginaires.

NOMBRES COMPLEXES : ADDITION ET SOUSTRACTION

Ajouter des nombres complexes :

\[(a+bi)+(c+di)=(a+c)+(b+d)i\]

Soustraction de nombres complexes :

\[(a+bi)−(c+di)=(a−c)+(b−d)i\]

Comment : à partir de deux nombres complexes, trouver la somme ou la différence

Identifiez les parties réelles et imaginaires de chaque numéro.
Ajoutez ou soustrayez les pièces réelles.
Ajoutez ou soustrayez les parties imaginaires.

Exemple$\PageIndex{3}$: Adding and Subtracting Complex Numbers

Ajoutez ou soustrayez comme indiqué.

$(3−4i)+(2+5i)$
$(−5+7i)−(−11+2i)$

Solution

\[\begin{align*} (3-4i)+(2+5i)&= 3-4i+2+5i\\[4pt] &= 3+2+(-4i)+5i\\[4pt] &= (3+2)+(-4+5)i\\[4pt] &= 5+i \end{align*}\]
\[\begin{align*} (-5+7i)-(-11+2i)&= -5+7i+11-2i\\[4pt] &= -5+11+7i-2i\\[4pt] &= (-5+11)+(7-2)i\\[4pt] &= 6+5i \end{align*}\]

Exercice$\PageIndex{3}$

Soustraire$2+5i$ de$3–4i$.

Réponse: $(3−4i)−(2+5i)=1−9i$

Multiplier des nombres complexes

Multiplier des nombres complexes est un peu comme multiplier des binômes. La principale différence est que nous travaillons séparément avec les parties réelles et imaginaires.

Multiplier un nombre complexe par un nombre réel

Commençons par multiplier un nombre complexe par un nombre réel. Nous distribuons le nombre réel comme nous le ferions avec un binôme. Considérez, par exemple, ce qui$3(6+2i)$ suit :

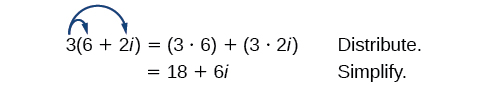
$Multiplication d'un nombre réel et d'un nombre complexe. Le 3 à l'extérieur des parenthèses comporte des flèches qui s'étendent à la fois au 6 et au 2i à l'intérieur des parenthèses. Cette expression est définie comme étant égale à la quantité trois fois six plus la quantité trois fois deux fois i ; il s'agit de la propriété distributive. La ligne suivante est égale à dix-huit plus six fois i ; la simplification.$

Comment : à partir d'un nombre complexe et d'un nombre réel, multipliez pour trouver le produit

Utilisez la propriété distributive.
Simplifiez.

Exemple$\PageIndex{4}$: Multiplying a Complex Number by a Real Number

Trouvez le produit$4(2+5i)$.

Solution

Distribuez le$4$.

\[\begin{align*} 4(2+5i)&= (4\cdot 2)+(4\cdot 5i)\\[4pt] &= 8+20i \end{align*}\]

Exercice$\PageIndex{4}$

Trouvez le produit :$\dfrac{1}{2}(5−2i)$

Réponse: $\dfrac{5}{2}-i$

Multiplier des nombres complexes ensemble

Maintenant, multiplions deux nombres complexes. Nous pouvons utiliser soit la propriété distributive, soit plus spécifiquement la méthode FOIL car nous avons affaire à des binômes. Rappelons que FOIL est un acronyme qui permet de multiplier les termes Premier, Intérieur, Externe et Dernier. La différence avec les nombres complexes est que lorsque nous obtenons un terme au carré$i^2$, il est égal$-1$.

\[\begin{align*} (a+bi)(c+di)&= ac+adi+bci+bdi^2\\[4pt] &= ac+adi+bci-bd(-1)\qquad i^2 = -1\\[4pt] &= ac+adi+bci-bd\\[4pt] &= (ac-bd)+(ad+bc)i \end{align*}\]

Regroupez les termes réels et les termes imaginaires.

Comment : à partir de deux nombres complexes, multipliez pour trouver le produit

Utilisez la propriété distributive ou la méthode FOIL.
N'oubliez pas cela$i^2=-1$.
Regroupez les termes réels et les termes imaginaires

Exemple$\PageIndex{5}$: Multiplying a Complex Number by a Complex Number

Multipliez$(4+3i)(2−5i)$.

Solution

\[\begin{align*} (4+3i)(2-5i)&= 4(2)-4(5i)+3i(2)-(3i)(5i)\\[4pt] &= 8-20i+6i-15(i^2)\\[4pt] &= (8+15)+(-20+6)i\\[4pt] &= 23-14i \end{align*}\]

Exercice$\PageIndex{5}$

Multipliez :$(3−4i)(2+3i)$.

Réponse: $18+i$

Diviser des nombres complexes

Diviser deux nombres complexes est plus compliqué que d'additionner, de soustraire ou de multiplier car nous ne pouvons pas diviser par un nombre imaginaire, ce qui signifie que toute fraction doit avoir un dénominateur réel pour écrire la réponse sous une forme standard$a+bi$. Nous devons trouver un terme par lequel nous pouvons multiplier le numérateur et le dénominateur qui éliminera la partie imaginaire du dénominateur afin d'obtenir un nombre réel comme dénominateur. Ce terme s'appelle le conjugué complexe du dénominateur, qui se trouve en modifiant le signe de la partie imaginaire du nombre complexe. En d'autres termes, le conjugué complexe de$a+bi$ est$a−bi$. Par exemple, le produit de$a+bi$ et$a−bi$ est

\[\begin{align*} (a+bi)(a-bi)&= a^2-abi+abi-b^2i^2\\[4pt] &= a^2+b^2 \end{align*}\]

Le résultat est un nombre réel.

Notez que les conjugués complexes ont une relation opposée : le conjugué complexe de$a+bi$ is$a−bi$ et le conjugué complexe de$a−bi$ is$a+bi$. De plus, lorsqu'une équation quadratique avec des coefficients réels comporte des solutions complexes, les solutions sont toujours des conjugués complexes les unes des autres.

Supposons que nous voulions diviser$c+di$ par$a+bi$, où ni$a$ ni$b$ égal à zéro. Nous écrivons d'abord la division sous forme de fraction, puis nous trouvons le conjugué complexe du dénominateur et nous multiplions.

$\dfrac{c+di}{a+bi}$où$a≠0$ et$b≠0$

Multipliez le numérateur et le dénominateur par le conjugué complexe du dénominateur.

\[\begin{align*} \dfrac{(c+di)}{(a+bi)}\cdot \dfrac{(a-bi)}{(a-bi)}&= \dfrac{(c+di)(a-bi)}{(a+bi)(a-bi)}\\[4pt] &= \dfrac{ca-cbi+adi-bdi^2}{a^2-abi+abi-b^2i^2} \qquad \text{Apply the distributive property}\\[4pt] &= \dfrac{ca-cbi+adi-bd(-1)}{a^2-abi+abi-b^2(-1)} \qquad \text{Simplify, remembering that } i^2=-1\\[4pt] &= \dfrac{(ca+bd)+(ad-cb)i}{a^2+b^2} \end{align*}\]

Définition : LE COMPLEXE CONJUGUÉ

Le conjugué complexe d'un nombre complexe$a+bi$ est$a−bi$. On le trouve en modifiant le signe de la partie imaginaire du nombre complexe. La partie réelle du nombre reste inchangée.

Lorsqu'un nombre complexe est multiplié par son conjugué complexe, le résultat est un nombre réel.
Lorsqu'un nombre complexe est ajouté à son conjugué complexe, le résultat est un nombre réel.

Exemple$\PageIndex{6}$: Finding Complex Conjugates

Détermine le conjugué complexe de chaque nombre.

$2+i\sqrt{5}$
$-\dfrac{1}{2}i$

Solution

Le numéro figure déjà dans le formulaire$a+bi$. Le conjugué complexe est$a−bi$, ou$2−i\sqrt{5}$.
Nous pouvons réécrire ce numéro sous la$a+bi$ forme$0−\dfrac{1}{2}i$. Le conjugué complexe est$a−bi$, ou$0+\dfrac{1}{2}i$. Cela peut être écrit simplement comme$\dfrac{1}{2}i$.

Analyse

Bien que nous ayons vu que nous pouvons trouver le conjugué complexe d'un nombre imaginaire, en pratique, nous trouvons généralement les conjugués complexes de nombres complexes uniquement avec une composante réelle et une composante imaginaire. Pour obtenir un nombre réel à partir d'un nombre imaginaire, il suffit de le multiplier par$i$.

Exercice$\PageIndex{6}$

Détermine le conjugué complexe de$−3+4i$.

Réponse: $−3−4i$

Comment : à partir de deux nombres complexes, divisez l'un par l'autre

Écrivez le problème de division sous forme de fraction.
Déterminez le conjugué complexe du dénominateur.
Multipliez le numérateur et le dénominateur de la fraction par le conjugué complexe du dénominateur.
Simplifiez.

Exemple$\PageIndex{7}$: Dividing Complex Numbers

Divisez$(2+5i)$ par$(4−i)$.

Solution

Nous commençons par écrire le problème sous forme de fraction.

\[\dfrac{(2+5i)}{(4−i)} \nonumber \]

Ensuite, nous multiplions le numérateur et le dénominateur par le conjugué complexe du dénominateur.

\[\dfrac{(2+5i)}{(4−i)}⋅\dfrac{(4+i)}{(4+i)} \nonumber \]

Pour multiplier deux nombres complexes, nous étendons le produit comme nous le ferions avec des polynômes (en utilisant FOIL).

\[\begin{align*} \dfrac{(2+5i)}{(4-i)}\cdot \dfrac{(4+i)}{(4+i)}&= \dfrac{8+2i+20i+5i^2}{16+4i-4i-i^2}\\[4pt] &= \dfrac{8+2i+20i+5(-1)}{16+4i-4i-(-1)}\; i^2=-1 \\[4pt] &= \dfrac{3+22i}{17}\\[4pt] &= \dfrac{3}{17}+\dfrac{22}{17i} \end{align*}\]

Séparez les parties réelles et imaginaires.

Notez que cela exprime le quotient sous forme standard.

Pouvoirs simplifiés de$i$

Les pouvoirs de$i$ sont cycliques. Regardons ce qui se passe lorsque nous accédons$i$ à des pouvoirs croissants.

\[i^1=i \nonumber \]\[i^2=-1 \nonumber \]\[i^3=i^2⋅i=-1⋅i=-i \nonumber \]\[i^4=i^3⋅i=-i⋅i=-i^2=-(-1)=1 \nonumber \]\[i^5=i^4⋅i=1⋅i=i \nonumber \]

Nous pouvons voir que lorsque nous arrivons à la cinquième puissance de i, elle est égale à la première puissance. Alors que nous continuons à nous multiplier$i$ en augmentant nos puissances, nous assisterons à un cycle de quatre. Examinons les quatre pouvoirs suivants de$i$.

\[i^6=i^5⋅i=i⋅i=i^2=-1 \nonumber \]\[i^7=i^6⋅i=i^2⋅i=i^3=-i \nonumber \]\[i^8=i^7⋅i=i^3⋅i=i^4=1 \nonumber \]\[i^9=i^8⋅i=i^4⋅i=i^5=i \nonumber \]

Le cycle se répète en continu :$i,−1,−i,1,$ toutes les quatre puissances.

Exemple$\PageIndex{8}$: Simplifying Powers of $i$

Évaluez :$i^{35}$.

Solution

Depuis$i^4=1$, nous pouvons simplifier le problème en tenant compte du plus grand nombre de facteurs$i^4$ possible. Pour ce faire, déterminez d'abord combien de fois$4$ il y a entrée$35: 35=4⋅8+3$.

\[i^{35}=i^{4⋅8+3}=i^{4⋅8}⋅i^3={(i^4)}^8⋅i^3=i^8⋅i^3=i^3=−i \nonumber \]

Exercice$\PageIndex{7}$

Évaluez :$i^{18}$

Réponse: $−1$

QUESTIONS-RÉPONSES

Pouvons-nous écrire$i^{35}$ d'une autre manière utile ?

Comme nous l'avons vu dans Exemple$\PageIndex{8}$, nous avons réduit$i^{35}$ à$i^3$ en divisant l'exposant par$4$ et en utilisant le reste pour trouver la forme simplifiée. Mais peut-être qu'une autre factorisation de$i^{35}$ pourrait être plus utile. Le tableau$\PageIndex{1}$ montre d'autres factorisations possibles.

Tableau$\PageIndex{1}$
Factorisation de$i^{35}$	$i^{34}⋅i$	$i^{33}⋅i^2$	$i^{31}⋅i^4$	$i^{19}⋅i^{16}$
Forme réduite	${(i^2)}^{17}⋅i$	$i^{33}⋅(−1)$	$i^{31}⋅1$	$i^{19}⋅{(i^4)}^4$
Formulaire simplifié	${(−1)}^{17}⋅i$	$−i^{33}$	$i^{31}$	$i^{19}$

Chacune d'entre elles aboutira finalement à la réponse que nous avons obtenue ci-dessus, mais peut nécessiter plusieurs étapes supplémentaires par rapport à notre méthode précédente.

Médias

Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner avec des nombres complexes.

Ajouter et soustraire des nombres complexes
Multiplier des nombres complexes
Multiplier des conjugués complexes
L'élever à deux pouvoirs

Concepts clés

La racine carrée de tout nombre négatif peut être écrite comme un multiple de $i$. Voir l'exemple.
Pour tracer un nombre complexe, nous utilisons deux lignes numériques, croisées pour former le plan complexe. L'axe horizontal est l'axe réel et l'axe vertical est l'axe imaginaire. Voir l'exemple.
Des nombres complexes peuvent être ajoutés et soustraits en combinant les parties réelles et les parties imaginaires. Voir l'exemple.
Les nombres complexes peuvent être multipliés et divisés.
- Pour multiplier des nombres complexes, distribuez-les comme pour les polynômes. Voir Exemple et Exemple.
- Pour diviser des nombres complexes, multipliez le numérateur et le dénominateur par le conjugué complexe du dénominateur afin d'éliminer le nombre complexe du dénominateur. Voir Exemple et Exemple.
Les puissances de i sont cycliques et se répètent toutes les quatre. Voir l'exemple.

Factorisation de\(i^{35}\)	\(i^{34}⋅i\)	\(i^{33}⋅i^2\)	\(i^{31}⋅i^4\)	\(i^{19}⋅i^{16}\)
Forme réduite	\({(i^2)}^{17}⋅i\)	\(i^{33}⋅(−1)\)	\(i^{31}⋅1\)	\(i^{19}⋅{(i^4)}^4\)
Formulaire simplifié	\({(−1)}^{17}⋅i\)	\(−i^{33}\)	\(i^{31}\)	\(i^{19}\)

Définition : NOMBRES IMAGINAIRES ET COMPLEXES

Comment : À partir d'un nombre imaginaire, exprimez-le sous la forme standard d'un nombre complexe

Exemple\(\PageIndex{1}\): Expressing an Imaginary Number in Standard Form

Exercice\(\PageIndex{1}\)