2.3 : Modèles et applications
- Page ID
- 195092
- Configurez une équation linéaire pour résoudre une application réelle.
- Utilisez une formule pour résoudre une application réelle.
Josh espère obtenir un cours\(A\) d'algèbre à l'université. Il a des scores de\(75\)\(82\),\(95\),\(91\), et\(94\) lors de ses cinq premiers tests. Il ne reste que l'examen final et le maximum de points pouvant être gagnés est de\(100\). Est-il possible pour Josh de terminer le cours avec un\(A\) ? Une simple équation linéaire donnera à Josh sa réponse.

De nombreuses applications du monde réel peuvent être modélisées par des équations linéaires. Par exemple, un forfait de téléphonie mobile peut inclure des frais de service mensuels plus des frais par minute de conversation ; le fabricant de widgets doit payer un certain montant pour produire x widgets par mois plus les frais d'exploitation mensuels ; une société de location de voitures facture des frais quotidiens plus un montant par kilomètre parcouru. Ce sont des exemples d'applications que nous rencontrons tous les jours et qui sont modélisées par des équations linéaires. Dans cette section, nous allons configurer et utiliser des équations linéaires pour résoudre ces problèmes.
Configuration d'une équation linéaire pour résoudre une application réelle
Pour configurer ou modéliser une équation linéaire adaptée à une application réelle, nous devons d'abord déterminer les quantités connues et définir la quantité inconnue en tant que variable. Ensuite, nous commençons à interpréter les mots comme des expressions mathématiques à l'aide de symboles mathématiques. Prenons l'exemple de location de voiture ci-dessus. Dans ce cas, un coût connu, tel que\($0.10/mi\), est multiplié par une quantité inconnue, le nombre de miles parcourus. Par conséquent, nous pouvons écrire\(0.10x\). Cette expression représente un coût variable car il change en fonction du nombre de miles parcourus.
Si une quantité est indépendante d'une variable, nous l'ajoutons ou la soustrayons généralement, en fonction du problème. Comme ces montants ne changent pas, nous les appelons coûts fixes. Pensez à une agence de location de voitures qui facture\($0.10/mi\) plus une redevance journalière de\($50\). Nous pouvons utiliser ces quantités pour modéliser une équation qui peut être utilisée pour déterminer le coût quotidien de location d'une voiture\(C\).
\(C=0.10x+50 \tag{2.4.1}\)
Lorsqu'il s'agit d'applications du monde réel, certaines expressions peuvent être traduites directement en mathématiques. Le tableau\(\PageIndex{1}\) répertorie certaines expressions verbales courantes et leurs expressions mathématiques équivalentes.
| Verbal | Translation vers les opérations mathématiques |
|---|---|
| Un chiffre dépasse un autre d'un | \(x,x+a\) |
| Deux fois un chiffre | \(2x\) |
| Un chiffre est\(a\) plus qu'un autre | \(x,x+a\) |
| Un chiffre est inférieur à deux fois un autre | \(x,2x−a\) |
| Le produit d'un nombre et\(a\), diminué de\(b\) | \(ax−b\) |
| Le quotient entre un nombre et le nombre plus\(a\) est trois fois le nombre | \(\dfrac{x}{x+a}=3x\) |
| Le produit de trois fois un nombre et du nombre diminué de\(b\) est\(c\) | \(3x(x−b)=c\) |
- Identifiez les quantités connues.
- Attribuez une variable pour représenter la quantité inconnue.
- S'il y a plus d'une quantité inconnue, trouvez un moyen d'écrire la seconde inconnue en fonction de la première.
- Rédigez une équation interprétant les mots comme des opérations mathématiques.
- Résolvez l'équation. Assurez-vous que la solution peut être expliquée avec des mots, y compris les unités de mesure.
Trouvez une équation linéaire à résoudre pour les quantités inconnues suivantes : Un nombre dépasse un autre nombre de\( 17\) et leur somme est de\( 31\). Trouve les deux numéros.
Solution
Soit\( x\) égal au premier chiffre. Ensuite, comme le deuxième nombre dépasse le premier de\(17\), nous pouvons écrire le deuxième nombre sous la forme\( x +17\). La somme des deux nombres est\(31\). Nous interprétons généralement le mot est comme un signe égal.
\[\begin{align*} x+(x+17)&= 31\\ 2x+17&= 31\\ 2x&= 14\\ x&= 7 \end{align*}\]
\[\begin{align*} x+17&= 7 + 17\\ &= 24\\ \end{align*}\]
Les deux chiffres sont\(7\) et\(24\).
Trouvez une équation linéaire à résoudre pour les quantités inconnues suivantes : Un nombre est trois de plus que deux fois un autre nombre. Si la somme des deux nombres est égale à\(36\), trouvez les nombres.
- Réponse
-
\(11\)et\(25\)
Deux compagnies de téléphonie mobile proposent des forfaits différents. La société A facture des frais de service mensuels\($34\) plus le\($.05/min\) temps de conversation. La société B facture des frais de service mensuels\($40\) plus le\($.04/min\) temps de conversation.
- Rédigez une équation linéaire qui modélise les packages proposés par les deux entreprises.
- Si le nombre moyen de minutes utilisées chaque mois est de\(1,160\), quelle entreprise propose le meilleur forfait ?
- Si le nombre moyen de minutes utilisées chaque mois est de\(420\), quelle entreprise propose le meilleur forfait ?
- Combien de minutes de conversation donneraient des relevés mensuels égaux pour les deux entreprises ?
Solution
un.
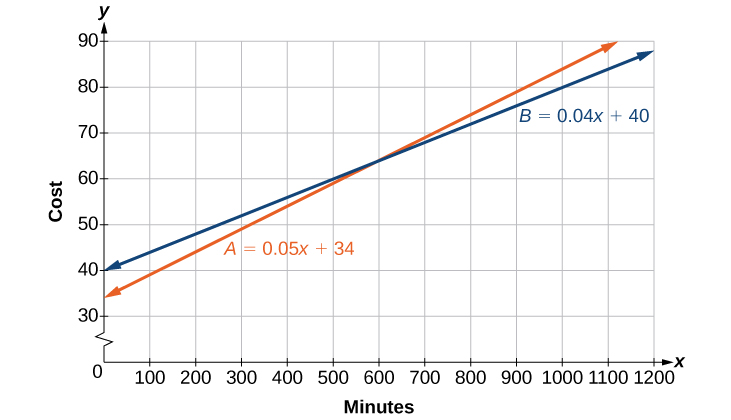
Le modèle de la société A peut être écrit sous la forme\( A =0.05x+34\). Cela inclut le coût variable de\( 0.05x\) plus les frais de service mensuels de\($34\). Le forfait de la société B facture des frais mensuels plus élevés de\($40\), mais un coût variable inférieur de\( 0.04x\). Le modèle de la société B peut être écrit comme\( B =0.04x+$40\).
b.
Si le nombre moyen de minutes utilisées chaque mois est de\(1,160\), voici ce qui suit :
\[\begin{align*} \text{Company A}&= 0.05(1.160)+34\\ &= 58+34\\ &= 92 \end{align*}\]
\[\begin{align*} \text{Company B}&= 0.04(1,1600)+40\\ &= 46.4+40\\ &= 86.4 \end{align*}\]
Ainsi, la société B offre le coût mensuel le plus bas par rapport au coût\($92\) mensuel proposé par l'entreprise A lorsque le nombre moyen de minutes utilisées chaque mois est de\(1,160\).\($86.40\)
c.
Si le nombre moyen de minutes utilisées chaque mois est de\(420\), voici ce qui suit :
\[\begin{align*} \text{Company A}&= 0.05(420)+34\\ &= 21+34\\ &= 55 \end{align*}\]
\[\begin{align*} \text{Company B}&= 0.04(420)+40\\ &= 16.8+40\\ &= 56.8 \end{align*}\]
Si le nombre moyen de minutes utilisées chaque mois est de\(420\), alors la société A propose un coût mensuel inférieur à\($55\) celui de la\($56.80\) société B.
d.
Pour répondre à la question de savoir combien de minutes de conversation rapporteraient la même facture aux deux entreprises, nous devrions réfléchir au problème en termes de\((x,y)\) coordonnées : à quel moment la\(x\) valeur et la\(y\) valeur -sont-elles égales ? Nous pouvons trouver ce point en mettant les équations égales les unes aux autres et en résolvant pour\(x\).
\[\begin{align*} 0.05x+34&= 0.04x+40\\ 0.01x&= 6\\ x&= 600 \end{align*}\]Vérifiez la\(x\) valeur -dans chaque équation.
\(0.05(600)+34=64\)
\(0.04(600)+40=64\)
Par conséquent, une moyenne mensuelle de\(600\) minutes de conversation rend les forfaits égaux. Voir la figure\(\PageIndex{2}\).
Trouvez une équation linéaire pour modéliser cette application du monde réel : la production d'une pièce utilisée dans une marque populaire d'ordinateurs de bureau coûte\($2.50\) par unité à ABC Electronics. La société a des dépenses d'exploitation mensuelles\($350\) pour les services publics et\($3,300\) pour les salaires. Quelles sont les dépenses mensuelles de l'entreprise ?
- Réponse
-
\(C=2.5x+3,650\)
Utiliser une formule pour résoudre une application réelle
De nombreuses applications sont résolues à l'aide de formules connues. Le problème est énoncé, une formule est identifiée, les quantités connues sont substituées dans la formule, l'équation est résolue pour l'inconnu et la réponse à la question du problème est résolue. Ces problèmes impliquent généralement deux équations représentant deux voyages, deux investissements, deux zones, etc. Des exemples de formules incluent l'aire d'une région rectangulaire,
\[A=LW \tag{2.4.2}\]
le périmètre d'un rectangle,
\[P=2L+2W \tag{2.4.3}\]
et le volume d'un solide rectangulaire,
\[V=LWH. \tag{2.4.4}\]
Lorsqu'il y a deux inconnues, nous trouvons un moyen d'écrire l'une en fonction de l'autre car nous ne pouvons résoudre que pour une seule variable à la fois.
Andrew\(30\; min\) doit se rendre au travail en voiture le matin. Il rentre chez lui en voiture en empruntant le même itinéraire, mais cela prend\(10\; min\) plus de temps et il fait en moyenne\(10\; mi/h\) moins que le matin. À quelle distance se rend au travail en voiture Andrew ?
Solution
Il s'agit d'un problème de distance, nous pouvons donc utiliser la formule\(d =rt\), où la distance est égale au taux multiplié par le temps. Notez que lorsque le taux est indiqué\(mi/h\), le temps doit être exprimé en heures. Des unités de mesure cohérentes sont essentielles pour obtenir une solution correcte.
Tout d'abord, nous identifions les quantités connues et inconnues. Le trajet matinal d'Andrew pour se rendre au travail prend\(30\; min\), ou\(12\; h\) au rythme\(r\). Son trajet pour rentrer chez lui prend\(40\; min\)\(23\; h\), ou, et sa vitesse moyenne\(10\; mi/h\) est inférieure à celle du matin. Les deux trajets couvrent la distance\(d\). Un tableau, tel qu'un tableau\(\PageIndex{2}\), est souvent utile pour suivre les informations relatives à ce type de problèmes.
| \(d\) | \(r\) | \(t\) | |
|---|---|---|---|
| Pour travailler | \ (d \) » style="text-align:center ; » class="lt-math-1632">\(d\) | \ (r \) » style="text-align:center ; » class="lt-math-1632">\(r\) | \ (t \) » style="text-align:center ; » class="lt-math-1632">\(12\) |
| À la maison | \ (d \) » style="text-align:center ; » class="lt-math-1632">\(d\) | \ (r \) » style="text-align:center ; » class="lt-math-1632">\(r−10\) | \ (t \) » style="text-align:center ; » class="lt-math-1632">\(23\) |
Écrivez deux équations, une pour chaque trajet.
\[d=r\left(\dfrac{1}{2}\right) \qquad \text{To work} \nonumber\]
\[d=(r-10)\left(\dfrac{2}{3}\right) \qquad \text{To home} \nonumber\]
Comme les deux équations sont égales à la même distance, nous les mettons égales l'une à l'autre et résolvons pour\(r\).
\[\begin{align*} r\left (\dfrac{1}{2} \right )&= (r-10)\left (\dfrac{2}{3} \right )\\ \dfrac{1}{2r}&= \dfrac{2}{3}r-\dfrac{20}{3}\\ \dfrac{1}{2}r-\dfrac{2}{3}r&= -\dfrac{20}{3}\\ -\dfrac{1}{6}r&= -\dfrac{20}{3}\\ r&= -\dfrac{20}{3}(-6)\\ r&= 40 \end{align*}\]
Nous avons résolu le taux de rapidité de travail,\(40\; mph\). La substitution par\(40\) le taux sur le trajet aller-retour donne des rendements\(30 mi/h\). Nous pouvons maintenant répondre à la question. Remplacez le taux dans l'une ou l'autre équation et résolvez pour\(d\).
\[\begin{align*}d&= 40\left (\dfrac{1}{2} \right )\\ &= 20 \end{align*}\]
La distance entre la maison et le travail est de\(20\; mi\).
Analyse
Notez que nous aurions pu effacer les fractions de l'équation en multipliant les deux côtés de l'équation par l'écran LCD à résoudre\(r\).
\[\begin{align*} r\left (\dfrac{1}{2} \right)&= (r-10)\left (\dfrac{2}{3} \right )\\ 6\times r\left (\dfrac{1}{2} \right)&= 6\times (r-10)\left (\dfrac{2}{3} \right )\\ 3r&= 4(r-10)\\ 3r&= 4r-40\\ r&= 40 \end{align*}\]
Samedi matin, Jennifer a dû\(3.6\; h\) se rendre en voiture chez sa mère pour le week-end. Dimanche soir, en raison de la circulation dense, Jennifer a dû\(4\; h\) rentrer chez elle. Sa vitesse était\(5\; mi/h\) plus lente le dimanche que le samedi. Quelle était sa vitesse dimanche ?
- Réponse
-
\(45\; mi/h\)
Le périmètre d'un patio extérieur rectangulaire est\(54\; ft\). La longueur est\(3\; ft\) supérieure à la largeur. Quelles sont les dimensions du patio ?
Solution
La formule périmétrique est standard :\(P=2L+2W\). Nous avons deux quantités inconnues, la longueur et la largeur. Cependant, nous pouvons écrire la longueur en termes de largeur sous la forme\(L =W+3\). Substituez la valeur du périmètre et l'expression de la longueur dans la formule. Il est souvent utile de faire un croquis et d'étiqueter les côtés comme sur la figure\(\PageIndex{3}\).
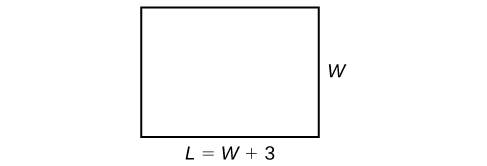
Nous pouvons maintenant résoudre la largeur puis calculer la longueur.
\[\begin{align*} P&= 2L + 2W\\ 54&= 2(W+3)+2W\\ 54&= 2W+6+2W\\ 54&= 4W+6\\ 48&= 4W\\ W&= 12 \end{align*}\]
\[\begin{align*} L&= 12+3\\ L&= 15 \end{align*}\]
Les dimensions sont\(L = 15\; ft\) et\(W = 12\; ft\).
Déterminez les dimensions d'un rectangle étant donné que le périmètre est\(110\; cm\) et que sa longueur est\(1\; cm\) supérieure à deux fois la largeur.
- Réponse
-
\(L=37\; cm\),\(W=18\; cm\)
Le périmètre d'une tablette de papier millimétré est\(48\space{in.}^2\). La longueur est\(6\; in\)... supérieure à la largeur. Trouvez la zone du papier millimétré.
Solution
La formule standard pour la superficie est\(A =LW\) ; cependant, nous allons résoudre le problème en utilisant la formule du périmètre. La raison pour laquelle nous utilisons la formule du périmètre est que nous connaissons suffisamment d'informations sur le périmètre pour que la formule nous permette de résoudre l'une des inconnues. Comme le périmètre et la surface utilisent la longueur et la largeur comme dimensions, ils sont souvent utilisés ensemble pour résoudre un problème comme celui-ci.
Nous savons que la longueur est\(6\; in\)... supérieure à la largeur, nous pouvons donc écrire la longueur sous la forme\(L =W+6\). Substituez la valeur du périmètre et l'expression de la longueur dans la formule du périmètre et trouvez la longueur.
\[\begin{align*} P&= 2L + 2W\\ 48&= 2(W+6)+2W\\ 48&= 2W+12+2W\\ 48&= 4W+12\\ 36&= 4W\\ W&= 9 \end{align*}\]
\[\begin{align*}L&= 9+6\\ L&= 15 \end{align*}\]
Maintenant, nous trouvons la zone en fonction des dimensions de\(L = 15\; in\). et\(W = 9\; in\).
\[\begin{align*} A&= LW\\ A&=15(9)\\ A&= 135\space{in.}^2 \end{align*}\]
La région est\(135\space{in.}^2\).
Une salle de jeux a un périmètre de\(70\; ft\). La longueur est cinq fois plus que deux fois la largeur. Combien\(ft^2\) de nouvelles moquettes faut-il commander ?
- Réponse
-
\(250\space{ft}^2\)
Déterminez les dimensions d'un carton d'expédition étant donné que la longueur est le double de la largeur, que la hauteur est\(8\; \) dedans et que le volume est\(1,600\space{in.}^3\).
Solution
La formule du volume d'une boîte est donnée comme\(V =LWH\) le produit de la longueur, de la largeur et de la hauteur. On nous donne cela\(L =2W\), et\(H =8\). Le volume est\(1,600\; \text{cubic inches}\).
\[\begin{align*} V&= LWH\\ 1600&= (2W)W(8)\\ 1600&= 16W^2\\ 100&= W^2\\ 10&= W \end{align*}\]Les dimensions sont\(L = 20\; in\)\(W= 10\; in\), et\(H = 8\; in\).
Analyse
Notez que la racine carrée de\(W^2\) produirait une valeur positive et une valeur négative. Cependant, comme nous décrivons la largeur, nous ne pouvons utiliser que le résultat positif.
Accédez à ces ressources en ligne pour obtenir des instructions et des exercices supplémentaires sur les modèles et les applications d'équations linéaires.
- Résolution de problèmes avec des équations linéaires
- Résolution de problèmes par des équations
- Déterminer les dimensions de la surface en fonction du périmètre
- Trouvez la distance entre les villes en utilisant la formule distance = tarif* temps
- Application d'une équation linéaire (Écrire une équation de coût)
Concepts clés
- Une équation linéaire peut être utilisée pour résoudre un problème inconnu dans un nombre. Voir l'exemple.
- Les applications peuvent être écrites sous forme de problèmes mathématiques en identifiant des quantités connues et en attribuant une variable à des quantités inconnues. Voir l'exemple.
- Il existe de nombreuses formules connues qui peuvent être utilisées pour résoudre des applications. Les problèmes de distance, par exemple, sont résolus à l'aide de la\(d = rt\) formule. Voir l'exemple.
- De nombreux problèmes de géométrie sont résolus à l'aide de la formule du périmètre\(P =2L+2W\), de la formule\(A =LW\) de la surface ou de la formule du volume\(V =LWH\). Voir Exemple, Exemple et Exemple.


