1.1 : Nombres réels - Les bases de l'algèbre
- Page ID
- 195336
- Classifiez un nombre réel en tant que nombre naturel, entier, rationnel ou irrationnel.
- Effectuez les calculs en utilisant l'ordre des opérations.
- Utilisez les propriétés suivantes des nombres réels : commutative, associative, distributive, inverse et identité.
- Évaluez les expressions algébriques.
- Simplifiez les expressions algébriques.
On dit souvent que les mathématiques sont le langage des sciences. Si c'est vrai, alors le langage des mathématiques, ce sont les nombres. La première utilisation des chiffres a eu lieu il y a\(100\) des siècles au Moyen-Orient pour compter ou énumérer des objets. Les fermiers, les éleveurs et les commerçants utilisaient des jetons, des pierres ou des marqueurs pour indiquer une seule quantité : une gerbe de grain, une tête de bétail ou une longueur fixe de tissu, par exemple. Cela a rendu possible le commerce, ce qui a permis d'améliorer les communications et de propager la civilisation.
Il y a trois à quatre mille ans, les Égyptiens ont introduit des fractions. Ils les ont d'abord utilisés pour montrer leurs réciproques. Plus tard, ils les ont utilisés pour représenter la quantité lorsqu'une quantité était divisée en parties égales.
Mais que se passerait-il s'il n'y avait pas de bétail à échanger ou si toute une récolte de céréales était perdue lors d'une inondation ? Comment pourrait-on indiquer l'existence de rien ? Dès les temps les plus reculés, les gens avaient pensé à un « état de base » lorsqu'ils comptaient et utilisaient divers symboles pour représenter cette condition nulle. Cependant, ce n'est qu'au Ve siècle environ de notre ère en Inde que le zéro a été ajouté au système numérique et utilisé comme chiffre dans les calculs.
De toute évidence, il fallait également des chiffres pour représenter les pertes ou les dettes. En Inde, au VIIe siècle de notre ère, les nombres négatifs étaient utilisés comme solutions aux équations mathématiques et aux dettes commerciales. Les contraires des nombres de comptage ont encore élargi le système de numérotation.
En raison de l'évolution du système numérique, nous pouvons désormais effectuer des calculs complexes en utilisant ces catégories et d'autres catégories de nombres réels. Dans cette section, nous allons explorer des ensembles de nombres, des calculs avec différents types de nombres et l'utilisation de nombres dans des expressions.
Classification d'un nombre réel
Les nombres que nous utilisons pour compter ou énumérer des éléments sont des nombres naturels,\(1, 2, 3, 4, 5\) et ainsi de suite. Nous les décrivons en notation d'ensemble comme\(\{1,2,3,...\}\) si les points de suspension\((\cdots)\) indiquent que les nombres continuent à l'infini. Les nombres naturels sont, bien entendu, également appelés nombres de comptage. Chaque fois que nous énumérons les membres d'une équipe, que nous comptons les pièces d'une collection ou que nous comptons les arbres d'un bosquet, nous utilisons l'ensemble des nombres naturels. L'ensemble des nombres entiers est l'ensemble des nombres naturels plus zéro :\(\{0,1,2,3,...\}\).
L'ensemble des nombres entiers ajoute les opposés des nombres naturels à l'ensemble des nombres entiers :\(\{\cdots,-3,-2,-1,0,1,2,3,\cdots\}\). Il est utile de noter que l'ensemble d'entiers est composé de trois sous-ensembles distincts : des entiers négatifs, des entiers nuls et des entiers positifs. En ce sens, les entiers positifs ne sont que des nombres naturels. Une autre façon de penser est que les nombres naturels sont un sous-ensemble des entiers.
\[ \overbrace{\cdots, -3,-2,-1}^{\text{negative integers}}, \underbrace{0}_{\text{zero}}, \overbrace{1,\, 2,\,3,\, \cdots}^{\text{positive integers}} \nonumber\]
L'ensemble des nombres rationnels s'écrit sous la forme\(\{\frac{m}{n}| \text{m and n are integers and } n \neq 0\}\) .Remarquez à partir de la définition que les nombres rationnels sont des fractions (ou quotients) contenant des entiers à la fois dans le numérateur et le dénominateur, et que le dénominateur n'est jamais\(0\). Nous pouvons également voir que chaque entier naturel, entier et entier est un nombre rationnel avec un dénominateur de\(1\).
Comme il s'agit de fractions, tout nombre rationnel peut également être exprimé sous forme décimale. Tout nombre rationnel peut être représenté comme suit :
- une décimale finale :\(\frac{15}{8} =1.875\), ou
- une décimale récurrente :\(\frac{4}{11} =0.36363636\cdots = 0.\bar{36}\)
Nous utilisons une ligne tracée au-dessus du bloc répétitif de nombres au lieu d'écrire le groupe plusieurs fois.
Écrivez chacun des éléments suivants sous forme de nombre rationnel. Ecrivez une fraction avec l'entier dans le numérateur et\(1\) in the denominator.
- \(7\)
- \(0\)
- \(-8\)
Solution
un.\(7= \frac{7}{1}\)
b.\(0= \frac{0}{1}\)
c.\(-8= \frac{-8}{1}\)
Écrivez chacun des éléments suivants sous forme de nombre rationnel.
- \(11\)
- \(3\)
- \(-4\)
- Réponse
-
- \(\frac{11}{1}\)
- \(\frac{3}{1}\)
- \(-\frac{4}{1}\)
Écrivez chacun des nombres rationnels suivants sous forme de décimale finale ou répétée.
- \(-\frac{5}{7}\)
- \(\frac{15}{5}\)
- \(\frac{13}{25}\)
Solution
a. une décimale récurrente
b.\(\frac{15}{5} = 3\) (ou\(3.0\)), une décimale finale
c.\(\frac{13}{25} =0.52\), une décimale finale
Écrivez chacun des nombres rationnels suivants sous forme de décimale finale ou répétée.
- \(\frac{68}{17}\)
- \(\frac{8}{13}\)
- \(-\frac{13}{25}\)
- Réponse
-
- \(4\)(ou\(4.0\)), se terminant
- \(0.\overline{615384}\), en répétant
- \(-0.85\), se terminant
Chiffres irrationnels
À un moment donné dans le passé ancien, quelqu'un a découvert que tous les nombres ne sont pas des nombres rationnels. Un constructeur, par exemple, peut avoir découvert que la diagonale d'un carré avec des côtés unitaires n'était pas\(2\) ou même\(32\), mais qu'elle était autre chose. Ou un fabricant de vêtements aurait pu remarquer que le rapport entre la circonférence et le diamètre d'un rouleau de tissu était légèrement supérieur\(3\), mais ce n'était toujours pas un chiffre rationnel. Ces nombres sont considérés comme irrationnels car ils ne peuvent pas être écrits sous forme de fractions. Ces nombres constituent l'ensemble des nombres irrationnels. Les nombres irrationnels ne peuvent pas être exprimés sous la forme d'une fraction de deux entiers. Il est impossible de décrire cet ensemble de nombres par une seule règle, sauf pour dire qu'un nombre est irrationnel s'il n'est pas rationnel. Nous écrivons donc ceci comme indiqué.
\[\{h\mid h \text { is not a rational number}\}\]
Déterminez si chacun des nombres suivants est rationnel ou irrationnel. Si c'est rationnel, déterminez s'il s'agit d'une décimale finale ou répétée.
- \(\sqrt{25}\)
- \(\frac{33}{9}\)
- \(\sqrt{11}\)
- \(\frac{17}{34}\)
- \(0.3033033303333…\)
Solution
- \(\sqrt{25}\): Cela peut être simplifié car,\(\sqrt{25} = 5\) par conséquent,\(\sqrt{25}\) c'est rationnel.
- \(\frac{33}{9}\): Parce que c'est une fraction,\(\frac{33}{9}\) c'est un nombre rationnel. Ensuite, simplifiez et divisez. \[\frac{33}{9}=\cancel{\frac{33}{9}} \nonumber\]Donc,\(\frac{33}{9}\) c'est rationnel et une décimale répétitive.
- \(\sqrt{11}\): Cela ne peut pas être simplifié davantage. C'\(\sqrt{11}\)est donc un nombre irrationnel.
- \(\frac{17}{34}\): Parce que c'est une fraction,\(\frac{17}{34}\) c'est un nombre rationnel. Simplifiez et divisez. \[\frac{17}{34} = 0.5 \nonumber\]Donc,\(\frac{17}{34}\) est rationnel et décimal final.
- \(0.3033033303333…\)n'est pas une décimale finale. Notez également qu'il n'y a pas de schéma répétitif car le groupe de\(3s\) augmente à chaque fois. Il ne s'agit donc ni d'une décimale finale ni d'une décimale répétée et, par conséquent, d'un nombre rationnel. C'est un chiffre irrationnel.
Déterminez si chacun des nombres suivants est rationnel ou irrationnel. Si c'est rationnel, déterminez s'il s'agit d'une décimale finale ou répétée.
- \(\frac{7}{77}\)
- \(\sqrt{81}\)
- \(4.27027002700027…\)
- \(\frac{91}{13}\)
- \(\sqrt{39}\)
- Réponse
-
- rationnel et répétitif ;
- rationnel et définitif ;
- irrationnel ;
- rationnel et définitif ;
- irrationnel
Nombres réels
Quel que soit le nombre\(n\), nous savons que\(n\) c'est rationnel ou irrationnel. Cela ne peut pas être les deux. Les ensembles de nombres rationnels et irrationnels forment ensemble l'ensemble des nombres réels. Comme nous l'avons vu avec les nombres entiers, les nombres réels peuvent être divisés en trois sous-ensembles : les nombres réels négatifs, les nombres réels nuls et les nombres réels positifs. Chaque sous-ensemble comprend des fractions, des décimales et des nombres irrationnels selon leur signe algébrique (+ ou —). Le zéro n'est considéré ni positif ni négatif.
Les nombres réels peuvent être visualisés sur une ligne numérique horizontale avec un point arbitraire choisi comme\(0\), avec des nombres négatifs à gauche\(0\) et des nombres positifs à droite de\(0\). Une distance unitaire fixe est ensuite utilisée pour marquer chaque entier (ou toute autre valeur de base) de chaque côté de\(0\). Tout nombre réel correspond à une position unique sur la ligne numérique. L'inverse est également vrai : chaque position sur la ligne numérique correspond exactement à un nombre réel. C'est ce que l'on appelle une correspondance individuelle. Nous appelons cela la ligne numérique réelle, comme le montre la figure (\(\PageIndex{1}\).

Classifiez chaque nombre comme positif ou négatif et comme rationnel ou irrationnel. Le numéro se trouve-t-il à gauche ou à\(0\) droite de la ligne numérique ?
- \(-\frac{10}{3}\)
- \(-\sqrt{5}\)
- \(-6π\)
- \(0.615384615384…\)
Solution
- \(-\frac{10}{3}\)est négatif et rationnel. Il se trouve à gauche de\(0\) la ligne numérique.
- \(-\sqrt{5}\)est positif et irrationnel. Il se trouve à droite de\(0\).
- \(-\sqrt{289} = -\sqrt{17^2} = -17\)est négatif et rationnel. Il se trouve à gauche de\(0\).
- \(-6π\)est négatif et irrationnel. Il se trouve à gauche de\(0\).
- \(0.615384615384…\)est une décimale répétitive, elle est donc rationnelle et positive. Il se trouve à droite de\(0\).
Classifiez chaque nombre comme positif ou négatif et comme rationnel ou irrationnel. Le numéro se trouve-t-il à gauche ou à\(0\) droite de la ligne numérique ?
- \(\sqrt{73}\)
- \(-11.411411411…\)
- \(\frac{47}{19}\)
- \(-\frac{\sqrt{5}}{2}\)
- \(6.210735\)
- Réponse
-
- positif, irrationnel
- droit, négatif, rationnel
- gauche positive, rationnelle
- droit, négatif, irrationnel
- gauche positif, rationnel ; droite
Ensembles de nombres en tant que sous-ensembles
En commençant par les nombres naturels, nous avons élargi chaque ensemble pour former un ensemble plus grand, ce qui signifie qu'il existe une relation de sous-ensemble entre les ensembles de nombres que nous avons rencontrés jusqu'à présent. Ces relations deviennent plus évidentes lorsqu'elles sont vues sous la forme d'un diagramme, tel que Figure (\(\PageIndex{2}\)).
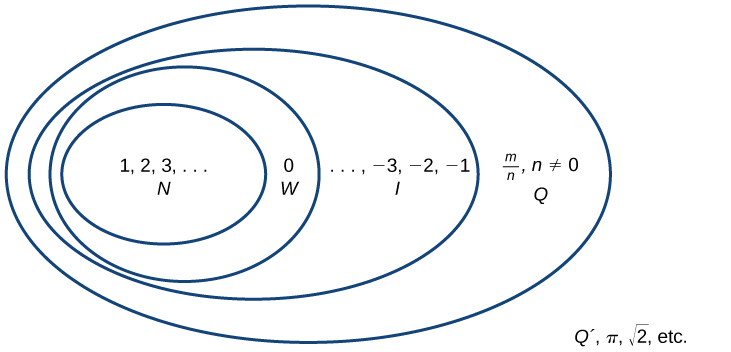
L'ensemble des nombres naturels comprend les nombres utilisés pour compter :\(\{1,2,3,...\}\).
L'ensemble des nombres entiers est l'ensemble des nombres naturels plus zéro :\(\{0,1,2,3,...\}\).
L'ensemble des entiers ajoute les nombres naturels négatifs à l'ensemble des nombres entiers :\(\{...,-3,-2,-1,0,1,2,3,...\}\).
L'ensemble des nombres rationnels comprend des fractions écrites sous la forme\(\{\frac{m}{n} | \text{m and n are integers and } n \neq 0\}\).
L'ensemble des nombres irrationnels est l'ensemble des nombres qui ne sont pas rationnels, qui ne se répètent pas et qui ne se terminent pas :\(\{h\parallel \text{h is not a rational number}\}\).
Classifiez chaque nombre comme étant un entier naturel (N), un nombre entier (W), un entier (I), un nombre rationnel (Q) et/ou un nombre irrationnel (Q′).
- \(\sqrt{36}\)
- \(\frac{8}{3}\)
- \(\sqrt{73}\)
- \(-6\)
- \(3.2121121112…\)
Solution
| N | W | JE | Q | Q' | |
|---|---|---|---|---|---|
| un.\(\sqrt{36} = 6\) | X | X | X | X | |
| b.\(\frac{8}{3} =2.\overline{6}\) | X | ||||
| c.\(\sqrt{73}\) | X | ||||
| d.\(-6\) | X | X | |||
| e.\(3.2121121112...\) | X |
Classifiez chaque nombre comme étant un entier naturel (N), un nombre entier (W), un entier (I), un nombre rationnel (Q) et/ou un nombre irrationnel (Q′).
- \(-\frac{35}{7}\)
- \(0\)
- \(\sqrt{169}\)
- \(\sqrt{24}\)
- \(4.763763763...\)
- Réponse
-
N W JE Q Q' un.\(-\frac{35}{7}\) X X b.\(0\) X X X c.\(\sqrt{169}\) X X X X d.\(\sqrt{24}\) X e.\(4.763763763...\) X
Exécution de calculs en utilisant l'ordre des opérations
Lorsque nous multiplions un nombre par lui-même, nous le mettons au carré ou l'élevons à une puissance de\(2\). Par exemple,\(4^2 =4\times4=16\). Nous pouvons augmenter n'importe quel chiffre à n'importe quelle puissance. En général, la notation exponentielle an signifie que le nombre ou la variable\(a\) est utilisé comme facteur\(n\) fois.
\[a^n=a\cdot a\cdot a\cdots a \qquad \text{ n factors} \nonumber \]
Dans cette notation,\(a^n\) est lu comme la\(n^{th}\) puissance de\(a\), où on\(a\) appelle la base et\(n\) l'exposant. Un terme en notation exponentielle peut faire partie d'une expression mathématique, qui est une combinaison de nombres et d'opérations. Par exemple,\(24+6 \times \dfrac{2}{3} − 4^2\) est une expression mathématique.
Pour évaluer une expression mathématique, nous effectuons les différentes opérations. Cependant, nous ne les exécutons pas dans un ordre aléatoire. Nous utilisons l'ordre des opérations. Il s'agit d'une séquence de règles permettant d'évaluer de telles expressions.
Souvenez-vous qu'en mathématiques, nous utilisons des parenthèses (), des crochets [] et des accolades {} pour regrouper des nombres et des expressions afin que tout ce qui apparaît dans les symboles soit traité comme une unité. De plus, les barres de fraction, les radicaux et les barres de valeurs absolues sont traités comme des symboles de regroupement. Lorsque vous évaluez une expression mathématique, commencez par simplifier les expressions au sein des symboles de regroupement.
L'étape suivante consiste à traiter tous les exposants ou radicaux. Ensuite, effectuez la multiplication et la division de gauche à droite et enfin l'addition et la soustraction de gauche à droite.
Jetons un coup d'œil à l'expression fournie.
\[24+6 \times \dfrac{2}{3} − 4^2 \nonumber\]
Il n'y a pas de symboles de regroupement, nous passons donc aux exposants ou aux radicaux. Le nombre\(4\) est augmenté à une puissance de\(2\), aussi simple\(4^2\) que\(16\).
\[24+6 \times \dfrac{2}{3} − 4^2 \nonumber \]
\[24+6 \times \dfrac{2}{3} − 16 \nonumber\]
Ensuite, effectuez une multiplication ou une division, de gauche à droite.
\[24+6 \times \dfrac{2}{3} − 16 \nonumber\]
\[24+4-16 \nonumber\]
Enfin, effectuez une addition ou une soustraction, de gauche à droite.
\[24+4−16 \nonumber\]
\[28−16 \nonumber\]
\[12 \nonumber\]
Par conséquent,
\[24+6 \times \dfrac{2}{3} − 4^2 =12 \nonumber\]
Pour certaines expressions complexes, plusieurs passages dans l'ordre des opérations seront nécessaires. Par exemple, il peut y avoir une expression radicale entre parenthèses qui doit être simplifiée avant que les parenthèses ne soient évaluées. Le respect de l'ordre des opérations garantit que toute personne simplifiant la même expression mathématique obtiendra le même résultat.
Les opérations dans les expressions mathématiques doivent être évaluées dans un ordre systématique, qui peut être simplifié à l'aide de l'acronyme PEMDAS :
- (parenthèses)
- E (Composants)
- M (multiplication) et D (Division)
- (Addition) et S (soustraction)
- Simplifiez toutes les expressions dans les symboles de regroupement
- Simplifiez toutes les expressions contenant des exposants ou des radicaux.
- Effectuez n'importe quelle multiplication et division dans l'ordre, de gauche à droite.
- Effectuez toutes les additions et soustractions dans l'ordre, de gauche à droite.
Utilisez l'ordre des opérations pour évaluer chacune des expressions suivantes.
- \(\dfrac{5^2-4}{7}- \sqrt{11-2}\)
- \(\dfrac{14-3 \times2}{2 \times5-3^2}\)
- \(7\times(5\times3)−2\times[(6−3)−4^2]+1\)
Solution
- \[\begin{align*} (3\times2)^2-4\times(6+2)&=(6)^2-4\times(8) && \qquad \text{Simplify parentheses}\\ &=36-4\times8 && \qquad \text{Simplify exponent}\\ &=36-32 && \qquad \text{Simplify multiplication}\\ &=4 && \qquad \text{Simplify subtraction}\\ \end{align*}\]
- \[\begin{align*} \dfrac{5^2-4}{7}- \sqrt{11-2}&= \dfrac{5^2-4}{7}-\sqrt{9} && \qquad \text{Simplify grouping symbols (radical)}\\ &=\dfrac{5^2-4}{7}-3 && \qquad \text{Simplify radical}\\ &=\dfrac{25-4}{7}-3 && \qquad \text{Simplify exponent}\\ &=\dfrac{21}{7}-3 && \qquad \text{Simplify subtraction in numerator}\\ &=3-3 && \qquad \text{Simplify division}\\ &=0 && \qquad \text{Simplify subtraction} \end{align*}\]
Notez que dans un premier temps, le radical est traité comme un symbole de regroupement, comme des parenthèses. De plus, dans la troisième étape, la barre de fraction est considérée comme un symbole de regroupement, de sorte que le numérateur est considéré comme groupé.
- \[\begin{align*} 6-\mid 5-8\mid +3\times(4-1)&=6-|-3|+3\times3 && \qquad \text{Simplify inside grouping symbols}\\ &=6-3+3\times3 && \qquad \text{Simplify absolute value}\\ &=6-3+9 && \qquad \text{Simplify multiplication}\\ &=3+9 && \qquad \text{Simplify subtraction}\\ &=12 && \qquad \text{Simplify addition}\\ \end{align*}\]
- \[\begin{align*} \dfrac{14-3 \times2}{2 \times5-3^2}&=\dfrac{14-3 \times2}{2 \times5-9} && \qquad \text{Simplify exponent}\\ &=\dfrac{14-6}{10-9} && \qquad \text{Simplify products}\\ &=\dfrac{8}{1} && \qquad \text{Simplify differences}\\ &=8 && \qquad \text{Simplify quotient}\\ \end{align*}\]
Dans cet exemple, la barre de fraction sépare le numérateur et le dénominateur, que nous simplifions séparément jusqu'à la dernière étape.
- \[\begin{align*} 7\times(5\times3)-2\times[(6-3)-4^2]+1&=7\times(15)-2\times[(3)-4^2]+1 && \qquad \text{Simplify inside parentheses}\\ &=7\times(15)-2\times(3-16)+1 && \qquad \text{Simplify exponent}\\ &=7\times(15)-2\times(-13)+1 && \qquad \text{Subtract}\\ &=105+26+1 && \qquad \text{Multiply}\\ &=132 && \qquad \text{Add} \end{align*}\]
Utilisez l'ordre des opérations pour évaluer chacune des expressions suivantes.
- \(\sqrt{5^2-4^2}+7\times(5-4)^2\)
- \(1+\dfrac{7\times5-8\times4}{9-6}\)
- \(|1.8-4.3|+0.4\times\sqrt{15+10}\)
- \(\dfrac{1}{2}\times[5\times3^2-7^2]+\dfrac{1}{3}\times9^2\)
- \([(3-8^2)-4]-(3-8)\)
- Réponse
-
- \(10\)
- \(2\)
- \(4.5\)
- \(25\)
- \(26\)
Utilisation des propriétés des nombres réels
Pour certaines activités que nous effectuons, l'ordre de certaines opérations n'a pas d'importance, mais l'ordre des autres opérations l'est. Par exemple, cela ne fait aucune différence si nous mettons la bonne chaussure avant la chaussure gauche ou vice versa. Cependant, peu importe que nous mettions d'abord des chaussures ou des chaussettes. Il en va de même pour les opérations en mathématiques.
Propriétés commutatives
La propriété commutative de l'addition indique que les nombres peuvent être ajoutés dans n'importe quel ordre sans affecter la somme.
\[a+b=b+a\]
Nous pouvons mieux voir cette relation en utilisant des nombres réels.
\((−2)+7 = 5 \text{ and } 7+(−2)=5\)
De même, la propriété commutative de la multiplication indique que les nombres peuvent être multipliés dans n'importe quel ordre sans affecter le produit.
\[a\times b=b\times a\]
Encore une fois, prenons un exemple avec des nombres réels.
Il est important de noter que ni la soustraction ni la division ne sont commutatives. Par exemple, ce n'\(17−5\)est pas la même chose que\(5−17\). De même,\(20÷5≠5÷20\).
Propriétés associatives
La propriété associative de la multiplication nous indique que peu importe la façon dont nous regroupons les nombres lors de la multiplication. Nous pouvons déplacer les symboles de regroupement pour faciliter le calcul, et le produit reste le même.
\[a(bc)=(ab)c\]
Prenons cet exemple.
\((3\times4)\times5=60 \text{ and } 3\times(4\times5)=60\)
La propriété associative de l'addition nous indique que les nombres peuvent être regroupés différemment sans affecter la somme.
\[a+(b+c)=(a+b)+c\]
Cette propriété peut être particulièrement utile lorsqu'il s'agit de nombres entiers négatifs. Prenons cet exemple.
\([15+(−9)]+23=29 \text{ and } 15+[(−9)+23]=29\)
La soustraction et la division sont-elles associatives ? Passez en revue ces exemples.
\[\begin{align*} 8-(3-15)\overset{?}{=}&(8-3)-15\\ 8-(-12)\overset{?}{=}&5-15\\ 20 \neq &10\\ 64\div (8\div 4)\overset{?}{=}&(64\div 8)\div 4\\ 64\div 2\overset{?}{=}&8\div 4\\ 32 \neq & 2 \end{align*}\]
Comme on peut le voir, ni la soustraction ni la division ne sont associatives.
Propriété distributive
La propriété distributive indique que le produit d'un facteur par une somme est la somme du facteur multipliée par chaque terme de la somme.
\[a\times(b+c)=a\times b+a\times c\]
Cette propriété combine à la fois l'addition et la multiplication (et est la seule propriété à le faire). Prenons un exemple.
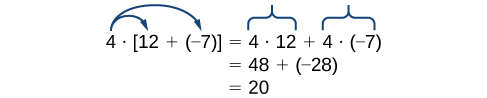
Notez que\(4\) is outside the grouping symbols, so we distribute the \(4\) by multiplying it by \(12\), multiplying it by \(–7\), and adding the products.
To be more precise when describing this property, we say that multiplication distributes over addition. The reverse is not true, as we can see in this example.
\[\begin{align*} 6+(3\times5)\overset{?}{=}&(6+3)\times(6\times5)\\ 6+(15)\overset{?}{=}&(9)\times(11)\\ 21 \neq &99 \end{align*}\]
Multiplication does not distribute over subtraction, and division distributes over neither addition nor subtraction.
A special case of the distributive property occurs when a sum of terms is subtracted.
\[a−b=a+(−b)\]
For example, consider the difference \(12−(5+3)\). We can rewrite the difference of the two terms \(12\) and \((5+3)\) by turning the subtraction expression into addition of the opposite. So instead of subtracting \( (5+3)\), we add the opposite.
Now, distribute \(-1\) and simplify the result.
\[\begin{align*} 12-(5+3)&=12+(-1)\times(5+3)\\ &=12+[(-1)\times5+(-1)\times3]\\ &=12+(-8)\\ &=4 \end{align*}\]
This seems like a lot of trouble for a simple sum, but it illustrates a powerful result that will be useful once we introduce algebraic terms. To subtract a sum of terms, change the sign of each term and add the results. With this in mind, we can rewrite the last example.
\[\begin{align*} 12-(5+3)&=12+(-5-3)\\ &=12-8\\ &=4 \end{align*}\]
Identity Properties
The identity property of addition states that there is a unique number, called the additive identity \((0)\) that, when added to a number, results in the original number.
\[a+0=a\]
The identity property of multiplication states that there is a unique number, called the multiplicative identity \((1)\) that, when multiplied by a number, results in the original number.
\[a\times 1=a\]
For example, we have \( (−6)+0=−6\) and\( 23\times1=23\). There are no exceptions for these properties; they work for every real number, including \(0\) and \(1\).
Inverse Properties
The inverse property of addition states that, for every real number a, there is a unique number, called the additive inverse (or opposite), denoted \(−a\), that, when added to the original number, results in the additive identity, \(0\).
\[a+(−a)=0\]
For example, if \(a =−8\), the additive inverse is \(8\), since \((−8)+8=0\).
The inverse property of multiplication holds for all real numbers except \(0\) because the reciprocal of \(0\) is not defined. The property states that, for every real number \(a\), there is a unique number, called the multiplicative inverse (or reciprocal), denoted \(1a\), that, when multiplied by the original number, results in the multiplicative identity, \(1\).
\[a\times \dfrac{1}{a}=1\]
For example, if \(a =−\dfrac{2}{3}\), the reciprocal, denoted \(\dfrac{1}{a}\), is \(-\dfrac{3}{2}\) because
\[a⋅\dfrac{1}{a}=\left(−\dfrac{2}{3}\right)\times\left(−\dfrac{3}{2}\right)=1 \nonumber\]
The following properties hold for real numbers \(a\), \(b\), and \(c\).
| Addition | Multiplication | |
|---|---|---|
| Commutative Property | \(a+b=b+a\) | \(a\times b=b\times a\) |
| Associative Property | \(a+(b+c)=(a+b)+c\) | \(a(bc)=(ab)c\) |
| Distributive Property | \(a\times (b+c)=a\times b+a\times c\) | |
| Identity Property |
There exists a unique real number called the additive identity, 0, such that, for any real number a \(a+0=a\)
|
There exists a unique real number called the multiplicative identity, 1, such that, for any real number a \(a\times 1=a\)
|
| Inverse Property |
Every real number a has an additive inverse, or opposite, denoted –a, such that \(a+(−a)=0\)
|
Every nonzero real number a has a multiplicative inverse, or reciprocal, denoted 1a , such that \(a\times \left(\dfrac{1}{a}\right)=1\)
|
Use the properties of real numbers to rewrite and simplify each expression. State which properties apply.
- \(3\times 6+3\times 4\)
- \((5+8)+(−8)\)
- \(6−(15+9)\)
- \(\dfrac{4}{7}\times\left(\dfrac{2}{3}\times \dfrac{7}{4}\right)\)
- \(100\times[0.75+(−2.38)]\)
Solution
- \[\begin{align*} 3\times6+3\times4&=3\times(6+4)\qquad \text{Distributive property}\\ &=3\times10\qquad \text{Simplify}\\ &=30\qquad \text{Simplify}\\ \end{align*}\]
- \[\begin{align*} (5+8)+(-8)&=5+[8+(-8)]\qquad \text{Associative property of addition}\\ &=5+0\qquad \text{Inverse property of addition}\\ &=5\qquad \text{Identity property of addition}\\ \end{align*}\]
- \[\begin{align*} 6-(15+9)&=6+[(-15)+(-9)]\qquad \text{Distributive property}\\ &=6+(-24)\qquad \text{Simplify}\\ &=-18\qquad \text{Simplify}\\ \end{align*}\]
- \[\begin{align*} \dfrac{4}{7}\times\left(\dfrac{2}{3}\times\dfrac{7}{4}\right)&=\dfrac{4}{7}\times\left(\dfrac{7}{4}\times\dfrac{2}{3}\right)\qquad \text{Commutative property of multiplication}\\ &=\left(\dfrac{4}{7}\times\dfrac{7}{4}\right)\times\dfrac{2}{3}\qquad \text{Associative property of multiplication}\\ &=1\times\dfrac{2}{3}\qquad \text{Inverse property of multiplication}\\ &=\dfrac{2}{3}\qquad \text{Identity property of multiplication}\\ \end{align*}\]
- \[\begin{align*} 100\times[0.75+(-2.38)]&=100\times0.75+100\times(-2.38)\qquad \text{Distributive property}\\ &=75+(-238)\qquad \text{Simplify}\\ &=-163\qquad \text{Simplify} \end{align*}\]
Use the properties of real numbers to rewrite and simplify each expression. State which properties apply.
- \(\left(-\dfrac{23}{5}\right)\times\left[11\times\left(-\dfrac{5}{23}\right)\right]\)
- \(5\times(6.2+0.4)\)
- \(18-(7-15)\)
- \(\dfrac{17}{18}+\left[\dfrac{4}{9}+\left(-\dfrac{17}{18}\right)\right]\)
- \(6\times(-3)+6\times3\)
- Answer
-
- \(11)\), commutative property of multiplication
- \(33\), distributive property
- \(26\), distributive property
- \(\dfrac{4}{9}\), commutative property of addition, associative property of addition, inverse property of addition, identity property of addition
- \(0\), distributive property, inverse property of addition, identity property of addition
Evaluating Algebraic Expressions
So far, the mathematical expressions we have seen have involved real numbers only. In mathematics, we may see expressions such as \(x +5\), \(\dfrac{4}{3}\pi r^3\), or \(\sqrt{2m^3 n^2}\). In the expression \(x +5\), \(5\) is called a constant because it does not vary and \(x\) is called a variable because it does. (In naming the variable, ignore any exponents or radicals containing the variable.) An algebraic expression is a collection of constants and variables joined together by the algebraic operations of addition, subtraction, multiplication, and division.
We have already seen some real number examples of exponential notation, a shorthand method of writing products of the same factor. When variables are used, the constants and variables are treated the same way.
\[\begin{align*} (-3)^5 &=(-3)\times(-3)\times(-3)\times(-3)\times(-3)\Rightarrow x^5=x\times x\times x\times x\times x\\ (2\times7)^3&=(2\times7)\times(2\times7)\times(2\times7)\qquad \; \; \Rightarrow (yz)^3=(yz)\times(yz)\times(yz) \end{align*}\]
In each case, the exponent tells us how many factors of the base to use, whether the base consists of constants or variables.
Any variable in an algebraic expression may take on or be assigned different values. When that happens, the value of the algebraic expression changes. To evaluate an algebraic expression means to determine the value of the expression for a given value of each variable in the expression. Replace each variable in the expression with the given value, then simplify the resulting expression using the order of operations. If the algebraic expression contains more than one variable, replace each variable with its assigned value and simplify the expression as before.
List the constants and variables for each algebraic expression.
- \(x + 5\)
- \(\dfrac{4}{3}\pi r^3\)
- \(\sqrt{2m^3 n^2}\)
Solution
| Constants | Variables | |
|---|---|---|
| a. \(x + 5\) | \(5\) | \(x\) |
| b. \(\dfrac{4}{3}\pi r^3\) | \(\dfrac{4}{3}\), \(\pi\) | \(r\) |
| c. \(\sqrt{2m^3 n^2}\) | \(2\) | \(m\),\(n\) |
List the constants and variables for each algebraic expression.
- \(2(L + W)\)
- \(4y^3+y\)
- Answer
-
Constants Variables a. \(2\pi r(r+h)\) \(2\),\(\pi\) \(r\),\(h\) b. \(2(L + W)\) \(2\) \(L\), \(W\) c. \(4y^3+y\) \(4\) \(y\)
Evaluate the expression \(2x−7\) for each value for \(x\).
- \(x=0\)
- \(x=1\)
- \(x=12\)
- \(x=−4\)
Solution
- Substitute \(0\) for \(x\). \[\begin{align*} 2x-7 &= 2(0)-7 \\ &= 0-7\\ &= -7\\ \end{align*}\]
- Substitute \(1\) for \(x\). \[\begin{align*} 2x-7 &= 2(1)-7 \\ &= 2-7\\ &= -5\\ \end{align*}\]
- Substitute \(\dfrac{1}{2}\) for \(x\). \[\begin{align*} 2x-7 &= 2\left (\dfrac{1}{2} \right )-7 \\ &= 1-7\\ &= -6\\ \end{align*}\]
- Substitute \(-4\) for \(x\). \[\begin{align*} 2x-7 &= 2(-4)-7 \\ &= -8-7\\ &= -15\\ \end{align*}\]
Evaluate the expression \(11−3y\) for each value for \(y\).
- \(y=2\)
- \(y=0\)
- \(y=\dfrac{2}{3}\)
- \(y=−5\)
- Answer
-
- \(11\)
- \(26\)
Evaluate each expression for the given values.
- \(x+5\) for \(x=-5\)
- \(\dfrac{t}{2t-1}\) for \(t=10\)
- \(\dfrac{4}{3}\pi r^3\) for \(r=5\)
- \(a+ab+b\) for \(a=11\), \(b=-8\)
- \(\sqrt{2m^3 n^2}\) for \(m=2\), \(n=3\)
Solution
- Substitute
\(-5\) for \(x\). \[\begin{align*} x+5 &= (-5)+5 \\ &= 0\\ \end{align*}\] - Substitute \(10\) for \(t\). \[\begin{align*} \dfrac{t}{2t-1} &= \dfrac{(10)}{2(10)-1} \\ &= \dfrac{10}{20-1}\\ &= \dfrac{10}{19}\\ \end{align*}\]
- Substitute \(5\) for \(r\)
. \[\begin{align*} \dfrac{4}{3} \pi r^3 &= \dfrac{4}{3}\pi (5)^3 \\ &= \dfrac{4}{3}\pi (125)\\ &= \dfrac{500}{3}\pi\\ \end{align*}\] - Substitute \(11\) for \(a\) and \(-8\) for \(b\)
. \[\begin{align*} a+ab+b &= (11)+(11)(-8)+(-8) \\ &= 11-88-8 \\ &= -85\\ \end{align*}\] - Substitute \(2\) for \(m\) and \(3\) for \(n\). \[\begin{align*} \sqrt{2m^3 n^2} &= \sqrt{2(2)^3 (3)^2} \\ &= \sqrt{2(8)(9)} \\ &= \sqrt{144} \\ &= 12 \end{align*}\]
Evaluate each expression for the given values.
- \(\dfrac{y+3}{y-3}\) for \(y=5\)
- \(7-2t\) for \(t=-2\)
- \(\dfrac{1}{3}\pi r^2\) for \(r=11\)
- \((p^2 q)^3\) for \(p=-2\), \(q=3\)
- \(4(m-n)-5(n-m)\) for \(m=\dfrac{2}{3}\) \(n=\dfrac{1}{3}\)
- Answer
-
- \(4\)
- \(11\)
- \(\dfrac{121}{3}\pi\)
- \(1728\)
- \(3\)
Formulas
An equation is a mathematical statement indicating that two expressions are equal. The expressions can be numerical or algebraic. The equation is not inherently true or false, but only a proposition. The values that make the equation true, the solutions, are found using the properties of real numbers and other results. For example, the equation \(2x +1= 7\) has the unique solution of \(3\) because when we substitute \(3\) for \(x\) in the equation, we obtain the true statement \(2(3)+1=7\).
A formula is an equation expressing a relationship between constant and variable quantities. Very often, the equation is a means of finding the value of one quantity (often a single variable) in terms of another or other quantities. One of the most common examples is the formula for finding the area \(A\) of a circle in terms of the radius \(r\) of the circle: \( A= \pi r^2\). For any value of \(r\), the area \(A\) can be found by evaluating the expression \(\pi r^2\).
A right circular cylinder with radius \(r\) and height \(h\) has the surface area \(S\) (in square units) given by the formula \(S=2\pi r(r+h)\). See Figure \(\PageIndex{3}\). Find the surface area of a cylinder with radius \(6\) in. and height \(9\) in. Leave the answer in terms of \(\pi\).
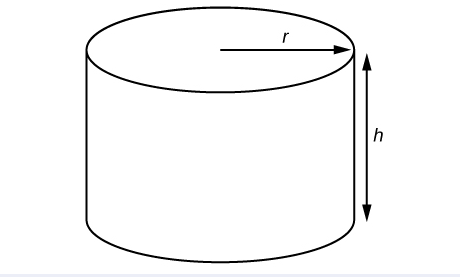
Evaluate the expression \(2\pi r(r+h)\) for \(r=6\) and \(h=9\).
Solution
\[\begin{align*} S &= 2\pi r(r+h) \\ &= 2\pi (6)[(6)+(9)] \\ &= 2\pi(6)(15) \\ &= 180\pi \end{align*}\]
The surface area is \(180\pi\) square inches.
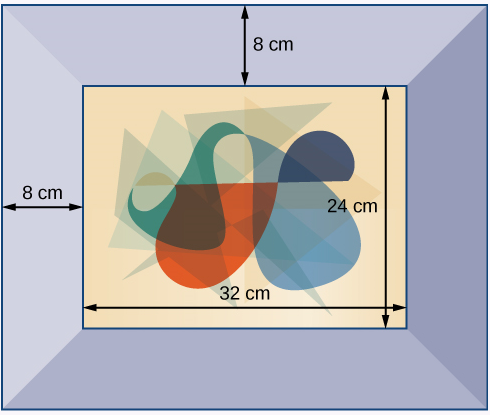
A photograph with length \(L\) and width \(W\) is placed in a matte of width \(8\) centimeters (cm). The area of the matte (in square centimeters, or \(cm^2\) is found to be \(A=(L+16)(W+16) - L\)⋅W
- Answer
-
\(1152cm^2\)
Simplifying Algebraic Expressions
Sometimes we can simplify an algebraic expression to make it easier to evaluate or to use in some other way. To do so, we use the properties of real numbers. We can use the same properties in formulas because they contain algebraic expressions.
Simplify each algebraic expression.
- \(3x-2y+x-3y-7\)
- \(2r-5(3-r)+4\)
- \(\left(4t-\dfrac{5}{4}s\right)-\left(\dfrac{2}{3}t+2s\right)\)
- \(2mn-5m+3mn+n\)
Solution
- \[\begin{align*} 3x-2y+x-3y-7&=3x+x-2y-3y-7 && \qquad \text{Commutative property of addition}\\ &=4x-5y-7 && \qquad \text{Simplify}\\ \end{align*}\]
- \[\begin{align*} 2r-5(3-r)+4&=2r-15+5r+4 && \qquad \qquad \qquad \text {Distributive property}\\ &=2r+5y-15+4 && \qquad \qquad \qquad \text{Commutative property of addition}\\ &=7r-11 && \qquad \qquad \qquad \text{Simplify}\\ \end{align*}\]
- \[\begin{align*} \left(4t-\dfrac{5}{4}s\right)-\left(\dfrac{2}{3}t+2s\right)&=4t-\dfrac{5}{4}s-\dfrac{2}{3}t-2s && \qquad \text{Distributive property}\\ &=4t-\dfrac{2}{3}t-\dfrac{5}{4}s-2s && \qquad \text{Commutative property of addition}\\ &=\dfrac{10}{3}t-\dfrac{13}{4}s && \qquad \text{Simplify}\\ \end{align*}\]
- \[\begin{align*} 2mn-5m+3mn+n&=2mn+3mn-5m+n && \qquad \text{Commutative property of addition}\\ &=5mn-5m+n && \qquad \text{Simplify}\\ \end{align*}\]
Simplify each algebraic expression.
- \(\dfrac{2}{3}y−2\left(\dfrac{4}{3}y+z\right)\)
- \(\dfrac{5}{t}−2−\dfrac{3}{t}+1\)
- \(4p(q−1)+q(1−p)\)
- \(9r−(s+2r)+(6−s)\)
- Answer
-
- \(−2y−2z\) or \(−2(y+z)\)
- \(\dfrac{2}{t}−1\)
- \(3pq−4p+q\)
- \(7r−2s+6\)
A rectangle with length \(L\) and width \(W\) has a perimeter \(P\) given by \(P =L+W+L+W\). Simplify this expression.
Solution
\[\begin{align*} P &=L+W+L+W\\ P &=L+L+W+W && \qquad \text{Commutative property of addition}\\ P &=2L+2W && \qquad \text{Simplify}\\ P &=2(L+W) && \qquad \text{Distributive property} \end{align*}\]
If the amount \(P\) is deposited into an account paying simple interest \(r\) for time \(t\), the total value of the deposit \(A\) is given by \(A =P+Prt\). Simplify the expression. (This formula will be explored in more detail later in the course.)
- Answer
-
\(A=P(1+rt)\)
Access these online resources for additional instruction and practice with real numbers.
Key Concepts
- Rational numbers may be written as fractions or terminating or repeating decimals. See Example and Example.
- Determine whether a number is rational or irrational by writing it as a decimal. See Example.
- The rational numbers and irrational numbers make up the set of real numbers. See Example. A number can be classified as natural, whole, integer, rational, or irrational. See Example.
- The order of operations is used to evaluate expressions. See Example.
- The real numbers under the operations of addition and multiplication obey basic rules, known as the properties of real numbers. These are the commutative properties, the associative properties, the distributive property, the identity properties, and the inverse properties. See Example.
- Algebraic expressions are composed of constants and variables that are combined using addition, subtraction, multiplication, and division. See Example. They take on a numerical value when evaluated by replacing variables with constants. See Example,Example, and Example
- Formulas are equations in which one quantity is represented in terms of other quantities. They may be simplified or evaluated as any mathematical expression. See Example and Example.
Glossary
- algebraic expression
- constants and variables combined using addition, subtraction, multiplication, and division
- associative property of addition
- the sum of three numbers may be grouped differently without affecting the result; in symbols,a+(b+c)=(a+b)+c
- associative property of multiplication
- the product of three numbers may be grouped differently without affecting the result; in symbols,a⋅(b⋅c)=(a⋅b)⋅c
- base
- in exponential notation, the expression that is being multiplied
- commutative property of addition
- two numbers may be added in either order without affecting the result; in symbols,a+b=b+a
- commutative property of multiplication
- two numbers may be multiplied in any order without affecting the result; in symbols,a⋅b=b⋅a
- constant
- a quantity that does not change value
- distributive property
- the product of a factor times a sum is the sum of the factor times each term in the sum; in symbols,a⋅(b+c)=a⋅b+a⋅c
- equation
- a mathematical statement indicating that two expressions are equal
- exponent
- in exponential notation, the raised number or variable that indicates how many times the base is being multiplied
- exponential notation
- a shorthand method of writing products of the same factor
- formula
- an equation expressing a relationship between constant and variable quantities
- identity property of addition
- there is a unique number, called the additive identity, 0, which, when added to a number, results in the original number; in symbols,a+0=a
- identity property of multiplication
- there is a unique number, called the multiplicative identity, 1, which, when multiplied by a number, results in the original number; in symbols,a⋅1=a
- integers
- the set consisting of the natural numbers, their opposites, and 0:{…,−3,−2,−1,0,1,2,3,…}
- inverse property of addition
- for every real numbera,there is a unique number, called the additive inverse (or opposite), denoted−a,which, when added to the original number, results in the additive identity, 0; in symbols,a+(−a)=0
- inverse property of multiplication
- for every non-zero real numbera,there is a unique number, called the multiplicative inverse (or reciprocal), denoted1a,which, when multiplied by the original number, results in the multiplicative identity, 1; in symbols,a⋅1a=1
- irrational numbers
- the set of all numbers that are not rational; they cannot be written as either a terminating or repeating decimal; they cannot be expressed as a fraction of two integers
- natural numbers
- the set of counting numbers:{1,2,3,…}
- order of operations
- a set of rules governing how mathematical expressions are to be evaluated, assigning priorities to operations
- rational numbers
- the set of all numbers of the formmn,wheremandnare integers andn≠0.Any rational number may be written as a fraction or a terminating or repeating decimal.
- real number line
- a horizontal line used to represent the real numbers. An arbitrary fixed point is chosen to represent 0; positive numbers lie to the right of 0 and negative numbers to the left.
- real numbers
- the sets of rational numbers and irrational numbers taken together
- variable
- a quantity that may change value
- whole numbers
- the set consisting of 0 plus the natural numbers:{0,1,2,3,…}


