6.1 : Énergie électromagnétique

Last updated
Save as PDF

Page ID: 193928

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objectifs d'apprentissage

Expliquer le comportement de base des vagues, y compris les ondes progressives et les ondes stationnaires
Décrire la nature ondulatoire de la lumière
Utilisez les équations appropriées pour calculer les propriétés des ondes lumineuses connexes, telles que la période, la fréquence, la longueur d'onde et l'énergie
Distinguer les spectres d'émission linéaires et continus
Décrire la nature particulaire de la lumière

La nature de la lumière fait l'objet de recherches depuis l'Antiquité. Au XVIIe siècle, Isaac Newton a réalisé des expériences avec des lentilles et des prismes et a pu démontrer que la lumière blanche est constituée des différentes couleurs de l'arc-en-ciel combinées. Newton a expliqué ses découvertes en optique en termes de vision « corpusculaire » de la lumière, dans laquelle la lumière était composée de flux de particules extrêmement minuscules se déplaçant à des vitesses élevées selon les lois du mouvement de Newton. D'autres au XVIIe siècle, comme Christiaan Huygens, avaient montré que les phénomènes optiques tels que la réflexion et la réfraction pouvaient être expliqués aussi bien en termes de lumière que d'ondes se déplaçant à grande vitesse dans un milieu appelé « éther luminifère » censé imprégner tout l'espace. Au début du XIXe siècle, Thomas Young a démontré que la lumière traversant des fentes étroites et rapprochées produisait des modèles d'interférence qui ne pouvaient pas être expliqués en termes de particules newtoniennes mais qui pouvaient être facilement expliqués en termes d'ondes. Plus tard au XIXe siècle, après que James Clerk Maxwell ait développé sa théorie du rayonnement électromagnétique et démontré que la lumière était la partie visible d'un vaste spectre d'ondes électromagnétiques, la vision des particules de la lumière a été complètement discréditée. À la fin du XIXe siècle, les scientifiques considéraient l'univers physique comme comprenant à peu près deux domaines distincts : la matière composée de particules se déplaçant selon les lois du mouvement de Newton et le rayonnement électromagnétique constitué d'ondes régies par les équations de Maxwell. Aujourd'hui, ces domaines sont appelés mécanique classique et électrodynamique classique (ou électromagnétisme classique). Bien que certains phénomènes physiques n'aient pas pu être expliqués dans ce cadre, les scientifiques de l'époque étaient tellement confiants dans la solidité globale de ce cadre qu'ils considéraient ces aberrations comme des paradoxes déroutants qui finiraient par être résolus d'une manière ou d'une autre dans ce cadre. Comme nous le verrons, ces paradoxes ont conduit à un cadre contemporain qui relie intimement les particules et les ondes à un niveau fondamental appelé dualité onde-particule, qui a dépassé la vision classique.

La lumière visible et d'autres formes de rayonnement électromagnétique jouent un rôle important en chimie, car elles peuvent être utilisées pour déduire l'énergie des électrons dans les atomes et les molécules. Une grande partie de la technologie moderne repose sur le rayonnement électromagnétique. Par exemple, les ondes radio émises par un téléphone portable, les rayons X utilisés par les dentistes, l'énergie utilisée pour cuire les aliments dans votre four à micro-ondes, la chaleur rayonnante des objets chauffés au rouge et la lumière de votre écran de télévision sont des formes de rayonnement électromagnétique qui présentent toutes un comportement ondulatoire.

Vagues

Une onde est une oscillation ou un mouvement périodique qui peut transporter de l'énergie d'un point de l'espace à un autre. Des exemples courants de vagues se trouvent tout autour de nous. Le fait de secouer le bout d'une corde permet de transférer l'énergie de votre main à l'autre bout de la corde, le fait tomber un caillou dans un étang provoque l'ondulation des vagues vers l'extérieur le long de la surface de l'eau, et l'expansion de l'air qui accompagne un coup de foudre génère des ondes sonores (tonnerre) qui peuvent se déplacer vers l'extérieur sur plusieurs kilomètres. Dans chacun de ces cas, l'énergie cinétique est transférée par la matière (la corde, l'eau ou l'air) alors que la matière reste essentiellement en place. Un exemple éloquent de vague se produit dans les stades de sport lorsque des supporters assis dans une zone étroite de sièges se lèvent simultanément et se tiennent debout les bras levés pendant quelques secondes avant de s'asseoir à nouveau, tandis que les supporters des sections voisines se lèvent et s'assoient également en séquence. Bien que cette vague puisse rapidement encercler un grand stade en quelques secondes, aucun des supporters ne voyage réellement avec la vague : ils restent tous assis ou au-dessus de leur siège.

Il n'est pas nécessaire que les vagues se déplacent à travers la matière. Comme Maxwell l'a montré, les ondes électromagnétiques consistent en un champ électrique oscillant au même rythme qu'un champ magnétique perpendiculaire, les deux étant perpendiculaires à la direction de déplacement. Ces ondes peuvent se déplacer dans le vide à une vitesse constante de 2,998 × 10 ⁸ m/s, la vitesse de la lumière (indiquée par c).

Toutes les ondes, y compris les formes de rayonnement électromagnétique, sont caractérisées par une longueur d'onde (désignée par λ, la lettre grecque minuscule lambda), une fréquence (désignée par νm, la lettre grecque minuscule nu) et une amplitude. Comme on peut le voir sur la figure\(\PageIndex{1}\), la longueur d'onde est la distance entre deux pics ou creux consécutifs d'une onde (mesurée en mètres dans le système SI). Les ondes électromagnétiques ont des longueurs d'onde qui se situent dans une gamme énorme : des longueurs d'onde allant de kilomètres (10 ³ m) à des picomètres (10 ^-12 m) ont été observées. La fréquence est le nombre de cycles d'ondes qui passent un point précis de l'espace dans un laps de temps donné (dans le système SI, cela est mesuré en secondes). Un cycle correspond à une longueur d'onde complète. L'unité de fréquence, exprimée en cycles par seconde [s ^-1], est le hertz (Hz). Les multiples courants de cette unité sont le mégahertz (1 MHz = 1 × 10 ⁶ Hz) et le gigahertz (1 GHz = 1 × 10 ⁹ Hz). L'amplitude correspond à l'amplitude du déplacement de l'onde et, sur la figure, cela correspond à la moitié de la hauteur entre les pics et les creux. L'amplitude est liée à l'intensité de l'onde, qui pour la lumière est la luminosité, et pour le son, le volume.

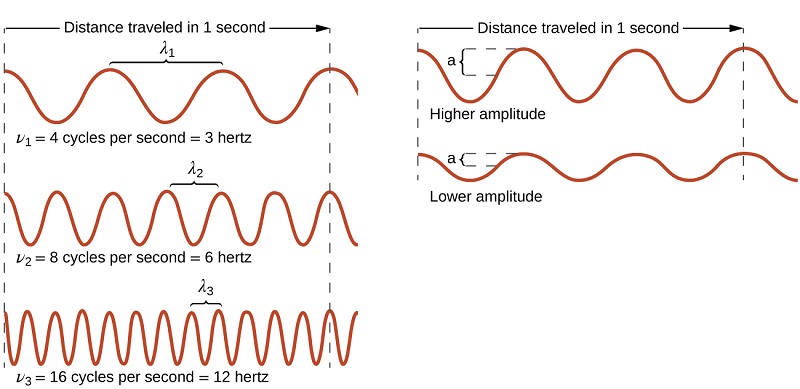
Figure\(\PageIndex{1}\) : Les ondes sinusoïdales unidimensionnelles montrent la relation entre la longueur d'onde, la fréquence et la vitesse. L'onde ayant la longueur d'onde la plus courte a la fréquence la plus élevée. L'amplitude correspond à la moitié de la hauteur de l'onde du pic au creux. (CC par 4.0 ; OpenStax)

Le produit de la longueur d'onde (λ) d'une onde et de sa fréquence (νm), λνm, est la vitesse de l'onde. Ainsi, pour le rayonnement électromagnétique dans le vide :

\[c=\mathrm{2.998×10^8\,ms^{−1}}=λν \label{6.2.1} \]

La longueur d'onde et la fréquence sont inversement proportionnelles : lorsque la longueur d'onde augmente, la fréquence diminue. La proportionnalité inverse est illustrée dans la figure\(\PageIndex{2}\). Cette figure montre également le spectre électromagnétique, la gamme de tous les types de rayonnements électromagnétiques. Chacune des différentes couleurs de lumière visible est associée à des fréquences et à des longueurs d'onde spécifiques, et vous pouvez constater que la lumière visible ne représente qu'une petite partie du spectre électromagnétique. Comme les technologies développées pour fonctionner dans différentes parties du spectre électromagnétique sont différentes, pour des raisons de commodité et d'héritage historique, différentes unités sont généralement utilisées pour différentes parties du spectre. Par exemple, les ondes radio sont généralement spécifiées sous forme de fréquences (généralement en unités de MHz), tandis que la région visible est généralement spécifiée en longueurs d'onde (généralement en unités de nm ou d'angströms).

Figure\(\PageIndex{2}\) : Les parties du spectre électromagnétique sont présentées par ordre décroissant de fréquence et longueur d'onde croissante. Parmi les applications pour différentes longueurs d'onde, citons la tomographie par émission de positons (TEP), l'imagerie par rayons X, les télécommandes, l'Internet sans fil, les téléphones cellulaires et les radios. (crédit « Rayon cosmique » : modification des travaux de la NASA ; crédit « PET scan » : modification des travaux du National Institute of Health ; crédit « X-ray » : modification des travaux du Dr Jochen Lengerke ; crédit « Dental cure » : modification des travaux par le ministère de la Marine ; crédit « Vision nocturne » : modification du travail par le Département de l'armée ; crédit « Remote » : modification de l'œuvre par Emilian Robert Vicol ; crédit « Téléphone portable » : modification de l'œuvre par Brett Jordan ; crédit « Four à micro-ondes » : modification de l'œuvre par Billy Mabray ; crédit « Ultrasound » : modification de l'œuvre par Jane Whitney ; crédit « Radio AM » : modification de l'œuvre par Dave Clausen)

Exemple\(\PageIndex{1}\): Determining the Frequency and Wavelength of Radiation

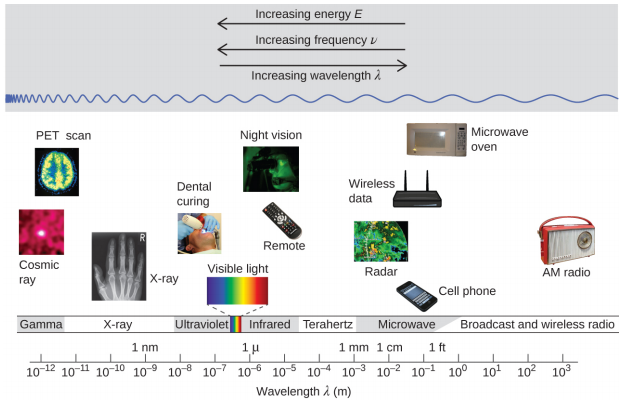
Un lampadaire au sodium émet une lumière jaune d'une longueur d'onde de 589 nm (1 nm = 1 × 10 ⁻⁹ m). Quelle est la fréquence de cette lumière ?

Solution

Nous pouvons réarranger l'équation \ ref {6.2.1} pour résoudre la fréquence :

\[ \nu=\dfrac{c}{λ} \nonumber \]

Puisque c est exprimé en mètres par seconde, il faut également convertir 589 nm en mètres.

\[ \nu=\mathrm{\left(\dfrac{2.998×10^8\:\cancel{m}s^{−1}}{589\cancel{nm}}\right)\left(\dfrac{1×10^9\cancel{nm}}{1\cancel{m}}\right)=5.09×10^{14}\,s^{−1}} \nonumber \]

Exercice\(\PageIndex{1}\)

L'une des fréquences utilisées pour transmettre et recevoir des signaux de téléphonie cellulaire aux États-Unis est la fréquence 850 MHz. Quelle est la longueur d'onde en mètres de ces ondes radio ?

Réponse: 0,353 m = 35,3 cm

Communication sans fil

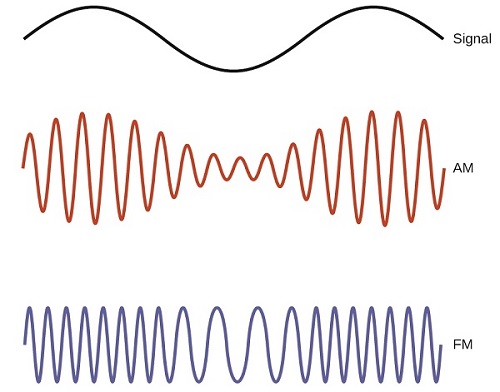
De nombreuses technologies intéressantes fonctionnent dans la région des fréquences radio (3 kHz-300 GHz) du spectre électromagnétique. À l'extrémité basse fréquence (basse énergie, longue longueur d'onde) de cette région se trouvent des signaux radio AM (modulation d'amplitude) (540-2830 kHz) qui peuvent parcourir de longues distances. Les signaux radio FM (modulation de fréquence) sont utilisés à des fréquences plus élevées (87,5-108,0 MHz). En radio AM, les informations sont transmises en faisant varier l'amplitude de l'onde (Figure\(\PageIndex{5}\)). En radio FM, en revanche, l'amplitude est constante et la fréquence instantanée varie.

alt — Figure\(\PageIndex{3}\) : Les tours radio et cellulaires sont généralement utilisées pour transmettre des rayonnements électromagnétiques de grande longueur d'onde. De plus en plus, les tours cellulaires sont conçues pour se fondre dans le paysage, comme c'est le cas pour la tour cellulaire de Tucson, en Arizona (à droite) déguisée en palmier. (crédit gauche : modification de l'œuvre de Sir Mildred Pierce ; crédit au milieu : modification de l'œuvre de M.O. Stevens)

D'autres technologies fonctionnent également dans la partie du spectre électromagnétique consacrée aux ondes radio. Par exemple, les signaux des téléphones cellulaires 4G sont d'environ 880 MHz, tandis que les signaux du système de positionnement mondial (GPS) fonctionnent à 1,228 et 1,575 GHz, les réseaux locaux sans fil (Wi-Fi) fonctionnent de 2,4 à 5 GHz et les capteurs de péage routier fonctionnent à 5,8 GHz. Les fréquences associées à ces applications sont pratiques car ces ondes ont tendance à être peu absorbées par les matériaux de construction courants.

alt — Figure\(\PageIndex{4}\) : Ce schéma montre comment la modulation d'amplitude (AM) et la modulation de fréquence (FM) peuvent être utilisées pour transmettre une onde radio.

Un phénomène particulièrement caractéristique des ondes se produit lorsque deux ondes ou plus entrent en contact : elles interfèrent les unes avec les autres. La figure\(\PageIndex{5}\) montre les modèles d'interférence qui se produisent lorsque la lumière passe à travers des fentes étroites étroitement espacées d'une longueur d'onde. Les motifs de franges produits dépendent de la longueur d'onde, les franges étant plus rapprochées pour que la lumière de longueur d'onde plus courte traverse un ensemble donné de fentes. Lorsque la lumière passe à travers les deux fentes, chaque fente agit efficacement comme une nouvelle source, ce qui fait que deux ondes rapprochées entrent en contact avec le détecteur (la caméra dans ce cas). Les régions sombres de la figure\(\PageIndex{5}\) correspondent aux régions où les pics de l'onde d'une fente coïncident avec les creux de l'onde provenant de l'autre fente (interférence destructrice), tandis que les régions les plus claires correspondent aux régions où les pics des deux ondes (ou de leurs deux creux) coïncident (interférence constructive). De même, lorsque deux pierres sont projetées l'une contre l'autre dans un étang, des motifs d'interférence sont visibles dans les interactions entre les vagues produites par les pierres. Ces modèles d'interférence ne peuvent pas être expliqués par le fait que les particules se déplacent selon les lois de la mécanique classique.

alt — Figure\(\PageIndex{5}\) : Des motifs de franges d'interférence sont illustrés pour la lumière traversant deux fentes étroites et rapprochées. L'espacement des franges dépend de la longueur d'onde, les franges étant plus rapprochées pour la lumière bleue de longueur d'onde plus courte. (crédit : PASCO)

Dorothy Hodgkin

Comme les longueurs d'onde des rayons X (10 à 10 000 picomètres [pm]) sont comparables à la taille des atomes, les rayons X peuvent être utilisés pour déterminer la structure des molécules. Lorsqu'un faisceau de rayons X traverse des molécules regroupées dans un cristal, les rayons X entrent en collision avec les électrons et se diffusent. Les interférences constructives et destructives de ces rayons X diffusés créent un diagramme de diffraction spécifique. En calculant à rebours à partir de ce schéma, les positions de chacun des atomes de la molécule peuvent être déterminées très précisément. Dorothy Crowfoot Hodgkin est l'une des pionnières qui ont contribué à la création de cette technologie.

Elle est née au Caire, en Égypte, en 1910, où ses parents britanniques étudiaient l'archéologie. Dès son plus jeune âge, elle était fascinée par les minéraux et les cristaux. Lorsqu'elle était étudiante à l'université d'Oxford, elle a commencé à étudier comment la cristallographie aux rayons X pouvait être utilisée pour déterminer la structure des biomolécules. Elle a inventé de nouvelles techniques qui lui ont permis, à elle et à ses étudiants, de déterminer les structures de la vitamine B ₁₂, de la pénicilline et de nombreuses autres molécules importantes. Le diabète, une maladie qui touche 382 millions de personnes dans le monde, implique l'hormone insuline. Hodgkin a commencé à étudier la structure de l'insuline en 1934, mais il a fallu plusieurs décennies de progrès dans le domaine avant de finalement présenter la structure en 1969. La compréhension de la structure a permis de mieux comprendre la maladie et les options de traitement.

Toutes les vagues ne sont pas des vagues progressives. Les ondes stationnaires (également appelées ondes stationnaires) restent limitées dans certaines régions de l'espace. Comme nous le verrons, les ondes stationnaires jouent un rôle important dans notre compréhension de la structure électronique des atomes et des molécules. L'exemple le plus simple d'onde stationnaire est une onde unidimensionnelle associée à une corde vibrante maintenue fixe à ses deux extrémités. La figure\(\PageIndex{6}\) montre les quatre ondes stationnaires de plus faible énergie (l'onde fondamentale et les trois harmoniques les plus faibles) pour une corde vibrante à une amplitude donnée. Bien que le mouvement de la corde se situe principalement dans un plan, l'onde elle-même est considérée comme unidimensionnelle, puisqu'elle se trouve sur toute la longueur de la corde. Le mouvement des segments de corde dans une direction perpendiculaire à la longueur de la corde génère les ondes et l'amplitude des ondes est donc visible comme le déplacement maximal des courbes visibles sur la figure\(\PageIndex{6}\). La principale observation de la figure est que seules les ondes ayant un nombre entier, n, de demi-longueurs d'onde entre les points d'extrémité peuvent se former. Un système avec des points d'extrémité fixes comme celui-ci limite le nombre et le type de formes d'onde possibles. Il s'agit d'un exemple de quantification, dans lequel seules les valeurs discrètes d'un ensemble plus général de valeurs continues d'une propriété sont observées. Une autre observation importante est que les ondes harmoniques (les ondes affichant plus de la moitié de la longueur d'onde) ont toutes un ou plusieurs points entre les deux extrémités qui ne sont pas en mouvement. Ces points spéciaux sont des nœuds. Les énergies des ondes stationnaires d'une amplitude donnée dans une corde vibrante augmentent avec le nombre de demi-longueurs d'onde n. Comme le nombre de nœuds est de n à 1, on peut également dire que l'énergie dépend du nombre de nœuds, augmentant généralement à mesure que le nombre de nœuds augmente.

alt — Figure\(\PageIndex{6}\) : Une corde vibrante montre des ondes stationnaires unidimensionnelles. Comme les deux extrémités de la chaîne sont maintenues fixes, seules des ondes ayant un nombre entier de demi-longueurs d'onde peuvent se former. Les points de la chaîne situés entre les extrémités qui ne bougent pas sont appelés nœuds.

Un exemple d'ondes stationnaires bidimensionnelles est illustré dans la figure\(\PageIndex{7}\) qui montre les modèles vibratoires sur une surface plane. Bien que les amplitudes vibratoires ne soient pas visibles comme elles le pouvaient dans la corde vibrante, les nœuds ont été rendus visibles en saupoudrant la surface du tambour d'une poudre qui s'accumule sur les zones de la surface ayant un déplacement minimal. Pour les ondes stationnaires unidimensionnelles, les nœuds étaient des points sur la ligne, mais pour les ondes stationnaires bidimensionnelles, les nœuds sont des lignes sur la surface (pour les ondes stationnaires tridimensionnelles, les nœuds sont des surfaces bidimensionnelles au sein du volume tridimensionnel). En raison de la symétrie circulaire de la surface du tambour, ses conditions limites (la surface du tambour étant étroitement limitée à la circonférence du tambour) se traduisent par deux types de nœuds : les nœuds radiaux qui balaient tous les angles à des rayons constants et sont donc considérés comme des cercles autour du centre, et les nœuds angulaires qui balayer tous les rayons à des angles constants et sont donc considérés comme des lignes passant par le centre. L'image en haut à gauche de la figure\(\PageIndex{7}\) montre deux nœuds radiaux, tandis que l'image en bas à droite montre le motif vibratoire associé à trois nœuds radiaux et à deux nœuds angulaires.

alt — Figure\(\PageIndex{7}\) : Des ondes stationnaires bidimensionnelles peuvent être visualisées sur une surface vibrante. La surface a été saupoudrée d'une poudre qui s'accumule près des lignes nodales. Il existe deux types de nœuds visibles : les nœuds radiaux (cercles) et les nœuds angulaires (rayons). Pour une vidéo plus animée, consultez ce lien.

Le rayonnement du corps noir et la catastrophe des ultraviolets

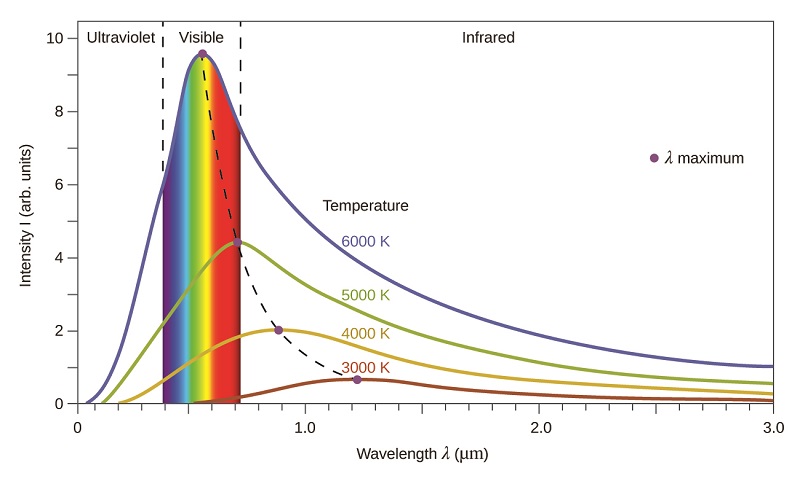
Les dernières décennies du XIXe siècle ont été marquées par une intense activité de recherche visant à commercialiser des éclairages électriques récemment découverts. Cela a nécessité de mieux comprendre les distributions de la lumière émise par les différentes sources considérées. L'éclairage artificiel est généralement conçu pour imiter la lumière naturelle du soleil dans les limites de la technologie sous-jacente. Cet éclairage consiste en une gamme de fréquences largement distribuées qui forment un spectre continu. La figure\(\PageIndex{8}\) montre la distribution des longueurs d'onde de la lumière solaire Le rayonnement le plus intense se trouve dans la région visible, l'intensité diminuant rapidement pour les rayons ultraviolets (UV) de plus courte longueur d'onde, et plus lentement pour les rayons infrarouges (IR) de plus grande longueur d'onde.

alt — Figure\(\PageIndex{8}\) : La distribution spectrale (intensité lumineuse par rapport à la longueur d'onde) de la lumière solaire atteint l'atmosphère de la Terre sous forme de lumière ultraviolette, de lumière visible et de lumière infrarouge. La lumière solaire non absorbée au sommet de l'atmosphère a une distribution qui correspond approximativement à la distribution théorique d'un corps noir à 5250 °C, représentée par la courbe bleue. (source : modification des travaux de l'American Society for Testing and Materials (ASTM) Terrestrial Reference Spectra for Photovoltaic Performance Evaluation)

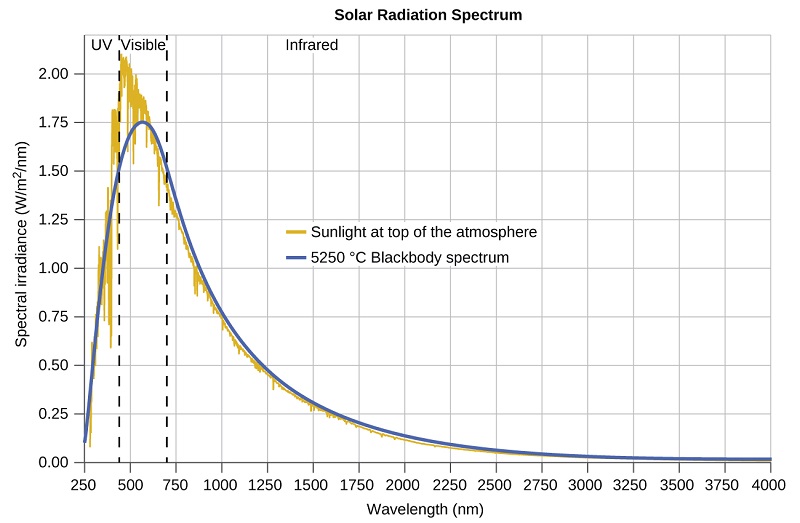
Sur la figure\(\PageIndex{8}\), la distribution solaire est comparée à une distribution représentative, appelée spectre du corps noir, qui correspond à une température de 5250 °C. Le spectre du corps noir correspond assez bien au spectre solaire. Un corps noir est un émetteur pratique et idéal qui se rapproche du comportement de nombreux matériaux lorsqu'il est chauffé. Il est « idéal » dans le même sens qu'un gaz idéal est une représentation simple et pratique de gaz réels qui fonctionne bien, à condition que la pression ne soit pas trop élevée ni que la température ne soit trop basse. Une bonne approximation d'un corps noir qui peut être utilisée pour observer le rayonnement du corps noir est un four métallique qui peut être chauffé à de très hautes températures. Le four comporte un petit trou permettant d'observer la lumière émise à l'intérieur du four à l'aide d'un spectromètre afin de mesurer les longueurs d'onde et leurs intensités. La figure\(\PageIndex{8}\) montre les courbes résultantes pour certaines températures représentatives. Chaque distribution ne dépend que d'un seul paramètre : la température. Les maxima des courbes du corps noir, λ _max, passent à des longueurs d'onde plus courtes à mesure que la température augmente, reflétant l'observation selon laquelle les métaux chauffés à des températures élevées commencent à briller d'un rouge plus foncé qui devient plus vif à mesure que la température augmente, pour finir par devenir blanc chaud à des températures très élevées lorsque les intensités de toutes les longueurs d'onde visibles deviennent appréciables. Cette observation commune a été au cœur du premier paradoxe qui a mis en évidence les limites fondamentales de la physique classique que nous allons examiner.

Les physiciens ont dérivé des expressions mathématiques pour les courbes du corps noir en utilisant des concepts bien acceptés issus des théories de la mécanique classique et de l'électromagnétisme classique. Les expressions théoriques en tant que fonctions de la température s'adaptent bien aux courbes expérimentales du corps noir observées à de plus grandes longueurs d'onde, mais présentent des différences significatives à des longueurs d'onde plus courtes. Non seulement les courbes théoriques ne montraient pas de pic, mais elles montraient de manière absurde que l'intensité devenait infiniment plus grande à mesure que la longueur d'onde diminuait, ce qui impliquerait que les objets du quotidien à température ambiante devraient émettre de grandes quantités de lumière ultraviolette. Cela a été connu sous le nom de « catastrophe ultraviolette » parce que personne n'a pu trouver de problèmes avec le traitement théorique qui pourrait conduire à un comportement aussi irréaliste sur les courtes longueurs d'onde. Enfin, vers 1900, Max Planck a dérivé une expression théorique du rayonnement du corps noir qui correspond exactement aux observations expérimentales (dans les limites de l'erreur expérimentale). Planck a développé son traitement théorique en prolongeant les travaux antérieurs qui reposaient sur la prémisse que les atomes composant le four vibraient à des fréquences croissantes (ou des longueurs d'onde décroissantes) à mesure que la température augmentait, ces vibrations étant la source du rayonnement électromagnétique émis . Mais là où les traitements antérieurs avaient permis aux atomes vibrants d'avoir n'importe quelle valeur énergétique obtenue à partir d'un ensemble continu d'énergies (parfaitement raisonnable, selon la physique classique), Planck a découvert qu'en limitant les énergies vibratoires à des valeurs discrètes pour chaque fréquence, il pouvait déduire un expression du rayonnement du corps noir dont l'intensité diminuait rapidement et correctement pour les courtes longueurs d'onde de la région des UV.

\[E=nhν,\:n=1,2,3,\:. . . \nonumber \]

La quantité h est une constante maintenant connue sous le nom de constante de Planck, en son honneur. Bien que Planck soit content d'avoir résolu le paradoxe des radiations du corps noir, il était troublé de devoir supposer que les atomes vibrants nécessitaient des énergies quantifiées, ce qu'il n'était pas en mesure d'expliquer. La valeur de la constante de Planck est très faible, 6,626 × 10 ⁻³⁴ joules secondes (J s), ce qui permet d'expliquer pourquoi la quantification de l'énergie n'avait pas été observée auparavant dans les phénomènes macroscopiques.

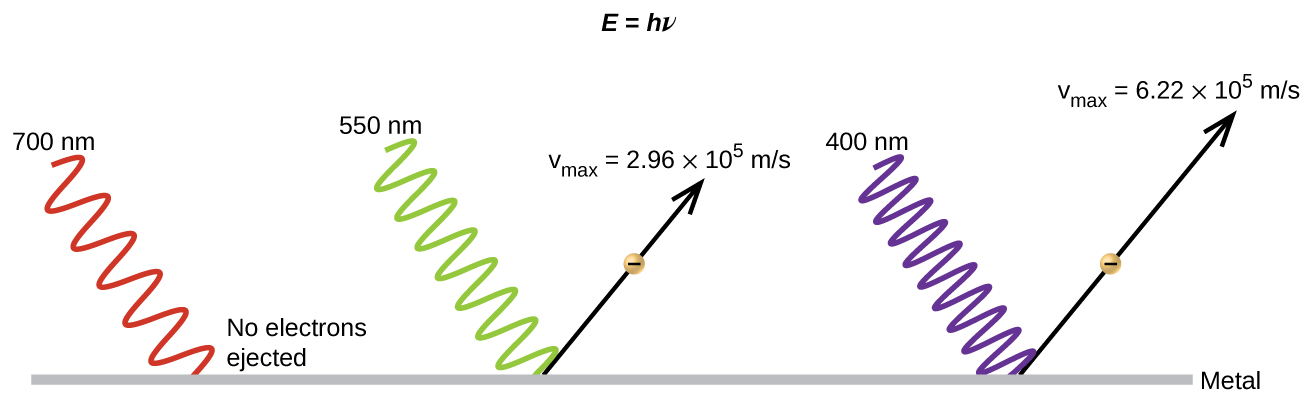
Figure\(\PageIndex{9}\) : Les courbes de distribution spectrale du corps noir sont présentées pour certaines températures représentatives.

L'effet photoélectrique

Le paradoxe suivant de la théorie classique à résoudre concerne l'effet photoélectrique (Figure\(\PageIndex{10}\)). Il avait été observé que des électrons pouvaient être éjectés de la surface propre d'un métal lorsque de la lumière d'une fréquence supérieure à une certaine fréquence seuil était projetée sur celui-ci. Étonnamment, l'énergie cinétique des électrons éjectés ne dépendait pas de la luminosité de la lumière, mais augmentait avec l'augmentation de la fréquence de la lumière. Comme les électrons du métal possédaient une certaine quantité d'énergie de liaison pour les maintenir, la lumière incidente avait besoin de plus d'énergie pour libérer les électrons. Selon la théorie classique des ondes, l'énergie d'une onde dépend de son intensité (qui dépend de son amplitude) et non de sa fréquence. Une partie de ces observations était que le nombre d'électrons éjectés à l'intérieur d'une période donnée augmentait à mesure que la luminosité augmentait. En 1905, Albert Einstein a réussi à résoudre le paradoxe en incorporant les résultats de quantification de Planck à la vision discréditée des particules de la lumière (Einstein a d'ailleurs remporté son prix Nobel pour cet ouvrage, et non pour ses théories de la relativité pour lesquelles il est le plus célèbre).

Einstein a soutenu que les énergies quantifiées que Planck avait postulées dans son traitement du rayonnement du corps noir pouvaient être appliquées à la lumière par effet photoélectrique, de sorte que la lumière frappant la surface métallique ne devait pas être considérée comme une onde, mais plutôt comme un flux de particules (appelées plus tard photons). ) dont l'énergie dépendait de leur fréquence, selon la formule de Planck, E = hβ (ou, en termes de longueur d'onde, en utilisant c = νλ,\(E=\dfrac{hc}{λ}\)). Les électrons étaient éjectés lorsqu'ils étaient touchés par des photons ayant une énergie suffisante (une fréquence supérieure au seuil). Plus la fréquence est élevée, plus l'énergie cinétique transmise aux électrons qui s'échappent par les collisions est importante. Einstein a également fait valoir que l'intensité lumineuse ne dépendait pas de l'amplitude de l'onde entrante, mais correspondait plutôt au nombre de photons frappant la surface au cours d'une période donnée. Cela explique pourquoi le nombre d'électrons éjectés augmentait avec l'augmentation de la luminosité, car plus le nombre de photons entrants était élevé, plus ils risquaient d'entrer en collision avec certains des électrons.

Avec les découvertes d'Einstein, la nature de la lumière a pris un nouvel air de mystère. Bien que de nombreux phénomènes lumineux puissent être expliqués en termes d'ondes ou de particules, certains phénomènes, tels que les diagrammes d'interférence obtenus lorsque la lumière passait à travers une double fente, étaient totalement contraires à une vision particulaire de la lumière, tandis que d'autres phénomènes, tels que l'effet photoélectrique, étaient totalement contraire à une vision ondulatoire de la lumière. D'une manière ou d'une autre, à un niveau fondamental encore mal compris, la lumière est à la fois ondulatoire et particulaire. C'est ce que l'on appelle la dualité onde-particule.

Figure\(\PageIndex{10}\) : Les photons de basses fréquences n'ont pas assez d'énergie pour provoquer l'éjection d'électrons par effet photoélectrique. Pour toute fréquence de lumière supérieure à la fréquence seuil, l'énergie cinétique d'un électron éjecté augmentera de façon linéaire avec l'énergie du photon entrant.

Exemple\(\PageIndex{2}\): Calculating the Energy of Radiation

Lorsque nous voyons de la lumière provenant d'un néon, nous observons le rayonnement des atomes de néon excités. Si ce rayonnement a une longueur d'onde de 640 nm, quelle est l'énergie du photon émis ?

Solution

Nous utilisons la partie de l'équation de Planck qui inclut la longueur d'onde, λ, et convertissons les unités de nanomètres en mètres afin que les unités de λ et de c soient identiques.

\[\begin{align*} E&=\dfrac{hc}{λ} \\[4pt] &=\mathrm{\dfrac{(6.626×10^{−34}\:J\cancel{s})(2.998×10^{8}\:m\cancel{s}^{−1})}{(640\cancel{nm})\left(\dfrac{1\:m}{10^9\cancel{nm}}\right)}}\\[4pt] &=\mathrm{3.10×10^{−19}\:J} \end{align*} \nonumber \]

Exercice\(\PageIndex{2}\)

Les micro-ondes d'un four ont une fréquence spécifique qui permet de chauffer les molécules d'eau contenues dans les aliments. (C'est pourquoi la plupart des plastiques et du verre ne chauffent pas dans un four à micro-ondes ; ils ne contiennent pas de molécules d'eau.) Cette fréquence est d'environ 3 × 10 ⁹ Hz. Quelle est l'énergie d'un photon dans ces micro-ondes ?

Réponse: 2 × 10 ⁻²⁴ J

Exemple\(\PageIndex{3}\): Photoelectric Effect

Identifiez les affirmations suivantes qui sont fausses et, si nécessaire, modifiez le mot ou la phrase en italique pour qu'ils soient vrais, conformément à l'explication d'Einstein sur l'effet photoélectrique.

L'augmentation de la luminosité de la lumière entrante augmente l'énergie cinétique des électrons éjectés.
L'augmentation de la longueur d'onde de la lumière entrante augmente l'énergie cinétique des électrons éjectés.
L'augmentation de la luminosité de la lumière entrante augmente le nombre d'électrons éjectés.
L'augmentation de la fréquence de la lumière entrante peut augmenter le nombre d'électrons éjectés.

Solution

Faux. L'augmentation de la luminosité de la lumière entrante n'a aucun effet sur l'énergie cinétique des électrons éjectés. Seule l'énergie, et non le nombre ou l'amplitude, des photons influence l'énergie cinétique des électrons.
Faux. L'augmentation de la fréquence de la lumière entrante augmente l'énergie cinétique des électrons éjectés. La fréquence est proportionnelle à l'énergie et inversement proportionnelle à la longueur d'onde. Les fréquences supérieures à la valeur seuil transfèrent l'énergie excédentaire dans l'énergie cinétique des électrons.
C'est vrai. Comme le nombre de collisions avec des photons augmente avec la luminosité, le nombre d'électrons éjectés augmente.
C'est vrai en ce qui concerne l'énergie seuil liant les électrons au métal. En dessous de ce seuil, les électrons ne sont pas émis et au-dessus de celui-ci, ils le sont. Une fois la valeur seuil atteinte, une nouvelle augmentation de la fréquence n'augmente pas le nombre d'électrons éjectés

Exercice\(\PageIndex{3}\)

Calculez l'énergie seuil en kJ/mol des électrons dans l'aluminium, étant donné que le photon de fréquence la plus basse pour lequel l'effet photoélectrique est observé est\(9.87 \times 10^{14}\; Hz\).

Réponse: \(3.94 \: kJ/mol\)

Gamme Spectra

Un autre paradoxe de la théorie électromagnétique classique à laquelle se débattaient les scientifiques à la fin du XIXe siècle concerne la lumière émise par les atomes et les molécules. Lorsque les solides, les liquides ou les gaz condensés sont suffisamment chauffés, ils émettent une partie de l'énergie excédentaire sous forme de lumière. Les photons produits de cette manière possèdent une gamme d'énergies et produisent ainsi un spectre continu dans lequel une série ininterrompue de longueurs d'onde est présente. La majeure partie de la lumière générée par les étoiles (y compris notre soleil) est produite de cette manière. Vous pouvez voir toutes les longueurs d'onde visibles de la lumière présente dans la lumière solaire en les séparant à l'aide d'un prisme. Comme le montre la figure\(\PageIndex{8}\), la lumière solaire contient également de la lumière UV (longueurs d'onde plus courtes) et de la lumière infrarouge (longueurs d'onde plus longues) qui peuvent être détectées à l'aide d'instruments mais qui sont invisibles à l'œil nu. Les solides incandescents (incandescents) tels que les filaments de tungstène des lampes à incandescence émettent également une lumière contenant toutes les longueurs d'onde de lumière visible. Ces spectres continus peuvent souvent être approximés par des courbes de rayonnement du corps noir à une température appropriée, comme celles illustrées sur la figure\(\PageIndex{9}\).

Contrairement aux spectres continus, la lumière peut également se présenter sous forme de spectres discrets ou linéaires avec des largeurs de raies très étroites entrecoupées dans les régions spectrales, comme celles illustrées sur la figure\(\PageIndex{5}\). L'excitation d'un gaz à basse pression partielle à l'aide d'un courant électrique, ou son chauffage, produira des spectres linéaires. Les ampoules fluorescentes et les enseignes au néon fonctionnent de cette manière (Figure\(\PageIndex{11}\)). Chaque élément présente son propre ensemble de raies caractéristiques, tout comme les molécules, bien que leurs spectres soient généralement beaucoup plus compliqués.

Cette figure montre une enseigne au néon colorée. Les tubes sont cintrés en différentes formes. — Figure\(\PageIndex{11}\) : Les enseignes au néon fonctionnent en excitant un gaz à basse pression partielle à l'aide d'un courant électrique. Ce panneau montre les effets artistiques élaborés qui peuvent être obtenus. (crédit : Dave Shaver)

Chaque raie d'émission est constituée d'une seule longueur d'onde de lumière, ce qui implique que la lumière émise par un gaz est constituée d'un ensemble d'énergies discrètes. Par exemple, lorsqu'une décharge électrique passe à travers un tube contenant de l'hydrogène gazeux à basse pression, les molécules de H ₂ se décomposent en atomes H distincts, et nous voyons une couleur bleu-rose. Le passage de la lumière à travers un prisme produit un spectre de raies, indiquant que cette lumière est composée de photons de quatre longueurs d'onde visibles, comme le montre la figure\(\PageIndex{12}\).

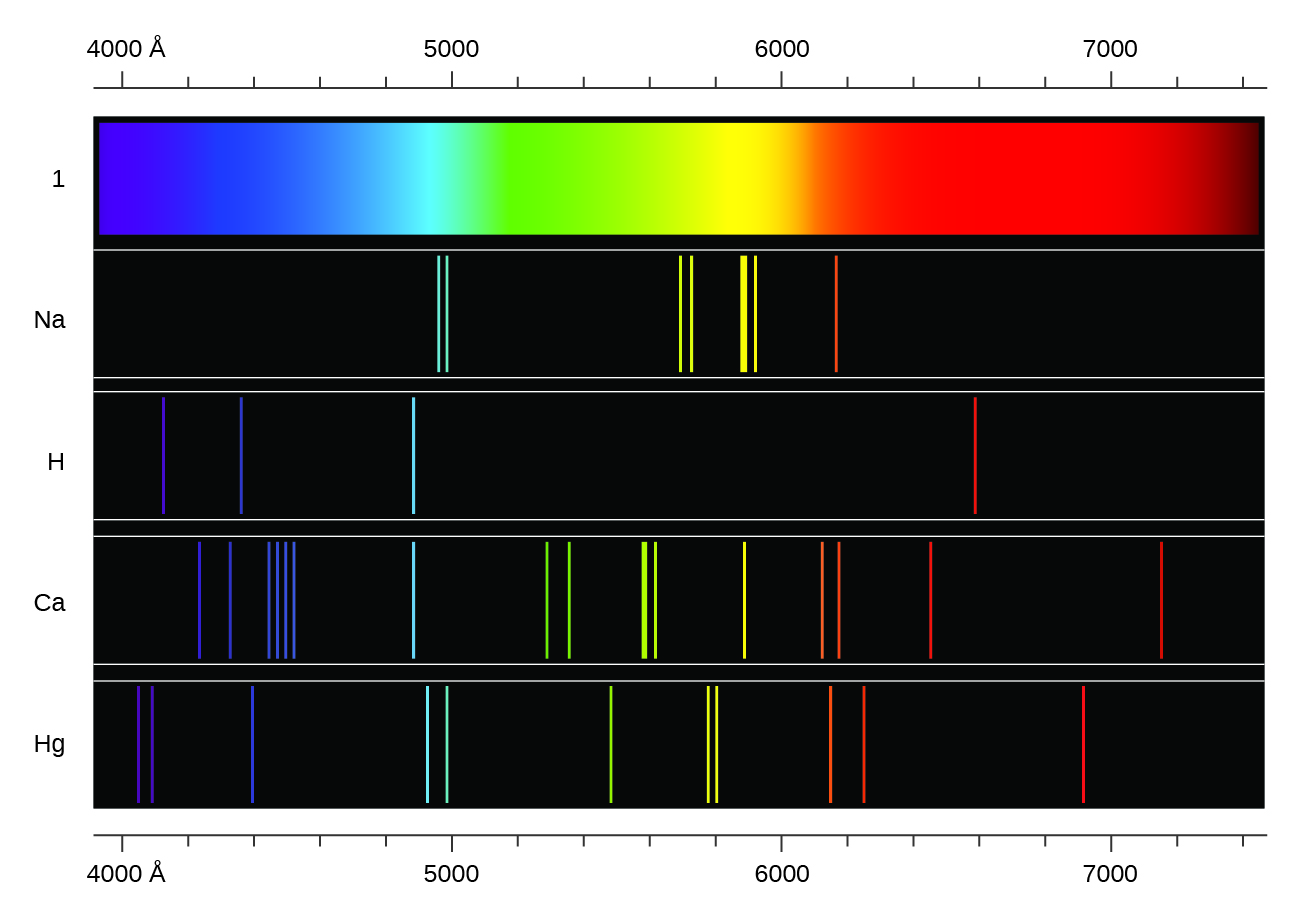
Figure\(\PageIndex{12}\) : Spectres linéaires de certains gaz. Comparez les deux types de spectres d'émission : le spectre continu de lumière blanche (en haut) et les spectres linéaires de la lumière provenant d'atomes de sodium, d'hydrogène, de calcium et de mercure excités.

L'origine des spectres discrets dans les atomes et les molécules était extrêmement déroutante pour les scientifiques à la fin du XIXe siècle, car selon la théorie électromagnétique classique, seuls les spectres continus devaient être observés. Ce qui est encore plus surprenant, c'est qu'en 1885, Johann Balmer a pu établir une équation empirique qui reliait les quatre longueurs d'onde visibles de la lumière émise par les atomes d'hydrogène à des nombres entiers. Cette équation est la suivante, dans laquelle k est une constante :

\[\dfrac{1}{λ}=k\left(\dfrac{1}{4}−\dfrac{1}{n^2}\right),\:n=3,\:4,\:5,\:6 \nonumber \]

D'autres raies discrètes pour l'atome d'hydrogène ont été trouvées dans les régions UV et IR. Johannes Rydberg a généralisé les travaux de Balmer et a développé une formule empirique qui prédisait toutes les raies d'émission d'hydrogène, et pas seulement celles limitées au domaine visible, où n ₁ et n ₂ sont des nombres entiers, n ₁ < n ₂, et\(R_∞\) est la constante de Rydberg (1,097 × 10 ⁷ m ⁻¹).

\[\dfrac{1}{λ}=R_∞\left(\dfrac{1}{n^2_1}−\dfrac{1}{n^2_2}\right) \nonumber \]

Même à la fin du XIXe siècle, la spectroscopie était une science très précise, de sorte que les longueurs d'onde de l'hydrogène étaient mesurées avec une très grande précision, ce qui impliquait que la constante de Rydberg pouvait également être déterminée très précisément. Le fait qu'une formule aussi simple que la formule de Rydberg puisse rendre compte de mesures aussi précises semblait étonnant à l'époque, mais c'est l'explication finale des spectres d'émission par Neils Bohr en 1913 qui a finalement convaincu les scientifiques d'abandonner la physique classique et a stimulé le développement de mécanique quantique moderne.

Résumé

La lumière et les autres formes de rayonnement électromagnétique se déplacent dans le vide à une vitesse constante, c, de 2,998 × 10 ⁸ m s ⁻¹. Ce rayonnement présente un comportement semblable à celui d'une onde, qui peut être caractérisé par une fréquence, νm, et une longueur d'onde, λ, telles que c = λβ. La lumière est un exemple d'onde progressive. Les autres phénomènes ondulatoires importants incluent les ondes stationnaires, les oscillations périodiques et les vibrations. Les ondes stationnaires présentent une quantification, car leurs longueurs d'onde sont limitées à des multiples entiers discrets de certaines longueurs caractéristiques. Le rayonnement électromagnétique qui passe à travers deux fentes étroites et rapprochées dont les dimensions sont à peu près similaires à la longueur d'onde présentera un diagramme d'interférence résultant de l'interférence constructive et destructrice des ondes. Le rayonnement électromagnétique démontre également les propriétés des particules appelées photons. L'énergie d'un photon est liée à la fréquence (ou bien à la longueur d'onde) du rayonnement sous la forme E = hνm (ou\(E=\dfrac{hc}{λ}\)), où h est la constante de Planck. Cette lumière démontre un comportement à la fois ondulatoire et particulaire, c'est ce que l'on appelle la dualité onde-particule. Toutes les formes de rayonnement électromagnétique partagent ces propriétés, bien que diverses formes, notamment les rayons X, la lumière visible, les micro-ondes et les ondes radio, interagissent différemment avec la matière et aient des applications pratiques très différentes. Le rayonnement électromagnétique peut être généré en excitant la matière à des énergies plus élevées, par exemple en la chauffant. La lumière émise peut être continue (sources incandescentes comme le soleil) ou discrète (provenant de types spécifiques d'atomes excités). Les spectres continus ont souvent des distributions qui peuvent être approximées sous forme de rayonnement du corps noir à une température appropriée. Le spectre linéaire de l'hydrogène peut être obtenu en faisant passer la lumière d'un tube électrifié d'hydrogène à travers un prisme. Ce spectre de raies était suffisamment simple pour qu'une formule empirique appelée formule de Rydberg puisse être dérivée du spectre. Trois paradoxes historiquement importants de la fin du XIXe siècle et du début du XXe siècle qui ne pouvaient être expliqués dans le cadre existant de la mécanique classique et de l'électromagnétisme classique étaient le problème du corps noir, l'effet photoélectrique et les spectres discrets des atomes. La résolution de ces paradoxes a finalement conduit à des théories quantiques qui ont supplanté les théories classiques.

Équations clés

c = λνm
\(E=hν=\dfrac{hc}{λ}\), où h = 6,626 × 10 ⁻³⁴ J s
\(\dfrac{1}{λ}=R_∞\left(\dfrac{1}{n^2_1}−\dfrac{1}{n^2_2}\right)\)

Lexique

amplitude: étendue du déplacement provoqué par une onde (pour les ondes sinusoïdales, il s'agit de la moitié de la différence entre la hauteur du pic et la profondeur du creux, et l'intensité est proportionnelle au carré de l'amplitude)

corps noir: absorbeur parfait idéalisé de tout rayonnement électromagnétique incident ; ces corps émettent un rayonnement électromagnétique dans des spectres continus caractéristiques appelés rayonnement du corps noir

spectre continu: rayonnement électromagnétique émis dans une série ininterrompue de longueurs d'onde (par exemple, lumière blanche émise par le soleil)

rayonnement électromagnétique: énergie transmise par des ondes qui ont une composante de champ électrique et une composante de champ magnétique

spectre électromagnétique: gamme d'énergies que peut comprendre le rayonnement électromagnétique, y compris les rayons radio, les micro-ondes, les infrarouges, le visible, les ultraviolets, les rayons X et les rayons gamma ; étant donné que l'énergie du rayonnement électromagnétique est proportionnelle à la fréquence et inversement proportionnelle à la longueur d'onde, le spectre peut également être spécifié par des plages de fréquences ou longueurs d'onde

fréquence (\(\nu\)): nombre de cycles d'ondes (pics ou creux) qui passent par un point précis de l'espace par unité de temps

hertz (Hz): l'unité de fréquence, qui est le nombre de cycles par seconde, s ^-1

intensité: propriété de l'énergie propagée par les ondes liée à l'amplitude de l'onde, telle que la luminosité de la lumière ou l'intensité du son

modèle d'interférence: motif généralement constitué d'une alternance de franges claires et foncées ; il résulte de l'interférence constructive et destructrice des ondes

spectre de lignes: rayonnement électromagnétique émis à des longueurs d'onde discrètes par un atome (ou des atomes) spécifique dans un état excité

nœud: tout point d'une onde stationnaire d'amplitude nulle

photon: le plus petit paquet possible de rayonnement électromagnétique, une particule de lumière

quantification: se produisant uniquement dans des valeurs discrètes spécifiques, et non en continu

vague stationnaire: (également, ondes stationnaires) phénomène d'ondes localisées caractérisé par des longueurs d'onde discrètes déterminées par les conditions limites utilisées pour générer les ondes ; les ondes stationnaires sont intrinsèquement quantifiées

vague: oscillation qui peut transporter de l'énergie d'un point à un autre dans l'espace

longueur d'onde (λ): distance entre deux pics ou creux consécutifs d'une vague

dualité onde-particule: terme utilisé pour décrire le fait que les particules élémentaires, y compris la matière, présentent des propriétés à la fois des particules (y compris la position localisée, la quantité de mouvement) et des ondes (y compris la non-localisation, la longueur d'onde