4.7 : Résoudre des systèmes d'équations en utilisant des déterminants
- Page ID
- 194174
À la fin de cette section, vous serez en mesure de :
- Évaluer le déterminant d'une matrice 2 × 2
- Évaluer le déterminant d'une matrice 3 × 3
- Utilisez la règle de Cramer pour résoudre des systèmes d'équations
- Résolvez des applications en utilisant
Avant de commencer, répondez à ce questionnaire de préparation.
Dans cette section, nous allons découvrir une autre méthode pour résoudre des systèmes d'équations linéaires appelée règle de Cramer. Avant de pouvoir commencer à utiliser la règle, nous devons apprendre de nouvelles définitions et de nouvelles notations.
Évaluer le déterminant d'une\(2×2\) matrice
Si une matrice comporte le même nombre de lignes et de colonnes, on l'appelle matrice carrée. Chaque matrice carrée est associée à un nombre réel appelé déterminant. Pour trouver le déterminant de la matrice carrée\(\left[ \begin{matrix} a &b \\ c&d \end{matrix} \right] \), nous l'écrivons d'abord comme\(\left| \begin{matrix} a &b \\ c&d \end{matrix} \right| \). Pour obtenir la valeur numérique réelle du déterminé, nous soustrayons les produits des diagonales, comme indiqué.
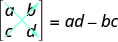
Le déterminant de toute matrice carrée\(\left[ \begin{matrix} a &b \\ c&d \end{matrix} \right] \), où a, b, c et d sont des nombres réels, est
\[\left| \begin{matrix} a &b \\ c&d \end{matrix} \right| =ad−bc \nonumber \]
Évaluez le déterminant de ⓐ\(\left[ \begin{matrix} 4 &-2 \\ 3&-1 \end{matrix} \right] \) ⓑ\(\left[ \begin{matrix} -3 &-4 \\ -2&0 \end{matrix} \right] \).
- Réponse
-
ⓐ

Écrivez le déterminant. 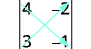
Soustrayez les produits des diagonales. 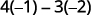
Simplifiez. 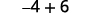
Simplifiez. 
ⓑ
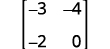
Écrivez le déterminant. 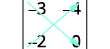
Soustrayez les produits des diagonales. 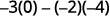
Simplifiez. 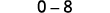
Simplifiez. 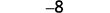
Évaluez le déterminant de ⓐ\(\left[ \begin{matrix} 5&−3\\2&−4 \end{matrix} \right] \) ⓑ\(\left[ \begin{matrix} −4&−6\\0&7 \end{matrix} \right] \).
- Réponse
-
ⓐ\(−14\) ; ⓑ\(−28\)
Évaluez le déterminant de ⓐ\(\left[ \begin{matrix} −1&3\\−2&4 \end{matrix} \right] \) ⓑ\(\left[ \begin{matrix} −7&−3\\−5&0 \end{matrix} \right] \).
- Réponse
-
ⓐ 2 ⓑ\(−15\)
Évaluer le déterminant d'une\(3×3\) matrice
Pour évaluer le déterminant d'une\(3×3\) matrice, nous devons être en mesure d'évaluer la mineure d'une entrée dans le déterminant. Le mineur d'une entrée est le\(2×2\) déterminant trouvé en éliminant la ligne et la colonne du\(3×3\) déterminant qui contient l'entrée.
Le mineur d'une entrée dans un\(3×3\) déterminant est le\(2×2\) déterminant trouvé en supprimant la ligne et la colonne du\(3×3\) déterminant qui contient l'entrée.
Pour trouver le mineur d'entrée\(a_1\), on élimine la ligne et la colonne qui la contiennent. Nous éliminons donc la première ligne et la première colonne. Ensuite, nous écrivons le\(2×2\) déterminant qui reste.

Pour trouver le mineur d'entrée\(b_2\), nous éliminons la ligne et la colonne qui la contiennent. Nous éliminons donc la\(2^{nd}\) ligne et\(2^{nd}\) la colonne. Ensuite, nous écrivons le\(2×2\) déterminant qui reste.

Pour le déterminant\(\left| \begin{matrix} 4&−2&3\\1&0&−3\\−2&−4&2 \end{matrix} \right|\), trouvez puis évaluez la mineure de ⓐ\(a_1\) ⓑ\(b_3\) ⓒ\(c_2\).
- Réponse
-
ⓐ
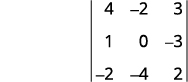
Éliminez la ligne et la colonne qui contiennent\(a_1\). 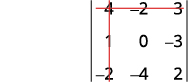
Écrivez le\(2×2\) déterminant qui reste. 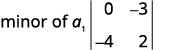
Évaluer. 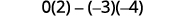
Simplifiez. 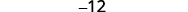
ⓑ
Éliminez la ligne et la colonne qui contiennent\(b_3\). 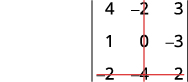
Écrivez le\(2×2\) déterminant qui reste. 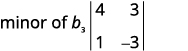
Évaluer. 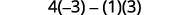
Simplifiez. 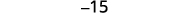
ⓒ
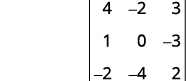
Éliminez la ligne et la colonne qui contiennent\(c_2\). 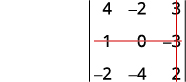
Écrivez le\(2×2\) déterminant qui reste. 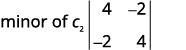
Évaluer. 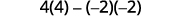
Simplifiez. 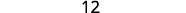
Pour le déterminant\(\left| \begin{matrix} 1&−1&4\\0&2&−1\\−2&−3&3 \end{matrix} \right|\), trouvez puis évaluez la mineure de ⓐ\(a_1\) ⓑ\(b_2\) ⓒ\(c_3\).
- Réponse
-
ⓐ 3 ⓑ 11 ⓒ 2
Pour le déterminant\(\left| \begin{matrix} −2&−1&0\\3&0&−1\\−1&−2&3 \end{matrix} \right|\), trouvez puis évaluez la mineure de ⓐ\(a_2\) ⓑ\(b_3\) ⓒ\(c_2\).
- Réponse
-
ⓐ\(−3\) ⓑ 2 ⓒ 3
Nous sommes maintenant prêts à évaluer un\(3×3\) déterminant. Pour ce faire, nous élargissons la liste des mineurs, ce qui nous permet d'évaluer le\(3×3\)\(2×2\) déterminant à l'aide de déterminants, que nous savons déjà comment évaluer !
Pour évaluer un\(3×3\) déterminant en l'élargissant par mineurs le long de la première rangée, nous utilisons le schéma suivant :
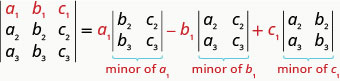
N'oubliez pas que pour trouver le mineur d'une entrée, nous éliminons la ligne et la colonne qui contiennent l'entrée.
Pour évaluer un\(3×3\) déterminant en élargissant par mineurs le long de la première rangée, le schéma suivant :
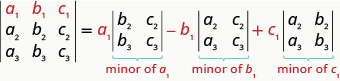
Évaluez le déterminant\(\left| \begin{matrix} 2&−3&−1\\3&2&0\\−1&−1&−2 \end{matrix} \right|\) en l'élargissant par mineurs le long de la première rangée.
- Réponse
-

À agrandir pour les mineurs le long de la première rangée 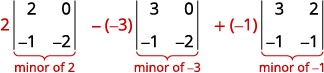
Évaluez chaque déterminant. 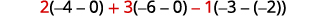
Simplifiez. 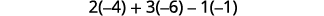
Simplifiez. 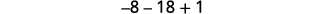
Simplifiez. 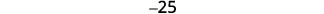
Évaluez le déterminant en\(\left| \begin{matrix} 3&−2&4\\0&−1&−2\\2&3&−1 \end{matrix} \right|\) l'élargissant par mineurs le long de la première rangée.
- Réponse
-
37
Évaluez le déterminant en\(\left| \begin{matrix} 3&−2&−2\\2&−1&4\\−1&0&−3 \end{matrix} \right|\) l'élargissant par mineurs le long de la première rangée.
- Réponse
-
7
Pour évaluer un\(3×3\) déterminant, nous pouvons l'étendre par mineurs en utilisant n'importe quelle ligne ou colonne. Le choix d'une ligne ou d'une colonne autre que la première ligne facilite parfois le travail.
Lorsque nous développons par ligne ou colonne, nous devons faire attention au signe des termes de l'extension. Pour déterminer le signe des termes, nous utilisons le schéma des signes suivant.
\[\left| \begin{matrix} +&−&+\\−&+&−\\+&−&+ \end{matrix} \right|\nonumber\]
Lorsque l'extension est réalisée par des mineurs à l'aide d'une ligne ou d'une colonne, le signe des termes de l'extension suit le schéma suivant. \[\left| \begin{matrix} +&−&+\\−&+&−\\+&−&+ \end{matrix} \right|\nonumber\]
Notez que le motif des signes de la première rangée correspond aux signes entre les termes de l'extension de la première rangée.
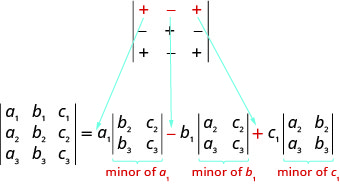
Étant donné que nous pouvons développer n'importe quelle ligne ou colonne, comment décidons-nous de la ligne ou de la colonne à utiliser ? Habituellement, nous essayons de choisir une ligne ou une colonne qui facilitera notre calcul. Si le déterminant contient un 0, l'utilisation de la ligne ou de la colonne contenant le 0 facilitera les calculs.
Évaluez le déterminant\(\left| \begin{matrix} 4&−1&−3\\3&0&2\\5&−4&−3 \end{matrix} \right|\) en l'élargissant aux mineurs.
- Réponse
-
Pour étendre par mineurs, nous recherchons une ligne ou une colonne qui facilitera nos calculs. Puisque 0 se trouve dans la deuxième ligne et la deuxième colonne, l'étendre par l'une ou l'autre de ces valeurs est un bon choix. Comme la deuxième ligne contient moins de points négatifs que la deuxième colonne, nous allons l'étendre à la deuxième ligne.

Développez à l'aide de la deuxième ligne. Fais attention aux signes. 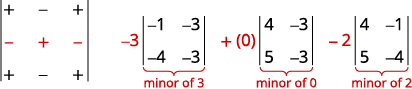
Évaluez chaque déterminant. 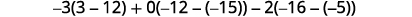
Simplifiez. 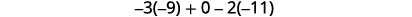
Simplifiez. 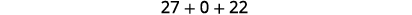
Ajoutez. 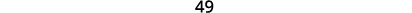
Évaluez le déterminant\(\left| \begin{matrix} 2&−1&−3\\0&3&−4\\3&−4&−3 \end{matrix} \right|\) en l'élargissant aux mineurs.
- Réponse
-
\(−11\)
Évaluez le déterminant\(\left| \begin{matrix} −2&−1&−3\\−1&2&2\\4&−4&0 \end{matrix} \right|\) en l'élargissant aux mineurs.
- Réponse
-
8
Utilisez la règle de Cramer pour résoudre des systèmes d'équations
La règle de Cramer est une méthode de résolution de systèmes d'équations à l'aide de déterminants. Il peut être dérivé en résolvant la forme générale des systèmes d'équations par élimination. Nous allons démontrer ici la règle pour les deux systèmes de deux équations à deux variables et pour les systèmes de trois équations à trois variables.
Commençons par les systèmes de deux équations à deux variables.
Pour le système d'équations\(\left\{\begin{array} {l} a_1x+b_1y=k_1 \\ a_2x+b_2y=k_2\end{array}\right.\), la solution\((x,y)\) peut être déterminée par

Notez que pour former le déterminant D, nous utilisons les coefficients des variables.
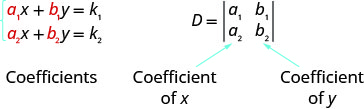
Notez que pour former le déterminant\(D_x\) et\(D_y\), nous substituons les constantes aux coefficients de la variable que nous trouvons.
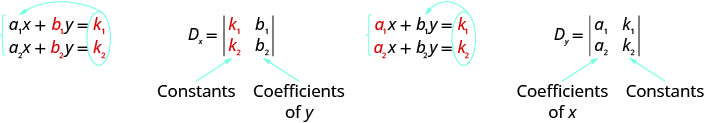
Résolvez en utilisant la règle de Cramer :\(\left\{ \begin{array} {l} 2x+y=−4\\3x−2y=−6\end{array}\right.\)
- Réponse
-






Résolvez en utilisant la règle de Cramer :\(\left\{\begin{array} {l} 3x+y=−3 \\ 2x+3y=6 \end{array} \right.\)
- Réponse
-
\((−\frac{15}{7},\frac{24}{7})\)
Résolvez en utilisant la règle de Cramer :\(\left\{\begin{array} {l} −x+y=2\\2x+y=−4 \end{array} \right.\)
- Réponse
-
\((−2,0)\)
- Évaluez le déterminant D en utilisant les coefficients des variables.
- Évaluez le déterminant\(D_x\). Utilisez les constantes à la place des coefficients x.
- Évaluez le déterminant\(D_y\). Utilisez les constantes à la place des coefficients y.
- Trouvez x et y. \(x=\frac{D_x}{D}\),\(y=\frac{D_y}{D}\)
- Écrivez la solution sous la forme d'une paire ordonnée.
- Vérifiez que la paire ordonnée est une solution aux deux équations d'origine.
Pour résoudre un système de trois équations à trois variables avec la règle de Cramer, nous faisons essentiellement ce que nous avons fait pour un système de deux équations. Cependant, nous devons maintenant résoudre trois variables pour obtenir la solution. Les déterminants seront également ceux\(3×3\) qui rendront notre travail plus intéressant !
Pour le système d'équations\(\left\{\begin{array} {l} a_1x+b_1y+c_1z=k_1\\a_2x+b_2y+c_2z=k_2\\a_3x+b_3y+c_3z=k_3\end{array}\right.\), la solution\((x,y,z)\) peut être déterminée par

Résolvez le système d'équations en utilisant la règle de Cramer :\(\left\{\begin{array} {l} 3x−5y+4z=5\\5x+2y+z=0\\2x+3y−2z=3 \end{array} \right.\)
- Réponse
-
Évaluez le déterminant D. 
Développez par mineurs en utilisant la colonne 1. 
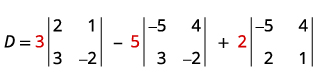
Évaluez les déterminants. 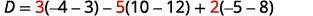
Simplifiez. 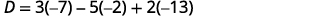
Simplifiez. 
Simplifiez. 
Évaluez le déterminant\(D_x\). Utilisez les
constantes pour remplacer les coefficients de x.
Développez par mineurs en utilisant la colonne 1. 
Évaluez les déterminants. 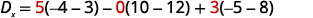
Simplifiez. 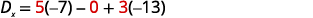
Simplifiez. 
Évaluez le déterminant Dy.Dy. Utilisez les
constantes pour remplacer les coefficients de y.

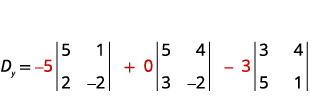
Évaluez les déterminants. 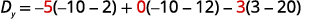
Simplifiez. 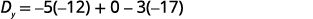
Simplifiez. 
Simplifiez. 
Évaluez le déterminant Dz.Dz. Utilisez les
constantes pour remplacer les coefficients de z.

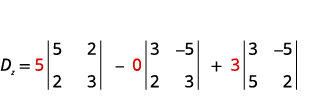
Évaluez les déterminants. 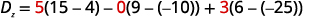
Simplifiez. 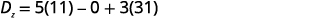
Simplifiez. 
Simplifiez. 
Trouvez x, y et z. 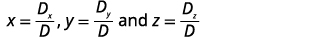
Substituez les valeurs. 
Simplifiez. 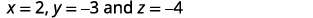
Écrivez la solution sous la forme d'un triple ordonné. 
Vérifiez que le triple ordonné est une solution
aux trois équations d'origine.Nous vous laissons le chèque. La solution est\((2,−3,−4)\).
Résolvez le système d'équations en utilisant la règle de Cramer :\(\left\{\begin{array} {l} 3x+8y+2z=−5\\2x+5y−3z=0\\x+2y−2z=−1 \end{array} \right.\)
- Réponse
-
\((−9,3,−1)\)
Résolvez le système d'équations en utilisant la règle de Cramer :\(\left\{\begin{array} {l} 3x+y−6z=−3\\2x+6y+3z=0\\3x+2y−3z=−6 \end{array} \right.\)
- Réponse
-
\((−6,3,−2)\)
La règle de Cramer ne fonctionne pas lorsque la valeur du déterminant D est 0, car cela signifierait que nous diviserions par 0. Mais quand\(D=0\), le système est soit incohérent, soit dépendant.
Lorsque les valeurs de\(D=0\) et\(D_x,\space D_y\) et D sont toutes nulles, le système est cohérent et dépendant et il existe une infinité de solutions.
Lorsque les valeurs de\(D=0\) et\(D_x,\space D_y\) et ne\(D_z\) sont pas toutes nulles, le système est incohérent et il n'y a pas de solution.
Pour tout système d'équations, où la valeur du déterminant\(D=0\),
\[ \begin{array} {lll} \textbf{Value of determinants} &\textbf{Type of system} &\textbf{Solution} \\ {D=0\text{ and }D_x,\space D_y\text{ and }D_z\text{ are all zero}} &\text{consistent and dependent} &\text{infinitely many solutions} \\ {D=0\text{ and }D_x,\space D_y\text{ and }D_z\text{ are not all zero}} &\text{inconsistent} &\text{no solution} \end{array} \nonumber\]
Dans l'exemple suivant, nous utiliserons les valeurs des déterminants pour trouver la solution du système.
Résolvez le système d'équations en utilisant la règle de Cramer :\(\left\{\begin{array} {l} x+3y=4\\−2x−6y=3 \end{array} \right.\)
- Réponse
-
\(\begin{array} {ll} {} &{\left\{\begin{array} {l} x+3y=4\\−2x−6y=3 \end{array} \right.} \\ {\begin{array} {l} \text{Evaluate the determinantD,using the} \\ \text{coefficients of the variables.} \end{array}} &{D=\left|\begin{matrix} 1&3\\−2&−6\end{matrix}\right|} \\ {} &{D=−6−(−6)} \\ {} &{D=0} \end{array} \)
Nous ne pouvons pas utiliser la règle de Cramer pour résoudre ce système. Mais en examinant la valeur des déterminants\(D_x\) et\(D_y\), nous pouvons déterminer si le système est dépendant ou incohérent.
\(\begin{array} {ll} {\text{Evaluate the determinant }D_x.} &{D_x=\left|\begin{matrix} 4&3\\3&−6\end{matrix}\right|} \\ {} &{D_x=−24−9} \\ {} &{D_x=15} \end{array} \)
Comme tous les déterminants ne sont pas nuls, le système est incohérent. Il n'y a pas de solution.
Résolvez le système d'équations en utilisant la règle de Cramer :\(\left\{\begin{array} {l} 4x−3y=8\\8x−6y=14 \end{array} \right.\)
- Réponse
-
aucune solution
Résolvez le système d'équations en utilisant la règle de Cramer :\(\left\{\begin{array} {l} x=−3y+4\\2x+6y=8 \end{array} \right.\)
- Réponse
-
des solutions infinies
Résolvez des applications en utilisant
Une application intéressante des déterminants nous permet de vérifier si les points sont colinéaires. Trois points\((x_1,y_1)\),\((x_2,y_2)\) et\((x_3,y_3)\) sont colinéaires si et seulement si le déterminant ci-dessous est zéro.
\[\left|\begin{matrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{matrix}\right|=0\nonumber\]
Trois points\((x_1,y_1)\),\((x_2,y_2)\) et\((x_3,y_3)\) sont colinéaires si et seulement si
\[\left|\begin{matrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{matrix}\right|=0\nonumber\]
Nous utiliserons cette propriété dans l'exemple suivant.
Déterminez si les points\((5,−5)\)\((4,−3)\), et\((3,−1)\) sont colinéaires.
- Réponse
-
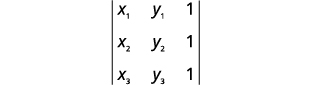
Remplacez les valeurs par le déterminant.
\((5,−5)\)\((4,−3)\), et\((3,−1)\)
Évaluez le déterminant en l'élargissant
par mineurs à l'aide de la colonne 3.
Évaluez les déterminants. 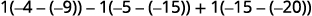
Simplifiez. 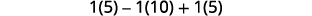
Simplifiez. 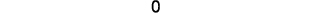
La valeur du déterminant est 0, donc les
points sont colinéaires.
Déterminez si les points\((3,−2)\)\((5,−3)\), et\((1,−1)\) sont colinéaires.
- Réponse
-
oui
Déterminez si les points\((−4,−1)\)\((−6,2)\), et\((−2,−4)\) sont colinéaires.
- Réponse
-
oui
Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner à résoudre des systèmes d'inégalités linéaires à l'aide de graphiques.
- Résolution de systèmes d'inégalités linéaires par représentation graphique
- Systèmes d'inégalités linéaires
Concepts clés
- Déterminant : Le déterminant de toute matrice carrée\(\left[\begin{matrix}a&b\\c&d\end{matrix}\right]\), où a, b, c et d sont des nombres réels, est
\[\left|\begin{matrix}a&b\\c&d\end{matrix}\right|=ad−bc\nonumber\]
- Expansion par mineurs le long de la première rangée pour évaluer un déterminant 3 × 3 : Pour évaluer un\(3×3\) déterminant en développant par mineurs le long de la première rangée, le schéma suivant :
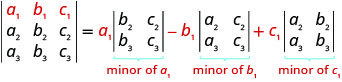
- Modèle de signes : Lorsque des mineurs utilisent une ligne ou une colonne pour agrandir, le signe des termes de l'extension suit le schéma suivant.
\[\left|\begin{matrix}+&−&+\\−&+&−\\+&−&+\end{matrix}\right|\nonumber\]
- Règle de Cramer : Pour le système d'équations\(\left\{\begin{array} {l} a_1x+b_1y=k_1\\a_2x+b_2y=k_2\end{array}\right.\), la solution\((x,y)\) peut être déterminée en

remarquant que pour former le déterminant D, nous utilisons les coefficients des variables. - Comment résoudre un système de deux équations en utilisant la règle de Cramer.
- Évaluez le déterminant D en utilisant les coefficients des variables.
- Évaluez le déterminant\(D_x\). Utilisez les constantes à la place des coefficients x.
- Évaluez le déterminant\(D_y\). Utilisez les constantes à la place des coefficients y.
- Trouvez x et y. \(x=\frac{D_x}{D}\),\(y=\frac{D_y}{D}\).
- Écrivez la solution sous la forme d'une paire ordonnée.
- Vérifiez que la paire ordonnée est une solution aux deux équations d'origine.
- Systèmes d'équations dépendants et incohérents : Pour tout système d'équations, où la valeur du déterminant\(D=0\),\[ \begin{array} {lll} \textbf{Value of determinants} &\textbf{Type of system} &\textbf{Solution} \\ {D=0\text{ and }D_x,\space D_y\text{ and }D_z\text{ are all zero}} &\text{consistent and dependent} &\text{infinitely many solutions} \\ {D=0\text{ and }D_x,\space D_y\text{ and }D_z\text{ are not all zero}} &\text{inconsistent} &\text{no solution} \end{array} \nonumber\]
- Test pour les points colinéaires : Trois points\((x_1,y_1)\)\((x_2,y_2)\), et\((x_3,y_3)\) sont colinéaires si et seulement si
\[\left|\begin{matrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{matrix}\right|=0\nonumber\]
Lexique
- déterminant
- Chaque matrice carrée est associée à un nombre réel appelé déterminant.
- mineur d'une entrée dans un déterminant 3×33×3
- Le mineur d'une entrée dans un déterminant 3×33×3 est le déterminant 2×22×2 obtenu en éliminant la ligne et la colonne du déterminant 3×33×3 qui contient l'entrée.
- matrice carrée
- Une matrice carrée est une matrice comportant le même nombre de lignes et de colonnes.


