Skip to main content
Global

4.6 : Résoudre des systèmes d'équations en utilisant des matrices

  1. Last updated
  2. Save as PDF
  • Page ID
    194148

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage

    À la fin de cette section, vous serez en mesure de :

    • Ecrire la matrice augmentée pour un système d'équations
    • Utiliser des opérations de ligne sur une matrice
    • Résoudre des systèmes d'équations à l'aide

    Avant de commencer, répondez à ce questionnaire de préparation.

    1. Résoudre :\(3(x+2)+4=4(2x−1)+9\).
      Si vous avez oublié ce problème, consultez [lien].
    2. Résoudre :\(0.25p+0.25(x+4)=5.20\).
      Si vous avez oublié ce problème, consultez [lien].
    3. Évaluez quand\(x=−2\) et\(y=3:2x^2−xy+3y^2\).
      Si vous avez oublié ce problème, consultez [lien].

    Ecrire la matrice augmentée pour un système d'équations

    La résolution d'un système d'équations peut être une opération fastidieuse où une simple erreur peut ruiner la recherche de la solution. Une méthode alternative utilisant les procédures de base d'élimination mais avec une notation plus simple est disponible. La méthode implique l'utilisation d'une matrice. Une matrice est un ensemble rectangulaire de nombres disposés en lignes et en colonnes.

    MATRICE

    Une matrice est un ensemble rectangulaire de nombres disposés en lignes et en colonnes.

    Une matrice comportant m lignes et n colonnes est ordonnée\(m\times n\). La matrice sur la gauche ci-dessous comporte 2 lignes et 3 colonnes et est donc ordonnée\(2\times 3\). Nous disons que c'est une matrice 2 par 3.

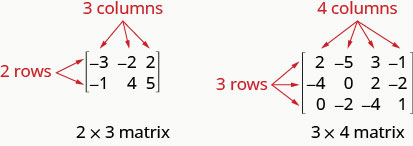
    La figure montre deux matrices. Celui de gauche a les chiffres moins 3, moins 2 et 2 dans la première rangée et les chiffres moins 1, 4 et 5 dans la deuxième rangée. Les lignes et les colonnes sont placées entre crochets. Il comporte donc 2 lignes et 3 colonnes. Il est étiqueté matrice 2 croix 3 ou matrice 2 par 3. La matrice de droite est similaire mais comporte 3 lignes et 4 colonnes. Il est étiqueté matrice 3 par 4.

    Chaque nombre de la matrice est appelé élément ou entrée de la matrice.

    Nous utiliserons une matrice pour représenter un système d'équations linéaires. Nous écrivons chaque équation sous forme standard et les coefficients des variables et la constante de chaque équation deviennent une ligne dans la matrice. Chaque colonne serait alors constituée des coefficients de l'une des variables du système ou des constantes. Une ligne verticale remplace les signes d'égalité. Nous appelons la matrice résultante la matrice augmentée du système d'équations.

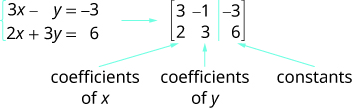
    Les équations sont les suivantes : 3x plus y est égal à moins 3 et 2x plus 3y est égal à 6. Une matrice de 2 x 3 est présentée. La première ligne est 3, 1, moins 3. La deuxième rangée est 2, 3, 6. La première colonne est étiquetée coefficients de x, la deuxième colonne est étiquetée coefficients de y et la troisième colonne est étiquetée constantes.

    Notez que la première colonne est composée de tous les coefficients de x, la deuxième colonne de tous les coefficients de y et la troisième colonne de toutes les constantes.

    Exemple\(\PageIndex{1}\)

    ⓐ\(\left\{ \begin{array} {l} 5x−3y=−1 \\ y=2x−2 \end{array} \right. \) ⓑ\( \left\{ \begin{array} {l} 6x−5y+2z=3 \\ 2x+y−4z=5 \\ 3x−3y+z=−1 \end{array} \right. \)

    Réponse

    ⓐ La deuxième équation n'est pas sous forme standard. Nous réécrivons la deuxième équation sous forme standard.

    \[\begin{aligned} y=2x−2 \\ −2x+y=−2 \end{aligned} \nonumber\]

    Nous remplaçons la deuxième équation par sa forme standard. Dans la matrice augmentée, la première équation nous donne la première ligne et la deuxième équation nous donne la deuxième ligne. La ligne verticale remplace les signes égaux.

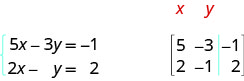
    Les équations sont les suivantes : 3x plus y est égal à moins 3 et 2x plus 3y est égal à 6. Une matrice de 2 x 3 est présentée. La première ligne est 3, 1, moins 3. La deuxième rangée est 2, 3, 6. La première colonne est étiquetée coefficients de x, la deuxième colonne est étiquetée coefficients de y et la troisième colonne est étiquetée constantes.

    ⓑ Les trois équations sont présentées sous forme standard. Dans la matrice augmentée, la première équation nous donne la première ligne, la deuxième équation nous donne la deuxième ligne et la troisième équation nous donne la troisième ligne. La ligne verticale remplace les signes égaux.

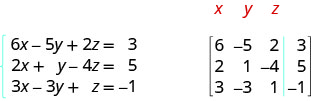
    Les équations sont les suivantes : 6x moins 5y plus 2z est égal à 3, 2x plus y moins 4z est égal à 5 et 3x moins 3y plus z est égal à moins 1. Une matrice de 4 par 3 est affichée dont la première ligne est 6, moins 5, 2, 3. Sa deuxième rangée est 2, 1, moins 4, 5. Sa troisième rangée est 3, moins 3, 1 et moins 1. Ses trois premières colonnes sont appelées x, y et z respectivement.

    Exemple\(\PageIndex{2}\)

    Écrivez chaque système d'équations linéaires sous forme de matrice augmentée :

    ⓐ\(\left\{ \begin{array} {l} 3x+8y=−3 \\ 2x=−5y−3 \end{array} \right. \) ⓑ\(\left\{ \begin{array} {l} 2x−5y+3z=8 \\ 3x−y+4z=7 \\ x+3y+2z=−3 \end{array} \right. \)

    Réponse

    ⓐ\(\left[ \begin{matrix} 3 &8 &-3 \\ 2 &5 &−3 \end{matrix} \right] \)

    ⓑ\(\left[ \begin{matrix} 2 &3 &1 &−5 \\ −1 &3 &3 &4 \\ 2 &8 &7 &−3 \end{matrix} \right] \)

    Exemple\(\PageIndex{3}\)

    Écrivez chaque système d'équations linéaires sous forme de matrice augmentée :

    ⓐ\(\left\{ \begin{array} {l} 11x=−9y−5 \\ 7x+5y=−1 \end{array} \right. \) ⓑ\(\left\{ \begin{array} {l} 5x−3y+2z=−5 \\ 2x−y−z=4 \\ 3x−2y+2z=−7 \end{array} \right. \)

    Réponse

    ⓐ\(\left[ \begin{matrix} 11 &9 &−5 \\ 7 &5 &−1 \end{matrix} \right] \)
    ⓑ\(\left[ \begin{matrix} 5 &−3 &2 &−5 \\ 2 &−1 &−1 &4 \\ 3 &−2 &2 &−7 \end{matrix} \right] \)

    Lorsque nous résolvons des systèmes d'équations à l'aide de matrices, il est important de pouvoir faire des allers-retours entre le système et la matrice. L'exemple suivant nous demande de prendre les informations de la matrice et d'écrire le système d'équations.

    Exemple\(\PageIndex{4}\)

    Écrivez le système d'équations qui correspond à la matrice augmentée :

    \(\left[ \begin{array} {ccc|c} 4 &−3 &3 &−1 \\ 1 &2 &−1 &2 \\ −2 &−1 &3 &−4 \end{array} \right] \).

    Réponse

    Nous nous souvenons que chaque ligne correspond à une équation et que chaque entrée est un coefficient d'une variable ou d'une constante. La ligne verticale remplace le signe égal. Comme cette matrice est un\(4\times 3\), nous savons qu'elle se traduira par un système de trois équations à trois variables.

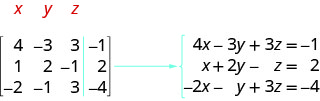
    Une matrice de 3 x 4 est présentée. Sa première rangée est 4, moins 3, 3, moins 1. Sa deuxième rangée est 1, 2, moins 1, 2. Sa troisième ligne est moins 2, moins 1, 3, moins 4. Les trois équations sont les suivantes : 4x moins 3y plus 3z est égal à moins 1, x plus 2y moins z est égal à 2 et moins 2x moins y plus 3z est égal à moins 4.

    Exemple\(\PageIndex{5}\)

    Ecrivez le système d'équations qui correspond à la matrice augmentée :\(\left[ \begin{matrix} 1 &−1 &2 &3 \\ 2 &1 &−2 &1 \\ 4 &−1 &2 &0 \end{matrix} \right] \).

    Réponse

    \(\left\{ \begin{array} {l} x−y+2z=3 \\ 2x+y−2z=1 \\ 4x−y+2z=0 \end{array} \right.\)

    Exemple\(\PageIndex{6}\)

    Ecrivez le système d'équations qui correspond à la matrice augmentée :\(\left[ \begin{matrix} 1 &1 &1 &4 \\ 2 &3 &−1 &8 \\ 1 &1 &−1 &3 \end{matrix} \right] \).

    Réponse

    \(\left\{ \begin{array} {l} x+y+z=4 \\ 2x+3y−z=8 \\ x+y−z=3 \end{array} \right.\)

    Utiliser des opérations de ligne sur une matrice

    Une fois qu'un système d'équations est sous sa forme matricielle augmentée, nous effectuerons des opérations sur les lignes qui nous mèneront à la solution.

    Pour les résoudre par élimination, peu importe l'ordre dans lequel nous plaçons les équations dans le système. De même, dans la matrice, nous pouvons échanger les lignes.

    Lorsque nous résolvons par élimination, nous multiplions souvent l'une des équations par une constante. Puisque chaque ligne représente une équation et que nous pouvons multiplier chaque côté d'une équation par une constante, de même, nous pouvons multiplier chaque entrée d'une ligne par n'importe quel nombre réel sauf 0.

    Lors de l'élimination, nous ajoutons souvent un multiple d'une ligne à une autre. Dans la matrice, nous pouvons remplacer une ligne par sa somme par un multiple d'une autre ligne.

    Ces actions sont appelées opérations sur les lignes et nous aideront à utiliser la matrice pour résoudre un système d'équations.

    OPÉRATIONS SUR LES LIGNES

    Dans une matrice, les opérations suivantes peuvent être effectuées sur n'importe quelle ligne et la matrice résultante sera équivalente à la matrice d'origine.

    1. Échangez deux lignes quelconques.
    2. Multipliez une ligne par n'importe quel nombre réel sauf 0.
    3. Ajoutez un multiple non nul d'une ligne à une autre ligne.

    Ces opérations sont faciles à effectuer, mais toutes les opérations arithmétiques peuvent entraîner une erreur. Si nous utilisons un système pour enregistrer le fonctionnement des lignes à chaque étape, il est beaucoup plus facile de revenir en arrière et de vérifier notre travail.

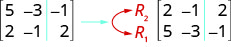
    Nous utilisons des lettres majuscules avec des indices pour représenter chaque ligne. Nous montrons ensuite le fonctionnement à gauche de la nouvelle matrice. Pour afficher l'échange d'une ligne :

    Une matrice de 2 x 3 est présentée. Sa première ligne, nommée R2, est égale à 2, moins 1, 2. Sa deuxième ligne, étiquetée R1, est 5, moins 3, moins 1.

    Pour multiplier la ligne 2 par\(−3\) :

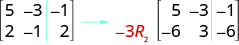
    Une matrice de 2 x 3 est présentée. Sa première ligne est 5, moins 3, moins 1. Sa deuxième ligne est 2, moins 1, 2. Une flèche pointe de cette matrice vers une autre sur la droite. La première ligne de la nouvelle matrice est identique. La deuxième ligne est précédée de moins 3 R2. C'est moins 6, 3, moins 6.

    Pour multiplier la ligne 2 par\(−3\) et l'ajouter à la ligne 1 :

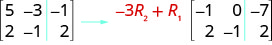
    Une matrice de 2 x 3 est présentée. Sa première ligne est 5, moins 3, moins 1. Sa deuxième ligne est 2, moins 1, 2. Une flèche pointe de cette matrice vers une autre sur la droite. La première ligne de la nouvelle matrice est précédée de moins 3 R2 plus R1. C'est moins 1, 0, moins 7. La deuxième ligne est 2, moins 1, 2.

    Exemple\(\PageIndex{7}\)

    Effectuez les opérations indiquées sur la matrice augmentée :

    ⓐ Échangez les rangées 2 et 3.

    ⓑ Multipliez la ligne 2 par 5.

    ⓒ Multipliez la ligne 3 par −2−2 et ajoutez-la à la ligne 1.

    \( \left[ \begin{array} {ccc|c} 6 &−5 &2 &3 \\ 2 &1 &−4 &5 \\ 3 &−3 &1 &−1 \end{array} \right] \)

    Réponse

    ⓐ Nous échangeons les rangées 2 et 3.

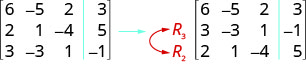
    Deux matrices de 3 x 4 sont présentées. Dans celle de gauche, la première rangée est 6, moins 5, 2, 3. La deuxième rangée est 2, 1, moins 4, 5. La troisième rangée est 3, moins 3, 1, moins 1. La deuxième matrice est similaire, sauf que les lignes 2 et 3 sont interchangées.

    ⓑ Nous multiplions la ligne 2 par 5.

    Deux matrices de 3 x 4 sont présentées. Dans celle de gauche, la première rangée est 6, moins 5, 2, 3. La deuxième rangée est 2, 1, moins 4, 5. La troisième rangée est 3, moins 3, 1, moins 1. La deuxième matrice est similaire à la première, sauf que la ligne 2, précédée de 5 R2, est égale à 10, 5, moins 20, 25.

    ⓒ Nous multiplions la ligne 3 par\(−2\) et l'ajoutons à la ligne 1.

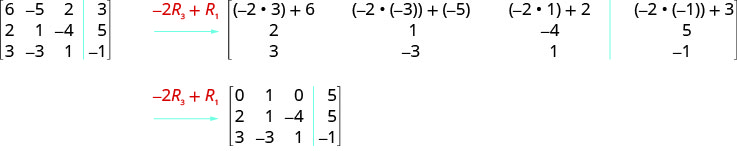
    Dans la matrice 3 x 4, la première ligne est 6, moins 5, 2, 3. La deuxième rangée est 2, 1, moins 4, 5. La troisième rangée est 3, moins 3, 1, moins 1. En effectuant l'opération moins 2 R3 plus R1 sur la première ligne, la première ligne devient 6 plus moins 2 fois 3, moins 5 plus moins 2 fois moins 3, 2 plus moins 2 fois 1 et 3 plus moins 2 fois moins 1 et 3 plus moins 2 fois moins 1. Cela devient 0, 1, 0, 5. Les deux lignes restantes de la nouvelle matrice sont identiques.

    Exemple\(\PageIndex{8}\)

    Effectuez les opérations indiquées sur la matrice augmentée :

    ⓐ Échangez les rangées 1 et 3.

    ⓑ Multipliez la ligne 3 par 3.

    ⓒ Multipliez la ligne 3 par 2 et ajoutez-la à la ligne 2.

    \( \left[ \begin{array} {ccc|c} 5 &−2 &-2 &-2 \\ 4 &-1 &−4 &4 \\ -2 &3 &0 &−1 \end{array} \right] \)

    Réponse

    ⓐ\( \left[ \begin{matrix} −2 &3 &0 &−2 \\ 4 &−1 &−4 &4 \\ 5 &−2 &−2 &−2 \end{matrix} \right] \)

    ⓑ\( \left[ \begin{matrix} −2 &3 &0 &−2 \\ 4 &−1 &−4 &4 \\ 15 &−6 &−6 &−6 \end{matrix} \right] \)

    ⓒ\( \left[ \begin{matrix} -2 &3 &0 &2 & \\ 3 &4 &-13 &-16 &-8 \\ 15 &-6 &-6 &-6 & \end{matrix} \right] \)

    Exemple\(\PageIndex{9}\)

    Effectuez les opérations indiquées sur la matrice augmentée :

    ⓐ Échangez les rangées 1 et 2,

    ⓑ Multipliez la ligne 1 par 2,

    ⓒ Multipliez la ligne 2 par 3 et ajoutez-la à la ligne 1.

    \( \left[ \begin{array} {ccc|c} 2 &−3 &−2 &−4 \\ 4 &1 &−3 &2 \\ 5 &0 &4 &−1 \end{array} \right] \)

    Réponse

    ⓐ\( \left[ \begin{matrix} 4 &1 &−3 &2 \\ 2 &−3 &−2 &−4 \\ 5 &0 &4 &−1 \end{matrix} \right] \)
    ⓑ\( \left[ \begin{matrix} 8 &2 &−6 &4 \\ 2 &−3 &−2 &−4 \\ 5 &0 &4 &−1 \end{matrix} \right] \)
    ⓒ\( \left[ \begin{matrix} 14 &−7 &−12 &−8 \\ 2 &−3 &−2 &−4 \\ 5 &0 &4 &−1 \end{matrix} \right] \)

    Maintenant que nous avons pratiqué les opérations sur les lignes, nous allons examiner une matrice augmentée et déterminer quelle opération nous allons utiliser pour atteindre un objectif. C'est exactement ce que nous avons fait lorsque nous avons procédé à l'élimination. Nous avons décidé par quel nombre multiplier une ligne afin qu'une variable soit éliminée lorsque nous additionnons les lignes.

    Avec ce système, que feriez-vous pour éliminer x ?

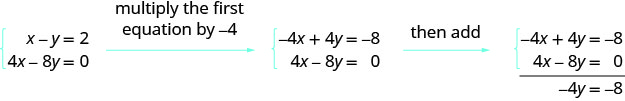
    Les deux équations sont les suivantes : x moins y est égal à 2 et 4x moins 8y est égal à 0. En multipliant le premier par moins 4, on obtient moins 4x plus 4y égal moins 8. En ajoutant cela à la deuxième équation, nous obtenons moins 4y égale moins 8.

    L'exemple suivant fait essentiellement la même chose, mais pour la matrice.

    Exemple\(\PageIndex{10}\)

    Effectuez l'opération de ligne nécessaire pour que la première entrée de la ligne 2 soit nulle dans la matrice augmentée :\( \left[ \begin{array} {cc|c} 1 &−1 &2 \\ 4 &−8 &0 \end{array} \right] \)

    Réponse

    Pour que le 4 soit 0, nous pouvons multiplier la ligne 1 par\(−4\) puis l'ajouter à la ligne 2.

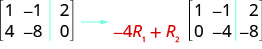
    La matrice 2 par 3 est 1, moins 1, 2 et 4, moins 8, 0. En effectuant l'opération moins 4R1 plus R2 sur la ligne 2, la deuxième ligne de la nouvelle matrice devient 0, moins 4, moins 8. La première rangée reste la même.

    Exemple\(\PageIndex{11}\)

    Effectuez l'opération de ligne nécessaire pour que la première entrée de la ligne 2 soit nulle dans la matrice augmentée :\( \left[ \begin{array} {cc|c} 1 &−1 &2 \\ 3 &−6 &2 \end{array} \right] \)

    Réponse

    \( \left[ \begin{matrix} 1 &−1 &2 \\ 0 &−3 &−4 \end{matrix} \right] \)

    Exemple\(\PageIndex{12}\)

    Effectuez l'opération de ligne nécessaire pour que la première entrée de la ligne 2 soit nulle dans la matrice augmentée :\( \left[ \begin{array} {cc|c} 1 &−1 &3 \\ -2 &−3 &2 \end{array} \right] \)

    Réponse

    \( \left[ \begin{matrix} 1 &−1 &3 \\ 0 &−5 &8 \end{matrix} \right] \)

    Résoudre des systèmes d'équations à l'aide

    Pour résoudre un système d'équations à l'aide de matrices, nous transformons la matrice augmentée en matrice sous forme d'échelons de ligne à l'aide d'opérations de ligne. Pour un système d'équations cohérent et indépendant, sa matrice augmentée se présente sous forme d'échelons de ligne lorsque, à gauche de la ligne verticale, chaque entrée de la diagonale est un 1 et toutes les entrées situées sous la diagonale sont des zéros.

    FORMULAIRE ROW-ECHELON

    Pour un système d'équations cohérent et indépendant, sa matrice augmentée se présente sous forme d'échelons de ligne lorsque, à gauche de la ligne verticale, chaque entrée de la diagonale est un 1 et toutes les entrées situées sous la diagonale sont des zéros.

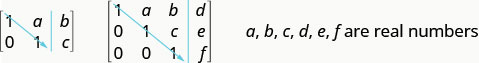
    Une matrice de 2 x 3 est montrée sur la gauche. Sa première ligne est 1, a, b et sa deuxième ligne est 0, 1, c. Une flèche pointe en diagonale vers le bas et vers la droite, superposant les deux 1 de la matrice. Une matrice de 3 x 4 est montrée sur la droite. Sa première ligne est 1, a, b, d. Sa deuxième ligne est 0, 1, c, e. Sa troisième ligne est 0, 0, 1, f. Une flèche pointe en diagonale vers le bas et vers la droite, superposant tous les 1 de la matrice. a, b, c, d, e, f sont des nombres réels.

    Une fois que nous avons obtenu la matrice augmentée sous forme d'échelons de ligne, nous pouvons écrire le système d'équations équivalent et lire la valeur d'au moins une variable. Nous substituons ensuite cette valeur dans une autre équation pour continuer à résoudre les autres variables. Ce processus est illustré dans l'exemple suivant.

    Comment résoudre un système d'équations à l'aide d'une matrice

    Résolvez le système d'équations en utilisant une matrice :\(\left\{ \begin{array} {l} 3x+4y=5 \\ x+2y=1 \end{array} \right. \)

    Réponse

    Les équations sont 3x plus 4y égale 5 et x plus 2y vaut 1. Étape 1. Ecrivez la matrice augmentée pour le système d'équations. Nous obtenons une matrice 2 par 3 avec la première ligne 3, 4, 5 et la deuxième ligne 1, 2, 1.Étape 2. À l'aide d'opérations de ligne, l'entrée de la ligne 1, colonne 1 prend la valeur 1. Échangez les lignes R1 et R2.Étape 3. À l'aide des opérations sur les lignes, obtenez des zéros dans la colonne 1 en dessous du 1. Multipliez la ligne 1 par moins 3 et ajoutez-la à la ligne 2. La ligne 2 devient 0, moins 2, 2.Étape 4. À l'aide des opérations de ligne, attribuez à l'entrée de la ligne 2, colonne 2 la valeur 1. Multipliez la ligne 2 par moins la moitié. La ligne 2 devient 0, 1, moins 1.Étape 5. Continuez le processus jusqu'à ce que la matrice se présente sous forme d'échelons de lignes. La matrice se présente désormais sous forme d'échelons de lignes.Étape 6. Écrivez le système d'équations correspondant. Nous obtenons x plus 2y égal 1 et y est égal à moins 1.Étape 7. Utilisez la substitution pour trouver les variables restantes. Substituer y est égal à moins 1 par x plus 2y est égal à 1. X plus 2 fois moins 1 est égal à 1. X moins 2 est égal à 1. On obtient x égal à 3.Étape 8. Écrivez la solution sous la forme d'une paire ordonnée ou d'un triple. La paire ordonnée est (3, moins 1).Étape 9. Vérifiez que la solution permet de vérifier que les équations d'origine sont vraies.

    Exemple\(\PageIndex{14}\)

    Résolvez le système d'équations en utilisant une matrice :\(\left\{ \begin{array} {l} 2x+y=7 \\ x−2y=6 \end{array} \right. \)

    Réponse

    La solution est\((4,−1)\).

    Exemple\(\PageIndex{15}\)

    Résolvez le système d'équations en utilisant une matrice :\(\left\{ \begin{array} {l} 2x+y=−4 \\ x−y=−2 \end{array} \right. \)

    Réponse

    La solution est\((−2,0)\).

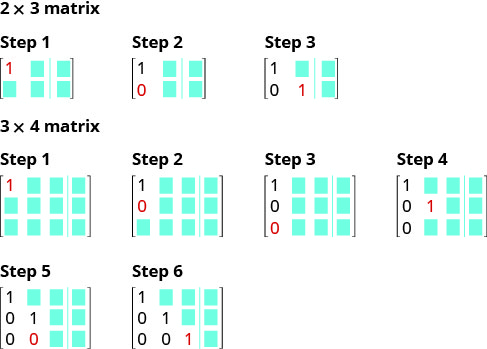
    Les étapes sont résumées ici.

    RÉSOLVEZ UN SYSTÈME D'ÉQUATIONS EN UTILISANT DES MATRICES.
    1. Ecrivez la matrice augmentée pour le système d'équations.
    2. À l'aide d'opérations de ligne, l'entrée de la ligne 1, colonne 1 prend la valeur 1.
    3. À l'aide des opérations sur les lignes, obtenez des zéros dans la colonne 1 en dessous du 1.
    4. À l'aide des opérations de ligne, attribuez à l'entrée de la ligne 2, colonne 2 la valeur 1.
    5. Continuez le processus jusqu'à ce que la matrice se présente sous forme d'échelons de lignes.
    6. Écrivez le système d'équations correspondant.
    7. Utilisez la substitution pour trouver les variables restantes.
    8. Écrivez la solution sous la forme d'une paire ordonnée ou d'un triple.
    9. Vérifiez que la solution permet de vérifier que les équations d'origine sont vraies.

    Voici un visuel qui montre l'ordre dans lequel les 1 et 0 sont placés dans la bonne position pour la forme à échelons de ligne.

    La figure montre 3 étapes pour une matrice 2 x 3 et 6 étapes pour une matrice 3 x 4. Pour le premier, l'étape 1 consiste à obtenir un 1 dans la ligne 1, colonne 1. L'étape to consiste à obtenir un 0 dans la ligne 2 de la colonne 1. L'étape 3 consiste à obtenir un 1 dans la colonne 2 de la ligne 2. Pour une matrice de 3 x 4, l'étape 1 consiste à obtenir un 1 dans la ligne 1, colonne 1. L'étape 2 consiste à obtenir un 0 dans la ligne 2, colonne 1. L'étape 3 consiste à obtenir un 0 dans la ligne 3, colonne 1. L'étape 4 consiste à obtenir un 1 dans la colonne 2 de la ligne 2. L'étape 5 consiste à obtenir un 0 dans la ligne 3, colonne 2. L'étape 6 consiste à obtenir un 1 dans la colonne 3 de la ligne 3.

    Nous utilisons la même procédure lorsque le système d'équations comporte trois équations.

    Exemple\(\PageIndex{16}\)

    Résolvez le système d'équations en utilisant une matrice :\(\left\{ \begin{array} {l} 3x+8y+2z=−5 \\ 2x+5y−3z=0 \\ x+2y−2z=−1 \end{array} \right. \)

    Réponse
      .
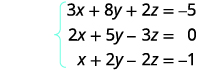
    Écrivez la matrice augmentée pour les équations. .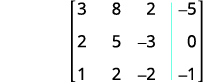
    Échangez les lignes 1 et 3 pour obtenir la valeur 1 de l'entrée de la
    ligne 1 et de la colonne 1.    		 .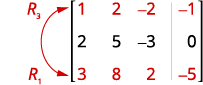
    À l'aide des opérations sur les lignes, obtenez des zéros dans la colonne 1 en dessous du 1. .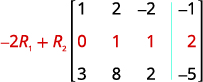
      .
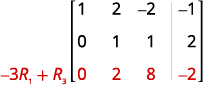
    L'entrée de la ligne 2, colonne 2 est désormais 1.  
    Continuez le processus jusqu'à ce que la matrice
    se présente sous forme d'échelons de lignes.    		 .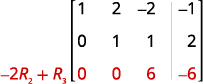
      .
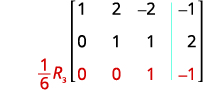
    La matrice se présente désormais sous forme d'échelons de lignes. .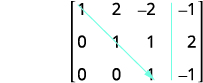
    Écrivez le système d'équations correspondant. .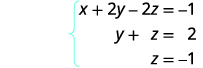
    Utilisez la substitution pour trouver les variables restantes. .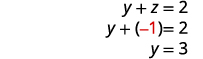
      .
    .
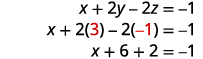
    Écrivez la solution sous la forme d'une paire ordonnée ou d'un triple. .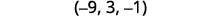
    Vérifiez que la solution permet de vérifier que les équations d'origine sont vraies. Nous vous laissons le chèque.
    Exemple\(\PageIndex{17}\)

    Résolvez le système d'équations en utilisant une matrice :\(\left\{ \begin{array} {l} 2x−5y+3z=8 \\ 3x−y+4z=7 \\ x+3y+2z=−3 \end{array} \right. \)

    Réponse

    \((6,−1,−3)\)

    Exemple\(\PageIndex{18}\)

    Résolvez le système d'équations en utilisant une matrice :\(\left\{ \begin{array} {l} −3x+y+z=−4 \\ −x+2y−2z=1 \\ 2x−y−z=−1 \end{array} \right. \)

    Réponse

    \((5,7,4)\)

    Jusqu'à présent, nous avons travaillé avec des matrices uniquement avec des systèmes cohérents et indépendants, ce qui signifie qu'ils n'ont qu'une seule solution. Voyons maintenant ce qui se passe lorsque nous utilisons une matrice pour un système dépendant ou incohérent.

    Exemple\(\PageIndex{19}\)

    Résolvez le système d'équations en utilisant une matrice :\(\left\{ \begin{array} {l} x+y+3z=0 \\ x+3y+5z=0 \\ 2x+4z=1 \end{array} \right. \)

    Réponse
      .
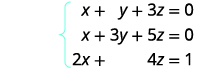
    Écrivez la matrice augmentée pour les équations. .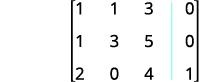
    L'entrée de la ligne 1, colonne 1 est 1.  
    À l'aide des opérations sur les lignes, obtenez des zéros dans la colonne 1 en dessous du 1. .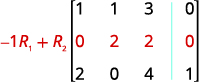
      .
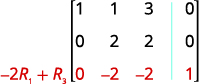
    Continuez le processus jusqu'à ce que la matrice se présente sous forme d'échelons de lignes. .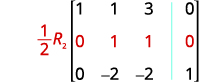
    Multipliez la ligne 2 par 2 et ajoutez-la à la ligne 3. .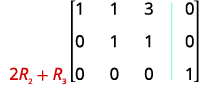
    À ce stade, nous avons tous les zéros à gauche de la rangée 3.  
    Écrivez le système d'équations correspondant. .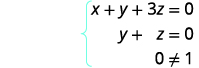
    Puisque\(0 \neq 1 \) nous avons une fausse déclaration. Tout comme lorsque nous résolvons un système à l'aide d'autres méthodes, cela nous indique que nous avons un système incohérent. Il n'y a pas de solution.
    Exemple\(\PageIndex{20}\)

    Résolvez le système d'équations en utilisant une matrice :\(\left\{ \begin{array} {l} x−2y+2z=1 \\ −2x+y−z=2 \\ x−y+z=5 \end{array} \right. \)

    Réponse

    aucune solution

    Exemple\(\PageIndex{21}\)

    Résolvez le système d'équations en utilisant une matrice :\(\left\{ \begin{array} {l} 3x+4y−3z=−2 \\ −2x+3y−z=−1 \\ 2x+y−2z=6 \end{array} \right. \)

    Réponse

    aucune solution

    Le dernier système était incohérent et il n'y avait donc aucune solution. L'exemple suivant est dépendant et propose une infinité de solutions.

    Exemple\(\PageIndex{22}\)

    Résolvez le système d'équations en utilisant une matrice :\(\left\{ \begin{array} {l} x−2y+3z=1 \\ x+y−3z=7 \\ 3x−4y+5z=7 \end{array} \right. \)

    Réponse
      .
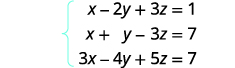
    Écrivez la matrice augmentée pour les équations. .
    L'entrée de la ligne 1, colonne 1 est 1.  
    À l'aide des opérations sur les lignes, obtenez des zéros dans la colonne 1 en dessous du 1. .
      .
    Continuez le processus jusqu'à ce que la matrice se présente sous forme d'échelons de lignes. .
    Multipliez la ligne 2 par\(−2\) et ajoutez-la à la ligne 3. .
    À ce stade, nous avons tous les zéros dans la rangée du bas.  
    Écrivez le système d'équations correspondant. .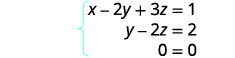
    Puisque\(0=0\) nous avons une déclaration vraie. Tout comme lorsque nous résolvons par substitution, cela nous indique que nous avons un système dépendant. Il existe une infinité de solutions.
    Résolvez y en termes de z dans la deuxième équation. .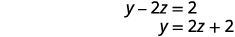
    Résolvez la première équation de x en termes de z. .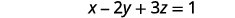
    Substitut\(y=2z+2\). .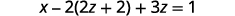
    Simplifiez. .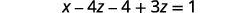
    Simplifiez. .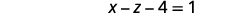
    Simplifiez. .
    Le système propose une infinité de solutions\((x,y,z)\), où se\(x=z+5;\space y=2z+2;\space z\) trouve n'importe quel nombre réel.
    Exemple\(\PageIndex{23}\)

    Résolvez le système d'équations en utilisant une matrice :\(\left\{ \begin{array} {l} x+y−z=0 \\ 2x+4y−2z=6 \\ 3x+6y−3z=9 \end{array} \right. \)

    Réponse

    infiniment de solutions\((x,y,z)\), où se\(x=z−3;\space y=3;\space z\) trouve n'importe quel nombre réel.

    Exemple\(\PageIndex{24}\)

    Résolvez le système d'équations en utilisant une matrice :\(\left\{ \begin{array} {l} x−y−z=1 \\ −x+2y−3z=−4 \\ 3x−2y−7z=0 \end{array} \right. \)

    Réponse

    infiniment de solutions\((x,y,z)\), où se\(x=5z−2;\space y=4z−3;\space z\) trouve n'importe quel nombre réel.

    Accédez à cette ressource en ligne pour obtenir des instructions et des exercices supplémentaires sur l'élimination gaussienne.

    • Élimination gaussienne

    Concepts clés

    • Matrice : Une matrice est un ensemble rectangulaire de nombres disposés en lignes et en colonnes. Une matrice comportant m lignes et n colonnes est ordonnée\(m\times n\). La matrice sur la gauche ci-dessous comporte 2 lignes et 3 colonnes et est donc ordonnée\(2\times 3\). Nous disons que c'est une matrice 2 par 3.
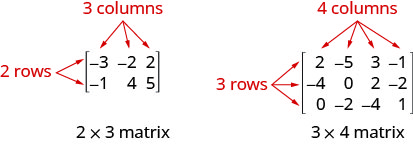
      La figure montre deux matrices. Celui de gauche a les chiffres moins 3, moins 2 et 2 dans la première rangée et les chiffres moins 1, 4 et 5 dans la deuxième rangée. Les lignes et les colonnes sont placées entre crochets. Il comporte donc 2 lignes et 3 colonnes. Il est étiqueté matrice 2 croix 3 ou matrice 2 par 3. La matrice de droite est similaire mais comporte 3 lignes et 4 colonnes. Il est étiqueté matrice 3 par 4.
      Chaque nombre de la matrice est appelé élément ou entrée de la matrice.
    • Opérations de ligne : Dans une matrice, les opérations suivantes peuvent être effectuées sur n'importe quelle ligne et la matrice résultante sera équivalente à la matrice d'origine.
      • Échangez deux lignes quelconques
      • Multipliez une ligne par n'importe quel nombre réel sauf 0
      • Ajouter un multiple non nul d'une ligne à une autre
    • Forme à échelons de ligne : Pour un système d'équations cohérent et indépendant, sa matrice augmentée se présente sous forme d'échelons de ligne lorsque, à gauche de la ligne verticale, chaque entrée de la diagonale est un 1 et que toutes les entrées situées sous la diagonale sont des zéros.
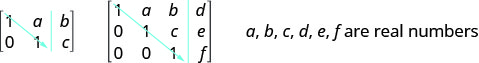
      La figure montre deux matrices. Celui de gauche a les chiffres moins 3, moins 2 et 2 dans la première rangée et les chiffres moins 1, 4 et 5 dans la deuxième rangée. Les lignes et les colonnes sont placées entre crochets. Il comporte donc 2 lignes et 3 colonnes. Il est étiqueté matrice 2 croix 3 ou matrice 2 par 3. La matrice de droite est similaire mais comporte 3 lignes et 4 colonnes. Il est étiqueté matrice 3 par 4.
    • Comment résoudre un système d'équations à l'aide de matrices.
      1. Ecrivez la matrice augmentée pour le système d'équations.
      2. À l'aide d'opérations de ligne, l'entrée de la ligne 1, colonne 1 prend la valeur 1.
      3. À l'aide des opérations sur les lignes, obtenez des zéros dans la colonne 1 en dessous du 1.
      4. À l'aide des opérations de ligne, attribuez à l'entrée de la ligne 2, colonne 2 la valeur 1.
      5. Continuez le processus jusqu'à ce que la matrice se présente sous forme d'échelons de lignes.
      6. Écrivez le système d'équations correspondant.
      7. Utilisez la substitution pour trouver les variables restantes.
      8. Écrivez la solution sous la forme d'une paire ordonnée ou d'un triple.
      9. Vérifiez que la solution permet de vérifier que les équations d'origine sont vraies.

    Lexique

    matrice
    Une matrice est un ensemble rectangulaire de nombres disposés en lignes et en colonnes.
    forme à échelons de ligne
    Une matrice se présente sous forme d'échelons de ligne lorsque, à gauche de la ligne verticale, chaque entrée de la diagonale est un 1 et que toutes les entrées situées sous la diagonale sont des zéros.