Skip to main content
Global

4.5 : Résoudre des systèmes d'équations à trois variables

  1. Last updated
  2. Save as PDF
  • Page ID
    194173

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage

    À la fin de cette section, vous serez en mesure de :

    • Déterminer si un triple ordonné est la solution d'un système de trois équations linéaires à trois variables
    • Résolvez un système d'équations linéaires à trois variables
    • Résolvez des applications en utilisant des systèmes d'équations linéaires à trois variables

    Avant de commencer, répondez à ce questionnaire de préparation.

    1. Évaluez\(5x−2y+3z\) quand\(x=−2, y=−4,\) et\(z=3.\)
      si vous avez oublié ce problème, consultez [lien].
    2. Classifiez les équations en tant qu'équation conditionnelle, identité ou contradiction, puis énoncez la solution. \( \left\{ \begin{array} {l} −2x+y=−11 \\ x+3y=9 \end{array} \right. \)
      Si vous avez oublié ce problème, consultez [lien].
    3. Classifiez les équations en tant qu'équation conditionnelle, identité ou contradiction, puis énoncez la solution. \(\left\{ \begin{array} {l} 7x+8y=4 \\ 3x−5y=27 \end{array} \right. \)
      Si vous avez oublié ce problème, consultez [lien].

    Déterminer si un triple ordonné est la solution d'un système de trois équations linéaires à trois variables

    Dans cette section, nous allons étendre notre travail de résolution d'un système d'équations linéaires. Jusqu'à présent, nous avons travaillé avec des systèmes d'équations à deux équations et à deux variables. Nous allons maintenant travailler avec des systèmes de trois équations à trois variables. Mais passons d'abord en revue ce que nous savons déjà sur la résolution d'équations et de systèmes impliquant jusqu'à deux variables.

    Nous avons appris plus tôt que le graphique d'une équation linéaire est une droite.\(ax+by=c\) Chaque point de la ligne, une paire ordonnée\((x,y)\), est une solution à l'équation. Pour un système de deux équations à deux variables, nous tracons deux lignes. Ensuite, nous pouvons voir que tous les points qui sont des solutions à chaque équation forment une droite. Et, en découvrant ce que les lignes ont en commun, nous trouverons la solution au système.

    La plupart des équations linéaires d'une variable ont une solution, mais nous avons vu que certaines équations, appelées contradictions, n'ont pas de solution et que pour d'autres équations, appelées identités, tous les nombres sont des solutions

    Nous savons que lorsque nous résolvons un système de deux équations linéaires représentées par un graphe de deux droites dans le même plan, il existe trois cas possibles, comme indiqué.

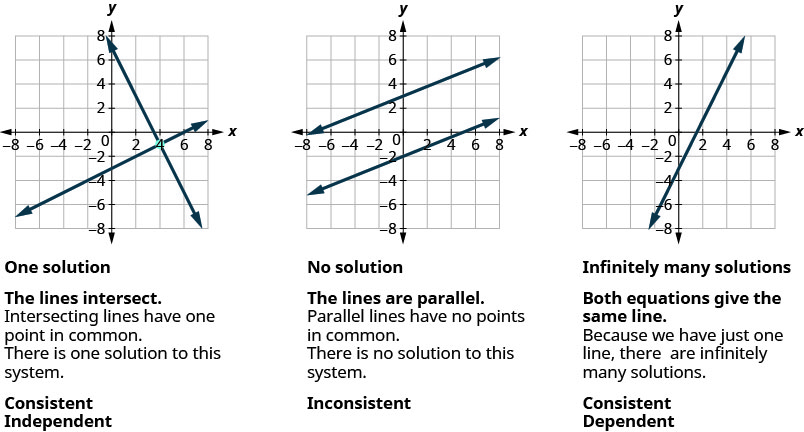
    La figure montre trois graphiques. Dans la première, deux lignes se croisent. Les lignes qui se croisent ont un point commun. Il existe une solution à ce système. Le graphique est intitulé Cohérent et indépendant. Dans le second graphique, deux droites sont parallèles. Les lignes parallèles n'ont aucun point commun. Il n'existe pas de solution à ce système. Le graphique est étiqueté « incohérent ». Dans le troisième graphique, il n'y a qu'une seule ligne. Les deux équations donnent la même droite. Comme nous n'avons qu'une seule ligne, il existe une infinité de solutions. Il est étiqueté dépendant de manière cohérente.

    De même, pour une équation linéaire comportant trois variables ax+by+cz=d, ax+by+cz=d, chaque solution de l'équation est un triple ordonné (x, y, z) (x, y, z) (x, y, z) qui rend l'équation vraie.

    ÉQUATION LINÉAIRE À TROIS VARIABLES

    Une équation linéaire à trois variables, où a, b, c et d sont des nombres réels et a, b et c ne sont pas tous 0, est de la forme

    \[ ax+by+cz=d\nonumber \]

    Chaque solution de l'équation est un triple ordonné,\((x,y,z)\) ce qui rend l'équation vraie.

    Tous les points qui sont des solutions à une équation forment un plan dans un espace tridimensionnel. Et, en découvrant ce que les avions ont en commun, nous trouverons la solution au système.

    Lorsque nous résolvons un système de trois équations linéaires représentées par un graphe de trois plans dans l'espace, trois cas sont possibles.

    Huit figures sont présentées. Le premier montre trois plans qui se croisent et qui ont un point commun. Il est étiqueté Système cohérent et Équations indépendantes. La deuxième figure comporte trois plans parallèles sans points communs. Il est étiqueté Système incohérent. Dans la troisième figure, deux plans coïncident et sont parallèles au troisième plan. Les avions n'ont aucun point commun. Dans la quatrième figure, deux plans sont parallèles et chacun croise le troisième plan. Les avions n'ont aucun point commun. Dans la cinquième figure, chaque plan croise les deux autres, mais les trois ne partagent aucun point. Les avions n'ont aucun point commun. Dans la sixième figure, trois plans se croisent en une seule ligne. Il n'y a qu'une seule ligne, il existe donc une infinité de solutions. Dans la septième figure, deux plans coïncident et coupent le troisième plan d'une ligne. Il n'y a qu'une seule ligne, il existe donc une infinité de solutions. Dans la dernière figure, trois plans coïncident. Il n'y a qu'un seul avion, il existe donc une infinité de solutions........

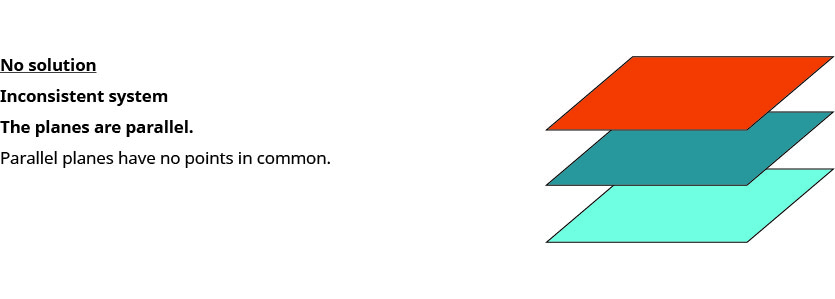
    Pour résoudre un système de trois équations linéaires, nous voulons trouver les valeurs des variables qui sont des solutions aux trois équations. En d'autres termes, nous recherchons le triple ordonné\((x,y,z)\) qui rend les trois équations vraies. On les appelle les solutions du système de trois équations linéaires à trois variables.

    SOLUTIONS D'UN SYSTÈME D'ÉQUATIONS LINÉAIRES À TROIS VARIABLES

    Les solutions d'un système d'équations sont les valeurs des variables qui rendent toutes les équations vraies. Une solution est représentée par un triple ordonné\((x,y,z)\).

    Pour déterminer si un triple ordonné est une solution à un système de trois équations, nous substituons les valeurs des variables dans chaque équation. Si le triple ordonné rend les trois équations vraies, il s'agit d'une solution pour le système.

    Exemple\(\PageIndex{1}\)

    Déterminez si le triple commandé est une solution pour le système :\( \left\{ \begin{array} {l} x−y+z=2 \\ 2x−y−z=−6 \\ 2x+2y+z=−3 \end{array} \right. \)

    ⓐ\((−2,−1,3)\) ⓑ\((−4,−3,4)\)

    Réponse

    ⓐ

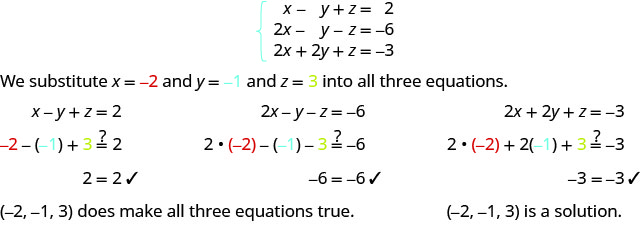
    Les équations sont les suivantes : x moins y plus z est égal à 2, 2x moins y moins z est égal à moins 6 et 2x plus 2y plus z est égal à moins 3. En substituant moins 2 pour x, moins 1 pour y et 3 pour z dans les trois équations, nous trouvons que les trois sont vraies. Par conséquent, moins 2, moins 1, 3 est une solution.

    ⓑ

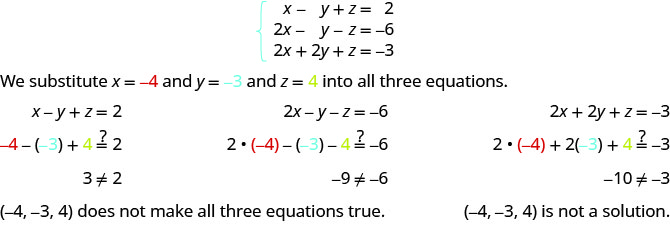
    Les équations sont les suivantes : x moins y plus z est égal à 2, 2x moins y moins z est égal à moins 6 et 2x plus 2y plus z est égal à moins 3. En substituant moins moins 4 pour x, moins 3 pour y et 4 pour z dans les trois équations, nous trouvons que les trois sont vraies. Par conséquent, moins 4, moins 3, 4 n'est pas une solution.

    Exemple\(\PageIndex{2}\)

    Déterminez si le triple commandé est une solution pour le système :\( \left\{ \begin{array} {l} 3x+y+z=2 \\ x+2y+z=−3 \\ 3x+y+2z=4 \end{array} \right. \)

    ⓐ\((1,−3,2)\) ⓑ\((4,−1,−5)\)

    Réponse

    ⓐ Oui ⓑ Non

    Exemple\(\PageIndex{3}\)

    Déterminez si le triple commandé est une solution pour le système :\( \left\{ \begin{array} {l} x−3y+z=−5 \\ −3x−y−z=1 \\ 2x−2y+3z=1 \end{array} \right. \)

    ⓐ\((2,−2,3)\) ⓑ\((−2,2,3)\)

    Réponse

    ⓐ non ⓑ oui

    Résolvez un système d'équations linéaires à trois variables

    Pour résoudre un système d'équations linéaires à trois variables, nous utilisons essentiellement les mêmes techniques que celles que nous avons utilisées avec des systèmes à deux variables. Nous commençons par deux paires d'équations et, dans chaque paire, nous éliminons la même variable. Cela nous donnera alors un système d'équations avec seulement deux variables et nous saurons ensuite comment résoudre ce système !

    Ensuite, nous utilisons les valeurs des deux variables que nous venons de trouver pour revenir à l'équation d'origine et trouver la troisième variable. Nous écrivons notre réponse sous la forme d'un triple ordonné, puis nous vérifions nos résultats.

    Exemple\(\PageIndex{4}\): How to Solve a System of Equations With Three Variables by Elimination

    Résolvez le système par élimination :\( \left\{ \begin{array} {l} x−2y+z=3 \\ 2x+y+z=4 \\ 3x+4y+3z=−1 \end{array} \right. \)

    Réponse

    Les équations sont les suivantes : x moins 2y plus z est égal à 3, 2x plus y plus z est égal à 4 et 3x plus 4y plus 3z est égal à moins 1. L'étape 1 consiste à écrire les équations sous forme standard. Ils le sont. Si certains coefficients sont des fractions, supprimez-les. Il n'y en a aucune.L'étape 2 consiste à éliminer la même variable de deux équations. Déterminez quelle variable vous allez éliminer. Nous pouvons éliminer les y des équations 1 et 2 en multipliant l'équation 2 par 2. Utilisez deux équations pour éliminer la variable choisie. Multipliez l'une des équations ou les deux de manière à ce que les coefficients de cette variable soient opposés. Ajoutez les équations résultant de l'étape 2 pour éliminer une variable. La nouvelle équation que nous obtenons est 5x plus 3z égale 11.L'étape 3 consiste à répéter l'étape 2 en utilisant deux autres équations et à éliminer la même variable qu'à l'étape 2. Nous pouvons à nouveau éliminer les y en utilisant les équations 1, 3 en multipliant l'équation 1 par 2. Ajoutez les nouvelles équations et le résultat sera 5x plus 5z est égal à 5.Étape 4. Les deux nouvelles équations forment un système de deux équations à deux variables. Résolvez ce système. En éliminant x, on obtient z égal à moins 3. En substituant cela dans l'une des nouvelles équations, on obtient x égal à 4.L'étape 5 consiste à utiliser les valeurs des deux variables trouvées à l'étape 4 pour trouver la troisième variable. 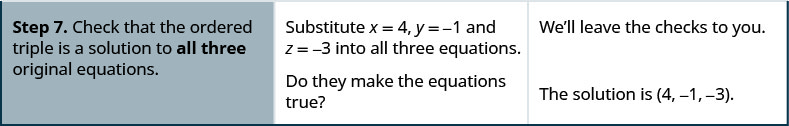En substituant les valeurs de x et de z dans l'une des équations d'origine, on obtient y égal à moins 1.L'étape 6 consiste à écrire la solution sous la forme d'un triple ordonné 4, moins 1, moins 3.L'étape 7 consiste à vérifier que le triple ordonné est une solution aux trois équations d'origine. Cela rend les trois équations vraies.

    Exemple\(\PageIndex{5}\)

    Résolvez le système par élimination :\( \left\{ \begin{array} {l} 3x+y−z=2 \\ 2x−3y−2z=1 \\ 4x−y−3z=0 \end{array} \right.\)

    Réponse

    \((2,−1,3)\)

    Exemple\(\PageIndex{6}\)

    Résolvez le système par élimination :\( \left\{ \begin{array} {l} 4x+y+z=−1 \\ −2x−2y+z=2 \\ 2x+3y−z=1 \end{array} \right. \)

    Réponse

    \((−2,3,4)\)

    Les étapes sont résumées ici.

    RÉSOLVEZ UN SYSTÈME D'ÉQUATIONS LINÉAIRES À TROIS VARIABLES.
    1. Écrivez les équations sous forme standard
      • Si certains coefficients sont des fractions, supprimez-les.
    2. Éliminez la même variable de deux équations.
      • Déterminez quelle variable vous allez éliminer.
      • Utilisez deux équations pour éliminer la variable choisie.
      • Multipliez l'une des équations ou les deux de manière à ce que les coefficients de cette variable soient opposés.
      • Ajoutez les équations résultant de l'étape 2 pour éliminer une variable
    3. Répétez l'étape 2 en utilisant deux autres équations et éliminez la même variable qu'à l'étape 2.
    4. Les deux nouvelles équations forment un système de deux équations à deux variables. Résolvez ce système.
    5. Utilisez les valeurs des deux variables trouvées à l'étape 4 pour trouver la troisième variable.
    6. Écrivez la solution sous la forme d'un triple ordonné.
    7. Vérifiez que le triple ordonné est une solution aux trois équations d'origine.
    Exemple\(\PageIndex{7}\)

    Résoudre :\( \left\{ \begin{array} {l} 3x−4z=0 \\ 3y+2z=−3 \\ 2x+3y=−5 \end{array} \right. \)

    Réponse

    \[ \left\{ \begin{array} {ll} 3x−4z=0 &(1) \\ 3y+2z=−3 &(2) \\ 2x+3y=−5 &(3) \end{array} \right. \nonumber \]

    Nous pouvons éliminer les\(z\) équations (1) et (2) en multipliant l'équation (2) par 2, puis en ajoutant les équations résultantes.

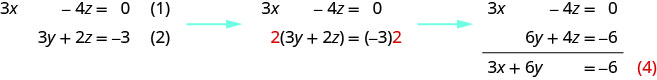
    Les équations sont les suivantes : 3 x moins 4 est égal à 0, 3y plus 2 z est égal à moins 3 et 2 x plus 3 y est égal à moins 5. Multipliez l'équation 2 par 2 et ajoutez-la à l'équation 1. Nous obtenons 3 x plus 6 y est égal à moins 6.

    Notez que les équations (3) et (4) contiennent toutes deux les variables\(x\) et\(y\). Nous allons résoudre ce nouveau système pour\(x\) et\(y\).

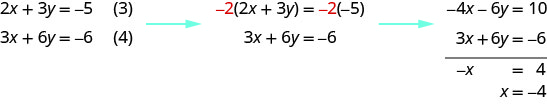
    Multipliez l'équation 3 par moins 2 et ajoutez-la à l'équation 4. On obtient x égal à moins 4.

    Pour résoudre y, nous le remplaçons\(x=−4\) dans l'équation (3).

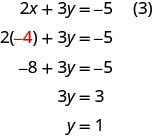
    Remplacez moins 4 dans l'équation 3 et résolvez pour y. Nous obtenons y égal à 1.

    Nous avons maintenant\(x=−4\) et\(y=1\). Nous devons résoudre pour z. Nous pouvons la remplacer par l'\(x=−4\)équation (1) pour trouver z.

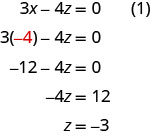
    En remplaçant x par moins 4 dans l'équation 1, on obtient z égal à moins 3.

    Nous écrivons la solution sous la forme d'un triple ordonné. \((−4,1,−3)\)

    Nous vérifions que la solution rend les trois équations vraies.

    \(\begin{array} {lll} {3x-4z=0 \space (1)} &{3y+2z=−3 \space (2)} &{2x+3y=−5 \space (3)} \\ {3(−4)−4(−3)\overset{?}{=} 0} &{3(1)+2(−3)\overset{?}{=} −3} &{2(−4)+3(1)\overset{?}{=} −5} \\ {0=0 \checkmark} &{−3=−3 \checkmark} &{−5=−5 \checkmark} \\ {} &{} &{\text{The solution is }(−4,1,−3)} \end{array}\)

    Exemple\(\PageIndex{8}\)

    Résoudre :\( \left\{ \begin{array} {l} 3x−4z=−1 \\ 2y+3z=2 \\ 2x+3y=6 \end{array} \right. \)

    Réponse

    \((−3,4,−2)\)

    Exemple\(\PageIndex{9}\)

    Résoudre :\( \left\{ \begin{array} {l} 4x−3z=−5 \\ 3y+2z=7 \\ 3x+4y=6 \end{array} \right. \)

    Réponse

    \((−2,3,−1)\)

    Lorsque nous résolvons un système et que nous nous retrouvons sans variables et avec une fausse déclaration, nous savons qu'il n'y a pas de solutions et que le système est incohérent. L'exemple suivant montre un système d'équations incohérent.

    Exemple\(\PageIndex{10}\)

    Résolvez le système d'équations :\( \left\{ \begin{array} {l} x+2y−3z=−1 \\ x−3y+z=1 \\ 2x−y−2z=2 \end{array} \right. \)

    Réponse

    \[\left\{ \begin{array} {ll} x+2y−3z=−1 &(1) \\ x−3y+z=1 &(2) \\ 2x−y−2z=2 &(3) \end{array} \right.\nonumber \]

    Utilisez les équations (1) et (2) pour éliminer z.

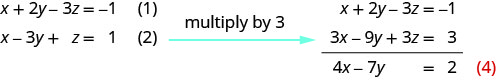
    Les équations sont les suivantes : x plus 2y moins 3z est égal à moins 1, x moins 3y plus z est égal à 1 et 2x moins y moins 2z est égal à 2.

    Utilisez (2) et (3) pour éliminer à\(z\) nouveau.

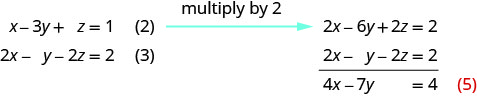
    En multipliant l'équation 2 par 3 et en l'ajoutant à l'équation 1, on obtient l'équation 4, 4x moins 7y égale 2. En multipliant l'équation 2 par 2 et en l'ajoutant à l'équation 3, on obtient l'équation 5, 4x moins 7y égale 4.

    Utilisez (4) et (5) pour éliminer une variable.

    Les équations 4 et 5 comportent toutes deux variables. Multipliez l'équation 5 par moins 1 et ajoutez-la à l'équation 4. On obtient 0 égal à moins 2, ce qui est faux.

    Il n'y a pas de solution.

    Il nous reste une fausse déclaration qui nous indique que le système est incohérent et qu'il n'y a aucune solution.

    Exemple\(\PageIndex{11}\)

    Résolvez le système d'équations :\( \left\{ \begin{array} {l} x+2y+6z=5 \\ −x+y−2z=3 \\ x−4y−2z=1 \end{array} \right. \)

    Réponse

    aucune solution

    Exemple\(\PageIndex{12}\)

    Résolvez le système d'équations :\( \left\{ \begin{array} {l} 2x−2y+3z=6 \\ 4x−3y+2z=0 \\ −2x+3y−7z=1 \end{array} \right. \)

    Réponse

    aucune solution

    Lorsque nous résolvons un système et que nous nous retrouvons sans variables mais avec une déclaration vraie, nous savons qu'il existe une infinité de solutions. Le système est cohérent avec les équations dépendantes. Notre solution montrera comment deux des variables dépendent de la troisième.

    Exemple\(\PageIndex{13}\)

    Résolvez le système d'équations :\( \left\{ \begin{array} {l} x+2y−z=1 \\ 2x+7y+4z=11 \\ x+3y+z=4 \end{array} \right. \)

    Réponse

    \[\left\{ \begin{array} {ll} x+2y−z=1 &(1) \\ 2x+7y+4z=11 &(2) \\ x+3y+z=4 &(3) \end{array} \right.\nonumber \]

    Utilisez les équations (1) et (3) pour éliminer x.

    Les équations sont les suivantes : x plus 2y moins z est égal à 1, 2x plus 7y plus 4z est égal à 11 et x plus 3y plus z est égal à 4. Multipliez l'équation 1 par moins 1 et ajoutez-la à l'équation 3. Nous obtenons l'équation 4, y plus 2z égale 3.

    Utilisez les équations (1) et (2) pour éliminer à nouveau x.

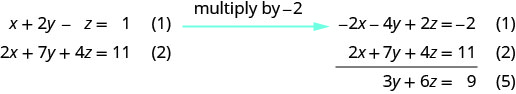
    Multipliez l'équation 1 par moins 2 et ajoutez-la à l'équation 2. Nous obtenons l'équation 5, 3y plus 6z égale 9.

    Utilisez les équations (4) et (5) pour éliminer\(y\).

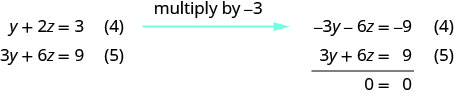
    Multipliez l'équation 4 par moins 3 et ajoutez-la à l'équation 5. Nous obtenons 0 égal à 0. Il existe une infinité de solutions. En résolvant l'équation 4 pour y, on obtient y égal à moins 2z plus 3. En le remplaçant dans l'équation 1, on obtient x égal à 5z moins 5. La vraie déclaration 0 égale à 0 nous indique qu'il s'agit d'un système dépendant qui a une infinité de solutions. Les solutions sont de la forme x, y, z où x est 5z moins 5, y est moins 2z plus 3 et z est un nombre réel quelconque.
      Il existe une infinité de solutions.
    Résolvez l'équation (4) pour y. Représentez la solution montrant comment x et y dépendent de z.
    \( \begin{aligned} y+2z &= 3 \\ y &= −2z+3 \end{aligned} \)
    Utilisez l'équation (1) pour résoudre x. \( x+2y−z=1\)
    Substitut\(y=−2z+3\). \( \begin{aligned} x+2(−2z+3)−z &= 1 \\ x−4z+6−z &= 1 \\ x−5z+6 &= 1 \\ x &= 5z−5 \end{aligned} \)

    La véritable affirmation nous\(0=0\) indique qu'il s'agit d'un système dépendant qui propose une infinité de solutions. Les solutions sont de la forme (x, y, z) (x, y, z) où\(x=5z−5;\space y=−2z+3\) et z est un nombre réel quelconque.

    Exemple\(\PageIndex{14}\)

    Résolvez le système par des équations :\( \left\{ \begin{array} {l} x+y−z=0 \\ 2x+4y−2z=6 \\ 3x+6y−3z=9 \end{array} \right. \)

    Réponse

    infiniment de solutions\((x,3,z)\) où se\(x=z−3;\space y=3;\space z\) trouve n'importe quel nombre réel

    Exemple\(\PageIndex{15}\)

    Résolvez le système par des équations :\( \left\{ \begin{array} {l} x−y−z=1 \\ −x+2y−3z=−4 \\ 3x−2y−7z=0 \end{array} \right. \)

    Réponse

    infiniment de solutions\((x,y,z)\) où se\(x=5z−2;\space y=4z−3;\space z\) trouve n'importe quel nombre réel

    Résolvez des applications en utilisant des systèmes d'équations linéaires à trois variables

    Les applications modélisées par un système d'équations peuvent être résolues en utilisant les mêmes techniques que celles que nous avons utilisées pour résoudre les systèmes. La plupart des applications ne sont que des extensions de trois variables des types que nous avons résolus précédemment.

    Exemple\(\PageIndex{16}\)

    Le département de théâtre du collège communautaire a vendu trois types de billets pour sa dernière production théâtrale. Les billets pour adultes se vendaient 15$, les billets étudiants 10$ et les billets pour enfants 8$. Le département du théâtre était ravi d'avoir vendu 250 billets et d'avoir rapporté 2 825 dollars en une nuit. Le nombre de billets étudiants vendus est le double du nombre de billets pour adultes vendus. Combien de produits de chaque type le ministère a-t-il vendus ?

    Réponse
    Nous utiliserons un tableau pour organiser les informations. .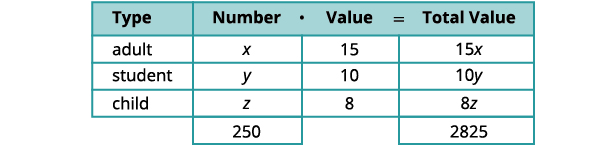
    Le nombre d'étudiants est le double du nombre d'adultes.  
    Réécrivez l'équation sous forme standard. \(\begin{aligned} y &= 2x \\ 2x−y &= 0 \end{aligned} \)
    .
    Utilisez les équations (1) et (2) pour éliminer z.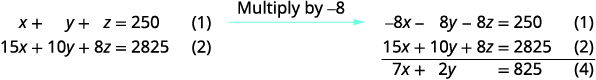  
    .
    Utilisez (3) et (4) pour éliminer\(y\).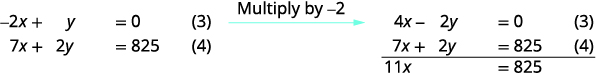  
    .
    Résolvez pour x. \(x=75 \)billets pour adultes
    Utilisez l'équation (3) pour trouver y. \(−2x+y=0\)
    Substitut\(x=75\). \(\begin{aligned} −2(75)+y &= 0 \\ −150+y &= 0 \\ y &= 150\text{ student tickets}\end{aligned} \)
    Utilisez l'équation (1) pour trouver z. \(x+y+z=250\)
    Substituer dans les valeurs
    \(x=75, \space y=150.\)
    \(\begin{aligned} 75+150+z &= 250 \\ 225+z &= 250 \\ z &= 25\text{ child tickets} \end{aligned} \)
    Écrivez la solution. Le département du théâtre a vendu 75 billets pour adultes,
    150 billets pour étudiants et 25 billets pour enfants.
    Exemple\(\PageIndex{17}\)

    Le département des beaux-arts du collège communautaire a vendu trois types de billets pour sa dernière présentation de danse. Les billets pour adultes se vendaient à 20 dollars, les billets étudiants à 12 dollars et les billets pour enfants à 10 dollars. Le département des beaux-arts était ravi d'avoir vendu 350 billets et d'avoir rapporté 4 650 dollars en une nuit. Le nombre de billets pour enfants vendus est le même que le nombre de billets pour adultes vendus. Combien de produits de chaque type le ministère a-t-il vendus ?

    Réponse

    Le département des beaux-arts a vendu 75 billets pour adultes, 200 billets pour étudiants et 75 billets pour enfants.

    Exemple\(\PageIndex{18}\)

    L'équipe de soccer du collège communautaire a vendu trois types de billets pour son dernier match. Les billets pour adultes se vendaient à 10$, les billets étudiants à 8 dollars et les billets pour enfants à 5 dollars. L'équipe de soccer était ravie d'avoir vendu 600 billets et d'avoir rapporté 4 900$ pour un match. Le nombre de billets pour adultes est le double du nombre de billets pour enfants. Combien de pièces de chaque type l'équipe de football a-t-elle vendues ?

    Réponse

    L'équipe de football a vendu 200 billets pour adultes, 300 billets pour étudiants et 100 billets pour enfants.

    Accédez à cette ressource en ligne pour obtenir des instructions supplémentaires et vous entraîner à résoudre un système linéaire à trois variables avec des solutions nulles ou infinies.

    • Résolution d'un système linéaire à trois variables avec des solutions nulles ou infinies
    • 3. Application variable

    Concepts clés

    • Équation linéaire à trois variables : Une équation linéaire à trois variables, où a, b, c et d sont des nombres réels et a, b et c ne sont pas tous 0, est de la forme

      \[ax+by+cz=d\nonumber \]


      Chaque solution de l'équation est un triple ordonné,\((x,y,z)\) ce qui rend l'équation vraie.
    • Comment résoudre un système d'équations linéaires à trois variables.
      1. Écrivez les équations sous forme standard.
        Si certains coefficients sont des fractions, effacez-les.
      2. Éliminez la même variable de deux équations.
        Déterminez quelle variable vous allez éliminer.
        Utilisez deux équations pour éliminer la variable choisie.
        Multipliez l'une des équations ou les deux de manière à ce que les coefficients de cette variable soient opposés.
        Ajoutez les équations résultant de l'étape 2 pour éliminer une variable
      3. Répétez l'étape 2 en utilisant deux autres équations et éliminez la même variable qu'à l'étape 2.
      4. Les deux nouvelles équations forment un système de deux équations à deux variables. Résolvez ce système.
      5. Utilisez les valeurs des deux variables trouvées à l'étape 4 pour trouver la troisième variable.
      6. Écrivez la solution sous la forme d'un triple ordonné.
      7. Vérifiez que le triple ordonné est une solution aux trois équations d'origine.

    Lexique

    solutions d'un système d'équations linéaires à trois variables
    Les solutions d'un système d'équations sont les valeurs des variables qui rendent toutes les équations vraies ; une solution est représentée par un triple ordonné (x, y, z).