4.4 : Résoudre des applications de mélange avec des systèmes d'équations
- Page ID
- 194163
À la fin de cette section, vous serez en mesure de :
- Résolvez les applications
- Résolvez les demandes
- Résoudre les applications des fonctions de coûts et de recettes
Avant de commencer, répondez à ce questionnaire de préparation.
- Multipliez :\(4.025(1,562)\).
Si vous avez oublié ce problème, consultez [lien]. - Ecrivez 8,2 % sous forme décimale.
Si vous avez oublié ce problème, consultez [lien]. - La facture du dîner d'Earl s'élevait à 32,50$ et il voulait laisser un pourboire de 18 %. Quel doit être le pourboire ?
Si vous avez oublié ce problème, consultez [lien].
Résolvez les applications
L'application du mélange implique la combinaison de deux quantités ou plus. Lorsque nous avons résolu des applications mixtes avec des pièces et des billets plus tôt, nous avons commencé par créer un tableau afin de pouvoir organiser les informations. Pour un exemple de pièce de monnaie avec des pièces de cinq cents et des pièces de dix cents, la table ressemblait à ceci :
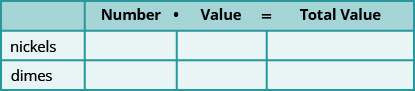
L'utilisation d'une variable signifiait que nous devions relier le nombre de nickels au nombre de dix cents. Nous devions décider si nous allions laisser n être le nombre de centimes et ensuite écrire le nombre de centimes en termes de n, ou si nous allions laisser d être le nombre de centimes et écrire le nombre de nickels en termes de d.
Maintenant que nous savons comment résoudre des systèmes d'équations à deux variables, nous allons simplement laisser n le nombre de nickel et d le nombre de dix cents. Nous allons écrire une équation basée sur la colonne de valeur totale, comme nous l'avons fait auparavant, et l'autre équation proviendra de la colonne des nombres.
Pour le premier exemple, nous allons résoudre un problème de ticket où les prix des billets sont en dollars entiers, de sorte que nous n'aurons pas besoin d'utiliser des décimales pour l'instant.
Traduisez en un système d'équations et résolvez :
Un centre scientifique a vendu 1 363 billets lors d'un week-end chargé. Les recettes s'élevaient à 12 146$. Combien de billets pour adultes à 12$ et combien de billets pour enfants à 7$ ont-ils été vendus ?
- Réponse
-
Étape 1. Lisez le problème. Nous allons créer un tableau pour organiser les informations. Étape 2. Identifiez ce que nous recherchons. Nous recherchons le nombre de billets pour adultes
et le nombre de billets pour enfants vendus.Étape 3. Nommez ce que nous recherchons. Laissez\(a= \text{the number of adult tickets.}\)
\(c= \text{the number of child tickets}\)Un tableau nous aidera à organiser les données.
Nous avons deux types de billets, adultes et enfants.Inscrivez en a et en c le nombre de billets. Inscrivez le nombre total de billets vendus en bas
de la colonne Numéro.Au total, 1 363 ont été vendus. Écrivez la valeur de chaque type de ticket dans la colonne
Valeur.La valeur de chaque billet adulte est de 12$.
La valeur de chaque billet pour enfant est de 7$.Le nombre multiplié par la valeur donne la valeur totale,
donc la valeur totale des billets pour adultes est\(a·12=12a\)
et la valeur totale des billets pour enfants est\(c·7=7c\).Renseignez la colonne Valeur totale. Au total, la valeur totale des billets était de 12 146$. 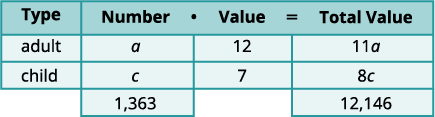
Étape 4. Traduisez en un système d'équations. La colonne Nombre et la colonne Valeur totale nous
donnent le système d'équations.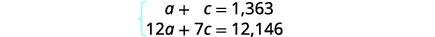
Nous utiliserons la méthode d'élimination pour résoudre
ce système. Multipliez la première équation par\(−7\).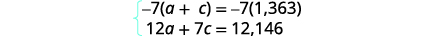
Simplifiez et ajoutez, puis résolvez pour un. 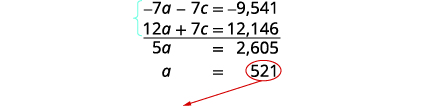
Substituez\(a=521\) dans la première équation, puis
résolvez pour c.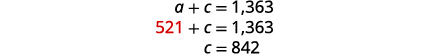
Étape 6. Vérifiez la réponse au
problème.
521 dollars par adulte à 12$ par billet font 6 252
842$ ; enfant à 7$ par billet fait 58 994 dollars
Le total des reçus est de 12 146$\(\checkmark\)Étape 7. Réponds à la question. Le centre scientifique a vendu 521 billets pour adultes et
842 billets pour enfants.
Traduisez en un système d'équations et résolvez :
La billetterie du zoo a vendu 553 billets par jour. Les recettes s'élevaient à 3 936 dollars. Combien de billets pour adultes à 9$ et combien de billets pour enfants à 6$ ont-ils été vendus ?
- Réponse
-
206 adultes, 347 enfants
Traduisez en un système d'équations et résolvez :
La billetterie d'un cinéma a vendu 147 billets pour le spectacle du soir et les recettes se sont élevées à 1 302 dollars. Combien de billets pour adultes de 11$ et combien de billets pour enfants de 8$ ont-ils été vendus ?
- Réponse
-
42 adultes, 105 enfants
Dans l'exemple suivant, nous allons résoudre un problème de pièces de monnaie. Maintenant que nous savons comment travailler avec des systèmes à deux variables, il sera facile de nommer les variables dans la colonne « nombre ».
Traduisez en un système d'équations et résolvez :
Juan a une poche pleine de pièces de cinq cents. La valeur totale des pièces est de 8,10$. Le nombre de pièces de dix cents est inférieur au double du nombre de pièces de nickel. Combien de pièces de monnaie et combien de centimes possède Juan ?
- Réponse
-
Étape 1. Lisez le problème.
Nous allons créer un tableau pour organiser les informations.Étape 2. Identifiez ce que nous recherchons. Nous cherchons le nombre de pièces de cinq
cents et le nombre de pièces de dix cents.Étape 3. Nommez ce que nous recherchons. Laissez\(n= \text{the number of nickels.}\)
\(d= \text{the number of dimes}\)Un tableau nous aidera à organiser les données.
Nous avons deux types de pièces, les pièces de cinq cents et les pièces de dix cents.Inscrivez n et d pour le numéro de
chaque type de pièce.Remplissez la colonne Valeur avec la valeur de chaque
type de pièce.La valeur de chaque nickel est de 0,05$.
La valeur de chaque centime est de 0,10$.Le nombre multiplié par la valeur donne la
valeur totale, donc, la valeur totale des nickels est
\(n(0.05)=0.05n\) et la valeur totale des dix cents est
\(d(0.10)=0.10d\).
Au total, la valeur totale des pièces est de 8,10$.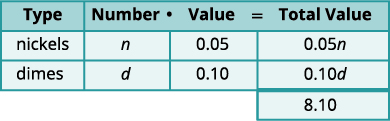
Étape 4. Traduisez en un système d'équations. La colonne Valeur totale fournit une équation. 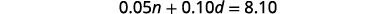
Nous savons également que le nombre de pièces de dix cents est inférieur à 9
fois le nombre de pièces de cinq cents.Traduisez pour obtenir la deuxième équation. 
Nous avons maintenant le système à résoudre. 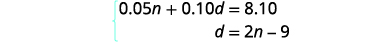
Étape 5. Résolvez le système d'équations
Nous utiliserons la méthode de substitution.Substituer\(d=2n−9\) dans la première équation. 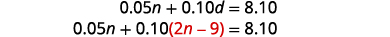
Simplifiez et résolvez pour n. 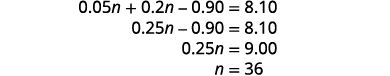
Pour trouver le nombre de pièces de dix cents,
\(n=36\) remplacez-le par la deuxième équation.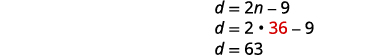
Étape 6. Vérifiez la réponse dans le problème
63 centimes à\($0.10=$6.30\)
36 centimes chez\($0.05=$1.80\)
Total\(=$8.10\checkmark\)Étape 7. Réponds à la question. Juan a 36 pièces de monnaie et 63 pièces de dix cents.
Traduisez en un système d'équations et résolvez :
Matilda possède une poignée de pièces et de dix cents, d'une valeur totale de 8,55 dollars. Le nombre de trimestres est de 3, soit plus du double du nombre de pièces de dix cents. Combien de centimes et combien de trimestres possède-t-elle ?
- Réponse
-
13 pièces de dix cents et 29 pièces
Traduisez en un système d'équations et résolvez :
Priam possède une collection de pièces de nickel et de pièces de rechange, d'une valeur totale de 7,30$. Le nombre de pièces de nickel est six fois inférieur à trois fois le nombre de quarts. Combien de pièces de monnaie et combien de pièces possède-t-il ?
- Réponse
-
19 pièces et 51 pièces de nickel
Certaines applications de mélanges impliquent de combiner des aliments ou des boissons. Des exemples de situations peuvent inclure la combinaison de raisins secs et de noix pour faire un mélange montagnard ou l'utilisation de deux types de grains de café pour faire un mélange.
Traduisez en un système d'équations et résolvez :
Carson veut fabriquer 20 livres de mélange montagnard à base de noix et de pépites de chocolat. Son budget exige que le mélange de sentiers lui coûte 7,60$ la livre. Les noix coûtent 9$ la livre et les pépites de chocolat 2$ la livre. Combien de kilos de noix et combien de kilos de pépites de chocolat devrait-il utiliser ?
- Réponse
-
Étape 1. Lisez le problème.
Nous allons créer un tableau pour organiser les informations.Étape 2. Identifiez ce que nous recherchons. Nous cherchons le nombre de livres de
noix et le nombre de livres de pépites de
chocolat.Étape 3. Nommez ce que nous recherchons. Laissez\(n= \text{the number of pound of nuts.}\)
\(c= \text{the number of pounds of chips}\)Carson mélangera des noix et des pépites de chocolat pour obtenir un mélange de
randonnée.
Écrivez en n et en c le nombre de livres de
noix et de pépites de chocolat.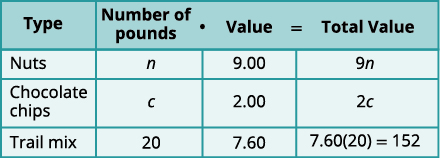
Il y aura 20 livres de mélange de randonnée.
Inscrivez le prix par livre de chaque article dans
la colonne Valeur.
Remplissez la dernière colonne en utilisant
\(\text{Number}•\text{Value}=\text{Total Value}\)Étape 4. Traduisez en un système d'équations.
Nous obtenons les équations à partir des colonnes Nombre
et Valeur totale.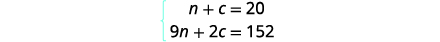
Étape 5. Résolvez le système d'équations
Nous utiliserons l'élimination pour résoudre le système.
Multipliez la première équation par\(−2\) pour éliminer c.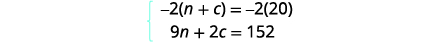
Simplifiez et ajoutez.
Résolvez pour n.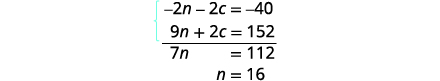
Pour trouver le nombre de livres de
pépites de chocolat,\(n=16\) remplacez-la dans la première équation,
puis résolvez par c.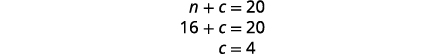
Étape 6 Vérifiez la réponse au problème.
\(\begin{array} {lll} 16+4 &= &20\checkmark \\ 9·16+2·4 &= &152\checkmark \end{array}\)Étape 7 Réponds à la question. Carson devrait mélanger 16 livres de noix avec 4
livres de pépites de chocolat pour créer le
mélange montagnard.
Traduisez en un système d'équations et résolvez :
Greta veut faire 5 livres d'un mélange de noix avec des cacahuètes et des noix de cajou. Son budget exige que le mélange lui coûte 6$ la livre. Les arachides coûtent 4 dollars la livre et les noix de cajou, 9 dollars la livre. Combien de kilos de cacahuètes et combien de livres de noix de cajou devrait-elle utiliser ?
- Réponse
-
3 livres de cacahuètes et 2 livres de noix de cajou
Traduisez en un système d'équations et résolvez :
Sammy possède la plupart des ingrédients dont il a besoin pour préparer une grande quantité de chili. Les seuls articles qui lui manquent sont les haricots et le bœuf haché. Il a besoin d'un total de 20 livres de haricots et de bœuf haché et dispose d'un budget de 3 dollars la livre. Le prix des haricots est de 1 dollar la livre et celui du bœuf haché de 5 dollars la livre. Combien de livres de haricots et combien de livres de bœuf haché devrait-il acheter ?
- Réponse
-
10 livres de haricots, 10 livres de bœuf haché
Une autre application des problèmes de mélange concerne les produits de nettoyage concentrés, d'autres produits chimiques et les boissons mélangées. La concentration est donnée en pourcentage. Par exemple, un nettoyant ménager concentré à 20 % signifie que 20 % de la quantité totale est du nettoyant et que le reste est de l'eau. Pour obtenir 35 onces d'une concentration de 20 %, vous devez mélanger 7 onces (20 % de 35) du nettoyant avec 28 onces d'eau.
Pour ce type de problèmes de mélange, nous utiliserons « pourcentage » au lieu de « valeur » pour l'une des colonnes de notre tableau.
Traduisez en un système d'équations et résolvez :
Sasheena est assistante de laboratoire dans son collège communautaire. Elle doit préparer 200 millilitres d'une solution d'acide sulfurique à 40 % pour une expérience en laboratoire. Le laboratoire ne dispose que de 25 % et 50 % de solutions dans l'entrepôt. Quelle quantité doit-elle mélanger des solutions à 25 % et à 50 % pour obtenir la solution à 40 % ?
- Réponse
-
Étape 1 Lisez le problème.
Un chiffre peut nous aider à visualiser la
situation, puis nous créerons un tableau pour
organiser les informations.Sasheena doit mélanger une partie de la\(25%\) solution et une
partie de la\(50%\) solution pour obtenir\(200\space ml\)
la\(40%\) solution.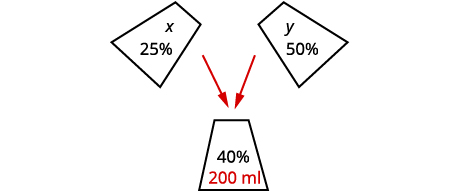
Étape 2 Identifiez ce que nous recherchons. Nous cherchons la quantité de chaque solution dont elle a
besoin.Étape 3 Nommez ce que nous recherchons. Laissez\(x= \text{number of }ml\text{ of }25% \text{ solution.}\)
\(y= \text{number of }ml\text{ of }50%\text{ solution\)Un tableau nous aidera à organiser les données. Elle
mélangera x\(ml\) of\(25%\) avec y\(ml\) of\(50%\) pour obtenir\(200 \space ml\)
la\(40%\) solution. Nous écrivons les pourcentages sous forme de décimales
dans le graphique.
Nous multiplions le nombre d'unités par la
concentration pour obtenir la quantité totale d'acide
sulfurique dans chaque solution.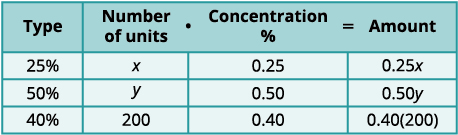
Étape 4. Traduisez en un système d'
équations.
Nous obtenons les équations de la
colonne Nombre et de la colonne Quantité.
Nous avons maintenant le système.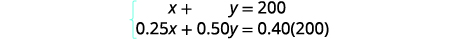
Étape 5. Résolvez le système d'équations
Nous allons résoudre le système par élimination.
Multipliez la première équation par\(−0.5\) pour
éliminer y.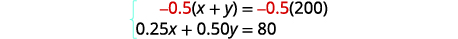
Simplifiez et ajoutez pour résoudre x. 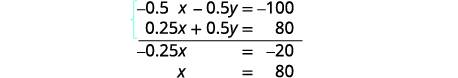
Pour résoudre y, remplacez-le\(x=80\) dans la première
équation.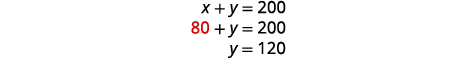
Étape 6 Vérifiez la réponse au problème.
\(\begin{array} {lll} 80+120 &= &200\checkmark \\ 0.25(80)+0.50(120) &= &200\checkmark \\ {} &{} &\text{Yes!} \end{array} \)Étape 7 Réponds à la question. Sasheena doit mélanger\(80 \space ml\) la\(25%\) solution avec
\(120 \space ml\) la\(50%\) solution pour obtenir\(200\space ml\) la
\(40%\) solution.
Traduisez en un système d'équations et résolvez :
LeBron a besoin de 150 millilitres d'une solution d'acide sulfurique à 30 % pour une expérience en laboratoire, mais n'a accès qu'à une solution à 25 % et à 50 %. Quelle quantité de solution à 25 % et quelle quantité de solution à 50 % doit-il mélanger pour obtenir la solution à 30 % ?
- Réponse
-
120 ml de solution à 25 % et 30 ml de solution à 50 %
Traduisez en un système d'équations et résolvez :
Anatole doit préparer 250 millilitres d'une solution d'acide chlorhydrique à 25 % pour une expérience en laboratoire. Le laboratoire ne dispose que d'une solution à 10 % et d'une solution à 40 % dans l'entrepôt. Quelle quantité de solution à 10 % et quelle quantité de solution à 40 % doit-il mélanger pour obtenir la solution à 25 % ?
- Réponse
-
125 ml de solution à 10 % et 125 ml de solution à 40 %
Résolvez les demandes
La formule pour modéliser des applications d'intérêt simples est\(I=Prt\). L'intérêt, I, est le produit du principal, P, du taux, r, et du temps, t. Dans notre travail ici, nous calculerons les intérêts gagnés en un an, donc ce sera 1.
Nous modifierons les titres des colonnes dans la table de mélange pour afficher la formule qui vous intéresse, comme vous le verrez dans l'exemple suivant.
Traduisez en un système d'équations et résolvez :
Adnan a 40 000 dollars à investir et espère gagner des\(7.1%\) intérêts par an. Il placera une partie de l'argent dans un fonds d'actions qui rapporte 8 % par an et le reste dans des obligations qui rapportent 3 % par an. Combien d'argent doit-il investir dans chaque fonds ?
- Réponse
-
Avez-vous remarqué que la colonne Principal représente le montant total investi alors que la colonne Intérêts représente uniquement les intérêts gagnés ? De même, la première équation de notre système,\(s+b=40,000\), represents the total amount of money invested and the second equation, \(0.08s+0.03b=0.071(40,000)\), represents the interest earned.Étape 1 Lisez le problème. Un tableau nous aidera à organiser l'information. Étape 2 Identifiez ce que nous recherchons. Nous cherchons le montant à investir dans chaque fonds. Étape 3 Nommez ce que nous recherchons. Laissez\(s= \text{the amount invested in stocks.}\)
\(b= \text{the amount invested in stocks}\)Inscrivez le taux d'intérêt sous forme décimale pour
chaque fonds.
Multipliez : Principal · Taux · Temps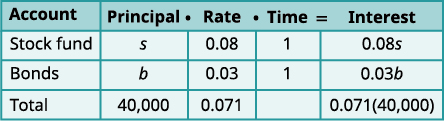
Étape 4. Traduisez en un système d'
équations.
Nous obtenons notre système d'équations à partir de
la colonne Principale et de la colonne
Intérêt.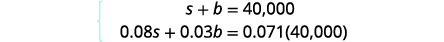
Étape 5. Résolvez le système d'équations
par élimination.
Multipliez l'équation supérieure par\(−0.03\).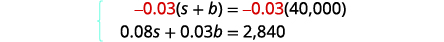
Simplifiez et ajoutez pour résoudre pour s. 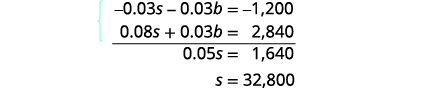
Pour trouver b, remplacez s = 32 800 dans
la première équation.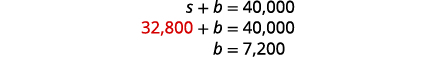
Étape 6 Vérifiez la réponse au
problème.Nous vous laissons le chèque. Étape 7 Réponds à la question. Adnan devrait investir 32 800 dollars en actions et
7 200 dollars en obligations.
Traduisez en un système d'équations et résolvez :
Leon avait 50 000$ à investir et espère gagner des\(6.2%\) intérêts par an. Il placera une partie de l'argent dans un fonds d'actions qui rapporte 7 % par an et le reste dans un compte d'épargne qui rapporte 2 % par an. Combien d'argent doit-il investir dans chaque fonds ?
- Réponse
-
42 000 dollars dans le fonds d'actions et 8 000 dollars dans le compte d'épargne
Traduisez en un système d'équations et résolvez :
Julius a investi 7 000$ dans deux placements en actions. Une action a payé 11 % d'intérêts et l'autre a payé 13 % d'intérêts. Il a gagné des\(12.5%\) intérêts sur l'investissement total. Combien d'argent a-t-il investi dans chaque action ?
- Réponse
-
1 750$ à 11 % et 5 250$ à 13 %
L'exemple suivant exige que nous trouvions le principal en fonction du montant des intérêts perçus.
Traduisez en un système d'équations et résolvez :
Rosie doit 21 540$ sur ses deux prêts étudiants. Le taux d'intérêt de son prêt bancaire est\(10.5%\) et le taux d'intérêt du prêt fédéral est\(5.9%\). Le montant total des intérêts qu'elle a payés l'année dernière était de\($1,669.68\). Quel était le principal de chaque prêt ?
- Réponse
-
Étape 1 Lisez le problème. Un tableau nous aidera à organiser l'information. Étape 2 Identifiez ce que nous recherchons. Nous recherchons le principal de chaque prêt. Étape 3 Nommez ce que nous recherchons. Laissez\(b= \text{the principal for the bank loan.}\)
\(f= \text{the principal on the federal loan}\)Le montant total des prêts s'élève à 21 540$. Enregistrez les taux d'intérêt sous forme de décimales
dans le graphique.
Multipliez en utilisant la formule I = Prt pour
obtenir l'intérêt.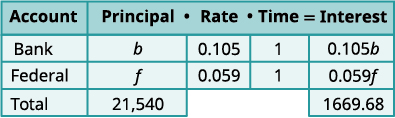
Étape 4. Traduisez en un système d'
équations.
Le système d'équations provient de
la colonne Principale et de la
colonne Intérêt.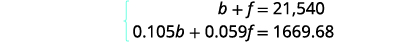
Étape 5. Résolvez le système d'équations
Nous utiliserons la substitution pour résoudre.
Résolvez la première équation pour b.
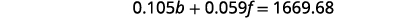
Substituez b = − f + 21,540 dans
la deuxième équation.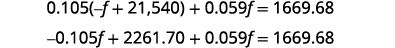
Simplifiez et résolvez pour f. 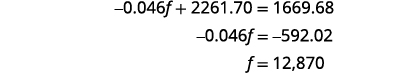
Pour trouver b, remplacez f = 12 870 dans la première équation. 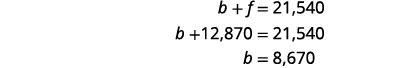
Étape 6 Vérifiez la réponse au
problème.Nous vous laissons le chèque. Étape 7 Réponds à la question. Le principal du prêt fédéral était de 12 870 dollars et
le principal du prêt bancaire était de 8 670 dollars.
Traduisez en un système d'équations et résolvez :
Laura doit 18 000$ sur ses prêts étudiants. Le taux d'intérêt du prêt bancaire est de 2,5 % et le taux d'intérêt du prêt fédéral est de 6,9 %. Le montant total des intérêts qu'elle a payés l'année dernière s'élevait à 1 066$. Quel était le principal de chaque prêt ?
- Réponse
-
Banque 4 000$ ; gouvernement fédéral 14 000$
Traduisez en un système d'équations et résolvez :
Jill's Sandwich Shoppe doit 65 200 dollars sur deux prêts commerciaux, l'un à 4,5 % d'intérêt et l'autre à 7,2 % d'intérêt. Le montant total des intérêts dus l'année dernière était de 3 582$. Quel était le principal de chaque prêt ?
- Réponse
-
41 200$ à 4,5 %, 24 000$ à 7,2 %
Résoudre les applications des fonctions de coûts et de recettes
Supposons qu'une entreprise fabrique et vend x unités d'un produit. Le coût pour l'entreprise est le coût total de production de x unités. Il s'agit du coût de fabrication pour chaque unité multiplié par x, du nombre d'unités fabriquées, plus les coûts fixes.
Le chiffre d'affaires est l'argent que l'entreprise rapporte à la suite de la vente de x unités. Il s'agit du prix de vente de chaque unité multiplié par le nombre d'unités vendues.
Lorsque les coûts sont égaux aux recettes, nous disons que l'entreprise a atteint le seuil de rentabilité.
La fonction coût est le coût de fabrication de chaque unité multiplié par x, le nombre d'unités fabriquées, plus les coûts fixes.
\[C(x)=(\text{cost per unit})·x+\text{fixed costs}\nonumber \]
La fonction des recettes est le prix de vente de chaque unité multiplié par x, le nombre d'unités vendues.
\[R(x)=(\text{selling price per unit})·x\nonumber \]
Le seuil de rentabilité est lorsque les recettes sont égales aux coûts.
\[C(x)=R(x)\nonumber\]
Le fabricant d'un banc de musculation dépense 105$ pour fabriquer chaque banc et le vend 245$. Le fabricant a également des coûts fixes de 7 000$ par mois.
ⓐ Trouvez la fonction de coût C lorsque x bancs sont fabriqués.
ⓑ Trouvez la fonction de revenus R lorsque x bancs sont vendus.
ⓒ Affichez le seuil de rentabilité en représentant graphiquement les fonctions Revenus et Cost sur la même grille.
ⓓ Trouvez le seuil de rentabilité. Interprétez ce que signifie le seuil de rentabilité.
- Réponse
-
ⓐ Le fabricant a des coûts fixes de 7 000$, quel que soit le nombre de bancs de musculation qu'il produit. Outre les coûts fixes, le fabricant dépense également 105$ pour produire chaque banc. Supposons que x bancs soient vendus.
\(\begin{array} {ll} {\text{Write the general Cost function formula.}} &{C(x)=(\text{cost per unit})·x+\text{fixed costs}} \\ {\text{Substitute in the cost values.}} &{C(x)=105x+7000} \\ \end{array}\)
ⓑ Le fabricant vend chaque banc de musculation pour 245$. Nous obtenons le chiffre d'affaires total en multipliant le chiffre d'affaires par unité par le nombre d'unités vendues.
\(\begin{array} {ll} {\text{Write the general Revenue function.}} &{C(x)=(\text{selling price per unit})·x} \\ {\text{Substitute in the revenue per unit.}} &{R(x)=245x} \\ \end{array}\)
ⓒ Nous avons essentiellement un système d'équations linéaires. Nous allons montrer le graphique du système car cela permet de rendre l'idée d'un seuil de rentabilité plus visuelle.
\[\left\{ \begin{array} {l} C(x)=105x+7000 \\ R(x)=245x \end{array} \right. \quad \text{or} \quad \left\{ \begin{array} {l} y=105x+7000 \\ y=245x \end{array} \right. \nonumber \]
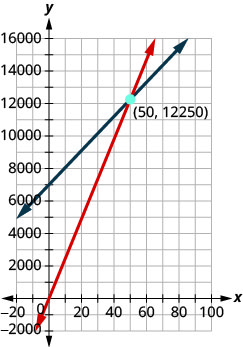
ⓓ Pour déterminer la valeur réelle, nous nous souvenons que le seuil de rentabilité se produit lorsque les coûts sont égaux aux revenus.
\(\begin{array} {ll} {\text{Write the break-even formula.}} &{\begin{array} {l} {C(x)=R(x)} \\ {105x+7000=245x} \end{array}} \\ {\text{Solve.}} &{\begin{array} {l} {7000=140x} \\ {50=x} \end{array}} \\ \end{array}\)
Lorsque 50 bancs sont vendus, les coûts sont égaux aux recettes.

Lorsque 50 bancs sont vendus, les recettes et les coûts s'élèvent à 12 250$. Notez que cela correspond à la paire commandée\((50,12250)\).
Le fabricant d'un banc de musculation dépense 15$ pour fabriquer chaque banc et le vend 32$. Le fabricant a également des coûts fixes mensuels de 25 500$.
ⓐ Trouvez la fonction de coût C lorsque x bancs sont fabriqués.
ⓑ Trouvez la fonction de revenus R lorsque x bancs sont vendus.
ⓒ Affichez le seuil de rentabilité en représentant graphiquement les fonctions Revenus et Cost sur la même grille.
ⓓ Trouvez le seuil de rentabilité. Interprétez ce que signifie le seuil de rentabilité.
- Réponse
-
ⓐ\(C(x)=15x+25,500\)
ⓑ\(R(x)=32x\)
ⓒ
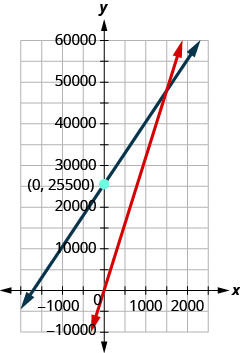
ⓓ 1 500 1 500 ; lorsque 1 500 bancs seront vendus, le coût et les recettes seront à la fois de 48 000
Le fabricant d'un banc de musculation dépense 120$ pour fabriquer chaque banc et le vend au prix de 170$. Le fabricant a également des coûts fixes mensuels de 150 000$.
ⓐ Trouvez la fonction de coût C lorsque x bancs sont fabriqués.
ⓑ Trouvez la fonction de revenus R lorsque x bancs sont vendus.
ⓒ Affichez le seuil de rentabilité en représentant graphiquement les fonctions Revenus et Cost sur la même grille.
ⓓ Trouvez le seuil de rentabilité. Interprétez ce que signifie le seuil de rentabilité.
- Réponse
-
ⓐ\(C(x)=120x+150,000\)
ⓑ\(R(x)=170x\)
ⓒ
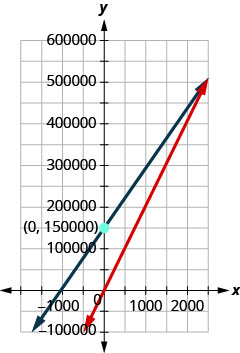
ⓓ\(3,000\) ; lorsque 3 000 bancs sont vendus, les revenus et les coûts s'élèvent à 510 000 dollars
Accédez à cette ressource en ligne pour obtenir des instructions et des exercices supplémentaires avec intérêt et mélanges.
- Intérêts et mélanges
Concepts clés
- Fonction de coût : La fonction de coût est le coût de fabrication de chaque unité multiplié par x, le nombre d'unités fabriquées, plus les coûts fixes.
\(C(x)=(\text{cost per unit})·x+\text{fixed costs}\)
- Revenus : La fonction des recettes est le prix de vente de chaque unité multiplié par x, le nombre d'unités vendues.
\(R(x)=(\text{selling price per unit})·x\)
- Point d'équilibre : Le seuil de rentabilité est lorsque les recettes sont égales aux coûts.
\(C(x)=R(x)\)
Lexique
- fonction de coût
- La fonction coût est le coût de fabrication de chaque unité multiplié par xx, le nombre d'unités fabriquées, plus les coûts fixes ; C (x) = (coût par unité) x + coûts fixes.
- recettes
- Le chiffre d'affaires est le prix de vente de chaque unité multiplié par x, le nombre d'unités vendues ; R (x) = (prix de vente par unité) x.
- seuil de rentabilité
- Le point où les recettes sont égales aux coûts est le seuil de rentabilité ; C (x) =R (x).


