4.3 : Résoudre des applications avec des systèmes d'équations

Objectifs d'apprentissage

À la fin de cette section, vous serez en mesure de :

• Résoudre des applications de traduction directe
• Résoudre des applications géométriques
• Résolvez des applications de mouvement

Avant de commencer, répondez à ce questionnaire de préparation.

1. La somme de deux fois un nombre et neuf est 31. Trouve le numéro.
   Si vous avez oublié ce problème, consultez [lien].
2. Les jumeaux Jon et Ron ont gagné ensemble 96 000$ l'an dernier. Ron a gagné 8 000$, soit plus de trois fois ce que Jon a gagné. Combien gagnait chacun des jumeaux ?
   Si vous avez oublié ce problème, consultez [lien].
3. Un train express et un train local partent de Pittsburgh pour se rendre à Washington, D.C. Le train express peut faire le trajet en quatre heures et le train local en cinq heures. La vitesse du train express est de 20 miles par heure plus rapide que la vitesse du train local. Déterminez la vitesse des deux trains.
   Si vous avez oublié ce problème, consultez [lien].

Résoudre des applications de traduction directe

Les systèmes d'équations linéaires sont très utiles pour résoudre des applications. Certaines personnes trouvent qu'il est plus facile de configurer des problèmes de mots avec deux variables que de les configurer avec une seule variable. Pour résoudre une application, nous allons d'abord traduire les mots en un système d'équations linéaires. Ensuite, nous déciderons de la méthode la plus pratique à utiliser, puis nous résoudrons le système.

RÉSOLVEZ DES APPLICATIONS AVEC DES SYSTÈMES D'ÉQUATIONS.

1. Lisez le problème. Assurez-vous que tous les mots et toutes les idées sont compris.
2. Déterminez ce que nous recherchons.
3. Nommez ce que nous recherchons. Choisissez des variables pour représenter ces quantités.
4. Traduisez en un système d'équations.
5. Résolvez le système d'équations en utilisant de bonnes techniques d'algèbre.
6. Vérifiez la réponse au problème et assurez-vous qu'elle est logique.
7. Répondez à la question par une phrase complète.

Nous avons résolu des problèmes de numérotation avec une variable plus tôt. Voyons comment cela fonctionne différemment en utilisant deux variables.

La somme de deux nombres est égale à zéro. Un chiffre est neuf de moins que l'autre. Trouve les numéros.

Réponse

Étape 1. Lisez le problème.
Étape 2. Identifiez ce que nous recherchons.	Nous recherchons deux chiffres.
Étape 3. Nommez ce que nous recherchons.	Laissez\(n= \text{the first number} \). \(m= \text{the second number} \)
Étape 4. Traduisez en un système d'équations.	La somme de deux nombres est égale à zéro.
	Un chiffre est neuf de moins que l'autre.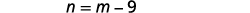
Le système est le suivant :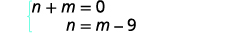
Étape 5. Résolvez le système d' équations. Nous utiliserons la substitution puisque la deuxième équation est résolue pour n.
Remplacez m − 9 par n dans la première équation.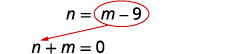
Résolvez pour moi.
Substituez\(m=\frac{9}{2}\) dans la deuxième équation, puis résolvez pour n.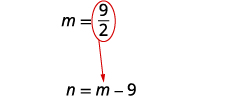
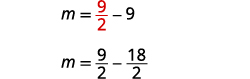
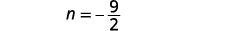
Étape 6. Vérifiez la réponse au problème.	Ces chiffres ont-ils un sens dans le problème ? Nous vous en remettons à vous !
Étape 7. Réponds à la question.	Les chiffres sont\(\frac{9}{2}\) et\(−\frac{9}{2}\).

Exemple\(\PageIndex{2}\)

La somme de deux nombres est de 10. Un chiffre est inférieur de 4 à l'autre. Trouve les numéros.

Réponse

\(3, 7\)

Exemple\(\PageIndex{3}\)

La somme de deux nombres est\(−6\). Un chiffre est inférieur de 10 à l'autre. Trouve les numéros.

Réponse

\(2, −8\)

Heather s'est vu offrir deux options pour son salaire en tant qu'entraîneuse au gymnase. L'option A lui verserait 25 000$ plus 15$ pour chaque séance de formation. L'option B la rémunérerait\($10,000+$40\) pour chaque séance de formation. Combien de sessions de formation rendraient les options salariales égales ?

Réponse

Étape 1. Lisez le problème.
Étape 2. Identifiez ce que nous recherchons.	Nous recherchons le nombre de sessions de formation qui permettraient d'obtenir un salaire égal.
Étape 3 Nommez ce que nous recherchons.	Soit s=s= le salaire d'Heather. n=n= le nombre de séances d'entraînement
Étape 4. Traduisez en un système d'équations.	L'option A lui verserait 25 000$ plus 15$ pour chaque séance de formation.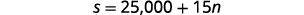
	L'option B lui verserait 10 000$ plus 40$ pour chaque séance de formation.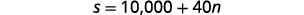
Le système s'affiche.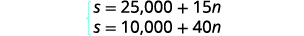
Étape 5. Résolvez le système d'équations. Nous utiliserons la substitution.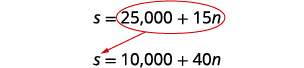
Remplacez 25 000 +15 n par s dans la deuxième équation.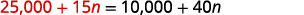
Résolvez pour n.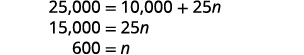
Étape 6 Vérifiez la réponse.	Est-ce que 600 sessions de formation par an sont raisonnables ? Les deux options sont-elles égales lorsque n = 600 ?
Étape 7 Réponds à la question.	Les options salariales seraient égales pour 600 sessions de formation.

Exemple\(\PageIndex{5}\)

Géraldine s'est vu proposer des postes par deux compagnies d'assurance. La première entreprise verse un salaire de 12 000$ plus une commission de 100$ pour chaque police vendue. Le second verse un salaire de 20 000$ plus une commission de 50$ pour chaque police vendue. Combien de polices devraient être vendues pour que le salaire total soit le même ?

Réponse

160 politiques

Exemple\(\PageIndex{6}\)

Kenneth vend actuellement des costumes pour l'entreprise A à un salaire de 22 000$ plus une commission de 10$ pour chaque costume vendu. La société B lui offre un poste avec un salaire de 28 000$ plus une commission de 4$ pour chaque costume vendu. Combien de costumes Kenneth devrait-il vendre pour que les options soient égales ?

Réponse

1000 costumes

Lorsque vous résolvez chaque application, n'oubliez pas d'analyser la méthode de résolution du système d'équations qui serait la plus pratique.

Exemple\(\PageIndex{7}\)

Traduisez en un système d'équations, puis résolvez :

Lorsque Jenna a passé 10 minutes sur l'appareil elliptique, puis a fait de l'entraînement en circuit pendant 20 minutes, son application de fitness indique qu'elle a brûlé 278 calories. Lorsqu'elle a passé 20 minutes sur le vélo elliptique et 30 minutes d'entraînement en circuit, elle a brûlé 473 calories. Combien de calories brûle-t-elle par minute sur le vélo elliptique ? Combien de calories pour chaque minute d'entraînement en circuit ?

Réponse

Étape 1 Lisez le problème.
Étape 2 Identifiez ce que nous recherchons.	Nous recherchons le nombre de calories brûlées par minute sur le vélo elliptique et par minute d'entraînement en circuit.
Étape 3 Nommez ce que nous recherchons.	Soit e = le nombre de calories brûlées par minute sur le vélo elliptique. c=c= nombre de calories brûlées par minute pendant l'entraînement en circuit
Étape 4. Traduisez en un système d'équations.	10 minutes d' entraînement sur vélo elliptique et sur circuit pendant 20 minutes, vous avez brûlé 278 calories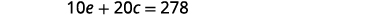
	20 minutes sur le vélo elliptique et 30 minutes d'entraînement en circuit ont brûlé 473 calories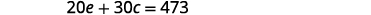
Le système est le suivant :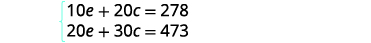
Étape 5. Résolvez le système d'équations.
Multipliez la première équation par −2 pour obtenir les coefficients opposés de e.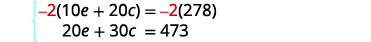
Simplifiez et ajoutez les équations. Résolvez pour c.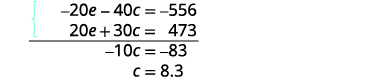
Remplacez c = 8,3 dans l'une des équations originales pour résoudre e.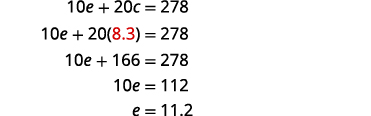
Étape 6 Vérifiez la réponse au problème.	Vérifiez vous-même les calculs.
Étape 7 Réponds à la question.	Jenna brûle 8,3 calories par minute en circuit et 11,2 calories par minute lorsqu'elle est sur un vélo elliptique.

Exemple\(\PageIndex{8}\)

Traduisez en un système d'équations, puis résolvez :

Mark est allé à la salle de sport et a fait 40 minutes de yoga chaud Bikram et 10 minutes de jump jacks. Il a brûlé 510 calories. La prochaine fois qu'il est allé à la salle de sport, il a fait 30 minutes de yoga chaud Bikram et 20 minutes de jump jacks brûlant 470 calories. Combien de calories ont été brûlées par minute de yoga ? Combien de calories ont été brûlées pour chaque minute passée à sauter ?

Réponse

Mark a brûlé 11 calories pour chaque minute de yoga et 7 calories pour chaque minute de saut d'obstacles.

Exemple\(\PageIndex{9}\)

Traduisez en un système d'équations, puis résolvez :

Erin a passé 30 minutes sur le rameur et 20 minutes à soulever des poids au gymnase et a brûlé 430 calories. Lors de sa prochaine visite au gymnase, elle a passé 50 minutes sur le rameur et 10 minutes à soulever des poids et a brûlé 600 calories. Combien de calories brûlait-elle par minute sur le rameur ? Combien de calories a-t-elle brûlées par minute d'haltérophilie ?

Réponse

Erin a brûlé 11 calories par minute passée sur le rameur et 5 calories par minute d'haltérophilie.

Résoudre des applications géométriques

Nous allons maintenant résoudre des applications de géométrie à l'aide de systèmes d'équations linéaires. Nous devrons ajouter des angles complémentaires et des angles supplémentaires à notre liste certaines propriétés des angles.

Les mesures de deux angles complémentaires s'ajoutent à 90 degrés. Les mesures de deux angles supplémentaires s'ajoutent à 180 degrés.

ANGLES COMPLÉMENTAIRES ET SUPPLÉMENTAIRES

Deux angles sont complémentaires si la somme des mesures de leurs angles est de 90 degrés.

Deux angles sont supplémentaires si la somme des mesures de leurs angles est de 180 degrés.

Si deux angles sont complémentaires, on dit qu'un angle est complémentaire de l'autre.

Si deux angles sont complémentaires, on dit qu'un angle est le complément de l'autre.

Exemple\(\PageIndex{10}\)

Traduisez en un système d'équations, puis résolvez.

La différence entre deux angles complémentaires est de 26 degrés. Trouvez les mesures des angles.

Réponse

\(\begin{array} {ll} {\textbf{Step 1. Read }\text{the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what we are looking for.}} &{\text{We are looking for the measure of each}} \\ {} &{\text{angle.}} \\ {\textbf{Step 3. Name }\text{what we are looking for.}} &{\text{Let} x=\text{ the measure of the first angle.}} \\ {} &{\hspace{3mm} y= \text{ the measure of the second angle}} \\ {\textbf{Step 4. Translate }\text{into a system of}} &{\text{The angles are complementary.}} \\ {\text{equations.}} &{\hspace{15mm} x+y=90} \\ {} &{\text{The difference of the two angles is 26}} \\ {} &{\text{degrees.}} \\ {} &{\hspace{15mm} x−y=26} \\ {} &{} \\ {} &{} \\ {\text{The system is shown.}} &{\hspace{15mm} \left\{ \begin{array} {l} x+y=90 \\ x−y=26 \end{array} \right. } \\ {} &{} \\ {} &{} \\ {\textbf{Step 5. Solve }\text{the system of equations} } &{\hspace{15mm} \left\{ \begin{array} {l} x+y=90 \\ \underline{x−y=26} \end{array} \right. } \\ {\text{by elimination.}} &{\hspace{21mm} 2x\hspace{4mm}=116} \\ {} &{\hspace{28mm} x=58} \\ {} &{} \\ {} &{} \\ {\text{Substitute }x=58\text{ into the first equation.}} &{\hspace{15mm} x+y=90} \\ {} &{\hspace{14mm} 58+y=90} \\ {} &{\hspace{22mm} y=32} \\ {\textbf{Step 6. Check }\text{the answer in the problem.}} &{} \\ {} &{} \\ {} &{} \\ {} &{} \\ {\hspace{15mm} 58+32=90\checkmark} &{} \\ {\hspace{15mm} 58−32=26\checkmark} &{} \\ {\textbf{Step 7. Answer }\text{the question.}} &{\text{The angle measures are 58 and 32 degrees.}} \end{array} \)

Exemple\(\PageIndex{11}\)

Traduisez en un système d'équations, puis résolvez :

La différence entre deux angles complémentaires est de 20 degrés. Trouvez les mesures des angles.

Réponse

Les mesures d'angle sont 55 et 35.

Exemple\(\PageIndex{12}\)

Traduisez en un système d'équations, puis résolvez :

La différence entre deux angles complémentaires est de 80 degrés. Trouvez les mesures des angles.

Réponse

Les mesures d'angle sont 5 et 85.

Dans l'exemple suivant, nous nous souvenons que les mesures des angles supplémentaires totalisent 180.

Exemple\(\PageIndex{13}\)

Traduisez en un système d'équations, puis résolvez :

Deux angles sont complémentaires. La mesure du plus grand angle est inférieure de douze degrés à cinq fois la mesure du plus petit angle. Trouvez les mesures des deux angles.

Réponse

Étape 1 Lisez le problème.
Étape 2 Identifiez ce que nous recherchons.	Nous recherchons la mesure de chaque angle.
Étape 3 Nommez ce que nous recherchons.	Soit x=x= la mesure du premier angle. y=y= la mesure du deuxième angle
Étape 4. Traduisez en un système d'équations.	Les angles sont complémentaires.
	L'angle le plus grand est douze fois moins que cinq fois l'angle le plus petit.
Le système s'affiche : Étape 5. Résolvez le système de substitution d'équations.
Dans la première équation, remplacez 5 x − 12 par y. Résolvez pour x.
Substituez 32 pour x dans la deuxième équation, puis résolvez pour y.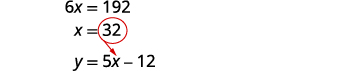
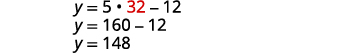
Étape 6 Vérifiez la réponse au problème.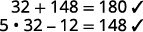
Étape 7 Réponds à la question.	Les mesures d'angle sont de 148 et 32 degrés.

Exemple\(\PageIndex{14}\)

Traduisez en un système d'équations, puis résolvez :

Deux angles sont complémentaires. La mesure de l'angle le plus grand est de 12 degrés, soit trois fois plus que le plus petit angle. Trouvez les mesures des angles.

Réponse

Les mesures d'angle sont de 42 et 138.

Exemple\(\PageIndex{15}\)

Traduisez en un système d'équations, puis résolvez :

Deux angles sont complémentaires. La mesure de l'angle le plus grand est 18 fois moins que le double de la mesure de l'angle le plus petit. Trouvez les mesures des angles.

Réponse

Les mesures d'angle sont 66 et 114.

Rappelez-vous que les angles d'un triangle totalisent 180 degrés. Un triangle droit possède un angle de 90 degrés. Qu'est-ce que cela nous apprend sur les deux autres angles ? Dans l'exemple suivant, nous allons trouver les mesures des deux autres angles.

Exemple\(\PageIndex{16}\)

La mesure de l'un des petits angles d'un triangle droit est dix fois plus que trois fois la mesure de l'autre petit angle. Trouvez les mesures des deux angles.

Réponse

Nous allons dessiner et étiqueter une figure.

Étape 1 Lisez le problème.
Étape 2 Identifiez ce que vous recherchez.	Nous recherchons les mesures des angles.
Étape 3 Nommez ce que nous recherchons.	Soit a=a= la mesure du premier angle. b=b= la mesure du deuxième angle
Étape 4. Traduisez en un système d'équations.	La mesure de l'un des petits angles d'un triangle droit est dix fois plus que trois fois la mesure de l'autre petit angle.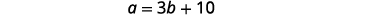
	La somme des mesures des angles d'un triangle est de 180.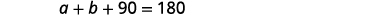
Le système s'affiche.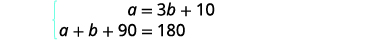
Étape 5. Résolvez le système d'équations. Nous utiliserons la substitution puisque la première équation est résolue pour a.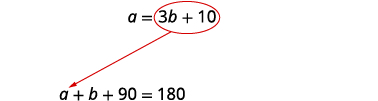
Remplacez 3b+103b+10 par a dans la deuxième équation.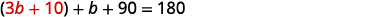
Résolvez pour b.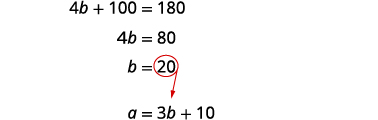
Substituez b=20b=20 dans la première équation, puis résolvez pour a.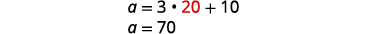
Étape 6 Vérifiez la réponse au problème.	Nous vous en remettons à vous !
Étape 7 Réponds à la question.	Les mesures des petits angles sont de 20 et 70 degrés.

Exemple\(\PageIndex{17}\)

La mesure de l'un des petits angles d'un triangle droit est 2 fois plus que 3 fois la mesure de l'autre petit angle. Détermine la mesure des deux angles.

Réponse

\(22, 68\)

Exemple\(\PageIndex{18}\)

La mesure de l'un des petits angles d'un triangle droit est inférieure de 18 à deux fois la mesure de l'autre petit angle. Détermine la mesure des deux angles.

Réponse

\(36, 54\)

Lors de la résolution d'applications de géométrie, il est souvent utile de dessiner une image pour visualiser la situation.

Exemple\(\PageIndex{19}\)

Traduisez en un système d'équations, puis résolvez :

Randall dispose de 125 pieds de clôture pour fermer la partie de son jardin adjacente à sa maison. Il n'aura besoin que de clôturer sur trois côtés, car le quatrième côté sera le mur de la maison. Il veut que la longueur de la cour clôturée (parallèle au mur de la maison) soit 5 pieds plus que quatre fois plus longue que la largeur. Trouvez la longueur et la largeur.

Réponse

Étape 1 Lisez le problème.
Étape 2 Identifiez ce que vous recherchez.	Nous recherchons la longueur et la largeur.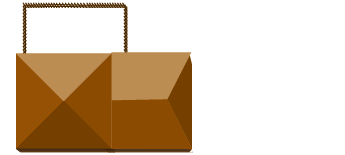
Étape 3 Nommez ce que nous recherchons.	Soit L=L= la longueur de la cour clôturée. W=W= la largeur de la cour clôturée
Étape 4. Traduisez en un système d'équations.	Une longueur et deux largeurs sont égales à 125.
	La longueur sera de 5 pieds de plus que quatre fois la largeur.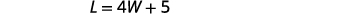
Le système s'affiche. Étape 5. Résolvez le système d'équations par substitution.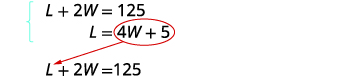
Substituez L = 4 W + 5 dans la première équation, puis résolvez pour W.
Remplacez W par 20 dans la deuxième équation, puis résolvez par L.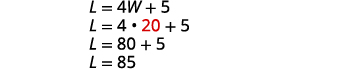
Étape 6 Vérifiez la réponse au problème.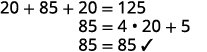
Étape 7 Répondez à l'équation.	La longueur est de 85 pieds et la largeur de 20 pieds.

Exemple\(\PageIndex{20}\)

Traduisez en un système d'équations, puis résolvez :

Mario veut installer une clôture autour de la piscine de son jardin. Comme un côté est adjacent à la maison, il n'aura besoin que de clôturer trois côtés. Il y a deux côtés longs et le côté le plus court est parallèle à la maison. Il a besoin de 155 pieds de clôture pour clôturer la piscine. La longueur du côté long est inférieure de 10 pieds au double de la largeur. Déterminez la longueur et la largeur de la zone de piscine à clôturer.

Réponse

La longueur est de 60 pieds et la largeur de 35 pieds.

Exemple\(\PageIndex{21}\)

Traduisez en un système d'équations, puis résolvez :

Alexis veut construire un parc à chiens rectangulaire dans sa cour, à côté de la clôture de son voisin. Elle utilisera 136 pieds de clôture pour clôturer complètement le parc à chiens rectangulaire. La longueur de la piste pour chiens le long de la clôture du voisin sera inférieure de 16 pieds au double de la largeur. Déterminez la longueur et la largeur du parc pour chiens.

Réponse

La longueur est de 60 pieds et la largeur de 38 pieds.

Résolvez des applications de mouvement

Nous avons utilisé un tableau pour organiser les informations en problèmes de mouvement uniformes lorsque nous les avons présentés plus tôt. Nous allons continuer à utiliser le tableau ici. L'équation de base était\(D=rt\) où D est la distance parcourue, r est le taux et t est le temps.

Notre premier exemple d'application de mouvement uniforme concernera une situation similaire à certaines que nous avons déjà vues, mais nous pouvons maintenant utiliser deux variables et deux équations.

Exemple\(\PageIndex{22}\)

Traduisez en un système d'équations, puis résolvez :

Joni a quitté Saint-Louis sur l'autoroute, se dirigeant vers l'ouest en direction de Denver à une vitesse de 110 miles à l'heure. Une demi-heure plus tard, Kelly a quitté Saint-Louis sur le même itinéraire que Joni, parcourant 78 miles à l'heure. Combien de temps faudra-t-il à Kelly pour rattraper Joni ?

Réponse

Un diagramme est utile pour nous aider à visualiser la situation.

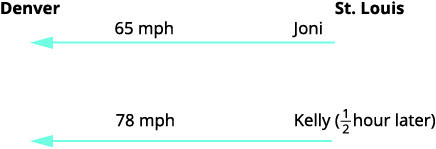
Identifiez et nommez ce que nous recherchons. Un graphique nous aidera à organiser les données. Nous connaissons les taux de Joni et de Kelly, et nous les inscrivons donc dans le graphique. Nous cherchons la durée pendant laquelle Kelly, k, et Joni, j, conduiront chacune.

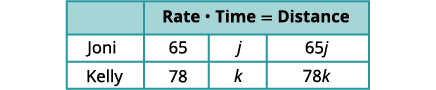
Puisque\(D=r·t\) nous pouvons remplir la colonne Distance.

Traduisez en un système d'équations.

Pour créer le système d'équations, il faut reconnaître que Kelly et Joni parcourront la même distance. Donc,

\(\hspace{85mm} 65j=78k \nonumber \)

De plus, puisque Kelly est partie plus tard, son temps sera inférieur d'\(\frac{1}{2}\)une heure à celui de Joni. Donc,

\( \hspace{105mm} k=j-\frac{1}{2} \nonumber \)

\(\begin{array} {ll} {\text{Now we have the system.}} &{\left\{ \begin{array} {l} k=j−\frac{1}{2} \\ 65j=78k \end{array} \right.} \\ {\textbf{Solve }\text{the system of equations by substitution.}} &{} \\ {} &{} \\ {\text{Substitute }k=j−12\text{ into the second equation,}} &{} \\ {\text{then solve for }j.} &{} \\ {} &{65j=78k} \\ {} &{65j=78(j−\frac{1}{2})} \\ {} &{65j=78j−39} \\ {} &{−13j=−39} \\ {} &{j=3} \\{\begin{array} {l} {\text{To find Kelly’s time, substitute }j=3 \text{ into the first}} \\ {\text{equation, then solve for }k.} \end{array} } &{k=j−\frac{1}{2}} \\ {} &{k=3−\frac{1}{2} } \\ {} &{k=\frac{5}{2} \text{ or } k=2\frac{1}{2}} \\ {\textbf{Check }\text{the answer in the problem.}} &{} \\ {\begin{array} {lllll} {\text{Joni}} &{3 \text{ hours}} &{(65\text{ mph})} &= &{195\text{ miles}} \\ {\text{Kelly}} &{2\frac{1}{2} \text{ hours}} &{(78\text{ mph})} &= &{195\text{ miles}} \end{array}} &{} \\ {\text{Yes, they will have traveled the same distance}} &{} \\{\text{when they meet.}} &{} \\ {\textbf{Answer }\text{the question.}} &{} \\ {} &{\text{Kelly will catch up to Joni in}} \\ {} &{2\frac{1}{2}\text{ hours. By then, Joni will}} \\ {} &{\text{have traveled }3 \text{ hours.}} \\ \end{array}\)

Exemple\(\PageIndex{23}\)

Traduisez en un système d'équations, puis résolvez :

Mitchell a quitté Détroit sur l'autoroute en direction du sud en direction d'Orlando à une vitesse de 60 miles à l'heure. Clark a quitté Détroit une heure plus tard, à une vitesse de 75 milles à l'heure, en suivant le même itinéraire que Mitchell. Combien de temps faudra-t-il à Clark pour attraper Mitchell ?

Réponse

Clark mettra 4 heures à attraper Mitchell.

Exemple\(\PageIndex{24}\)

Traduisez en un système d'équations, puis résolvez :

Charlie a quitté la maison de sa mère en voyageant à une vitesse moyenne de 58 miles par heure. Sa sœur Sally est partie 15 minutes\((\frac{1}{4} \text{ hour})\) plus tard en empruntant le même itinéraire à une vitesse moyenne de 42 miles par heure. Combien de temps avant que Sally ne rattrape Charlie ?

Réponse

Sally mettra des\(112\) heures à rattraper Charlie.

De nombreuses applications réelles du mouvement uniforme sont dues aux effets des courants, de l'eau ou de l'air, sur la vitesse réelle d'un véhicule. Les vols d'avion de fond aux États-Unis prennent généralement plus de temps vers l'ouest que vers l'est en raison des courants de vent dominants.

Jetons un coup d'œil à un bateau qui circule sur une rivière. Selon la direction que prend le bateau, le courant de l'eau le ralentit ou l'accélère.

Les images ci-dessous montrent comment un courant fluvial affecte la vitesse à laquelle un bateau se déplace réellement. Nous appellerons la vitesse du bateau en eau calme b et la vitesse du courant de la rivière c.

Le bateau se dirige vers l'aval, dans le même sens que le courant de la rivière. Le courant aide à pousser le bateau, de sorte que la vitesse réelle du bateau est plus rapide que sa vitesse en eau calme. La vitesse réelle à laquelle le bateau se déplace est de\(b+c\).

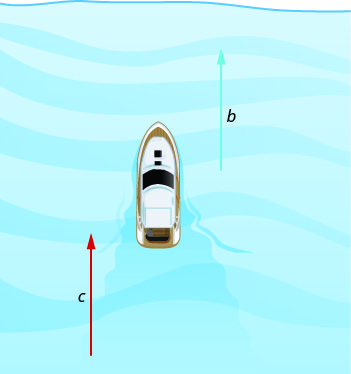
Maintenant, le bateau remonte, à l'opposé du courant de la rivière. Le courant va à contre-courant, de sorte que la vitesse réelle du bateau est plus lente que sa vitesse en eau calme. La vitesse réelle du bateau est de\(b−c\).

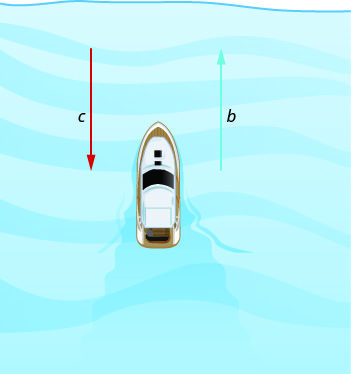
Nous allons donner quelques chiffres à cette situation dans l'exemple suivant.

Exemple\(\PageIndex{25}\)

Traduisez en un système d'équations, puis résolvez.

Un bateau de croisière fluviale a navigué à 60 milles en aval pendant 4 heures, puis a mis 5 heures de navigation en amont pour regagner le quai. Trouvez la vitesse du navire en eau calme et la vitesse du courant de la rivière.

Réponse

Lisez le problème.	Il s'agit d'un problème de mouvement uniforme et une image nous aidera à visualiser la situation.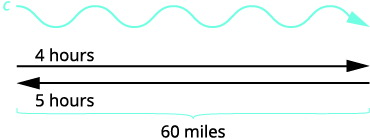
Déterminez ce que nous recherchons.	Nous recherchons la vitesse du navire en eau calme et la vitesse du courant.
Nommez ce que nous recherchons.	Laissez\(s= \text{the rate of the ship in still water.}\) \(c= \text{the rate of the current}\)
Un tableau nous aidera à organiser l'information. Le navire part vers l'aval puis vers l'amont. En aval, le courant aide le navire et le débit réel du navire est donc s + c. En remontant, le courant ralentit le navire et le débit réel est donc s − c.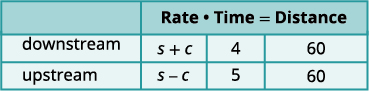
En aval, cela prend 4 heures. En amont, cela prend 5 heures. Dans chaque sens, la distance est de 60 miles.
Traduisez en un système d'équations. Puisque la vitesse multipliée par le temps est une distance, nous pouvons écrire le système d'équations.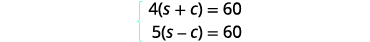
Résolvez le système d'équations. Distribuez pour mettre les deux équations sous forme standard, puis résolvez par élimination.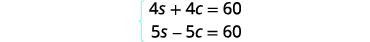
Multipliez l'équation du haut par 5 et l'équation du bas par 4. Ajoutez les équations, puis résolvez pour s.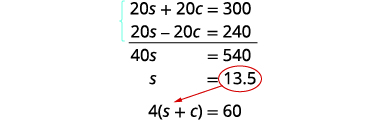
Remplacez s = 13,5 dans les équations d'origine.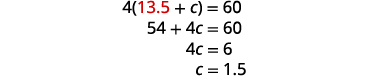
Vérifiez la réponse au problème. Le débit en aval serait de \(13.5+1.5=15\) mi/h. En 4 heures, le navire parcourrait des \(15·4=60\) kilomètres. Le débit en amont serait de \(13.5−1.5=12\) mi/h. En 5 heures, le navire parcourrait des \(12·5=60\) kilomètres.
Réponds à la question.	La vitesse du navire est de 13,5 mi/h et la vitesse du courant est de 1,5 mi/h.

Exemple\(\PageIndex{26}\)

Traduisez en un système d'équations, puis résolvez :

Une croisière en bateau sur le Mississippi a navigué à 120 milles en amont pendant 12 heures, puis a mis 10 heures pour retourner au quai. Trouvez la vitesse du bateau fluvial en eau calme et la vitesse du courant de la rivière.

Réponse

La vitesse du bateau est de 11 mi/h et la vitesse du courant est de 1 mi/h.

Exemple\(\PageIndex{27}\)

Traduisez en un système d'équations, puis résolvez :

Jason a pagayé son canot à 24 milles en amont pendant 4 heures. Il lui a fallu 3 heures pour rentrer en pagaie. Trouvez la vitesse du canot en eau calme et la vitesse du courant de la rivière.

Réponse

La vitesse du canot est de 7 mi/h et la vitesse du courant est de 1 mi/h.

Les courants de vent affectent la vitesse des avions de la même manière que les courants d'eau influent sur la vitesse des bateaux. Nous allons voir cela dans l'exemple suivant. Un courant de vent dans la même direction que celle de l'avion est appelé vent arrière. Un courant de vent soufflant dans la direction opposée à celle de l'avion est appelé vent de face.

Exemple\(\PageIndex{28}\)

Traduisez en un système d'équations, puis résolvez :

Un jet privé peut parcourir 1 095 miles en trois heures avec un vent arrière, mais seulement 987 miles en trois heures dans un vent de face. Trouvez la vitesse du jet dans l'air calme et la vitesse du vent.

Réponse

Lisez le problème.	Il s'agit d'un problème de mouvement uniforme et une image nous aidera à le visualiser.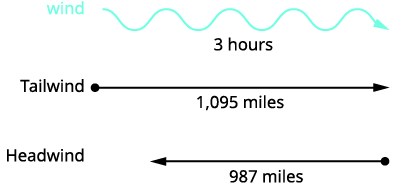
Déterminez ce que nous recherchons.	Nous recherchons la vitesse du jet dans l'air calme et la vitesse du vent.
Nommez ce que nous recherchons.	Soit j=j= la vitesse du jet dans l'air calme. w=w= la vitesse du vent.
Un tableau nous aidera à organiser l'information. Le jet effectue deux voyages, l'un par vent arrière et l'autre par vent de face. Dans un vent arrière, le vent aide le jet et la vitesse est donc j + w. Dans un vent de face, le vent ralentit le jet et la vitesse est donc de j ‒ w.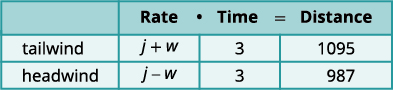
Chaque trajet dure 3 heures. Dans un vent arrière, le jet parcourt 1 095 miles. Dans un vent de face, le jet parcourt 987 miles.
Traduisez en un système d'équations. Puisque le rythme multiplié par le temps est une distance, nous obtenons le système d'équations.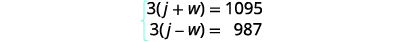
Résolvez le système d'équations. Distribuez, puis résolvez par élimination. Ajoutez et résolvez pour j.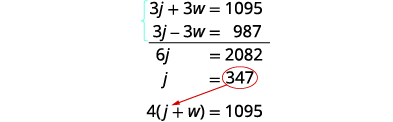
Remplacez j = 347 dans l'une des équations d'origine, puis résolvez pour w.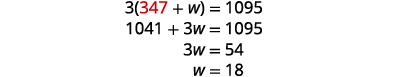
Vérifiez la réponse au problème. Avec le vent arrière, la vitesse réelle du jet serait de \(347+18=365\) mi/h. En 3 heures, le jet parcourrait des \(365·3=1,095\) miles . Face au vent de face, la vitesse réelle du jet serait de \(347−18=329\) mi/h. En 3 heures, le jet parcourrait des \(329·3=987\) kilomètres.
Réponds à la question.	La vitesse du jet est de 347 mi/h et la vitesse du vent est de 18 mi/h.

Exemple\(\PageIndex{29}\)

Traduisez en un système d'équations, puis résolvez :

Un petit jet peut parcourir 1 325 miles en 5 heures avec un vent arrière, mais seulement 1 035 miles en 5 heures dans un vent de face. Trouvez la vitesse du jet dans l'air calme et la vitesse du vent.

Réponse

La vitesse du jet est de 235 mi/h et la vitesse du vent est de 30 mi/h.

Exemple\(\PageIndex{30}\)

Traduisez en un système d'équations, puis résolvez :

Un jet commercial peut parcourir 1 728 miles en 4 heures avec un vent arrière, mais seulement 1 536 miles en 4 heures dans un vent de face. Trouvez la vitesse du jet dans l'air calme et la vitesse du vent.

Réponse

La vitesse du jet est de 408 mi/h et la vitesse du vent est de 24 mi/h.

Accédez à cette ressource en ligne pour obtenir des instructions et des exercices supplémentaires sur les systèmes d'équations.

• Systèmes d'équations

Concepts clés

• Comment résoudre des applications avec des systèmes d'équations
  1. Lisez le problème. Assurez-vous que tous les mots et toutes les idées sont compris.
  2. Déterminez ce que nous recherchons.
  3. Nommez ce que nous recherchons. Choisissez des variables pour représenter ces quantités.
  4. Traduisez en un système d'équations.
  5. Résolvez le système d'équations en utilisant de bonnes techniques d'algèbre.
  6. Vérifiez la réponse au problème et assurez-vous qu'elle est logique.
  7. Répondez à la question par une phrase complète.

Lexique

angles complémentaires

Deux angles sont complémentaires si la somme des mesures de leurs angles est de 90 degrés.

angles supplémentaires

Deux angles sont supplémentaires si la somme des mesures de leurs angles est de 180 degrés.