4.2 : Résoudre des systèmes d'équations linéaires à deux variables
- Page ID
- 194187
À la fin de cette section, vous serez en mesure de :
- Déterminer si une paire ordonnée est la solution d'un système d'équations
- Résolvez un système d'équations linéaires en traçant un graphique
- Résoudre un système d'équations par substitution
- Résoudre un système d'équations par élimination
- Choisissez la méthode la plus pratique pour résoudre un système d'équations linéaires
Avant de commencer, répondez à ce questionnaire de préparation.
- Pour l'équation\(y=\frac{2}{3}x−4\),
ⓐ Est-ce\((6,0)\) une solution ? ⓑ Est-ce\((−3,−2)\) une solution ?
Si vous avez oublié ce problème, consultez [lien]. - Détermine la pente et l'intersection y de la ligne\(3x−y=12\).
Si vous avez oublié ce problème, consultez [lien]. - Trouvez les points d'intersection x et y de la ligne\(2x−3y=12\).
Si vous avez oublié ce problème, consultez [lien].
Déterminer si une paire ordonnée est la solution d'un système d'équations
Dans la section Résolution d'équations linéaires, nous avons appris à résoudre des équations linéaires avec une variable. Nous allons maintenant travailler avec au moins deux équations linéaires regroupées, ce que l'on appelle un système d'équations linéaires.
Lorsque deux équations linéaires ou plus sont regroupées, elles forment un système d'équations linéaires.
Dans cette section, nous concentrerons nos travaux sur les systèmes de deux équations linéaires dans deux inconnues. Nous allons résoudre de plus grands systèmes d'équations plus loin dans ce chapitre.
Un exemple de système de deux équations linéaires est présenté ci-dessous. Nous utilisons une accolade pour montrer que les deux équations sont regroupées pour former un système d'équations.
\[ \left\{ \begin{aligned} 2x+y & = 7 \\ x−2y & = 6 \end{aligned} \right. \nonumber \]
Une équation linéaire à deux variables, par exemple\(2x+y=7\), possède un nombre infini de solutions. Son graphique est une ligne. N'oubliez pas que chaque point de la ligne est une solution à l'équation et que chaque solution à l'équation est un point sur la ligne.
Pour résoudre un système de deux équations linéaires, nous voulons trouver les valeurs des variables qui sont des solutions aux deux équations. En d'autres termes, nous recherchons les paires ordonnées\((x,y)\) qui rendent les deux équations vraies. C'est ce que l'on appelle les solutions d'un système d'équations.
Les solutions d'un système d'équations sont les valeurs des variables qui rendent toutes les équations vraies. La solution d'un système de deux équations linéaires est représentée par une paire ordonnée\((x,y)\).
Pour déterminer si une paire ordonnée est une solution à un système de deux équations, nous substituons les valeurs des variables dans chaque équation. Si la paire ordonnée rend les deux équations vraies, c'est une solution pour le système.
Déterminez si la paire commandée constitue une solution pour le système\(\left \{ \begin{array} {l} x−y = −1 \\ 2x−y = −5 \end{array} \right. \).
ⓐ\((−2,−1)\) ⓑ\((−4,−3)\)
- Réponse
-
ⓐ
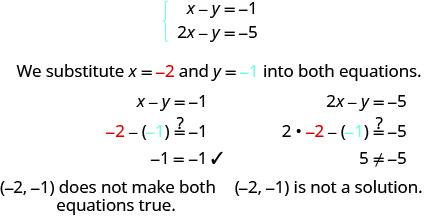
ⓑ
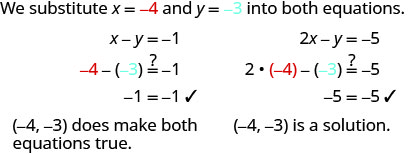
Déterminez si la paire commandée constitue une solution pour le système\(\left \{ \begin{array} 3x+y = 0 \\ x+2y = −5 \end{array} \right. \).
ⓐ\((1,−3)\) ⓑ\((0,0)\)
- Réponse
-
ⓐ Oui ⓑ Non
Déterminez si la paire commandée constitue une solution pour le système\(\left \{ \begin{array} x−3y = −8 \\ −3x−y = 4 \end{array} \right. \).
ⓐ\((2,−2)\) ⓑ\((−2,2)\)
- Réponse
-
ⓐ non ⓑ oui
Résolvez un système d'équations linéaires en graphiant
Dans cette section, nous utiliserons trois méthodes pour résoudre un système d'équations linéaires. La première méthode que nous utiliserons est la création graphique.
Le graphique d'une équation linéaire est une droite. Chaque point de la ligne est une solution à l'équation. Pour un système de deux équations, nous allons représenter graphiquement deux droites. Ensuite, nous pouvons voir tous les points qui sont des solutions à chaque équation. Et, en découvrant ce que les lignes ont en commun, nous trouverons la solution au système.
La plupart des équations linéaires d'une variable ont une solution, mais nous avons vu que certaines équations, appelées contradictions, n'ont pas de solution et que pour d'autres équations, appelées identités, tous les nombres sont des solutions.
De même, lorsque nous résolvons un système de deux équations linéaires représentées par un graphe de deux droites dans le même plan, trois cas sont possibles, comme indiqué.
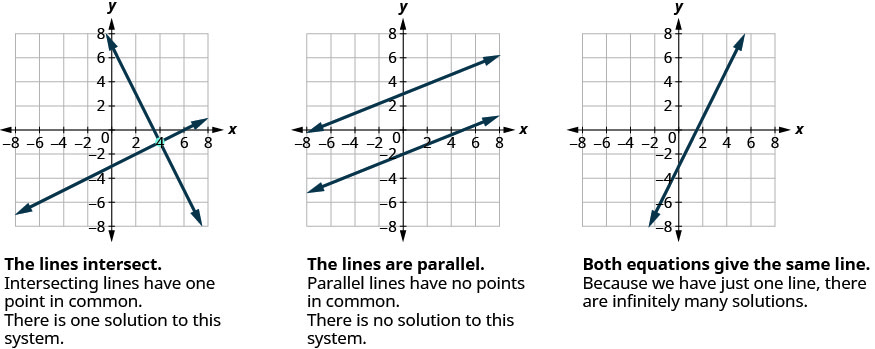
Chaque fois que nous démontrerons une nouvelle méthode, nous l'utiliserons sur le même système d'équations linéaires. À la fin de la section, vous déciderez quelle méthode est la plus pratique pour résoudre ce système.
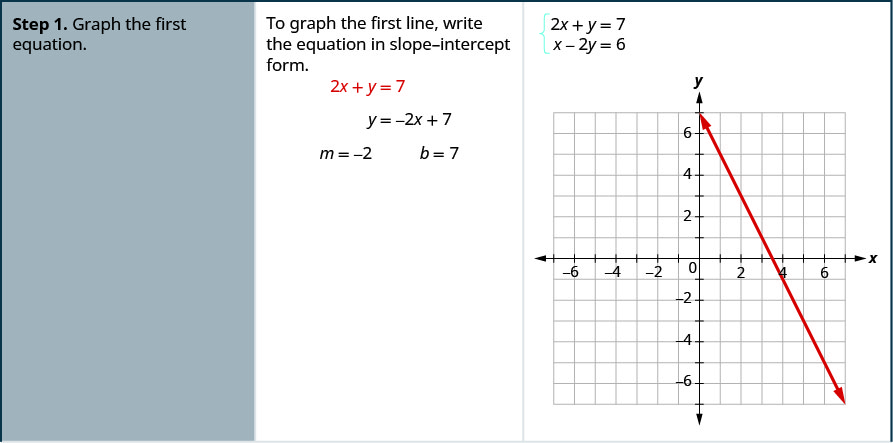
Résolvez le système en dessinant un graphique\( \left\{ \begin{array} {l} 2x+y = 7 \\ x−2y = 6 \end{array} \right. \).
- Réponse
-
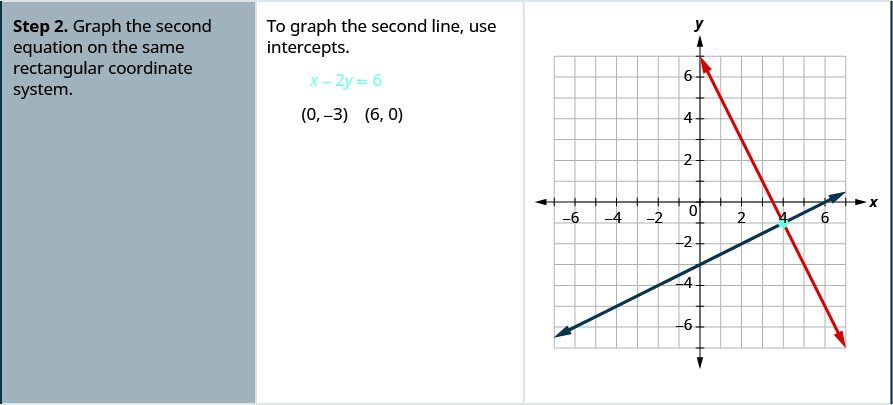


Résolvez le système en graphiquant :\( \left\{ \begin{array} {l} x−3y = −3 \\ x+y = 5 \end{array} \right. \).
- Réponse
-
\((3,2)\)
Résolvez le système en représentant graphiquement :\( \left\{ \begin{array} {l} −x+y = 1 \\ 3x+2y = 12 \end{array} \right.\)
- Réponse
-
\((2,3)\)
Les étapes à suivre pour résoudre un système d'équations linéaires par représentation graphique sont présentées ici.
- Tracez la première équation.
- Tracez la deuxième équation sur le même système de coordonnées rectangulaires.
- Déterminez si les lignes se croisent, sont parallèles ou constituent la même ligne.
- Identifiez la solution du système.
- Si les lignes se croisent, identifiez le point d'intersection. C'est la solution au système.
- Si les lignes sont parallèles, le système n'a pas de solution.
- Si les lignes sont identiques, le système dispose d'un nombre infini de solutions.
- Vérifiez la solution dans les deux équations.
Dans l'exemple suivant, nous allons d'abord réécrire les équations sous forme pente-intersection, afin de pouvoir tracer rapidement les lignes.
Résolvez le système en représentant graphiquement :\(\left\{ \begin{array} {l} 3x+y = −1 \\ 2x+y = 0 \end{array}\right.\)
- Réponse
-
Nous allons résoudre ces deux équations\(y\) afin de pouvoir facilement les représenter graphiquement à l'aide de leurs pentes et de leurs\(y\) interceptions.
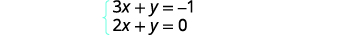
Résolvez la première équation pour y. 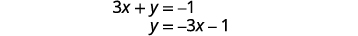
Trouvez la pente et l'intersection y. 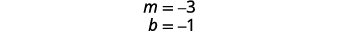
Résolvez la deuxième équation pour y. 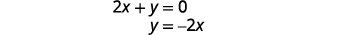
Trouvez la pente et l'intersection y. 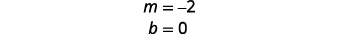
Tracez les lignes. 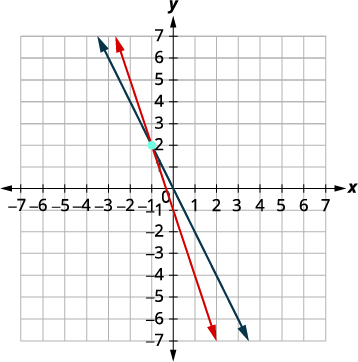
Déterminez le point d'intersection. Les lignes se croisent à\((−1,2)\). Vérifiez la solution dans les deux équations.
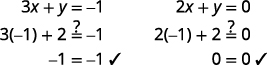
La solution est\((−1,2)\).
Résolvez le système en graphiquant :\(\left\{ \begin{array} {l} −x+y = 1 \\2x+y = 10 \end{array}\right. \).
- Réponse
-
\((3,4)\)
Résolvez le système en graphiquant :\(\left\{ \begin{array} {l} 2x+y = 6 \\x+y = 1 \end{array}\right. \).
- Réponse
-
\((5,−4)\)
Jusqu'à présent, dans tous les systèmes d'équations linéaires, les lignes se croisaient et la solution était un point. Dans les deux exemples suivants, nous allons examiner un système d'équations qui n'a pas de solution et un système d'équations qui possède un nombre infini de solutions.
Résolvez le système en graphiquant :\(\left\{ \begin{array} {l} y = \tfrac{1}{2}x-3 \\ x-2y = 4 \end{array}\right. \).
- Réponse
-
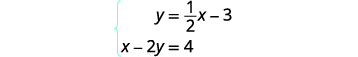
Pour représenter graphiquement la première équation, nous utiliserons sa
pente et son intersection y.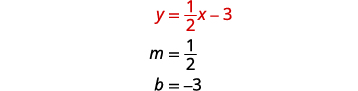
Pour représenter graphiquement la deuxième équation, nous utiliserons
les interceptions.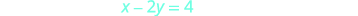
Tracez les lignes. 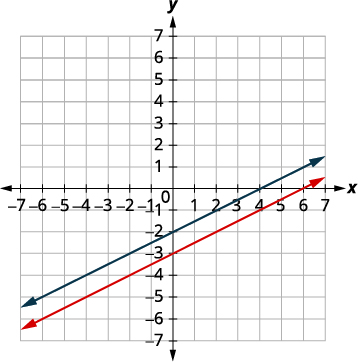
Déterminez les points d'intersection. Les lignes sont parallèles.
Comme aucun point ne se trouve sur les deux lignes, aucune paire
ordonnée ne rend les deux équations
vraies. Il n'existe pas de solution à ce système.
Résolvez le système en graphiquant :\(\left\{ \begin{array} {l} y = -\tfrac{1}{4}x+2 \\ x+4y = 4 \end{array}\right. \).
- Réponse
-
aucune solution
Résolvez le système en graphiquant :\(\left\{ \begin{array} {l} y = 3x-1 \\ 6x-2y = 6 \end{array}\right. \).
- Réponse
-
aucune solution
Parfois, les équations d'un système représentent la même droite. Comme chaque point de la ligne rend les deux équations vraies, il existe une infinité de paires ordonnées qui rendent les deux équations vraies. Il existe une infinité de solutions au système.
Résolvez le système en graphiquant :\(\left\{ \begin{array} {l} y = 2x-3 \\ -6x+3y = 9 \end{array}\right. \).
- Réponse
-
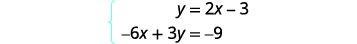
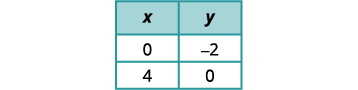
Détermine la pente et l'intersection y de la première équation. 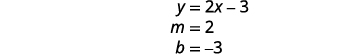
Trouvez les points d'intersection de la deuxième équation. 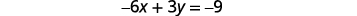
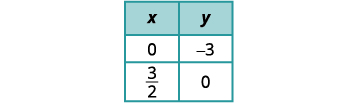
Tracez les lignes. 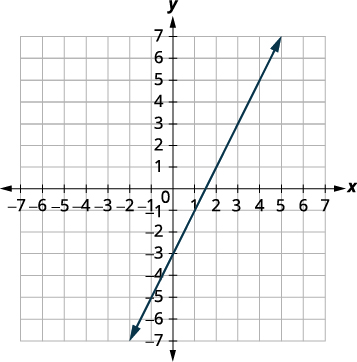
Les lignes sont les mêmes !
Comme chaque point de la ligne rend les deux
équations vraies, il existe une infinité de paires
ordonnées qui rendent les deux équations vraies.
Il existe une infinité de solutions à ce système.Si vous écrivez la deuxième équation sous forme d'intersection de pente, vous reconnaîtrez peut-être que les équations ont la même pente et la même intersection y.
Résolvez le système en graphiquant :\(\left\{ \begin{array} {l} y = -3x-6 \\ 6x+2y = -12 \end{array}\right. \).
- Réponse
-
une infinité de solutions
Résolvez le système en graphiquant :\(\left\{ \begin{array} {l} y = \tfrac{1}{2}x-4 \\ 2x-4y = 16 \end{array}\right. \).
- Réponse
-
une infinité de solutions
Lorsque nous avons représenté graphiquement la deuxième ligne dans le dernier exemple, nous l'avons dessinée juste au-dessus de la première ligne. Nous disons que les deux lignes coïncident. Les lignes coïncidentes ont la même pente et la même intersection y.
Les droites coïncidentes ont la même pente et la même intersection y.
Les systèmes d'équations de l'exemple et de l'exemple comportaient chacun deux lignes qui se croisent. Chaque système avait une solution.
Dans l'exemple, les équations donnaient des lignes coïncidentes, et le système avait donc une infinité de solutions.
Les systèmes de ces trois exemples comportaient au moins une solution. Un système d'équations comportant au moins une solution est appelé système cohérent.
Un système avec des lignes parallèles, comme Example, n'a pas de solution. Nous appelons un système d'équations comme celui-ci incohérent. Il n'y a pas de solution.
Un système d'équations cohérent est un système d'équations comportant au moins une solution.
Un système d'équations incohérent est un système d'équations sans solution.
Nous classons également les équations dans un système d'équations en les qualifiant d'indépendantes ou de dépendantes. Si deux équations sont indépendantes, elles ont chacune leur propre ensemble de solutions. Les lignes qui se croisent et les lignes parallèles sont indépendantes.
Si deux équations sont dépendantes, toutes les solutions d'une équation sont également des solutions de l'autre équation. Lorsque nous tracons deux équations dépendantes, nous obtenons des droites coïncidentes.
Résumons cela en examinant les graphiques des trois types de systèmes. Voir ci-dessous et tableau.
| Lignes | Croisement | Parallèle | coïncident |
|---|---|---|---|
| Nombre de solutions | 1 point | Aucune solution | Infiniment nombreux |
| Cohérent/incohérent | Constant | Incohérent | Constant |
| Dépendant/indépendant | Indépendant | Indépendant | Dépendant |
Sans créer de graphique, déterminez le nombre de solutions, puis classez le système d'équations.
ⓐ\( \left\{ \begin{array} {l} y = 3x−1 \\ 6x−2y = 12 \end{array}\right. \) ⓑ\( \left\{ \begin{array} {l} 2x+y=−3 \\ x−5y=5 \end{array} \right. \)
- Réponse
-
ⓐ Nous allons comparer les pentes et les intersections des deux lignes.
\(\begin{array} {lll} {} &{} &{ \left\{ \begin{array} {l} {y=3x-1} \\ {6x−2y=12} \end{array} \right. } \\ {} &{} &{y = 3x-1} \\ {\text{The first equation is already in slope-intercept form.}} &{} &{} \\ {\text{Write the second equation in slope-intercept form.}} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{6x-2y=12} \\ {} &{} &{-2y=-6x+12} \\ {} &{} &{\frac{-2y}{-2}=\frac{-6x+12}{-2}} \\ {} &{} &{y=3x-6} \\ {} &{y=3x-1} &{y=3x-6} \\ {} &{m=3} &{m=3} \\ {} &{b=-1} &{b=-6} \\ {\text{Find the slope and intercept of each line.}} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{\text{Since the slopes are the same andy-intercepts are}} &{} \\ {} &{\text{different, the lines are parallel.}} &{} \\ \end{array}\)
ⓑ Nous allons comparer la pente et les intersections des deux lignes.
\(\begin{array} {lll} {} &{} &{} \\ {} &{ \left\{ \begin{array} {l} 2x+y=-3 \\ x-5y=5 \\ \end{array} \right. } &{} \\ {\text{Write both equations in slope–intercept form.}} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{2x+y=-3} &{x-5y=5} \\ {} &{y=-2x-3} &{-5y=-x+5} \\ {} &{} &{\frac{-5y}{-5}=\frac{-x+5}{-5}} \\ {} &{} &{y=\frac{1}{5}-1} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {\text{Find the slope and intercept of each line.}} &{} &{} \\ {} &{} &{} \\ {} &{y=-2x-3} &{y=\frac{1}{5}-1} \\ {} &{m=-2} &{m=\frac{1}{5}} \\ {} &{b=-3} &{b=-1} \\ {} &{} &{} \\ {} &{\text{Since the slopes are different, the lines intersect.}} &{} \\ \end{array}\)
Un système d'équations dont les graphes se croisent n'a qu'une solution et est cohérent et indépendant.
Sans créer de graphique, déterminez le nombre de solutions, puis classez le système d'équations.
ⓐ\(\left\{ \begin{array} {l} y=−2x−4 \\ 4x+2y=9 \end{array} \right. \) ⓑ\(\left\{ \begin{array} {l} 3x+2y=2 \\ 2x+y=1 \end{array} \right. \)
- Réponse
-
ⓐ aucune solution, incohérente, indépendante ⓑ une solution, cohérente, indépendante
Sans créer de graphique, déterminez le nombre de solutions, puis classez le système d'équations.
ⓐ\(\left\{ \begin{array} {l} y=\frac{1}{3}x−5 \\ x−3y=6 \end{array} \right. \) ⓑ\(\left\{ \begin{array} {l} x+4y=12 \\ −x+y=3 \end{array} \right. \)
- Réponse
-
ⓐ aucune solution, incohérente, indépendante ⓑ une solution, cohérente, indépendante
La résolution de systèmes d'équations linéaires à l'aide de graphiques est un bon moyen de visualiser les types de solutions qui peuvent en résulter. Cependant, dans de nombreux cas, la résolution graphique d'un système n'est pas pratique ou imprécise. Si les graphes s'étendent au-delà de la petite grille avec x et y compris entre\(−10\) et 10, la représentation graphique des lignes peut s'avérer fastidieuse. Et si les solutions du système ne sont pas des nombres entiers, il peut être difficile de lire leurs valeurs avec précision à partir d'un graphique.
Résoudre un système d'équations par substitution
Nous allons maintenant résoudre des systèmes d'équations linéaires par la méthode de substitution.
Nous utiliserons le même système que celui que nous avons utilisé en premier pour la création de graphiques.
\[ \left\{ \begin{array} {l} 2x+y=7 \\ x−2y=6 \end{array} \right. \nonumber \]
Nous allons d'abord résoudre l'une des équations pour x ou y. Nous pouvons choisir l'une ou l'autre des équations et résoudre l'une ou l'autre variable, mais nous essaierons de faire un choix qui facilitera le travail.
Ensuite, nous substituons cette expression dans l'autre équation. Le résultat est une équation avec une seule variable, et nous savons comment les résoudre !
Après avoir trouvé la valeur d'une variable, nous la remplacerons dans l'une des équations d'origine et la résoudrons pour l'autre variable. Enfin, nous vérifions notre solution et nous nous assurons qu'elle rend les deux équations vraies.
Résolvez le système par substitution :\( \left\{ \begin{array} {l} 2x+y=7 \\ x−2y=6 \end{array} \right. \)
- Réponse
-






Résolvez le système par substitution :\( \left\{ \begin{array} {l} −2x+y=−11 \\ x+3y=9 \end{array} \right. \)
- Réponse
-
\((6,1)\)
Résolvez le système par substitution :\( \left\{ \begin{array} {l} 2x+y=−1 \\ 4x+3y=3 \end{array} \right. \)
- Réponse
-
\((−3,5)\)
- Résolvez l'une des équations pour chaque variable.
- Remplacez l'expression de l'étape 1 dans l'autre équation.
- Résolvez l'équation résultante.
- Remplacez la solution de l'étape 3 dans l'une des équations d'origine pour trouver l'autre variable.
- Écrivez la solution sous la forme d'une paire ordonnée.
- Vérifiez que la paire ordonnée est une solution aux deux équations d'origine.
Soyez très prudent avec les signes de l'exemple suivant.
Résolvez le système par substitution :\( \left\{ \begin{array} {l} 4x+2y=4 \\ 6x−y=8 \end{array} \right. \)
- Réponse
-
Nous devons résoudre une équation pour une variable. Nous allons résoudre la première équation pour y.
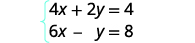
Résolvez la première équation pour y.
Remplacez\(−2x+2\) y dans la deuxième équation.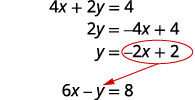
Remplacez le y par\(−2x+2\). 
Résolvez l'équation pour x. 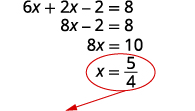
\(x=54\)Remplacez par\(4x+2y=4\) pour trouver y. 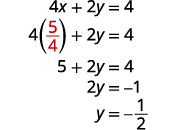
La paire commandée est\((54,−12)\). Vérifiez la paire ordonnée dans les deux équations.
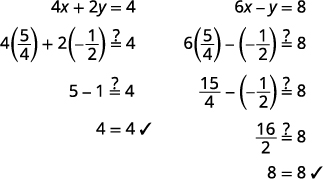
La solution est\((54,−12)\).
Résolvez le système par substitution :\( \left\{ \begin{array} {l} x−4y=−4 \\ −3x+4y=0 \end{array} \right. \)
- Réponse
-
\((2,32)\)
Résolvez le système par substitution :\( \left\{ \begin{array} {l} 4x−y=0 \\ 2x−3y=5 \end{array} \right. \)
- Réponse
-
\((−12,−2)\)
Résoudre un système d'équations par élimination
Nous avons résolu des systèmes d'équations linéaires par graphes et par substitution. La représentation graphique fonctionne bien lorsque les coefficients variables sont faibles et que la solution comporte des valeurs entières. La substitution fonctionne bien lorsque nous pouvons facilement résoudre une équation pour l'une des variables sans avoir trop de fractions dans l'expression résultante.
La troisième méthode de résolution de systèmes d'équations linéaires s'appelle la méthode d'élimination. Lorsque nous avons résolu un système par substitution, nous avons commencé avec deux équations et deux variables et nous l'avons réduit à une équation avec une variable. C'est ce que nous ferons également avec la méthode d'élimination, mais nous aurons une autre façon d'y parvenir.
La méthode d'élimination est basée sur la propriété d'addition d'égalité. La propriété d'addition de l'égalité indique que lorsque vous ajoutez la même quantité des deux côtés d'une équation, vous obtenez toujours l'égalité. Nous allons étendre la propriété d'addition de l'égalité pour indiquer que lorsque vous ajoutez des quantités égales des deux côtés d'une équation, les résultats sont égaux.
Pour toutes les expressions a, b, c et d.
\[\begin{array} {ll} {\text{if}} &{a=b} \\ {\text{and}} &{c=d} \\ {\text{then}} &{a+c=b+d.} \\ \nonumber \end{array}\]
Pour résoudre un système d'équations par élimination, nous commençons par les deux équations sous forme standard. Ensuite, nous décidons quelle variable sera la plus facile à éliminer. Comment décidons-nous ? Nous voulons que les coefficients d'une variable soient opposés, afin de pouvoir additionner les équations et éliminer cette variable.
Remarquez comment cela fonctionne lorsque nous ajoutons ces deux équations :
\[\left\{ \begin{array} {l} 3x+y=5 \\ \underline{2x−y=0} \end{array} \right. \nonumber\]
\[5x=5 \nonumber\]
Les y s'additionnent à zéro et nous avons une équation avec une variable.
Essayons-en un autre :
\[ \left\{ \begin{array} x+4y=2 \\ 2x+5y=−2 \end{array} \right. \nonumber\]
Cette fois, nous ne voyons pas de variable qui puisse être immédiatement éliminée si nous ajoutons les équations.
Mais si nous multiplions la première équation par\(−2\), nous ferons en sorte que les coefficients de x soient opposés. Nous devons multiplier chaque terme des deux côtés de l'équation par\(−2\).
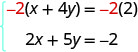
Réécrivez ensuite le système d'équations.
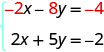
Nous voyons maintenant que les coefficients des termes x sont opposés, donc x sera éliminé lorsque nous ajouterons ces deux équations.
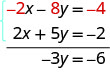
Une fois que nous obtenons une équation avec une seule variable, nous la résolvons. Ensuite, nous remplaçons cette valeur dans l'une des équations d'origine pour résoudre la variable restante. Et, comme toujours, nous vérifions notre réponse pour nous assurer qu'elle est une solution aux deux équations d'origine.
Nous allons maintenant voir comment utiliser l'élimination pour résoudre le même système d'équations que nous avons résolu par graphe et par substitution.
Résolvez le système par élimination :\(\left\{ \begin{array} {l} 2x+y=7 \\ x−2y=6 \end{array} \right. \)
- Réponse
-






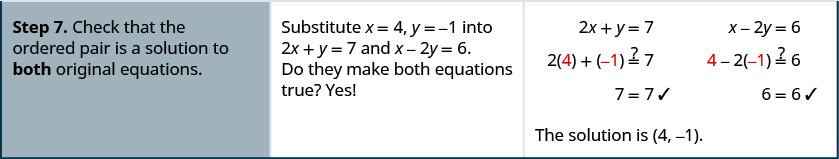
Résolvez le système par élimination :\(\left\{ \begin{array} {l} 3x+y=5 \\ 2x−3y=7 \end{array} \right.\)
- Réponse
-
\((2,−1)\)
Résolvez le système par élimination :\(\left\{ \begin{array} {l} 4x+y=−5 \\ −2x−2y=−2 \end{array} \right.\)
- Réponse
-
\((−2,3)\)
Les étapes sont répertoriées ici pour faciliter la consultation.
- Écrivez les deux équations sous forme standard. Si certains coefficients sont des fractions, supprimez-les.
- Faites en sorte que les coefficients d'une variable soient opposés.
- Déterminez quelle variable vous allez éliminer.
- Multipliez l'une des équations ou les deux de manière à ce que les coefficients de cette variable soient opposés.
- Ajoutez les équations résultant de l'étape 2 pour éliminer une variable.
- Résolvez pour la variable restante.
- Remplacez la solution de l'étape 4 par l'une des équations d'origine. Résolvez ensuite pour l'autre variable.
- Écrivez la solution sous la forme d'une paire ordonnée.
- Vérifiez que la paire ordonnée est une solution aux deux équations d'origine.
Nous allons maintenant faire un exemple où nous devons multiplier les deux équations par des constantes afin de rendre les coefficients d'une variable opposés.
Résolvez le système par élimination :\(\left\{ \begin{array} {l} 4x−3y=9 \\ 7x+2y=−6 \end{array} \right. \)
- Réponse
-
Dans cet exemple, nous ne pouvons pas multiplier une seule équation par n'importe quelle constante pour obtenir des coefficients opposés. Nous allons donc multiplier stratégiquement les deux équations par différentes constantes pour obtenir les contraires.
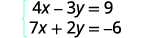
Les deux équations sont présentées sous forme standard.
Pour obtenir les coefficients opposés de y, nous allons
multiplier la première équation par 2 et la
deuxième équation par 3.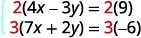
Simplifiez. 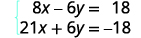
Ajoutez les deux équations pour éliminer y. 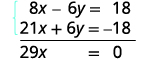
Résolvez pour x. 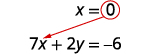
Remplacez x=0x=0 dans l'une des équations d'origine. 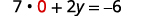
Résolvez pour y. 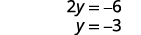
Écrivez la solution sous la forme d'une paire ordonnée. La paire commandée est\((0,−3)\).
Vérifiez que la paire ordonnée est une solution aux
deux équations d'origine.
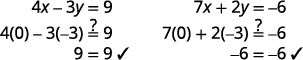
La solution est\((0,−3)\).
Résolvez le système par élimination :\(\left\{ \begin{array} {l} 3x−4y=−9 \\ 5x+3y=14\end{array} \right. \)
- Réponse
-
\((1,3)\)
Résolvez chaque système par élimination :\(\left\{ \begin{array} {l} 7x+8y=4 \\ 3x−5y=27 \end{array} \right.\)
- Réponse
-
\((4,−3)\)
Lorsque le système d'équations contient des fractions, nous allons d'abord effacer les fractions en multipliant chaque équation par l'écran LCD de toutes les fractions de l'équation.
Résolvez le système par élimination :\(\left\{ \begin{array} {l} x+\tfrac{1}{2}y=6 \\ \tfrac{3}{2}x+\tfrac{2}{3}y=\tfrac{17}{2} \end{array} \right.\)
- Réponse
-
Dans cet exemple, les deux équations comportent des fractions. Notre première étape sera de multiplier chaque équation par l'écran LCD de toutes les fractions de l'équation pour effacer les fractions.
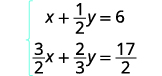
Pour effacer les fractions, multipliez chaque
équation par son écran LCD.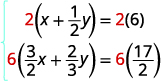
Simplifiez. 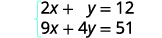
Nous sommes maintenant prêts à éliminer l'une
des variables. Notez que les deux équations sont sous forme
standard.Nous pouvons éliminer y en multipliant l'équation supérieure par\(−4\). 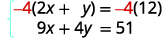
Simplifiez et ajoutez.
Remplacez\(x=3\) par l'une des équations d'origine.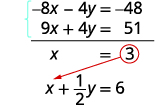
Résolvez pour y. 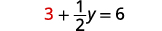
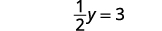
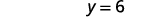
Écrivez la solution sous la forme d'une paire ordonnée. La paire commandée est\((3,6)\). Vérifiez que la paire ordonnée est une solution aux
deux équations d'origine.

La solution est\((3,6)\).
Résolvez chaque système par élimination :\(\left\{ \begin{array} {l} \tfrac{1}{3}x−\tfrac{1}{2}y=1 \\ \tfrac{3}{4}x−y=\tfrac{5}{2} \end{array} \right.\)
- Réponse
-
\((6,2)\)
Résolvez chaque système par élimination :\(\left\{ \begin{array} {l} x+\tfrac{3}{5}y=−\tfrac{1}{5} \\ −\tfrac{1}{2}x−\tfrac{2}{3}y=\tfrac{5}{6} \end{array} \right.\)
- Réponse
-
\((1,−2)\)
Lorsque nous avons résolu le système à l'aide d'un graphique, nous avons constaté que tous les systèmes d'équations linéaires n'ont pas une seule paire ordonnée comme solution. Lorsque les deux équations étaient vraiment identiques, il y avait une infinité de solutions. C'est ce que nous avons appelé un système cohérent. Lorsque les deux équations décrivaient des lignes parallèles, il n'y avait pas de solution. Nous avons dit que c'était un système incohérent.
Il en va de même pour la substitution ou l'élimination. Si l'équation à la fin de la substitution ou de l'élimination est vraie, nous avons un système cohérent mais dépendant et le système d'équations propose une infinité de solutions. Si l'équation à la fin de la substitution ou de l'élimination est une fausse déclaration, nous avons un système incohérent et le système d'équations n'a pas de solution.
Résolvez le système par élimination :\(\left\{ \begin{array} {l} 3x+4y=12 \\ y=3−\tfrac{3}{4}x \end{array} \right. \)
- Réponse
-
\(\begin{array} {ll} {} &{ \left\{ \begin{array} {l} 3x+4y=12 \\ y=3−\frac{3}{4}x \end{array} \right.} \\ {} &{} \\ {\text{Write the second equation in standard form.}} &{\left\{ \begin{array} {l} 3x+4y=12 \\ \frac{3}{4}x+y=3 \end{array} \right. } \\ {} &{} \\ {\text{Clear the fractions by multiplying the } \\ \text{second equation by 4.}} &{\left\{ \begin{array} {l} 3x+4y=12 \\ 4(\frac{3}{4}x+y)=4(3) \end{array} \right. } \\ {} &{} \\ {\text{Simplify.}} &{\left\{ \begin{array} {l} 3x+4y=12 \\ 3x+4y=12 \end{array} \right. } \\ {} &{} \\ {\text{To eliminate a variable, we multiply the} \\ \text{second equation by−1. Simplify and add.}} &{\begin{array} {l} {\left\{ \begin{array} {l} 3x+4y=12 \\ \underline{-3x-4y=-12 } \end{array} \right.} \\ {\hspace{16mm} 0=0} \end{array}} \\ \end{array} \)
C'est une affirmation vraie. Les équations sont cohérentes mais dépendantes. Leurs graphiques seraient sur la même ligne. Le système propose une infinité de solutions.
Après avoir effacé les fractions de la deuxième équation, avez-vous remarqué que les deux équations étaient identiques ? Cela signifie que nous avons des lignes coïncidentes.
Résolvez le système par élimination :\(\left\{ \begin{array} {l} 5x−3y=15 \\ 5y=−5+\tfrac{5}{3}x \end{array} \right. \)
- Réponse
-
une infinité de solutions
Résolvez le système par élimination :\(\left\{ \begin{array} {l} x+2y=6 \\ y=−\tfrac{1}{2}x+3\end{array} \right. \)
- Réponse
-
une infinité de solutions
Choisissez la méthode la plus pratique pour résoudre un système d'équations linéaires
Lorsque vous résolvez un système d'équations linéaires dans une application, vous ne serez pas informé de la méthode à utiliser. Vous devrez prendre cette décision vous-même. Vous devez donc choisir la méthode la plus simple à utiliser et qui minimise les risques d'erreur.
\[ \textbf{Choose the Most Convenient Method to Solve a System of Linear Equations} \\ \begin{array} {lll} {\underline{\textbf{Graphing}}} &{\underline{\textbf{Substitution}}} &{\underline{\textbf{Elimination}}} \\ {\text{Use when you need a}} &{\text{Use when one equation is}} &{\text{Use when the equations a}} \\ {\text{picture of the situation.}} &{\text{already solved or can be}} &{\text{rein standard form.}} \\ {\text{}} &{\text{easily solved for one}} &{\text{}} \\ {\text{}} &{\text{variable.}} &{\text{}} \\ \end{array} \nonumber \]
Pour chaque système d'équations linéaires, décidez s'il serait plus pratique de le résoudre par substitution ou par élimination. Expliquez votre réponse.
ⓐ\(\left\{ \begin{array} {l} 3x+8y=40 \\ 7x−4y=−32 \end{array} \right.\) ⓑ\(\left\{ \begin{array} {l} 5x+6y=12 \\ y=\tfrac{2}{3}x−1 \end{array} \right.\)
- Réponse
-
ⓐ
\[\left\{ \begin{array} {l} 3x+8y=40 \\ 7x−4y=−32 \end{array} \right.\nonumber\]
Comme les deux équations se présentent sous une forme standard, l'élimination sera plus pratique.
ⓑ
\[\left\{ \begin{array} {l} 5x+6y=12 \\ y=\tfrac{2}{3}x−1 \end{array} \right.\nonumber \]
Comme une équation est déjà résolue pour y, l'utilisation de la substitution sera plus pratique.
Pour chaque système d'équations linéaires, décidez s'il serait plus pratique de le résoudre par substitution ou par élimination. Expliquez votre réponse.
ⓐ\(\left\{ \begin{array} {l} 4x−5y=−32 \\ 3x+2y=−1 \end{array} \right.\) ⓑ\(\left\{ \begin{array} {l} x=2y−1 \\ 3x−5y=−7 \end{array} \right.\)
- Réponse
-
ⓐ Comme les deux équations sont de forme standard, l'élimination sera plus pratique. ⓑ Comme une équation est déjà résolue pour x, le recours à la substitution sera plus pratique.
Pour chaque système d'équations linéaires, décidez s'il serait plus pratique de le résoudre par substitution ou par élimination. Expliquez votre réponse.
ⓐ\(\left\{ \begin{array} {l} y=2x−1 \\ 3x−4y=−6 \end{array} \right.\) ⓑ\(\left\{ \begin{array} {l} 6x−2y=12 \\ 3x+7y=−13 \end{array} \right.\)
- Réponse
-
ⓐ Comme une équation est déjà résolue pour y, l'utilisation de la substitution sera plus pratique. ⓑ Comme les deux équations sont sous forme standard, l'élimination sera plus pratique.
Concepts clés
- Comment résoudre un système d'équations linéaires par représentation graphique.
- Tracez la première équation.
- Tracez la deuxième équation sur le même système de coordonnées rectangulaires.
- Déterminez si les lignes se croisent, sont parallèles ou constituent la même ligne.
- Identifiez la solution du système.
Si les lignes se croisent, identifiez le point d'intersection. C'est la solution au système.
Si les lignes sont parallèles, le système n'a pas de solution.
Si les lignes sont identiques, le système dispose d'un nombre infini de solutions. - Vérifiez la solution dans les deux équations.
- Comment résoudre un système d'équations par substitution.
- Résolvez l'une des équations pour chaque variable.
- Remplacez l'expression de l'étape 1 dans l'autre équation.
- Résolvez l'équation résultante.
- Remplacez la solution de l'étape 3 dans l'une des équations d'origine pour trouver l'autre variable.
- Écrivez la solution sous la forme d'une paire ordonnée.
- Vérifiez que la paire ordonnée est une solution aux deux équations d'origine.
- Comment résoudre un système d'équations par élimination.
- Écrivez les deux équations sous forme standard. Si certains coefficients sont des fractions, supprimez-les.
- Faites en sorte que les coefficients d'une variable soient opposés.
Déterminez quelle variable vous allez éliminer.
Multipliez l'une des équations ou les deux de manière à ce que les coefficients de cette variable soient opposés. - Ajoutez les équations résultant de l'étape 2 pour éliminer une variable.
- Résolvez pour la variable restante.
- Remplacez la solution de l'étape 4 par l'une des équations d'origine. Résolvez ensuite pour l'autre variable.
- Écrivez la solution sous la forme d'une paire ordonnée.
- Vérifiez que la paire ordonnée est une solution aux deux équations d'origine. \[ \textbf{Choose the Most Convenient Method to Solve a System of Linear Equations} \\ \begin{array} {lll} {\underline{\textbf{Graphing}}} &{\underline{\textbf{Substitution}}} &{\underline{\textbf{Elimination}}} \\ {\text{}} &{\text{Use when one equation is}} &{\text{}} \\ {\text{Use when you need a}} &{\text{already solved or can be}} &{\text{Use when the equations a}} \\ {\text{picture of the situation.}} &{\text{easily solved for one}} &{\text{rein standard form.}} \\ {\text{}} &{\text{variable.}} &{\text{}} \\ \end{array} \nonumber \]
Lexique
- lignes coïncidentes
- Les droites coïncidentes ont la même pente et la même intersection y.
- systèmes cohérents et incohérents
- Un système d'équations cohérent est un système d'équations comportant au moins une solution ; un système d'équations incohérent est un système d'équations sans solution.
- solutions d'un système d'équations
- Les solutions d'un système d'équations sont les valeurs des variables qui rendent toutes les équations vraies ; la solution est représentée par une paire ordonnée (x, y). (x, y).
- système d'équations linéaires
- Lorsque deux équations linéaires ou plus sont regroupées, elles forment un système d'équations linéaires.