3.3E : Exercices

Last updated
Save as PDF

Page ID: 194126

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

La pratique permet de perfectionner

Trouvez la pente d'une ligne

Dans les exercices suivants, déterminez la pente de chaque ligne affichée.

1.
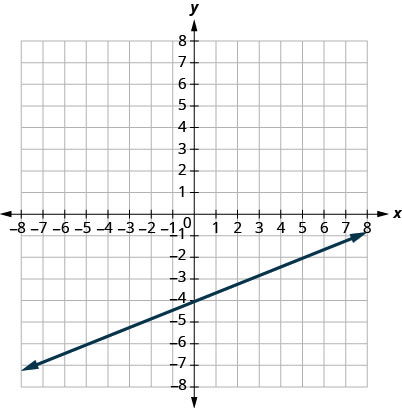
$Cette figure montre le graphique d'une ligne droite sur le plan de coordonnées x. L'axe X va de moins 8 à 8. L'axe Y va de moins 8 à 8. La ligne passe par les points (0, moins 4) et (5, moins 2).$

Réponse: $m=\frac{2}{5}$

2.
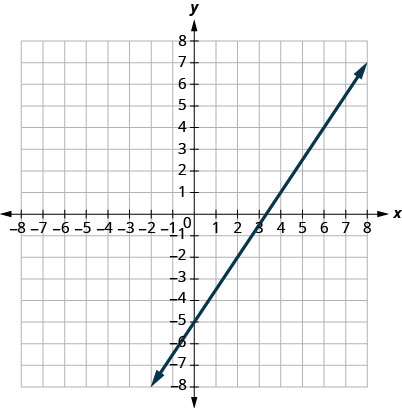
$Cette figure montre le graphique d'une ligne droite sur le plan de coordonnées x. L'axe X va de moins 8 à 8. L'axe Y va de moins 8 à 8. La ligne passe par les points (0, moins 5) et (2, moins 2).$

3.
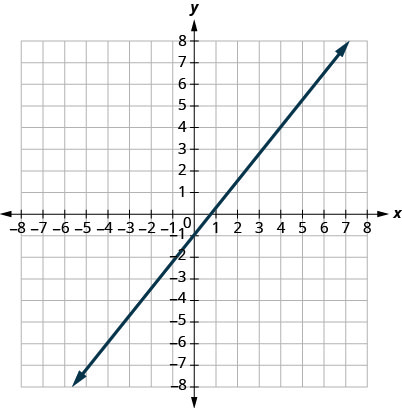
$Cette figure montre le graphique d'une ligne droite sur le plan de coordonnées x. L'axe X va de moins 8 à 8. L'axe Y va de moins 8 à 8. La ligne passe par les points (0, moins 1) et (4, 4).$

Réponse: $m=\frac{5}{4}$

4.
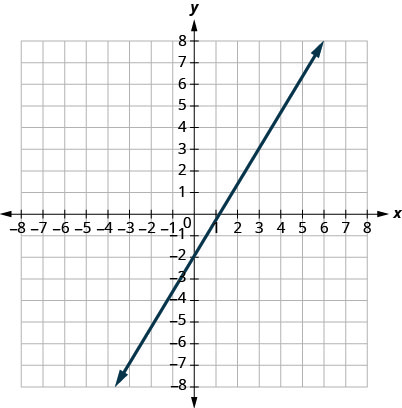
$Cette figure montre le graphique d'une ligne droite sur le plan de coordonnées x. L'axe X va de moins 8 à 8. L'axe Y va de moins 8 à 8. La ligne passe par les points (0, moins 2) et (3, 3).$

5.
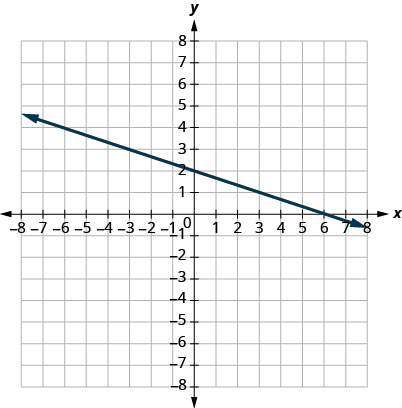
$Cette figure montre le graphique d'une ligne droite sur le plan de coordonnées x. L'axe X va de moins 8 à 8. L'axe Y va de moins 8 à 8. La ligne passe par les points (0, 2) et (3, 1).$

Réponse: $m = -\frac{1}{3}$

6.
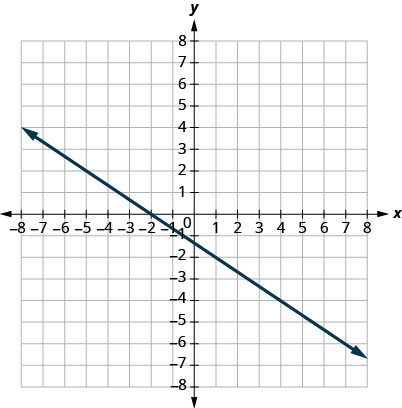
$Cette figure montre le graphique d'une ligne droite sur le plan de coordonnées x. L'axe X va de moins 8 à 8. L'axe Y va de moins 8 à 8. La ligne passe par les points (0, moins 1) et (3, moins 3).$

7.
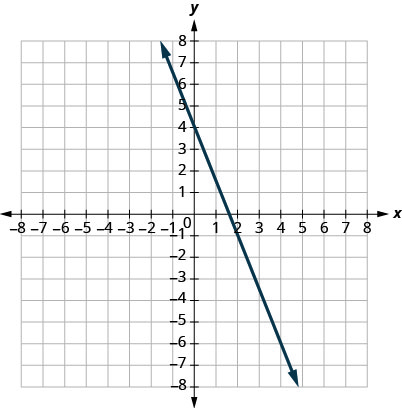
$Cette figure montre le graphique d'une ligne droite sur le plan de coordonnées x. L'axe X va de moins 8 à 8. L'axe Y va de moins 8 à 8. La ligne passe par les points (0, 4) et (2, moins 1).$

Réponse: $m = -\frac{5}{2}$

8.
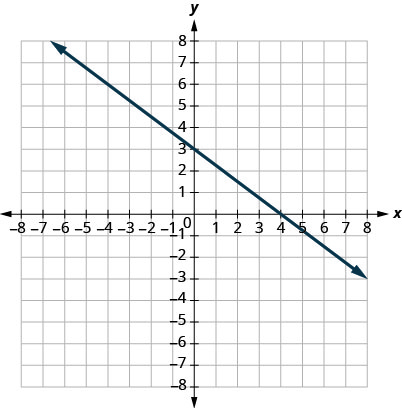
$Cette figure montre le graphique d'une ligne droite sur le plan de coordonnées x. L'axe X va de moins 8 à 8. L'axe Y va de moins 8 à 8. La ligne passe par les points (0, 2) et (4, moins 1).$

Dans les exercices suivants, déterminez la pente de chaque ligne.

9. $y=3$

Réponse: $m = 0$

10. $y=−2$

11. $x=−5$

Réponse: indéfini

12. $x=4$

Dans les exercices suivants, utilisez la formule de pente pour déterminer la pente de la ligne entre chaque paire de points.

13. $(2,5),\;(4,0)$

Réponse: $m = -\frac{5}{2}$

14. $(3,6),\;(8,0)$

15. $(−3,3),\;(4,−5)$

Réponse: $m = -\frac{8}{7}$

16. $(−2,4),\;(3,−1)$

17. $(−1,−2),\;(2,5)$

Réponse: $m = \frac{7}{3}$

18. $(−2,−1),\;(6,5)$

19. $(4,−5),\;(1,−2)$

Réponse: $m = -1$

20. $(3,−6),\;(2,−2)$

Tracez une droite en fonction d'un point et de la pente

Dans les exercices suivants, tracez chaque ligne avec le point et la pente donnés.

21. $(2,5)$;$m=−\frac{1}{3}$

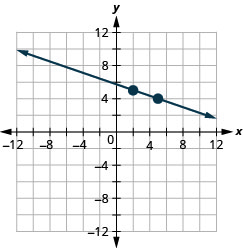
Réponse: $Cette figure montre le graphique d'une ligne droite sur le plan de coordonnées x. L'axe X va de moins 12 à 12. L'axe Y va de moins 12 à 12. La ligne passe par les points (2, 5) et (5, 4).$

22. $(1,4)$;$m=−\frac{1}{2}$

23. $(−1,−4)$;$m=\frac{4}{3}$

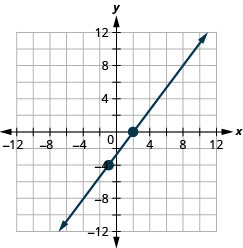
Réponse: $Cette figure montre le graphique d'une ligne droite sur le plan de coordonnées x. L'axe X va de moins 12 à 12. L'axe Y va de moins 12 à 12. La ligne passe par les points (moins 1, moins 4) et (2, 0).$

24. $(−3,−5)$;$m=\frac{3}{2}$

25. $y$-intercepter :$(0, 3)$ ;$m=−\frac{2}{5}$

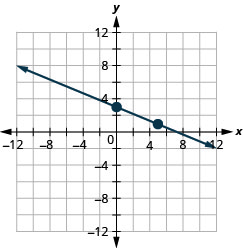
Réponse: $Cette figure montre le graphique d'une ligne droite sur le plan de coordonnées x. L'axe X va de moins 12 à 12. L'axe Y va de moins 12 à 12. La ligne passe par les points (0, 3) et (5, 1).$

26. $x$-intercepter :$(−2,0)$ ;$m=\frac{3}{4}$

27. $(−4,2)$;$m=4$

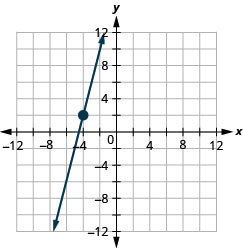
Réponse: $Cette figure montre le graphique d'une ligne droite sur le plan de coordonnées x. L'axe X va de moins 12 à 12. L'axe Y va de moins 12 à 12. La ligne passe par les points (moins 4, 2) et (moins 3, 6).$

28. $(1,5)$;$m=−3$

Tracez une ligne en utilisant sa pente et son intersection

Dans les exercices suivants, identifiez la pente et l'intersection y de chaque ligne.

29. $y=−7x+3$

Réponse: $m=−7$;$(0,3)$

30. $y=4x−10$

31. $3x+y=5$

Réponse: $m=−3$;$(0,5)$

32. $4x+y=8$

33. $6x+4y=12$

Réponse: $m=−\frac{3}{2}$;$(0,3)$

34. $8x+3y=12$

35. $5x−2y=6$

Réponse: $m=\frac{5}{2}$;$(0,−3)$

36. $7x−3y=9$

Dans les exercices suivants, tracez la droite de chaque équation en utilisant sa pente et son intersection y.

37. $y=3x−1$

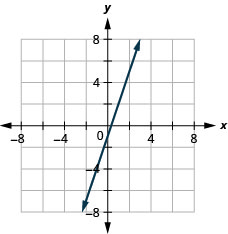
Réponse: $Cette figure montre le graphique d'une ligne droite sur le plan de coordonnées x. L'axe X va de moins 10 à 10. L'axe Y va de moins 10 à 10. La ligne passe par les points (0, moins 1) et (1, 2).$

38. $y=2x−3$

39. $y=−x+3$

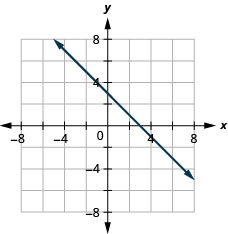
Réponse: $Cette figure montre le graphique d'une ligne droite sur le plan de coordonnées x. L'axe X va de moins 10 à 10. L'axe Y va de moins 10 à 10. La ligne passe par les points (0, 3) et (1, 2).$

40. $y=−x−4$

41. $y=−\frac{2}{5}x−3$

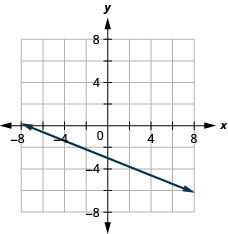
Réponse: $Cette figure montre le graphique d'une ligne droite sur le plan de coordonnées x. L'axe X va de moins 10 à 10. L'axe Y va de moins 10 à 10. La ligne passe par les points (0, moins 3) et (5, moins 5).$

42. $y=−\frac{3}{5}x+2$

43. $3x−2y=4$

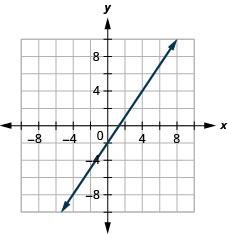
Réponse: $Cette figure montre le graphique d'une ligne droite sur le plan de coordonnées x. L'axe X va de moins 10 à 10. L'axe Y va de moins 10 à 10. La ligne passe par les points (0, moins 2) et (2, 1).$

44. $3x−4y=8$

Choisissez la méthode la plus pratique pour tracer une ligne

Dans les exercices suivants, déterminez la méthode la plus pratique pour représenter graphiquement chaque ligne.

45. $x=2$

Réponse: ligne verticale

46. $y=5$

47. $y=−3x+4$

Réponse: interception de pente

48. $x−y=5$

49. $x−y=1$

Réponse: intercepte

50. $y=\frac{2}{3}x−1$

51. $3x−2y=−12$

Réponse: intercepte

52. $2x−5y=−10$

Applications graphiques et interprétatives de Slope—Intercept

53. L'équation$P=31+1.75w$ modélise la relation entre le montant de la facture d'eau mensuelle de Tuyet$P$, en dollars, et le nombre d'unités d'eau utilisées.$w$

a. Trouvez le paiement mensuel de Tuyet lorsque des$0$ unités d'eau sont utilisées.

b. Trouvez le paiement mensuel de Tuyet lorsque des$12$ unités d'eau sont utilisées.

c. Interprétez la pente et$P$ l'intersection de l'équation.

d. Représentez l'équation sous forme graphique.

Réponse

a.$$31$
b.$$52$
c. La pente signifie que le paiement augmente$$1.75$ lorsque le nombre d'unités d'eau utilisées augmente de$1$.$1.75$$P$$w$ Le$P$ -intercept signifie que lorsque le nombre d'unités d'eau utilisées par Tuyet est égal à$0$, le paiement est$$31$.
d.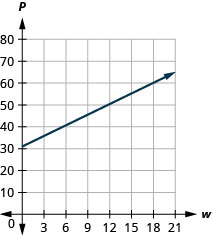

$Cette figure montre le graphique d'une ligne droite sur le plan de coordonnées x. L'axe X va de moins 1 à 21. L'axe Y va de moins 1 à 80. La ligne passe par les points (0, 31) et (12, 52).$

54. L'équation$P=28+2.54w$ modélise la relation entre le montant de la facture d'eau mensuelle de Randy$P$, en dollars, et le nombre d'unités d'eau utilisées.$w$

a. Trouvez le paiement pour un mois lorsque Randy a utilisé des$0$ unités d'eau.

b. Trouvez le paiement pour un mois lorsque Randy a utilisé des$15$ unités d'eau.

c. Interprétez la pente et$P$ l'intersection de l'équation.

d. Représentez l'équation sous forme graphique.

55. Bruce conduit sa voiture pour son travail. L'équation$R=0.575m+42$ modélise la relation entre le montant en dollars qu'il est remboursé et le nombre de miles qu'il parcourt en une journée.$R$$m$

a. Déterminez le montant remboursé à Bruce un jour où il parcourt des$0$ miles.

b. Déterminez le montant remboursé à Bruce un jour où il parcourt des$220$ miles.

c. Interprétez la pente et$R$ l'intersection de l'équation.

d. Représentez l'équation sous forme graphique.

Réponse

a.$$42$
b.$$168.50$
c. La pente$0.575$ signifie que le montant qui lui est remboursé augmente$$0.575$ lorsque le nombre de miles parcourus augmente de$1$.$R$$m$ Le$R$ -intercept signifie que lorsque le nombre de miles parcourus est$0$ égal à, le montant remboursé est$$42$.
d.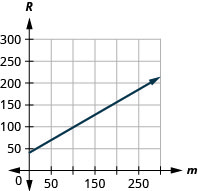

$Cette figure montre le graphique d'une ligne droite sur le plan de coordonnées x. L'axe X va de moins 50 à 250. L'axe Y va de moins 50 à 300. La ligne passe par les points (0, 42) et (220, 168,5).$

56. Janelle prévoit de louer une voiture pendant ses vacances. L'équation$C=0.32m+15$ modélise la relation entre le coût en dollars$C$, par jour et le nombre de miles$m$ parcourus par elle en une journée.

a. Déterminez le coût si Janelle parcourt des$0$ kilomètres en voiture un jour.

b. Déterminez le coût d'une journée où Janelle parcourt des$400$ kilomètres en voiture.

c. Interprétez la pente et$C$ l'intersection de l'équation.

d. Représentez l'équation sous forme graphique.

57. Cherie travaille dans le commerce de détail et son salaire hebdomadaire comprend une commission pour le montant qu'elle vend. L'équation$S=400+0.15c$ modélise la relation entre son salaire hebdomadaire$S$, en dollars, et le montant de ses ventes$c$, en dollars.

a. Trouvez le salaire de Cherie pour une semaine alors qu'elle vendait$$0$.

b. Trouvez le salaire de Cherie pour une semaine alors qu'elle vendait$$3,600$.

c. Interprétez la pente et$S$ l'intersection de l'équation.

d. Représentez l'équation sous forme graphique.

Réponse

a.$$400$
b.$$940$
c. La pente signifie que le salaire de Cherie, S, augmente$$0.15$ à chaque$$1$ augmentation de ses ventes.$0.15$ Le$S$ -intercepter signifie que lorsque ses ventes sont effectuées$$0$, son salaire est de$$400$.
d.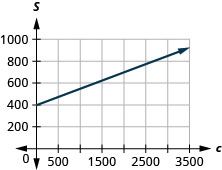

$Cette figure montre le graphique d'une ligne droite sur le plan de coordonnées x. L'axe X s'étend de moins 500 à 3500. L'axe Y va de moins 200 à 1 000. La ligne passe par les points (0, 400) et (3600, 940).$

58. Le salaire hebdomadaire de Patel comprend un salaire de base plus une commission sur ses ventes. L'équation$S=750+0.09c$ modélise la relation entre son salaire hebdomadaire$S$, en dollars, et le montant de ses ventes$c$, en dollars.

a. Trouvez le salaire de Patel pour une semaine pendant laquelle il vendait$0$.

b. Trouvez le salaire de Patel pour une semaine lorsque ses ventes étaient$18,540$.

c. Interprétez la pente et$S$ l'intersection de l'équation.

d. Représentez l'équation sous forme graphique.

59. Costa prépare un banquet pour le déjeuner. L'équation$C=450+28g$ modélise la relation entre le coût$C$ en dollars du banquet et le nombre d'invités$g$.

a. Déterminez le coût si le nombre d'invités est de$40$.

b. Déterminez le coût si le nombre d'invités est de$80$.

c. Interprétez la pente et$C$ l'intersection de l'équation.

d. Représentez l'équation sous forme graphique.

Réponse

a.$$1570$
b.$$5690$
c. La pente indique le coût par personne. La pente signifie que le coût augmente$$28$ lorsque le nombre d'invités augmente$1$.$28$$C$ Le$C$ -intercept signifie que si le nombre d'invités était$0$, le coût serait$$450$.
d.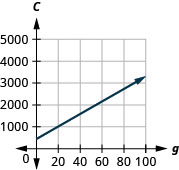

$Cette figure montre le graphique d'une ligne droite sur le plan de coordonnées x. L'axe X va de moins 20 à 100. L'axe Y va de 1 000 à 7 000 points négatifs. La ligne passe par les points (0, 450) et (40, 1570).$

60. Margie prépare un dîner de banquet. L'équation$C=750+42g$ modélise la relation entre le coût$C$ en dollars du banquet et le nombre d'invités$g$.

a. Déterminez le coût si le nombre d'invités est de$50$.

b. Déterminez le coût si le nombre d'invités est de$100$.

c. Interprétez la pente et$C$ l'intersection de l'équation.

d. Représentez l'équation sous forme graphique.

Utiliser les pentes pour identifier les lignes parallèles et perpendiculaires

Dans les exercices suivants, utilisez les pentes et$y$ les interceptions pour déterminer si les lignes sont parallèles, perpendiculaires ou aucune des deux.

61. $y=\frac{3}{4}x−3$;$3x−4y=−2$

Réponse: parallèle

62. $3x−4y=−2$;$y=\frac{3}{4}x−3$

63. $2x−4y=6$;$x−2y=3$

Réponse: ni

64. $8x+6y=6$;$12x+9y=12$

65. $x=5$;$x=−6$

Réponse: parallèle

66. $x=−3$;$x=−2$

67. $4x−2y=5$;$3x+6y=8$

Réponse: perpendiculaire

68. $8x−2y=7$;$3x+12y=9$

69. $3x−6y=12$;$6x−3y=3$

Réponse: ni

70. $9x−5y=4$;$5x+9y=−1$

71. $7x−4y=8$;$4x+7y=14$

Réponse: perpendiculaire

72. $5x−2y=11$;$5x−y=7$

73. $3x−2y=8$;$2x+3y=6$

Réponse: perpendiculaire

74. $2x+3y=5$;$3x−2y=7$

75. $3x−2y=1$;$2x−3y=2$

Réponse: ni

76. $2x+4y=3$;$6x+3y=2$

77. $y=2$;$y=6$

Réponse: parallèle

78. $y=−1$;$y=2$

Exercices d'écriture

79. En quoi le graphique d'une droite avec pente$m=12$ diffère-t-il du graphique d'une droite avec pente$m=2$ ?

Réponse: Les réponses peuvent varier.

80. Pourquoi la pente d'une ligne verticale est-elle « indéfinie » ?

81. Expliquez comment représenter graphiquement une droite en fonction d'un point et de sa pente.

Réponse: Les réponses peuvent varier.

82. Expliquez avec vos propres mots comment choisir la méthode à utiliser pour tracer une courbe.

Auto-vérification

a. Une fois les exercices terminés, utilisez cette liste de contrôle pour évaluer votre maîtrise des objectifs de cette section.

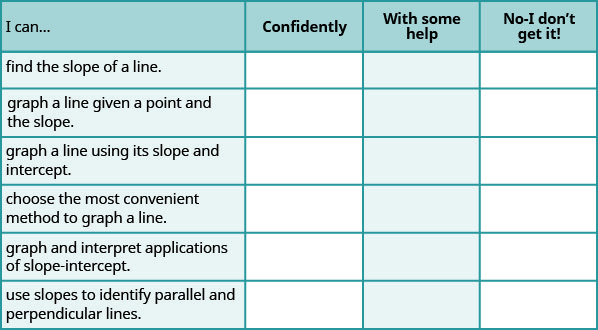
$Ce tableau comporte 7 lignes et 4 colonnes. La première ligne est une ligne d'en-tête et elle étiquette chaque colonne. Le premier en-tête de colonne est « Je peux... », le second est « En toute confiance », le troisième est « Avec de l'aide » et le quatrième est « Non, je ne comprends pas ». Sous la première colonne se trouvent les phrases « trouver la pente d'une ligne », « tracer une ligne en fonction d'un point et de la pente », « tracer une ligne en utilisant sa pente et son intersection », « choisissez la méthode la plus pratique pour tracer une ligne », « tracez et interprétez les applications de l'interception de pente » et « utilisez les pentes pour identifier les parallèles et lignes perpendiculaires ». Les autres colonnes sont laissées vides afin que l'apprenant puisse indiquer son niveau de maîtrise pour chaque sujet.$

b. Après avoir examiné cette liste de contrôle, que ferez-vous pour atteindre tous les objectifs en toute confiance ?