Chapitre 2 Exercices de révision

Last updated
Save as PDF

Page ID: 194423

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Exercices de révision des

Utiliser une stratégie générale pour résoudre des équations linéaires

Résoudre des équations en utilisant la stratégie générale de résolution d'équations linéaires

Dans les exercices suivants, déterminez si chaque nombre est une solution à l'équation.

1. $10x−1=5x,\quad x= \frac{1}{5}$

2. $−12n+5=8n,\quad n=−\frac{5}{4}$

Réponse: non

Dans les exercices suivants, résolvez chaque équation linéaire.

3. $6(x+6)=24$

4. $−(s+4)=18$

Réponse: $s=−22$l'ensemble de solutions est donc :$ \{-22\} $.

5. $23−3(y−7)=8$

6. $\frac{1}{3}(6m+21)=m−7$

Réponse: $m=−14$

7. $4(3.5y+0.25)=365$

8. $0.25(q−8)=0.1(q+7)$

Réponse: $q=18$

9. $8(r−2)=6(r+10)$

10. $5+7(2−5x)=2(9x+1)−(13x−57)$

Réponse: $x=−1$

11. $(9n+5)−(3n−7)=20−(4n−2)$

12. $2[−16+5(8k−6)]=8(3−4k)−32$

Réponse: $k=\frac{3}{4}$

Classer les équations

Dans les exercices suivants, classez chaque équation en tant qu'équation conditionnelle, identité ou contradiction, puis énoncez la solution.

13. $17y−3(4−2y)=11(y−1)+12y−1$

14. $9u+32=15(u−4)−3(2u+21)$

Réponse: contradiction ; pas de solution

15. $−8(7m+4)=−6(8m+9)$

Résolvez des équations avec des coefficients de fraction

Dans les exercices suivants, résolvez chaque équation.

16. $\frac{2}{5}n−\frac{1}{10}=\frac{7}{10}$

Réponse: $n=2$

17. $\frac{3}{4}a−\frac{1}{3}=\frac{1}{2}a+\frac{5}{6}$

18. $\frac{1}{2}(k+3)=\frac{1}{3}(k+16)$

Réponse: $k=23$

19. $\frac{5y−1}{3}+4=\frac{-8y+4}{6}$

20. $0.8x−0.3=0.7x+0.2$

Réponse: $x=5$

21. $0.10d+0.05(d−4)=2.05$

Utilisez une stratégie de résolution de problèmes

Utiliser une stratégie de résolution de problèmes pour les problèmes de mots

Dans les exercices suivants, résolvez en utilisant la stratégie de résolution de problèmes pour les problèmes de mots.

22. Les trois quarts des personnes qui assistent à un concert sont des enfants. S'il y a 87 enfants, quel est le nombre total de personnes présentes au concert ?

Réponse: Il y a 116 personnes.

23. Le groupe compte neuf saxophonistes. Le nombre de saxophonistes est inférieur au double du nombre de tubistes. Détermine le nombre de joueurs de tuba.

Résoudre des problèmes de mots numériques

Dans les exercices suivants, résolvez chaque problème de mot numérique.

24. La somme d'un nombre et de trois est de quarante et un. Trouve le numéro.

Réponse: 38

25. Un chiffre est neuf de moins qu'un autre. Leur somme est négative de vingt-sept. Trouve les numéros.

26. Un chiffre est deux fois plus que quatre fois un autre. Leur somme est négative de treize. Trouve les numéros.

Réponse: $−3,−10$

27. La somme de deux entiers consécutifs est$−135$. Trouve les numéros.

28. Trouvez trois entiers pairs consécutifs dont la somme est de 234.

Réponse: 76, 78, 80

29. Trouve trois entiers impairs consécutifs dont la somme est 51.

30. Koji a 5 502$ sur son compte d'épargne. C'est 30$ de moins de six fois le montant de son compte courant. Combien d'argent a Koji sur son compte courant ?

Réponse: 922$

Résolvez les demandes

Dans les exercices suivants, traduisez et résolvez.

31. Quel est le chiffre 67 % de 250 ?

32. 12,5 % de quel nombre est 20 ?

Réponse: $160$

33. Quel pourcentage de 125 vaut 150 ?

Dans les exercices suivants, résolvez.

34. La facture du déjeuner de Dino était de 19,45$. Il voulait laisser 20 % de la facture totale sous forme de pourboire. Quel doit être le pourboire ?

Réponse: $$3.89$

35. Dolores a acheté un berceau en vente pour 350$. Le prix de vente était de 40 % du prix initial. Quel était le prix initial du berceau ?

36. Jaden gagne 2 680$ par mois. Il paie 938$ par mois pour le loyer. Quel pourcentage de son salaire mensuel est consacré au loyer ?

Réponse: $35%$

37. Angel a reçu une augmentation de son salaire annuel de 55 400$ à 56 785$. Trouvez la variation en pourcentage.

38. La facture mensuelle d'essence de Rowena est passée de 83,75$ le mois dernier à 56,95$ ce mois-ci. Trouvez la variation en pourcentage.

Réponse: $32%$

39. Emmett a acheté une paire de chaussures en solde à 40 % de rabais par rapport au prix initial de 138$. Trouvez ⓐ le montant de la réduction et ⓑ le prix de vente.

40. Lacey a acheté une paire de bottes en solde pour 95$. Le prix initial des bottes était de 200$. Trouvez ⓐ le montant de la réduction et ⓑ le taux d'escompte. (Si nécessaire, arrondissez au dixième de pour cent le plus proche.)

Réponse: ⓐ$$105$ ⓑ$52.5%$

41. Nga et Lauren ont acheté un coffre dans un marché aux puces pour 50$. Ils l'ont refait, puis ont ajouté une majoration de 350 %. Trouvez ⓐ le montant de la majoration et ⓑ le prix catalogue.

Résoudre des demandes d'intérêt simples

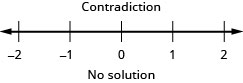
Dans les exercices suivants, résolvez.

42. Winston a déposé 3 294$ sur un compte bancaire avec un taux d'intérêt de 2,6 % Combien d'intérêts a été gagné en cinq ans ?

Réponse: $$428.22$

43. Moira a emprunté 4 500$ à son grand-père pour payer sa première année d'université. Trois ans plus tard, elle a remboursé les 4 500$ plus 243$ d'intérêts. Quel était le taux d'intérêt ?

44. Le relevé de prêt frigorifique de Jaime indiquait qu'il paierait 1 026 dollars d'intérêts pour un prêt de quatre ans à 13,5 %. Combien Jaime a-t-il emprunté pour acheter le réfrigérateur ?

Réponse: $$1,900$

Résoudre une formule pour une variable spécifique

Résoudre une formule pour une variable spécifique

Dans les exercices suivants, résolvez la formule pour la variable spécifiée.

45. Résolvez la formule
$V=LWH$ pour L.

46. Résolvez la formule
$A=\frac{1}{2}d_1d_2$ pour$d_2$.

Réponse: $d_2=\frac{2A}{d_1}$

47. Résolvez la formule
$h=48t+\frac{1}{2}at^2$ pour t.

48. Résolvez la formule
4x−3y=12 pour y.

Réponse: $y=\frac{4x}{3}−4$

Utiliser des formules pour résoudre des applications de géométrie

Dans les exercices suivants, résolvez à l'aide d'une formule géométrique.

49. Quelle est la hauteur d'un triangle d'une superficie de 67,567,5 mètres carrés et d'une base de 9 mètres ?

50. La mesure du plus petit angle d'un triangle droit est inférieure de 45°45° à la mesure de l'angle supérieur suivant. Trouvez les mesures des trois angles.

Réponse: $22.5°,\; 67.5°,\; 90°$

51. Le périmètre d'un triangle est de 97 pieds. Un côté du triangle mesure onze pieds de plus que le plus petit côté. Le troisième côté mesure six pieds de plus que le double du plus petit côté. Trouvez la longueur de tous les côtés.

52. Détermine la longueur de l'hypoténuse.

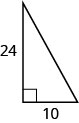
$La figure est un triangle droit avec une base de 10 unités et une hauteur de 24 unités.$

Réponse: $26$

53. Détermine la longueur du côté manquant. Si nécessaire, arrondissez au dixième le plus proche.

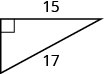
$La figure est un triangle droit d'une hauteur de 15 unités et d'une hypoténuse de 17 unités.$

54. Sergio doit attacher un fil pour maintenir l'antenne sur le toit de sa maison, comme le montre la figure. L'antenne mesure huit pieds de haut et Sergio a 10 pieds de fil. À quelle distance de la base de l'antenne peut-il fixer le fil ? Environ le dixième le plus proche, si nécessaire.

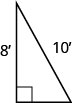
$La figure est un triangle droit d'une hauteur de 8 pieds et d'une hypoténuse de 10 pieds.$

Réponse: 6 pieds

55. Seong construit des étagères dans son garage. Les étagères mesurent 36 pouces de largeur et 15 pouces de hauteur. Il veut placer une attelle diagonale à l'arrière pour stabiliser les étagères, comme indiqué. Quelle doit être la longueur de l'attelle ?

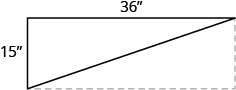
$La figure illustre des étagères rectangulaires dont la largeur de 36 pouces et la hauteur de 15 pouces forment un triangle droit avec une entretoise diagonale.$

56. La longueur d'un rectangle est supérieure de 12 cm à sa largeur. Le périmètre est de 74 cm. Trouvez la longueur et la largeur.

Réponse: $24.5$cm,$12.5$ cm

57. La largeur d'un rectangle est trois fois plus grande que deux fois la longueur. Le périmètre est de 96 pouces. Trouvez la longueur et la largeur.

58. Le périmètre d'un triangle est de 35 pieds. Un côté du triangle mesure cinq pieds de plus que le second côté. Le troisième côté est plus long de trois pieds que le second côté. Déterminez la longueur de chaque côté.

Réponse: 9 pieds, 14 pieds, 12 pieds

Résolvez les applications à mouvements mixtes et uniformes

Résoudre les problèmes de Coin Word

Dans les exercices suivants, résolvez.

59. Paulette a 140$ en billets de 5$ et 10$. Le nombre de billets de 10$ est inférieur au double du nombre de billets de 5$. Combien en possède-t-elle ?

60. Lenny a 3,69$ en centimes, dix cents et quatre pièces. Le nombre de centimes est supérieur de trois cents au nombre de dix cents. Le nombre de trimestres est le double du nombre de pièces de dix cents. Combien de pièces de chaque pièce possède-t-il ?

Réponse: neuf centimes, six centimes, 12 quarts

Résoudre les problèmes liés aux tickets et aux timbres

Dans les exercices suivants, résolvez chaque problème de ticket ou de mot de timbre.

61. Les billets pour un match de basket coûtent 2$ pour les étudiants et 5$ pour les adultes. Le nombre d'étudiants était trois fois moins de dix fois supérieur à celui des adultes. Le montant total provenant de la vente de billets était de 619$. Combien de billets ont été vendus par billet ?

62. 125 billets ont été vendus pour le concert du groupe de jazz pour un total de 1 022 dollars. Les billets étudiants coûtent 6$ chacun et les billets d'admission générale coûtent 10$ chacun. Combien de billets de chaque type ont été vendus ?

Réponse: 57 étudiants, 68 adultes

63. Yumi a dépensé 34,15$ pour acheter des timbres. Le nombre de timbres de 0,56$ qu'elle a achetés était 10 fois inférieur à quatre fois le nombre de timbres de 0,41$. Combien en a-t-elle acheté ?

Résolvez les problèmes de mélange

Dans les exercices suivants, résolvez.

64. Marquese fabrique 10 livres de mélange montagnard à partir de raisins secs et de noix. Les raisins secs coûtent 3,45$ la livre et les noix 7,95$ la livre. Combien de livres de raisins secs et combien de livres de noix Marquese devrait-il utiliser pour le mélange de randonnée pour lui coûter 6,96 dollars la livre ?

Réponse: $2.2$livres de raisins secs,$7.8$ livres de noix

65. Amber veut poser des carreaux sur le dosseret de ses comptoirs de cuisine. Elle aura besoin de 36 pieds carrés de carreaux. Elle utilisera des carreaux de base qui coûtent 8$ le pied carré et des carreaux de décoration qui coûtent 20$ le pied carré. Combien de pieds carrés de chaque carreau doit-elle utiliser pour que le coût global du dosseret soit de 10$ le pied carré ?

66. Enrique a emprunté 23 500$ pour acheter une voiture. Il paie à son oncle 2 % d'intérêt sur les 4 500$ qu'il lui a empruntés, et il paie à la banque 11,5 % d'intérêt sur le reste. Quel taux d'intérêt moyen paie-t-il sur un total de 23 500$ ? (Arrondissez votre réponse au dixième de pour cent le plus proche.)

Réponse: $9.7%$

Résolvez des applications de mouvements

Dans les exercices suivants, résolvez.

67. Lorsque Gabe conduit de Sacramento à Redding, il lui faut 2,2 heures. Il faut deux heures à Elsa pour parcourir la même distance. La vitesse d'Elsa est de 11 miles à l'heure plus rapide que celle de Gabe. Trouve la vitesse de Gabe et celle d'Elsa.

68. Louellen et Tracy se sont rencontrées dans un restaurant sur la route entre Chicago et Nashville. Louellen avait quitté Chicago et avait fait 3,2 heures de route en direction de Nashville. Tracy avait quitté Nashville et avait roulé 4 heures en direction de Chicago, à une vitesse d'un mille à l'heure plus rapide que celle de Louellen. La distance entre Chicago et Nashville est de 472 miles. Trouvez la vitesse de Louellen et celle de Tracy.

Réponse: Louellen 65 mi/h, Tracy 66 mi/h

69. Deux bus partent d'Amarillo en même temps. Le bus d'Albuquerque se dirige vers l'ouest sur l'I-40 à une vitesse de 112 miles à l'heure, et le bus d'Oklahoma City se dirige vers l'est sur l'I-40 à une vitesse de 78 miles par heure. Combien d'heures leur faudra-t-il pour se retrouver à 375 miles l'un de l'autre ?

70. Kyle a ramé son bateau en amont pendant 50 minutes. Il lui a fallu 30 minutes pour redescendre à la rame. Sa vitesse en amont est de deux milles à l'heure plus lente que sa vitesse en aval. Trouvez les vitesses en amont et en aval de Kyle.

Réponse: en amont 3 mi/h, en aval 5 mi/h

71. À 6 h 30, Devon a quitté sa maison et a fait du vélo sur la route plate jusqu'à 7 h 30. Puis elle a commencé à monter la pente et a roulé jusqu'à 8 heures. Elle a parcouru un total de 15 miles. Sa vitesse sur la route plate était de cinq milles à l'heure plus rapide que sa vitesse en montée. Trouvez la vitesse de Devon sur la route plate et en montée.

72. Anthony a conduit de New York à Baltimore, soit une distance de 192 miles. Il est parti à 3 h 45 et la circulation était dense jusqu'à 17 h 30. La circulation était faible pendant le reste du trajet et il est arrivé à 7 h 30. Sa vitesse dans la circulation légère était de quatre milles à l'heure, soit plus du double de sa vitesse dans la circulation dense. Trouvez la vitesse de conduite d'Anthony dans un trafic dense et léger.

Réponse: circulation dense 32 mi/h, circulation légère 66 mi/h

Résoudre les inégalités linéaires

Représenter graphiquement les inégalités sur la droite numérique

Dans les exercices suivants, tracez l'inégalité sur la droite numérique et écrivez en notation par intervalles.

73. $x<−1$

74. $x\geq −2.5$

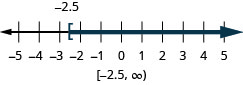
Réponse: $La solution est si x est supérieur ou égal à moins 2,5. La ligne numérique montre un crochet gauche à moins 2,5 avec un ombrage à droite. La notation des intervalles va de moins 2,5 à l'infini entre crochets et parenthèses.$

75. $x\leq \frac{5}{4}$

76. $x>2$

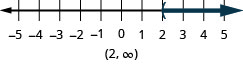
Réponse: $La solution est que x est supérieur à 2. La ligne numérique montre une parenthèse gauche à 2 avec un ombrage à droite. La notation par intervalles est comprise entre 2 et l'infini entre parenthèses.$

77. $−2<x<0$

78. $-5\leq x<−3$

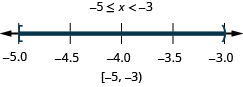
Réponse: $La solution est négative ; 5 est inférieure ou égale à x, qui est inférieure à moins 3. La ligne numérique montre un cercle fermé à moins 5, un cercle ouvert à moins 3 et un ombrage entre les cercles. La notation des intervalles va de moins 5 à moins 3 entre crochets et parenthèses.$

79. $0\leq x\leq 3.5$

Résoudre les inégalités linéaires

Dans les exercices suivants, résolvez chaque inégalité, tracez la solution sur la ligne numérique et écrivez la solution en notation par intervalles.

80. $n−12\leq 23$

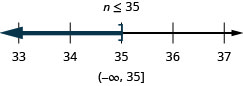
Réponse: $La solution est que n est inférieur ou égal à 35. La ligne numérique représente un crochet droit à 35 avec un ombrage à gauche. La notation par intervalles est une valeur infinie négative à 35 entre parenthèses et crochets.$

81. $a+\frac{2}{3}\geq \frac{7}{12}$

82. $9x>54$

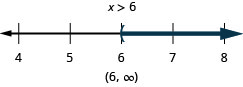
Réponse: $La solution est que x est supérieur à 6. La ligne numérique montre une parenthèse gauche à 6 avec un ombrage à droite. La notation par intervalles est comprise entre 6 et l'infini entre parenthèses.$

83. $\frac{q}{−2}\geq −24$

84. $6p>15p−30$

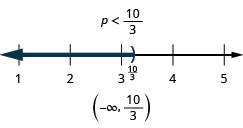
Réponse: $La solution est que p est inférieur aux dix tiers. La ligne numérique montre une parenthèse droite aux dix tiers avec un ombrage à gauche. La notation par intervalles est de l'infini négatif aux dix tiers entre parenthèses.$

85. $9h−7(h−1)\leq 4h−23$

86. $5n−15(4−n)<10(n−6)+10n$

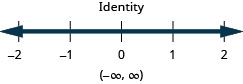
Réponse: $La solution, c'est l'identité. Sa solution sur la ligne numérique est ombrée pour toutes les valeurs. La solution en notation par intervalles est de l'infini négatif à l'infini entre parenthèses.$

87. $\frac{3}{8}a−\frac{1}{12}a>\frac{5}{12}a+\frac{3}{4}$

Traduisez les mots en une inégalité et résolvez

Dans les exercices suivants, traduisez et résolvez. Écrivez ensuite la solution en notation par intervalles et graphiquez sur la ligne numérique.

88. Cinq de plus$z$ que 19 au plus.

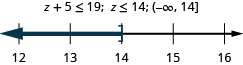
Réponse: $L'inégalité est Z plus 5 est inférieure ou égale à 19. Sa solution est que z est inférieur ou égal à 14. La ligne numérique représente un crochet droit au 14 avec un ombrage à gauche. La notation par intervalles est une valeur infinie négative à 14 entre parenthèses et crochets.$

89. Trois de moins$c$ que 360 au moins.

90. Neuf fois$n$ plus que 42.

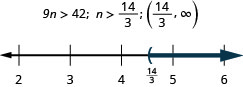
Réponse: $L'inégalité est de 9 n est supérieure à 42. Sa solution est que n est supérieur aux quatorze tiers. La ligne numérique montre des parenthèses gauches aux quatorze tiers avec un ombrage à droite. La notation par intervalles est comprise entre quatorze tiers et l'infini entre parenthèses.$

91. Négatif deux fois ne$a$ vaut pas plus de huit.

Résoudre des applications présentant des inégalités linéaires

Dans les exercices suivants, résolvez.

92. Julianne dispose d'un budget alimentaire hebdomadaire de 231$ pour sa famille. Si elle prévoit de prévoir le même montant pour chacun des sept jours de la semaine, quel est le montant maximum qu'elle peut dépenser chaque jour en nourriture ?

Réponse: 33$ par jour

93. Rogelio peint des aquarelles. Il a reçu une carte-cadeau de 100$ au magasin de fournitures artistiques et veut l'utiliser pour acheter des toiles de 12 pouces × 16 pouces. Chaque toile coûte 10,99$. Quel est le nombre maximum de toiles qu'il peut acheter avec sa carte-cadeau ?

94. Briana s'est vu proposer un poste de vendeuse dans une autre ville. L'offre était de 42 500$ plus 8 % de ses ventes totales. Pour que le déménagement en vaille la peine, Briana doit avoir un salaire annuel d'au moins 66 500 dollars. Quel devrait être son chiffre d'affaires total pour qu'elle déménage ?

Réponse: au moins 300 000$

95. La voiture de Renee lui coûte 195$ par mois plus 0,09$ par mile. Combien de kilomètres Renee peut-elle parcourir pour que ses dépenses de voiture mensuelles ne dépassent pas 250$ ?

96. Costa est comptable. Pendant la saison des impôts, il facture 125$ pour faire une simple déclaration de revenus. Ses dépenses pour l'achat de logiciels, la location d'un bureau et la publicité s'élèvent à 6 000$. Combien de déclarations de revenus doit-il faire s'il veut réaliser un bénéfice d'au moins 8 000$ ?

Réponse: au moins 112 emplois

97. Jenna prévoit des vacances de cinq jours en villégiature avec trois de ses amies. Cela lui coûtera 279$ pour le billet d'avion, 300$ pour la nourriture et les divertissements et 65 dollars par jour pour sa part de l'hôtel. Elle a économisé 550 dollars pour ses vacances et peut gagner 25 dollars de l'heure en tant qu'assistante dans le studio de photographie de son oncle. Combien d'heures doit-elle travailler pour avoir suffisamment d'argent pour ses vacances ?

Résoudre les inégalités composées

Résolvez les inégalités composées avec « et »

Dans chacun des exercices suivants, résolvez chaque inégalité, représentez la solution sous forme graphique et écrivez la solution en notation par intervalles.

98. $x\leq 5$et$x>−3$

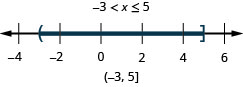
Réponse: $La solution est négative, 3 est inférieure à x qui est inférieure ou égale à 5. La ligne numérique montre un cercle ouvert à moins 3 et un cercle fermé à 5. La notation des intervalles est négative de 3 à 5 entre parenthèses et crochets.$

99. $4x−2\leq 4$et$7x−1>−8$

100. $5(3x−2)\leq 5$et$4(x+2)<3$

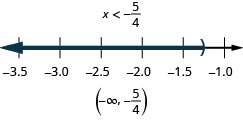
Réponse: $La solution est négative x est inférieure à moins de cinq quarts. La ligne numérique montre un cercle ouvert aux cinq quarts négatifs avec un ombrage à sa gauche. La notation par intervalles va de l'infini négatif à moins cinq quarts entre parenthèses.$

101. $34(x−8)\leq 3$et$15(x−5)\leq 3$

102. $34x−5\geq −2$et$−3(x+1)\geq 6$

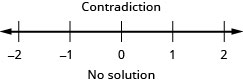
Réponse: $La solution est contradictoire. Il n'y a donc pas de solution. Par conséquent, il n'y a pas de graphique sur la notation numérique, linéaire ou par intervalle.$

103. $−5\leq 4x−1<7$

Résolvez les inégalités composées avec « ou »

Dans les exercices suivants, résolvez chaque inégalité, tracez la solution sur la ligne numérique et écrivez la solution en notation par intervalles.

104. $5−2x\leq −1$ou$6+3x\leq 4$

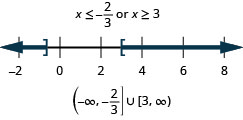
Réponse: $La solution est si x est inférieur aux deux tiers négatifs ou si x est supérieur ou égal à 3. La ligne numérique montre un cercle fermé à moins deux tiers avec un ombrage à sa gauche et un cercle fermé à 3 avec un ombrage à sa droite. La notation par intervalles est l'union de l'infini négatif à moins deux tiers entre parenthèses et crochets et de 3 à l'infini entre parenthèses et parenthèses.$

105. $3(2x−3)<−5$ou$4x−1>3$

106. $34x−2>4$ou$4(2−x)>0$

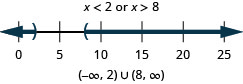
Réponse: $La solution est si x est inférieur à 2 ou x est supérieur à 8. La ligne numérique montre un cercle ouvert à 2 avec un ombrage à gauche et un cercle ouvert à 8 avec un ombrage à sa droite. La notation par intervalles est l'union de l'infini négatif à 8 entre parenthèses et de 8 à l'infini entre parenthèses.$

107. $2(x+3)\geq 0$ou$3(x+4)\leq 6$

108. $12x−3\leq 4$ou$13(x−6)\geq −2$

Réponse: $La solution, c'est l'identité. Sa solution sur la ligne numérique est ombrée pour toutes les valeurs. La solution en notation par intervalles est de l'infini négatif à l'infini entre parenthèses.$

Résoudre des applications présentant des inégalités composées

Dans les exercices suivants, résolvez.

109. Liam joue à un jeu de chiffres avec sa sœur Audry. Liam pense à un chiffre et veut qu'Audry le devine. Cinq fois plus que trois fois son nombre se situe entre 2 et 32. Écrivez une inégalité composée qui montre la gamme de nombres auxquels Liam pourrait penser.

110. Elouise crée un jardin rectangulaire dans son jardin. La longueur du jardin est de 12 pieds. Le périmètre du jardin doit être d'au moins 36 pieds et pas plus de 48 pieds. Utilisez une inégalité composée pour déterminer la plage de valeurs pour la largeur du jardin.

Réponse: $6\leq w\leq 12$

Résoudre les inégalités de valeur absolue

Résolvez des équations de

Dans les exercices suivants, résolvez.

111. $|x|=8$

112. $|y|=−14$

Réponse: aucune solution

113. $|z|=0$

114. $|3x−4|+5=7$

Réponse: $x=2,x=\frac{2}{3}$

115. $4|x−1|+2=10$

116. $−2|x−3|+8=−4$

Réponse: $x=9,x=−3$

117. $|12x+5|+4=1$

118. $|6x−5|=|2x+3|$

Réponse: $x=2,x=14$

Résolvez les inégalités de valeur absolue avec « moins de »

Dans les exercices suivants, résolvez chaque inégalité. Représentez la solution sous forme graphique et écrivez la solution en notation par intervalles.

119. $|x|\leq 8$

120. $|2x−5|\leq 3$

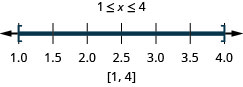
Réponse: $La solution est 1 est inférieure ou égale à x qui est inférieur ou égal à 4. La ligne numérique montre un cercle fermé à 1, un cercle fermé à 4 et un ombrage entre les cercles. La notation des intervalles est de 1 à 4 entre parenthèses.$

121. $|6x−5|<7$

122. $|5x+1|\leq −2$

Réponse: $La solution est contradictoire. Il n'y a donc pas de solution. Par conséquent, il n'y a pas de graphique, de ligne numérique ou de notation par intervalles.$

Résolvez les inégalités de valeur absolue avec « supérieur à »

Dans les exercices suivants, résolvez. Représentez la solution sous forme graphique et écrivez la solution en notation par intervalles.

123. $|x|>6$

124. $|x|\geq 2$

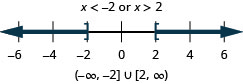
Réponse: $La solution est si x est inférieur à moins 2 ou x est supérieur à 6. La ligne numérique montre un cercle fermé à moins 2 avec un ombrage à gauche et un cercle fermé à 2 avec un ombrage à sa droite. La notation par intervalles est l'union de l'infini négatif à moins 2 entre parenthèses et crochets et de 2 à l'infini entre crochets et parenthèses.$

125. $|x−5|>−2$

126. $|x−7|\geq 1$

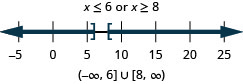
Réponse: $La solution est si x est inférieur ou égal à 6 ou x est supérieur ou égal à 8. La ligne numérique montre un cercle fermé à 6 avec un ombrage à gauche et un cercle fermé à 8 avec un ombrage à droite. La notation par intervalles est l'union de l'infini négatif à moins 6 entre parenthèses et crochets et de 8 à l'infini entre parenthèses et parenthèses.$

127. $3|x|+4\geq 1$

Résolvez des applications à valeur absolue

Dans les exercices suivants, résolvez.

128. Un brasseur de bière artisanale a besoin de 215 000 bouteilles par jour. Mais ce total peut varier jusqu'à 5 000 bouteilles. Quelle est la consommation maximale et minimale prévue par l'entreprise d'embouteillage ?

Réponse: L'utilisation minimale et maximale prévue est de 210 000 à 220 000 bouteilles

129. Chez Fancy Grocery, le poids idéal d'une miche de pain est de 16 onces. Selon la loi, le poids réel peut varier de 1,5 once par rapport à l'idéal. Quelle fourchette de poids sera acceptable pour l'inspecteur sans que la boulangerie soit condamnée à une amende ?

Test d'entraînement

Dans les exercices suivants, résolvez chaque équation.

1. $−5(2x+1)=45$

Réponse: $x=−5$

2. $\frac{1}{4}(12m+28)=6+2(3m+1)$

3. $8(3a+5)−7(4a−3)=20−3a$

Réponse: $a=41$

4. $0.1d+0.25(d+8)=4.1$

5. $14n−3(4n+5)=−9+2(n−8) $

Réponse: contradiction ; pas de solution

6. $3(3u+2)+4[6−8(u−1)]=3(u−2)$

7. $\frac{3}{4}x−\frac{2}{3}=\frac{1}{2}x+\frac{5}{6}$

Réponse: $x=6$

8. $|3x−4|=8$

9. $|2x−1|=|4x+3|$

Réponse: $x=−2,x=−13$

10. Résolvez la formule
$x+2y=5$ pour y.

Dans les exercices suivants, tracez l'inégalité sur la droite numérique et écrivez en notation par intervalles.

11. $x\geq −3.5$

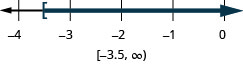
Réponse: $L'inégalité si x est supérieure ou égale à moins 3,5. La ligne numérique montre un crochet gauche à moins 3,5 et un ombrage vers la droite. La notation des intervalles va de 3,5 à l'infini entre crochets et parenthèses.$

12. $x<\frac{11}{4}$

13. $−2\leq x<5$

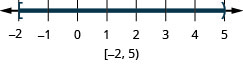
Réponse: $L'inégalité est négative : deux est inférieur ou égal à x qui est inférieur à 5. La ligne numérique montre un cercle fermé à moins 2 et un cercle ouvert à 5 avec un ombrage entre les cercles. La notation des intervalles est négative de 2 à 5 entre crochets et parenthèses.$

Dans les exercices suivants, résolvez chaque inégalité, tracez la solution sur la ligne numérique et écrivez la solution en notation par intervalles.

14. $8k\geq 5k−120$

15. $3c−10(c−2)<5c+16$

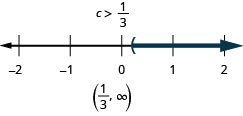
Réponse: $La solution est supérieure à un tiers. La ligne numérique montre une parenthèse gauche au tiers avec un ombrage à droite. La notation par intervalles est comprise entre un tiers et l'infini entre parenthèses.$

16. $\frac{3}{4}x−5\geq −2$et$−3(x+1)\geq 6$

17. $3(2x−3)<−5$ou$4x−1>3$

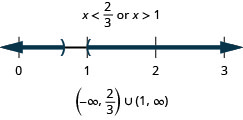
Réponse: $La solution est si x est inférieur aux deux tiers ou x est supérieur à 1. La ligne numérique montre un cercle ouvert aux deux tiers avec un ombrage à gauche et un cercle ouvert à 1 avec un ombrage à droite. La notation par intervalles est l'union de l'infini négatif aux deux tiers entre parenthèses et de 1 à l'infini entre parenthèses.$

18. $\frac{1}{2}x−3\leq 4$ou$\frac{1}{3}(x−6)\geq −2$

19. $|4x−3|\geq 5$

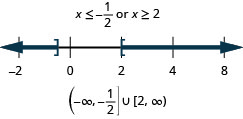
Réponse: $La solution est si x est inférieur ou égal à moins la moitié ou x est supérieur ou égal à 2. La ligne numérique montre un cercle fermé à moins la moitié avec un ombrage à sa gauche et un cercle fermé à 2 avec un ombrage à sa droite. La notation par intervalles est l'union de l'infini négatif à moins la moitié entre parenthèses et crochets et de 2 à l'infini entre parenthèses et parenthèses.$

Dans les exercices suivants, traduisez en une équation ou une inégalité et résolvez.

20. Quatre de moins de deux fois x vaut 16.

21. Détermine la longueur du côté manquant.

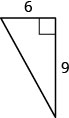
$La figure est un triangle droit avec une base de 6 unités et une hauteur de 9 unités.$

Réponse: $10.8$

22. Un chiffre est quatre de plus que deux fois un autre. Leur somme est$−47$. Trouve les numéros.

23. La somme de deux entiers impairs consécutifs est$−112$. Trouve les numéros.

Réponse: $−57,−55$

24. Marcus a acheté un téléviseur en vente pour 626,50$. Le prix initial du téléviseur était de 895$. Trouvez ⓐ le montant de la réduction et ⓑ le taux d'escompte.

25. Bonita a 2,95 dollars en pièces de dix cents en poche. Si elle a cinq cents de plus que des quarts, combien de pièces de chaque pièce possède-t-elle ?

Réponse: 12 centimes, sept quarts

26. Kim prépare huit gallons de punch à partir de jus de fruits et de soda. Le jus de fruits coûte 6,04 dollars le gallon et le soda coûte 4,28 dollars le gallon. Combien de jus de fruits et de soda devrait-elle utiliser pour que le punch coûte 5,71$ le gallon ?

27. La mesure d'un angle d'un triangle est le double de la mesure du plus petit angle. La mesure du troisième angle est trois fois la mesure du plus petit angle. Trouvez les mesures des trois angles.

Réponse: $30°,60°,90°$

28. La longueur d'un rectangle est de cinq pieds de plus que quatre fois la largeur. Le périmètre est de 60 pieds. Trouvez les dimensions du rectangle.

29. Deux avions quittent Dallas en même temps. On se dirige vers l'est à une vitesse de 428 milles à l'heure. L'autre avion se dirige vers l'ouest à une vitesse de 382 milles à l'heure. Combien d'heures leur faudra-t-il pour se retrouver à 2 025 miles l'un de l'autre ?

Réponse: $2.5$heures

30. Leon s'est rendu en voiture de sa maison de Cincinnati à celle de sa sœur à Cleveland, sur une distance de 252 miles. Cela lui a pris des$4\frac{1}{2}$ heures. Pendant la première demi-heure, la circulation était dense et, le reste du temps, sa vitesse était de cinq milles à l'heure, soit deux fois moins que dans un trafic dense. Quelle était sa vitesse dans un trafic dense ?

31. Sara dispose d'un budget de 1 000 dollars pour les costumes des 18 membres de sa troupe de théâtre musical. Quel est le montant maximum qu'elle peut dépenser pour chaque costume ?

Réponse: Au plus 55,56$ par costume.