Skip to main content
Global

2.8 : Résoudre les inégalités de valeurs absolues

  1. Last updated
  2. Save as PDF
  • Page ID
    194424

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage

    À la fin de cette section, vous serez en mesure de :

    • Résolvez des équations de
    • Résolvez les inégalités de valeur absolue avec « moins de »
    • Résolvez les inégalités de valeur absolue avec « supérieur à »
    • Résolvez des applications à valeur absolue

    Avant de commencer, répondez à ce questionnaire de préparation.

    1. Évaluez :\(−|7|\).
      Si vous avez oublié ce problème, consultez [lien].
    2. Remplissez\(<,>,<,>,\) ou\(=\) pour chacune des paires de chiffres suivantes.
      ⓐ\(|−8|\text{___}−|−8|\) ⓑ\(12\text{___}−|−12|\) ⓒ\(|−6|\text{___}−6\) ⓓ\(−(−15)\text{___}−|−15|\)
      Si vous avez oublié ce problème, consultez [lien].
    3. Simplifiez :\(14−2|8−3(4−1)|\).
      Si vous avez oublié ce problème, consultez [lien].

    Résolvez des équations de

    Alors que nous nous préparons à résoudre des équations de valeurs absolues, nous revoyons notre définition de la valeur absolue.

    VALEUR ABSOLUE

    La valeur absolue d'un nombre est sa distance par rapport à zéro sur la ligne numérique.

    La valeur absolue d'un nombre n s'écrit comme\(|n|\) et\(|n|\geq 0\) pour tous les nombres.

    Les valeurs absolues sont toujours supérieures ou égales à zéro.

    Nous avons appris qu'un nombre et son opposé se trouvent à la même distance de zéro sur la droite numérique. Comme ils ont la même distance par rapport à zéro, ils ont la même valeur absolue. Par exemple :

    • \(−5\)est à 5 unités de 0, donc\(|−5|=5\).
    • \(5\)est à 5 unités de 0, donc\(|5|=5\).

    La figure\(\PageIndex{1}\) illustre cette idée.

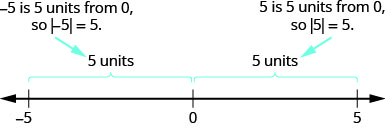
    La figure est une ligne numérique avec des coches aux points 5, 0 et 5 négatifs. La distance entre moins 5 et 0 est exprimée en 5 unités, de sorte que la valeur absolue de moins 5 est 5. La distance entre 5 et 0 est de 5 unités, donc la valeur absolue de 5 est 5.
    Figure\(\PageIndex{1}\) : Les chiffres 5 et 3\(−5\) se situent tous deux à cinq unités de zéro.

    Pour l'équation |x|=5, |x|=5, nous recherchons tous les nombres qui en font une affirmation vraie. Nous recherchons les nombres dont la distance par rapport à zéro est de 5. Nous venons de voir que 5 et −5−5 sont tous deux cinq unités à partir de zéro sur la droite numérique. Ce sont les solutions à l'équation.

    \(\begin{array} {ll} {\text{If}} &{|x|=5} \\ {\text{then}} &{x=−5\text{ or }x=5} \\ \end{array}\)

    La solution peut être simplifiée en une seule déclaration écrite\(x=\pm 5\). Cela se lit comme suit : « x est égal à 5 positif ou négatif ».

    Nous pouvons généraliser cela à la propriété suivante pour les équations de valeurs absolues.

    ÉQUATIONS DE VALEURS ABSOL

    Pour toute expression algébrique, u, et tout nombre réel positif, a,

    \[\begin{array} {ll} {\text{if}} &{|u|=a} \\ {\text{then}} &{u=−a \text{ or }u=a} \\ \nonumber \end{array}\]

    N'oubliez pas qu'une valeur absolue ne peut pas être un nombre négatif.

    Exemple\(\PageIndex{1}\)

    Résoudre :

    1. \(|x|=8\)
    2. \(|y|=−6\)
    3. \(|z|=0\)
    Solution a

    \(\begin{array} {ll} {} &{|x|=8} \\ {\text{Write the equivalent equations.}} &{x=−8 \text{ or } x=8} \\ {} &{x=\pm 8} \\ \end{array}\)

    Solution b

    \(\begin{array} {ll} {} &{|y|=−6} \\ {} &{\text{No solution}} \\ \end{array}\)
    Comme une valeur absolue est toujours positive, il n'existe aucune solution à cette équation.

    Solution c

    \(\begin{array} {ll} {} &{|z|=0} \\ {\text{Write the equivalent equations.}} &{z=−0\text{ or }z=0} \\ {\text{Since }−0=0,} &{z=0} \\ \end{array}\)
    Les deux équations nous indiquent que z=0z=0 et il n'y a donc qu'une seule solution.

    EXERCICE\(\PageIndex{2}\)

    Résoudre :

    1. \(|x|=2\)
    2. \(|y|=−4\)
    3. \(|z|=0\)
    Répondez à une

    \(\pm 2\)

    Réponse b

    aucune solution

    Réponse c

    0

    EXERCICE\(\PageIndex{3}\)

    Résoudre :

    1. \(|x|=11\)
    2. \(|y|=−5\)
    3. \(|z|=0\)
    Répondez à une

    \(\pm 11\)

    Réponse b

    aucune solution

    Réponse c

    0

    Pour résoudre une équation de valeur absolue, nous isolons d'abord l'expression de la valeur absolue en utilisant les mêmes procédures que celles que nous avons utilisées pour résoudre des équations linéaires. Une fois que nous avons isolé l'expression de valeur absolue, nous la réécrivons sous forme de deux équations équivalentes.

    Comment résoudre des équations de valeurs absolues

    Exemple\(\PageIndex{4}\)

    Résoudre\(|5x−4|−3=8\).

    Solution

    L'étape 1 consiste à isoler l'expression de valeur absolue. La différence entre la valeur absolue de la quantité 5 x moins 4 et 3 est égale à 8. Ajoutez-en 3 des deux côtés. Le résultat est que la valeur absolue de la quantité 5 x moins 4 est égale à 11.L'étape 2 consiste à écrire les équations équivalentes, 5 x moins 4 est égal à moins 11 et 5 x moins 4 est égal à 11.L'étape 3 consiste à résoudre chaque équation. Ajoutez 4 de chaque côté. 5 x est égal à moins 7 ou 5 x est égal à 15. Divisez chaque côté par 5. Le résultat est que x est égal à moins sept cinquièmes ou x est égal à 3.L'étape 4 consiste à vérifier chaque solution. Remplacez 3 et moins sept cinquièmes dans l'équation d'origine, la différence entre la valeur absolue de la quantité 5 x moins 4 et 3 est égale à 8. Remplacez 3 par x. La différence entre la valeur absolue de la quantité 5 fois 3 moins 4 et 3 est-elle égale à 8 ? La différence entre la valeur absolue de la quantité 15 moins 4 et 3 est-elle égale à 8 ? La différence entre la valeur absolue du 11 et du 3 est-elle égale à 8 ? Est-ce que 11 moins 3 est égal à 8 ? 8 est égal à 8, donc la solution x est égale à 3 contrôles. Remplacez x. par moins sept cinquièmes. La différence entre la valeur absolue de la quantité 5 fois moins sept cinquièmes moins 4 et 3 est-elle égale à 8 ? La différence entre la valeur absolue de la quantité négative 7 moins 4 et 3 est-elle égale à 8 ? La différence entre la valeur absolue du négatif 11 et celle de 3 est-elle égale à 8 ? Est-ce que 11 moins 3 est égal à 8 ? 8 est égal à 8, donc la solution x est égale à sept cinquièmes de contrôles négatifs.

    EXERCICE\(\PageIndex{5}\)

    Résoudre :\(|3x−5|−1=6\).

    Réponse

    \(x=4, \space x=−\frac{2}{3}\)

    EXERCICE\(\PageIndex{6}\)

    Résoudre :\(|4x−3|−5=2\).

    Réponse

    \(x=−1,\space x=\frac{5}{2}\)

    Les étapes de résolution d'une équation de valeur absolue sont résumées ici.

    RÉSOUDRE DES ÉQUATIONS DE VALEURS ABSOLUES
    1. Isolez l'expression de valeur absolue.
    2. Écrivez les équations équivalentes.
    3. Résolvez chaque équation.
    4. Vérifiez chaque solution.
    Exemple\(\PageIndex{7}\)

    Résoudre\(2|x−7|+5=9\).

    Solution
      \(2|x−7|+5=9\)
    Isolez l'expression de valeur absolue. \(2|x−7|=4\)
      \(|x−7|=2\)
    Écrivez les équations équivalentes. \(x−7=−2\)ou\(x−7=2\)
    Résolvez chaque équation. \(x=5\)ou\(x=9\)
    Vérifiez :
    .    		  
    Exercice\(\PageIndex{8}\)

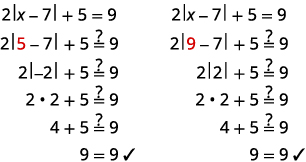
    Résoudre :\(3|x−4|−4=8\).

    Réponse

    \(x=8,\space x=0\)

    Exercice\(\PageIndex{9}\)

    Résoudre :\(2|x−5|+3=9\).

    Réponse

    \(x=8,\space x=2\)

    N'oubliez pas qu'une valeur absolue est toujours positive !

    Exemple\(\PageIndex{10}\)

    Résoudre :\(|\frac{2}{3}x−4|+11=3\).

    Solution

    \(\begin{array} {ll} {} &{|\frac{2}{3}x−4|=−8} \\ {\text{Isolate the absolute value term.}} &{|\frac{2}{3}x−4|=−8} \\ {\text{An absolute value cannot be negative.}} &{\text{No solution}} \\ \end{array}\)

    Exercice\(\PageIndex{11}\)

    Résoudre :\(|\frac{3}{4}x−5|+9=4\).

    Réponse

    Aucune solution

    Exercice\(\PageIndex{12}\)

    Résoudre :\(|\frac{5}{6}x+3|+8=6\).

    Réponse

    Aucune solution

    Certaines de nos équations de valeurs absolues peuvent être de la forme\(|u|=|v|\) où u et v sont des expressions algébriques. Par exemple,\(|x−3|=|2x+1|\).

    Comment pourrions-nous les résoudre ? Si deux expressions algébriques sont égales en valeur absolue, elles sont soit égales l'une à l'autre, soit négatives l'une par rapport à l'autre. La propriété des équations de valeurs absolues indique que pour toute expression algébrique, u, et un nombre réel positif, a, si\(|u|=a\), alors\(u=−a\) ou\(u=a\).

    Cela nous indique que

    \ (\ begin {array} {llll}
    {\ text {if}} & {|u|=|v|} & {} & {} & {}
     \ \ {\ text {alors}} & {|u|=v} & {\ text {ou}} & {|u|=−v}
    \ \ {\ text {et ainsi de suite}} & {u=v \ text {ou} u = −v} & {\ text {ou}} & {u=−v \ text {ou} u = − (−v)}
     \ \ \ end {tableau} \)

    Cela nous amène à la propriété suivante pour les équations à deux valeurs absolues.

    ÉQUATIONS À DEUX VALEURS ABSOLUES

    Pour toutes les expressions algébriques, u et v,

    \[\begin{array} {ll} {\text{if}} &{|u|=|v|} \\ {\text{then}} &{u=−v\text{ or }u=v} \\ \nonumber \end{array}\]

    Lorsque nous prenons le contraire d'une quantité, nous devons faire attention aux signes et ajouter des parenthèses si nécessaire.

    Exemple\(\PageIndex{13}\)

    Résoudre :\(|5x−1|=|2x+3|\).

    Solution

    \(\begin{array} {ll} {} &{} &{|5x−1|=|2x+3|} &{} \\ {} &{} &{} &{} \\ {\text{Write the equivalent equations.}} &{5x−1=−(2x+3)} &{\text{or}} &{5x−1=2x+3} \\ {} &{5x−1=−2x−3} &{\text{or}} &{3x−1=3} \\ {\text{Solve each equation.}} &{7x−1=−3} &{} &{3x=4} \\ {} &{7x=−2} &{} &{x=43} \\ {} &{x=−27} &{\text{or}} &{x=43} \\ {\text{Check.}} &{} &{} &{} \\ {\text{We leave the check to you.}} &{} &{} &{} \\ \end{array}\)

    Exercice\(\PageIndex{14}\)

    Résoudre :\(|7x−3|=|3x+7|\).

    Réponse

    \(x=−\frac{2}{5}, \space x=\frac{5}{2}\)

    Exercice\(\PageIndex{15}\)

    Résoudre :\(|6x−5|=|3x+4|\).

    Réponse

    \(x=3, x=19\)

    Résolvez les inégalités de valeur absolue avec « Moins de »

    Voyons maintenant ce qui se passe lorsque nous avons une inégalité de valeur absolue. Tout ce que nous avons appris sur la résolution des inégalités est toujours valable, mais nous devons tenir compte de l'impact de la valeur absolue sur notre travail. Encore une fois, nous examinerons notre définition de la valeur absolue. La valeur absolue d'un nombre est sa distance par rapport à zéro sur la ligne numérique. Pour l'équation\(|x|=5\), nous avons vu que 5 et\(−5\) sont tous deux cinq unités à partir de zéro sur la droite numérique. Ce sont les solutions à l'équation.

    \[\begin{array} {lll} {} &{|x|=5} &{} \\ {x=−5} &{\text{or}} &{x=5} \\ \nonumber \end{array}\]

    Qu'en est-il de l'inégalité\(|x|\leq 5\) ? Où sont les nombres dont la distance est inférieure ou égale à 5 ? Nous savons\(−5\) et 5 sont tous deux cinq unités à partir de zéro. Tous les nombres compris entre\(−5\) 1 et 5 sont inférieurs à cinq unités à partir de zéro (Figure\(\PageIndex{2}\)).

    La figure est une ligne numérique avec 5, 0 et 5 négatifs affichés. Il y a un crochet gauche à moins 5 et un crochet droit à 5. La distance entre 5 et 0 est donnée en 5 unités et la distance entre 5 et 0 est donnée en 5 unités. Il montre que si la valeur absolue de x est inférieure ou égale à 5, alors moins 5 est inférieur ou égal à x qui est inférieur ou égal à 5.
    Chiffre\(\PageIndex{2}\).

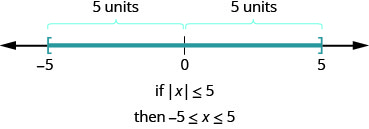
    D'une manière plus générale, nous pouvons voir que si\(|u|\leq a\), alors\(−a\leq u\leq a\) (Figure\(\PageIndex{3}\)).

    La figure est une ligne numérique avec un 0 négatif et un affiché. Il y a un crochet gauche à moins a et un crochet droit à a. La distance entre moins a et 0 est donnée en unités et la distance entre a et 0 est donnée en unités. Il montre que si la valeur absolue de u est inférieure ou égale à a, alors la valeur négative de a est inférieure ou égale à u qui est inférieur ou égal à a.
    Chiffre\(\PageIndex{3}\).

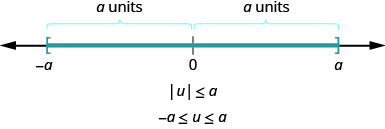
    Ce résultat est résumé ici.

    INÉGALITÉS DE VALEUR ABSOLUE AVEC\(<\) OR \(\leq\)

    Pour toute expression algébrique, u, et tout nombre réel positif, a,

    \[ \text{if} \quad |u|<a, \quad \text{then} \space −a<u<a \\ \text{if} \quad |u|\leq a, \quad \text{then} \space−a\leq u\leq a \nonumber\]

    Après avoir résolu une inégalité, il est souvent utile de vérifier certains points pour voir si la solution a du sens. Le graphique de la solution divise la ligne numérique en trois sections. Choisissez une valeur dans chaque section et remplacez-la par l'inégalité d'origine pour voir si cela rend l'inégalité vraie ou non. Bien que cette vérification ne soit pas complète, elle permet souvent de vérifier la solution.

    Exemple\(\PageIndex{16}\)

    Résoudre\(|x|<7\). Tracez la solution et écrivez la solution en notation par intervalles.

    Solution
      .
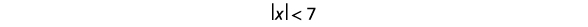
    Écrivez l'inégalité équivalente. .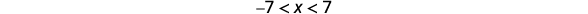
    Tracez la solution. .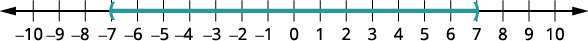
    Écrivez la solution en utilisant la notation par intervalles. .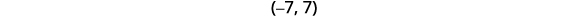

    Vérifiez :

    Pour vérifier, vérifiez une valeur dans chaque section de la ligne numérique indiquant la solution. Choisissez des nombres tels que −8, −8, 1 et 9.

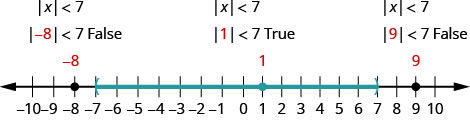
    La figure est une ligne numérique avec une parenthèse gauche à moins 7, une parenthèse droite à 7 et un ombrage entre les parenthèses. Les valeurs négatives 8, 1 et 9 sont marquées par des points. La valeur absolue de moins 8 est inférieure à 7 est fausse. Elle ne satisfait pas à la valeur absolue de x inférieure à 7. La valeur absolue de 1 est inférieure à 7, c'est vrai. Il vérifie que la valeur absolue de x est inférieure à 7. La valeur absolue de 9 est inférieure à 7 est fausse. Elle ne satisfait pas à la valeur absolue de x inférieure à 7.

    EXERCICE\(\PageIndex{17}\)

    Représentez graphiquement la solution et écrivez la solution en notation par intervalles :\(|x|<9\).

    Réponse

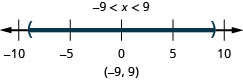
    La solution est négative ; 9 est inférieur à x, qui est inférieur à 9. La ligne numérique montre les cercles ouverts aux valeurs négatives 9 et 9 avec un ombrage entre les cercles. La notation des intervalles est négative de 9 à 9 entre parenthèses.

    EXERCICE\(\PageIndex{18}\)

    Représentez graphiquement la solution et écrivez la solution en notation par intervalles :\(|x|<1\).

    Réponse

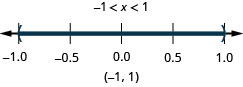
    La solution est négative, 1 est inférieur à x qui est inférieur à 1. La ligne numérique montre les cercles ouverts aux valeurs négatives 1 et 1 avec un ombrage entre les cercles. La notation des intervalles est négative de 1 à 1 entre parenthèses.

    Exemple\(\PageIndex{19}\)

    Résoudre\(|5x−6|\leq 4\). Tracez la solution et écrivez la solution en notation par intervalles.

    Solution
    Étape 1. Isolez l'expression de valeur absolue.
    Elle est isolée.    		 \(|5x−6|\leq 4\)
    Étape 2. Ecrivez l'inégalité composée équivalente. \(−4\leq 5x−6\leq 4\)
    Étape 3. Résolvez l'inégalité composée. \(2\leq 5x\leq 10\)
    \(\frac{2}{5}\leq x\leq 2\)
    Étape 4. Tracez la solution. .
    Étape 5. Écrivez la solution en utilisant la notation par intervalles. \([\frac{2}{5}, 2]\)
    Chèque :
    Le chèque vous est laissé.    		  
    EXERCICE\(\PageIndex{20}\)

    Résoudre\(|2x−1|\leq 5\). Représentez graphiquement la solution et écrivez la solution en notation par intervalles :

    Réponse

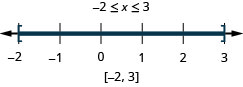
    La solution est négative, 2 est inférieure ou égale à x qui est inférieur ou égal à 3. La ligne numérique montre les cercles fermés aux points 2 et 3 négatifs, avec un ombrage entre les cercles. La notation des intervalles est négative de 2 à 3 entre parenthèses.

    EXERCICE\(\PageIndex{21}\)

    Résoudre\(|4x−5|\leq 3\). Représentez graphiquement la solution et écrivez la solution en notation par intervalles :

    Réponse

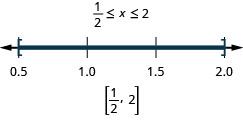
    La solution est que la moitié est inférieure ou égale à x qui est inférieur ou égal à 2. La ligne numérique montre des cercles fermés à la moitié et à 2, avec un ombrage entre les cercles. La notation par intervalles est comprise entre un demi et deux entre crochets.

    RÉSOLVEZ LES INÉGALITÉS DE VALEUR ABSOL\(<\) OR \(\leq\)
    1. Isolez l'expression de valeur absolue.
    2. Ecrivez l'inégalité composée équivalente.

      \[\begin{array} {lll} {|u|<a} &{\quad \text{is equivalent to}} &{−a<u<a} \\ {|u|\leq a} &{\quad \text{is equivalent to}} &{−a\leq u\leq a} \\ \nonumber \end{array}\]

    3. Résolvez l'inégalité composée.
    4. Tracez la solution
    5. Écrivez la solution en utilisant la notation par intervalles.

    Résolvez les inégalités de valeur absolue avec « supérieur à »

    Que se passe-t-il pour les inégalités de valeur absolue qui sont « supérieures à » ? Encore une fois, nous examinerons notre définition de la valeur absolue. La valeur absolue d'un nombre est sa distance par rapport à zéro sur la ligne numérique.

    Nous avons commencé par l'inégalité\(|x|\leq 5\). Nous avons vu que les nombres dont la distance est inférieure ou égale à cinq par rapport à zéro sur la ligne numérique étaient\(−5\) et 5 et tous les nombres compris entre\(−5\) et 5 (Figure\(\PageIndex{4}\)).

    La figure est une ligne numérique avec 5, 0 et 5 négatifs affichés. Il y a un crochet droit à moins 5 avec un ombrage à droite et un crochet droit à 5 avec un ombrage à gauche. Il montre que si la valeur absolue de x est inférieure ou égale à 5, alors moins 5 est inférieur ou égal à x est inférieur ou égal à 5.
    Chiffre\(\PageIndex{4}\).

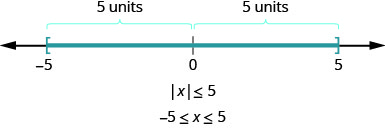
    Nous voulons maintenant examiner l'inégalité\(|x|\geq 5\). Où sont les nombres dont la distance par rapport à zéro est supérieure ou égale à cinq ?

    Encore une fois, les deux\(−5\) et 5 sont cinq unités à partir de zéro et sont donc inclus dans la solution. Les nombres dont la distance par rapport à zéro est supérieure à cinq unités seraient inférieurs\(−5\) et supérieurs à 5 sur la ligne numérique (Figure\(\PageIndex{5}\)).

    La figure est une ligne numérique avec 5, 0 et 5 négatifs affichés. Il y a un crochet droit à moins 5 avec un ombrage à gauche et un crochet gauche à 5 avec un ombrage à droite. La distance entre 5 et 0 est donnée en 5 unités et la distance entre 5 et 0 est donnée en 5 unités. Elle montre que si la valeur absolue de x est supérieure ou égale à 5, alors x est inférieur ou égal à moins 5 ou x est supérieur ou égal à 5.
    Chiffre\(\PageIndex{5}\).

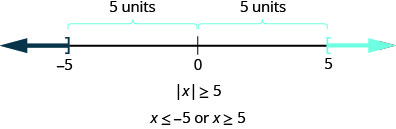
    D'une manière plus générale, nous pouvons voir si\(|u|\geq a\), alors\(u\leq −a\) ou\(u\leq a\). Voir la figure.

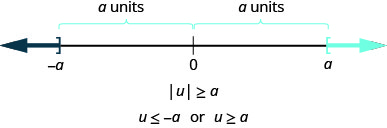
    La figure est une ligne numérique avec un a, 0 et un négatif affiché. Il y a un crochet droit au niveau du négatif a qui a un ombrage à gauche et un crochet gauche au point a avec un ombrage à sa droite. La distance entre a et 0 est donnée en unités et la distance entre a et 0 est donnée en unités. Il montre que si la valeur absolue de u est supérieure ou égale à a, alors u est inférieur ou égal à moins a ou u est supérieur ou égal à a.
    Chiffre\(\PageIndex{6}\).

    Ce résultat est résumé ici.

    INÉGALITÉS DE VALEUR ABSOLUE AVEC\(>\) OR \(\geq\)

    Pour toute expression algébrique, u, et tout nombre réel positif, a,

    \[\begin{array} {lll} {\text{if}} &{\quad |u|>a,} &{\quad \text{then } u<−a \text{ or } u>a} \\ {\text{if}} &{\quad |u|\geq a,} &{\quad \text{then } u\leq −a \text{ or } u\geq a} \\ \nonumber \end{array}\]

    Exemple\(\PageIndex{22}\)

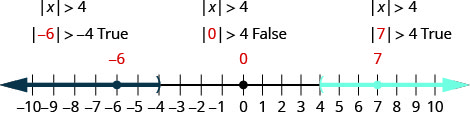
    Résoudre\(|x|>4\). Tracez la solution et écrivez la solution en notation par intervalles.

    Solution
      \(|x|>4\)
    Écrivez l'inégalité équivalente. \(x<−4\)ou\(x>4\)
    Tracez la solution. .
    Écrivez la solution en utilisant la notation par intervalles. \((−\inf ,−4)\cup (4,\inf )\)
    Vérifiez :  

    Pour vérifier, vérifiez une valeur dans chaque section de la ligne numérique indiquant la solution. Choisissez des nombres tels que −6, −6, 0 et 7.

    La figure est une ligne numérique avec une parenthèse droite à moins 4 avec un ombrage à gauche et une parenthèse gauche à 4 ombrée à droite. Les valeurs négatives 6, 0 et 7 sont marquées par des points. La valeur absolue de moins 6 est supérieure à celle de moins 4 est vraie. Il ne satisfait pas à la valeur absolue de x supérieur à 4. La valeur absolue de 0 est supérieure à 4 est fausse. Il ne satisfait pas à la valeur absolue de x supérieur à 4. La valeur absolue de 7 est inférieure à 4 est vraie. Il vérifie que la valeur absolue de x est supérieure à 4.

    EXERCICE\(\PageIndex{23}\)

    Résoudre\(|x|>2\). Tracez la solution et écrivez la solution en notation par intervalles.

    Réponse

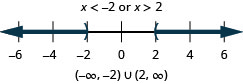
    La solution est si x est inférieur à moins 2 ou x est supérieur à 2. La ligne numérique montre un cercle ouvert à moins 2 avec un ombrage à gauche et un cercle ouvert à 2 avec un ombrage à sa droite. La notation par intervalles est l'union de l'infini négatif à moins 2 entre parenthèses et de 2 à l'infini entre parenthèses.

    EXERCICE\(\PageIndex{24}\)

    Résoudre\(|x|>1\). Tracez la solution et écrivez la solution en notation par intervalles.

    Réponse

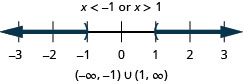
    La solution est si x est inférieur à moins 1 ou x est supérieur à 1. La ligne numérique montre un cercle ouvert à moins 1 avec un ombrage à gauche et un cercle ouvert à 1 avec un ombrage à sa droite. La notation par intervalles est l'union de l'infini négatif à moins 1 entre parenthèses et de 1 à l'infini entre parenthèses.

    Exemple\(\PageIndex{25}\)

    Résoudre\(|2x−3|\geq 5\). Tracez la solution et écrivez la solution en notation par intervalles.

    Solution
      \(|2x−3|\geq 5\)
    Étape 1. Isolez l'expression de valeur absolue. Elle est isolée.  
    Étape 2. Ecrivez l'inégalité composée équivalente. \(2x−3\leq −5\)ou\(2x−3\geq 5\)
    Étape 3. Résolvez l'inégalité composée. \(2x\leq −2\)ou\(2x\geq 8\)
    \(x\leq −1\) ou\(x\geq 4\)
    Étape 4. Tracez la solution. .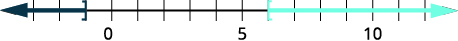
    Étape 5. Écrivez la solution en utilisant la notation par intervalles. \((−\inf ,−1]\cup [4,\inf )\)
    Chèque :
    Le chèque vous est laissé.    		  
    EXERCICE\(\PageIndex{26}\)

    Résoudre\(|4x−3|\geq 5\). Tracez la solution et écrivez la solution en notation par intervalles.

    Réponse

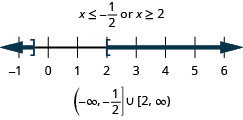
    La solution est si x est inférieur ou égal à moins la moitié ou x est supérieur ou égal à 2. La ligne numérique montre un cercle fermé à moins la moitié avec un ombrage à sa gauche et un cercle fermé à 2 avec un ombrage à sa droite. La notation par intervalles est l'union de l'infini négatif à moins la moitié entre parenthèses et crochets et de 2 à l'infini entre parenthèses et parenthèses.

    EXERCICE\(\PageIndex{27}\)

    Résoudre\(|3x−4|\geq 2\). Tracez la solution et écrivez la solution en notation par intervalles.

    Réponse

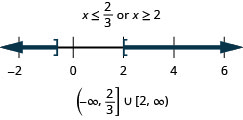
    La solution est si x est inférieur ou égal aux deux tiers ou x est supérieur ou égal à 2. La ligne numérique montre un cercle fermé aux deux tiers avec un ombrage à gauche et un cercle fermé à 2 avec un ombrage à droite. La notation par intervalles est l'union de l'infini négatif aux deux tiers entre parenthèses et crochets et de 2 à l'infini entre parenthèses et parenthèses.

    RÉSOLVEZ LES INÉGALITÉS DE VALEUR ABSOL\(>\) OR \(\geq\).
    1. Isolez l'expression de valeur absolue.
    2. Ecrivez l'inégalité composée équivalente.

      \ [\ begin {array} {lll}
      {|u| >a} & {\ quad \ text {est équivalent à}} & {u<−a \ quad \ text {ou} \ quad u>a}
       \ \ {|u| \ geq a} & {\ quad \ text {est équivalent à}} & {u \ leq −a \ quad \ text {ou} \ quad u \ geq a}
      \ \ {|u| >a} & {\ quad \ text {est équivalent à}} & {u<−a \ quad \ text {ou} \ quad u>a}
       \ \ {|u| \ geq a} & {\ quad \ text {est équivalent à}} & {u \ leq −a \ quad \ text {ou} \ quad u \ geq a}
       \ \ \ nonumber \ end {array} \]

    3. Résolvez l'inégalité composée.
    4. Tracez la solution
    5. Écrivez la solution en utilisant la notation par intervalles.

    Résolvez des applications à valeur absolue

    Les inégalités de valeur absolue sont souvent utilisées dans le processus de fabrication. Un article doit être fabriqué avec des spécifications presque parfaites. Il existe généralement une certaine tolérance de différence par rapport aux spécifications autorisées. Si la différence par rapport aux spécifications dépasse la tolérance, l'article est rejeté.

    \[|\text{actual-ideal}|\leq \text{tolerance} \nonumber\]

    Exemple\(\PageIndex{28}\)

    Le diamètre idéal d'une tige nécessaire à une machine est de 60 mm. Le diamètre réel peut varier du diamètre idéal en\(0.075\) mm. Quelle gamme de diamètres sera acceptable pour le client sans que la tige ne soit rejetée ?

    Solution

    \(\begin{array} {ll} {} &{\text{Let }x=\text{ the actual measurement}} \\ {\text{Use an absolute value inequality to express this situation.}} &{|\text{actual-ideal}|\leq \text{tolerance}} \\ {} &{|x−60|\leq 0.075} \\ {\text{Rewrite as a compound inequality.}} &{−0.075\leq x−60\leq 0.075} \\ {\text{Solve the inequality.}} &{59.925\leq x\leq 60.075} \\ {\text{Answer the question.}} &{\text{The diameter of the rod can be between}} \\ {} &{59.925 mm \text{ and } 60.075 mm.} \\ \end{array}\)

    Exercice\(\PageIndex{29}\)

    Le diamètre idéal d'une tige nécessaire à une machine est de 80 mm. Le diamètre réel peut varier de 0,009 mm par rapport au diamètre idéal. Quelle gamme de diamètres sera acceptable pour le client sans que la tige ne soit rejetée ?

    Réponse

    Le diamètre de la tige peut être compris entre 79,991 et 80,009 mm.

    Exercice\(\PageIndex{30}\)

    Le diamètre idéal d'une tige nécessaire à une machine est de 75 mm. Le diamètre réel peut varier de 0,05 mm par rapport au diamètre idéal. Quelle gamme de diamètres sera acceptable pour le client sans que la tige ne soit rejetée ?

    Réponse

    Le diamètre de la tige peut être compris entre 74,95 et 75,05 mm.

    Accédez à cette ressource en ligne pour obtenir des instructions et des exercices supplémentaires sur la résolution d'équations et d'inégalités linéaires en valeur absolue.

    • Résolution d'équations et d'inégalités linéaires en valeur absolue

    Concepts clés

    • Valeur absolue
      La valeur absolue d'un nombre est sa distance par rapport à 0 sur la ligne numérique.
      La valeur absolue d'un nombre n s'écrit comme\(|n|\) et\(|n|\geq 0\) pour tous les nombres.
      Les valeurs absolues sont toujours supérieures ou égales à zéro.
    • Équations de valeurs absolues
      Pour toute expression algébrique, u, et tout nombre réel positif, a,
      \(\begin{array} {ll} {\text{if}} &{\quad |u|=a} \\ {\text{then}} &{\quad u=−a \text{ or } u=a} \\ \end{array}\)
      Rappelez-vous qu'une valeur absolue ne peut pas être un nombre négatif.
    • Comment résoudre des équations de valeurs absolues
      1. Isolez l'expression de valeur absolue.
      2. Écrivez les équations équivalentes.
      3. Résolvez chaque équation.
      4. Vérifiez chaque solution.
    • Équations à deux valeurs absolues
      Pour toutes les expressions algébriques, u et v,
      \(\begin{array} {ll} {\text{if}} &{\quad |u|=|v|} \\ {\text{then}} &{\quad u=−v \text{ or } u=v} \\ \end{array}\)
    • Inégalités de valeurs absolues avec\(<\) ou\(\leq\)
      pour toute expression algébrique, u, et tout nombre réel positif, a,
      \(\begin{array} {llll} {\text{if}} &{\quad |u|=a} &{\quad \text{then}} &{−a<u<a} \\ {\text{if}} &{\quad |u|\leq a} &{\quad \text{then}} &{−a\leq u\leq a} \\ \end{array}\)
    • Comment résoudre les inégalités de valeur absolue avec\(<\) ou\(\leq\)
      1. Isolez l'expression de valeur absolue.
      2. Ecrivez l'inégalité composée équivalente.
        \(\begin{array} {lll} {|u|<a} &{\quad \text{is equivalent to}} &{\quad −a<u<a} \\ {|u|\leq a} &{\quad \text{is equivalent to}} &{\quad −a\leq u\leq a} \\ \end{array}\)
      3. Résolvez l'inégalité composée.
      4. Tracez la solution
      5. Écrivez la solution en utilisant la notation par intervalles
    • Inégalités de valeurs absolues avec\(>\) ou\(\geq\)
      pour toute expression algébrique, u, et tout nombre réel positif, a,
      \(\begin{array} {lll} {\text{if}} &{\quad |u|>a,} &{\text{then } u<−a\text{ or }u>a} \\ {\text{if}} &{\quad |u|\geq a,} &{\text{then } u\leq −a\text{ or }u\geq a} \\ \end{array}\)
    • Comment résoudre les inégalités de valeur absolue avec\(>\) ou\(\geq\)
      1. Isolez l'expression de valeur absolue.
      2. Ecrivez l'inégalité composée équivalente.
        \(\begin{array} {lll} {|u|>a} &{\quad \text{is equivalent to}} &{\quad u<−a\text{ or }u>a} \\ {|u|\geq a} &{\quad \text{is equivalent to}} &{\quad u\leq −a\text{ or }u\geq a} \\ \end{array}\)
      3. Résolvez l'inégalité composée.
      4. Tracez la solution
      5. Écrivez la solution en utilisant la notation par intervalles