Skip to main content
Global

2.7 : Résoudre les inégalités composées

  1. Last updated
  2. Save as PDF
  • Page ID
    194454

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage

    À la fin de cette section, vous serez en mesure de :

    • Résolvez les inégalités composées avec « et »
    • Résolvez les inégalités composées avec « ou »
    • Résoudre des applications présentant des inégalités composées

    Avant de commencer, répondez à ce questionnaire de préparation.

    1. Simplifiez :\(\frac{2}{5}(x+10)\).
      Si vous avez oublié ce problème, consultez [lien].
    2. Simplifiez :\(−(x−4)\).
      Si vous avez oublié ce problème, consultez [lien].

    Résolvez les inégalités composées avec « et »

    Maintenant que nous savons comment résoudre les inégalités linéaires, l'étape suivante consiste à examiner les inégalités composées. Une inégalité composée est constituée de deux inégalités reliées par le mot « et » ou par le mot « ou ». Par exemple, les inégalités suivantes sont des inégalités composées.

    \[\begin{array} {lll} {x+3>−4} &{\text{and}} &{4x−5\leq 3} \\ {2(y+1)<0} &{\text{or}} &{y−5\geq −2} \\ \end{array} \nonumber\]

    INÉGALITÉ COMPOSÉE

    Une inégalité composée est constituée de deux inégalités reliées par le mot « et » ou par le mot « ou ».

    Résoudre une inégalité composée signifie trouver toutes les valeurs de la variable qui font de l'inégalité composée une affirmation vraie. Nous résolvons les inégalités composées en utilisant les mêmes techniques que celles que nous avons utilisées pour résoudre les inégalités linéaires. Nous résolvons chaque inégalité séparément, puis nous examinons les deux solutions.

    Pour résoudre une inégalité composée à l'aide du mot « et », nous recherchons tous les chiffres qui confirment les deux inégalités. Pour résoudre une inégalité composée à l'aide du mot « ou », nous recherchons tous les nombres qui confirment que l'une ou l'autre inégalité est vraie.

    Commençons par les inégalités composées par « et ». Notre solution sera les chiffres qui sont des solutions aux deux inégalités, appelées intersection des deux inégalités. Supposons que l'intersection de deux rues, c'est-à-dire la partie où les rues se chevauchent, appartient aux deux rues.

    La figure est une illustration de deux rues dont l'intersection est ombrée.

    Pour trouver la solution à une inégalité composée « et », nous examinons les graphes de chaque inégalité, puis nous trouvons les nombres qui appartiennent aux deux graphes, là où les graphes se chevauchent.

    Pour l'inégalité composée\(x>−3\) et\(x\leq 2\), nous graphions chaque inégalité. Nous cherchons ensuite où les graphiques « se chevauchent ». Les nombres ombrés sur les deux graphiques seront ombrés sur le graphique de la solution de l'inégalité composée. Voir la figure\(\PageIndex{1}\).

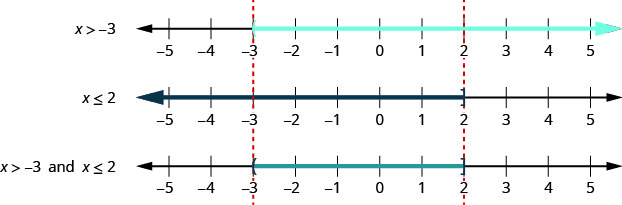
    La figure montre que le graphique de x est supérieur à moins 3 avec une parenthèse gauche à moins 3 et un ombrage à sa droite, le graphique de x est inférieur ou égal à 2 avec un crochet à 2 et un ombrage à sa gauche, et le graphique de x est supérieur à moins 3 et x est inférieur ou égal à 2 avec une parenthèse gauche. à moins 3 et une parenthèse droite à 2 et un ombrage entre moins 3 et 2. Les points 3 et 2 négatifs sont marqués par des lignes sur chaque ligne numérique.
    Figurine\(\PageIndex{1}\)

    Nous pouvons voir que les nombres entre\(−3\) et\(2\) sont ombrés sur les deux premiers graphiques. Ils seront ensuite ombrés sur le graphique de la solution.

    Le nombre n'\(−3\)est pas ombré sur le premier graphique et, comme il n'est pas ombré sur les deux graphiques, il n'est pas inclus sur le graphique de solution.

    Le chiffre deux est ombré sur les premier et deuxième graphiques. Par conséquent, il doit être ombré sur le graphe des solutions.

    C'est ainsi que nous allons montrer notre solution dans les prochains exemples.

    Exemple\(\PageIndex{1}\)

    Résolvez\(6x−3<9\) et\(2x+7\geq 3\). Tracez la solution et écrivez la solution en notation par intervalles.

    Réponse
      \(6x−3<9\) et \(2x+9\geq 3\)
    Étape 1. Résolvez chaque
    inégalité.    		 \(6x−3<9\)   \(2x+9\geq 3\)
      \(6x<12\)   \(2x\geq −6\)
      \(x<2\) et \(x\geq −3\)
    Étape 2. Tracez chaque solution. Représentez ensuite graphiquement les chiffres qui confirment les deux inégalités. Le graphique final affichera tous les chiffres qui confirment les deux inégalités : les chiffres ombrés sur les deux premiers graphiques. .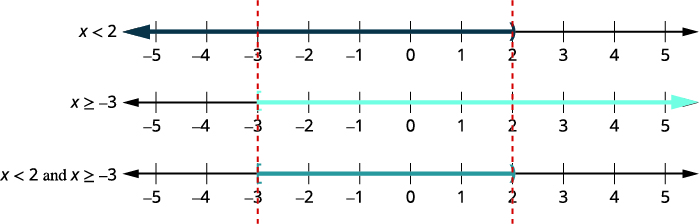
    Étape 3. Écrivez la solution en notation par intervalles. \([−3,2)\)
    Tous les chiffres qui confirment les deux inégalités constituent la solution à l'inégalité composée.
    Exemple\(\PageIndex{2}\)

    Résolvez l'inégalité composée. Représentez graphiquement la solution et écrivez la solution en notation par intervalles :\(4x−7<9\) et\(5x+8\geq 3\).

    Réponse

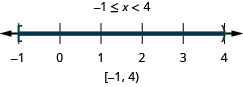
    La solution est négative : 1 est inférieur ou égal à x qui est inférieur à 4. Sur une ligne numérique, il est représenté par un cercle fermé à moins 1 et un cercle ouvert à 4, avec un ombrage entre les cercles fermés et ouverts. Sa notation par intervalles est négative de 1 à 4 entre crochets et parenthèses.

    Exemple\(\PageIndex{3}\)

    Résolvez l'inégalité composée. Représentez graphiquement la solution et écrivez la solution en notation par intervalles :\(3x−4<5\) et\(4x+9\geq 1\).

    Réponse

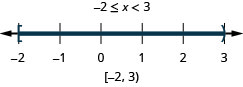
    La solution est négative, 2 est inférieure ou égale à x qui est inférieur à 3. Sur une ligne numérique, il est représenté par un cercle fermé au négatif 2 et un cercle ouvert au point 3, avec un ombrage entre les cercles fermés et ouverts. Sa notation par intervalles est négative de 2 à 3 entre crochets et parenthèses.

    RÉSOLVEZ UNE INÉGALITÉ COMPOSÉE AVEC « ET ».
    1. Résolvez chaque inégalité.
    2. Tracez chaque solution. Représentez ensuite graphiquement les chiffres qui confirment les deux inégalités.
      Ce graphique montre la solution à l'inégalité composée.
    3. Écrivez la solution en notation par intervalles.
    Exemple\(\PageIndex{4}\)

    Résolvez\(3(2x+5)\leq 18\) et\(2(x−7)<−6\). Tracez la solution et écrivez la solution en notation par intervalles.

    Réponse
      \(3(2x+5)\leq 18\) et \(2(x−7)<−6\)
    Résolvez chaque
    inégalité.    		 \(6x+15\leq 18\)   \(2x−14<−6\)
      \(6x\leq 3\)   \(2x<8\)
      \(x\leq \frac{1}{2}\) et \(x<4\)
    Tracez chaque
    solution.    		 .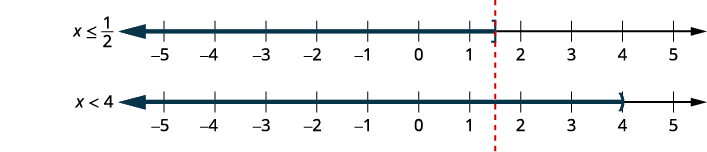
    Représentez graphiquement
    les chiffres qui confirment
    les deux inégalités.    		 .
    Écrivez la solution
    en notation par intervalles.    		 \((−\infty, \frac{1}{2}]\)
    Exemple\(\PageIndex{5}\)

    Résolvez l'inégalité composée. Représentez graphiquement la solution et écrivez la solution en notation par intervalles :\(2(3x+1)\leq 20\) et\(4(x−1)<2\).

    Réponse

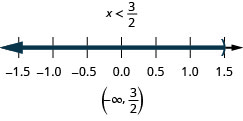
    La solution est que x est inférieur à trois moitiés. Sur une ligne numérique, il est représenté par un cercle ouvert aux trois moitiés avec un ombrage à gauche. Sa notation par intervalles est de l'infini négatif à trois moitiés entre parenthèses.

    Exemple\(\PageIndex{6}\)

    Résolvez l'inégalité composée. Représentez graphiquement la solution et écrivez la solution en notation par intervalles :\(5(3x−1)\leq 10\) et\(4(x+3)<8\).

    Réponse

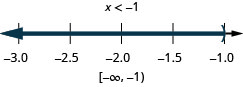
    La solution est que x est inférieur à moins 1. Sur une ligne numérique, il est représenté par un cercle ouvert à 1 avec un ombrage à gauche. Sa notation par intervalles va de l'infini négatif à moins 1 entre parenthèses.

    Exemple\(\PageIndex{7}\)

    Résolvez\(\frac{1}{3}x−4\geq −2\) et\(−2(x−3)\geq 4\). Tracez la solution et écrivez la solution en notation par intervalles.

    Réponse
      \(\frac{1}{3}x−4\geq −2\) et \(−2(x−3)\geq 4\)
    Résolvez chaque inégalité. \(\frac{1}{3}x−4\geq −2\)   \(−2x+6\geq 4\)
      \(\frac{1}{3}x\geq 2\)   \(−2x\geq −2\)
      \(x\geq 6\) et \(x\leq 1\)
    Tracez chaque solution. ...
    Représentez graphiquement les chiffres qui
    confirment les deux
    inégalités.    		 ...
      Aucun chiffre ne confirme que les deux inégalités sont vraies.

    C'est une contradiction donc il n'y a pas de solution. Il n'y a pas de chiffres qui confirment les deux inégalités.

    C'est une contradiction donc il n'y a pas de solution. Il n'y a pas de chiffres qui confirment les deux inégalités.

    C'est une contradiction et il n'y a donc pas de solution.
    Exemple\(\PageIndex{8}\)

    Résolvez l'inégalité composée. Représentez graphiquement la solution et écrivez la solution en notation par intervalles :\(\frac{1}{4}x−3\geq −1\) et\(−3(x−2)\geq 2\).

    Réponse

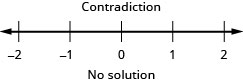
    L'inégalité est contradictoire. Il n'y a donc pas de solution. Par conséquent, il n'existe aucun graphique de la ligne numérique ou de la notation des intervalles.

    Exemple\(\PageIndex{9}\)

    Résolvez l'inégalité composée. Représentez graphiquement la solution et écrivez la solution en notation par intervalles :\(\frac{1}{5}x−5\geq −3\) et\(−4(x−1)\geq −2\).

    Réponse

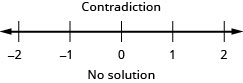
    L'inégalité est contradictoire. Il n'y a donc pas de solution. Par conséquent, il n'y a pas de graphique, de ligne numérique ou de notation par intervalles.

    Parfois, nous avons une inégalité composée qui peut être écrite de manière plus concise. Par exemple,\(a<x\) et\(x<b\) peut être écrit simplement comme,\(a<x<b\) puis nous l'appelons une double inégalité. Les deux formes sont équivalentes.

    DOUBLE INÉGALITÉ

    Une double inégalité est une inégalité composée telle que\(a<x<b\). C'est équivalent à\(a<x\) et\(x<b\).

    \[\text{Other forms:} \quad \begin{array} {lllll} {a<x<b} &{\text{is equivalent to }} &{a<x} &{\text{and}} &{x<b} \\ {a\leq x\leq b} &{\text{is equivalent to }} &{a\leq x} &{\text{and}} &{x\leq b} \\ {a>x>b} &{\text{is equivalent to }} &{a>x} &{\text{and}} &{x>b} \\ {a\geq x\geq b} &{\text{is equivalent to }} &{a\geq x} &{\text{and}} &{x\geq b} \\ \end{array} \nonumber\]

    Pour résoudre une double inégalité, nous effectuons la même opération sur les trois « parties » de la double inégalité dans le but d'isoler la variable au centre.

    Exemple\(\PageIndex{10}\)

    Résoudre\(−4\leq 3x−7<8\). Tracez la solution et écrivez la solution en notation par intervalles.

    Réponse
      \(-4 \leq 3x - 7 < 8\)
    Ajoutez 7 aux trois parties. \( -4 \,{\color{red}{+\, 7}} \leq 3x - 7 \,{\color{red}{+ \,7}} < 8 \,{\color{red}{+ \,7}}\)
    Simplifiez. \( 3 \le 3x < 15 \)
    Divisez chaque partie par trois. \( \dfrac{3}{\color{red}{3}} \leq \dfrac{3x}{\color{red}{3}} < \dfrac{15}{\color{red}{3}} \)
    Simplifiez. \( 1 \leq x < 5 \)
    Tracez la solution. .
    Écrivez la solution en notation par intervalles. \( [1, 5) \)

    Lorsqu'elle est écrite comme une double inégalité\(1\leq x<5\), il est facile de voir que les solutions sont les nombres compris entre un et cinq, y compris un, mais pas cinq. Nous pouvons ensuite représenter graphiquement la solution immédiatement, comme nous l'avons fait ci-dessus.

    Une autre façon de représenter graphiquement la solution de\(1\leq x<5\) est de représenter graphiquement à la fois la solution de\(x\geq 1\) et la solution de\(x<5\). Nous trouverions ensuite les chiffres qui confirment les deux inégalités, comme nous l'avons fait dans les exemples précédents.

    Exemple\(\PageIndex{11}\)

    Résolvez l'inégalité composée. Représentez graphiquement la solution et écrivez la solution en notation par intervalles :\(−5\leq 4x−1<7\).

    Réponse

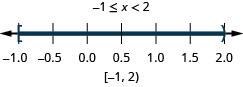
    La solution est négative : 1 est inférieur ou égal à x qui est inférieur à 2. Son graphique comporte un cercle fermé à moins 1 et un cercle ouvert à 2 avec un ombrage entre les cercles fermés et ouverts. Sa notation par intervalles est négative de 1 à 2 entre crochets et parenthèses.

    Exemple\(\PageIndex{12}\)

    Résolvez l'inégalité composée. Représentez graphiquement la solution et écrivez la solution en notation par intervalles :\(−3<2x−5\leq 1\).

    Réponse

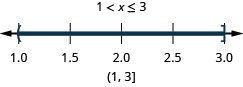
    La solution est 1 est inférieure à x qui est inférieure ou égale à 3. Son graphique comporte un cercle ouvert à 1 et un cercle fermé à 3 avec un ombrage entre les cercles fermés et ouverts. Sa notation par intervalles est négative de 1 à 3 entre parenthèses et crochets.

    Résolvez les inégalités composées avec « ou »

    Pour résoudre une inégalité composée par « ou », nous commençons comme nous l'avons fait pour les inégalités composées par « et » : nous résolvons les deux inégalités. Ensuite, nous trouvons tous les chiffres qui confirment que l'une ou l'autre inégalité est vraie.

    Tout comme les États-Unis sont l'union des 50 États, la solution sera l'union de tous les chiffres qui confirment l'une ou l'autre des inégalités. Pour trouver la solution de l'inégalité composée, nous examinons les graphes de chaque inégalité, trouvons les nombres qui appartiennent à l'un ou l'autre graphique et assemblons tous ces nombres.

    Pour écrire la solution en notation par intervalles, nous utiliserons souvent le symbole de l'union\(\cup\),, pour montrer l'union des solutions présentées dans les graphiques.

    RÉSOLVEZ UNE INÉGALITÉ COMPOSÉE AVEC « OU ».
    1. Résolvez chaque inégalité.
    2. Tracez chaque solution. Représentez ensuite graphiquement les chiffres qui confirment l'une ou l'autre inégalité
    3. Écrivez la solution en notation par intervalles.
    Exemple\(\PageIndex{13}\)

    Résolvez\(5−3x\leq −1\) ou\(8+2x\leq 5\). Tracez la solution et écrivez la solution en notation par intervalles.

    Réponse
      \(5−3x\leq −1\) ou \(8+2x\leq 5\)
    Résolvez chaque inégalité. \(5−3x\leq −1\)   \(8+2x\leq 5\)
      \(−3x\leq −6\)   \(2x\leq −3\)
      \(x\geq 2\) ou \(x\leq −\frac{3}{2}\)
    Tracez chaque solution. .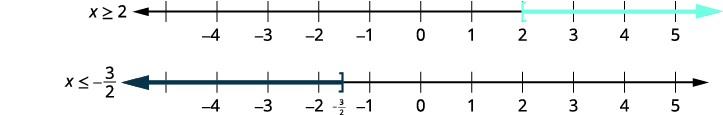
    Représentez graphiquement
    les nombres qui confirment l'
    une ou l'    		 .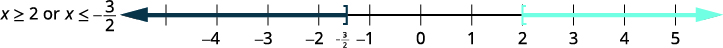
      \((−\infty,−32]\cup[2,\infty)\)
    Exemple\(\PageIndex{14}\)

    Résolvez l'inégalité composée. Représentez la solution sous forme graphique et écrivez la solution en notation par intervalles :\(1−2x\leq −3\) ou\(7+3x\leq 4\).

    Réponse

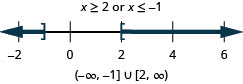
    La solution est si x est supérieur ou égal à 2 ou x est inférieur ou égal à 1. Le graphique des solutions sur une droite numérique présente un cercle fermé à moins 1 et ombré vers la gauche et un cercle fermé à 2 avec un ombrage vers la droite. La notation par intervalles est l'union de l'infini négatif à moins 1 entre parenthèses et crochets et de 2 et de l'infini entre crochets et parenthèses.

    Exemple\(\PageIndex{15}\)

    Résolvez l'inégalité composée. Représentez la solution sous forme graphique et écrivez la solution en notation par intervalles :\(2−5x\leq −3\) ou\(5+2x\leq 3\).

    Réponse

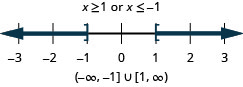
    La solution est si x est supérieur ou égal à 1 ou x est inférieur ou égal à moins 1. Le graphique des solutions sur une droite numérique présente un cercle fermé à moins 1 et ombré vers la gauche et un cercle fermé à 1 avec un ombrage vers la droite. La notation par intervalles est l'union de l'infini négatif à moins 1 entre parenthèses et crochets et de 1 et de l'infini entre crochets et parenthèses.

    Exemple\(\PageIndex{16}\)

    Résolvez\(\frac{2}{3}x−4\leq 3\) ou\(\frac{1}{4}(x+8)\geq −1\). Tracez la solution et écrivez la solution en notation par intervalles.

    Réponse
      \(\frac{2}{3}x−4\leq 3\) ou \(\frac{1}{4}(x+8)\geq −1\)
    Résolvez chaque
    inégalité.    		 \(3(\frac{2}{3}x−4)\leq 3(3)\)   \(4⋅\frac{1}{4}(x+8)\geq 4⋅(−1)\)
      \(2x−12\leq 9\)   \(x+8\geq −4\)
      \(2x\leq 21\)   \(x\geq −12\)
      \(x\leq \frac{21}{2}\)    
      \(x\leq \frac{21}{2}\) ou \(x\geq −12\)
    Tracez chaque
    solution.    		 .
    Représentez graphiquement les nombres
    qui
    confirment l'une ou l'    		 .
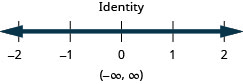
      La solution couvre tous les nombres réels.
      \((−\infty ,\infty )\)
    Exemple\(\PageIndex{17}\)

    Résolvez l'inégalité composée. Représentez la solution sous forme graphique et écrivez la solution en notation par intervalles :\(\frac{3}{5}x−7\leq −1\) ou\(\frac{1}{3}(x+6)\geq −2\).

    Réponse

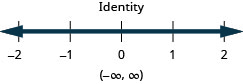
    La solution, c'est l'identité. Sa solution sur la ligne numérique est ombrée pour toutes les valeurs. La solution en notation par intervalles est de l'infini négatif à l'infini entre parenthèses.

    Exemple\(\PageIndex{18}\)

    Résolvez l'inégalité composée. Représentez la solution sous forme graphique et écrivez la solution en notation par intervalles :\(\frac{3}{4}x−3\leq 3\) ou\(\frac{2}{5}(x+10)\geq 0\).

    Réponse

    La solution, c'est l'identité. Sa solution sur la ligne numérique est ombrée pour toutes les valeurs. La solution en notation par intervalles est de l'infini négatif à l'infini entre parenthèses.

    Résoudre des applications présentant des inégalités composées

    Les situations du monde réel impliquent également des inégalités aggravées. Nous utiliserons la même stratégie de résolution de problèmes que celle que nous avons utilisée pour résoudre les applications d'équations linéaires et d'inégalités.

    Rappelez-vous que les stratégies de résolution de problèmes consistent à d'abord lire le problème et à s'assurer que tous les mots sont compris. Ensuite, identifiez ce que nous recherchons et attribuez une variable pour le représenter. Ensuite, reformulez le problème en une phrase pour qu'il se traduise facilement par une inégalité composée. Enfin, nous allons résoudre l'inégalité composée.

    Exemple\(\PageIndex{19}\)

    En raison de la sécheresse qui sévit en Californie, de nombreuses communautés ont des tarifs d'eau échelonnés. Il existe différents taux pour l'utilisation à des fins de conservation, l'utilisation normale et l'utilisation excessive. L'utilisation est mesurée en nombre de centaines de pieds cubes (hcf) utilisés par le propriétaire.

    Pendant l'été, un propriétaire paiera 24,72$ plus 1,54$ par hcf pour une utilisation normale. La facture pour une utilisation normale serait comprise entre 57,06$ et 171,02$. Combien de hcf le propriétaire peut-il utiliser s'il souhaite que son utilisation reste dans la fourchette normale ?

    Réponse
    Déterminez ce que nous recherchons. Le nombre de CHF qu'il peut utiliser et rester dans la fourchette de facturation « utilisation normale ».
    Nommez ce que nous recherchons. Soit x=x= le nombre de hcf qu'il peut utiliser.
    Cela se traduit par une inégalité. La facture est de 24,72$ plus 1,54 fois le nombre de hcf qu'il utilise ou\(24.72+1.54x\).
     

    \(\color{Cerulean}{\underbrace{\color{black}{\text{His bill will be between or equal to }$57.06\text{ and }$171.02.}}}\)

    \(57.06 \leq 24.74 + 1.54x \leq 171.02 \)
    Résolvez l'inégalité.

    \(57.06 \leq 24.74 + 1.54x \leq 171.02\)

    \(57.06 \,{\color{red}{- \,24.72}}\leq 24.74 \,{\color{red}{- \,24.72}} + 1.54x \leq 171.02 \,{\color{red}{- \,24.72}}\)

    \( 32.34 \leq 1.54x \leq 146.3\)

    \( \dfrac{32.34}{\color{red}{1.54}} \leq \dfrac{1.54x}{\color{red}{1.54}} \leq \dfrac{146.3}{\color{red}{1.54}}\)

    \( 21 \leq x \leq 95 \)
    Réponds à la question. Le propriétaire peut utiliser le\(21–95\) hcf tout en restant dans la fourchette de facturation « utilisation normale ».
    Exemple\(\PageIndex{20}\)

    En raison de la sécheresse qui sévit en Californie, de nombreuses communautés ont désormais des tarifs d'eau différenciés. Il existe différents taux pour l'utilisation à des fins de conservation, l'utilisation normale et l'utilisation excessive. L'utilisation est mesurée en nombre de centaines de pieds cubes (hcf) utilisés par le propriétaire.

    Au cours de l'été, un propriétaire paiera 24,72$ plus 1,32$ par hcf pour une utilisation à des fins de conservation. La facture pour l'utilisation à des fins de conservation serait comprise entre 31,32$ et 52,12$. Combien de hcf la propriétaire peut-elle utiliser si elle souhaite que son utilisation reste dans la zone de conservation ?

    Réponse

    Le propriétaire peut utiliser le\(5–20\) hcf tout en se situant dans la fourchette de facturation « utilisation de conservation ».

    Exemple\(\PageIndex{21}\)

    En raison de la sécheresse qui sévit en Californie, de nombreuses communautés ont des tarifs d'eau échelonnés. Il existe différents taux pour l'utilisation à des fins de conservation, l'utilisation normale et l'utilisation excessive. L'utilisation est mesurée en nombre de centaines de pieds cubes (hcf) utilisés par le propriétaire.

    Pendant l'hiver, un propriétaire paiera 24,72$ plus 1,54$ par hcf pour une utilisation normale. La facture pour une utilisation normale serait comprise entre 49,36$ et 86,32$. Combien de hcf sera-t-il autorisé à utiliser s'il veut que sa consommation reste dans la fourchette normale ?

    Réponse

    Le propriétaire peut utiliser le\(16–40\) hcf tout en restant dans la fourchette de facturation « utilisation normale ».

    Accédez à cette ressource en ligne pour obtenir des instructions et des exercices supplémentaires sur la résolution des inégalités composées.

    • Inégalités accrues

    Concepts clés

    • Comment résoudre une inégalité composée avec « et »
      1. Résolvez chaque inégalité.
      2. Tracez chaque solution. Représentez ensuite graphiquement les chiffres qui confirment les deux inégalités. Ce graphique montre la solution à l'inégalité composée.
      3. Écrivez la solution en notation par intervalles.
    • Double inégalité
      • Une double inégalité est une inégalité composée telle que\(a<x<b\). Il est équivalent à\(a<x\) et aux\(x<b.\)

        autres formes : \ [\ begin {align*} a<x<b & & \ text {est équivalent à} & & a<x \ ; \ text {et} \ ; x<b \ \
        a≤x≤b & & \ text {est équivalent à} & & a≤x \ ; \ text {et} \ ; x≤b \ \
        a>x>b & & \ text {est équivalent à} & & a>x \ ; \ text {et} \ ; x>b \ \
        a≥x≥b & & \ text {est équivalent à} & & a≥x \ ; \ text {et} \ ; x≥b \ end {align*} \]
    • Comment résoudre une inégalité composée avec « ou »
      1. Résolvez chaque inégalité.
      2. Tracez chaque solution. Représentez ensuite graphiquement les chiffres qui confirment l'une ou l'autre inégalité
      3. Écrivez la solution en notation par intervalles.

    Lexique

    inégalité aggravée
    Une inégalité composée est constituée de deux inégalités reliées par le mot « et » ou par le mot « ou ».