2.6 : Résoudre les inégalités linéaires

Last updated
Save as PDF

Page ID: 194429

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

À la fin de cette section, vous serez en mesure de :

Représenter graphiquement les inégalités sur la ligne numérique
Résoudre les inégalités linéaires
Traduisez les mots en une inégalité et résolvez
Résoudre des applications présentant des inégalités linéaires

Avant de commencer, répondez à ce questionnaire de préparation.

Traduire de l'algèbre vers l'anglais :$15>x$.
Si vous avez oublié ce problème, consultez [lien].
Traduisez en une expression algébrique :$15$ est inférieur à$x$.
Si vous avez oublié ce problème, consultez [lien].

Représenter graphiquement les inégalités sur la droite numérique

Quel chiffre confirmerait l'$x>3$inégalité ? Pensez-vous que « ça$x$ pourrait être quatre » ? C'est exact, mais$x$ cela pourrait aussi être 6, ou 37, ou même 3,001. Tout nombre supérieur à trois est une solution à l'inégalité$x>3$. Nous montrons toutes les solutions à l'inégalité$x>3$ sur la ligne numérique en ombrant tous les nombres situés à droite de trois, pour montrer que tous les nombres supérieurs à trois sont des solutions. Comme le chiffre trois lui-même n'est pas une solution, nous avons placé trois entre parenthèses.

Nous pouvons également représenter les inégalités en utilisant la notation par intervalles. Il n'y a pas de solution optimale à cette inégalité. En notation par intervalles, nous exprimons$x>3$ comme$(3,\infty)$. Le symbole$\infty$ se lit comme « infini ». Il ne s'agit pas d'un chiffre réel. La figure$\PageIndex{1}$ montre à la fois la ligne numérique et la notation des intervalles.

La figure montre l'inégalité, x est supérieur à 3, représentée sur une ligne numérique allant de moins 5 à 5. Il y a un ombrage qui commence à 3 et s'étend jusqu'aux chiffres situés à sa droite. La solution de l'inégalité est écrite en notation par intervalles. C'est l'intervalle de 3 à l'infini, sans compter 3. — Figure$\PageIndex{1}$ : L'inégalité$x>3$ est représentée graphiquement sur cette ligne numérique et écrite en notation par intervalles.

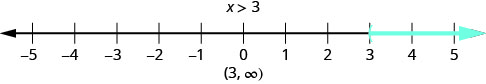
Nous utilisons le symbole de la parenthèse gauche, (, pour montrer que le point final de l'inégalité n'est pas inclus. Le symbole entre crochets, [, indique que le point de terminaison est inclus.

L'inégalité$x\leq 1$ signifie tous les nombres inférieurs ou égaux à un. Ici, nous devons montrer que l'une d'entre elles est également une solution. Pour ce faire, nous mettons un crochet à$x=1$. Nous ombrons ensuite tous les nombres situés à gauche de un, pour montrer que tous les nombres inférieurs à un sont des solutions (Figure$\PageIndex{2}$). Il n'y a pas de limite inférieure à ces chiffres. Nous écrivons$x\leq 1x\leq 1 $ en notation par intervalles comme$(−\infty,1]$. Le symbole$−\infty$ se lit comme « infini négatif ».

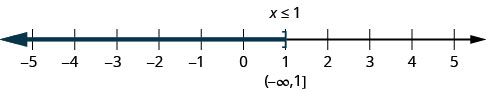
La figure montre l'inégalité, x est inférieur ou égal à l, représentée sur une ligne numérique allant de moins 5 à 5. Il existe un ombrage qui commence à 1 et s'étend jusqu'aux nombres situés à gauche. La solution de l'inégalité est écrite en notation par intervalles. C'est l'intervalle entre l'infini négatif et un, y compris 1. — Figure$\PageIndex{2}$ : L'inégalité$x\leq 1$ est représentée graphiquement sur cette ligne numérique et écrite en notation par intervalles.

La figure$\PageIndex{3}$ montre à la fois la ligne numérique et la notation des intervalles.

INÉGALITÉS, LIGNES NUMÉRIQUES ET NOTATION PAR INTERVALLES

$La figure montre que la solution de l'inégalité x est supérieure à a est indiquée sur une ligne numérique avec une parenthèse gauche en a et un ombrage vers la droite, et que la solution en notation par intervalles est l'intervalle de a à l'infini entre parenthèses. Il montre que la solution de l'inégalité x est supérieur ou égal à a est indiqué sur une ligne numérique avec un crochet gauche en a et un ombrage vers la droite, et que la solution en notation par intervalles est l'intervalle a à l'infini entre crochets gauche et parenthèses droites. Cela montre que la solution de l'inégalité x est inférieure à a est indiquée sur une ligne numérique avec une parenthèse droite en a et un ombrage vers la gauche, et que la solution en notation par intervalles est l'intervalle entre l'infini négatif et a entre parenthèses. Cela montre que la solution de l'inégalité x est inférieure ou égale à a est indiquée sur une ligne numérique avec un crochet droit en a et un ombrage vers la gauche, et que la solution en notation par intervalles est négative de l'infini à a entre parenthèses gauche et droite.$

La notation des inégalités sur une ligne numérique et dans la notation par intervalles utilise les mêmes symboles pour exprimer les extrémités des intervalles.

Exemple$\PageIndex{1}$

Représentez graphiquement chaque inégalité sur la ligne numérique et écrivez en notation par intervalles.

$x\geq −3$
$x<2.5$
$x\leq −\frac{3}{5}$

Réponse

ⓐ

	$ x \geq -3 $
Ombrez à droite de$−3$, et placez un support sur$−3$.	$.$
Écrivez en notation par intervalles.	$ [-3, \infty) $

ⓑ

	$ x < 2.5 $
Ombrez vers la gauche de 2,5 et placez une parenthèse à 2,5.	$.$
Écrivez en notation par intervalles.	$ (-\infty, 2.5) $

ⓒ

	$ x \leq -\dfrac{3}{5} $
Ombrez à gauche de$−\frac{3}{5}$, et placez un support sur$−\frac{3}{5}$.	$.$
Écrivez en notation par intervalles.	$ \bigg( -\infty, \dfrac{3}{5}\bigg] $

Représentez graphiquement chaque inégalité sur la ligne numérique et écrivez en notation par intervalles :

$x>2$
$x\leq −1.5$
$x\geq \frac{3}{4}$.

Réponse

ⓐ

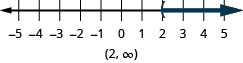
$Le graphique de l'inégalité x est supérieur à 2 est indiqué sur une ligne numérique avec une parenthèse gauche à 2 et un ombrage vers la droite. La solution en notation par intervalles est l'intervalle de 2 à l'infini entre parenthèses.$

ⓑ

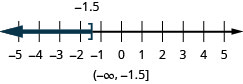
$Le graphique de l'inégalité x est inférieur ou égal à moins 1,5 est indiqué sur une ligne numérique avec un crochet droit à moins 1,5 et un ombrage vers la gauche. La solution en notation par intervalles est l'intervalle entre l'infini négatif et moins 1,5 entre une parenthèse gauche et un crochet droit.$

ⓒ

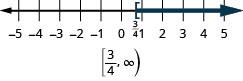
$Le graphique de l'inégalité x est supérieure ou égale aux trois quarts est indiqué sur une ligne numérique avec un crochet gauche aux trois quarts et un ombrage vers la droite. La solution en notation par intervalles est l'intervalle des trois quarts à l'infini entre un crochet gauche et des parenthèses gauches.$

Exemple$\PageIndex{3}$

Représentez graphiquement chaque inégalité sur la ligne numérique et écrivez en notation par intervalles :

$x\leq −4$
$x\geq 0.5$
$x<−\frac{2}{3}$.

Réponse

ⓐ

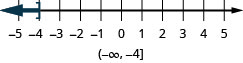
$Le graphique de l'inégalité x est inférieur ou égal à moins 4 est indiqué sur une ligne numérique avec un crochet droit à moins 4 et un ombrage vers la gauche. La solution en notation par intervalles est l'intervalle entre l'infini négatif et moins 4 entre une parenthèse gauche et une parenthèse droite.$

ⓑ

$Le graphique de l'inégalité x est supérieure ou égale à 0,5 est indiqué sur une ligne numérique avec un crochet gauche à 0,5 et un ombrage vers la droite. La solution en notation par intervalles est l'intervalle de 0,5 à l'infini entre un crochet gauche et une parenthèse droite.$

ⓒ

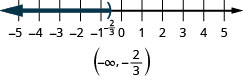
$Le graphique de l'inégalité x est inférieur à moins deux tiers est indiqué sur une ligne numérique avec une parenthèse droite aux deux tiers moins et un ombrage vers la gauche. La solution en notation par intervalles est l'intervalle entre l'infini négatif et les deux tiers négatifs entre parenthèses.$

Quels nombres sont supérieurs à deux mais inférieurs à cinq ? Tu penses à dire,$2.5,\space 3,\space 3\frac{2}{3},\space 4,\space 4,\space 99$ ? Nous pouvons représenter tous les nombres entre deux et cinq avec l'inégalité$2<x<5$. Nous pouvons afficher$2<x<5$ sur la ligne numérique en ombrant tous les nombres compris entre deux et cinq. Encore une fois, nous utilisons les parenthèses pour montrer que les chiffres deux et cinq ne sont pas inclus. Voir la figure.

Le graphique de l'inégalité 2 est inférieur à x, qui est inférieur à 5, montre les cercles ouverts a 2 et 5 et un ombrage entre les deux. — Figurine$\PageIndex{3}$

Représentez graphiquement chaque inégalité sur la ligne numérique et écrivez en notation par intervalles.

ⓐ$−3<x<4$ ⓑ$−6\leq x<−1$ ⓒ$0\leq x\leq 2.5$

Réponse

ⓐ

		$-3 < x < 4$
Ombre entre$−3$ et 4. Mettez une parenthèse à$−3$ et 4.		$.$
Écrivez en notation par intervalles.		$ (-3,4) $

ⓑ

			$ -6 \leq x < -1 $
Ombre entre$−6$ et −1. Placez un crochet à$−6$ et une parenthèse à −1.			$.$
Écrivez en notation par intervalles.			$ [-6,1) $

ⓒ

			$ 0 \leq x \leq 2.5 $
Ombre entre 0 et 2,5. Placez un crochet à 0 et à 2,5.			$.$
Écrivez en notation par intervalles.			$ [0, 2.5] $

Exemple$\PageIndex{5}$

Représentez graphiquement chaque inégalité sur la ligne numérique et écrivez en notation par intervalles :

ⓐ$−2<x<1$ ⓑ$−5\leq x<−4$ ⓒ$1\leq x\leq 4.25$

Réponse

ⓐ

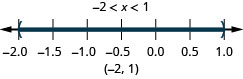
$Négatif 2 est inférieur à x qui est inférieur à 1. Il y a des cercles ouverts aux points négatifs 2 et 1 et un ombrage entre moins 2 et 1 sur la ligne numérique. Mettez des parenthèses à moins 2 et 1. Écrivez en notation par intervalles.$

ⓑ

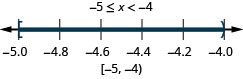
$Le négatif 5 est inférieur ou égal à x qui est inférieur au négatif 4. Il y a un cercle fermé à moins 6 et un cercle ouvert à moins 4 et un ombrage entre moins 5 et moins 4 sur la ligne numérique. Mettez un crochet à moins 5 et une parenthèse à moins 4. Écrivez en notation par intervalles.$

ⓒ

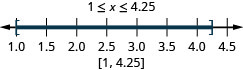
$1 est inférieur ou égal à x qui est inférieur à 4,25. Il y a un cercle fermé à 1 et un cercle fermé à 4,25 et un ombrage entre 1 et 4,25 sur la ligne numérique. Placez les crochets à 1 et 4,25. Écrivez en notation par intervalles.$

Exemple$\PageIndex{6}$

Représentez graphiquement chaque inégalité sur la ligne numérique et écrivez en notation par intervalles :

ⓐ$−6<x<2$ ⓑ$−3\leq x< −1$ ⓒ$2.5\leq x\leq 6$

Réponse

ⓐ

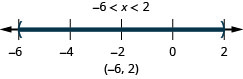
$Négatif 6 est inférieur à x qui est inférieur à 2. Il y a un cercle ouvert à moins 6 et un cercle ouvert à 2 et un ombrage entre moins 6 et 2 sur la ligne numérique. Mettez des parenthèses à moins 6 et 2. Écrivez en notation par intervalles.$

ⓑ

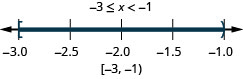
$Le négatif 3 est inférieur ou égal à x qui est inférieur au négatif 1. Il y a un cercle fermé à moins 3 et un cercle ouvert à moins 1 et un ombrage entre moins 3 et moins 1 sur la ligne numérique. Mettez un crochet à moins 3 et une parenthèse à moins 1. Écrivez en notation par intervalles.$

ⓒ

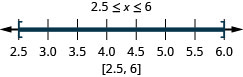
$2,5 est inférieur ou égal à x qui est inférieur ou égal à 6. Il y a un cercle fermé à 2,5 et un cercle fermé à 6 et un ombrage entre 2,5 et 6 sur la ligne numérique. Placez les crochets à 2,5 et 6. Écrivez en notation par intervalles.$

Résoudre les inégalités linéaires

Une inégalité linéaire ressemble beaucoup à une équation linéaire, mais le signe égal est remplacé par un signe d'inégalité. Une inégalité linéaire est une inégalité dans une variable qui peut être écrite sous l'une des formes suivantes :$ax+b<c$$ax+b\leq c$,$ax+b>c$, ou$ax+b\geq c$.

INÉGALITÉ LINÉAIRE

Une inégalité linéaire est une inégalité dans une variable qui peut être écrite sous l'une des formes suivantes où$a, \, b,$ et$c$ sont des nombres réels et$a≠0$ :

\[ \begin{array} {llll} {ax+b<c,} &{ax+b\leq c,} &{ax+b>c,} &{ax+b\geq c.} \\ \nonumber \end{array}\]

Lorsque nous avons résolu des équations linéaires, nous avons pu utiliser les propriétés de l'égalité pour ajouter, soustraire, multiplier ou diviser les deux côtés tout en conservant l'égalité. Des propriétés similaires sont valables pour les inégalités.

Nous pouvons ajouter ou soustraire la même quantité des deux côtés d'une inégalité tout en conservant l'inégalité. Par exemple :

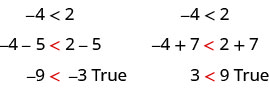
$Négatif 4 est inférieur à 2. Moins 4 moins 5 est inférieur à 2 moins 5. Négatif 9 est inférieur au négatif 3, ce qui est vrai. Négatif 4 est inférieur à 2. Négatif 4 plus 7 est inférieur à 2 plus 7. 3 est inférieur à 9, ce qui est vrai.$

Notez que le signe d'inégalité est resté le même.

Cela nous amène aux propriétés d'addition et de soustraction de l'inégalité.

PROPRIÉTÉ D'ADDITION ET DE SOUSTRACTION DE L'

Pour tous les nombres$a, \, b,$ et$c,$ si$a<b$, alors

\[\begin{array} {ll} {a+c<b+c} &{a−c<b−c} \\ {a+c>b+c} &{a−c>b−c} \\ \nonumber \end{array}\]

Nous pouvons ajouter ou soustraire la même quantité des deux côtés d'une inégalité tout en conservant l'inégalité

Qu'arrive-t-il à une inégalité lorsque nous divisons ou multiplions les deux côtés par une constante ?

Multiplions d'abord et divisons les deux côtés par un nombre positif.

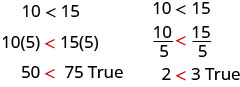
$10 est inférieur à 15. 10 fois 5 est inférieur à 15 fois 5. 50 est inférieur à 75 est vrai. 10 est inférieur à 15. 10 divisé par 5 est inférieur à 15 est inférieur à 15 divisé par 5. 2 est inférieur à 3 est vrai.$

Les signes d'inégalité sont restés les mêmes.

L'inégalité reste-t-elle la même lorsque nous divisons ou multiplions par un nombre négatif ?

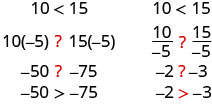
$10 est inférieur à 15 10 fois négatif 5 est vide 15 fois négatif 5 ? Le négatif 50 correspond à un négatif vide de 75. Moins 50 est supérieur à moins 75. 10 est inférieur à 15. 10 divisé par moins 5 est vide 15 divisé par moins 5. Le négatif 2 est vide, le négatif 3. Le négatif 2 est vide, le négatif 3.$

Remarquez que lorsque nous avons rempli les signes d'inégalité, les signes d'inégalité ont inversé leur direction.

Lorsque nous divisons ou multiplions une inégalité par un nombre positif, le signe d'inégalité reste le même. Lorsque nous divisons ou multiplions une inégalité par un nombre négatif, le signe d'inégalité s'inverse.

Cela nous donne la propriété de multiplication et de division de l'inégalité.

PROPRIÉTÉ DE MULTIPLICATION ET DE DIVISION DES INÉGALITÉS

Pour tous les numéros$a, \, b,$ et$c,$

\[\begin{array} {l} {\text{multiply or divide by a positive}} \\ \\ \space\space\space\space\text{if }a<b\text{ and }c>0\text{, then }ac<bc \text{ and }\frac{a}{c}<\frac{b}{c}. \\ \space\space\space\space\text{if }a>b\text{ and }c>0\text{, then }ac>bc \text{ and }\frac{a}{c}>\frac{b}{c}. \\ \\ \text{ multiply or divide by a negative } \\ \\ \space\space\space\space\text{if }a<b\text{ and }c<0\text{, then }ac>bc \text{ and }\frac{a}{c}>\frac{b}{c}.\\ \space\space\space\space\text{if }a>b\text{ and }c<0\text{, then }ac<bc \text{ and }\frac{a}{c}<\frac{b}{c}.\\ \nonumber \end{array}\]

Lorsque nous divisons ou multiplions une inégalité par$a$ :

nombre positif, l'inégalité reste la même.
nombre négatif, l'inégalité s'inverse.

Parfois, lors de la résolution d'une inégalité, comme dans l'exemple suivant, la variable se termine à droite. Nous pouvons réécrire l'inégalité à l'envers pour placer la variable vers la gauche.

\[x>a \text{ has the same meaning as } a<x \nonumber \]

Réfléchissez ainsi : « Si Xander est plus grand qu'Andy, alors Andy est plus petit que Xander ».

Exemple$\PageIndex{7}$

Résolvez chaque inégalité. Tracez la solution sur la ligne numérique et écrivez la solution en notation par intervalles.

ⓐ$x−\frac{3}{8}\leq \frac{3}{4}$ ⓑ$9y<54$ ⓒ$−15<\frac{3}{5}z$

Réponse

ⓐ

	$.$
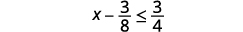
Ajoutez 3838 aux deux côtés de l'inégalité.	$.$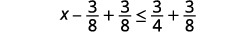
Simplifiez.	$.$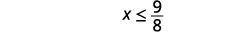
Représentez graphiquement la solution sur la ligne numérique.	$.$
Écrivez la solution en notation par intervalles.	$.$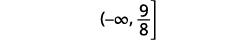

ⓑ

	$.$
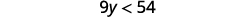
Divisez les deux côtés de l'inégalité par 9 ; puisque 9 est positif, l'inégalité reste la même.	$.$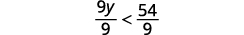
Simplifiez.	$.$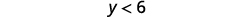
Représentez graphiquement la solution sur la ligne numérique.	$.$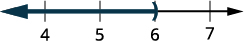
Écrivez la solution en notation par intervalles.	$.$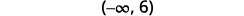

ⓒ

	$.$
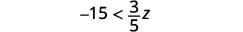
Multipliez les deux côtés de l'inégalité par$\frac{5}{3}$. Puisque$\frac{5}{3}$ c'est positif, l'inégalité reste la même.	$.$
Simplifiez.	$.$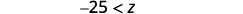
Réécrivez avec la variable sur la gauche.	$.$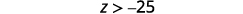
Représentez graphiquement la solution sur la ligne numérique.	$.$
Écrivez la solution en notation par intervalles.	$.$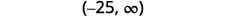

Résolvez chaque inégalité, tracez la solution sur la ligne numérique et écrivez la solution en notation par intervalles :

ⓐ$p−\frac{3}{4}\geq \frac{1}{6}$ ⓑ$9c>72$ ⓒ$24\leq \frac{3}{8}m$

Réponse

ⓐ

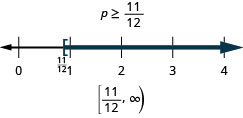
$p est inférieur à onze douzièmes. La solution sur la ligne numérique comporte un crochet droit aux onze douzièmes avec un ombrage vers la droite. La solution en notation par intervalles est de onze douzièmes à l'infini entre crochets et parenthèses.$

ⓑ

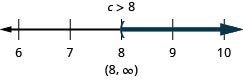
$c est inférieur à 8. La solution sur la ligne numérique comporte un crochet gauche à 8 avec un ombrage vers la droite. La solution en notation par intervalles est de 8 à l'infini entre parenthèses.$

ⓒ

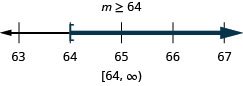
$m est supérieur ou égal à 8. La solution sur la ligne numérique a un crochet droit à 64 avec un ombrage vers la droite. La solution en notation par intervalles est de 64 à l'infini entre crochets et parenthèses.$

Exemple$\PageIndex{9}$

Résolvez chaque inégalité, tracez la solution sur la ligne numérique et écrivez la solution en notation par intervalles :

ⓐ$r−\frac{1}{3}\leq \frac{7}{12}$ ⓑ$12d\leq 60$ ⓒ$−24<\frac{4}{3}n$

Réponse

ⓐ

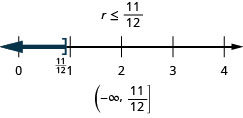
$r est inférieur ou égal à onze douzièmes. La solution sur la ligne numérique comporte un crochet gauche aux onze douzièmes avec un ombrage vers la gauche. La solution en notation par intervalles est de l'infini négatif à onze douzièmes entre parenthèses et crochets.$

ⓑ

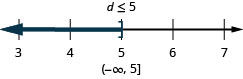
$c est inférieur ou égal à 5. La solution sur la ligne numérique a un crochet droit à 5 avec un ombrage vers la gauche. La solution en notation par intervalles est de l'infini négatif à 5 entre parenthèses et crochets.$

ⓒ

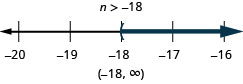
$n est supérieur à moins 18. La solution sur la ligne numérique a une parenthèse gauche à moins 18 avec un ombrage vers la droite. La solution en notation par intervalles est négative de 18 à l'infini entre parenthèses.$

Soyez prudent lorsque vous multipliez ou divisez par un nombre négatif. N'oubliez pas d'inverser le signe d'inégalité.

Exemple$\PageIndex{10}$

Résolvez chaque inégalité, tracez la solution sur la ligne numérique et écrivez la solution en notation par intervalles.

ⓐ$−\frac{1}{3}m\geq \frac{6}{5}$ ⓑ$\frac{n}{−2} \geq 8$

Réponse

ⓐ

	$.$
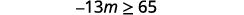
Divisez les deux côtés de l'inégalité par$−\frac{1}{3}$. Puisque$−\frac{1}{3}$ c'est négatif, l'inégalité s'inverse.	$.$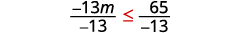
Simplifiez.	$.$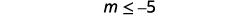
Représentez graphiquement la solution sur la ligne numérique.	$.$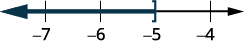
Écrivez la solution en notation par intervalles.	$.$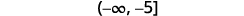

ⓑ

	$.$
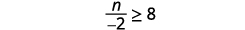
Multipliez les deux côtés de l'inégalité par$−2$. Puisque$−2$ c'est négatif, l'inégalité s'inverse.	$.$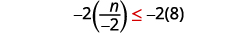
Simplifiez.	$.$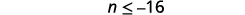
Représentez graphiquement la solution sur la ligne numérique.	$.$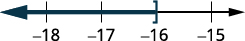
Écrivez la solution en notation par intervalles.	$.$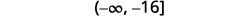

Exemple$\PageIndex{11}$

Résolvez chaque inégalité, tracez la solution sur la ligne numérique et écrivez la solution en notation par intervalles :

ⓐ$−8q<32$ ⓑ$\frac{k}{−12} \leq 15$.

Réponse

ⓐ

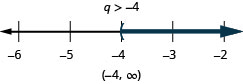
$q est supérieur ou égal à moins 4. La solution sur la ligne numérique a une parenthèse gauche au point négatif 4 avec un ombrage vers la droite. La solution en notation par intervalles est de moins 4 à l'infini entre parenthèses.$

ⓑ

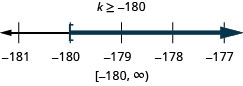
$k est supérieur ou égal à moins 180. La solution sur la ligne numérique a un crochet gauche à moins 180 avec un ombrage vers la droite. La solution en notation par intervalles est de 180 à l'infini entre crochets et parenthèses.$

Exemple$\PageIndex{12}$

Résolvez chaque inégalité, tracez la solution sur la ligne numérique et écrivez la solution en notation par intervalles :

ⓐ$−7r\leq −70$ ⓑ$\frac{u}{−4}\geq −16$.

Réponse

ⓐ

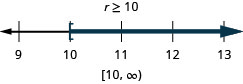
$r est supérieur ou égal à 10. La solution sur la ligne numérique comporte un crochet gauche à 10 avec un ombrage vers la droite. La solution en notation par intervalles est de 10 à l'infini entre crochets et parenthèses.$

ⓑ

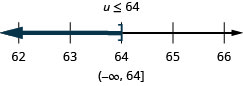
$u est inférieur ou égal à 64. La solution sur la ligne numérique a un crochet droit au 64 avec un ombrage vers la gauche. La solution en notation par intervalles est de l'infini négatif à 64 entre parenthèses et entre crochets.$

La plupart des inégalités nécessiteront plus d'une étape pour être résolues. Nous suivons les mêmes étapes que celles utilisées dans la stratégie générale de résolution d'équations linéaires, mais nous veillons à faire très attention lorsque nous multiplions ou divisons pour isoler la variable.

Résolvez l'inégalité$6y\leq 11y+17$, tracez la solution sur la ligne numérique et écrivez la solution en notation par intervalles.

Réponse

	$.$
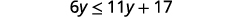
Soustrayez 11y11y des deux côtés pour collecter les variables sur la gauche.	$.$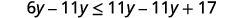
Simplifiez.	$.$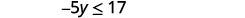
Divisez les deux côtés de l'inégalité par −5, −5 et inversez l'inégalité.	$.$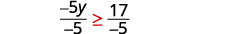
Simplifiez.	$.$
Représentez graphiquement la solution sur la ligne numérique.	$.$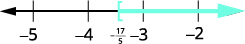
Écrivez la solution en notation par intervalles.	$.$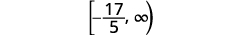

Résolvez l'inégalité, tracez la solution sur la ligne numérique et écrivez la solution en notation par intervalles :$3q\geq 7q−23$.

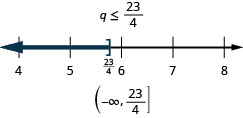
Réponse: $q est inférieur ou égal à 23 divisé par 4. La solution sur la ligne numérique comporte un crochet droit à 23 divisé par 4 avec un ombrage vers la gauche. La solution en notation par intervalles est une infinité négative à 23 divisée par 4 entre parenthèses et crochets.$

Exemple$\PageIndex{15}$

Résolvez l'inégalité, tracez la solution sur la ligne numérique et écrivez la solution en notation par intervalles :$6x<10x+19$.

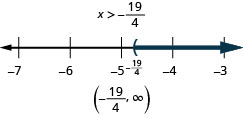
Réponse: $x est supérieur à moins 19 divisé par 4. La solution sur la ligne numérique a une parenthèse gauche à moins 19 divisée par 4 avec un ombrage vers la droite. La solution en notation par intervalles est négative 19 divisée par 4 à l'infini entre parenthèses.$

Lors de la résolution d'inégalités, il est généralement plus facile de collecter les variables du côté où le coefficient de la variable est le plus élevé. Cela élimine les coefficients négatifs et nous n'avons donc pas à multiplier ou à diviser par un négatif, ce qui signifie que nous n'avons pas à penser à inverser le signe d'inégalité.

Exemple$\PageIndex{16}$

Résolvez l'inégalité$8p+3(p−12)>7p−28$, tracez la solution sur la ligne numérique et écrivez la solution en notation par intervalles.

Réponse

	$8p+3(p−12)>7p−28$
Simplifiez chaque côté autant que possible.
Distribuez.	$8p+3p−36>7p−28$
Combinez les mêmes termes.	$11p−36>7p−28$
Soustrayez$7p$ des deux côtés pour collecter les variables sur la gauche, puisque$11>7$.	$11p−36−7p>7p−28−7p$
Simplifiez.	$4p−36>−28$
Ajoutez$36$ des deux côtés pour collecter les constantes sur la droite.	$4p−36+36>−28+36$
Simplifiez.	$4p>8$
Divisez les deux côtés de l'inégalité par $4$ : l'inégalité reste la même.	$\dfrac{4p}{4}>\dfrac{8}{4}$
Simplifiez.	$p>2$
Représentez graphiquement la solution sur la ligne numérique.	$.$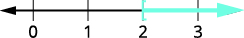
Écrivez la solution en notation par intervalles.	$(2,\infty)$

Exemple$\PageIndex{17}$

Résolvez l'inégalité$9y+2(y+6)>5y−24$, tracez la solution sur la ligne numérique et écrivez la solution en notation par intervalles.

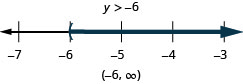
Réponse: $y est supérieur à moins 6. La solution sur la ligne numérique a une parenthèse gauche au point négatif 6 avec un ombrage vers la droite. La solution en notation par intervalles est de moins 6 à l'infini entre parenthèses.$

Exemple$\PageIndex{18}$

Résolvez l'inégalité$6u+8(u−1)>10u+32$, tracez la solution sur la ligne numérique et écrivez la solution en notation par intervalles.

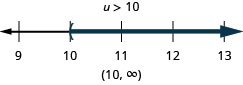
Réponse: $u est supérieur à moins 10. La solution sur la ligne numérique a une parenthèse gauche à 10 avec un ombrage vers la droite. La solution en notation par intervalles est de 10 à l'infini entre parenthèses.$

Tout comme certaines équations sont des identités et d'autres des contradictions, les inégalités peuvent également être des identités ou des contradictions. Nous reconnaissons ces formes lorsqu'il ne nous reste que des constantes lorsque nous résolvons l'inégalité. Si le résultat est une affirmation vraie, nous avons une identité. Si le résultat est une fausse déclaration, nous sommes en présence d'une contradiction.

Exemple$\PageIndex{19}$

Résolvez l'inégalité$8x−2(5−x)<4(x+9)+6x$, tracez la solution sur la ligne numérique et écrivez la solution en notation par intervalles.

Réponse

Simplifiez chaque côté autant que possible.		$8x−2(5−x)<4(x+9)+6x$
Distribuez.		$8x−10+2x<4x+36+6x$
Combinez les mêmes termes.		$10x−10<10x+36$
Soustrayez${\color{red}{10x}}$ des deux côtés pour collecter les variables sur la gauche.		$10x−10\,{\color{red}{-\,10x}}<10x+36\,{\color{red}{-\,10x}}$
Simplifiez.		$−10<36$
Ils$x$ ont disparu, et nous avons une déclaration vraie.		L'inégalité est une identité. La solution, ce sont tous des nombres réels.
Représentez graphiquement la solution sur la ligne numérique.		$.$
Écrivez la solution en notation par intervalles.		$(−\infty,\infty)$

Exemple$\PageIndex{20}$

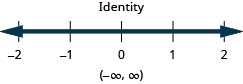
Résolvez l'inégalité$4b−3(3−b)>5(b−6)+2b$, tracez la solution sur la ligne numérique et écrivez la solution en notation par intervalles.

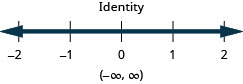
Réponse: $L'inégalité est une identité. Sa solution sur la ligne numérique est ombrée pour toutes les valeurs. La solution en notation par intervalles est de l'infini négatif à l'infini entre parenthèses.$

Exemple$\PageIndex{21}$

Résolvez l'inégalité$9h−7(2−h)<8(h+11)+8h$, tracez la solution sur la ligne numérique et écrivez la solution en notation par intervalles.

Réponse: $L'inégalité est une identité. Sa solution sur la ligne numérique est ombrée pour toutes les valeurs. La solution en notation par intervalles est de l'infini négatif à l'infini entre parenthèses.$

Nous pouvons éliminer les fractions dans les inégalités comme nous l'avons fait dans les équations. Encore une fois, faites attention aux signes lorsque vous multipliez ou divisez par un négatif.

Exemple$\PageIndex{22}$

Résolvez l'inégalité$\frac{1}{3}a−\frac{1}{8}a>\frac{5}{24}a+\frac{3}{4}$, tracez la solution sur la ligne numérique et écrivez la solution en notation par intervalles.

Réponse

	$\frac{1}{3}a−\frac{1}{8}a>\frac{5}{24}a+\frac{3}{4}$
Multipliez les deux côtés par l'écran LCD, 24, pour effacer les fractions.	${\color{red}{24}}\left(\dfrac{1}{3}a−\dfrac{1}{8}a\right)>\,{\color{red}{24}}\left(\dfrac{5}{24}a+\dfrac{3}{4}\right)$
Simplifiez.	$ 8a - 3a > 5a + 18 $
Combinez les mêmes termes.	$ 5a > 5a + 18$
Soustrayez$5a$ des deux côtés pour collecter les variables sur la gauche.	$ 5a \,{\color{red}{-\,5a}} > 5a \,{\color{red}{-\,5a}} + 18$
Simplifiez.	$0 > 18 $
La déclaration est fausse.	L'inégalité est contradictoire. Il n'y a pas de solution.
Représentez graphiquement la solution sur la ligne numérique.	$.$
Écrivez la solution en notation par intervalles.	Il n'y a pas de solution.

Exemple$\PageIndex{23}$

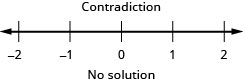
Résolvez l'inégalité$\frac{1}{4}x−\frac{1}{12}x>\frac{1}{6}x+\frac{7}{8}$, tracez la solution sur la ligne numérique et écrivez la solution en notation par intervalles.

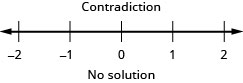
Réponse: $L'inégalité est contradictoire. Il n'y a donc pas de solution. Par conséquent, il n'y a pas de graphique sur la ligne numérique ou la notation des intervalles.$

Exemple$\PageIndex{24}$

Résolvez l'inégalité$\frac{2}{5}z−\frac{1}{3}z<\frac{1}{15}z−\frac{3}{5}$, tracez la solution sur la ligne numérique et écrivez la solution en notation par intervalles.

Réponse: $L'inégalité est contradictoire. Il n'y a donc pas de solution. Par conséquent, il n'y a pas de graphique sur la ligne numérique ou la notation des intervalles.$

Traduisez en une inégalité et résolvez

Pour traduire des phrases anglaises en inégalités, nous devons reconnaître les phrases qui indiquent l'inégalité. Certains mots sont simples, comme « plus que » et « moins que ». Mais d'autres ne sont pas aussi évidents. Le tableau présente quelques expressions courantes qui indiquent des inégalités.

$>$	$\geq$	$<$	$\leq$
\ (> \) "> \) » data-valign="middle » class="lt-math-17389">est supérieur à ce qui est supérieur à ce qui est supérieur à	\ (\ geq \) » data-valign="middle">est supérieur ou égal à est au moins égal au minimum	\ (est < \) » data-valign="middle"> inférieur à est inférieur à ce qui est inférieur à	\ (\ leq \) » data-valign="middle">est inférieur ou égal à est au plus égal au maximum

Exemple$\PageIndex{25}$

Traduisez et résolvez. Tracez ensuite la solution sur la ligne numérique et écrivez la solution en notation par intervalles.

\[\text{Twenty-seven less than }x\text{ is at least }48.\nonumber\]

Réponse

	$.$
Traduisez.	$x - 27 \geq 48$
Résoudre : ajoutez-en 27 des deux côtés.	$ x - 27 \, {\color{red}{+\, 27}} \geq 48 \, {\color{red}{+\, 27}}$
Simplifiez.	$x \geq 75$
Graphique sur la ligne numérique.	$.$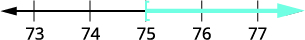
Écrivez en notation par intervalles.	$[75, \infty)$

Traduisez et résolvez. Tracez ensuite la solution sur la ligne numérique et écrivez la solution en notation par intervalles.

\[\text{Nineteen less than } p \text{ is no less than }47.\nonumber\]

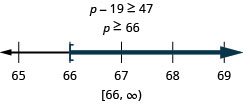
Réponse: $p moins 19 est supérieur ou égal à 47. Sa solution est que p est supérieur ou égal à 66. La solution sur la ligne numérique comporte un crochet gauche à 66 avec un ombrage vers la droite. La solution en notation par intervalles est de 66 à l'infini entre crochets et parenthèses.$

Exemple$\PageIndex{27}$

Traduisez et résolvez. Tracez ensuite la solution sur la ligne numérique et écrivez la solution en notation par intervalles.

\[\text{Four more than }a\text{ is at most }15.\nonumber\]

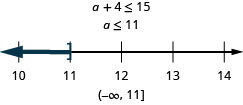
Réponse: $a plus 4 est inférieur ou égal à 15. Sa solution est inférieure ou égale à 11. La solution sur la ligne numérique a un crochet droit à 11 avec un ombrage vers la gauche. La solution en notation par intervalles est de l'infini négatif à 11 entre parenthèses et crochets.$

Résoudre des applications présentant des inégalités linéaires

De nombreuses situations de la vie réelle nous obligent à résoudre les inégalités. La méthode que nous utiliserons pour résoudre des applications avec des inégalités linéaires est très similaire à celle que nous avons utilisée pour résoudre des applications avec des équations.

Nous allons lire le problème et nous assurer que tous les mots sont compris. Ensuite, nous allons identifier ce que nous recherchons et assignerons une variable pour le représenter. Nous allons reformuler le problème en une phrase pour qu'il se traduise facilement par une inégalité. Ensuite, nous résoudrons l'inégalité.

Parfois, une application exige que la solution soit un nombre entier, mais la solution algébrique à l'inégalité n'est pas un nombre entier. Dans ce cas, il faut arrondir la solution algébrique à un nombre entier. Le contexte de l'application déterminera si nous arrondissons vers le haut ou vers le bas.

Exemple$\PageIndex{28}$

Dawn a remporté une mini-subvention de 4 000$ pour acheter des tablettes électroniques pour sa classe. Les tablettes qu'elle aimerait acheter coûtent 254,12$ chacune, taxes et livraison incluses. Quel est le nombre maximum de tablettes que Dawn peut acheter ?

Réponse: \(\begin{array} {ll} {\textbf{Step 1. Read }\text{ the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what you are looking for.}} &{\text{the maximum number of tablets Dawn can buy}} \\ {\textbf{Step 3. Name}\text{ what you are looking for.}} &{} \\ {} &{} \\ {} &{\text{Let }n= \text{ the number of tablets.}} \\ {\text{Choose a variable to represent that}} &{} \\{\text{quantity.}} &{} \\ {\textbf{Step 4. Translate.}\text{Write a sentence that gives the}} &{} \\ {\text{information to find it.}} &{$254.12\text{ times the number of tablets is}} \\ {} &{\text{no more than }$4,000.} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space 254.12n\leq 4000} \\ {\text{Translate into an inequality.}} &{} \\ {\textbf{Step 5. Solve }\text{the inequality.}} &{} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space n\leq 15.74} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space n\leq 15} \\{\text{But }n\text{ must be a whole number of}} &{} \\ {\text{tablets, so round to }15.} &{} \\ {\textbf{Step 6. Check }\text{the answer in the problem}} &{} \\ {\text{and make sure it makes sense.}} &{} \\ {} &{} \\ {} &{} \\ {\space\space\space \text{Rounding down the price to } $250, 15} &{} \\ {\space\space\space \text{tablets would cost }$3,750,\text{ while } 16} &{} \\ {\space\space\space \text{tablets would be }$4,000.\text{So a}} &{} \\ {\space\space\space \text{maximum of 15 tablets at }$254.12} &{} \\ {\space\space\space \text{seems reasonable.}} &{} \\ {\textbf{Step 7. Answer }\text{the question with a complete sentence.}} &{\text{Dawn can buy a maximum of 15 tablets.}} \\ \end{array}\)

Exemple$\PageIndex{29}$

Angie a 20$ à dépenser en boîtes de jus pour le pique-nique préscolaire de son fils. Chaque paquet de boîtes de jus coûte 2,63$. Quel est le nombre maximum de packs qu'elle peut acheter ?

Réponse: Angie peut acheter 7 sachets de jus.

Exemple$\PageIndex{30}$

Daniel veut faire une surprise à sa copine avec une fête d'anniversaire dans son restaurant préféré. Le dîner coûtera 42,75$ par personne, pourboire et taxes compris. Son budget pour le parti est de 500$. Quel est le nombre maximum de personnes que Daniel peut avoir à la fête ?

Réponse: Daniel peut avoir 11 personnes à la fête.

Exemple$\PageIndex{31}$

Le forfait téléphonique de Taleisha lui coûte 28,80$ par mois plus 0,20$ par SMS. Combien de textos peut-elle envoyer/recevoir et garder sa facture de téléphone mensuelle ne dépassant pas 50$ ?

Réponse: \(\begin{array} {ll} {\textbf{Step 1. Read }\text{the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what you are looking for.}} &{\text{the number of text messages Taleisha can make}} \\ {\textbf{Step 3. Name }\text{what you are looking for.}} &{} \\ {} &{} \\ {} &{\text{Let }t= \text{the number of text messages.}} \\ {\text{Choose a variable to represent that}} &{} \\ {\text{quantity.}} &{} \\ {\textbf{Step 4. Translate }\text{Write a sentence that}} &{} \\ {\text{gives the information to find it.}} &{$28.80\text{ plus }$0.20\text{ times the number of}} \\ {} &{\text{text messages is less than or equal to }$50.} \\ {} &{28.80+0.20t \leq 50} \\ {\space\space\space \text{Translate into an inequality.}} &{} \\ {\textbf{Step 5. Solve }\text{the inequality.}} &{} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 0.2t\leq 21.2} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space t\leq 106\text{ text messages}} \\ {} &{} \\ {\textbf{Step 6. Check }\text{the answer in the problem}} &{} \\ {\text{and make sure it makes sense.}} &{} \\ {} &{} \\ {} &{} \\{\space\space\space \text{Yes, }28.80+0.20(106)=50.} &{} \\ {\textbf{Step 7. Write }\text{a sentence that answers the question.}} &{} \\ {} &{\text{Taleisha can send/receive no more than}} \\ {} &{106\text{ text messages to keep her bill no}} \\ {} &{\text{more than } $50.} \\ \end{array}\)

Exemple$\PageIndex{32}$

Sergio et Lizeth ont un budget de vacances très serré. Ils prévoient de louer une voiture auprès d'une entreprise qui facture 75$ par semaine plus 0,25$ le mile. Combien de miles peuvent-ils parcourir pendant la semaine tout en respectant leur budget de 200$ ?

Réponse: Sergio et Lizeth ne peuvent pas parcourir plus de 500 miles.

Exemple$\PageIndex{33}$

La facture de chauffage de Rameen est de 5,42$ par mois plus 1,08$ par chauffage. Combien de thermes Rameen peut-il utiliser s'il veut que sa facture de chauffage ne dépasse pas 87,50$ ?

Réponse: La facture de chauffage de Rameen est de 5,42$ par mois plus 1,08$ par chauffage. Combien de thermes Rameen peut-il utiliser s'il veut que sa facture de chauffage ne dépasse pas 87,50$ ?

Le profit est l'argent qui reste lorsque les coûts ont été soustraits des recettes. Dans l'exemple suivant, nous déterminerons le nombre d'emplois qu'une petite femme d'affaires doit occuper chaque mois pour réaliser un certain profit.

Exemple$\PageIndex{34}$

Felicity a une entreprise de calligraphie. Elle facture 2,50$ par invitation de mariage. Ses dépenses mensuelles s'élèvent à 650$. Combien d'invitations doit-elle écrire pour réaliser un bénéfice d'au moins 2 800$ par mois ?

Réponse: \(\begin{array} {ll} {\textbf{Step 1. Read }\text{the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what you are looking for.}} &{\text{the number of invitations Felicity needs to write}} \\ {\textbf{Step 3. Name }\text{what you are looking for.}} &{\text{Let }j=\text{ the number of invitations.}} \\ {} &{} \\ {\space\space\space\text{Choose a variable to represent it.}} &{} \\ {\textbf{Step 4. Translate. }\text{Write a sentence that}} &{} \\ {\text{gives the information to find it.}} &{$2.50 \text{ times the number of invitations}} \\ {} &{\text{minus }$650\text{ is at least }$2,800.} \\ {} &{\space\space\space 2.50j−650\geq 2,800} \\ {\space\space\space \text{Translate into an inequality.}} &{} \\ {\textbf{Step 5. Solve }\text{the inequality.}} &{} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 2.5j\geq 3,450} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space j\geq 1,380 \text{ invitations}} \\ {\textbf{Step 6. Check }\text{the answer in the problem}} &{} \\ {\text{and make sure it makes sense.}} &{} \\ {} &{} \\ {} &{} \\ {\space\space\space \text{If Felicity wrote }1400\text{ invitations, her}} &{} \\ {\space\space\space \text{profit would be }2.50(1400)−650, \text{or}} &{} \\ {\space\space\space $2,850.\text{ This is more than }$2800.} &{} \\ {\textbf{Step 7. Write }\text{a sentence that answers the question.}} &{\text{Felicity must write at least }1,380\text{ invitations.}} \\ \end{array}\)

Exemple$\PageIndex{35}$

Caleb a une entreprise de garde d'animaux de compagnie. Il facture 32$ de l'heure. Ses dépenses mensuelles s'élèvent à 2 272$. Combien d'heures doit-il travailler pour réaliser un bénéfice d'au moins 800$ par mois ?

Réponse: Caleb doit travailler au moins 96 heures.

Exemple$\PageIndex{36}$

Elliot possède une entreprise d'entretien paysager. Ses dépenses mensuelles s'élèvent à 1 100$. S'il facture 60$ par emploi, combien d'emplois doit-il occuper pour réaliser un bénéfice d'au moins 4 000 dollars par mois ?

Réponse: Elliot doit occuper au moins 85 emplois.

Il existe de nombreuses situations dans lesquelles plusieurs quantités contribuent à la dépense totale. Nous devons nous assurer de prendre en compte toutes les dépenses individuelles lorsque nous résolvons de tels problèmes.

Exemple$\PageIndex{37}$

Malik prévoit un voyage de vacances d'été de six jours. Il a des économies de 840$ et gagne 45$ de l'heure pour le tutorat. Le voyage lui coûtera 525$ pour le billet d'avion, 780$ pour la nourriture et les visites touristiques et 95$ par nuit pour l'hôtel. Combien d'heures doit-il donner des cours pour avoir suffisamment d'argent pour payer le voyage ?

Réponse: \(\begin{array} {ll} {} &{} \\ {\textbf{Step 1. Read }\text{the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what you are looking for.}} &{\text{the number of hours Malik must tutor}} \\ {\textbf{Step 3. Name }\text{what you are looking for.}} &{} \\ {} &{} \\ {} &{\text{Let }h=\text{ the number of hours.}} \\ {\space\space\space\space\space\space\space \text{Choose a variable to represent that}} &{} \\ {\space\space\space\space\space\space\space \text{quantity.}} &{} \\ {\textbf{Step 4. Translate. }\text{Write a sentence that}} &{} \\ {\text{gives the information to find it.}} &{} \\ {} &{\text{The expenses must be less than or equal to}} \\{} &{\text{the income. The cost of airfare plus the}} \\{} &{\text{cost of food and sightseeing and the hotel}} \\{} &{\text{bill must be less than the savings plus the}} \\{} &{\text{amount earned tutoring.}} \\{} &{} \\ {} &{} \\ {} &{} \\ {} &{} \\ {\space\space\space\space\space\space\space \text{Translate into an inequality.}} &{525+780+95(6)\leq 840+45h} \\ {\textbf{Step 5. Solve }\text{the inequality.}} &{} \\ {} &{} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 1,875\leq 840+45h} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 1,035\leq 45h} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 23\leq h} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space h\geq 23} \\ {} &{} \\ {} &{} \\ {\textbf{Step 6. Check }\text{the answer in the problem}} &{} \\ {\text{and make sure it makes sense.}} &{} \\ {\text{We substitute 23 into the inequality.}} &{} \\ {} &{} \\ {} &{} \\ {\space\space\space\space\space\space\space\space 1,875\leq 840+45h} &{} \\ {\space\space\space\space\space\space\space\space 1,875\leq 840+45(23)} &{} \\ {\space\space\space\space\space\space\space\space 1,875\leq 1875} &{} \\ {\textbf{Step 7. Write }\text{a sentence that answers the question.}} &{\text{Malik must tutor at least }23\text{ hours.}} \\ \end{array}\)

Exemple$\PageIndex{38}$

La meilleure amie de Brenda organise un mariage à destination et l'événement durera trois jours. Brenda a des économies de 500$ et peut gagner 15$ de l'heure en faisant du baby-sitting. Elle s'attend à payer 350$ par billet d'avion, 375$ pour la nourriture et les divertissements et 60$ par nuit pour sa part d'une chambre d'hôtel. Combien d'heures doit-elle faire du baby-sitting pour avoir assez d'argent pour payer le voyage ?

Réponse: Brenda doit garder les enfants pendant au moins 27 heures.

Exemple$\PageIndex{39}$

Josue veut faire un road trip de 10 nuits avec des amis au printemps prochain. Cela lui coûtera 180$ pour l'essence, 450$ pour la nourriture et 49$ par nuit pour partager une chambre de motel. Il a économisé 520$ et peut gagner 30$ par allée en pelletant de la neige. Combien d'allées doit-il déblayer pour avoir assez d'argent pour payer le voyage ?

Réponse: Josue doit déblayer au moins 20 allées.

Concepts clés

Inégalités, lignes numériques et notation par intervalles
$x>a \quad x\geq a\quad x<a\quad x\leq a$
$La figure montre que la solution de l'inégalité x est supérieure à a est indiquée sur une ligne numérique avec une parenthèse gauche en a et un ombrage vers la droite, et que la solution en notation par intervalles est l'intervalle de a à l'infini entre parenthèses. Il montre que la solution de l'inégalité x est supérieur ou égal à a est indiqué sur une ligne numérique avec un crochet gauche en a et un ombrage vers la droite, et que la solution en notation par intervalles est l'intervalle a à l'infini entre crochets gauche et parenthèses droites. Cela montre que la solution de l'inégalité x est inférieure à a est indiquée sur une ligne numérique avec une parenthèse droite en a et un ombrage vers la gauche, et que la solution en notation par intervalles est l'intervalle entre l'infini négatif et a entre parenthèses. Cela montre que la solution de l'inégalité x est inférieure ou égale à a est indiquée sur une ligne numérique avec un crochet droit en a et un ombrage vers la gauche, et que la solution en notation par intervalles est négative de l'infini à a entre parenthèses gauche et droite.$
Inégalités linéaires
- Une inégalité linéaire est une inégalité dans une variable qui peut être écrite sous l'une des formes suivantes où a, b et c sont des nombres réels et$a\neq 0$ :
  \[ax+b<c, \qquad ax+b\leq c, \qquad ax+b>c, \qquad ax+b\geq c.\nonumber\]
Propriété d'addition et de soustraction de l'inégalité
- Pour tous les nombres a, b et c, si a<b, alors a<b, alors
  \[\begin{array} {ll} {a+c<b+c} &{a−c<b−c} \\ {a+c>b+c} &{a−c>b−c} \\ \end{array} \nonumber\]
- Nous pouvons ajouter ou soustraire la même quantité des deux côtés d'une inégalité tout en conservant l'inégalité.
Propriété de multiplication et de division de l'inégalité
- Pour tous les nombres a, b et c,
  $\begin{array} {l} \text{multiply or divide by a }\textbf{positive} \\ \\ \space\space\space\space\space\space\space\text{if }a<b\text{ and }c>0,\text{ then } ac<bc\text{ and }\frac{a}{c}<\frac{b}{c}. \\ \space\space\space\space\space\space\space\text{if }a>b\text{ and }c>0,\text{ then } ac>bc\text{ and }\frac{a}{c}>\frac{b}{c}. \\ \text{multiply or divide by a }\textbf{negative} \\ \\ \space\space\space\space\space\space\space\text{if }a<b\text{ and }c<0,\text{ then } ac>bc\text{ and }\frac{a}{c}>\frac{b}{c}. \\ \space\space\space\space\space\space\space\text{if }a>b\text{ and }c<0,\text{ then } ac<bc\text{ and }\frac{a}{c}<\frac{b}{c}. \\ \end{array}$

Phrases indiquant des inégalités

$>$	$\geq$	$<$	$\leq$
\ (> \) « >est supérieur à ce qui est supérieur à ce qui dépasse	\ (\ geq \) » data-valign="middle">est supérieur ou égal à est au moins égal au minimum	\ (est < \) » data-valign="middle"> inférieur à est inférieur à ce qui est inférieur à	\ (\ leq \) » data-valign="middle">est inférieur ou égal à est au plus égal au maximum

	\( x \geq -3 \)
Ombrez à droite de\(−3\), et placez un support sur\(−3\).	$.$
Écrivez en notation par intervalles.	\( [-3, \infty) \)

	\( x \leq -\dfrac{3}{5} \)
Ombrez à gauche de\(−\frac{3}{5}\), et placez un support sur\(−\frac{3}{5}\).	$.$
Écrivez en notation par intervalles.	\( \bigg( -\infty, \dfrac{3}{5}\bigg] \)

		\(-3 < x < 4\)
Ombre entre\(−3\) et 4. Mettez une parenthèse à\(−3\) et 4.		$.$
Écrivez en notation par intervalles.		\( (-3,4) \)

			\( -6 \leq x < -1 \)
Ombre entre\(−6\) et −1. Placez un crochet à\(−6\) et une parenthèse à −1.			$.$
Écrivez en notation par intervalles.			\( [-6,1) \)

	\(8p+3(p−12)>7p−28\)
Simplifiez chaque côté autant que possible.
Distribuez.	\(8p+3p−36>7p−28\)
Combinez les mêmes termes.	\(11p−36>7p−28\)
Soustrayez\(7p\) des deux côtés pour collecter les variables sur la gauche, puisque\(11>7\).	\(11p−36−7p>7p−28−7p\)
Simplifiez.	\(4p−36>−28\)
Ajoutez\(36\) des deux côtés pour collecter les constantes sur la droite.	\(4p−36+36>−28+36\)
Simplifiez.	\(4p>8\)
Divisez les deux côtés de l'inégalité par \(4\) : l'inégalité reste la même.	\(\dfrac{4p}{4}>\dfrac{8}{4}\)
Simplifiez.	\(p>2\)
Représentez graphiquement la solution sur la ligne numérique.	$.$
Écrivez la solution en notation par intervalles.	\((2,\infty)\)

INÉGALITÉS, LIGNES NUMÉRIQUES ET NOTATION PAR INTERVALLES

Exemple\(\PageIndex{1}\)

Exemple\(\PageIndex{3}\)

Exemple\(\PageIndex{5}\)

Exemple\(\PageIndex{6}\)

INÉGALITÉ LINÉAIRE

PROPRIÉTÉ D'ADDITION ET DE SOUSTRACTION DE L'

PROPRIÉTÉ DE MULTIPLICATION ET DE DIVISION DES INÉGALITÉS

Exemple\(\PageIndex{7}\)

Exemple\(\PageIndex{9}\)

Exemple\(\PageIndex{10}\)

Exemple\(\PageIndex{11}\)

Exemple\(\PageIndex{12}\)

Exemple\(\PageIndex{15}\)

Exemple\(\PageIndex{16}\)

Exemple\(\PageIndex{17}\)

Exemple\(\PageIndex{18}\)

Exemple\(\PageIndex{19}\)

Exemple\(\PageIndex{20}\)

Exemple\(\PageIndex{21}\)

Exemple\(\PageIndex{22}\)

Exemple\(\PageIndex{23}\)

Exemple\(\PageIndex{24}\)

Exemple\(\PageIndex{25}\)

Exemple\(\PageIndex{27}\)

Exemple\(\PageIndex{28}\)

Exemple\(\PageIndex{29}\)

Exemple\(\PageIndex{30}\)

Exemple\(\PageIndex{31}\)

Exemple\(\PageIndex{32}\)

Exemple\(\PageIndex{33}\)

Exemple\(\PageIndex{34}\)

Exemple\(\PageIndex{35}\)

Exemple\(\PageIndex{36}\)

Exemple\(\PageIndex{37}\)

Exemple\(\PageIndex{38}\)

Exemple\(\PageIndex{39}\)

	\( x < 2.5 \)
Ombrez vers la gauche de 2,5 et placez une parenthèse à 2,5.	$.$
Écrivez en notation par intervalles.	\( (-\infty, 2.5) \)

			\( 0 \leq x \leq 2.5 \)
Ombre entre 0 et 2,5. Placez un crochet à 0 et à 2,5.			$.$
Écrivez en notation par intervalles.			\( [0, 2.5] \)

Simplifiez chaque côté autant que possible.		\(8x−2(5−x)<4(x+9)+6x\)
Distribuez.		\(8x−10+2x<4x+36+6x\)
Combinez les mêmes termes.		\(10x−10<10x+36\)
Soustrayez\({\color{red}{10x}}\) des deux côtés pour collecter les variables sur la gauche.		\(10x−10\,{\color{red}{-\,10x}}<10x+36\,{\color{red}{-\,10x}}\)
Simplifiez.		\(−10<36\)
Ils\(x\) ont disparu, et nous avons une déclaration vraie.		L'inégalité est une identité. La solution, ce sont tous des nombres réels.
Représentez graphiquement la solution sur la ligne numérique.		$.$
Écrivez la solution en notation par intervalles.		\((−\infty,\infty)\)

	\(\frac{1}{3}a−\frac{1}{8}a>\frac{5}{24}a+\frac{3}{4}\)
Multipliez les deux côtés par l'écran LCD, 24, pour effacer les fractions.	\({\color{red}{24}}\left(\dfrac{1}{3}a−\dfrac{1}{8}a\right)>\,{\color{red}{24}}\left(\dfrac{5}{24}a+\dfrac{3}{4}\right)\)
Simplifiez.	\( 8a - 3a > 5a + 18 \)
Combinez les mêmes termes.	\( 5a > 5a + 18\)
Soustrayez\(5a\) des deux côtés pour collecter les variables sur la gauche.	\( 5a \,{\color{red}{-\,5a}} > 5a \,{\color{red}{-\,5a}} + 18\)
Simplifiez.	\(0 > 18 \)
La déclaration est fausse.	L'inégalité est contradictoire. Il n'y a pas de solution.
Représentez graphiquement la solution sur la ligne numérique.	$.$
Écrivez la solution en notation par intervalles.	Il n'y a pas de solution.

	$.$
Traduisez.	\(x - 27 \geq 48\)
Résoudre : ajoutez-en 27 des deux côtés.	\( x - 27 \, {\color{red}{+\, 27}} \geq 48 \, {\color{red}{+\, 27}}\)
Simplifiez.	\(x \geq 75\)
Graphique sur la ligne numérique.	$.$
Écrivez en notation par intervalles.	\([75, \infty)\)