2.2 : Utiliser une stratégie générale pour résoudre des équations linéaires
- Page ID
- 194407
À la fin de cette section, vous serez en mesure de :
- Utiliser les propriétés commutatives et associatives
- Utilisez les propriétés d'identité, d'inverse et de zéro
- Simplifier les expressions en utilisant la propriété distributive
Avant de commencer, répondez à ce questionnaire de préparation.
- Simplifiez :\(\frac{3}{2}(12x+20)\).
- Simplifiez :\(5−2(n+1)\).
- Trouvez l'écran LCD de\(\frac{5}{6}\) et\(\frac{1}{4}\).
Résoudre des équations linéaires en utilisant une stratégie générale
Résoudre une équation, c'est comme découvrir la réponse à un casse-tête. Le but de la résolution d'une équation est de trouver la ou les valeurs de la variable qui en fait une déclaration vraie. Toute valeur de la variable qui rend l'équation vraie est appelée solution de l'équation. C'est la réponse au casse-tête !
La solution d'une équation est la valeur d'une variable qui fournit une déclaration vraie lorsqu'elle est substituée dans l'équation.
Pour déterminer si un nombre est une solution à une équation, nous substituons la valeur à la variable de l'équation. Si l'équation qui en résulte est une déclaration vraie, le nombre est une solution de l'équation.
- Remplacez la variable par un nombre dans l'équation.
- Simplifiez les expressions des deux côtés de l'équation.
- Déterminez si l'équation résultante est vraie.
- Si c'est vrai, le nombre est une solution.
- Si ce n'est pas vrai, le nombre n'est pas une solution.
Déterminez si les valeurs sont des solutions à l'équation :\(5y+3=10y−4\).
- \(y=\frac{3}{5}\)
- \(y=\frac{7}{5}\)
Comme la solution d'une équation est la valeur de la variable qui rend l'équation vraie, commencez par remplacer la valeur de la solution par la variable.
un.
| \(5 y+3=10 y-4\) | |
| Substitut\(\color{rec}\frac{3}{5}\) de\(y\) | \(5\left( \color{red} \frac{3}{5} \color{black}\right)+3 \stackrel{?}{=} 10\left( \color{red}\frac{3}{5} \color{black}\right)-4\) |
| Multipliez. | \(3+3\stackrel{?}{=} 6-4\) |
| Simplifiez. | \(6 \neq 2\) |
Puisque\(y=\frac{3}{5}\) n'aboutit pas à une véritable équation, n'\(y=\frac{3}{5}\)est pas une solution à l'équation\(5y+3=10y−4.\)
b.
| \(5 y+3=10 y-4\) | |
| Substitut\(\color{red} \frac{7}{5}\) de\(y\) | \(5\left(\color{red} \frac{7}{5} \color{black}\right)+3 \stackrel{?}{=} 10\left(\color{red}\frac{7}{5}\color{back}\right)-4\) |
| Multipliez. | \(7+3 \stackrel{?}{=} 14-4\) |
| Simplifiez. | \(10=10 \checkmark\) |
Puisque le\(y=\frac{7}{5}\) résultat est une vraie équation,\(y=\frac{7}{5}\) est une solution à l'équation\(5y+3=10y−4.\)
Déterminez si les valeurs sont des solutions à l'équation :\(9y+2=6y+3.\)
- \(y=\frac{4}{3}\)
- \(y=\frac{1}{3}\)
- Répondez à une
-
non
- Réponse b
-
oui
Déterminez si les valeurs sont des solutions à l'équation :\(4x−2=2x+1\).
- \(x=\frac{3}{2}\)
- \(x=−\frac{1}{2}\)
- Répondez à une
-
oui
- Réponse b
-
non
Il existe de nombreux types d'équations que nous allons apprendre à résoudre. Dans cette section, nous allons nous concentrer sur une équation linéaire.
Une équation linéaire est une équation à une variable qui peut être écrite, où\(a\) et\(b\) sont des nombres réels et\(a≠0\), comme suit :
\[ax+b=0\]
Pour résoudre une équation linéaire, il est conseillé de disposer d'une stratégie globale qui peut être utilisée pour résoudre n'importe quelle équation linéaire. Dans l'exemple suivant, nous allons donner les étapes d'une stratégie générale pour résoudre n'importe quelle équation linéaire. Simplifier chaque côté de l'équation autant que possible facilite d'abord le reste des étapes.
Résoudre :\(7(n−3)−8=−15\)
- Réponse
-




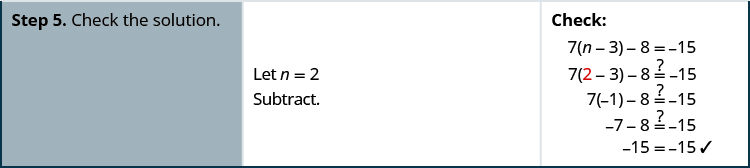
Résoudre :\(2(m−4)+3=−1.\)
- Réponse
-
\(m=2\)
Résoudre :\(5(a−3)+5=−10.\)
- Réponse
-
\(a=0\)
Ces étapes sont résumées dans la stratégie générale de résolution d'équations linéaires ci-dessous.
- Simplifiez chaque côté de l'équation autant que possible.
Utilisez la propriété distributive pour supprimer les parenthèses.
Combinez les mêmes termes. - Collectez tous les termes variables d'un côté de l'équation.
Utilisez la propriété d'addition ou de soustraction de l'égalité.
- Recueillez tous les termes constants de l'autre côté de l'équation.
Utilisez la propriété d'addition ou de soustraction de l'égalité.
- Rendre le coefficient du terme variable égal à 1.
Utilisez la propriété de multiplication ou de division de l'égalité.
Indiquez la solution de l'équation.
- Vérifiez la solution.
Remplacez la solution dans l'équation d'origine pour vous assurer que le résultat est vrai.
Résoudre :\(\frac{2}{3}(3m−6)=5−m\).
- Réponse
-
\(\frac{2}{3}(3 m-6)=5-m\) Distribuez. \(2 m-4=5-m\) Ajoutez\(m\) des deux côtés pour obtenir les variables uniquement sur la gauche. 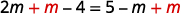
Simplifiez. \(3 m-4=5\) Ajoutez\(4\) des deux côtés pour obtenir des constantes uniquement sur la droite. 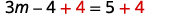
Simplifiez. \(3 m=9\) Divisez les deux côtés par trois. 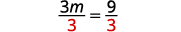
Simplifiez. \(m=3\)
| Vérifiez : | 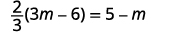 |
| Laissez\(m=3\). | 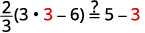 |
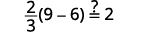 |
|
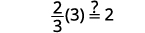 |
|
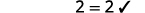 |
Résoudre :\(\frac{1}{3}(6u+3)=7−u\).
- Réponse
-
\(u=2\)
Résoudre :\(\frac{2}{3}(9x−12)=8+2x\).
- Réponse
-
\(x=4\)
Nous pouvons résoudre des équations en plaçant tous les termes variables de chaque côté du signe égal. En rassemblant les termes des variables du côté où le coefficient de la variable est le plus grand, nous évitons de travailler avec certains négatifs. Ce sera une bonne stratégie lorsque nous résoudrons les inégalités plus loin dans ce chapitre. Cela nous aide également à prévenir les erreurs avec des négatifs.
Résoudre :\(4(x−1)−2=5(2x+3)+6\).
- Réponse
-
\(4(x-1)-2=5(2 x+3)+6\) Distribuez. \(4 x-4-2=10 x+15+6\)
Combinez les mêmes termes. \(4 x-6=10 x+21\) Soustrayez\(4x\) de chaque côté pour obtenir les variables uniquement sur la droite depuis\(10>4\). \(4 x \color{red} -4 \color{black} x-6=10 x \color{red}-4 x \color{black}+21\) Simplifiez. \(-6=6 x+21\) Soustrayez\(21\) de chaque côté pour obtenir les constantes sur la gauche. \(-6 \color{red} -21 \color{black} =6 x+21 \color{red}-21\)
Simplifiez. \(-27=6 x\) Divisez les deux côtés par\(6\). \(\frac{-27}{\color{red}6} \color{black}=\frac{6 x}{\color{red}6}\) Simplifiez. \(-\frac{9}{2}=x\) Vérifiez : \(4(x-1)-2=5(2 x+3)+6\)\) Laissez\(x=−92\). 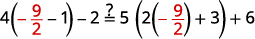
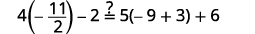
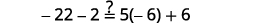
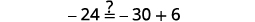
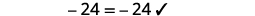
Résoudre :\(6(p−3)−7=5(4p+3)−12.\)
- Réponse
-
\(p=−2\)
Résoudre :\(8(q+1)−5=3(2q−4)−1.\)
- Réponse
-
\(q=−8\)
Résoudre :\(10[3−8(2s−5)]=15(40−5s)\).
- Réponse
-
\(10[3-8(2 s-5)]=15(40-5 s)\) Simplifiez d'abord à partir des parenthèses les plus intérieures. \(10[3-16 s+40]=15(40-5 s)\) Combinez des termes similaires entre crochets. \(10[43-16 s]=15(40-5 s)\) Distribuez. \(430-160 s=600-75 s\) Ajoutez\(160s\) des deux côtés pour\(160s\) obtenir les deux côtés et obtenir les variables vers la droite. 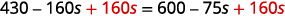
Simplifiez. \(430=600+85 s\) Soustrayez\(600\) des deux côtés pour obtenir les constantes vers la gauche. 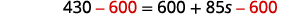
Simplifiez. \(-170=85 s\) Divisez les deux côtés par\(85\). 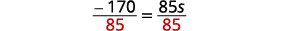
Simplifiez. \(-2=s,\)donc\(s = -2\) Vérifiez : \(10[3-8(2 s-5)]=15(40-5 s)\) Laissez\(s=−2\). 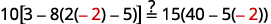
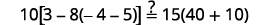
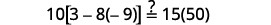
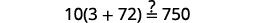
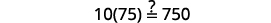
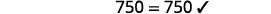
Résoudre :\(6[4−2(7y−1)]=8(13−8y)\).
- Réponse
-
\(y=−\frac{17}{5}\)
Résoudre :\(12[1−5(4z−1)]=3(24+11z).\)
- Réponse
-
\(z=0\)
Classer les équations
La véracité ou non d'une équation dépend de la valeur de la variable. L'équation\(7x+8=−13\) est vraie lorsque nous remplaçons la variable, x, par la valeur\(−3\), mais elle n'est pas vraie lorsque nous remplaçons x par une autre valeur. Une telle équation est appelée équation conditionnelle. Toutes les équations que nous avons résolues jusqu'à présent sont des équations conditionnelles.
Une équation vraie pour une ou plusieurs valeurs de la variable et fausse pour toutes les autres valeurs de la variable est une équation conditionnelle.
Examinons maintenant l'équation\(7y+14=7(y+2)\). Reconnaissez-vous que le côté gauche et le côté droit sont équivalents ? Voyons ce qui se passe lorsque nous résolvons pour y.
Résoudre :
| \(7 y+14=7(y+2)\) | |
| Distribuez. | \(7 y+14=7 y+14\) |
| Soustrayez\(7y\) de chaque côté pour obtenir le\(y’\) s d'un côté. | \(7 y \color{red}-7 y \color{black} +14=7 y \color{red} -7 y \color{black}+14\) |
| Simplifiez-vous : les\(y\) A sont éliminés. | \(14=14\) |
| Mais\(14=14\) c'est vrai. |
Cela signifie que l'équation\(7y+14=7(y+2)\) est vraie pour toute valeur de\(y\). Nous disons que la solution à l'équation se trouve dans tous les nombres réels. Une équation qui est vraie pour n'importe quelle valeur de la variable est appelée identité.
Une équation qui est vraie pour n'importe quelle valeur de la variable est appelée identité.
La solution d'une identité est valable pour tous les nombres réels.
Que se passe-t-il lorsque nous résolvons l'équation\(−8z=−8z+9?\)
Résoudre :
| \(-8 z=-8 z+9\) | |
| Ajoutez\(8z\) des deux côtés pour laisser la constante seule sur la droite. | \(-8 z \color{red} +8 z \color{black}=-8 z \color{red}+8 z \color{black} +9\) |
| Simplifiez-vous : les\(z\) A sont éliminés. | \(0 \neq 9\) |
| Mais\(0≠9\). |
La résolution de l'équation\(−8z=−8z+9\) a conduit à la fausse déclaration\(0=9\). L'équation ne\(−8z=−8z+9\) sera vraie pour aucune valeur de\(z\). Il n'y a pas de solution. Une équation qui n'a pas de solution ou qui est fausse pour toutes les valeurs de la variable est appelée contradiction.
Une équation qui est fausse pour toutes les valeurs de la variable est appelée contradiction.
Une contradiction n'a pas de solution.
Les exemples suivants nous demanderont de classer une équation comme conditionnelle, une identité ou une contradiction.
Classifiez l'équation comme une équation conditionnelle, une identité ou une contradiction, puis énoncez la solution :\(6(2n−1)+3=2n−8+5(2n+1)\).
- Réponse
-
\(6(2 n-1)+3=2 n-8+5(2 n+1)\) Distribuez. \(12 n-6+3=2 n-8+10 n+5\) Combinez les mêmes termes. \(12 n-3=12 n-3\) Soustrayez\(12n\) de chaque côté pour obtenir les\(n\) « d'un côté ». 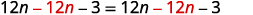
Simplifiez. \(-3=-3\) C'est une affirmation vraie. L'équation est une identité. La solution, ce sont tous des nombres réels.
Classifiez l'équation en tant qu'équation conditionnelle, identité ou contradiction, puis énoncez la solution :\(4+9(3x−7)=−42x−13+23(3x−2).\)
- Réponse
-
identité ; tous les nombres réels
Classifiez l'équation en tant qu'équation conditionnelle, identité ou contradiction, puis énoncez la solution :\(8(1−3x)+15(2x+7)=2(x+50)+4(x+3)+1.\)
- Réponse
-
identité ; tous les nombres réels
Classifiez l'équation comme une équation conditionnelle, une identité ou une contradiction, puis énoncez la solution :\(8+3(a−4)=0\).
- Réponse
-
\(8+3(a-4)=0\) Distribuez. \(8+3 a-12=0\) Combinez les mêmes termes. \(3 a-4=0\) Ajouter\(4\) des deux côtés. \(3 a-4 \color{red}+4 \color{black}=0 \color{red}+4\) Simplifiez. \(3 a=4\) Diviser. \(\frac{3 a}{\color{red}3} \color{black}=\frac{4}{\color{red}3}\) Simplifiez. \(a=\frac{4}{3}\) L'équation est vraie quand\(a=\frac{4}{3}\). Il s'agit d'une équation conditionnelle. La solution est\(a=\frac{4}{3}\).
Classifiez l'équation comme une équation conditionnelle, une identité ou une contradiction, puis énoncez la solution :\(11(q+3)−5=19\).
- Réponse
-
équation conditionnelle ;\(q=−\frac{9}{11}\)
Classifiez l'équation comme une équation conditionnelle, une identité ou une contradiction, puis énoncez la solution :\(6+14(k−8)=95\).
- Réponse
-
équation conditionnelle ;\(k=\frac{201}{14}\)
Classifiez l'équation comme une équation conditionnelle, une identité ou une contradiction, puis énoncez la solution :\(5m+3(9+3m)=2(7m−11)\).
- Réponse
-
\(5 m+3(9+3 m)=2(7 m-11)\) Distribuez. \(5 m+27+9 m=14 m-22\) Combinez les mêmes termes. \(14 m+27=14 m-22\) Soustrayez\(14m\) des deux côtés. \(14 m+27 \color{red}-14 m \color{black}=14 m-22 \color{red}-14 m\) Simplifiez. \(27 \neq-22\) Mais\(27≠−22\). L'équation est contradictoire. Il n'y a pas de solution.
Classifiez l'équation comme une équation conditionnelle, une identité ou une contradiction, puis énoncez la solution :\(12c+5(5+3c)=3(9c−4)\).
- Réponse
-
contradiction ; pas de solution
Classifiez l'équation comme une équation conditionnelle, une identité ou une contradiction, puis énoncez la solution :\(4(7d+18)=13(3d−2)−11d\).
- Réponse
-
contradiction ; pas de solution
Nous résumons les méthodes de classification des équations dans le tableau.
| Type d'équation | Que se passe-t-il lorsque vous le résolvez ? | Solution |
|---|---|---|
| Équation conditionnelle | Vrai pour une ou plusieurs valeurs des variables et faux pour toutes les autres valeurs | Une ou plusieurs valeurs |
| Identité | Vrai pour n'importe quelle valeur de la variable | Tous les nombres réels |
| Contro | Faux pour toutes les valeurs de la variable | Aucune solution |
Résolvez des équations avec des coefficients de fraction
Nous pourrions utiliser la stratégie générale pour résoudre l'exemple suivant. Cette méthode fonctionnerait bien, mais de nombreux étudiants ne se sentent pas très confiants lorsqu'ils voient toutes ces fractions. Nous allons donc montrer une méthode alternative pour résoudre des équations avec des fractions. Cette méthode alternative élimine les fractions.
Nous appliquerons la propriété de multiplication de l'égalité et multiplierons les deux côtés d'une équation par le plus petit dénominateur commun (LCD) de toutes les fractions de l'équation. Le résultat de cette opération sera une nouvelle équation, équivalente à la première, mais sans fractions. Ce processus s'appelle effacer l'équation des fractions.
Pour effacer une équation de décimales, nous pensons à toutes les décimales sous forme de fraction, puis nous trouvons l'écran LCD de ces dénominateurs.
Résoudre :\(\frac{1}{12}x+\frac{5}{6}=\frac{3}{4}\).
- Réponse
-



Résoudre :\(\frac{1}{4}x+\frac{1}{2}=\frac{5}{8}\).
- Réponse
-
\(x=\frac{1}{2}\)
Résoudre :\(\frac{1}{8}x+\frac{1}{2}=\frac{1}{4}\).
- Réponse
-
\(x=−2\)
Remarquez que dans l'exemple précédent, une fois que nous avons effacé l'équation des fractions, l'équation était similaire à celles que nous avons résolues plus tôt dans ce chapitre. Nous avons remplacé le problème par un problème que nous savions déjà résoudre. Nous avons ensuite utilisé la stratégie générale pour résoudre des équations linéaires.
- Déterminez le plus petit dénominateur commun (LCD) de toutes les fractions et décimales (sous forme de fraction) de l'équation.
- Multipliez les deux côtés de l'équation par cet écran LCD. Cela efface les fractions et les décimales.
- Résolvez en utilisant la stratégie générale de résolution d'équations linéaires.
Résoudre :\(5=\frac{1}{2}y+\frac{2}{3}y−\frac{3}{4}y\).
- Réponse
-
Nous voulons effacer les fractions en multipliant les deux côtés de l'équation par l'écran LCD de toutes les fractions de l'équation.
Trouvez l'écran LCD de toutes les fractions de l'équation. \(5=\frac{1}{2} y+\frac{2}{3} y-\frac{3}{4} y\) L'écran LCD est\(12\). Multipliez les deux côtés de l'équation par\(12\). \(\color{red}12 \color{black}(5)=\color{red}12 \color{black} \cdot\left(\frac{1}{2} y+\frac{2}{3} y-\frac{3}{4} y\right)\) Distribuez. \(12(5)=12 \cdot \frac{1}{2} y+12 \cdot \frac{2}{3} y-12 \cdot \frac{3}{4} y\) Simplifier : remarquez qu'il n'y a plus de fractions. \(60=6 y+8 y-9 y\) Combinez les mêmes termes. \(60=5 y\) Divisez par cinq. \(\frac{60}{\color{red}5} \color{black}=\frac{5 y}{\color{red}5}\) Simplifiez. \(12=y\) Vérifiez : \(5=\frac{1}{2} y+\frac{2}{3} y-\frac{3}{4} y\) Laissez\(y=12\). 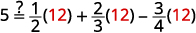
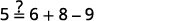

Résoudre :\(7=\frac{1}{2}x+\frac{3}{4}x−\frac{2}{3}x\).
- Réponse
-
\(x=12\)
Résoudre :\(−1=\frac{1}{2}u+\frac{1}{4}u−\frac{2}{3}u\).
- Réponse
-
\(u=−12\)
Dans l'exemple suivant, nous allons distribuer avant d'effacer les fractions.
Résoudre :\(\frac{1}{2}(y−5)=\frac{1}{4}(y−1)\).
- Réponse
-
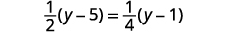
Distribuez. 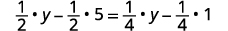
Simplifiez. 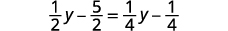
Multipliez par l'écran LCD, quatre. 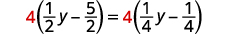
Distribuez. 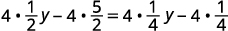
Simplifiez. 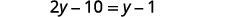
Collectez les variables sur la gauche. 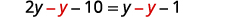
Simplifiez. 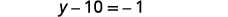
Collectez les constantes sur la droite. 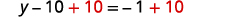
Simplifiez. 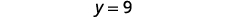
Une autre façon de résoudre cette équation consiste à effacer les fractions sans les distribuer au préalable. Si vous multipliez correctement les facteurs, cette méthode sera plus facile. 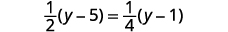
Multipliez par l'écran LCD,\(4\). 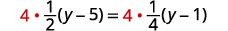
Multipliez quatre fois les fractions. 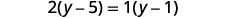
Distribuez. 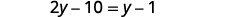
Collectez les variables sur la gauche. 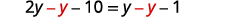.jpg)
Simplifiez. 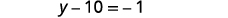
Collectez les constantes sur la droite. 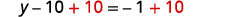
Simplifiez. 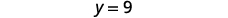
Vérifiez : 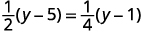
Laissez\(y=9\). 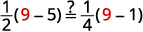
Terminez la vérification vous-même.
Résoudre :\(\frac{1}{5}(n+3)=\frac{1}{4}(n+2)\).
- Réponse
-
\(n=2\)
Résoudre :\(\frac{1}{2}(m−3)=\frac{1}{4}(m−7)\).
- Réponse
-
\(m=−1\)
Lorsque vous multipliez les deux côtés d'une équation par l'écran LCD des fractions, assurez-vous de multiplier chaque terme par l'écran LCD, même s'il ne contient aucune fraction.
Résoudre :\(\frac{4q+3}{2}+6=\frac{3q+5}{4}\)
- Réponse
-
\(\frac{4 q+3}{2}+6=\frac{3 q+5}{4}\) Multipliez les deux côtés par l'écran LCD,\(4\). 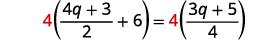
Distribuez. 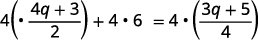
Simplifiez. \(2(4 q+3)+24=3 q+5\) \(8 q+6+24=3 q+5\) \(8 q+30=3 q+5\) Collectez les variables sur la gauche. 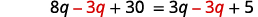
Simplifiez. \(5 q+30=5\) Collectez les constantes sur la droite. 
Simplifiez. \(5 q=-25\) Divisez les deux côtés par cinq. 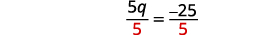
Simplifiez. \(q=-5\) Vérifiez : \(\frac{4 q+3}{2}+6=\frac{3 q+5}{4}\) Laissez\(q=−5.\) 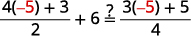
Terminez la vérification vous-même.
Résoudre :\(\frac{3r+5}{6}+1=\frac{4r+3}{3}\).
- Réponse
-
\(r=3\)
Résoudre :\(\frac{2s+3}{2}+1=\frac{3s+2}{4}\).
- Réponse
-
\(s=−8\)
Certaines équations contiennent des décimales. Ce type d'équation peut se produire lorsque nous résolvons des problèmes liés à l'argent ou aux pourcentages. Mais les décimales peuvent également être exprimées sous forme de fractions. Par exemple,\(0.7=\frac{7}{10}\) et\(0.29=\frac{29}{100}\). Ainsi, avec une équation avec des décimales, nous pouvons utiliser la même méthode que celle que nous avons utilisée pour effacer les fractions : multiplier les deux côtés de l'équation par le plus petit dénominateur commun.
L'exemple suivant utilise une équation typique de celles que nous verrons dans les applications monétaires dans une section ultérieure. Notez que nous allons effacer toutes les décimales en multipliant par l'écran LCD leur forme de fraction.
Résoudre :\(0.25x+0.05(x+3)=2.85\).
- Réponse
-
Regardez les décimales et pensez aux fractions équivalentes :
\[0.25=\frac{25}{100}, \; \; \; \;\;\;\;\; 0.05=\frac{5}{100}, \;\;\;\;\;\;\;\; 2.85=2\frac{85}{100}.\]
Remarquez que l'écran LCD est\(100\). En multipliant par l'écran LCD, nous supprimerons les décimales de l'équation.
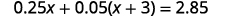
Distribuez d'abord. 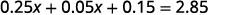
Combinez les mêmes termes. 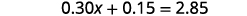
Pour effacer les décimales, multipliez par\(100\). 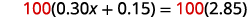
Distribuez. 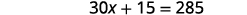
Soustrayez\(15\) des deux côtés. 
Simplifiez. 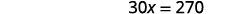
Divisez par\(30\). 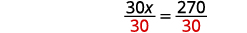
Simplifiez. 
Vérifiez-le vous-même en le remplaçant\(x=9\) dans l'équation d'origine.
Résoudre :\(0.25n+0.05(n+5)=2.95.\)
- Réponse
-
\(n=9\)
Résoudre :\(0.10d+0.05(d−5)=2.15.\)
- Réponse
-
\(d=16\)
Concepts clés
- Comment déterminer si un nombre est une solution à une équation
- Remplacez la variable dans l'équation par le nombre.
- Simplifiez les expressions des deux côtés de l'équation.
- Déterminez si l'équation résultante est vraie.
Si c'est vrai, le nombre est une solution.
Si ce n'est pas vrai, le nombre n'est pas une solution.
- Comment résoudre des équations linéaires à l'aide d'une stratégie générale
- Simplifiez chaque côté de l'équation autant que possible.
Utilisez la propriété distributive pour supprimer les parenthèses.
Combinez les mêmes termes.
- Collectez tous les termes variables d'un côté de l'équation.
Utilisez la propriété d'addition ou de soustraction de l'égalité.
- Recueillez tous les termes constants de l'autre côté de l'équation.
Utilisez la propriété d'addition ou de soustraction de l'égalité.
- Rendre le coefficient du terme variable égal à 1.
Utilisez la propriété de multiplication ou de division de l'égalité.
Indiquez la solution de l'équation.
- Vérifiez la solution.
Remplacez la solution dans l'équation d'origine pour vous assurer que le résultat est vrai.
- Simplifiez chaque côté de l'équation autant que possible.
- Comment résoudre des équations avec des coefficients fractionnels ou décimaux
- Déterminez le plus petit dénominateur commun (LCD) de toutes les fractions et décimales (sous forme de fraction) de l'équation.
- Multipliez les deux côtés de l'équation par cet écran LCD. Cela efface les fractions et les décimales.
- Résolvez en utilisant la stratégie générale de résolution d'équations linéaires.
Lexique
- équation conditionnelle
- Une équation vraie pour une ou plusieurs valeurs de la variable et fausse pour toutes les autres valeurs de la variable est une équation conditionnelle.
- contradiction
- Une équation qui est fausse pour toutes les valeurs de la variable est appelée contradiction. Une contradiction n'a pas de solution.
- identité
- Une équation qui est vraie pour n'importe quelle valeur de la variable est appelée identité. La solution d'une identité réside dans les vrais nombres.
- équation linéaire
- Une équation linéaire est une équation à une variable qui peut être écrite, où a et b sont des nombres réels et\(a≠0\), as\(ax+b=0\).
- solution d'une équation
- La solution d'une équation est la valeur d'une variable qui fournit une déclaration vraie lorsqu'elle est substituée dans l'équation.


