Skip to main content
Global

11.2：粒子物理学概论

  1. Last updated
  2. Save as PDF
  • Page ID
    201954

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    学习目标

    在本节结束时，您将能够：

    • 描述四种基本力以及参与其中的粒子
    • 识别和描述费密子和玻色子
    • 识别并描述夸克和轻子家族
    • 区分粒子和反粒子，并描述它们的相互作用

    基本粒子物理学是研究基本粒子及其在自然界中的相互作用。 那些研究基本粒子物理学的人——粒子物理学家——在他们所研究的系统的规模上与其他物理学家不同。 粒子物理学家不满足于研究细胞、分子、原子甚至原子核的微观世界。 他们对规模甚至比原子核还小的物理过程感兴趣。 同时，它们揭开了自然界中最深刻的奥秘：宇宙是如何开始的？ 是什么解释了宇宙中的质量模式？ 为什么宇宙中的物质比反物质还多？ 为什么能量和动量是保守的？ 宇宙将如何演变？

    四种基本力量

    回答这些问题的重要步骤是了解粒子及其相互作用。 粒子相互作用以四种基本力表示。 按强度递减顺序排列，这些力是强核力、电磁力、弱核力和引力。

    1. 强大的核力量。 强大的核力量是一种非常强大的吸引力，只能在很短的距离（大约\(10^{-15}m\)）内起作用。 强大的核力量负责在原子核中将质子和中子结合在一起。 并非所有粒子都参与强大的核力量；例如，电子和中微子不受其影响。 顾名思义，这支力量比其他力量强得多。
    2. 电磁力。 电磁力可以在很远的距离内起作用（它的射程是无限的），但其强度仅为强核力量的1/100。 据说通过这种力相互作用的粒子具有 “电荷”。 在经典的静电理论（库仑定律）中，电力随相互作用粒子电荷的乘积和它们之间距离的反平方而变化。 与强力形成鲜明对比的是，电磁力可以具有吸引力或排斥性（相反的电荷会吸引，就像电荷一样击退）。 磁力在更复杂的方式上取决于电荷及其运动。 将电力和磁力统一为单一的电磁力（詹姆斯·克莱克·麦克斯韦的成就）是十九世纪最伟大的智力成就之一。 这种力是原子结构和分子键的科学模型的核心。
    3. 核力量弱。 薄弱的核力量在很短的距离\((10^{-15}m)\)内起作用，顾名思义，它非常弱。 它大致相当\(10^{-6}\)于强大的核力量的力量。 这种力最明显地表现为基本粒子的衰变和中微子相互作用。 例如，中子可以通过弱力衰变为质子、电子和电子中微子。 弱力至关重要，因为它对于理解恒星核合成至关重要，恒星核合成是在恒星核心中产生新原子核的过程。
    4. 引力。 与电磁力一样，引力可以在无限远的距离内起作用；但是，它的强度只能\(10^{-38}\)与强大的核力一样强。 在牛顿的经典重力理论中，重力随相互作用粒子质量的乘积和它们之间距离的反平方而变化。 这种力是一种吸引力，在所有有质量的粒子之间起作用。 在现代重力理论中，这种力行为被认为是低能宏观相互作用的特例。 与其他自然力量相比，重力是迄今为止最弱的。

    基本力量可能不是真正的 “基本” 力量，但实际上可能是同一力量的不同方面。 正如电力和磁力被统一为电磁力一样，物理学家在20世纪70年代将电磁力和弱核力统一为电弱力。 任何试图统一 electroweak 力量和强核力的科学理论都被称为宏伟的统一理论，任何试图统一所有四种力量的理论都被称为万物理论。 我们将在本章后面重新讨论统一的概念。

    基本粒子的分类

    自然界中存在大量的亚原子粒子。 这些粒子可以通过两种方式进行分类：自旋特性和参与四种基本力。 回想一下，粒子的自旋类似于宏观物体绕其自身轴线旋转。 下文分别描述了这些分类类型。

    按旋转分类

    物质粒子可以分为费密子和玻色子 s。 费密子具有半积分自旋\((\frac{1}{2}\hbar, \frac{1}{2}\hbar,. . . )\)，玻色子具有积分自旋\((0\hbar, 1\hbar, 2\hbar, . . . )\)。

    费密子的常见例子是电子、质子和中子。 一个熟悉的玻色子例子是光子。 费密子和玻色子在群体中的行为截然不同。 例如，当电子被限制在很小的空间区域时，保利的排除原理指出，没有两个电子可以占据相同的量子力学状态。 但是，当光子局限于较小的空间区域时，就没有这样的限制。

    费密子和玻色子成群的行为可以用难以区分的特性来理解。 如果粒子彼此相同，则说它们是 “无法区分的”。 例如，电子是无法区分的，因为宇宙中的每个电子的质量和自旋都与所有其他电子完全相同—— “当你看见一个电子时，你就全部看见了。” 如果在同一个小空间区域内切换两个无法区分的粒子，则描述该系统且可以测量的波函数的平方将保持\((|\psi|^2)\)不变。 如果不是这样，我们可以分辨出粒子是否已切换，粒子就无法真正区分了。 费密子和玻色子的不同之处在于波浪函数\((\psi)\)（不可直接观察）的符号是否会翻转：

    \[\psi \rightarrow - \psi \, (indistinguishable \, fermions), \nonumber \]

    \[\psi \rightarrow + \psi \, (indistinguishable \, bosons). \nonumber \]

    据说费密子 “在交换时是反对称的”，而玻色子 “在交换时是对称的”。 保利的排除原理是费密子交换对称性的结果，费密子的交换对称性是在现代物理学更高级的课程中发展出来的。 原子的电子结构以保利的排除原理为前提，因此与电子的不可区分性直接相关。

    按力相互作用分类

    费密子可以进一步分为夸克和轻子 s。 这两种粒子之间的主要区别在于夸克通过强力相互作用，而轻子不能。 夸克和轻子（以及稍后将讨论的玻色子）组织在图中\(\PageIndex{1}\)。 上面的两行（前三列用紫色表示）包含六个夸克。 这些夸克分为两个粒子家族：向上、魅力和顶部（u、c、t），以及向下、奇怪和底部（d、s、b）。 同一粒子族的成员具有相同的属性，但质量不同（在中给出\(MeV/c^2\)）。 例如，顶级夸克的质量远大于魅力夸克的质量，而魅力夸克的质量远大于向上夸克的质量。 所有夸克都通过强大的核力量相互作用。

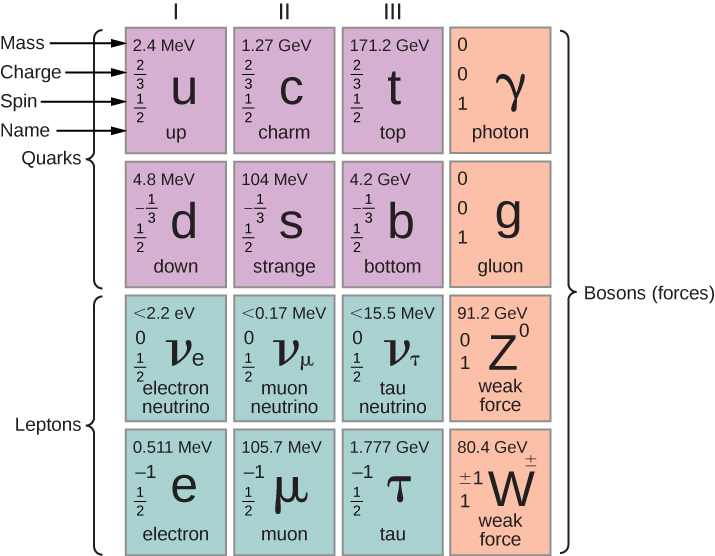
    这是一个有四行四列的表。 第一行和第二行中的前三个单元被标记为夸克。 第三行和第四行的前三个细胞被标记为轻子。 最后一列标有 “玻色子，力量”。 每个细胞都有粒子的名称，它的符号、质量、电荷和自旋。 在第一行中，这些值按顺序为：单元格一：向上、u、2.4 meV、2 x 3、1 x 2；单元格二：charm、c、1.27 GeV、2 x 3、1 x 2；单元格三、top、t、171.2 GeV、2 x 3、1 x 2；单元格四：光子、伽玛、0、0、1。 在第二行中，这些值按顺序为：单元格一：向下、d、4.8 meV、减去 1 x 3、1 x 2；单元格二：奇怪、s、104 meV、减去 1 x 3、1 x 2；单元格三：bottom、b、4.2 GeV、减去 1 x 3、1 x 2；单元格四：gluon、0、1。 在第三行中，这些值按顺序为：细胞一：电子中微子，v 下标 e，小于 2.2 eV，0，1 x 2；细胞二：μ子中微子，v 下标 mu，小于 0.17 meV，0，1 x 2；细胞三：tau neutrino，v 下标 tau，小于 15.5 meV，0，1 x 2；细胞四：弱力，z 上升到 0, 91.2 GeV,0,1。 在第四行中，这些值按顺序为：单元一：电子，e，0.511 meV，减去 1，1 x 2；单元格二：μon、mu、105.7 meV、减去 1、1 x 2；单元格三：tau、tau、1.777 GeV、减去 1、1 x 2；弱力，w 加负 1、1。
    图\(\PageIndex{1}\)：亚原子粒子家族，按它们相互作用的力类型分类。 （来源：“MissMJ” /Wikimedia Commons 对作品的修改）

    普通物质由两种类型的夸克组成：向上夸克（基本冲锋\(q = +2/3\)）和向下夸克（\(q = -1/3\)）。 较重的夸克是不稳定的，会通过弱力迅速衰减为较轻的夸克。 夸克通过强力以二和三为一组的形式绑定在一起，称为强子。 由两个夸克组成的强子被称为介子，由三个夸克组成的强子被称为重子。 介子的例子包括介子和 kaon，重子的例子包括熟悉的质子和中子。 质子是两个向上夸克和一个向下夸克\((p = uud, \, q = +1)\)，中子是一个向上夸克和两个向下夸克（\(n = udd, \, q = 0\)）。 表中给出了样本介子和重子的性质\(\PageIndex{1}\)。 夸克参与所有四种基本力：强、弱、电磁和引力。

    图中下两行（绿色）包含排列成两个粒子族的六个轻子：电子、μ子和 tau (\(e, \mu, \tau\))，以及电子中微子、μ子中微子和 tau 中微子 (\(\nu_e, \nu_{\mu}, \nu_T\))。

    μ子比电子重200倍以上，但在其他方面与电子相似。 tau 比电子重约 3500 倍，但在其他方面与μ子和电子相似。 一旦生成，μ子和 tau 就会通过弱力迅速衰减为更轻的粒子。 轻子不参与强大力量。 夸克和轻子将在本章后面讨论。 轻子参与弱力、电磁力和引力，但不参与强力。

    玻色子（以红色显示）是费密子的载力器。 在这个模型中，轻子和夸克通过发送和接收玻色子相互作用。 例如，当两个带正电荷的粒子发送和接收（交换）光子时，就会发生库伦比克相互作用。 据说光子在带电粒子之间 “携带” 力。 同样，当两个夸克发送和接收 g luon s 时，就会发生原子核中两个夸克之间的吸引。 其他例子包括 W 和 Z 玻色子 s（携带弱核力）和引力子（携带引力）。 希格斯玻色子是一种特殊的粒子：当它与其他粒子相互作用时，它赋予的不是力，而是赋予它们质量。 换句话说，希格斯玻色子有助于解释为什么粒子有质量。 这些断言是稍后讨论的试探性但非常有成效的科学模型（标准模型）的一部分。

    粒子和反颗粒

    在20世纪20年代后期，狭义相对论和量子力学被合并为相对论的电子量子理论。 该理论的一个令人惊讶的结果是预测了每个电子的两种能量态：一种与电子有关，另一种与另一个电子质量相同但电荷为的粒子有关\(e^+\)。 这个粒子被称为反电子或正电子。 正电子是在 20 世纪 30 年代通过实验发现的。

    很快人们发现，自然界中的每一个粒子都有相应的反粒子。 反粒子的质量和寿命与其关联粒子相同，而电荷的征兆恰恰相反。 这些粒子是在高能反应中产生的。 高能粒子的例子包括 antimuon\((\mu^+\))、anti-up quark (\(u\)) 和 anti-down quark (\(d\))。 （请注意，夸克的反粒子是用上杠来指定的。） 许多介子和重子都含有反粒子。 例如，反质子 (\ overline {p}\) 是\(\overline{u}\overline{u}\overline{d}\)，带正电荷的 pion (\(\pi^+\)) 是\(u\overline{d}\)。 一些中性粒子，例如光子和\(\pi^0\)介子，是它们自己的反粒子。 表中列出了样品颗粒、反粒子及其特性\(\PageIndex{1}\)。

    表\(\PageIndex{1}\)：粒子及其特性
    粒子名称 符号 反粒子 弥撒 (\(MeV/c^2\)) 平均使用寿命
    Leptons
    电子 \(e^-\) \(e^+\) \ (mev/c^2\))” style= “text-align: center; 垂直对齐:middle;” class= “lt-phys-4555” >0.511 稳定
    电子中微子 \(\nu_e\) \(\overline{\nu}_e\) \ (mev/c^2\))” style= “text-align: center; 垂直对齐:middle;” class= “lt-phys-4555” >\(\approx 0\) 稳定
    Muon \(\mu^-\) \(\mu^+\) \ (mev/c^2\))” style= “text-align: center; 垂直对齐:middle;” class= “lt-phys-4555” >105.7 \(2.20 \times 10^{-6}\)
    μon 中微子 \(\nu_{\mu}\) \(\overline{\nu_{\mu}}\) \ (mev/c^2\))” style= “text-align: center; 垂直对齐:middle;” class= “lt-phys-4555” >\(\approx 0\) 稳定
    Tau \(\tau^-\) \(\tau^+\) \ (mev/c^2\))” style= “text-align: center; 垂直对齐:middle;” class= “lt-phys-4555” >1784 \(<4 \times 10^{-13}\)
    Tau 中微子 \(\nu_{\tau}\) \(\overline{\nu_{\tau}}\) \ (mev/c^2\))” style= “text-align: center; 垂直对齐:middle;” class= “lt-phys-4555” >\(\approx 0\) 稳定
    Hadrons
    重子 质子 p \(\overline{p}\) \ (mev/c^2\))” style= “text-align: center; 垂直对齐:middle;” class= “lt-phys-4555” >938.3 稳定
    中子 n \(\overline{n}\) \ (mev/c^2\))” style= “text-align: center; 垂直对齐:middle;” class= “lt-phys-4555” >939.6 920
    兰姆达 \(\Lambda^0\) \(\overline{\Lambda^0}\) \ (mev/c^2\))” style= “text-align: center; 垂直对齐:middle;” class= “lt-phys-4555” >1115.6 \(2.6 \times 10^{-10}\)
    西格玛 \(\sum^+\) \(\sum^-\) \ (mev/c^2\))” style= “text-align: center; 垂直对齐:middle;” class= “lt-phys-4555” >1189.4 \(0.80 \times 10^{-10}\)
    Xi \(\Xi^+\) \(\Xi^-\) \ (mev/c^2\))” style= “text-align: center; 垂直对齐:middle;” class= “lt-phys-4555” >1315 \(2.9 \times 10^{-10}\)
    欧米茄 \(\Omega^+\) \(\Omega^-\) \ (mev/c^2\))” style= “text-align: center; 垂直对齐:middle;” class= “lt-phys-4555” >1672 \(0.82 \times 10^{-10}\)
    介子 Pion \(\pi^+\) \(\pi^-\) \ (mev/c^2\))” style= “text-align: center; 垂直对齐:middle;” class= “lt-phys-4555” >139.6 \(2.60 \times 10^{-8}\)
    \(\pi\)-零 \(\pi^0\) \(\pi^0\) \ (mev/c^2\))” style= “text-align: center; 垂直对齐:middle;” class= “lt-phys-4555” >135.0 \(0.83 \times 10^{-16}\)
    卡恩 \(K^+\) \(K^-\) \ (mev/c^2\))” style= “text-align: center; 垂直对齐:middle;” class= “lt-phys-4555” >493.7 \(1.24 \times 10^{-8}\)
    K 短裤 \(K_S^0\) \(\overline{K_S^0}\) \ (mev/c^2\))” style= “text-align: center; 垂直对齐:middle;” class= “lt-phys-4555” >497.6 \(0.89 \times 10^{-10}\)
    K-long \(K_L^0\) \(\overline{K_L^0}\) \ (mev/c^2\))” style= “text-align: center; 垂直对齐:middle;” class= “lt-phys-4555” >497.6 \(5.2 \times 10^{-8}\)
    J/\(\psi\) \(J/\psi\) \(J/\psi\) \ (mev/c^2\))” style= “text-align: center; 垂直对齐:middle;” class= “lt-phys-4555” >3100 \(7.1 \times 10^{-21}\)
    Upsilon \(\Upsilon\) \(\Upsilon\) \ (mev/c^2\))” style= “text-align: center; 垂直对齐:middle;” class= “lt-phys-4555” >9460 \(1.2 \times 10^{-20}\)

    粒子及其特性

    将普通物质凝聚在一起的同样力量也将反物质凝聚在一起。 在适当的条件下，有可能产生抗原子，例如抗氢、抗氧甚至反水。 在反原子中，正电子绕着带负电荷的反质子和反中子核。 图中\(\PageIndex{2}\)比较了原子和反原子。

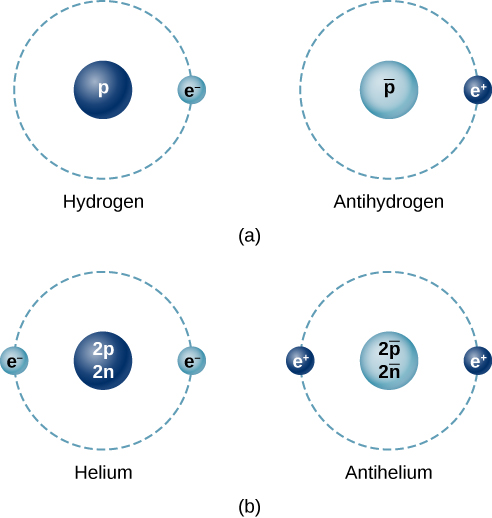
    图 a 显示了氢原子和反氢原子。 前者在中心有一个标有 p 的圆，另一个较小的圆在围绕它的轨道上标有 e minus。 后者的中心有一个标有 p bar 的圆圈，另一个标有 e plus 的小圆在围绕它的轨道上。 图 b 显示了氦原子和反氦原子。 前者的中心有一个标有 2p 2n 的圆圈，在其周围的轨道上有两个标有 e minus 的小圆圈。 后者在中心有一个标有 2p bar 2 n bar 的圆圈，在围绕它的轨道上有两个标有 e plus 的小圆圈。
    图\(\PageIndex{2}\)：最简单的物质原子和反物质原子的比较。 (a) 在玻尔模型中，反氢原子由绕反质子运行的正电子组成。 (b) 反氦原子由两个正电子组成，它们绕两个反质子和两个反中子的原子核运行。

    反物质不可能在自然界中长期存在，因为粒子和反粒子相互消灭以产生高能辐射。 一个常见的例子是电子-正电子歼灭。 这个过程由反应进行

    \[e^- + e^+ \rightarrow 2\gamma. \nonumber \]

    电子和正电子完全消失，取而代之的是两个光子。 （事实证明，产生单个光子会违反能量守恒和动量。） 这种反应也可以朝相反的方向进行：两个光子可以相互消灭，产生电子和正电子对。 或者，单个光子可以在原子核场中产生电子-正电子对，这种过程称为配对产生。 这种反应通常在现代粒子探测器中测量。 自然界中反粒子的存在不是科幻小说。

    观看此视频，了解有关物质和反物质粒子的更多信息。