9.9: 超导

Last updated
Save as PDF

Page ID: 201959

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

学习目标

在本节结束时，您将能够：

描述超导体的主要特征
描述 BCS 的超导理论
根据磁场数据确定 T = 0 K 的临界磁场
计算电线保持超导的最大电动势或电流

电阻可以看作是衡量电流中摩擦力的一种方法。因此，电阻是电磁铁、电动机和传输线路等电气系统中能量消耗的主要来源。铜线通常用于电线，因为它是普通导体中室温电阻率最低的之一。（实际上，银的电阻率低于铜，但是与铜相比，银的高成本和有限的可用性超过了其节省的能量。）

尽管我们对电导率的讨论似乎意味着所有材料都必须具有电阻，但我们知道事实并非如此。当许多材料的温度降至临界值以下时，它们的电阻率降至零，材料就会变成超导体。

观看这段 NOVA 视频摘录《让东西变冷》，介绍超导及其众多应用。

超导体的性质

除了零电阻外，超导体还具有完美的抗磁性。换句话说，在存在施加磁场的情况下，超导体内的净磁场始终为零（图\(\PageIndex{1}\)）。因此，任何在超导样品处于正常状态时穿过该样品的磁场线在样品变为超导时都会被排出。这些是迈斯纳效应的表现形式，你在关于电流和电阻的章节中学到了这一点。

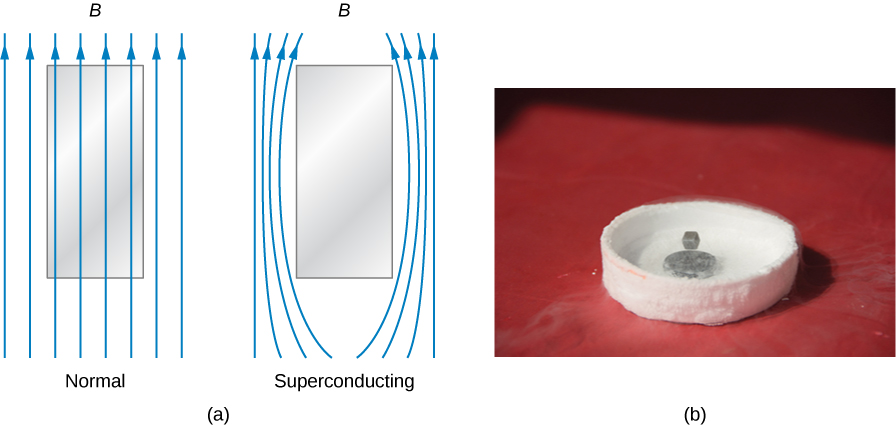
图 a 有两个相似的矩形板。指向上方的垂直箭头显示在第一个板的前面。箭头围绕第二个板块弯曲。图 b 是一张照片，显示了一个悬浮在空中的小球在金属板上方。 — 图\(\PageIndex{1}\) :( a) 在迈斯纳效应中，一旦材料变为超导，磁场就会从材料中排出。 (b) 在驱逐磁场的力的支撑下，磁体可以悬浮在超导材料上方。

有趣的是，迈斯纳效应不是阻力为零的结果。要了解原因，假设放置在磁场中的样品经历了过渡，其电阻降至零。根据欧姆定律，样本中的电流密度 j 与净内部电场 E 有关，I\(j = E/\rho\) f 的电阻率\(\rho\)\(\rho\)为零，E 也必须为零，这样 j 才能保持有限。现在，根据法拉第定律，E 和样品中的磁\(\Phi_m\)通量相关联为

\[\oint E\,dI = - \dfrac{d\Phi_m}{dt} \nonumber \]

如果 E 为零，\(d\Phi_m/dt\)也为零，也就是说，通过样品的磁通量不会改变。因此，过渡发生时，不应排出样品内的磁场线。因此，这并不意味着阻力为零的材料必须表现出迈斯纳效应。相反，迈斯纳效应是超导体的特殊特性。

超导材料的另一个重要特性是其临界温度\(T_c\)，即材料的超导温度低于该温度。已知的临界温度范围从 1 K 的几分之一到略高于 100 K 不等。临界温度接近这个上限的超导体通常被称为 “高温” 超导体。从实际的角度来看，超导体\(T_c \gg 77 \, K\)对其非常重要。目前，涉及超导体的应用通常仍要求将超导材料浸入液氦中（4.2 K）以使其低于临界温度。由于蒸发，必须持续补充液氦浴，冷却成本很容易超过使用超导体所节省的费用。但是，77 K 是液氮的温度，它比液氦更丰富、更便宜。如果我们能够轻松地制造和使用只需要保存在液氮浴中即可保持其超导性的高温超导组件，则成本效益会大大提高。

高温超导材料目前用于各种应用。例如，某些粒子加速器产生磁场。最终目标是发现室温下具有超导性的材料。在没有任何冷却要求的情况下，大部分电子元件和传输线路可以是超导的，从而显著提高效率和性能，这是前所未有的。

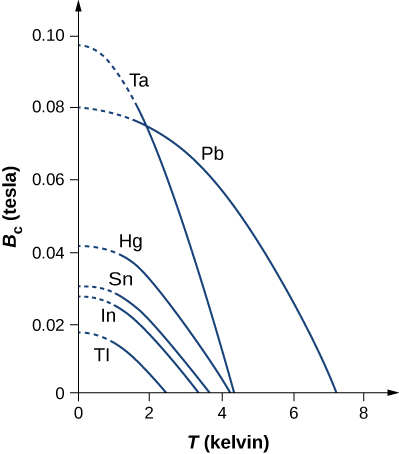
特斯拉中的 B 下标 c 与开尔文中的 T 的图表。它有 6 条曲线。曲线 Tl 从 x 轴上刚好高于 2 开始，在 y 轴上刚好低于 0.02 结束。 Curve In 和 Sn 从 x 轴上刚好高于 3 开始，在 y 轴上以 0.03 左右结束。曲线 Hg 在 x 轴上刚好高于四点开始，在 y 轴上刚好高于 0.04 结束。曲线 Ta 在 x 轴上刚好高于 4 开始，在 y 轴上刚好低于 0.1 结束。曲线 Pb 在 x 轴上刚好高于 7 开始，在 y 轴上以 0.08 结束。 — 图\(\PageIndex{2}\)：多个超导体临界场的温度依赖性。超导发生在低于所示曲线的磁场和温度下。

超导材料的另一个重要特性是其临界磁场\(B_c(T)\)，临界磁场是温度 T 下允许材料保持超导的最大施加磁场。大于临界场的施加场将摧毁超导性。临界场在临界温度下为零，并随着温度的降低而增加。图中显示了几种超导材料的临界场与温度的关系图\(\PageIndex{2}\)。临界场的温度依赖性可以大致描述为

\[B_c(T) = B_c(0) \left[1 - \left(\frac{T}{T_c}\right)^2\right] \nonumber \]

哪里\(B_0\)是绝对零温度下的临界场。表中\(\PageIndex{1}\)列出了两类超导体的临界温度和磁场：I 型超导体和 II 型超导体。通常，I 型超导体是元素，例如铝和汞。它们在临界磁场 B _C (T) 下具有完全的抗磁性，一旦超过该磁场，它们就会进入正常的非超导状态。 I 型超导体的临界场通常很低（远低于一特斯拉）。出于这个原因，它们不能用于需要产生高磁场的应用，这会破坏它们的超导状态。

表\(\PageIndex{1}\)：各种超导体的临界温度和临界磁场\(T = 0 \, K\)
材质	临界温度 (K)	临界磁场 (T)
I 型
阿尔	1.2	0.011
Ga	1.1	0.0051
\(Hg(\alpha)\)	4.2	0.041
在	3.4	0.029
注意	9.3	0.20
Pb	7.2	0.080
太阳	3.7	0.031
Th	1.4	0.00016
锌	0.87	0.0053
二型
\(Nb_3Al\)	18	32
\(Nb_3Ge\)	23	38
\(Nb_3Sn\)	18	25
\(NbTi\)	9.3	15
\(YBa_2Cu_3O_7\)	92	>100

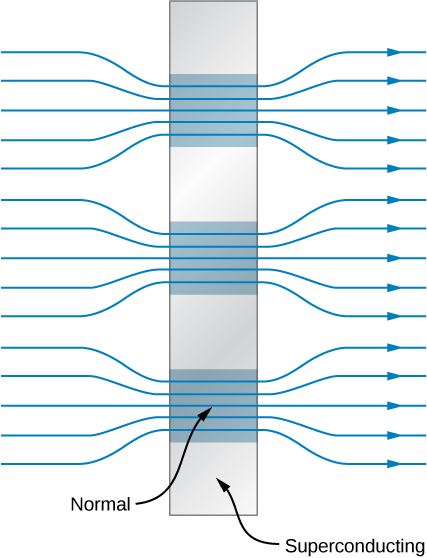
II 型超导体通常是涉及过渡金属或 actinide 系列元素的化合物或合金。几乎所有临界温度相对较高的超导体都是 II 型。它们有两个关键字段，用\(B_{c1}(T)\)和表示\(B_{c2}(T)\)。当磁场低于磁场时\(B_{c1}(T)\)，II 型超导体具有完全的抗磁性，不会发生磁通渗透到材料中。如果场地超过\(B_{c2}(T)\)，它们就会进入正常状态。当磁场大于\(B_{c1}(T)\)但小于时\(B_{c2}(T)\)，II 型超导体被认为处于混合状态。尽管在混合状态下会有一些磁通穿透，但材料的电阻为零。在超导体中，存在具有正常电学和磁学特性的灯丝状区域，穿插在具有完美抗磁性的超导区域之间。该状态的表示如图所示\(\PageIndex{3}\)。磁场从超导区域排出，但存在于正常区域。总的\(B_{c2}(T)\)来说，与 I 型超导体的临界场相比，它非常大，因此由 II 型超导材料制成的导线适用于高场磁体的绕组。

图中显示了一条竖线，其中蓝色和灰色方块交替放置，一个位于另一个之上。蓝色方块被标记为正态，灰色方块被标记为超导。箭头从左边进入，汇聚在一起，只穿过普通方块。在酒吧的右边，它们分开。 — 图\(\PageIndex{3}\)：II 型超导体混合态的示意图。超导体（灰色方块）在其附近排出磁场。

示例\(\PageIndex{1}\): Niobium Wire

在实验中，半径为 0.25 mm 的铌线（Nb）浸入液氦\(T = 4.2 \, K)\)中，需要承载 300 A 的电流。该导线是否保持超导状态？

策略

施加的磁场可以通过电线和电流的半径来确定。临界磁场可以通过 [链接]、超导体的特性和温度来确定。如果施加的磁场大于临界场，则Nb线中的超导性将被破坏。

解决方案

在\(T = 4.2 \, K\)，Nb 的关键字段是，来自表\(\PageIndex{1}\)：

\[B_c(4.2 \, K) = B_c(0)\left[1 - \left(\frac{4.2 \, K}{9.3 \, K}\right)^2\right] = (0.20 \, T)(0.80) = 0.16 \, T. \nonumber \]

在前面的章节中，我们了解到半径\(a\)为的载流线内的磁场由下式给出

\[B = \frac{\mu_0I}{2\pi a}, \nonumber \]

其中 r 是距导线中心轴的距离。因此，电线表面的磁场是\(\frac{\mu_0I}{2\pi a}\)。对于铌线来说，这个字段是

\[B = \frac{(4\pi \times 10^{-7} T m/A)(300 \, A)}{2\pi(2.5 \times 10^{-4}m)} = 0.24 \, T. \nonumber \]

由于这超过了临界的 0.16 T，因此导线不会保持超导状态。

意义

超导需要低温和低磁场。与许多其他金属相比，铌不容易同时满足这些条件。例如，铝的超导体温度低7倍，磁场低18倍。

练习\(\PageIndex{1}\)

超导需要什么条件？

回答: 低温低磁场

超导体理论

约翰·巴丁、莱昂·库珀和罗伯特·施里弗在20世纪50年代成功地提出了超导理论，并因此于1972年获得了诺贝尔奖。这个理论被称为 BCS 理论。 BCS 理论很复杂，因此我们在下面对其进行了定性总结。

在普通导体中，材料的电学特性归因于费米能量附近的能量最高的电子。 1956 年，库珀表明，如果两个电子在费米水平上存在任何有吸引力的相互作用，那么电子就可以形成总能量小于 2EF2EF 的绑定态。两个这样的电子被称为库珀对。

很难想象两个电子会相互吸引，因为它们具有类似的电荷并且应该能击退。但是，拟议的相互作用仅在原子晶格的背景下发生。该景点的描绘如图所示\(\PageIndex{4}\)。由于库仑的吸引，Electron 1 在经过时会稍微将带正电荷的原子核移向自身。电子 2 “看见” 了一个相对于周围环境具有更高正电荷密度的区域，因此被吸引到该区域，因此间接地被电子 1 吸引。由于排除原理，库珀对中的两个电子必须具有相反的自旋。

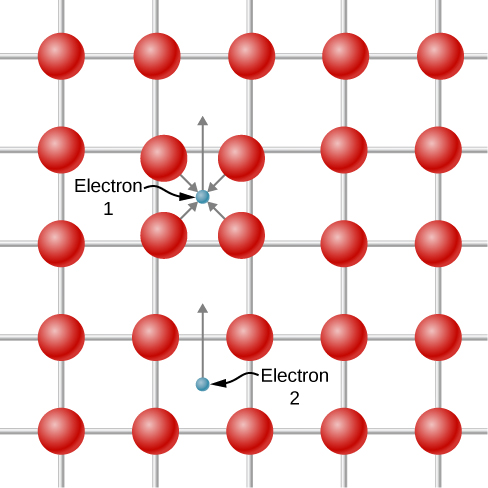
显示了一个包含 25 个红点的网格。共有 5 列和 5 行，每列由背景中的格子框架连接。在标有电子 1 的 4 个点之间有一个点，其中一个箭头来自周围的每个点，然后另一个箭头指向上方。下方 2 行，另一个点被标记为电子 2，还有一个箭头也指向上方。 — 图\(\PageIndex{4}\)：正原子核的位移可能形成库珀对。由于库仑的吸引，Electron 1 在经过时会稍微将带正电荷的原子核移向自身。 Electron 2 “看见” 了一个相对于周围环境具有更高正电荷密度的区域，因此被吸引到该区域

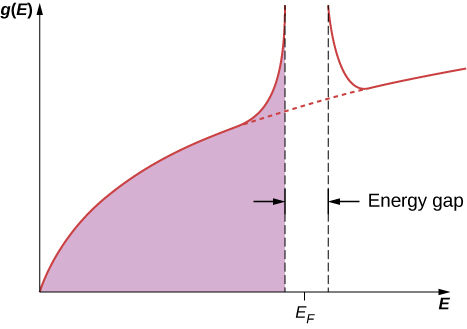
BCS 理论将库珀的想法（即一对电子）扩展到了整个自由电子气。当过渡到超导态时，所有电子配对形成库珀对。在原子尺度上，组成库珀对的两个电子之间的距离相当大。这些电子之间通常是关于\(10^6\)其他电子的，每个电子也与一个遥远的电子配对。因此，单个 Cooper 对的波函数之间存在相当大的重叠，导致波函数对的运动之间存在很强的相关性。他们都像游行乐队的成员一样 “步调一致” 地走到一起。在超导过渡中，态的密度在费米水平附近发生了巨大变化。如图所示\(\PageIndex{5}\)，周围出现了能量缺口，\(E_F\)因为库珀对的集合的基态能量低于非相互作用电子的费米气体。这种间隙的出现是超导态的特征。如果这种状态被破坏，则间隙消失，状态的密度将恢复为自由电子气的密度。

圆括号 E 与 E 中的 g 图。该图从原点开始，向上和向右弯曲。图表上显示了两条垂直线。它们之间的距离被标记为能量间隙。曲线的 y 值在间隙之前和之后都非常高。间隙中心的 x 值为 E 下标 F。间隙左侧曲线下方的区域为阴影。 — 图\(\PageIndex{5}\): A relatively large energy gap is formed around the Fermi energy when a material becomes superconducting. If this state is destroyed, then the gap disappears, and the density of states reverts to that of the free electron gas.

The BCS theory is able to predict many of the properties observed in superconductors. Examples include the Meissner effect, the critical temperature, the critical field, and, perhaps most importantly, the resistivity becoming zero at a critical temperature. We can think about this last phenomenon qualitatively as follows. In a normal conductor, resistivity results from the interaction of the conduction electrons with the lattice. In this interaction, the energy exchanged is on the order of \(k_BT\), the thermal energy. In a superconductor, electric current is carried by the Cooper pairs. The only way for a lattice to scatter a Cooper pair is to break it up. The destruction of one pair then destroys the collective motion of all the pairs. This destruction requires energy on the order of \(10^{-3}eV\), which is the size of the energy gap. Below the critical temperature, there is not enough thermal energy available for this process, so the Cooper pairs travel unimpeded throughout the superconductor.

Finally, it is interesting to note that no evidence of superconductivity has been found in the best normal conductors, such as copper and silver. This is not unexpected, given the BCS theory. The basis for the formation of the superconducting state is an interaction between the electrons and the lattice. In the best conductors, the electron-lattice interaction is weakest, as evident from their minimal resistivity. We might expect then that in these materials, the interaction is so weak that Cooper pairs cannot be formed, and superconductivity is therefore precluded.