4.E:衍射(练习)
- Page ID
- 201992
概念性问题
4.1 单缝衍射
1。 随着产生单缝衍射图案的狭缝宽度的减小,产生的衍射图案将如何变化?
2。 比较干涉和衍射。
3。 如果你和朋友在山的对面,你可以用对讲机通信,但不能用手电筒交流。 解释一下。
4。 当整个光学设备浸入水中时,单个狭缝的衍射图案会怎样?
5。 在我们研究单缝衍射时,我们假设狭缝的长度远大于宽度。 如果这两个维度具有可比性,衍射图案会怎样?
6。 矩形狭缝的宽度是其高度的两倍。 中央衍射峰在垂直方向还是水平方向上更宽?
4.2 单缝衍射中的强度
7。 在方程式 4.4 中,参数 ββ 看起来像一个角度,但不是一个可以在物理世界中用量角器测量的角度。 解释 ββ 代表什么。
4.3 双缝衍射
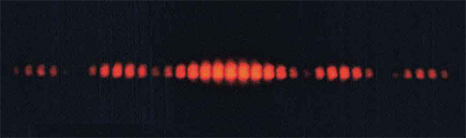
8。 下图显示的是投射到双狭缝上的纯波长红光的干涉图案的中心部分。 该图案实际上是单缝和双缝干涉的组合。 请注意,亮点间隔均匀。 这是双缝还是单缝特征? 请注意,有些亮点在中心两侧都很暗。 这是单缝还是双缝特征? 哪个更小,是狭缝宽度还是狭缝之间的间隔? 解释你的回应。 图为黑色背景上显示红色干涉图案的图像。 中心部分有更亮的线条。 这些线条在顶部和底部被切断,似乎封闭在两个相位相反的正弦波之间。
4.5 圆孔径和分辨率
9。 在红光或蓝光的显微镜中能否获得更高的分辨率? 解释你的答案。
10。 折射望远镜的分辨率随着物镜大小的增加而增加。 更大的镜头还能获得什么其他好处?
11。 分子中原子之间的距离约为\(\displaystyle 10^{−8}cm\)。 可见光可以用来 “看见” 分子吗?
12。 一束光总是散开。 为什么不能用平行光线生成光束来防止扩散? 为什么不能使用镜头、镜子或光圈来校正扩散?
4.6 X 射线衍射
13。 晶格可以用 X 射线检查,但不能用 UV 进行检查。 为什么?
4.7 全息术
14。 你怎么能分辨出全息图是真正的三维图像,而三维电影中的全息图不是?
15。 如果全息图是在一个波长使用单色光录制的,但其图像是在另一个波长下观看的,\(\displaystyle 10%\)比如说更短,你会看到什么? 如果使用正好是原始波长一半的光来观看呢?
16。 如果使用单色光录制全息图,但其图像是在白光下观看,人们会看到什么图像? 解释一下。
问题
4.1 单缝衍射
17。 (a) 550 nm 光落在单个宽度狭缝上的第一个最小角度是多\(\displaystyle 1.00μm\)少?
(b) 会有第二个最低限度吗?
18。 (a) 计算\(\displaystyle 2.00-μm\)宽缝在 410 纳米紫光下产生第一个最小值的角度。
(b) 700-nm 红光的第一个最小值在哪里?
19。 (a) 单个狭缝在角度为 633 nm 的光下产生第一个最小值的宽度有多大\(\displaystyle 28.0°\)?
(b) 第二个最小值将处于什么角度?
20。 (a) 在 600 纳米光下产生第一个最小值的单个狭缝\(\displaystyle 60.0°\)的宽度是多少?
(b) 找出第一个最小值为的光的波长\(\displaystyle 62.0°\)。
21。 找出其第三个最小值的光的波长,其角度为落在单个宽度狭缝上\(\displaystyle 48.6°\)时的角度\(\displaystyle 3.00μm\)。
22。 (a) 平均波长为589 nm的钠蒸气光落在单个宽度狭缝上\(\displaystyle 7.50μm\)。 它在什么角度产生第二个最小值?
(b) 最高订单的最低产量是多少?
23。 以单缝衍射图案为例\(\displaystyle λ=589nm\),投射在距离宽度为 0.25 mm 的狭缝 1.00 m 的屏幕上。 第一个和第二个深色条纹的中心离图案中心有多远?
24。 (a) 找出波长为589.1和589.6 nm的两条钠蒸气线落在单个宽度狭缝上时的第一个最小值之间的角度\(\displaystyle 2.00μm\)。
(b) 如果衍射图案落在距离狭缝 1.00 米的屏幕上,这些最小值之间的距离是多少?
(c) 讨论测量这种距离的难易程度。
25。 (a) 产生波长第一个最小值的单个狭缝(以倍数为单位\(\displaystyle λ\))的最小宽度是多少\(\displaystyle λ\)?
(b) 如果它产生 50 个最小宽度,它的最小宽度是多少?
(c) 最低 1000 个?
26。 (a) 如果单个狭缝产生第一个最小值\(\displaystyle 14.5°\),则二阶最小值的角度是多少?
(b) 三阶最小值的角度是多少?
(c) 有四阶最低值吗?
(d) 使用你的答案来说明中心最大值的角宽度大约是下一个最大值(即第一个和第二个最小值之间的角度)的角宽度的两倍。
27。 如果单缝衍射图案的第一个和第二个最小值之间的间隔为 6.0 mm,那么屏幕和狭缝之间的距离是多少? 光波长为 500 纳米,狭缝宽度为 0.16 毫米。
28。 港口入口处的防水处由一个开口为 50.0 米的岩石屏障组成。 波长为 20.0 米的海浪直接接近开口。 港口内的船只在入射方向的哪个角度最能抵御海浪作用?
29。 一名飞机维修技术人员走过一扇高大的机库门,这扇门就像是进入机库的声音的单个缝隙。 在门外,在一条垂直于门口的线上,喷气发动机发出 600-Hz 的声音。 如果垂直开口宽度为 0.800 m,声速为 340 m/s,技术人员将观察到门的第一个最小角度?
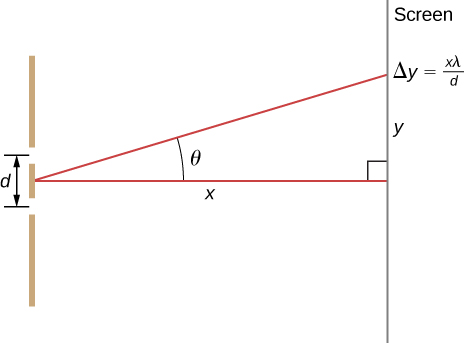
4.2 单缝衍射中的强度
30。 波长\(\displaystyle 3.0μm\)为 589 nm 的钠黄光照亮一条宽度的狭缝。 根据中心最大值的强度找到与轴成\(\displaystyle 15°\)一定角度的强度。
31。 宽度为 0.1 mm 的单个狭缝由波长为 576 nm 的水银光照亮。 根据中心最大值的强度计算与轴成10°10°角的强度。
32。 单缝衍射图案中中心峰的宽度为 5.0 mm。 光的波长为 600 nm,屏幕距离狭缝 2.0 m。 (a) 缝隙的宽度是多少? (b) 确定从图案中心 4.5 mm 处的强度与中心强度的比率。
33。 以和的单缝衍射图案\(\displaystyle λ=600nm, a=0.025m\)为例\(\displaystyle x=2.0m\)。 用 a\(\displaystyle I_o\) t 和. 来计算强\(\displaystyle θ=0.5°\)\(\displaystyle 1.0°, 1.5°, 3.0°,\)度\(\displaystyle 10.0°\)。
4.3 双缝衍射
34。 两条宽度狭缝\(\displaystyle 2μm\),每个缝隙均为不透明材质,中心到中心的距离为\(\displaystyle 6μm\)。 波长为 450 nm 的单色光入射在双缝上。 人们可以在屏幕上找到混合的干涉和衍射图案。
(a) 在衍射图案的中心最大值中会观察到多少干扰峰?
(b) 如果狭缝宽度增加一倍,同时保持狭缝之间的距离不变,将观察到多少个干扰峰值?
(c) 如果狭缝间隔两倍的距离,也就是说,在保持狭缝宽度不变的情况下\(\displaystyle 12μm\),会观察到多少干扰峰?
(d) 如果使用 680 nm 波长为 680 nm 的光而不是 450 纳米的光,在 (a) 中会发生什么?
(e) (a) 中中心峰的强度与下一个亮峰强度的比值是多少?
(f) 这个比率是否取决于光的波长?
(g) 这个比率是否取决于缝隙的宽度或间隔?
35。 双缝产生的衍射图案是单缝和双缝干涉的组合。 如果单缝图案的第一个最小值落在双缝图案的第五个最大值上,则求出狭缝宽度与它们之间的间距之比。 (这将大大降低第五个最大值的强度。)
36。 对于狭缝间距为狭缝宽度的四倍的双缝配置,衍射图案的中心峰中有多少干涉条纹?
37。 波长为 500 nm 的光通常落在 50 个\(\displaystyle 2.5×10^{−3}mm\)宽且间\(\displaystyle 5.0×10^{−3}mm\)隔开的狭缝上。 衍射图案的中心峰中有多少干涉条纹?
38。 波长为 589 nm 的单色光入射在具有狭缝宽\(\displaystyle 2.5μm\)度和未知分离的双缝上,会产生在中心最大值内包含九个干扰峰的衍射图案。 找到缝隙的间隔。
39。 当波长为 430 nm 的单色光入射在狭缝分离的双缝上时\(\displaystyle 5μm\),其中心最大值有 11 个干涉条纹。 波长和狭缝宽度相同但又有新的狭缝分离的光的中心最大值中会有多少干涉条纹\(\displaystyle 4 μm\)?
40。 如果可能,当波长为 628 nm 的光入射到宽度为 500 nm 且间隔为 1500 nm 的双缝上时,确定除衍射中心最大值中的中心峰以外的两个干扰峰的强度。 使用中心点的强度为\(\displaystyle 1mW/cm^2\)。
4.4 衍射光栅
41。 衍射光栅每厘米有 2000 条线。 对于波长为 520 nm 的绿光,一阶最大值将处于什么角度?
42。 找出落在每厘米有 1500 条线的折射光栅上的 580 nm 波长的黄光的三阶最大角度。
43。 衍射光栅上每厘米有多少条线,该光栅在一阶最大角度为 470-nm 的蓝光下得出一阶最大值\(\displaystyle 25.0°\)?
44。 如果衍射光栅在角度为 760 nm 的红光下产生二阶最大值,则衍射光栅上的线之间的距离是\(\displaystyle 60.0°\)多少?
45。 计算落在每厘米有 5000 条线的衍射光栅上\(\displaystyle 45.0°\)时具有二阶最大值的光的波长。
46。 通过氢气的电流会产生几种不同波长的可见光。 如果氢光谱在角度上形成一阶最大值,\(\displaystyle 24.2°,25.7°,29.1°,\)并且投射到每厘米有 10,000 条线的衍射光栅上,\(\displaystyle 41.0°\)则氢光谱的波长是多少?
47。 (a) 如果使用每厘米5000线的衍射光栅,前面问题中的四个角度会变成什么?
(b) 使用这个光栅,二阶最大值的角度是多少?
(c) 讨论以每厘米线为单位的积分缩减与不同阶最大值的新角度之间的关系。
48。 假设羽毛中充当反射光栅的结构之间的间距是多少,假设它们在一定\(\displaystyle 30.0°\)角度下产生525纳米光的一阶最大值?
49。 图 4.15 所示的蛋白石就像反射光栅一样,行间隔约\(\displaystyle 8μm.\)如果蛋白石正常照亮,
(a) 在什么角度可以看到红光以及
(b) 在什么角度会看到蓝光?
50。 对于具有一阶最大值的光,衍射光栅会在什么角度产生二阶最大值\(\displaystyle 20.0°\)?
51。 (a) 找出衍射光栅每厘米可以具有的最大线数,并为最小波长的可见光生成最大线数。
(b) 这种光栅对紫外光谱有用吗?
(c) 用于红外光谱?
52。 (a) 表明每厘米30,000线的光栅不会产生最大可见光。
(b) 它产生一阶最大值的最长波长是多少?
(c) 衍射光栅每厘米的最大线数是多少,可以产生完整的可见光二阶光谱?
53。 下图所示的分析也适用于线段间隔为 d 的衍射光栅。 如果屏幕距离1.50米,则衍射光栅每厘米有125条线,600纳米光产生的条纹之间的距离是多少? (提示:假设狭缝间隔 d 与 d 相当\(\displaystyle Δy=xλ/d\),相邻条纹之间的距离为\(\displaystyle λ\)。)
4.5 圆孔径和分辨率
54。 图4.20所示的直径为305米的阿雷西博射电望远镜可探测平均波长为4.00厘米的无线电波。
(a) 这台望远镜的两个刚刚可分辨的点源之间的角度是多少?
(b) 在 Andromeda Galaxy 的 200 万光年距离处,这些点源的距离能有多近?
55。 假设在示例 4.6 中找到了哈勃望远镜的角分辨率,那么在月球上可以观测到的最小细节是什么?
56。 与手电筒的其他光学限制(例如镜子中的球面像差)相比,手电筒的衍射扩散微不足道。 要显示这一点,请计算最初直径为 5.00 cm、平均波长为 600 nm 的手电筒光束的最小角度展开。
57。 (a) 最初直径为 1.00 mm 的 633 纳米波长 He-Ne 激光束的最小角度分布是多少? (b) 如果激光瞄准15.0公里外的山崖,照明点会有多大? (c) 忽视大气效应,月球上的一个点会被照亮多大? (这可能是为了击中角反射镜来测量往返时间,从而测量距离。)
58。 望远镜可用于扩大激光束的直径和限制衍射扩散。 激光束通过望远镜以与正常方向相反的方向发送,然后可以投射到卫星或月球上。 (a) 如果这是用威尔逊山望远镜完成的,产生直径为2.54米的633纳米光束,那么光束的最小角度分布是多少? (b) 忽略大气效应,假设月球距离为,这束光束在月球上产生的点大小是多少\(\displaystyle 3.84×10^8m\)。?
59。 眼睛敏锐度的极限实际上与瞳孔的衍射有关。
(a) 假设平均波长为 550 nm,对于直径为 3.00 mm 的瞳孔,两个刚可分辨的光点之间的角度是多少?
(b) 把你的结果当作眼睛的实际极限。 如果你能分辨出汽车的两个大灯相距 1.30 米,那么汽车与你的最大距离是多少?
(c) 距离你的眼睛一臂之长(0.800 m)的两个刚解的点之间的距离是多少?
(d) 你对 (c) 的回答与你在日常环境中通常观察到的细节相比如何?
60。 望远镜上的最小直径是多少,它能让你看到大约 384,000 公里外的月球上小至 5.00 千米的细节? 假设接收到的光的平均波长为 550 nm。
61。 在眼睛视网膜上找出星星图像的半径,如果它的瞳孔张开到0.65厘米,并且从瞳孔到视网膜的距离为2.8厘米。 假设\(\displaystyle λ=550nm\)。
62。 (a) 矮行星冥王星及其卫星 Charon 相隔19,600千米。 忽视大气效应,直径为5.08米的帕洛玛山望远镜是否能够解析这些\(\displaystyle 4.50×10^9km\)来自地球的天体? 假设平均波长为 550 nm。
(b) 实际上,使用地面望远镜几乎不可能辨别冥王星和Charon是分开的天体。 造成这种情况的原因是什么?
63。 一颗间谍卫星在180公里的高度绕地球运行。 为了解析相距 2.0 m 的部队纵队,必须使用望远镜中的物镜的最小直径是多少? 假设 λ=550nm.λ=550nm。
64。 如果大气效应不限制分辨率,8.1 m Gemini South 望远镜刚好可以分辨的两颗恒星的最小角度间隔是多少? 使用 550 nm 作为来自恒星的光的波长。
65。 汽车的大灯相距 1.3 米。 眼睛分辨这两个大灯的最大距离是多少? 将瞳孔直径设为 0.40 厘米。
66。 当激光打印机在页面上放置点时,它们必须足够近,这样你就看不到单个墨水点。 要做到这一点,点的分离必须小于罗利的标准。 将眼睛的瞳孔设为 3.0 mm,纸张到眼睛的距离为 35 cm;找出两个点的最小间隔,这样它们就无法分辨出来。 这相当于每英寸 (dpi) 多少点?
67。 假设你从一架高度为 6.0 km 的喷气式飞机往下看高速公路。 如果你能区分两辆车,它们必须相隔多远? 假设\(\displaystyle λ=550nm\)你的瞳孔直径为 4.0 mm。
68。 宇航员能否在距离地表 180 千米的距离处乘坐卫星绕地球运行,区分两座相距 20 米的摩天大楼? 假设宇航员眼睛的瞳孔直径为 5.0 mm,并且大部分光线集中在 500 nm 左右。
69。 体育场记分牌的角色由间隔紧密的灯泡组成,主要辐射黄光。 (使用\(\displaystyle λ=600nm\)。) 灯泡间隔多近,这样 80 米外的观察者才能看到连续线条的显示屏而不是单个灯泡? 假设观察者眼睛的瞳孔直径为 5.0 mm。
70。 如果显微镜能够以最大角度接收来自物体的光\(\displaystyle α=70°\),那么用波长为 500 nm 的光照射时能分辨出的最小结构是什么
(a) 标本在空气中?
(b) 当试样浸入油中时,折射率为 1.52?
71。 相机使用光圈为 2.0 cm 的镜头。 在 700 nm 波长下拍摄的照片的角度分辨率是多少? 它能否分辨放置在 35 米外的尺子上的毫米标记?
4.6 X 射线衍射
72。 波长为 0.103 nm 的 X 射线从晶体上反射,二阶最大值以布拉格角记录下来\(\displaystyle 25.5°\)。 这个晶体中散射面之间的间距是多少?
73。 当单色 X 射线与反射面成\(\displaystyle 32.3°\)一定角度落在晶体上时,可以观察到一阶布拉格反射最大值。 这张 X 射线的波长是多少?
74。 对原子形成分隔 0.440 nm 的平面的晶体进行 X 射线散射实验。 使用波长为0.548 nm的X射线源,实验者需要在多大角度(相对于相关平面)照亮晶体才能观察到一阶最大值?
75。 NaCl 晶体的结构形成相距 0.541 nm 的反射面。 如果使用波长为 0.085 nm 的 X 射线,则从这些平面测量,可以观察到 X 射线衍射的最小角度是多少?
76。 在某种晶体上,使用未知波长的 X 射线源,以\(\displaystyle 27.1°\)相对于其表面的角度观察到一级 X 射线衍射最大值。 此外,当用不同的已知波长为0.137 nm的时间照亮时,检测到二阶最大值为\(\displaystyle 37.3°\)。 确定 (a) 反射面之间的间距,以及 (b) 未知波长。
77。 方解石晶体含有分隔 0.30 nm 的散射面。 当使用 0.130 nm 波长的 X 射线时,一阶衍射最大值和二阶衍射最大值之间的角度间隔是多少?
78。 某晶体的一阶布拉格角是\(\displaystyle 12.1°\)。 二阶角度是多少?
其他问题
79。 白光落在两条相隔 0.40 mm 的狭缝上。 在 3.0 米外的屏幕上观察到干扰模式。 (a) 红光 () 和紫光 (\(\displaystyle λ=700nm\)\(\displaystyle λ=400nm\)) 的第一个最大值之间的间隔是多少? (b) 在最接近中心最大值的哪个点上,黄光的最大值 (\(\displaystyle λ=600nm\)) 会与紫光的最大值重合? 确定每个最大值的顺序。
80。 波长 10.0 mm 的微波通常落在包含 25 mm 宽狭缝的金属板上。
(a) 衍射图案的第一个最小值在哪里?
(b) 如果波长为30.0 mm,会有最小值吗?
81。 类星体或准恒星无线电源是1960年发现的天体。 它们是遥远但强大的无线电波发射器,角大小很小,它们最初没有得到解决,就像恒星一样。 类星体 3C405 实际上是两个离散的无线电源,其角度为 82 弧秒。 如果使用频率为410 MHz的无线电发射来研究这个物体,那么能够分辨这两个源的射电望远镜的最小直径是多少?
82。 两条宽度各为 1800 nm 的狭缝由波长为 461.9 nm 的K型离子激光器发出的平面波照亮。 找出中心衍射峰中的干扰峰数。
83。 波长未知的微波入射在宽度为 6 cm 的单个狭缝上。 发现中心峰的角宽度为\(\displaystyle 25°\)。 找到波长。
84。 氦霓激光器发出的红光(空气中波长 632.8 nm)入射到宽度为 0.05 mm 的单个狭缝上。 整个设备浸入折射率为1.333的水中。 确定中心峰的角宽度。
85。 一束波长为 461.9 nm 的光线从一颗 2 毫米的原子离子激光器的圆孔中产生。 由于衍射,光束在向外移动时会膨胀。 中心亮点有多大
(a) 1 米,
(b) 1 千米,
(c) 1000 千米,以及
(d) 在距离地球 400,000 千米的月球表面。
86。 如果只有眼睛瞳孔的衍射效应限制了分辨率,那么两个物体在月球上的距离必须有多远才能被眼睛区分? 假设光的波长为 550 nm,瞳孔直径为 5.0 mm,距离月球的距离为 400,000 km。
87。 如果只有望远镜孔径的衍射效应限制了分辨率,那么位于夏威夷莫纳克亚岛的直径为8.1米的Gemini North望远镜必须分辨出月球上的两个物体相距多远? 假设光的波长为 550 nm,与月球的距离为 400,000 km。
88。 众所周知,间谍卫星能够解析相距 10 厘米的物体,同时在地球表面上空 197 千米处运行。 如果分辨率仅受衍射效应的限制,望远镜孔径的直径是多少? 使用 550 nm 作为灯光。
89。 波长为 530 nm 的单色光穿过不透明板\(\displaystyle 1.5μm\)中的水平单个宽度狭缝。 屏幕尺寸\(\displaystyle 2.0m×2.0m\)与缝隙相距 1.2 m。
(a) 衍射图案在屏幕上以哪种方式展开?
(b) 最小值相对于中心的角度是多少?
(c) 最大值的角度是多少?
(d) 屏幕上的中央亮边有多宽?
(e) 屏幕上下一个亮边有多宽?
90。 波长未知的单色光入射在宽度狭缝上\(\displaystyle 20μm\)。 在 2.5 米外的屏幕上可以看到衍射图案,其中中心最大值分布在 10.0 cm 的距离内。 找到波长。
91。 具有相同强度的两个波长 550 nm 和 600 nm 的光源入射到宽度狭缝上\(\displaystyle 1.8μm\)。 在 30.0 厘米外的屏幕上找到两个波长的\(\displaystyle m=1\)亮点的分离。
92。 宽度为 2100 nm 的单个狭缝通常由波长为 632.8 nm 的波浪照亮。 找出从缝隙底部到屏幕上水平距离为 2.0 m、垂直距离中心 10.0 厘米处的波浪之间的相位差。
93。 波长\(\displaystyle 3.0μm\)为 589 nm 的钠黄光照亮一条宽度的狭缝。 根据中心最大值的强度找到与轴成\(\displaystyle 15°\)一定角度的强度。
94。 宽度为 0.10 mm 的单个狭缝由波长为 576 nm 的水银灯照亮。 根据中心最大值的强度找到与轴成\(\displaystyle 10°\)一定角度的强度。
95。 在距离2.0米的屏幕上,衍射光栅产生的第二个最大值距离中心最大值89.7厘米。 如果光栅每厘米有 600 条线,那么产生衍射图案的光的波长是多少?
96。 每厘米有 4000 条线的光栅用于衍射包含 400 到 650 nm 之间所有波长的光。 屏幕上距离光栅 3.0 m 的一阶光谱有多宽?
97。 每厘米有 2000 条线的衍射光栅用于测量氢气放电管发射的波长。 (a) 你会在什么角度找到波长 410 和 434 nm 的两条一阶蓝线的最大值? (b) 在 rad 和\(\displaystyle θ_1=0.097\) rad 处找到另外两条一阶线的最大值。\(\displaystyle θ_2=0.132\) 这些线的波长是多少?
98。 对于正常落在衍射光栅上的白光 (\(\displaystyle 400nm<λ<700nm\)),显示无论光栅常数 d 是多少,二阶和三阶光谱都会重叠。
99。 使用每厘米包含 5000 条线的衍射光栅可以产生多少完整的可见光谱 (\(\displaystyle 400nm<λ<700nm\))?
100。 两盏产生波长为589 nm的光的灯固定在木板上,相距1.0米。 如果分辨率仅受进入眼睛的光的衍射的影响,那么观察者能够将灯泡分辨为两个独立的光源的最大距离是多少? 假设光线通过直径为 4.5 mm 的瞳孔进入眼睛。
101。 在晴朗的日子里,你站在山顶,望着一座12公里外的城市。 这座城市有两座相距 20.0 米的高塔。 如果瞳孔直径为 4.0 mm,你的眼睛能分辨出两座塔吗? 如果不是,解析两座塔所需的望远镜的最小放大倍率应该是多少? 在计算中,使用 550 nm 作为光的波长。
102。 射电望远镜是用于探测来自太空的无线电发射的望远镜。 由于无线电波的波长比可见光长得多,因此射电望远镜的直径必须非常大才能提供良好的分辨率。 例如,加拿大不列颠哥伦比亚省彭蒂克顿的射电望远镜直径为 26 m,可在高达 6.6 GHz 的频率下运行。
(a) 这个频率对应的波长是多少?
(b) 这台望远镜可以分辨的两个无线电源的角间隔是多少?
(c) 将望远镜的分辨率与月球的角度大小进行比较。

103。 计算落在单个宽度狭缝上\(\displaystyle 36.9°\)时产生第一个最小值的光的波长\(\displaystyle 1.00μm\)。
104。 (a) 找出落在宽度狭缝上的 633 nm 光的第三个最小衍射角度\(\displaystyle 20.0μm\)。
(b) 将此最小值设置为多大的狭缝宽度\(\displaystyle 85.0°\)?
105。 以日常尺寸的孔径衍射为例,以宽度为 1.0 m 的门口为例。
(a) 600-nm 光的衍射图案中第一个最小值的角度位置是多少?
(b) 对频率为 440 Hz(A 高于中间 C)的音符重复此计算。 将声速设为 343 m/s。
106。 在由 400 nm 光照射的宽度为 0.20 mm 的狭缝产生的衍射图案中,第一个和第二个最小值的角度位置是多少? 中心峰的角宽度是多少?
107。 你会将屏幕放置在距离前一个问题的缝隙多远,这样第二个最小距离就是距离衍射图案中心 2.5 mm 的距离?
108。 在 1.8 m 以外、中心峰宽 1.0 m 的屏幕上产生衍射图案的缝隙有多窄? 假设\(\displaystyle λ=589nm\)。
109。 假设单缝衍射图案的中心峰很宽,可以假设第一个最小值出现在±90°±90°的角度位置。 在这种情况下,狭缝宽度与光波长的比率是多少?
110。 双缝干涉图案的中心衍射峰恰好包含九条条纹。 狭缝间距与狭缝宽度的比率是多少?
111。 如果可能,当波长为 500 nm 的光正常入射到宽度为 1000 nm 且间隔为 1500 nm 的双缝上时,确定除衍射中心最大值中的中心峰以外的三个干扰峰的强度。 使用中心点的强度为\(\displaystyle 1mW/cm^2\)。
112。 钠蒸气灯发出的黄光似乎是纯波长,但是\(\displaystyle 36.129°\)当投射到每厘米10,000线的衍射光栅上时,它会产生两个一阶最大值。\(\displaystyle 36.093°\) 精度为 0.1 nm 的两个波长是多少?
113。 鸟羽上的结构就像反射光栅一样,每厘米有 8000 条线。 600-nm 光的一阶最大角度是多少?
114。 如果衍射光栅在可见光的最短波长处产生一阶最大值\(\displaystyle 30.0°\),那么对于最大波长的可见光,一阶最大值将在多大角度下呢?
115。 (a) 在每厘米25,000线的衍射光栅上投射\(\displaystyle 25.0°\)时,哪个可见波长的四阶最大值为四阶最大值?
(b) 这个结果有什么不合理之处?
(c) 哪些假设不合理或不一致?
116。 以基于衍射光栅的光谱仪为例。 构造一个问题,在其中计算光谱仪中两个波长电磁辐射之间的距离。 需要考虑的因素包括你希望能够分辨的波长、衍射光栅上每米的线数以及从光栅到屏幕或探测器的距离。 讨论该设备在能够辨别感兴趣的波长方面的实用性。
117。 一位业余天文学家想建造一台具有衍射极限的望远镜,这样他就可以看到木星的卫星上是否有人。
(a) 需要多大直径的镜子才能在距离地球的距离处看到木星月球上的 1.00 米细节?\(\displaystyle 7.50×10^8km\) 光的波长平均为 600 nm。
(b) 这个结果有什么不合理之处?
(c) 哪些假设不合理或不一致?
挑战问题
118。 波长为 450 nm 的蓝光落在宽度为 0.25 mm 的狭缝上。 在狭缝后面放置一个焦距为 20 cm 的会聚镜头,并将衍射图案聚焦在屏幕上。
(a) 屏幕离镜头有多远?
(b) 衍射图案的第一个最小值和第三个最小值之间的距离是多少?
119。 (a) 假设最大值介于单缝衍射图案的最小值之间。 如单缝衍射强度中所述,使用相量图的直径和周长,根据中心最大值的强度来确定第三和第四最大值的强度。
(b) 使用公式 4.4 进行同样的计算。
120。 (a) 通过微分方程 4.4,表明单缝衍射图案的高阶最大值出现在满足\(\displaystyle β\)的值处\(\displaystyle tanβ=β\)。
(b) 绘制\(\displaystyle y=tanβ\)\(\displaystyle β\)和\(\displaystyle y=β\)对比图,然后找出这两条曲线的交点。 他们向您提供了有关最大值位置的哪些信息?
(c) 说服自己,这些点并不是精确出现在\(\displaystyle β=(n+\frac{1}{2})π\)、哪里,\(\displaystyle n=0,1,2,…,\)而是与这些值非常接近。
121。 衍射光栅每厘米的最大线数是多少,可以为可见光生成完整的一阶光谱?
122。 表明,除非一阶最大值的角度小于,否则衍射光栅无法为给定波长的光产生二阶最大值\(\displaystyle 30.0°\)。
123。 He-Ne 激光束从 CD 表面反射到墙上。 最亮的光点是角度等于入射角的反射光束。 但是,也可以观察到条纹。 如果墙距离 CD 1.50 m,第一个条纹距离中心最大值 0.600 m,那么 CD 上的凹槽间距是多少?
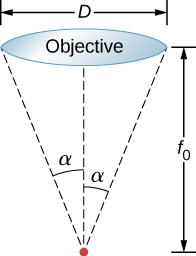
124。 通过显微镜观察的物体放置在非常靠近物镜焦点的位置。 显示可通过显微镜分辨的两个物体的最小间距 x 由下式给出
\[x=\frac{1.22λf_0}{D}, \nonumber \]
其中\(\displaystyle f_0\)是焦距,D 是物镜的直径,如下所示。