Skip to main content
Global

1.2: 光的传播

  1. Last updated
  2. Save as PDF
  • Page ID
    202050

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    学习目标

    在本节结束时，您将能够：

    • 根据介质中的光速，确定折 射率
    • 列出光从光源传播到另一个 位置的方式

    光速：早期测量

    1675 年， 丹麦天文学家奥莱·罗默（Ole Roemer）（1644—1710 年）首次测量了光速。 他研究了木星四颗大卫星之一艾奥的 轨道，发现 它围绕木星的旋转周期为42.5小时。 他还 发现，该值会波动几秒钟，具体 取决于地球在绕太阳轨道上的位置。 Roemer 意识到这种波动是由于光速有限造成的 ，可以用来确定 c。

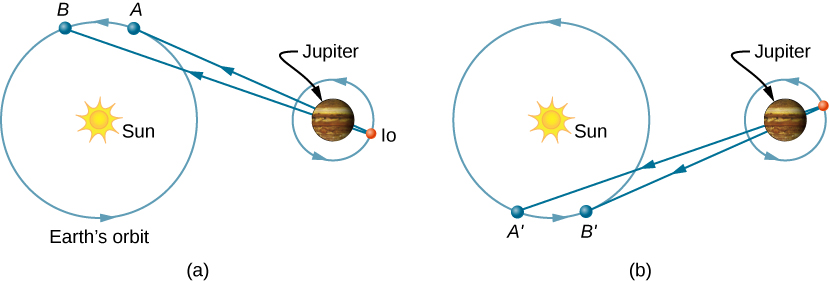
    罗默通过测量木星连续日食之间的 时间间隔，找到了艾奥的革命时期。 该图 \(\PageIndex{1a}\)显示了在地球从木星 后退的轨道部分进行此类 测量时的行星结构。 当地球处于 A 点时，地球、 木星和艾奥对齐。 下次进行这种对齐时， 地球位于 B 点，将这些 信息传送到地球的光必须传播到该点。 由于 B 比 A 离木星 更远，因此当地球在 B 处时，光 到达地球所需的时间更长。 现在想象一下大约 6 个月后，行星的排列方式如图所示 \(\PageIndex{1b}\)。 对艾奥周期的测量始于地 球 A 点，艾奥被木星黯然失色。 然后，下一次日食 发生在地球处于 B 点时，携带这次日食 信息的光必须传送到该点。 由于 B' 比 A 更接近 木星，因此光在 B 处时到达地球所需的时间更短。 因此， 在 “A” 和 “B” 看到的艾奥连续日食之间的时间间隔小于在 A 和 B 看到的 日食之间的时间间隔。 通过测量这些时间间隔的 差异并适当了解 木星和地球之间的距离，罗默计算出光速仅比当今接受的值 低33％。 \(2.0 \times 10^8\,m/s\)

    该图说明了使用 Roemer 方法时地球绕太阳的轨道和位置，以及艾奥围绕木星的轨道和位置。 显示了两种配置。 在这两者中，木星都位于艾奥和太阳之间。 在图 a 中，地球、木星和艾奥对齐，当地球位于 A 位置时，地球正在远离木星，然后在地球轨道 B 稍晚一点的位置，因此 A 比 B 更接近艾奥。在图 b 中，地球有两个相似的位置，但位于地球的另一侧标注了图 a 所示的轨道，当时地球、木星和艾奥再次对齐，但地球正在向木星移动。 第一个位置被标记为位置 A 素数，后来的位置被标记为 B 素数，因此 A 素数比 B 素数距离 Io 稍远一些。 显示了从 Io 到位置 A、B、A 素数和 B 素数的光线。
    图\(\PageIndex{1}\)：Roemer 用于确定光速的天文学方法。 使用部分 (a) 和 (b) 的配置对 Io 周期 的测量有所不同，因为 光路长度和相关的行程时间从 A 增加到 B (a)，但从 A'A′ 减少到 B'B′ (b)。

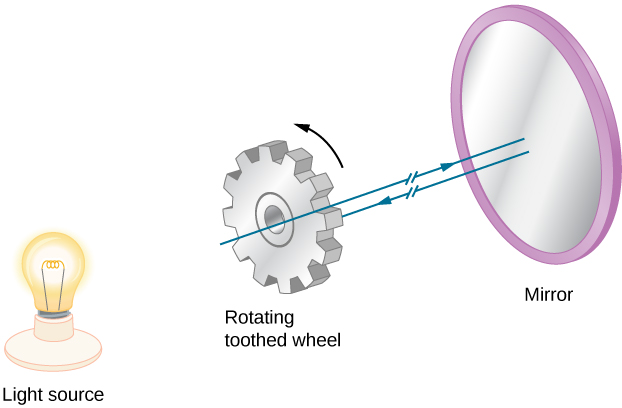
    1849 年，Armand Fizeau（1819—1896 年）首次成功地对 光速进行了地面测量。 他在一个山顶上放置了一个可以快速旋转的 齿轮，在 8 公里外的第二个山顶上放 了一面镜子（图\(\PageIndex{2}\)）。 在方向盘后面放置了一个强烈的光源，这样当 轮子旋转时，它会将光束切成连续的 脉冲。 然后调整方向盘的速度，直到没有光线 返回到方向盘后面的观察者身上。 只有当轮子旋转一个与 (n+½) 齿 位移相对应的角度，而脉冲向下移动到 镜子然后返回时，才会 发生这种情况。 Fizeau 知道了车轮的旋转速度、车轮上的齿 数以及与镜子的距离，因此确定光速为\（3.15\ times 10^8\，m/s\），这只太高了 5％。

    该图说明了 Fizeau 方法的设置。 旋转齿轮位于光源（图中显示为灯泡）和镜子之间。 镜子和轮子彼此平行且垂直于光束。 在通往镜子的路上，光线在牙齿之间穿过，但是从镜子回来时会被轮齿挡住。
    图\(\PageIndex{2}\)：Fizeau 测量 光速的方法。 当车轮以与 光线进出镜子的行进时间相匹配的速度旋转时，车轮 的齿在返回时会阻挡反射光。

    法国物理学家让·伯纳德·莱昂·福柯（1819—1868 年） 修改了菲佐的仪器，用 旋转镜代替了齿轮。 1862年，他测得的光速为 2.98×10 8 m/s，在目前可 接受值的0.6％以内。 阿尔伯特·迈克尔森（1852-1931）还多次使用福柯 的方法来测量光速。 他的 第一批实验是在1878年进行的；到1926年，他对这项技术进行了很好的完善 ，以至于他发现 c 为 (2.99796±4) ×10 8 m/s。

    今天，人们已经非常精确地知道光速。 实际 上，真空 c 中的光速非常重要，以至于 它被接受为基本物理量之一并具有 价值

    \ [c=2.99792458\ times 10^8m/s\ equiv 3.00\ times 10^8m/s \ label {speed}\]

    其中， 只要三位数的精度足够使用 3.00×10 8 m/s 的近似值。

    物质中的光速

    光穿过物质的速度小于在 真空中的速度，因为光与材料中的原子相互作用。 光速 在很大程度上取决于材料的类型，因为其 相互作用因不同的原子、晶格 和其他子结构而异。 我们可以定义一个 描述其中的光速的材质常数，称为折射率 n：

    \[n=\dfrac{c}{v} \label{index} \]

    哪里\(v\)是材料中观测到的光速。

    由于 物质中的光速始终小于 c，并且仅在真空中等于 c，因此 折射率始终大于或等于 1；即 n≤1。 表中列\(\PageIndex{1}\)出了一些 代表性物质的折射指数。 列出了特定光 波长的值，因为它们随波长的变化略有不同。 （这可能会产生重要的影响，例如由 棱镜分隔的颜色，正如我们将在色 散中看到的那样。） 请注意，对于气体，n 接近 1.0。 这似乎是合理的，因为气体中的原子被广泛分离， 光在原子之间的真空中以 c 处传播。 除非需要很高的精度，否则 通常使用气体。\(n=1\) 尽管介质中的光速 v 与真空中的值 c 有 很大差异，但它仍然是一个很 大的速度。

    图\(\PageIndex{1}\)：各种介质中的 折射率对于真空中波长为 589 nm 的光
    中等 n
    气体温度 为 0°C，1 atm
    空气 1.000293
    二氧化碳 1.00045
    氢气 1.000139
    氧气 1.000271
    20 摄氏度的液体
    苯 1.501
    二 硫化碳 1.628
    四氯化碳 1.461
    乙醇 1.361
    甘油 1.473
    淡水 1.333
    20°C 时的固体物质
    钻石 2.419
    萤石 1.434
    玻璃、皇冠 1.52
    玻璃、火石 1.66
    冰（ 0°C 时）0°C 1.309
    聚苯乙烯 1.49
    有机玻璃 1.51
    石英， 结晶 1.544
    石英，熔融石英 1.458
    氯化钠 1.544
    锆石 1.923

    示例\(\PageIndex{1}\)： 珠宝首饰中的光速

    计算锆石中的光速，锆石是 珠宝中用来模仿钻石的材料。

    策略

    我们可以使用方程 \ red { index} 根据材料\(n\)的折射率计算出材料中的光速\(v\)

    解决方案

    重新排列方程\ ref {index} for\(v\) 可以给我们

    \[v=\dfrac{c}{n}. \nonumber \]

    锆石的折射率在表中以 1.923 给出 \(\PageIndex{1}\)，在方程式\ ref {speed} 中给出。\(c\) 在方程中输入这些值可以得到

    \ [\ begin {align*} v &=\ dfrac {3.00×10^8m/s} {1.923}\\ [4pt] &=1.56×10^8m/s。\ end {align*}\ nonumber\]

    意义

    这个速度略高于 真空中光速的一半，并且与我们平时 体验的速度相比仍然很高。 表\(\PageIndex{1}\) 中列出的唯一折射率高于锆石的物质是钻石。 稍后 我们将看到，锆石的大折射率 使其比玻璃更闪耀，但比钻石更闪耀。

    练习\(\PageIndex{1}\)

    该表 \(\PageIndex{1}\)显示乙醇和淡水的折射指数非常 相似。 这些液体中的 光速相差多少百分比？

    回答

    2.1%（达到两个重要数字）

    光的射线模型

    在上一章关于 电磁波的章节中，你已经研究了 光的一些波浪特性。 在本章中，我们主要从射线 特性开始。 光线可以通过 三种方式从一个光源传播到另一个位置（图 \(\PageIndex{1}\)）。 它可以直接从源头穿过 空旷的空间，例如从太阳到地球。 或者光线可以 穿过各种媒体，例如空气和玻璃，传递给观察者。 光线也可以在被反射后到达，例如被镜子反射。 在所有这些情况下，我们可以将光路建模为一条称为射 线的直线。

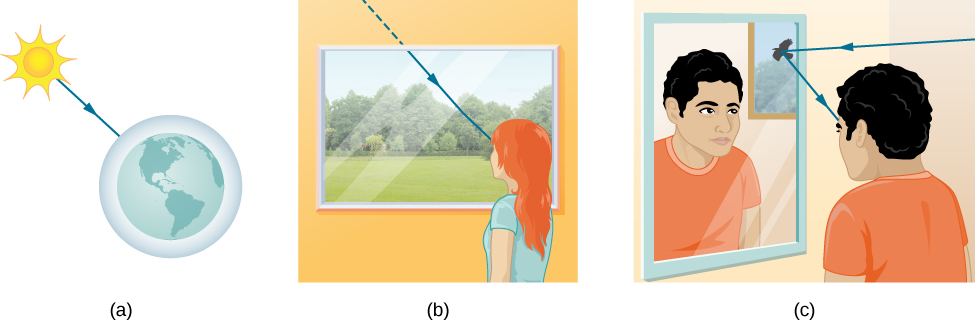
    该图的图纸说明了光从一个源头传播到另一个位置的三种方法。 图 a 显示了来自太阳的光到达地球大气层，直线穿过太空。 图 b 显示光线穿过窗户到达观察者。 图 c 显示光线从物体传播到镜子并向观察者反射。
    图\(\PageIndex{3}\)：光从光源传播 到另一个位置的三种方法。 (a) 光线到达地球 高层大气层，直接 从光源穿过空白空间。 (b) 光线可以通过空气和玻璃等 介质传递到人身上。 (c) 光也可以从镜子 等物体反射。 在此处所示的情形中，光线与足够大的 物体相互作用，使其像 射线一样以直线传播。

    实验表明，当光与比其波长大 几倍的物体相互作用时，它会以直 线传播并像射线一样起作用。 在这种情况下，它的波浪特性并不 明显。 由于可见 光的波长小于一微米（千分之一毫米），因此在许多常见情况下，它会遇到大于一微米的 物体， 就像射线一样。 例如，当可见光 遇到任何大到足以让我们用 肉眼观察到的东西时，例如硬币，它的作用就像射线，波浪特性通常 可以忽略不计。

    在所有这些情况下，我们可以将光路建模为 直线。 当光线遇到 物体（例如镜子）或从一种材质传递到 另一种材质时（例如从空气传递到玻璃）时，它可能会改变方向，但随后它会以直线或光线形式 继续。 “射线” 一词来自 数学，这里的意思是一条起源于某个 点的直线。 将光线可视化为激光射线是可以接受的。 光的 射线模型将光路描述为直 线。

    由于光线以直线移动，与材质 相互作用时会改变方向，因此其路径由几何和 简单的三角学来描述。 因此，光的射线方面占主导地位的 光学部分被称为几何光学。 两条定律 规定了光与物质相互作用时如何改变方向。 这些是反射定律，用于 光从物质上反射的情况，以及折射定律，适用于光穿过物质 的情况。 我们将在本章接下来的 章节中 详细介绍每项法律。