8.2: 系统的潜在能量
- Page ID
- 204977
- 将势能的差异与系统在没有摩擦或空气阻力的粒子上所做的工作相关联
- 解释系统势能函数零的含义
- 计算并应用地球表面附近物体的引力势能和质量弹簧系统的弹性势能
在 Work 中,我们看到,在地球表面附近,在任何位移上,在恒定引力下对物体所做的工作仅是位移终点位置差异的函数。 这个属性允许我们为系统定义一种与其动能(称为势能)不同的能量。 我们在以下小节中考虑势能的各种属性和类型。
潜在能量基础知识
在《二维与三维运动》中,我们分析了弹丸的运动,比如在 Figure 中踢足球\(\PageIndex{1}\)。 在这个例子中,让我们忽略摩擦和空气阻力。 随着足球的升起,足球的引力所起的作用是负的,因为球的垂直位移是正的,而重力产生的力在垂直方向上是负的。 我们还注意到,球会减速直到达到运动中的最高点,从而降低了球的动能。 这种动能的损失转化为 Football-Earth 系统的引力势能的增加。
随着足球落向地球,现在在足球上所做的工作是积极的,因为位移和引力都指向垂直向下。 球也会加速,这表明动能增加。 因此,能量从引力势能转换回动能。
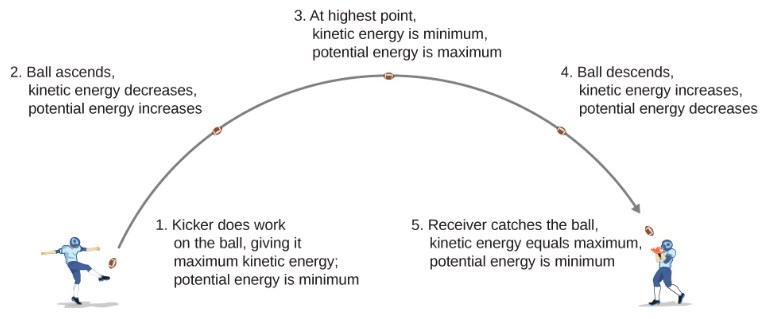
基于这个场景,我们可以将从A点到 B 点的势能差定义为已完成工作的负值:
\[ \Delta U_{A B}=U_{B}-U_{A}=-W_{A B} \label{8.1} \]
这个公式明确说明了潜在的能量差,而不仅仅是绝对的势能。 因此,我们需要定义给定位置的势能,以便自己陈述势能的标准值,而不是潜在的能量差。 我们通过用任意常数重写势能函数来做到这一点,
\[ \Delta U=U(\overrightarrow{\mathbf{r}})-U\left(\overrightarrow{\mathbf{r}}_{0}\right) \label{8.2} \]
在给定问题中,选择起始位置的势能\(\vec{r}_0\)是出于方便考虑。 最重要的是,无论做出什么选择,都应该陈述并在整个给定问题中保持一致。 对于初始势能,有一些公认的选择。 例如,问题中的最低高度通常定义为零势能,或者如果物体在太空中,则距离系统的最远点通常被定义为零势能。 那么,相对于零点\(\vec{r}_0\)的势能是公正的\(U(\vec{r})\)。
只要没有摩擦力或空气阻力,足球动能的变化等于足球引力势能变化的负值。 这可以概括为任何潜在能量:
\[\Delta K_{A B}=-\Delta U_{A B} \label{8.3}\]
让我们来看一个具体的例子,在方便点选择零势能作为引力势能。
粒子在 F =-a x 2 给出的力的作用下沿 x 轴移动,其中 a = 3 N/m 2。 (a) 当它从 x A = 1 m 移动到 x B = 2 m 时,它的势能有什么区别? (b) 相对于给定的 0.5 J 在 x=0 处的势能,粒子在 x = 1 m 处的势能是多少?
策略
(a) 如方程式\ ref {8.1} 所定义,势能之差是已完成工作的负值。 在上一章中,该功被定义为力与距离的点积。 由于粒子在 x 方向上向前移动,因此点积简化为乘法 (\(\hat{i} \cdot \hat{i}\)= 1)。 为了找出已完成的全部工作,我们需要在给定的极限之间整合函数。 整合后,我们可以陈述功效或势能的变化。 (b) 势能函数在 x=0 处相对于零,是 (a) 部分中遇到的不定积分,积分常数由方程\ ref {8.3} 确定。 然后,我们将 x 值替换为势能函数,以计算 x = 1 时的势能。
解决方案
a. 当粒子在一维上从坐标 x 移动到 x + dx 时,给定力所做的工作是
\[d W=\overrightarrow{\mathbf{F}} \cdot d \overrightarrow{\mathbf{r}}=F d x=-a x^{2} d x \nonumber \]
将这个表达式代入方程\ ref {8.1},我们得到
\[\Delta U=-W=\int_{x_{1}}^{x_{2}} a x^{2} d x=\left.\frac{1}{3}\left(3 \: \mathrm{N} / \mathrm{m}^{2}\right) x^{3}\right|_{1 \mathrm{m}} ^{2\mathrm{m}}=7 \: \mathrm{J} \nonumber \]
b. (a) 部分中势能函数的不定积分为
\[U(x)=\frac{1}{3} a x^{3}+\text { const. }, \nonumber \]
而且我们希望常数由下式确定
\[ U(0) = 0.5 \: J. \nonumber \]
因此,x = 0 时相对于零的势能仅为
\[U(x)=\frac{1}{3} a x^{3}+0.5 \: \mathrm{J} \nonumber \]
因此,x = 1 m 处的势能为
\[U(1 \: \mathrm{m})=\frac{1}{3}\left(3 \: \mathrm{N} / \mathrm{m}^{2}\right)(1 \: \mathrm{m})^{3}+0.5 \: \mathrm{J}=1.5 \: \mathrm{J}. \nonumber \]
意义
在这个一维的例子中,我们可以整合的任何函数,与路径无关,都是保守的。 注意我们是如何应用势能差的定义来确定选定点相对于零的势能函数的。 另请注意,在 (b) 部分中确定,在 x = 1 m 处的势能为 U (1 m) = 1 J,x = 2 m 处的势能为 U (2 m) = 8 J;它们的差异是 (a) 部分的结果。
在示例中\(\PageIndex{1}\),在 x = 1 m 和 x = 2 m 时,粒子在 x = 1.5 m 时相对于零的势能是多少? 验证势能之差是否仍为 7 J。
由多个粒子组成的系统
通常,一个感兴趣的系统可能由几个粒子组成。 系统势能的差异是引力或弹性力所做工作的负值,正如我们将在下一节中看到的那样,引力或弹性力是保守力。 势能差仅取决于粒子的初始位置和最终位置,以及表征相互作用的某些参数(例如重力的质量或胡克定律力的弹簧常数)。
重要的是要记住,势能是选定系统中物体之间相互作用的特性,而不仅仅是每个物体的属性。 对于电力来说尤其如此,尽管在下面我们考虑的势能示例中,系统的各个部分要么很大(比如地球,与其表面的物体相比),要么太小(比如无质量弹簧),以至于这些部分所经历的变化可以忽略不计系统。
势能的类型
对于系统中存在的每种相互作用类型,您可以标记相应类型的势能。 系统的总势能是所有类型的势能之和。 (这源于已完成工作的表达式中点积的加法特性。) 让我们来看看 Work 中讨论的潜在能量类型的一些具体示例。 首先,我们在分开行动时考虑每种力量,然后在两者共同作用时考虑其中的每一种力量。
地球表面附近的引力势能
兴趣系统由我们的星球、地球及其表面附近的一个或多个粒子(或与地球相比小到足以被视为粒子的物体)组成。 每个粒子(或物体)上的引力仅为其在地球表面附近的重量毫克,垂直向下起作用。 根据牛顿第三定律,每个粒子在地球上施加的力大小相等,但方向相反。 牛顿第二定律告诉我们,地球上每种力产生的加速度大小为毫克除以地球的质量。 由于任何普通物体的质量与地球质量的比例都非常小,因此可以完全忽略地球的运动。 因此,我们认为该系统是一组单粒子系统,受地球均匀引力的影响。
在 Work 中,地球在其表面附近的均匀引力对天体所做的工作取决于物体的质量、重力引起的加速度以及物体穿越的高度差,如方程式 7.2.4 所示。 顾名思义,这项工作是引力势能差异的负值,所以这种差异是
\[\Delta U_{\mathrm{grav}}=-W_{\mathrm{grav}, A B}=m g\left(y_{B}-y_{A}\right) \label{8.4}.\]
由此可以看出,地球表面附近的引力势能函数是
\[U(y)=m g y+\text { const. } \label{8.5}\]
您可以选择常量的值,如方程\ ref {8.2} 的讨论中所述;但是,为了求解大多数问题,当 y=0(问题中最低的垂直位置)时,最方便选择的常量是零。
位于马萨诸塞州米尔顿的 Great Blue Hill 山顶比其底部高出 147 米,海拔 195 米(图\(\PageIndex{2}\))。 (它的美洲原住民名字马萨诸塞州被定居者用来命名海湾殖民地及其所在地附近的州。) 一个 75 公斤的徒步旅行者从基地上升到山顶。 当徒步旅行者(a)在山底,(b)在山顶,(c)之后在海平面时,相对于基本高度的零引力势能,徒步旅行者-地球系统的引力势能是多少?
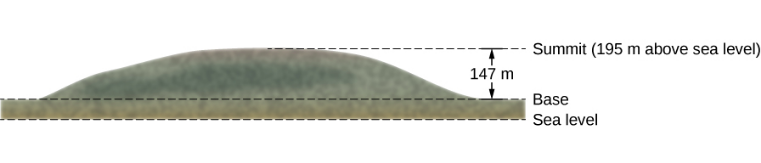
策略
首先,我们需要为 y 轴选择一个原点,然后确定使基数高度处势能为零的常数的值。 然后,我们可以根据零势能高度与徒步旅行者所在高度之间的关系,根据方程\ ref {8.5} 确定势能。
解决方案
a. 让我们在基本高度处选择 y 轴的原点,我们也希望势能的零为零。 此选择使常量等于零,
\[U(\text { base })=U(0)=0 \nonumber\]
b. 在山顶上,y = 147 m,所以
\[ U(\text { summit }) = U(147 \: \mathrm{m})=m g h=(75 \times 9.8 \: \mathrm{N})(147 \: \mathrm{m})=108 \: \mathrm{kJ}. \nonumber \]
c. 在海平面上,y = (147-195) m = -48 m,所以
\[ U \text { (sea-level) }=(75 \times 9.8 \mathrm{N})(-48 \mathrm{m})=-35.3 \mathrm{kJ} .\nonumber \]
意义
除了说明方程\ ref {8.4} 和方程\ ref {8.5} 的用法外,我们发现的引力势能值是合理的。 山顶的引力势能高于底部,海平面上的引力势能比底部的引力势能低。 在你上升的路上,Gravity 也会对你起作用! 它的作用是负面的,不如你的肌肉那么多(按幅度计算)。 但它确实有效。 同样,你的肌肉确实会在你向下的路上起作用,就像负面作用一样。 势能的数值取决于势能零的选择,但势能的物理意义差异不是。 [请注意,由于方程\ ref {8.2} 存在差异,因此数值不取决于坐标的原点。]
相对于潜在能量为零的海平面,徒步旅行者在底部、山顶和海平面的引力势能值是多少?
弹性势能
在 Work 中,我们看到,完全弹性弹性弹簧在一维上所做的工作仅取决于弹簧常数和从未拉伸位置的位移平方,如方程式 7.2.5 所示。 这项工作仅涉及胡克定律相互作用的属性,而不涉及真实弹簧和附着在它们上的任何物体的属性。 因此,在考虑体现这种力的系统之前,我们可以将弹簧力的弹性势能之差定义为该方程中弹簧力所做功的负值。 因此,
\[\Delta U=-W_{A B}=\frac{1}{2} k\left(x_{B}^{2}-x_{A}^{2}\right) \label{8.6} \]
物体从 A 点移动到 B 点的位置。 与该差异对应的势能函数为
\[U(x)=\frac{1}{2} k x^{2}+\text { const. } \label{8.7} \]
如果弹簧力是唯一起作用的力,那么当弹簧处于未拉伸长度时,最简单的方法是在 x = 0 处取位能为零。 然后,常数为方程\ ref {8.7} 为零。 (如果其他力量在起作用,其他选择可能更方便。)
系统包含一个弹性极好的弹簧,其未拉伸长度为 20 cm,弹簧常数为 4 N/cm。 (a) 当弹簧的长度为 23 厘米时,弹簧会产生多少弹性势能? (b) 如果它的长度增加到26厘米,它会产生多少潜在能量?
策略
当弹簧处于未拉伸长度时,它对系统的势能没有任何贡献,因此我们可以使用方程\ ref {8.7},常数等于零。 x 的值是长度减去未拉伸的长度。 当弹簧膨胀时,在计算弹簧的势能时,应使用弹簧的位移或其松弛长度与拉伸长度之间的差作为 x 值。
解决方案
- 弹簧的位移为 x = 23 cm − 20 cm = 3 cm,因此贡献的势能为 U =\(\frac{1}{2}\) kx 2 =\(\frac{1}{2}\) (4 N/cm) (3 cm) 2 = 0.18 J
- 当弹簧的位移为 x = 26 cm − 20 cm = 6 cm 时,势能为 U =\(\frac{1}{2}\) kx 2 =\(\frac{1}{2}\) (4 N/cm) (6 cm) 2 = 0.72 J,比 (a) 部分中的量增加了 0.54-J。
意义
计算方程\ ref {8.7} 中的弹性势能和势能差涉及根据给定的弹簧长度求解势能。 由于 U 依赖于 x 2,因此压缩(负 x)的势能与等幅延伸的势能相同。
当示例 8.2.3 中弹簧的长度从 22.0 cm 的初始值变为最终值时,它产生的弹性势能会变化 −0.0800J。 找到最终长度。
引力和弹性势能
同时体现引力和弹性势能的简单系统是一维垂直质量弹簧系统。 它由一个巨大的粒子(或方块)组成,悬挂在一个弹性极好、无质量的弹簧的一端,弹簧的另一端是固定的,如图所示\(\PageIndex{3}\)。
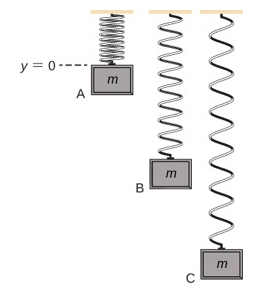
首先,让我们考虑系统的潜在能量。 我们需要在方程\ ref {8.5} 的势能函数中定义常数。 通常,当引力势能为零时,地面是合适的选择;但是,在这种情况下,最高点或 y = 0 是零引力势能的便捷位置。 请注意,这个选择是任意的,即使选择了另一个选项,问题也可以正确解决。
我们还必须定义系统的弹性势能和相应的常数,详见方程\ ref {8.7}。 这是弹簧未拉伸的地方,或者处于 y = 0 的位置。
如果我们认为系统的总能量是守恒的,那么 A 点的能量等于 C 点。方块正好放置在弹簧上,因此其初始动能为零。 根据前面讨论的问题的构成,引力势能和弹性势能都等于零。 因此,系统的初始能量为零。 当方块到达 C 点时,其动能为零。 但是,它现在既有引力势能,又有弹性势能。 因此,我们可以求解方块在停靠点之前行进的距离 y:
\ [\ begin {aligned}
K_ {\ mathrm {A}} &+U_ {A} =K_ {C} +U_ {\ mathrm {C}}\\
0 &=0+m g y_ {C} +\ frac {1} {2}\\ y_ {\
mathrm {C}} &=\ frac {-2 m g} {k}
\ end {aligned}\]

重达 1.2 N 的块悬挂在弹簧上,弹簧常数为 6.0 N/m,如图所示\(\PageIndex{3}\)。 (a) 如C点所示,弹簧的最大膨胀率是多少? (b) 介于 A 和 C 之间 B 点的总势能是多少? (c) B点区块的速度是多少?
策略
在 (a) 部分中,我们计算了前文中讨论的距离 y C。 然后在 (b) 部分中,我们使用方程式\ ref {8.4} 和方程\ ref {8.6} 使用 y 值的一半来计算 B 点的势能。 该能量必须等于 B 点处的动能,即方程 7.3.1,因为系统的初始能量为零。 通过计算 B 点的动能,我们现在可以计算出 B 点方块的速度。
解决方案
a. 如前所述,由于系统在 A 点的总能量为零,因此弹簧的最大膨胀计算公式为:
\ begin {arra
y} {l} y_ {\ mathrm {C}} =\ frac {-2 m g} {k}\\
y_ {\ mathrm {C}} =\ frac {-2 (1.2\:\ mathrm {N}/\ mathrm {m})} =-0.40\:\ mathrm {m}
\ end {array}
b. y B 的位置是 y C 位置的一半或 -0.20 m。因此 B 点的总势能为:
\ begin {aligned}
U_ {B} &=m g y_ {B} +\ 左 (\ frac {1} {2} k y_ {B}\ 右) ^ {2}\\
U_ {B} & =( 1.2\:\ mathrm {N}) (-0.20\:\ mathrm {m}) +\ frac {1} {2} (6\:\ mathrm {N}/\ mathrm {m}) (-0.20\:\ mathrm {m}) ^ {2}\\
U_ {B} &=-0.12\:\ mathrm {J}
\ end {aligned}
c. 方块的质量等于重量除以重力。
\[m=\frac{F_{w}}{g}=\frac{1.2 \: \mathrm{N}}{9.8 \: \mathrm{m} / \mathrm{s}^{2}}=0.12 \: \mathrm{kg} \nonumber \]
因此,B 点的动能为 0.12 J,因为总能量为零。 因此,B点处方块的速度等于
\ begin {array} {l}
K=\ frac {1} {2} m
v^ {2}\\ v=\ sqrt {\ frac {2 K} {m}} =\ sqrt {\ frac {2 (0.12\:\ mathrm {k})}} =1.4\:\ mathrm {m}/\ mathrm {s}
\ end {array}
意义
尽管重力产生的势能是相对于选定的零位置的,但如果在不同的位置选择零能量点,则这个问题的解决方案是相同的。
假设方程\ ref {8.6} 中的质量翻了一番,同时保持所有其他条件不变。 弹簧的最大膨胀率会增加、减少还是保持不变? 与原始质量相比,B 点的速度会更大、更小还是相同?
观看这个模拟,了解滑冰运动员的能量守恒吧! 为滑冰运动员建造赛道、坡道和跳跃点,查看他移动时的动能、势能和摩擦力。 您也可以将滑冰运动员带到不同的星球甚至太空!
表中显示了各种能量的样本图,\(\PageIndex{1}\)可让您了解与某些事件相关的典型能量值。 其中一些是使用动能计算出来的,而另一些则是使用目前可能尚未讨论过的以势能形式发现的量计算得出的。
| 物体/现象 | 以焦耳为单位的能量 |
|---|---|
| 大爆炸 | 10 68 |
| 世界每年的能源消耗 | 4.0 x 10 20 |
| 大型聚变炸弹(9 兆吨) | 3.8 x 10 16 |
| 广岛大小的裂变炸弹(10 千吨) | 4.2 x 10 13 |
| 1 桶原油 | 5.9 x 10 9 |
| 1 吨 TNT | 4.2 x 10 9 |
| 1 加仑汽油 | 1.2 x 10 8 |
| 成人每日食物摄入量(推荐) | 1.2 x 10 7 |
| 1000 千克的汽车,时速为 90 kg | 3.1 x 10 5 |
| 网球时速为 100 km/h | 22 |
| 蚊子(0.5 m/s 时为 10 −2 g) | 1.3 x 10 -6 |
| 电视管光束中的单个电子 | 4.0 x 10 -15 |
| 分解一条 DNA 链的能量 | 10 -19 |


