2.3:估计可变和固定成本方程式并预测未来成本
- Page ID
- 199290
有时,企业需要使用成本估算技术,尤其是在混合成本的情况下,这样它们才能将固定和可变组成部分分开,因为短期内只有可变成分会发生变化。 估算对于使用当前数据预测未来生产变化对总成本的影响也很有用。 可以使用的三种估计技术包括散点图、高低法和回归分析。 在这里,我们将演示散点图和高低法(你将在高级管理会计课程中学习回归分析技术)。
成本方程的函数
成本方程是一个线性方程,它考虑了总固定成本、混合成本的固定部分和单位可变成本。 成本方程式可以使用过去的数据来确定过去的成本模式,然后可以预测未来的成本,也可以使用估计或预期的未来数据来估算未来的成本。 回想一下混合成本方程式:
\[y=a+b x\]
其中\(Y\)是总混合成本,\(a\)是固定成本,\(b\)是单位可变成本,\(x\)是活动水平。
让我们通过研究Eagle Electronics在制造家庭安全系统时产生的成本,更深入地了解成本方程式,如表所示\(\PageIndex{1}\)。
| 产生的成本 | 固定或可变 | 成本 |
|---|---|---|
| 制造设备租赁 | 已修复 | 每年 50,000 美元 |
| 主管工资 | 已修复 | 每年 75,000 美元 |
| 直接材料 | 变量 | 每单位 50 美元 |
| 直接劳动 | 变量 | 每单位 20 美元 |
通过应用成本方程式,Eagle Electronics 可以预测其在任何活动水平上的成本 (\(x\)),如下所示:
- 确定总固定成本:\(\$50,000 + \$75,000 = \$125,000\)
- 确定每单位可变成本:\(\$50 + \$20 = \$70\)
- 完成成本方程式:\(Y = \$125,000 + \$70x\)
使用这个方程式,Eagle Electronics 现在可以预测任何给定活动水平 (\(x\)) 的总成本 (),如图\(\PageIndex{1}\):\(Y\)
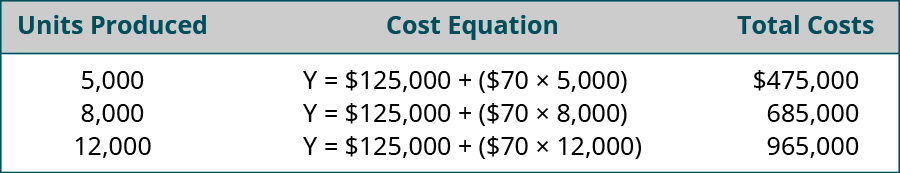
在使用这种方法时,Eagle Electronics必须确定它只预测其相关区间的成本。 例如,如果他们必须雇用第二位主管来生产\(12,000\)单位,则他们必须回去调整等式中使用的总固定成本。 同样,如果单位可变成本发生变化,也必须对其进行调整。
同样的方法可用于预测服务和销售公司的成本,如表所示,通过检查J&L Accounting为准备企业所得税申报表而产生的成本所示\(\PageIndex{2}\)。
| 产生的成本 | 固定或可变 | 成本 |
|---|---|---|
| 建筑物租金 | 已修复 | 每月 1,000 美元 |
| 直接劳动(适用于注册会计师) | 变量 | 每份纳税申报表 250 美元 |
| 秘书人员 | 已修复 | 每月 2,000 美元 |
| 会计文员 | 变量 | 每张退货 100 美元 |
如果他们在2月份完成\(25\)公司纳税申报表,J&L希望预测他们的总成本。
- 确定总固定成本:\(\$1,000 + \$2,000 = \$3,000\)
- 确定每份纳税申报单的可变成本:\(\$250 + \$100 = \$350\)
- 完成成本方程式:\(Y = \$3,000 + \$350x\)
使用这个方程式,强生现在可以在预计准备\(25\)公司纳税申报表时预测其2月份的总成本(\(Y\)):
\(\begin{array}{l}{Y=\$ 3,000+(\$ 350 \times 25)} \\ {Y=\$ 3,000+\$ 8,750} \\ {Y=\$ 11,750}\end{array}\)
强生现在可以使用这个预测的总成本数字\(\$11,750\)来决定向客户收取多少费用或他们需要多少现金来支付费用。 同样,强生必须谨慎行事,在未调整相应的总成本组成部分的情况下,尽量不要预测超出相关区间的成本。
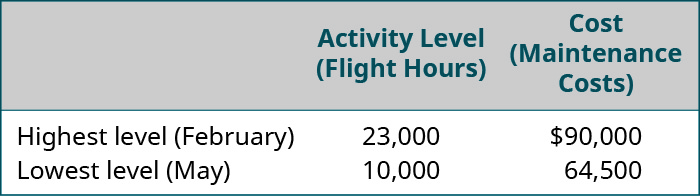
强生可以预测自己的成本,因为他们拥有所需的数据,但是当企业想要估算总成本但没有收集有关单位成本的数据时会发生什么? 位于南卡罗来纳州海岸的一家小型酒店Beach Inn的经理就是这种情况。 他们知道六月份的成本是多少,但现在他们想预测7月的成本。 他们收集了图中的信息\(\PageIndex{2}\)。
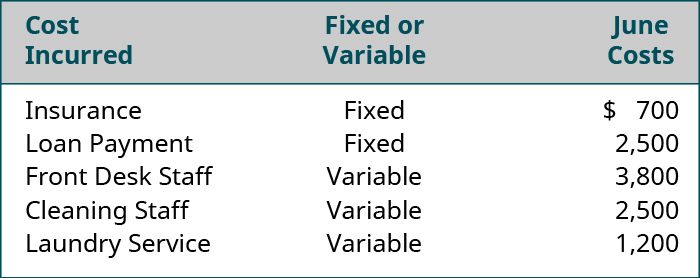
6月,他们\(75\)住了几晚。 对于海滩客栈来说,入住率(租用的房间)是成本驱动因素。 由于他们知道是什么推动了他们的成本,他们可以确定每单位可变成本以预测未来的成本:
\(\begin{array}{l}{\dfrac{\text { Front Desk Staff }}{75\text { nights }}=\dfrac{\$ 3,800}{75}=\$ 50.67 \text { variable front desk staff costs per night }} \\ {\dfrac{\text { Cleaning Staff }}{75\text {nights }}=\dfrac{\$ 2,500}{75}=\$ 33.33 \text { variable cleaning staff costs per night }} \\ {\dfrac{\text { Laundry Service }}{75 \text { nights }}=\dfrac{\$ 1,200}{75}=\$ 16.00 \text { variable laundry service costs per night }}\end{array}\)
现在,Beach Inn可以应用成本方程式来预测相关范围内任意数量的总费用。
- 确定总固定成本:\(\$700 + \$2,500 = \$3,200\)
- 确定每晚入住的可变费用:\(\$50.67 + \$33.33 + \$16.00 = \$100\)
- 完成成本方程式:\(Y = \\$3,200 + $100x\)
使用这个方程式,Beach Inn现在可以预测其7月份的总费用(\(Y\)),届时他们预计会有\(93\)夜晚入住。
\(\begin{array}{l}{Y=\$ 3,200+(\$ 100 \times 93)} \\ {Y=\$ 3,200+\$ 9,300} \\ {Y=\$ 12,500}\end{array}\)
在所有三个示例中,经理都使用他们收集的成本数据来预测不同活动级别的未来成本。
示例\(\PageIndex{1}\): Waymaker Furniture
Waymaker Furniture 已经从其生产过程中收集了成本信息,现在想预测不同活动水平的成本。 他们计划使用成本方程来制定这些预测。 表中列出了从三月份收集的信息\(\PageIndex{3}\)。
| 产生的成本 | 固定或可变 | 三月成本 |
|---|---|---|
| 工厂主管工资 | 已修复 | 每月 12,000 美元 |
| 木材(直接材料) | 变量 | 总计 75,000 美元 |
| 生产工人的工资 | 变量 | 每小时 11.00 美元 |
| 机器维护 | 变量 | 每生产一件 5.00 美元 |
| 工厂租赁 | 已修复 | 每月 15,000 美元 |
3月,Waymaker生产了\(1,000\)单位并使用了\(2,000\)数小时的生产劳动力。
使用这些信息和成本方程式,在表中预测Waymaker的生产水平的总成本\(\PageIndex{4}\)。
| 月 | 活动级别 |
|---|---|
| 四月 | 1,500 个单位 |
| 可能 | 2,000 个单位 |
| 六月 | 2500 个单位 |
解决方案
\(\text {Total Fixed Cost} = \$12,000 + \$15,000 = \$27,000\)。
\(\text { Direct Materials per Unit }=\dfrac {\$ 75,000 }{1,000} \text { Units }=\$ 75 \text { per unit}\)。
\(\text {Direct Labor per Hour} = \$11.00\)。
\(\text {Machine Maintenance} = \$5.00 \text {per unit}\)。
\(\text {Total Variable Cost per Unit} = \$75 + \$11 + \$5 = \$91 \text {per unit}\)。

演示在不同活动水平下计算未来成本的散点图方法
为了使用成本方程式,管理者必须做出的假设之一是,活动与成本之间的关系是线性的。 换句话说,成本的增长与活动成正比。 用于验证此假设的诊断工具是散点图。
散点图显示了代表不同活动水平产生的实际成本的点图。 构造散点图后,我们画出一条看起来最适合点状图案的线(通常称为趋势线)。 由于趋势线有些主观,散点图通常被用作探索成本与活动之间的关系通常为线性关系的可能性的初步工具。 在解释散点图时,重要的是要记住,不同的人可能会划出不同的线条,这会导致对固定成本和可变成本的估算不同。 与另一个人相比,任何人的路线和成本估算都不一定是对还是错;它们只会有所不同。 在使用散点图确定成本和活动是否存在线性关系之后,经理通常会转向更精确的成本估算流程,例如高低法或最小二乘回归分析。
为了演示一家公司将如何使用散点图,让我们来看看丽晶航空的数据,该公司运营着一支为美国东北部服务的支线飞机机队。 联邦航空管理局根据飞行时数制定了飞机例行维护指导方针。 因此,Regent发现其每月维护成本随飞行时数的变化而变化,如图所示\(\PageIndex{4}\)。
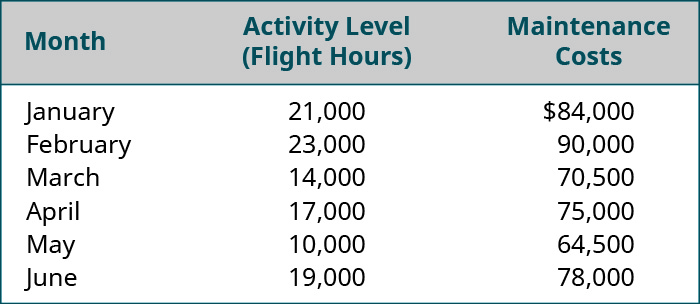
创建散点图时,每个点将代表一对活动和成本值。 维护成本绘制在垂直轴 (\(Y\)) 上,而飞行时数绘制在水平轴 (\(X\)) 上。 例如,一分代表\(21,000\)工时\($84,000\)和成本。 在绘制完所有数据对之前,图表上的下一个点将代表\(23,000\)工时和成本,依此类推。\(\$90,000\) 最后,在图表中添加一条趋势线,以帮助经理查看活动水平和成本之间是否存在正、负或零的关系。 \(\PageIndex{5}\)该图显示了丽晶航空的散点图。
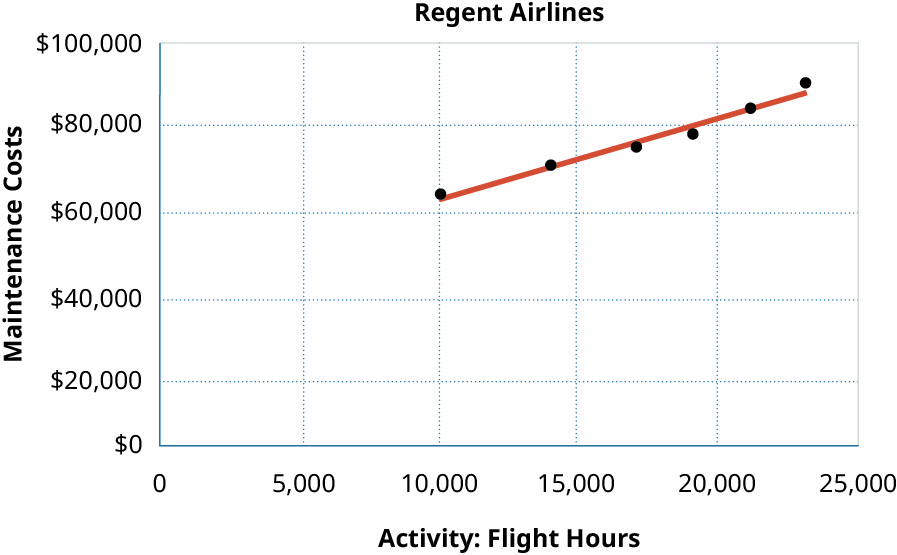
在散点图中,成本被视为因变量,因为成本取决于活动水平。 该活动被视为自变量,因为它是成本变化的原因。 Regent的散点图显示了飞行时数和维护成本之间的正关系,因为随着飞行时间的增加,维护成本也会增加。 这被称为正线性关系或线性成本行为。
所有成本和活动关系是否都是线性的? 仅当活动与该特定成本之间存在关系时。 相反,如果将跑道的除雪费用与飞行时数相比会怎样? 假设除雪成本如表中所列\(\PageIndex{5}\)。
| 月 | 活动等级:飞行时间 | 除雪费用 |
|---|---|---|
| 一月 | 21,000 | 40,000 美元 |
| 二月 | 23,000 | 50,000 |
| 三月 | 14,000 | 8,000 |
| 四月 | 17,000 | 0 |
| 可能 | 10,000 | 0 |
| 六月 | 19,000 | 0 |
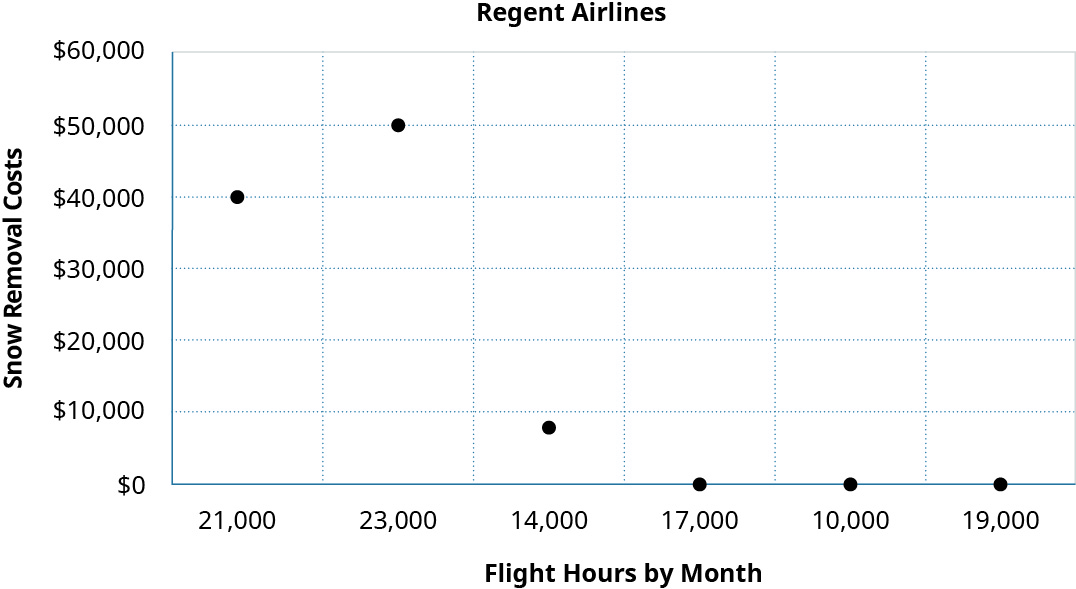
从散点图中可以看出,飞行时数与除雪成本之间实际上没有线性关系。 这是有道理的,因为除雪成本与积雪量以及起飞和降落的航班数量有关,但与飞机的飞行时数无关。
使用散点图确定这种线性关系是否存在是成本行为分析中必不可少的第一步。 如果散点图显示线性成本行为,则经理可以继续进行更复杂的分析,将混合成本分为固定和可变成分。 但是,如果不存在这种线性关系,则不适合使用其他分析方法。 让我们使用高低法检查摄政航空的成本数据。
演示在不同活动水平下计算未来成本的高低方法
如你所知,确定成本的目的是控制成本,经理经常使用过去的成本来预测未来的成本。 由于我们知道可变成本会随活动水平而变化,因此我们可以得出结论,成本和活动之间通常存在正关系:随着一个成本的上升,另一个也会增加。 理想情况下,可以在散点图上确认这一点。 分析成本的最简单方法之一是使用 h igh-low 方法,该方法用于分离混合成本中的固定成本和可变成本组成部分。 使用最高和最低活动水平及其相关成本,我们能够估算混合成本的可变成本组成部分。
一旦我们确定存在线性成本行为,我们就可以将可变成本等同于线的斜率,表示为线在运行过程中的上升。 该线的斜率越陡坡,随着活动的变化,成本上升的速度就越快。 回想一下散点图,成本是因\(Y\)变量,活动是自\(X\)变量。 通过检查相\(Y\)对于变化的变化\(X\),我们可以预测成本:
\[\text { Variable cost }=\dfrac{\text { Rise of the line }}{\text { Run of the line }}=\dfrac{Y_{2}-Y_{1}}{X_{2}-X_{1}}\]
其中\(Y_2\)是最高活动级别的总成本;\(Y_1\)是最低活动级别的总成本;\(X_2\)是最高活动级别的单位数、工时等;\(X_1\)是最低活动级别的单位数、工时等。
使用图中所示的摄政航空公司的维护成本数据\(\PageIndex{7}\),我们将研究这种方法在实践中的工作原理。
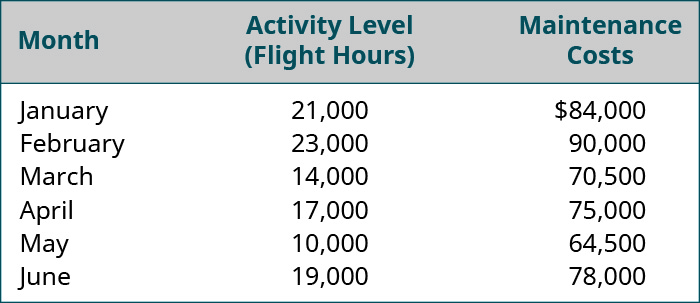
使用高低法分析混合成本的第一步是确定活动水平最高和最低的时段。 在这种情况下,将是 2 月和 5 月,如图所示\(\PageIndex{8}\)。 我们总是选择最高和最低的活动以及与这些活动水平相对应的成本,即使它们不是最高和最低的成本。
现在,我们可以使用以下公式将最高时段和低点成本之间的差额除以活动变化,从而估算可变成本:
\[\text { Variable cost }=\dfrac{\text { Change in cost }}{\text { Change in Activity }}=\dfrac{\text { Cost at the high activity level- cost at the low activity level }}{\text { Highest activity level -Lowest activity level }}\]
对于丽晶航空来说,这是:
\(\text { Variable Cost}=\dfrac{\$ 90,000-\$ 64,500}{23,000-10,000}=\$ 1.96 \text { per flight hour }\)
在确定每个飞行小时的可变成本为之后\(\$1.96\),我们现在可以确定固定成本的金额。 我们可以通过将活动水平高或低的总成本减去这个可变成分来确定这些固定成本。 你会记得,总成本=固定成本+可变成本,因此丽晶航空的固定成本部分可以分离出来,如下所示:
\(\begin{array}{l}{\text { Fixed cost }=\text { total cost-variable cost }} \\ {\text { Fixed cost }=\$ 90,000-(23,000 \times \$ 1.96)} \\ {\text { Fixed cost }=\$ 44,920}\end{array}\)
请注意,如果我们选择了另一个数据点,即低成本和低活动,我们仍将获得相同的固定成本\(\$44,920 = [\$64,500 – (10,000 × \$1.96)]\)。
既然我们已经隔离了固定部分和可变组件,我们可以使用总成本方程式来表示丽晶航空的维护成本:
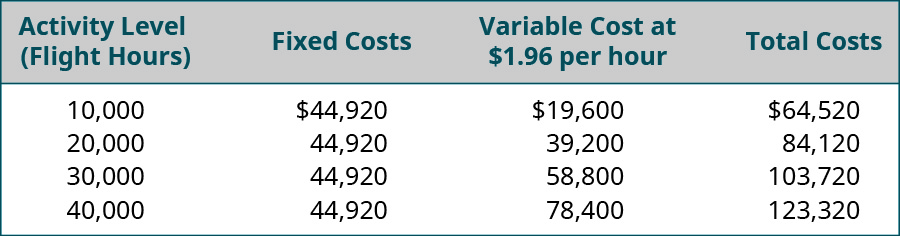
\(Y=\$ 44,920+\$ 1.96 x\)
哪里\(Y\)是总成本,\(x\)是飞行时数。
因为我们确认丽晶的成本与活动之间的关系在散点图上表现出线性成本行为,因此该方程式使丽晶航空的经理得出结论,活动每增加一个单位,可变成本就会相应增加\(\$1.96\)。 付诸实践后,Regent Airlines的经理们现在可以预测他们在任何活动级别上的总成本,如图所示\(\PageIndex{9}\)。
尽管经理经常使用这种方法,但它并不是预测未来成本的最准确方法,因为它仅基于两条成本数据:活动的最高水平和最低水平。 实际成本可能与这些估计值有很大差异,尤其是在高或低活动水平不能代表企业内部通常的活动水平的情况下。 对于更精确的模型,将使用最小二乘回归法将混合成本分为固定和可变分量。 最小二乘回归法是一种统计技术,可用于根据过去的成本数据估算给定活动水平的总成本。 最小二乘回归可以最大限度地减少尝试在数据点之间拟合一条直线的错误,从而使该线更接近所有数据点。
了解各种成本标签是使用成本评估业务决策的第一步。 在本课程中继续学习管理会计时,您将更多地了解这些不同的标签以及它们如何应用于决策过程。


