在研究经济统计数据时，有一个关键的区别值得强调。 区别在于名义和实际衡量标准，后者指的是通货膨胀是否扭曲了给定的统计数据。 在不考虑通货膨胀的情况下查看经济统计数据就像透过双筒望远镜试图猜测某物有多近：除非你知道镜头有多强，否则你无法非常准确地猜出距离。 同样，如果你不知道通货膨胀率，就很难弄清楚国内生产总值的上涨主要是由于总体价格水平的上涨还是商品产量的增加。 任何经济统计数据的名义价值意味着该统计数据是根据当时存在的实际价格来衡量的。 实际价值是指经通货膨胀调整后的相同统计数据。 通常，更重要的是实际价值。
将名义国内生产总值转换为实际
表1显示了自1960年以来每隔五年以名义美元计算的美国国内生产总值；也就是说，使用每个规定年份的实际市场价格衡量的国内生产总值。 此数据也反映在图 1 所示的图表中
| 年 |
名义国内生产总值（十亿美元） |
国内生产总值平减指数（2005 = 100） |
| 1960 |
543.3 |
19.0 |
| 1965 |
743.7 |
20.3 |
| 1970 |
1,075.9 |
24.8 |
| 1975 |
1,688.9 |
34.1 |
| 1980 |
2,862.5 |
48.3 |
| 1985 |
4,346.7 |
62.3 |
| 1990 |
5,979.6 |
72.7 |
| 1995 |
7,664.0 |
81.7 |
| 2000 |
10,289.7 |
89.0 |
| 2005 |
13,095.4 |
100.0 |
| 2010 |
14,958.3 |
110.0 |
表 1：美国名义国内生产总值和国内生产总值平减指数（来源：www.bea.gov）
1960-2010 年美国名义国内生产总值
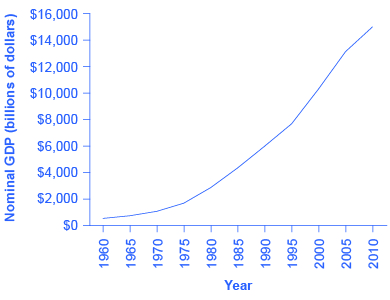图1：根据东亚银行的数据，从1960年到2010年，名义国内生产总值呈指数级增长。
如果一位粗心的分析师将1960年的名义GDP与2010年的名义GDP进行比较，那么在这段时间内，国民产出似乎增长了27倍（也就是说，2010年的GDP为149.58亿美元除以1960年的5,430亿美元的GDP）。 这个结论极具误导性。 回想一下，名义GDP的定义是生产的每种商品或服务的数量乘以其销售价格，再加上所有商品和服务的总和。 为了了解产量实际增长了多少，我们需要提取价格上涨对名义GDP的影响。 使用GDP平减指数，这很容易做到。
GDP平减指数是一种价格指数，用于衡量经济中包含的所有商品和服务的平均价格。 我们将详细探讨价格指数以及如何在通货膨胀中计算这些指数，但这个定义将在本章的背景下进行。 GDP平减指数的数据在表1中给出，并在图2中以图形方式显示。
1960-2010 年美国国内生产总值平减指数
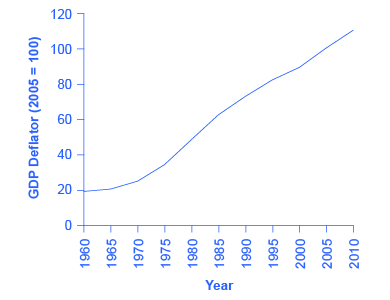图2：与名义国内生产总值非常相似，从1960年到2010年，国内生产总值平减指数呈指数上升。 （资料来源：BEA）
图 2 显示，自 1960 年以来，价格水平急剧上升。 2010年的价格水平比1960年高出近六倍（2010年的平减指数为110，而1960年的水平为19）。 显然，名义GDP的明显增长在很大程度上是由于通货膨胀，而不是商品和服务生产数量的实际变化，换句话说，不是实际GDP的变化。 回想一下，名义GDP的增长可能有两个原因：产出增加和/或价格上涨。 需要的是从名义GDP中提取物价的上涨，以便仅衡量产出的变化。 毕竟，1960年用来衡量名义GDP的美元比1990年膨胀的美元更有价值，而价格指数准确地说明了多少。 如果你明白标称测量值是按价值计算的，那么这种调整就很容易做到，其中
\[Value=Price\,\times\,Quantity\]
\[or\]
\[Nominal\,GDP=GDP\,Deflator\,\times\,Real\,GDP\]
让我们来看一个微观层面的例子。 假设 T 恤公司 Coolshirts 以每件 9 美元的价格出售 10 件 T 恤。
\[Coolshirt's\,nominal\,revenue\,from\,sales=Price\,\times\,Quantity\]
\[=\$9\times10\]
\[=\$90\]
然后，
\[Coolshirt's\,real\,income=\dfrac{Nominal\,revenue}{Price}\]
\[=\dfrac{\$90}{\$9}\]
\[=10\]
换句话说，当我们计算 “实际” 测量值时，我们试图得出实际数量，在本例中为 10 件 T 恤。
对于国内生产总值来说，情况稍微复杂一点。 我们从与上面相同的公式开始：
\[Real\,GDP=\dfrac{Nominal\,GDP}{Price\,Index}\]
出于下文将详细解释的原因，从数学上讲，价格指数是一个两位数的十进制数字，例如1.00、0.85或1.25。 因为有些人在处理小数时遇到了麻烦，所以在发布价格指数时，传统上将其乘以 100 得到 100、85 或 125 之类的整数。 这意味着当我们 “缩小” 名义数字以获得真实数字（通过名义数字除以价格指数）时。 我们还需要记住将公布的价格指数除以100，以使数学起作用。 所以公式变成：
\[Real\,GDP=\dfrac{Nominal\,GDP}{Price\,Index/100}\]
现在阅读以下 Work It Out 功能，了解更多计算实际国内生产总值的练习。
注意：计算国内生产总值
可以使用表 1 中的数据来计算实际的 GDP。
第 1 步。 看看表1，可以看出，1960年，名义国内生产总值为5,433亿美元，物价指数（GDP平减指数）为19.0。
第 2 步。 要计算1960年的实际国内生产总值，请使用以下公式：
\[Real\,GDP=\dfrac{Nominal\,GDP}{Price\,Index/100}\]
\[=\dfrac{\$543.3\,billion}{19/100}\]
\[=\$2,859.5\,billion\]
为了清楚起见，我们将分为两部分。 首先调整价格指数：19 除以 100 = 0.19。 然后分为名义国内生产总值：5,433亿美元/0.19亿美元 = 28.595亿美元。
第 3 步。 使用相同的公式来计算 1965 年的实际国内生产总值。
\[Real\,GDP=\dfrac{Nominal\,GDP}{Price\,Index/100}\]
\[=\dfrac{\$743.7\,billion}{20.3/100}\]
\[=\$3,663.5\,billion\]
第 4 步。 继续使用此公式来计算 1960 年至 2010 年期间的所有实际国内生产总值值。 计算和结果如表 2 所示。
| 年 |
名义国内生产总值（十亿美元） |
国内生产总值平减指数（2005 = 100） |
计算 |
实际国内生产总值（2005 年十亿美元） |
| 1960 |
543.3 |
19.0 |
543.3/(19.0/100) |
2859.5 |
| 1965 |
743.7 |
20.3 |
743.7/(20.3/100) |
3663.5 |
| 1970 |
1075.9 |
24.8 |
1,075.9/(24.8/100) |
4338.3 |
| 1975 |
1688.9 |
34.1 |
1,688.9/(34.1/100) |
4952.8 |
| 1980 |
2862.5 |
48.3 |
2,862.5/(48.3/100) |
5926.5 |
| 1985 |
4346.7 |
62.3 |
4,346.7/(62.3/100) |
6977.0 |
| 1990 |
5979.6 |
72.7 |
5,979.6/(72.7/100) |
8225.0 |
| 1995 |
7664.0 |
82.0 |
7,664/(82.0/100) |
9346.3 |
| 2000 |
10289.7 |
89.0 |
10,289.7/(89.0/100) |
11561.5 |
| 2005 |
13095.4 |
100.0 |
13,095.4/(100.0/100) |
13095.4 |
| 2010 |
14958.3 |
110.0 |
14,958.3/(110.0/100) |
13598.5 |
表 2：将名义国内生产总值转换为实际国内生产总值（资料来源：经济分析局，www.bea.gov）
这里有几件事要注意。 每当你计算实数统计数据时，一年（或周期）都起着特殊作用。 它被称为基准年（或基准期）。 基准年是使用其价格来计算实际统计数据的年份。 例如，当我们计算实际GDP时，我们用每年（例如，1960年或1973年）生产的商品和服务的数量乘以它们在基准年（在本例中为2005年）的价格，这样我们就可以得出一个使用每年不变化的价格来衡量GDP。 这就是为什么实际GDP被标记为 “固定美元” 或 “2005美元” 的原因，这意味着实际GDP是使用2005年的价格计算的。 使用的公式是：
\[GDP\,deflator=\dfrac{Nominal\,GDP}{Real\,GDP}\times100\]
重新排列公式并使用 2005 年的数据：
\[Real\,GDP=\dfrac{Nominal\,GDP}{Price\,Index/100}\]
\[=\dfrac{\$13,095.4\,billion}{100/100}\]
\[=\$13,095.4\,billion\]
比较2005年的实际国内生产总值和名义国内生产总值，你会发现它们是一样的。 这绝非偶然。 这是因为在本示例中，2005 年被选为 “基准年”。 由于基准年的价格指数始终为100（顾名思义），因此基准年的名义和实际GDP始终相同。
看看 2010 年的数据。
\[Real\,GDP=\dfrac{Nominal\,GDP}{Price\,Index/100}\]
\[=\dfrac{\$14,958.3\,billion}{110/100}\]
\[=\$13,598.5\,billion\]
使用这些数据进行另一个观察：只要通货膨胀率为正，这意味着物价每年平均上涨，则基准年之后的任何一年的实际GDP都应低于名义GDP。 其原因应该很明确：名义GDP的价值被通货膨胀 “膨胀”。 同样，只要通货膨胀率为正，在基准年之前的任何一年，实际GDP都应高于名义GDP。
图 3 显示了 1960 年以来的美国名义和实际国内生产总值。 由于 2005 年是基准年，因此该年的名义值和实际值完全相同。 但是，随着时间的推移，名义GDP的增长看起来比实际GDP的增长要大得多（也就是说，名义GDP 线比实际GDP线增长幅度更大），因为通货膨胀的存在夸大了名义GDP的增长，尤其是在1970年代。
1960-2012 年美国名义和实际国内生产总值
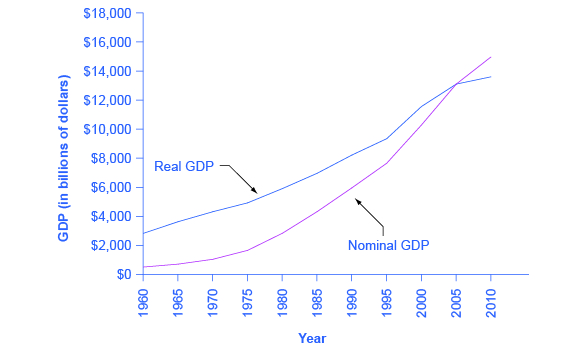图 3：红线以名义美元衡量美国国内生产总值。 黑线以实际美元衡量美国国内生产总值，其中所有美元价值均转换为2005美元。 由于实际国内生产总值以2005年的美元表示，因此这两条线在2005年交叉。 但是，在2005年之前的几年中，实际GDP似乎将高于名义GDP，因为2005年的美元价值低于往年。 相反，在2005年之后的几年中，实际GDP将显得更低，因为2005年的美元价值要高于以后的几年。
让我们回到最初提出的问题：按实际价值计算，国内生产总值增长了多少？ 从1960年到2010年，实际国内生产总值的增长率是多少？ 为了得出实际增长率，我们使用百分比变化公式：
\[\dfrac{2010\,real\,GDP-1960\,real\,GDP}{1960\,real\,GDP}\times100=\%\,change\]
\[\dfrac{13,598.5-2,859.5}{2,859.5}\times100=376\%\]
换句话说，自1960年以来，美国经济将商品和服务的实际产量增加了近四倍。 当然，这低估了物质改进，因为它未能体现产品质量和新产品发明的改进。
有一种更快的方法可以用另一种数学技巧来大致回答这个问题。 因为：
\[Nominal=Price\times\,Quantity\]
\[\%\,change\,in\,Nominal= \%\,change\,in\,Price+\%\,change\,in\,Quantity\]
\[\%\,change\,in\,Quantity= \%\,change\,in\,Nominal-\%\,change\,in\,Price\]
因此，实际GDP的增长率（数量变化百分比）等于名义GDP的增长率（价值变动百分比）减去通货膨胀率（价格变动百分比）。
请注意，使用此方程可为水平的微小变化提供近似值。 为了获得更准确的测量，应使用所示的第一个公式。
关键概念和摘要
经济统计数据的名义价值是通常公布的价值。 实际价值是根据通货膨胀变化进行调整后的价值。 要将来自几个不同年份的名义经济数据转换为经通胀调整的真实数据，起点是任意选择基准年，然后使用价格指数来转换衡量标准，以便以基准年通行货币来衡量。
词汇表
- 名义价值
- 当时实际公布的经济统计数据，未根据通货膨胀进行调整；与实际价值形成对比
- 实际价值
- 经通货膨胀调整后的经济统计数据；与名义价值形成对比
