(请在初读后查阅本附录欢迎来到经济学!) 经济学不是数学。 本课程中没有没有没有没有数学就无法解释的重要概念。 也就是说,数学是一种可以用来说明经济概念的工具。 还记得那句话一张照片胜过千言万语吗? 与其说是图片,不如想一张图表。 这是同样的事情。 经济学家使用模型作为获得有关经济问题和问题的见解的主要工具。 数学是处理(或操纵)经济模型的一种方法。
还有其他表示模型的方式,例如文字或叙事。 但是,如果你有锤子,为什么要用拳头敲钉子呢? 与文本相比,数学有一定的优势。 它通过让你准确说明你的意思来约束你的思维。 你可以通过脑海中的模糊思维逃脱,但是当你将模型简化为代数方程时,你就无法摆脱困境。 同时,数学也有缺点。 数学模型必然基于简化的假设,因此它们不太可能完全现实。 数学模型也缺乏叙事模型中可以找到的细微差别。 关键是数学是一种工具,但它不是经济学家可以使用的唯一工具,甚至不是最好的工具。 那么你需要什么数学来写这本书呢? 答案是:只不过是高中代数和图表而已。 你需要知道:
什么是函数
如何解释直线方程(即斜率和截距)
如何操作直线(即改变斜率或截距)
如何计算和解释增长率(即百分比变化)
如何读取和操作图表
在本文中,我们将使用尽可能简单的数学运算,并将在本附录中对其进行介绍。 因此,如果你在书中发现了一些你无法理解的数学运算,请回到本附录中复习。 像大多数事物一样,数学的收益递减。 一点数学能力有很长的路要走;你引入的数学越高级,你获得的额外知识就越少。 也就是说,如果你要主修经济学,你应该考虑学习一点微积分。 在帮助你更快地学习高级经济学方面,值得你花点时间。
代数模型
经济模型(或模型的一部分)通常以数学函数表示。 什么是函数? 函数
在经济学中,函数通常描述因果关系。 左边的变量就是正在解释的内容(“效果”)。 右边是解释什么(“原因”)。 例如,假设您的 GPA 按如下方式确定:
\[GPA=0.25\times combined\,SAT+0.05\times class\,attendance+0.50\times hours\,spent\,studying\]
这个方程式表明,你的 GPA 取决于三件事:你的 SAT 综合分数、你的课堂出勤率和你花在学习上的时数。 它还说,学习时间的重要性(0.50)是组合_Sat分数(0.25)或课堂出勤率(0.25)的两倍。 如果这种关系是真的,你怎么能提高你的GPA? 不要逃课多学习。 请注意,你无法对自己的SAT成绩做任何事情,因为如果你在上大学,你(大概)已经参加了SAT考试。
当然,经济模型使用经济变量来表达关系,比如预算 = money_spent_on_econ_books + money_spent_on_music,假设你唯一购买的东西是经济学书籍和音乐。
\[y=b+mx\]
以图形方式表示方程
图表有两个用途。 第一个是直观地表示方程,第二个是显示统计数据或数据。 本节将讨论直观地表示方程式。
对于数学家或经济学家来说,变量
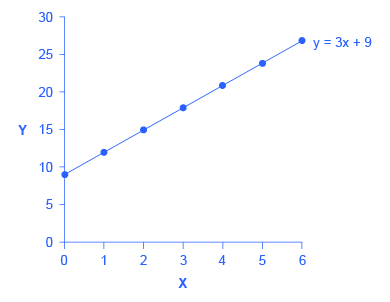
\[y=9+3x\]
在此特定直线的方程中,b 项设置为 9,m 项设置为 3。 表 1 显示了这个给定方程的 x 和 y 的值。 图 1 在图表中显示了这个方程和这些值。 要构造表,只需为 x 插入一系列不同的值,然后计算 y 的结果是多少。 在图中,绘制了这些点并画了一条穿过它们的直线。
x y
0
9
1
12
2
15
3
18
4
21
5
24
6
27
表 1:斜率截距方程的值
斜率和直线代数
图 1:此折线图的水平轴上有 x ,垂直轴上有 y。 y 截距(即直线与 y 轴相交的点)为 9。 直线的斜率为 3;也就是说,水平轴每增加 1,垂直轴上就会上升 3。 沿直线的斜率是相同的。 此示例说明了直线方程中的 b 和 m 项如何确定直线的形状。 b 项称为 y 截距。 这个名字的原因是,如果 x = 0,那么 b 项将显示直线在 y 轴上的交叉位置或交叉位置。 在此示例中,直线在 9 点处到达垂直轴。 直线方程中的 m 项是斜率。 请记住,斜率
解释斜率
斜率的概念在经济学中非常有用,因为它衡量两个变量之间的关系。 正斜率
负斜率
斜率为零意味着 x 和 y 之间没有关系。图形上,这条线是平坦的;也就是说,在游程中上升为零。 本附录稍后显示的失业率图 4 说明了许多折线图的常见模式:有些分段的斜率为正,其他分段的斜率为负,还有其他分段的斜率接近于零。
两点之间的直线的斜率可以用数值计算。 要计算斜率,首先将一个点指定为 “起点”,将另一个点指定为 “终点”,然后计算这两个点之间的上升幅度。 例如,以空气密度图表示海拔 4,000 米和海拔 6,000 米的点之间的斜率为例:
上升:垂直轴变量的变化(终点减去原始点)
\[=0.100-0.307\]
\[=-0.207\]
运行:更改水平轴上的变量(终点减去原始点)
\[=6,000-4,000\]
\[=2,000\]
因此,这两点之间的直线的斜率将是,从海拔 4,000 米到 6,000 米,接下来的 1000 米中,空气密度每减少大约 0.1 千克/立方米
假设一条线的斜率要增加。 从图形上看,这意味着它会变得更陡峭。 假设一条线的斜率要减小。 然后它会变得更平坦。 无论斜率一开始是正还是负,这些条件都是正确的。 较高的正斜率意味着向直线的向上倾斜度越大,而较小的正斜率意味着向直线的向上倾斜度越平坦。 绝对值越大(即负值越大)的负斜率意味着向直线的向下倾斜度越大。 零的斜率是一条水平平线。 垂直线具有无限斜率。
假设一条线的截距更大。 从图形上讲,这意味着它将从旧原点向外(或向上)移动,平行于旧线。 如果一条直线的截距较小,它将向内(或向下)移动,与旧线平行。
用代数求解模型
经济学家经常使用模型来回答一个具体的问题,比如:如果经济以每年3%的速度增长,失业率会是多少? 回答特定问题需要求解代表模型的方程的 “系统”。
假设对个人披萨的需求由以下方程式给出:
\[Qd=16-2P\]
其中 Qd 是消费者想要购买的个人披萨数量(即需求数量),P 是披萨的价格。 假设个人披萨的供应量是:
\[Qs=2+5P\]
其中 Qs 是披萨生产商将供应的数量(即供应量)。
最后,假设个人披萨市场在供应等于需求的地方运作,或者
\[Qd=Qs\]
我们现在有了一个由三个方程和三个未知数(Qd、Qs 和 P)组成的系统,我们可以用代数求解:
由于 Qd = Qs,我们可以将需求和供应方程设置为相等:
\[Qd=Qs\]
\[16-2P=2+5P\]
从两边减去 2 并在两边加上 2P 得出:
\[16-2P-2=2+5P-2\]
\[14-2P=5P\]
\[14-2P+2P=5P+2P\]
\[14=7P\]
\[\dfrac{14}{7}=\dfrac{7P}{7}\]
\[2=P\]
换句话说,每个个人披萨的价格将为2美元。 消费者会买多少?
以2美元的价格将其插入需求方程式中,我们得到:
\[Qd=16-2P\]
\[=16-2(2)\]
\[=16-4\]
\[=12\]
因此,如果每张价格为2美元,消费者将购买12美元。 生产商将供应多少? 假设2美元的价格,并将其纳入供应方程式,我们得到:
\[Qs=2+5P\]
\[=2+5(2)\]
\[=2+10\]
\[=12\]
因此,如果每个价格为2美元,生产商将提供12个个人披萨。 这意味着我们的数学运算是正确的,因为 Qd = Qs。
使用图表求解模型
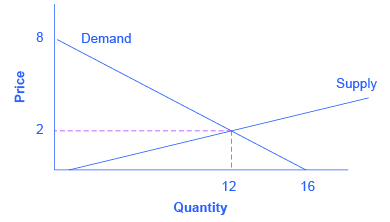
如果代数不是你的强项,你可以使用图表得到同样的答案。 取出 Qd 和 Qs 的方程并将它们绘制在同一组轴上,如图 2 所示。 由于 P 位于垂直轴上,最简单的方法是求解 P 的每个方程。然后,需求曲线为 P = 8 — 0.5Qd,需求曲线为 P = —0.4 + 0.2Qs。 请注意,垂直截距为 8 和 —0.4,需求斜率为 —0.5,供应斜率为 0.2。 如果你仔细绘制图表,你会看到它们的交叉位置(Qs = Qd),价格为2美元,数量为12,就像代数预测的那样。
供应和需求图
图 2:Qd 和 Qs 的方程由斜线以图形方式显示。 在本书中,我们将比代数更频繁地使用图表,但是现在您知道了图表背后的数学原理。
增长率
在现实世界的经济学中,增长率经常出现。 增长率
\[Percentage\,change=\dfrac{Change\,in\,quantity}{Quantity}\]
假设你的工作每小时支付 10 美元。 但是,你的老板对你的工作印象非常深刻,以至于他给你每小时加薪2美元。 工资的百分比变化(或增长率)为2美元/10美元 = 0.20美元或20%。
为了计算数据在很长一段时间内的增长率,例如,十年或更长时间内 GDP 的平均年增长率,分母的定义通常略有不同。 在前面的示例中,我们将数量定义为初始数量,或者我们开始时的数量。 这对于一次性计算来说没问题,但是当我们一遍又一遍地计算增长时,将数量定义为相关时间段内的平均数量更有意义,也就是定义为介于初始数量和下一个数量之间的数量。 用文字解释比用一个例子来说明更难。 假设一个国家的国内生产总值在2005年为1万亿美元,在2006年为1.03万亿美元。 2005年至2006年的增长率将是国内生产总值的变化(1.03万亿美元——1.00万亿美元)除以2005年至2006年的平均国内生产总值(1.03万亿美元+1.00万亿美元)/2。 换句话说:
\[=\dfrac{\$1.03\,trillion-\$1.00\,trillion}{(\$1.03\,trillion+\$1.00\,trillion)/2}\]
\[=\dfrac{0.03}{1.015}\]
\[=0.0296\]
\[=2.966\%\,growth\]
请注意,如果我们使用第一种方法,计算方法将是(1.03万亿美元-1.00万亿美元)/1.00万亿美元 = 3%的增长,这与第二种更复杂的方法大致相同。 如果你需要粗略的近似值,请使用第一种方法。 如果你需要精度,请使用第二种方法。
需要记住的几件事:正增长率意味着数量在增长。 较小的增长率意味着数量的增长速度更慢。 更高的增长率意味着数量增长得更快。 负增长率意味着数量在减少。
随着时间的推移,同样的变化会产生较小的增长率。 如果你每年加薪2美元,那么第一年的增长率将为2美元/10美元= 20%,如上所示。 但是在第二年,增长率将为2美元/12美元=0.167美元或16.7%的增长。 在第三年,同样的2美元加薪将相当于2美元/14美元= 14.2%。 这个故事的寓意是:为了保持增长率不变,每个时期的变化都必须增加。
以图形方式显示数据并解释图表
图表还用于显示数据或证据。 图表是一种呈现数值模式的方法。 它们将详细的数字信息浓缩成一种视觉形式,在这种形式中,可以更轻松地看到关系和数字模式。 例如,哪些国家的人口较多或更少? 仔细的读者可以查看代表许多国家人口的一长串数字,但是世界上有200多个国家,搜索这样的列表需要集中精力和时间。 将这些相同的数字放在图表上可以快速揭示人口模式。 经济学家使用图表既可以简洁易读地呈现数字组,又可以直观地掌握关系和联系。
本书使用三种类型的图表:折线图、饼图和条形图。 下文将逐一讨论。 我们还提供警告,说明如何操纵图表以改变观众对数据中关系的看法。
折线图
我们到目前为止讨论的图表被称为折线图
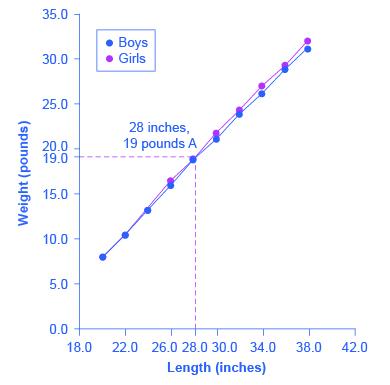
有时,在同一个坐标轴上显示多组数据会很有用。 表 2 中的数据显示在图 3 中,该图显示了两个变量之间的关系:美国男婴和女婴在出生后头三年的身长和中位体重。 (中位数
美国男孩和女孩的长重关系
图 3:折线图显示了男孩和女孩从出生到 3 岁的身高和体重之间的关系。 例如,点 A 表明,身高 28 英寸(在水平轴上测量)的男孩的体重通常为 19 磅(在垂直轴上测量)。 这些数据仅适用于出生后头三年的儿童。
从出生到 36 个月的男孩 从出生到 36 个月的女孩
长度(英寸)
重量(磅)
长度(英寸)
重量(磅)
20.0
8.0
20.0
7.9
22.0
10.5
22.0
10.5
24.0
13.5
24.0
13.2
26.0
16.4
26.0
16.0
28.0
19.0
28.0
18.8
30.0
21.8
30.0
21.2
32.0
24.3
32.0
24.0
34.0
27.0
34.0
26.2
36.0
29.3
36.0
28.9
38.0
32.0
38.0
31.3
表 2:美国男孩和女孩的身长与体重的关系
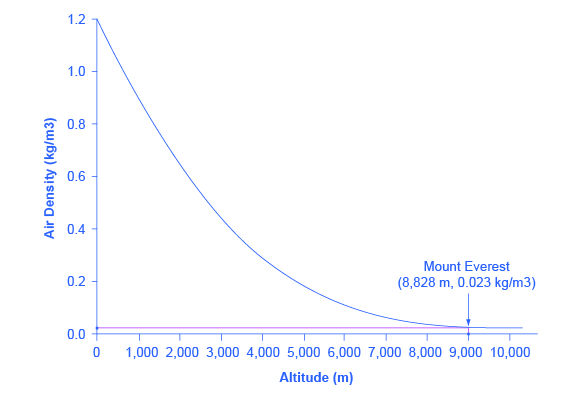
并非经济学中的所有关系都是线性的。 有时它们是曲线。 图 4 显示了另一个折线图示例,表示表 3 中的数据。 在这种情况下,折线图显示了你爬山时空气变得多么稀薄。 图中的水平轴显示海拔,以海拔米为单位测量。 垂直轴测量每个高度的空气密度。 空气密度是通过一立方米空间(即高度、宽度和深度为一米的盒子)中的空气重量来衡量的。 如图所示,地面上的气压最大,攀爬时气压会变轻。 图 4 显示,在 500 米的高度,一立方米的空气重约为一千克(约 2.2 磅)。 但是,随着海拔的增加,空气密度会降低。 珠穆朗玛峰顶部约为8,828米的一立方米空气重量仅为0.023千克。 高海拔地区的稀薄空气解释了为什么许多登山者在到达山顶时需要使用氧气罐。
海拔-空气密度关系
图 4:此折线图显示了海拔(以海拔米为单位测量)与空气密度(以每立方米空气千克为单位测量)之间的关系。 随着海拔的升高,空气密度下降。 珠穆朗玛峰顶部的点高度约为海拔 8,828 米(水平轴),空气密度为每立方米 0.023 千克(垂直轴)。
海拔(米) 空气密度(kg/立方米)
0
1.200
500
1.093
1,000
0.831
1,500
0.678
2,000
0.569
2500
0.484
3,000
0.415
3500
0.357
4,000
0.307
4,500
0.231
5,000
0.182
5,500
0.142
6,000
0.100
6,500
0.085
7,000
0.066
7,500
0.051
8,000
0.041
8,500
0.025
9,000
0.022
9,500
0.019
10,000
0.014
表 3:海拔与空气密度的关系
这两个图中的长度-重量关系和海拔-空气密度关系代表平均值。 如果你要收集不同高度气压的实际数据,那么不同地理位置的相同海拔的空气密度将略有不同,这取决于你离赤道的距离、当地天气条件和空气中的湿度等因素。 同样,在上一个折线图中测量孩子的身高和体重时,特定身高的孩子会有一系列不同的体重,有些高于平均水平,有些低于平均水平。 在现实世界中,这种数据变化很常见。 研究人员的任务是以有助于理解典型模式的方式组织数据。 统计学研究,尤其是与计算机统计和电子表格程序结合使用时,对组织此类数据、绘制折线图和寻找典型的潜在关系有很大帮助。 对于大多数经济学和社会科学专业的学生,在某个时候都需要一门统计学课程。
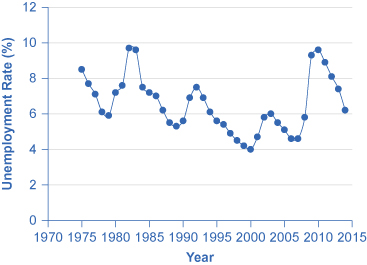
一种常见的折线图称为时间序列
1975-2014 年美国失业率
图 5:该图提供了失业数据的快速直观摘要。 有了这样的图表,很容易发现高失业率和低失业率的时代。 饼图
饼图 饼图
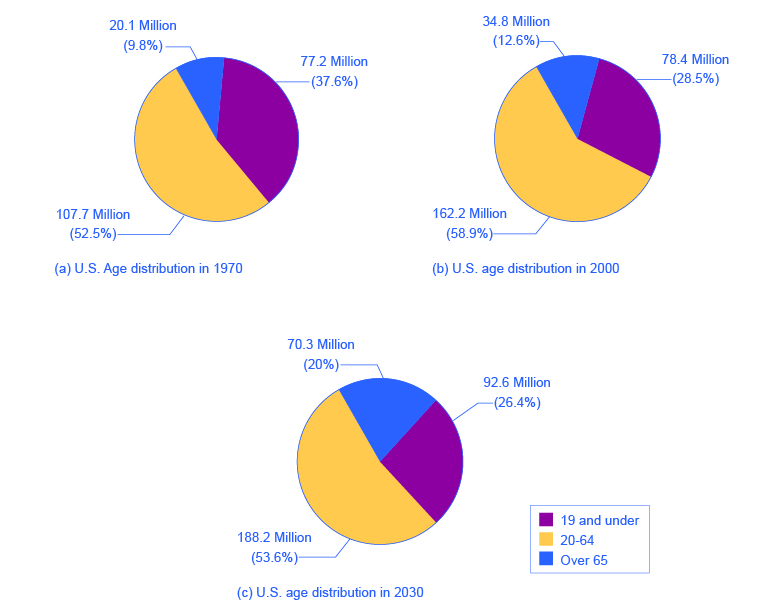
图 6 显示了 1970 年、2000 年美国人口在儿童、工作年龄成人和老年人之间的划分情况,以及对 2030 年的预测。 信息首先在表 4 中用数字传达,然后在三个饼图中传达。 表 4 的第一列显示了三年中每年的美国总人口。 第 2-4 列按年龄组对总数进行分类:从出生到 18 岁、19 到 64 岁以及 65 岁及以上。 在第 2-4 列中,第一个数字显示每个年龄组的实际人数,而括号中的数字显示该年龄组在总人口中所占的百分比。
年 总人口 19 岁及以下 20—64 岁 65 岁以上
1970
2.05 亿
77.2 (37.6%)
107.7 (52.5%)
20.1 (9.8%)
2000
2.754 亿
78.4 (28.5%)
162.2 (58.9%)
34.8 (12.6%)
2030
3.511 亿
92.6 (26.4%)
188.2 (53.6%)
70.3 (20.0%)
表 4:1970 年、2000 年和 2030 年的美国年龄分布(预测)
美国年龄分布的饼图(以百万为单位的数字)
图 6:三个饼图说明了在三个不同年份将总人口分为三个年龄组的情况。 在饼图中,饼图的每个分区代表总数的份额或百分比。 例如,50% 是饼的一半,20% 是饼的五分之一。 图 6 中的三张饼图显示,65 岁及以上美国人口的比例正在增长。 饼图使您可以了解从1970年到2000年至2030年不同年龄组的相对规模,而无需仔细查看表中的具体数字和百分比。 如何使用饼图的一些常见例子包括按年龄、收入水平、种族、宗教、职业将人口分为几组;按规模、行业、雇员人数将不同的公司分为几类;以及将政府支出或税收分为主要类别。
条形图
条形图
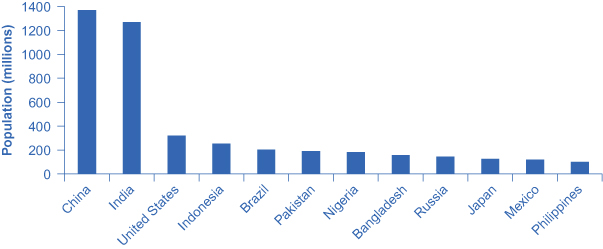
2015 年按人口排列的世界领先国家(以百万计)
图 7:该图显示了世界上人口最多的12个国家。 条形图中条形的高度显示了每个国家的人口规模。
国家 人口
中国
1,369
印度
1,270
美国
321
印度尼西亚
255
巴西
204
巴基斯坦
190
尼日利亚
184
孟加拉国
158
俄国
146
日本
127
墨西哥
121
菲律宾
101
表 5:按人口分列的世界领先12个国家
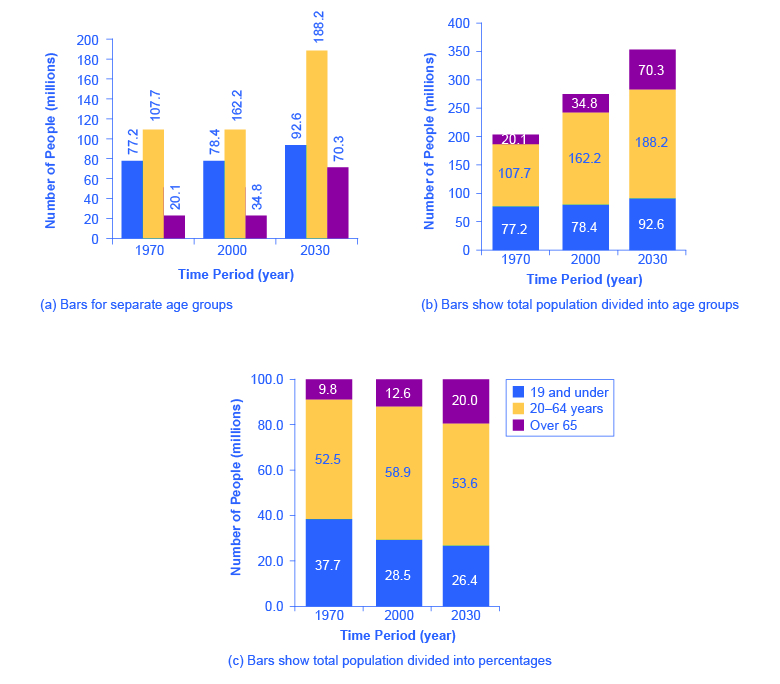
可以对条形图进行细分,以显示类似于我们可以从饼图中获得的信息。 图 8 根据图 6 中有关 1970 年、2000 年和 2030 年美国年龄分布的信息,提供了三个条形图。 图8 (a) 显示了每年的三个条形,代表每年每个年龄段的总人数。 图 8 (b) 仅显示了每年的一个条形图,但不同年龄组现在在条形内有阴影。 在图 8 (c) 中,仍然基于相同的数据,垂直轴衡量百分比而不是人数。 在这种情况下,所有三个条形图的高度相同,代表人口的100%,每个条形图根据每个年龄组的人口百分比进行划分。 有时,读者更容易看到几个条形图,比较阴影区域,而不是尝试比较几个饼图。
带有条形图的美国人口
图 8:人口数据可以用不同的方式表示。 (a) 显示每年的三个条形图,代表每年每个年龄段的总人数。 (b) 每年只显示一个条形图,但不同年龄组现在在条形图内有阴影。 (c) 将垂直轴设定为百分比而不是人数的度量。 所有三个条形图的高度相同,每个条形是根据每个年龄组的人口百分比进行划分的。 图 7 和图 8 显示了条形图如何表示国家或年份,以及垂直轴如何表示数值或百分比值。 条形图还可以比较大小、数量、速率、距离和其他定量类别。
比较折线图与饼图和条形图
既然您已经熟悉了饼图、条形图和折线图,那么如何知道要使用哪个图表作为数据? 在显示整个群组的划分方式方面,饼图通常比折线图更好。 但是,如果饼图的切片过多,则可能难以解释。
条形图在比较数量时特别有用。 例如,如果您正在研究不同国家的人口,如图 7 所示,条形图可以显示多个国家的人口规模之间的关系。 它不仅可以显示这些关系,还可以显示人口中不同群体的细分情况。
折线图通常是说明两个都在变化的变量之间关系的最有效格式。 例如,时间序列图可以显示时间变化的模式,例如一段时间内的失业率。 折线图在经济学中被广泛用于呈现有关价格、工资、买入和卖出数量、经济规模的连续数据。
图表如何具有误导性
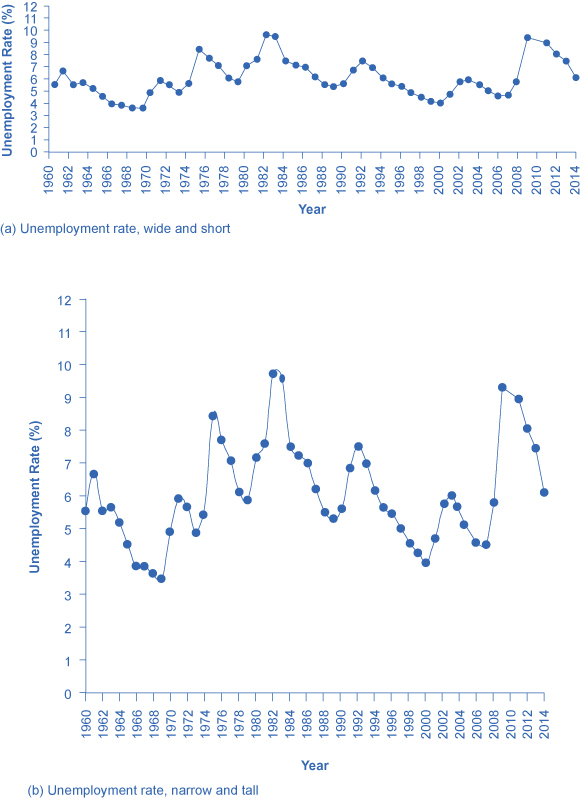
图表不仅可以揭示模式;还可以改变人们对模式的感知方式。 要了解实现此目的的一些方法,请考虑图 9、图 10 和图 11 中的折线图。 这些图表都说明了失业率,但从不同的角度来看。
图 9 以不同的方式呈现失业率,所有方法都准确
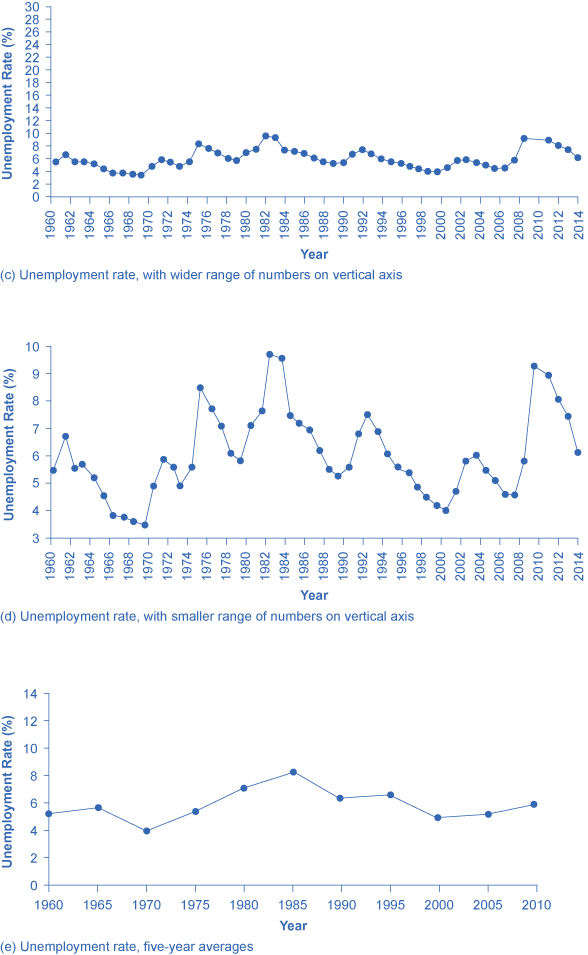
图 10:只要改变显示数据的区域的宽度和高度,就可以改变人们对数据的感知。 以不同的方式呈现失业率,所有方法都准确
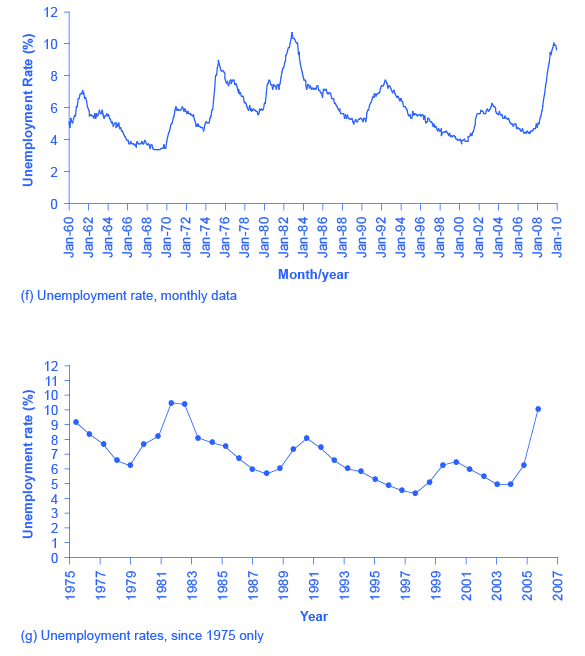
图 11:只要改变显示数据的区域的宽度和高度,就可以改变人们对数据的感知。 假设你想要一张图表,给人的印象是,2009 年失业率的上升幅度并不那么大,或者按历史标准来看没有那么不寻常。 您可以选择显示数据,如图 9 (a) 所示。 图 9 (a) 包含了与图 5 前面所示的大部分相同数据,但水平轴相对于垂直轴向外延伸得更长。 通过将图表广泛而平坦地展开,视觉效果是失业率的上升幅度不大,与过去失业率的上升相似。 现在想象一下,你想强调一下2009年失业率是如何大幅上升的。 在这种情况下,使用相同的数据,您可以将垂直轴相对于水平轴向外延伸,如图 9 (b) 所示,这使得失业率的所有上升和下降都显得更大。
无需更改轴的长度,而是通过更改垂直轴上的比例即可达到类似的效果。 在图 10 (c) 中,垂直轴上的比例从 0% 到 30% 不等,而在图 10 (d) 中,垂直轴从 3% 到 10% 不等。 与图5相比,垂直比例从0%到12%不等,图10(c)使失业率的波动看起来更小,而图10(d)则使失业率的波动看起来更大。
改变图形感知的另一种方法是通过更改图表上绘制的点的数量来减少变化量。 图10 (e) 显示了根据五年平均值计算的失业率。 通过平均一些逐年变化,这条线显得更平滑,高点和低点也更少。 实际上,失业率是按月报告的,图11(f)显示了自1960年以来的月度数字,其波动幅度超过了五年平均水平。 图 11 (f) 也生动地说明了图表如何压缩大量数据。 该图包括自1960年以来的月度数据,在将近50年的时间里,这些数据得出了近600个数据点。 以数字形式读取包含600个数据点的列表真是太催眠了。 但是,您可以很快从图表中直观地了解这 600 个数据点。
操纵图形信息感知的最后一个技巧是,通过仔细选择起点和终点,你可以影响对变量是上升还是下降的感知。 原始数据显示了总体模式,失业率在1960年代处于低水平,但在1970年代中期、1980年代初、1990年代初、21世纪初和21世纪末激增。 但是,图11(g)显示了一张仅可追溯到1975年的图表,它给人的印象是,失业率随着时间的推移或多或少地逐渐下降,直到2009年的经济衰退将其推回到 “原始” 水平——如果从1975年左右的最高点开始,这是一种合理的解释。
这些技巧——或者我们可以称之为 “演示选择” ——不仅限于折线图。 在包含许多小切片和一个大切片的饼图中,首先必须有人决定应该使用哪些类别来制作这些切片,从而使一些切片看起来比其他切片更大。 如果您正在制作条形图,则可以使垂直轴变高或变短,这往往会使条形高度的变化或多或少地出现。
无论是在经济学还是在生活中,能够阅读图表都是一项必不可少的技能。 图表只是一种视角或视角,由本节中讨论的选项所塑造。 不要总是相信图表中的第一印象。 请谨慎查看。
关键概念和摘要
数学是一种理解经济学的工具,经济关系可以使用代数或图表以数学方式表达。 直线的代数方程为 y = b + mx,其中 x 是水平轴上的变量,y 是垂直轴上的变量,b 项是 y 截距,m 项是斜率。 直线上任何一点的斜率都是相同的,它表示两个经济变量之间的关系(正、负或零)。
经济模型可以通过代数或图形求解。 图表允许您直观地说明数据。 他们可以通过压缩数值数据并在数据中提供直观的关系感来说明模式、比较、趋势和分配。 折线图显示两个变量之间的关系:一个显示在水平轴上,另一个显示在垂直轴上。 饼图显示了某些东西是如何分配的,例如一笔钱或一群人。 绘制饼的每个切片的大小以表示整体的相应百分比。 条形图使用条形的高度来显示关系,其中每个条形代表一个特定的实体,例如一个国家或一群人。 条形图上的条形也可以分成段以显示子组。
任何图表都是拍摄对象的单一视觉视角。 它给人的印象将基于许多选择,例如包含哪些数据或时间范围,如何划分数据或组,垂直轴和水平轴的相对大小,垂直方向上使用的比例是否从零开始。 因此,应该对任何图表持怀疑态度,记住潜在的关系可能会有不同的解释。
查看问题
练习
命名三种图表,并简要说明何时最适合使用每种类型的图表。