（在初读《总需求/总供应模型》和《凯恩斯主义视角》之后，应查阅本附录。） 凯恩斯主义经济学的基本思想是在AD/AS模型普及之前发展起来的。 从20世纪30年代到1970年代，凯恩斯主义经济学通常用另一种模型来解释，即支出产出法。 这种方法深深植根于凯恩斯主义经济学的基本假设：它侧重于经济中的总支出额，没有明确提及总供应量或价格水平（尽管如你所见，可以对总供应和价格得出一些推论）关卡（基于图表）。
支出-产出图的轴心
支出-产出模型，有时也称为凯恩斯主义交叉图，它根据经济中的总支出或总支出等于生产的产出量来确定实际GDP的均衡水平。 图1所示的凯恩斯主义交叉图的轴线在水平轴上显示了实际GDP作为产出的衡量标准，在垂直轴上显示了总支出，以衡量支出。
支出-产出图
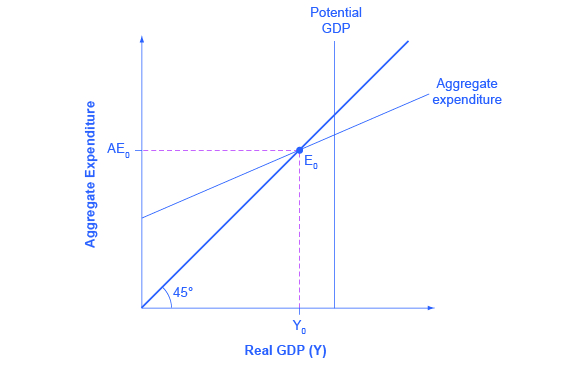图 1：总支出-产出模型在纵轴上显示总支出，在横轴上显示实际国内生产总值。 垂直线显示出现充分就业的潜在国内生产总值。 45 度线显示总支出和产出相等的所有点。 总支出表显示总支出或总支出如何随着产出或实际国内生产总值的增加而增加。 总支出计划和45度线的交叉点将是平衡。 平衡发生在 E 0，其中总支出 AE 0 等于产出水平 Y 0。
请记住，可以用几种等效的方式来看待GDP：它既衡量最终产品的支出价值，也衡量最终产品的生产价值。 构成国内生产总值的最终商品和服务的所有销售最终将成为工人、管理者、投资者和企业所有者的收入。 为国内生产总值贡献资源所获得的所有收入之和称为国民收入（Y）。 在接下来的讨论的某些时刻，将实际GDP称为 “国民收入” 是有用的。 这两个轴均以实际（经通胀调整后）计量。
潜在的国内生产总值线和 45 度线
凯恩斯主义交叉图包含两条线，它们是指导讨论的概念路标。 第一条是显示潜在GDP 水平的垂直线。 潜在GDP在这里的含义与AD/AS图表中的含义相同：它指的是经济在充分利用劳动力和实物资本的情况下可以产生的产出数量。
凯恩斯十字图上的第二条概念线是 45 度线，它从原点开始，向上和向右延伸。 以 45 度角向上延伸的直线代表一组点 (1、1)、(2、2)、(3、3) 等，其中垂直轴上的测量值等于水平轴上的测量值。 在此图中，45 度线显示了一组点，在这些点中，以垂直轴衡量的经济中的总支出水平等于经济中的产出或国民收入水平（以横轴上的 GDP 衡量）。
当宏观经济处于平衡状态时，经济中的总支出必须等于实际GDP ——因为顾名思义，GDP是衡量经济中商品和服务最终销售支出的标准。 因此，使用凯恩斯主义交叉图计算的均衡将始终在总支出和产出相等的情况下结束，而这只会发生在45度线上。
总支出明细表
凯恩斯主义交叉图或支出产出图的最后一个要素是总支出表，它将显示每个实际GDP水平的经济总支出。 总支出线与45度线的交点（图1中的E 0 点）将显示经济的均衡，因为这是总支出等于产出或实际GDP的点。 在了解了总支出表的含义之后，我们将回到这个平衡以及如何解释它。
建立总支出明细表
总支出是支出收入模型的关键。 总支出表以表格或图表的形式显示了经济中的总支出如何随着实际GDP或国民收入的增加而增加。 因此，在考虑总支出项目的组成部分——消费、投资、政府支出、出口和进口——时，关键问题是随着国民收入的增加，每个类别的支出将如何调整。
消费作为国民收入的函数
随着国民收入的增加，消费支出如何增加？ 人们可以用自己的收入做两件事：消费或储蓄（目前，让我们忽略用其中一部分纳税的必要性）。 每个获得额外一美元的人都将面临这个选择。 边际消费倾向（MPC）是一个人决定将额外收入用于消费支出的份额。 边际储蓄倾向（MPS）是一个人决定储蓄的额外美元中所占的份额。 以下情况必须始终成立：
\[MPC+MPS=1\]
例如，如果边际收入的边际消费倾向为0.9，则边际储蓄倾向为0.1。
考虑到这种关系，请考虑图 2 所示的收入、消费和储蓄之间的关系。 （请注意，在本图和下图中，我们在垂直轴上使用 “总支出”，因为所有消费支出都是总支出的一部分。）
该模型中通常做出的假设是，即使收入为零，人们也必须消费一些东西。 在此示例中，即使收入为零，消费也将为600美元。 然后，MPC 为 0.8，MPS 为 0.2。 因此，当收入增加1,000美元时，消费增加800美元，储蓄增加200美元。 如果收入为4,000美元，总消费将是即使没有任何收入也能消耗的600美元，再加上4,000美元乘以0.8或3,200美元的边际消费倾向，总计为3,800美元。 消费和储蓄的总额必须始终等于总收入金额。 （零收入和负储蓄的情况在实践中究竟会如何运作并不重要，因为即使是低收入社会也不是真正的零收入，所以问题是假设性的。） 如图 2 和表 1 所示，收入与消费之间的这种关系称为消费函数。
消耗函数
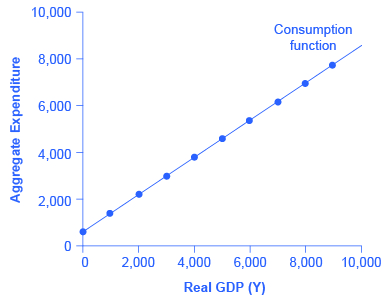图2：在支出产出模型中，消费如何随着国民收入水平而增加？ 横轴上的产出在概念上与国民收入相同，因为生产和出售的所有最终产出的价值必须是经济中某个地方某人的收入。 在国民收入为零的情况下，消耗600美元。 然后，每当收入增加1,000美元，消费就会增加800美元，因为在本例中，边际消费倾向为0.8。
表 1 所示的消耗模式如图 2 所示。 要计算消费，将收入水平乘以0.8，得出边际消费倾向，再加上600美元，得出即使收入为零也能消耗的金额。 消费加储蓄必须等于收入。
| 收入 |
消费 |
储蓄 |
| $0 |
600 美元 |
—600 美元 |
| 1,000 美元 |
1,400 美元 |
—400 美元 |
| 2,000 美元 |
2,200 美元 |
—200 美元 |
| 3,000 美元 |
3,000 美元 |
$0 |
| 4,000 美元 |
3,800 美元 |
200 美元 |
| 5,000 美元 |
4,600 美元 |
400 美元 |
| 6,000 美元 |
5,400 美元 |
600 美元 |
| 7,000 美元 |
6,200 美元 |
800 美元 |
| 8,000 美元 |
7,000 美元 |
1,000 美元 |
| 9,000 美元 |
7,800 美元 |
1,200 美元 |
表 1：消耗函数
但是，收入以外的许多因素也可能导致整个消费功能发生变化。 这些因素在先前关于消费的讨论中进行了总结，并列于表1。 当消耗函数移动时，它可以通过两种方式移动：要么整个消耗函数可以平行地向上或向下移动，要么消耗函数的斜率可以移动，使其变得更陡峭或更平。 例如，如果减税导致消费者增加支出，但不影响他们的边际消费倾向，则会导致向上转移到与原始消费功能平行的新消费功能。 但是，家庭储蓄偏好的变化降低了边际储蓄倾向，这将导致消费函数的斜率变得更大：也就是说，如果储蓄率降低，那么收入的每一次增加都会导致消费的更大增长。
投资是国民收入的函数
投资决策是前瞻性的，基于预期的回报率。 正是因为投资决策主要取决于对未来经济状况的看法，所以它们并不主要取决于本年度的GDP水平。 因此，在凯恩斯主义交叉图上，投资函数可以绘制为固定支出水平的水平线。 图 3 显示了一个投资函数，为了具体起见，该函数的投资水平设定为 500 的特定水平。 正如消费函数显示消费水平与实际GDP（或国民收入）之间的关系一样，投资函数显示投资水平与实际GDP之间的关系。
投资职能
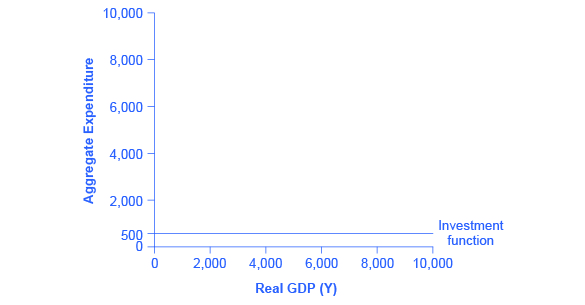图 3：投资函数被描绘成一条平线，因为投资是基于利率和对未来的预期，因此它不会随当前国民收入水平而变化。 在本例中，投资支出水平为500。 但是，技术机会、对短期经济增长的预期和利率等因素的变化都将导致投资功能向上或向下移动。
投资功能呈现为水平线并不意味着投资水平永远不会变动。 这只是意味着，在这张二维图的背景下，纵向总支出轴上的投资水平不会根据横轴上当前的实际国内生产总值水平而变化。 但是，所有其他影响投资的因素——新技术机会、对短期经济增长的预期、利率、关键投入的价格和投资的税收优惠——都可能导致横向投资功能向上或向下移动。
政府支出和税收与国民收入的关系
在凯恩斯主义交叉图中，政府支出显示为一条水平线，如图 4 所示，其中政府支出设定为 1,300。 与投资支出一样，这条水平线并不意味着政府支出不变。 这只是意味着当国会决定改变预算时，政府支出会发生变化，而不是在横轴上显示当前实际GDP规模的情况下以可预测的方式发生变化。
政府支出职能
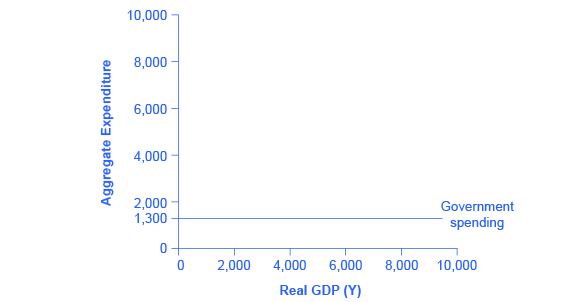图4：政府支出水平是由政治因素决定的，而不是由给定年份的实际GDP水平决定的。 因此，政府支出被划为一条水平线。 在这个例子中，政府支出水平为1,300。 国会增加政府支出的决定将导致这条水平线向上移动，而削减支出的决定将导致其向下移动。
税收情况有所不同，因为税收往往随着经济活动量的增加或下降。 例如，所得税以所得收入水平为基础，销售税基于销售额，经济增长时收入和销售额往往更高，而在经济衰退时收入和销售额往往更低。 为了构建基本的凯恩斯主义交叉图，将税收视为GDP的比例是有帮助的。 例如，在美国，将联邦、州和地方税加在一起，政府通常征收收入的30-35％作为税收。
表 5 修订了先前关于消费函数的表，以便将税收考虑在内。 第一列显示国民收入。 第二列计算税费，在本例中，税率设置为 30% 或 0.3。 第三列显示税后收入；即总收入减去税款。 然后，第四列以与以前相同的方式计算消费：将税后收入乘以0.8，表示边际消费倾向，然后加上600美元，得出即使收入为零也能消耗的金额。 如果将税收包括在内，边际消费倾向会减去税率的金额，因此，每增加一美元的收入，消费的增长幅度小于税前。 因此，含税的消费函数比不含税的消费函数更平坦，如图 5 所示。
税前和税后的消费函数
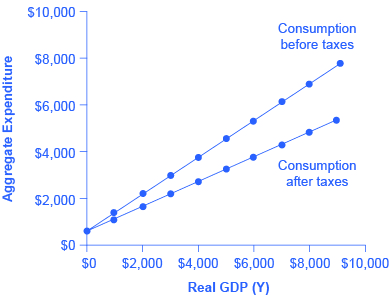图 2。 如果必须首先对收入缴税，然后根据税后收入进行消费，则下线显示了消费函数。
| 收入 |
税收 |
税后收入 |
消费 |
储蓄 |
| $0 |
$0 |
$0 |
600 美元 |
—600 美元 |
| 1,000 美元 |
300 美元 |
700 美元 |
1,160 美元 |
—460 美元 |
| 2,000 美元 |
600 美元 |
1,400 美元 |
1,720 美元 |
—320 美元 |
| 3,000 美元 |
900 美元 |
2,100 美元 |
2,280 美元 |
—180 美元 |
| 4,000 美元 |
1,200 美元 |
2,800 美元 |
2,840 美元 |
—40 美元 |
| 5,000 美元 |
1,500 美元 |
3,500 美元 |
3,400 美元 |
100 美元 |
| 6,000 美元 |
1,800 美元 |
4,200 美元 |
3,960 美元 |
240 美元 |
| 7,000 美元 |
2,100 美元 |
4,900 美元 |
4,520 美元 |
380 美元 |
| 8,000 美元 |
2,400 美元 |
5,600 美元 |
5,080 美元 |
520 美元 |
| 9,000 美元 |
2,700 美元 |
6,300 美元 |
5,640 美元 |
660 美元 |
表 2：税前和税后的消费函数
进出口与国民收入的关系
出口函数显示出口如何随一国自身实际国内生产总值水平而变化，该函数以水平线绘制，如图 6 (a) 中的示例，其中出口的绘制水平为 840 美元。 同样，与投资支出和政府支出一样，将出口功能划为横向并不意味着出口永远不会改变。 这只是意味着它们不会因为横向轴线（即一个国家自身的国内生产水平）而改变，而是由其他国家的总需求水平决定的。 对其他国家出口需求的增加将导致出口功能向上移动；对其他国家出口需求的减少将导致出口功能下降。
导出和导入功能
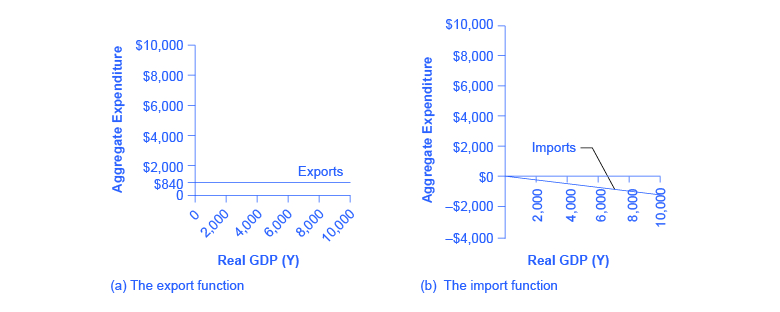图6：(a) 出口功能被画成一条横线，因为出口是由其他国家的购买力决定的，因此不会随国内经济规模的变化而变化。 在此示例中，导出设置为 840。 但是，出口可以向上或向下移动，这取决于其他国家的购买模式。 (b) 进口功能处于负值区间，因为进口产品的支出是从国内经济支出中减去的。 在此示例中，边际进口倾向为 0.1，因此进口是通过将收入水平乘以 —0.1 来计算的。
在凯恩斯主义十字图中，进口被描绘成一条向下倾斜的线，下降的斜率由国民收入的边际进口倾向（MPI）决定。 在图 6 (b) 中，边际进口倾向为 0.1。 因此，如果实际国内生产总值为5,000美元，则进口为500美元；如果国民收入为6,000美元，则进口为600美元，依此类推。 进口函数被划分为向下倾斜和负值，因为它是从国内经济总支出中减去的。 边际进口倾向的改变，可能是由于优惠的变化，将改变进口功能的斜率。
注意：对支出产出模型使用代数方法
在支出-产出或凯恩斯主义交叉模型中，均衡发生在总支出线（AE 线）与45度线交叉的地方。 给定两条线的代数方程，可以很容易地计算出它们的交叉点。 想象一下具有以下特征的经济体。
Y = 实际国内生产总值或国民收入
T = 税收 = 0.3 年
C = 消耗量 = 140 + 0.9 (Y — T)
I = 投资 = 400
G = 政府支出 = 800
X = 出口 = 600
M = 进口 = 0.15Y
第 1 步。 确定总支出函数。 在这种情况下，它是：
\[AE=C+I+G+X-M\]
\[AE=140+0.9(Y-T)+400+800+600-0.15Y\]
第 2 步。 45 度线的方程是一组点，其中横轴上的国内生产总值或国民收入等于垂直轴上的总支出。 因此，45 度线的方程为：AE = Y。
第 3 步。 下一步是求解 Y（或 AE，因为它们将彼此相等）的这两个方程。 用 Y 代替 AE：
\[Y=140+0.9(Y-T)+400+800+600-0.15Y\]
第 4 步。 为税率 T 插入 0.3Y 一词。这会生成一个只有一个变量 Y 的方程式
第 5 步。 仔细计算代数并求解 Y。
\[Y=140+0.9(Y-0.3Y)+400+800+600-0.15Y\]
\[Y=140+0.9Y-0.27Y+1800-0.15Y\]
\[Y=1940+0.48Y\]
\[0.52Y=1940\]
\[Y=3730\]
这个代数框架在预测经济事件和政策行动将如何影响实际GDP方面非常灵活，很有用。
第 6 步。 比如说，由于国内外商品相对价格的变化，边际进口倾向降至0.1。 计算边际进口倾向更改为 0.1 时的均衡产出。
\[Y=140+0.9(Y-0.3Y)+400+800+600-0.1Y\]
\[Y=1940-0.53Y\]
\[0.47Y=1940\]
\[Y=4127\]
第 7 步。 由于商业信心的激增，投资上升至500。 计算均衡输出。
\[Y=140+0.9(Y-0.3Y)+500+800+600-0.15Y\]
\[Y=2040+0.48Y\]
\[0.52Y=2040\]
\[Y=3923\]
对于政策问题，关键问题将是如何调整政府支出水平或税率，使产出的均衡水平为充分就业水平。 在这种情况下，假设经济参数为：
Y = 国民收入
T = 税收 = 0.3 年
C = 消耗量 = 200 + 0.9 (Y — T)
I = 投资 = 600
G = 政府支出 = 1,000
X = 出口 = 600
Y = 进口 = 0.1 (Y — T)
第 8 步。 计算这个经济体的均衡（记住 Y = AE）。
\[Y=200+0.9(Y-0.3Y)+600+1000+600-0.1(Y-0.3Y)\]
\[0.44Y=2400\]
\[Y=5454\]
第 9 步。 假设产出的充分就业水平为6,000。 要达到这个水平，需要什么水平的政府支出？ 要回答这个问题，请插入 6,000 作为等于 Y，但保留 G 作为变量，然后求解 G。因此：
\[6000=200+0.9(6000-0.3(6000))+600+G+600-0.1(6000-0.3(6000))\]
第 10 步。 用算术解决这个问题。 答案是：G = 1,240。 换句话说，将政府支出从最初的1,000增加到1,240个，将把产出提高到GDP的充分就业水平。
事实上，增加多少政府支出以使均衡产出从5,454增加到6,000的问题，只要使用乘数公式就可以不用计算代数就能得到解答。 在这种情况下，乘数方程为：
\[\dfrac{1}{1-0.56}=2.27\]
因此，要将产出提高546％，就需要将政府支出增加546/2.27=240，这与代数计算得出的答案相同。
这个代数框架非常灵活。 例如，可以将税收视为政治考虑（如政府支出）的总和，而不依赖于国民收入。 进口可能基于税前收入，而不是税后收入。 出于某些目的，分析没有进出口的经济可能会有所帮助。 更复杂的方法可以将消费、投资、政府、出口和进口分为较小的类别，或者增加税率、储蓄率和进口率的某些变动。 一位明智的经济学家将根据正在调查的具体问题来塑造模型。
建立合并总支出函数
总需求的所有组成部分——消费、投资、政府支出和贸易平衡——现已准备就绪，可以构建凯恩斯主义交叉图。 图 7 根据本文中使用的 C、I、G、X 和 M 的数值插图构建了一个总支出函数。 表 3 中的前三列取自之前的表 2，该表显示了如何将税收纳入消费函数。 第一列是实际GDP或国民收入，这是收入支出图的水平轴上显示的内容。 第二列根据以下假设计算税后收入：在这种情况下，实际GDP的30％是税收的。 第三列基于0.8的MPC，因此，随着税后收入从一行到下一行增加700美元，消费从一行到下一行增加了560美元（700×0.8）。 投资、政府支出和出口不会随当前国民收入水平而变化。 在之前的讨论中，投资为500美元，政府支出为1300美元，出口为840美元，总额为2,640美元。 该总数显示在第四列中。 在此示例中，进口占实际GDP的0.1，进口水平在第五列中计算。 最后一栏 “总支出” 汇总了 C + I + G + X — M。该总支出项目如图 7 所示。
凯恩斯主义交叉图
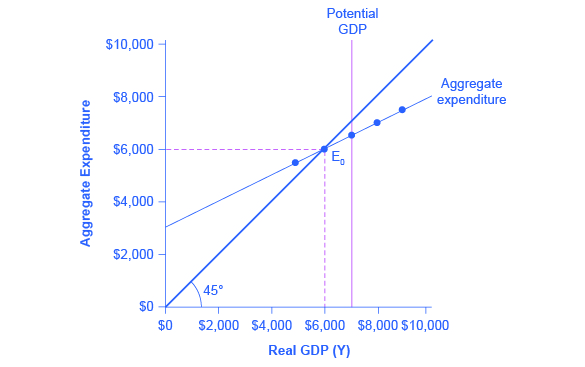图 7：绘制了国民收入和总支出（税后消费、政府支出、投资、出口和进口）的每种组合。 平衡发生在总支出等于国民收入的地方；当总支出计划跨越45度线，实际GDP为6,000美元时，就会发生这种平衡。 本例中的潜在GDP为7,000美元，因此均衡发生在产出水平或实际GDP低于潜在GDP水平的水平上。
| 国民收入 |
税后收入 |
消费 |
政府支出 + 投资 + 出口 |
进口 |
总支出 |
| 3,000 美元 |
2,100 美元 |
2,280 美元 |
2,640 美元 |
300 美元 |
4,620 美元 |
| 4,000 美元 |
2,800 美元 |
2,840 美元 |
2,640 美元 |
400 美元 |
5,080 美元 |
| 5,000 美元 |
3,500 美元 |
3,400 美元 |
2,640 美元 |
500 美元 |
5,540 美元 |
| 6,000 美元 |
4,200 美元 |
3,960 美元 |
2,640 美元 |
600 美元 |
6,000 美元 |
| 7,000 美元 |
4,900 美元 |
4,520 美元 |
2,640 美元 |
700 美元 |
6,460 美元 |
| 8,000 美元 |
5,600 美元 |
5,080 美元 |
2,640 美元 |
800 美元 |
6,920 美元 |
| 9,000 美元 |
6,300 美元 |
5,640 美元 |
2,640 美元 |
900 美元 |
7,380 美元 |
表 3：国民收入总支出平衡
总支出函数是通过将消费函数（税后）、投资函数、政府支出函数、出口函数和进口函数叠加在一起而形成的。 总支出函数与垂直轴的交叉点将由投资、政府和出口支出水平决定，这些水平不会随国民收入而变化。 总支出函数的向上斜率将由边际储蓄倾向、税率和边际进口倾向决定。 更高的边际储蓄倾向、更高的税率和更高的边际进口倾向都将使总支出函数的斜率变得更平淡——因为在任何额外收入中，更多的用于储蓄、税收或进口，而更少的用于国内商品和服务的支出。
平衡发生在国民收入等于总支出的情况下，总支出在图表中显示为总支出计划跨越45度线的点。 在此示例中，均衡发生在 6,000 处。 也可以从图下方的表格中看出这种均衡；总支出等于国民收入的是国民收入水平。
凯恩斯交叉模型中的均衡
总支出线到位后，下一步是将其与凯恩斯主义交叉图的另外两个要素联系起来。 因此，第一小节解释了总支出函数与 45 度线的交点，而下一小节则将这个交叉点与潜在的 GDP 线联系起来。
平衡发生的地方
由C + I + G + X — M构成的总支出线穿过45度线的点将是经济的均衡。 这是总支出项目上唯一一个用于总需求的总支出等于总生产水平的点。 在图 7 中，这个平衡点（E 0）发生在 6,000 处，也可以从表 3 中读出。
“均衡” 的含义保持不变；也就是说，均衡是一个平衡点，不存在偏离该结果的动机。 要理解为什么总支出函数和45度线之间的交点是宏观经济均衡，可以考虑如果一个经济体发现自己位于均衡点E的右边，比如图8中的H点，产出高于均衡，会发生什么。 在H点，总支出水平低于45度线，因此经济中的总支出水平低于产出水平。 结果，在H点，产出堆积未售出，这不是一种可持续的状况。
凯恩斯交叉图中的均衡
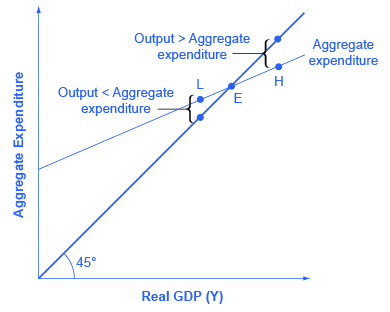图8：如果产出在H处高于均衡水平，则实际产出大于经济中的总支出。 这种模式不成立，因为这意味着商品已经生产出来但堆积起来未售出。 如果产出低于L的均衡水平，那么总支出将大于产出。 这种模式也不能成立，因为这意味着支出超过生产的商品数量。 只有E点可以处于平衡状态，即产出或国民收入和总支出相等。 均衡（E）必须位于45度线上，这是国民收入和总支出相等的点集。
相反，请考虑一下产出水平在L点的情况，即实际产出低于均衡。 在这种情况下，经济中的总需求水平高于45度线，这表明经济中的总支出水平高于产出水平。 当总需求水平已耗尽商店货架时，也无法维持。 企业将通过提高生产水平来作出回应。 因此，均衡必须是总支出函数和45度线交汇处产生的金额和支出金额保持平衡的点。
注意：寻找平衡
表 4 提供了一些有关经济的信息。 凯恩斯主义模型假设，即使没有收入，也有一定程度的消费。 该金额为236美元——216美元=20美元。当国民收入等于零时，将消耗20美元。 假设税收占实际国内生产总值的0.2％。 假设税后收入的边际储蓄倾向为0.1。 投资水平为70美元，政府支出水平为80美元，出口水平为50美元。 进口占税后收入的0.2％。 鉴于这些值，您需要完成表 4，然后回答以下问题：
- 什么是消耗功能？
- 什么是均衡？
- 为什么300美元的国民收入没有达到平衡？
- 此时的支出和产出相比如何？
| 国民收入 |
税收 |
税后收入 |
消费 |
我 + G + X |
进口 |
总支出 |
| 300 美元 |
|
|
236 美元 |
|
|
|
| 400 美元 |
|
|
|
|
|
|
| 500 美元 |
|
|
|
|
|
|
| 600 美元 |
|
|
|
|
|
|
| 700 美元 |
|
|
|
|
|
|
表 4
第 1 步。 使用以下示例计算每个国民收入水平的每个国民收入水平（提醒：GDP = 国民收入）的税额：
| \(National\,Income\,(Y)\) |
\(\$300\) |
| \(Taxes=0.2\,or\,20\%\) |
\(\times 0.2\) |
| \(Tax\,amount\,(T)\) |
\(\$60\) |
第 2 步。 使用以下例子，通过从每个国民收入水平的国民收入中减去税额来计算税后收入：
| \(National\,Income\minus\,taxes\) |
\(\$300\) |
| |
\(-\$60\) |
| \(After-tax\,income\) |
\(\$240\) |
第 3 步。 计算消耗。 边际储蓄倾向为 0.1。 这意味着边际消费倾向为0.9，因为 MPS + MPC = 1。 因此，使用以下示例将0.9乘以税后收入金额：
| \(After-tax\,Income\) |
\(\$240\) |
| \(MPC\) |
\(\times 0.9\) |
| \(Consumption\) |
\(\$216\) |
第 4 步。 考虑一下为什么表中的第一行显示消费为236美元。 如前所述，凯恩斯主义模型假设即使没有收入，也有一定程度的消费。 这个金额是236美元 — 216美元 = 20美元。
第 5 步。 现在有足够的信息来编写消耗函数。 消费函数是通过计算收入为零时将发生的消费水平来找到的。 请记住：
\[C=Consumption\,when\,national\,income\,is\,zero+MPC\,(after-tax\,income)\]
假设 C 表示消费函数，Y 代表国民收入，T 代表税收。
\[C=\$20+0.9(Y-T)\]
\[=\$20+0.9(\$300-\$60)\]
\[=\$236\]
第 6 步。 使用消费函数查找每个国民收入水平的消费。
第 7 步。 加上投资（I）、政府支出（G）和出口（X）。 请记住，这些不会随着国民收入的变化而改变：
第 8 步。 找出进口，在每个国民收入水平上，进口占税后收入的0.2％。 例如：
| \(After-tax\,Income\) |
\(\$240\) |
| \(Imports\,of\,0.2\,or\,20\%\,of\,Y-T\) |
\(\times 0.2\) |
| \(Imports\) |
\(\$48\) |
第 9 步。 通过将每个国民收入水平的 C + I + G + X — I 相加，得出总支出。 您完成的表格应与表 5 类似。
| 国民收入 (Y) |
税 = 0.2 × Y (T) |
税后收入（Y — T） |
消费 C = 20 美元 + 0.9 (Y — T) |
我 + G + X |
减去进口量 (M) |
总支出 AE = C + I + G + X — M |
| 300 美元 |
60 美元 |
240 美元 |
236 美元 |
200 美元 |
48 美元 |
388 美元 |
| 400 美元 |
80 美元 |
320 美元 |
308 美元 |
200 美元 |
64 美元 |
444 美元 |
| 500 美元 |
100 美元 |
400 美元 |
380 美元 |
200 美元 |
80 美元 |
500 美元 |
| 600 美元 |
120 美元 |
480 美元 |
452 美元 |
200 美元 |
96 美元 |
556 美元 |
| 700 美元 |
140 美元 |
560 美元 |
524 美元 |
200 美元 |
112 美元 |
612 美元 |
表 5
第 10 步。 回答问题：什么是均衡？ 均衡发生在AE = Y的地方。表5显示，当国民收入等于500美元的总支出时，就会出现平衡。
第 11 步。 知道国民收入等于总支出，用数学方法找到均衡。
\[Y=AE\]
\[=C+I+G+X-M\]
\[=\$20+0.9(Y-T)+\$70+\$80+\$50-0.2(Y-T)\]
\[=\$220+0.9(Y-T)-0.2(Y-T)\]
由于 T 是国民收入的 0.2，所以用 0.2 Y 代替 T，这样：
\[Y=\$220+0.9(Y-0.2Y)-0.2(Y-0.2Y)\]
\[=\$220+0.9Y-0.18Y-0.2Y+0.04Y\]
\[=\$220+0.56Y\]
求解 Y。
\[Y=\$220+0.56Y\]
\[0.44Y=\$220\]
\[Y=\$500\]
第 12 步。 回答这个问题：为什么300美元的国民收入不是均衡？ 国民收入为300美元，总支出为388美元。
第 13 步。 回答这个问题：目前支出和产出相比如何？ 从长远来看，总支出不能超过产出（GDP），因为没有足够的商品可供购买。
衰退和通货膨胀缺口
在凯恩斯主义十字图中，如果总支出线在潜在GDP水平上与45度线相交，则经济状况良好。 没有衰退，失业率很低。 但无法保证平衡会在潜在的GDP产出水平上发生。 均衡可能更高或更低。
例如，图9 (a) 说明了总支出线在E 0 点与45度线相交的情况，即实际国内生产总值为6,000美元，低于7,000美元的潜在国内生产总值。 在这种情况下，总支出水平太低，国内生产总值无法达到充分就业水平，就会出现失业。 像E 0 这样的低于潜在GDP的产出水平与潜在GDP水平之间的距离被称为衰退缺口。 由于实际GDP的均衡水平如此之低，企业不希望雇用充分就业人数的员工，失业率将很高。
解决衰退和通货膨胀缺口
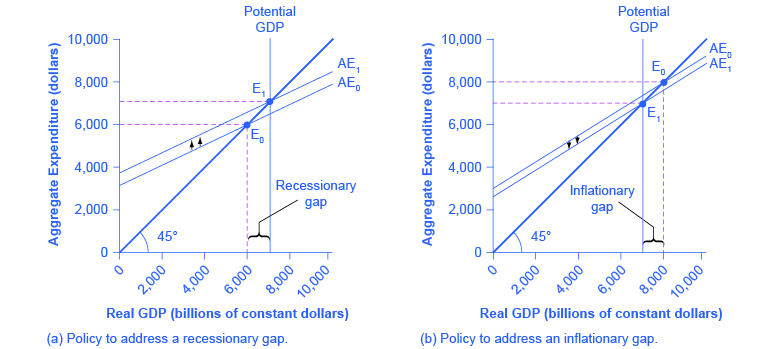图9：（a）如果均衡发生在产出低于潜在GDP的地方，则存在衰退缺口。 解决衰退缺口的政策办法是利用减税或增加政府支出等政策，将总支出计划从零上调至AE 1。 然后，新的均衡E 1 出现在潜在的GDP上。 (b) 如果在产出高于潜在国内生产总值时出现均衡，则存在通货膨胀缺口。 解决通货膨胀缺口的政策办法是使用增税或减支等政策，将总支出计划从零下调至AE 1。 然后，新的均衡E 1 出现在潜在的GDP上。
什么可能导致衰退缺口？ 任何使总支出线向下移动的因素都是衰退的潜在原因，包括消费下降、储蓄增加、投资减少、政府支出下降或税收增加、出口下降或进口增加。 此外，一个处于平衡状态但存在衰退缺口的经济体可能只会停留在那里，长期遭受高失业率；请记住，均衡的含义是，没有对经济中的价格或数量进行特别调整来赶走衰退。
应对衰退缺口的适当对策是政府减少税收或增加支出，使总支出功能从AE 0 向上转移到AE 1。 当这种转变发生时，新的均衡E 1 现在出现在潜在的GDP上，如图9 (a) 所示。
相反，图9 (b) 显示了总支出计划（AE 0）与潜在国内生产总值上方45度线相交的情况。 均衡E 0 的实际GDP水平与潜在GDP之间的差距称为通货膨胀缺口。 通货膨胀差距也需要一些解释。 毕竟，对凯恩斯主义交叉图的天真解读可能表明，如果将总支出函数推高到足够高的水平，实际GDP可以达到预期的水平，甚至是经济潜在GDP水平的两倍或三倍。 这种含义显然是错误的。 一个经济体在利用现有劳动力、物质和人力资本、技术和市场机构在给定时间能生产多少方面面临一些供给侧限制。
通货膨胀缺口不应被解释为对实际GDP将有多大的字面预测，而应解释为经济中有多少额外总支出超出达到潜在GDP所需的金额的陈述。 通货膨胀缺口表明，由于经济无法生产足够的商品和服务来吸收这种水平的总支出，支出反而会导致物价水平的通货膨胀上升。 这样，尽管价格水平的变化没有明确出现在凯恩斯主义交叉方程中，但通货膨胀的概念隐含在通货膨胀缺口的概念中。
凯恩斯主义对通货膨胀缺口的适当反应如图9（b）所示。 总支出线AE 0 和45度线的原始交点为8,000美元，高于潜在GDP的7,000美元。 如果AE 0 向下移动到AE 1，使新均衡为E 1，那么经济将达到潜在的GDP，而不会受到通货膨胀价格上涨的压力。 政府可以通过增加对消费者或企业的税收或通过减少政府支出来实现总支出的向下移动。
乘数效应
凯恩斯主义的政策处方还有最后一个转折点。 假设对于某个经济体，总支出函数和45度线的交点为GDP为700，而该经济体的潜在GDP水平为800美元。 政府支出需要增加多少才能使经济达到充分就业的GDP？ 显而易见的答案似乎是800美元——700美元=100美元；因此，将政府支出增加100美元。 但是这个答案是不正确的。 例如，100美元的政府支出变化将对实际GDP的均衡水平产生超过100美元的影响。 原因是总支出的变化贯穿整个经济：家庭从企业购买商品，企业向工人和供应商付款，工人和供应商从其他公司购买商品，这些公司向员工和供应商支付工资，依此类推。 这样，总支出的最初变化实际上是不止一次的支出。 这就是所谓的乘数效应：支出的初始增加，在整个经济中反复循环，其影响大于最初的美元支出。
乘数是如何工作的？
要了解乘数效应是如何起作用的，请回到凯恩斯主义交叉图中的当前均衡是实际GDP为700美元，比实现充分就业所需的800美元（潜在GDP）少100美元。 如果政府花费100美元来缩小这一缺口，那么经济中有人就会收到这笔支出并将其视为收入。 假设获得这笔收入的人缴纳30％的税款，储蓄10％的税后收入，将总收入的10％用于进口，然后将其余的花在国产商品和服务上。
如图10和表6的计算所示，在最初的100美元政府支出中，有53美元用于购买国产商品和服务。 花费的53美元变成了经济中某个地方某人的收入。 获得该收入的人还要缴纳30％的税款，节省10％的税后收入，并将总收入的10％用于进口，如图10所示，因此在第三轮中将额外花费28.09美元（即0.53×53美元）。 然后，获得该收入的人纳税，储蓄和购买进口商品，第四轮的支出金额为14.89美元（即0.53×28.09美元）。
乘数效应
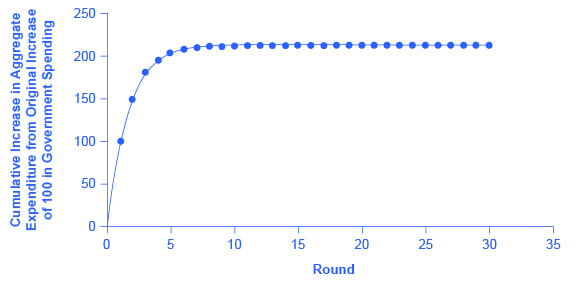图10：政府支出最初增加100美元，导致总支出增加100美元。 但是这100美元是经济中其他人的收入，在他们储蓄、纳税和购买进口商品之后，他们在第二轮中花费了100美元中的53美元。 反过来，这53美元是他人的收入。 因此，最初的100美元政府支出乘以这些支出周期，但每个连续周期的影响越来越小。 鉴于本例中的数字，最初的政府支出增加100美元，使总支出增加了213美元；因此，本例中的乘数为213美元/100美元 = 2.13美元。
| 政府开支总支出的最初增加 |
100 |
| 这是整个经济中人们的收入：缴纳30％的税款。 节省税后收入的10％。 将收入的10％用于进口。 第二轮增加... |
70 — 7 — 10 = 53 |
| 这是经济中人们收入的53美元：缴纳30％的税款。 节省税后收入的10％。 将收入的10％用于进口。 第三轮增加... |
37.1 — 3.71 — 5.3 = 28.09 |
| 这是整个经济中人们收入的28.09美元：缴纳30％的税款。 节省税后收入的10％。 将收入的10％用于进口。 第四轮增加... |
19.663 — 1.96633 — 2.809 = 14.89 |
表 6：计算乘数效应
因此，在前四轮总支出中，最初增加100美元的政府支出所产生的影响使总支出增加了100美元+ 53美元+ 28.09美元+ 14.89美元 = 195.98美元。 图 10 显示了前四轮之后的总支出，然后该图显示了 30 轮之后的总支出。 在每轮消费中，总支出的额外增长正在减少。 经过大约 10 轮后，额外的增量确实非常小，肉眼几乎看不见。 30 回合后，每回合的额外增量非常小，没有任何实际影响。 经过30轮，总支出初始增长的累计价值约为213美元。 因此，经过多次周期，100美元的政府支出最终增加了213美元，使总支出和实际GDP增加了213美元。 在本示例中，乘数为 213美元/100 美元 = 2.13。
计算乘数
幸运的是，对于那些没有随身携带装有电子表格程序的计算机来预测最初超过20、50或100轮支出增加的影响的人来说，有一个计算乘数的公式。
\[Spending\,Multiplier=1/(1-MPC*(1-tax\,rate)+MPI)\]
图 10 和表 6 中的数据是：
- 边际储蓄倾向 (MPS) = 30%
- 税率 = 10%
- 边际进口倾向 (MPI) = 10%
MPC 等于 1 — MPS 或 0.7。 因此，支出乘数为：
\[Spending\,Multiplier=\dfrac{1}{1-(0.7-(0.10)(0.7)-0.10)}\]
\[=\dfrac{1}{0.47}\]
\[=2.13\]
100美元的支出变化乘以支出乘数2.13等于国内生产总值的变化213美元。 并非巧合的是，这个结果正是图 10 中在经济中经历了多轮支出循环之后计算得出的结果。
乘数的大小取决于边际收入中有多少比例用于税收、储蓄和进口。 这三个因素被称为 “泄漏”，因为它们决定了每轮乘数效应中 “泄漏” 多少需求。 如果泄漏量相对较小，那么每轮连续的乘数效应都会产生更多的需求，而乘数将很高。 相反，如果泄漏量相对较大，则需求的任何初始变化将在第二、第三和以后的回合中更快地减少，乘数也将很小。 泄漏规模的变化——边际储蓄倾向、税率或边际进口倾向的变化——将改变乘数的大小。
计算凯恩斯主义政策干预
回到最初的问题：政府支出应该增加多少才能使实际GDP总共增加100美元？ 如果目标是将总需求增加100美元，乘数为2.13，那么为实现该目标而增加的政府支出将为100美元/2.13美元 = 47美元。 政府支出约为47美元，再加上2.13的乘数（请记住，基于对税收、储蓄和进口税率的具体假设），实际GDP总体增长100美元，使经济恢复到800美元的潜在GDP，如图11所示。
支出-产出模型中的乘数效应
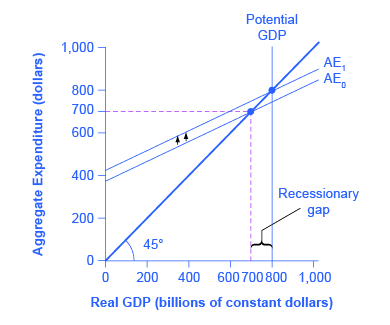图11：乘数效应的力量在于，支出的增加对均衡产出的增加幅度更大。 支出的增加是从AE 0 到AE 1 的垂直增长。 但是，水平轴上显示的平衡产出的增加显然更大。
乘数效应在凯恩斯主义交叉图上也可见。 图11显示了我们一直在讨论的例子：均衡为700美元的衰退缺口，潜在的GDP为800美元，总支出函数（AE 0）的斜率由以下假设确定：税收占收入的30％，储蓄占税后收入的0.1％，进口为0.1％税前收入。 在 AE 1 中，总支出函数向上移动以达到潜在的 GDP。
现在，将总支出函数的垂直向上移动（47美元）与实际GDP的水平向外移动（100美元）进行比较（这些数字是先前计算的）。 实际国内生产总值的增长是总支出函数增长的两倍多。 （同样，如果你回头看图 9，你会发现总支出函数的垂直移动小于水平轴上产生的均衡产出的变化。 再说一遍，这是起作用的乘数效应。） 这样，乘数的功效在收入支出图和算术计算中显而易见。
乘数不仅影响政府支出，还适用于经济的任何变化。 假设商业信心下降而投资下降，或者说主要贸易伙伴的经济放缓导致出口销售下降。 这些变化将减少总支出，然后由于乘数效应而对实际GDP产生更大的影响。 阅读以下 Clear It Up 功能，了解如何应用乘数效应来分析职业体育的经济影响。
注意：如何使用乘数来分析职业体育的经济影响？
吸引职业运动队和建造体育场以创造就业机会和刺激业务增长是美国许多社区采用的一项经济发展战略。 环城公路外的詹姆斯·乔伊纳在他最近的文章《私人体育场的公共融资》中探讨了美国国家橄榄球联盟球队的公共融资。 乔伊纳的发现证实了范德比尔特大学的约翰·齐格弗里德和史密斯学院的安德鲁·津巴利斯特早些时候的工作。
齐格弗里德和津巴利斯特使用乘数来分析这个问题。 他们考虑了在当地缴纳的税款和花费的金额，以确定是否产生了积极的乘数效应。 由于大多数职业运动员和运动队老板都足够富有，可以欠很多税，所以假设他们赚取的任何边际收入中有40％是用税收缴纳的。 由于运动员通常是职业生涯短的高收入者，所以让我们假设他们储蓄了税后收入的三分之一。
但是，许多职业运动员并不是全年都住在他们参加比赛的城市，因此，假设他们花的钱中有一半花在了当地以外。 在这个例子中，人们可以认为本地经济之外的支出相当于国民经济的进口商品。
现在，考虑一下在除职业体育以外的当地娱乐场所花费的钱会产生的影响。 尽管这些其他企业的所有者可能属于中等收入企业，但他们中很少有人处于职业运动员的经济平流层。 因为他们的收入较低，他们的税收也较低；假设他们只缴纳边际收入的35％作为税款。 他们没有和职业运动员一样的储蓄能力或需求，所以假设他们的 MPC 只有 0.8。 最后，由于更多的人生活在当地，他们将把更高比例的收入花在当地商品上，比如说65％。
如果这些一般假设成立，那么花在职业体育上的钱对当地经济的影响将小于花在其他形式的娱乐上的钱。 对于职业运动员来说，在赚到的一美元中，40美分用于税收，剩下60美分。 在这60美分中，三分之一可以储蓄，剩下40美分，一半在区域外消费，剩下20美分。 在第一轮中，每1美元中只有20美分循环进入当地经济。 对于本地经营的娱乐活动，在赚取的一美元中，35美分用于税收，剩下65美分。 其余部分中，有20％被储蓄，剩下52美分，其中65％用于当地，因此每1美元收入中有33.8美分被循环用于当地经济。
齐格弗里德和津巴利斯特提出了合理的论点，即在家庭预算中，人们有固定的娱乐开支。 如果这个假设成立，那么在给定大都市区花在参加职业体育赛事上的钱就是没有花在其他娱乐选择上的钱。 由于职业体育的乘数低于其他当地娱乐选择，因此职业体育进入城市将重新分配娱乐支出，从而导致当地经济萎缩而不是增长。 因此，他们的发现似乎证实了乔伊纳报道的内容以及全国各地的报纸正在报道什么。 在互联网上快速搜索 “体育的经济影响” 将产生大量质疑这一经济发展战略的报告。
乘数权衡：稳定与宏观经济政策的力量
乘数高还是低乘数的经济更健康？ 如果乘数高，总需求的任何变化都往往会被大幅放大，因此经济将更加不稳定。 相比之下，在乘数较低的情况下，总需求的变化不会成倍增加，因此经济往往会更加稳定。
但是，在乘数较低的情况下，政府在税收或支出方面的政策变化往往对实际产出的均衡水平的影响较小。 随着乘数的提高，政府提高或减少总支出的政策将产生更大的影响。 因此，低乘数意味着更稳定的经济，但也意味着更弱的政府宏观经济政策，而高乘数意味着更不稳定的经济，但也意味着政府宏观经济政策更有力的经济。
关键概念和摘要
支出-产出模型或凯恩斯主义交叉图显示了总支出水平（在垂直轴上）如何随经济产出水平（在横轴上显示）而变化。 由于所有宏观经济产出的价值也代表经济中其他地方的收入，因此横向轴也可以解释为国民收入。 图中的均衡将发生在总支出线与45度线交叉的地方，45度线代表经济中的总支出等于产出（或国民收入）的一组点。 凯恩斯交叉图中的均衡可能发生在潜在的GDP上，或者低于或高于该水平。
消费函数显示了国民收入和消费之间向上倾斜的关系。 边际消费倾向（MPC）是指从额外一美元收入中消耗的金额。 较高的边际消费倾向意味着更陡峭的消费函数；较低的边际消费倾向意味着更平坦的消费函数。 边际储蓄倾向（MPS）是从额外一美元收入中储蓄的金额。 MPC + MPS = 1 必然是事实。 投资职能以一条平线绘制，表明本年度的投资相对于当前的国民收入水平没有变化。 但是，投资功能将根据未来的预期回报率上下移动。 在凯恩斯主义交叉图中，政府支出被画成一条水平线，因为其水平是由政治考虑决定的，而不是由当前的经济收入水平决定的。 通过调整消费函数，将基本凯恩斯主义交叉图中的税收考虑在内。 在凯恩斯主义交叉图中，出口函数被绘制为一条水平线，因为出口不是因为国内收入的变化而发生变化，而是由于国外收入的变化以及汇率的变化而变化。 进口函数被描绘成一条向下倾斜的线，因为进口随着国民收入的增长而增加，但进口是总需求的减法。 因此，较高的进口水平意味着较低的国内商品支出水平。
在凯恩斯主义交叉图中，均衡可能处于低于潜在GDP的水平，这称为衰退缺口，也可能高于潜在GDP的水平，即所谓的通货膨胀缺口。
乘数效应描述了总需求的初始变化所产生的GDP是累计GDP的几倍。 支出乘数的大小由三个漏洞决定：储蓄、税收和进口支出。 乘数的公式是：
\[Multiplier=\dfrac{1}{1-(MPC \times (1-tax\,rate)+MPI)}\]
乘数较低的经济体更稳定——与乘数较高的经济体相比，它受经济事件或政府政策的影响较小。
自查问题
解决方案
下图显示了带有衰退缺口的总支出产出图。
图 12
解决方案
下图显示了带有通货膨胀缺口的总支出产出图。
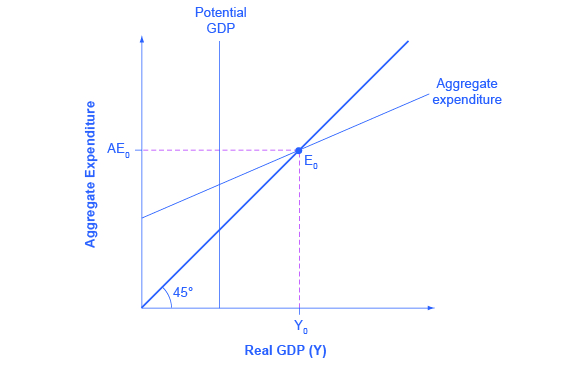图 13
练习
经济具有以下特征：
Y = 国民收入
税收 = T = 0.25 年
C = 消耗量 = 400 + 0.85 (Y — T)
I = 300
G = 200
X = 500
M = 0.1 (Y — T)
找到这个经济的均衡。 如果潜在的GDP为3,500，那么要达到这个水平，需要对政府支出进行哪些改变？ 用两种方法解决这个问题。 首先，在方程中插入 3,500 然后求解 G. 其次，计算乘数然后用这种方式计算出来。
解决方案
首先，设置计算。
\[AE=400+0.85(Y-T)+300+200+500-0.1(Y-T)\]
\[AE=Y\]
然后为 AE 插入 Y，为 T 插入 0.25Y
\[Y=400+0.85(Y-0.25Y)+300+200+500-0.1(Y-0.25Y)\]
\[Y=1400+0.6375Y-0.075Y\]
\[Y=3200\]
如果充分就业率为 3,500，则一种方法是在整个方程中为 Y 插入 3,500，但将 G 保留为单独的变量。
\[Y=400+0.85(Y-0.25Y)+300+G+500+0.1(Y-0.25Y)\]
\[3500=400+0.85(3500-0.25(3500))+300+G+500-0.1(3500-0.25(3500))\]
\[G=3500-400-2231.25-1300-500+262.5\]
\[G=331.25\]
G 值为 331.25 比原来的水平 200 增加了 131.25。
或者，乘数是，在每花费1美元中，0.25用于税收，剩下0.75美元；在税后收入中，0.15用于储蓄，0.1用于进口。 因为 (0.75) (0.15) = 0.1125 且 (0.75) (0.1) = 0.075，这意味着每花费一美元：1 —0.25 —0.1125 —0.075 = 0.5625。
因此，使用该公式，乘数为：
\[\dfrac{1}{1-0.5625}=2.2837\]
要将均衡国内生产总值提高300，需要提振300/2.2837，再次达到131.25。
练习
表 7 显示了凯恩斯交叉图背后的数据。 假设税率为国民收入的0.4；税后收入中的货币政策委员会为0.8；投资为2,000美元；政府支出为1,000美元；出口为2,000美元，进口为税后收入的0.05。 这个经济体的均衡产出水平是多少？
| 国民收入 |
税后收入 |
消费 |
我 + G + X |
减去进口 |
总支出 |
| 8,000 美元 |
|
4,340 美元 |
|
|
|
| 9,000 美元 |
|
|
|
|
|
| 10,000 |
|
|
|
|
|
| 11,000 美元 |
|
|
|
|
|
| 12,000 美元 |
|
|
|
|
|
| 13,000 美元 |
|
表 7
解决方案
下表说明了已完成的表。 均衡是水平用斜体表示。
| 国民收入表 |
税后收入 |
消费 |
我 + G + X |
减去进口 |
总支出 |
| 8,000 美元 |
4,800 美元 |
4,340 美元 |
5,000 美元 |
240 美元 |
9,100 美元 |
| 9,000 美元 |
5,400 美元 |
4,820 美元 |
5,000 美元 |
270 美元 |
9,550 美元 |
| 10,000 |
6,000 美元 |
5,300 美元 |
5,000 美元 |
300 美元 |
10,000 |
| 11,000 美元 |
6,600 美元 |
5,780 美元 |
5,000 美元 |
330 美元 |
10,450 美元 |
| 12,000 美元 |
7,200 美元 |
6,260 美元 |
5,000 美元 |
360 美元 |
10,900 美元 |
| 13,000 美元 |
7,800 美元 |
46,740 美元 |
5,000 美元 |
4,390 美元 |
11,350 美元 |
表 8
确定均衡的另一种方法是求解 Y，其中 Y = 国民收入，使用：Y = AE = C + I + G + X — M
\[Y=\$500+0.8(Y-T)+\$2,000+\$1,000+\$2,000-0.05(Y-T)\]
求解 Y，我们可以看到产出的均衡水平为 Y = 10,000 美元。
练习
解释乘数是如何工作的。 在示例中使用 80% 的 MPC。
解决方案
乘数是指一美元将在经济中营业额的多少倍。 它基于 “边际消费倾向”（MPC），它表明收到的每一美元中有多少将花费。 如果MPC为80％，那么这意味着消费者每收到一美元，将花费0.80美元。 这 0.80 美元由其他人收到。 反过来，收到的0.80美元（即0.64美元）中的80％将被花掉，依此类推。 如果考虑到税收和支出对进口的影响，乘数的影响就会被淡化。 要得出乘数，请使用 1/1 — F；其中 F 等于进口储蓄、税收和支出的百分比。
查看问题
练习
为什么投资职能、政府支出职能和出口职能都被划成平线？
练习
为什么导入功能会向下倾斜？ 进口的边际倾向是什么？
练习
凯恩斯交叉图中的均衡通常预计等于或接近潜在GDP吗？
练习
为什么在计算乘数效应时将储蓄、税收和进口称为 “流失”？
练习
在应对经济或政府政策变化时，乘数高的经济体会比乘数低的经济体更稳定还是更不稳定？
批判性思维问题
练习
当总支出线穿过45度线时，这意味着什么？ 换句话说，你会如何用语言解释十字路口？
练习
哪种模型，AD/AS或AE模型，可以更好地解释物价上涨与GDP之间的关系？ 为什么？
练习
经济可能陷入衰退的原因有哪些？政府采取了哪些适当的行动来缓解衰退？
练习
如果总支出大于潜在GDP，政府应该做些什么来缓解通货膨胀压力？
练习
两个国家正处于衰退之中。 国家 A 的 MPC 为 0.8，国家 B 的 MPC 为 0.6。 哪个国家的政府支出将产生最大的影响？
练习
比较一下两项政策：收入减税或增加政府在道路和桥梁上的支出。 这些政策对经济的短期和长期影响是什么？
练习
政府在稳定经济方面发挥了什么作用？必须考虑哪些权衡？
练习
如果出现1000亿美元的衰退缺口，政府是否应该增加1000亿美元的支出来缩小缺口？ 为什么？ 为什么不呢？
