24.5:黑洞
- Page ID
- 203176
学习目标
在本节结束时,您将能够:
- 解释黑洞周围的事件视野
- 讨论为什么流行的将黑洞视为可以在离黑洞很远的地方摄取物质的伟大吸怪物的观念是错误的
- 使用黑洞附近时空扭曲的概念来追踪任何可能掉入黑洞的物体会发生什么
- 认识为什么奇点的概念(具有无限密度和零体积)对我们对物质的理解构成了重大挑战
现在,让我们把我们学到的关于重力和时空曲率的知识应用于我们刚开始讨论的问题:一颗非常大的恒星中的崩溃核心。 我们看到,如果核心的质量大于大约 3\(M_{\text{Sun}}\),理论上说没有什么能阻止核心永远崩溃。 我们将从两个角度研究这种情况:首先从爱因斯坦之前的角度来看,然后借助广义相对论。
经典崩溃
让我们从思想实验开始。 我们想知道逃离不同物体的引力需要多大的速度。 火箭要想逃避地球引力的牵引,就必须以非常高的速度从地球表面发射。 实际上,任何以低于每秒 11 千米的速度投掷到空中的物体,无论是火箭、球、天文学书,都将很快回落到地球表面。 只有那些以大于该逃生速度发射的物体才能逃离地球。
但太阳表面的逃逸速度更高——每秒 618 千米。 现在想象一下,我们开始压缩太阳,迫使太阳直径缩小。 回想一下,重力的拉力既取决于拉动你的质量,也取决于你与该质量重心的距离。 如果太阳被压缩,其质量将保持不变,但是太阳表面上的某个点与中心之间的距离将越来越小。 因此,当我们压缩恒星时,物体在收缩表面上的重力会越来越强(图\(\PageIndex{1}\))。
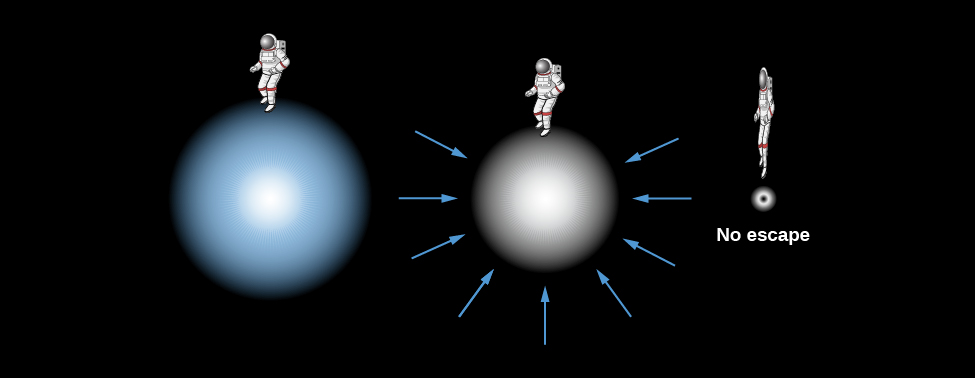
当收缩的太阳达到中子星的直径(大约 20 千米)时,逃避其引力所需的速度约为光速的一半。 假设我们继续将太阳压缩到越来越小的直径。 (我们看到,在现实世界中,像我们的太阳这样的恒星不可能发生这种情况,因为电子退化,即紧密包装的电子之间的相互排斥;这只是一个快速的 “思想实验”,以了解我们的方向)。
最终,随着太阳的收缩,地表附近的逃逸速度将超过光速。 如果你需要逃脱的速度比宇宙中最快的速度快,那么任何东西,甚至光都无法逃脱。 逃生速度如此之大的物体不会发光,任何落入其中的物体都永远无法返回。
在现代术语中,我们将光线无法逃脱的物体称为黑洞,这个名字由美国科学家约翰·惠勒从20世纪60年代末开始普及(图\(\PageIndex{2}\))。 但是,这种物体可能存在的想法并不是一个新想法。 剑桥大学教授兼业余天文学家约翰·米歇尔(John Michell)在1783年写了一篇论文,论述了逃逸速度超过光速的恒星存在的可能性。 1796年,法国数学家皮埃尔-西蒙拉普拉斯侯爵用牛顿的引力理论做了类似的计算;他称由此产生的物体为 “暗体”。

尽管这些早期的计算提供了有力的暗示,即如果非常大的物体在自身重力下崩溃,应该会发生一些奇怪的事情,但我们确实需要广义相对论来充分描述在这种情况下会发生什么。
用相对论崩溃
广义相对论告诉我们,重力实际上是时空的曲率。 随着重力的增加(比如我们的思想实验中正在崩溃的太阳),曲率越来越大。 最终,如果太阳能够缩小到大约 6 千米的直径,那么只有垂直于地表发出的光束才能逃脱。 所有其他人都会掉到星星上(图\(\PageIndex{3}\))。 如果太阳能再缩小一点,那么即使剩下的一束光束也无法逃脱。

请记住,重力不会拉动光线。 物质的集中是弯曲的时空,而光(就像我们前面例子中训练有素的蚂蚁一样)正在 “尽最大努力” 沿直线移动,但现在面临着一个世界,过去向外移动的直线变成了通向的弯曲路径。 在这个视图中,倒塌的星是一个黑洞,因为 “退出” 的概念本身没有几何意义。 这颗恒星被困在自己的时空小口袋里,无法逃脱。
正是在我们之前的照片中,逃逸速度等于光速的那一刻,恒星的几何形状切断了与宇宙其他部分的通信。 此时恒星的大小决定了我们称之为事件视野的表面。 这是一个奇妙的描述性名称:就像在地球上看不到沉入我们地平线以下的物体一样,事件视野内发生的任何事物都无法再与宇宙的其余部分相互作用。
想象一下,未来的航天器愚蠢到足以降落在一颗巨星的表面,就像它开始像我们描述的那样崩溃一样。 也许船长在重力计前睡着了,在机组人员说出 “阿尔伯特·爱因斯坦” 之前,他们已经倒塌了,恒星进入了事件视野。 疯狂的是,他们直接向外派出了一个逃生舱。 但是向外的路径会扭曲变成向内的路径,然后吊舱转身向黑洞的中心掉落。 他们向亲人发送电台消息,向他们道别。 但是无线电波,就像光一样,必须穿越时空,而弯曲的时空不允许任何东西流出。 他们的最后信息仍未被听见。 事件视野内的事件永远不会再影响事件视野之外的事件。
天文学家和数学家卡尔·施瓦茨柴尔德(Karl Schwarzschild)首先确定了事件视野的特征(图\(\PageIndex{4}\))。 作为第一次世界大战期间的德国军队成员,他在1916年死于在俄罗斯战线进行炮弹计算时感染的疾病。 他关于事件视野理论的论文是他临终时完成的最后一件事之一;这是爱因斯坦广义相对论方程的第一个精确解。 在他的记忆中,事件视野的半径被称为施瓦茨柴尔德半径。

事件视野是黑洞的边界;计算表明,一旦整颗恒星在黑洞内部塌陷,事件视野不会变小。 它是将困在其中的事物与宇宙其他部分分开的区域。 任何来自外部的东西一旦进入事件视野,也会被困住。 事实证明,地平线的大小仅取决于其内部的质量。 如果质量为1的太阳变成黑洞(幸运的是它不能\(M_{\text{Sun}}\),这只是一个思想实验),施瓦茨柴尔德半径将约为3千米;因此,整个黑洞的大小约为相同质量的中子星的三分之一。 给黑洞喂一些质量,地平线就会扩大,但不是很多。 质量翻倍将使黑洞半径为6千米,在宇宙尺度上仍然很小。
更大的黑洞的事件视野具有更大的半径。 例如,如果一个由100,000颗恒星(太阳质量)组成的球状星团能够崩溃成黑洞,则其半径将为300,000千米,略小于太阳半径的一半。 如果整个银河系能够崩溃成黑洞,那么它的半径将只有大约\(10^{12}\)千米,大约是光年的十分之一。 相应地,较小的群体的视野也相对较小:要使地球变成黑洞,就必须将其压缩到半径仅为1厘米——小于葡萄的大小。 典型的小行星如果被压碎到足够小的大小以至于成为黑洞,其尺寸将相当于原子核。
示例\(\PageIndex{1}\):银河系的黑洞
黑洞事件视野的大小取决于黑洞的质量。 质量越大,事件视野的半径越大。 广义相对论的计算表明,事件视野的 Schwarzschild 半径 (\(R_S\)) 的公式为
\[R_S=\dfrac{2GM}{c^2} \label{RS}\]
其中\(c\)是光速,\(G\)是引力常数,M 是黑洞的质量。 请注意,在此公式中,2\(G\)、和\(c\)都是恒定的;只有质量从黑洞变为黑洞。
正如我们将在银河系章节中看到的那样,天文学家追踪了银河系中心附近几颗恒星的路径,发现它们似乎正在绕一个看不见的物体运行,这个物体被称为 Sgr A*(发音为 “射手座 A 星”),其质量约为 400 万个太阳质量。 它的 Schwarzschild 半径是多少?
解决方案
我们可以将\(G\)\(M\)、和\(c\)(来自附录 E)的数据直接替换到方程式\ ref {RS} 中:
\[\begin{aligned} R_S & =\dfrac{2GM}{c^2}=\dfrac{2 \left( 6.67 \times 10^{−11} \text{ N} \cdot ·\text{ m}^2/\text{kg}^2 \right) \left( 4 \times 10^6\right) \left( 1.99 \times 10^{30} \text{ kg} \right)}{ \left( 3.00 \times 10^8 \text{ m}/\text{s} \right)^2} \\ = 1.18×10^{10} \text{ m} \end{aligned} \nonumber\]
这个距离大约是水星绕太阳轨道半径的五分之一,但该天体包含400万个太阳质量,用我们最大的望远镜看不见。 你可以明白为什么天文学家确信这个天体是一个黑洞。
练习\(\PageIndex{1}\)
如果黑洞的重量仅与普通皮卡车一样大(大约 3000 千克),那么黑洞的大小会是多少? (请注意,质量如此之小的东西实际上不可能形成黑洞,但考虑一下结果很有趣。)
- 回答
-
将数据代入我们的方程式可以得到
\[ \begin{aligned} R_S=\dfrac{2GM}{c^2}=\dfrac{2 \left( 6.67 \times 10^{−11} \text{ N} \cdot \text{ m}^2/\text{kg}^2 \right) \left( 3000 \text{ kg} \right)}{ \left( 3.00 \times 10^8 \text{ m}/\text{s} \right)^2}=1.33 \times 10^{−23} \text{ m.} \end{aligned} \nonumber\]
相比之下,通常认为质子的大小约\(8 \times 10^{−16} \text{ m}\)为一千万倍。
黑洞神话
许多关于黑洞的现代民间传说都具有误导性。 你可能听说过的一个想法是,黑洞会用它们的重力吸收东西。 实际上,我们一直在讨论的奇怪效果才开始发挥作用,离黑洞很近。 远离黑洞的引力吸引力与为形成黑洞而崩溃的恒星的引力吸引力相同。
请记住,一段距离之外的任何恒星的重力都好像它的所有质量都集中在中心的某个点,我们称之为重心。 对于真正的恒星,我们只是想象所有质量都集中在那里;对于黑洞来说,所有的质量实际上都集中在中心的某个点。
因此,如果你是一颗恒星或遥远的行星,绕着一颗变成黑洞的恒星运行,那么你的轨道可能不会受到恒星崩溃的重大影响(尽管它可能会受到崩溃之前的任何质量损失的影响)。 另一方面,如果你冒险接近事件视野,那么你很难抗拒黑洞附近扭曲的时空的 “拉力”。 你必须非常靠近黑洞才能体验到任何显著的效果。
如果另一颗恒星或太空飞船从黑洞穿过一两个太阳半径,牛顿定律足以描述它会发生什么。 只有在黑洞的事件视野附近,引力才如此强烈,以至于牛顿定律崩溃了。 对我们来说,一颗巨星进入我们附近的黑洞残余物比它早些时候化身为一颗灿烂的炙手可热的恒星要安全得多。
重力和时间机器
时间机器是科幻小说中最受欢迎的设备之一。 这样的设备可以让你以与其他人不同的速度或不同的方向穿越时空。 广义相对论表明,从理论上讲,利用重力建造一台可以带你走向未来的时光机器是可能的。
让我们想象一下重力非常强的地方,比如在黑洞附近。 广义相对论预测,重力越强,时间步伐越慢(如遥远的观察者所见)。 所以,想象一下未来的宇航员,他拥有一艘快速而坚固的太空飞船,自愿前往如此高重力的环境执行任务。 这位宇航员在22岁大学毕业后于2222年离开。 比方说,她花了整整10年的时间才能进入黑洞。 到达那里后,她会与它运行一段距离,注意不要被拉进去。
她现在处在一个高重力领域,时间流逝的速度比在地球上慢得多。 这不只是对她的时钟机制的影响,时间本身运行得很慢。 这意味着,与地球上时间流逝相比,她测量时间的所有方法都会给出同样的减慢读数。 她的心跳会更慢,头发长得更慢,她的古董手表会更慢地滴答作响,依此类推。 她没有意识到这种减速,因为她所有的时间读数,无论是通过自己的身体机能还是用机械设备得出,都在测量相同的时间——更慢——的时间。 同时,回到地球,时间一如既往地流逝。
我们的宇航员现在从黑洞区域出来,她的探索任务完成,然后返回地球。 在离开之前,她仔细地注意到(根据她的钟表)她在黑洞里呆了大约两个星期。 然后,她需要整整10年的时间才能返回地球。 她的计算告诉她,自从她离开地球时22岁起,她返回地球后将达到42周以上。 因此,她认为,地球上的年份应该是2242年,她的同学们现在应该正在接近中年危机。
但是我们的宇航员在她的天文课上应该多加关注! 因为黑洞附近的时间变慢了,所以她过去的时间比地球上的人要少得多。 虽然她的时钟在黑洞附近停留了2周,但地球上很可能已经过去了2000多周(取决于她离得多近)。 这相当于40年,这意味着当她(只有42岁)回来时,她的同学将在80多岁时成为老年人。 在地球上,不是2242,而是2282,她会说她将来已经到了。
这种情况是真的吗? 好吧,它有一些实际的挑战:我们认为任何黑洞都不够近,十年后我们无法到达,而且我们认为任何太空飞船或人类都无法在黑洞附近生存。 但是时间放缓的关键点是爱因斯坦广义相对论的自然结果,我们看到它的预测已经被一个又一个的实验所证实。
科学理解方面的这种发展也成为科幻小说作家的灵感来源。 最近,电影《星际穿越》的特色是主角在一个巨大的黑洞附近旅行;由此导致的他相对于地球家庭的衰老延迟是剧情的关键部分。
科幻小说,例如弗雷德里克·波尔的《盖特威》和拉里·尼文的《时光倒流的世界》,也利用黑洞附近时间的放缓作为故事的主要转折点。 有关基于优秀天文学的科幻故事清单,你可以访问 www.astrosociety.org/scifi。
黑洞之旅
科学家看不见黑洞内部的事实并没有阻止他们尝试计算黑洞的样子。 这些计算显示的第一件事是,黑洞的形成几乎抹去了关于崩溃形成它的恒星的所有信息。 物理学家喜欢说 “黑洞没有头发”,这意味着黑洞中没有任何东西可以向我们提供线索,说明是什么恒星产生了黑洞或者里面掉了什么物质。 黑洞能揭示的关于自身的唯一信息是其质量、自旋(旋转)以及它是否有电荷。
造成黑洞的崩溃星芯会怎样? 我们的最佳计算预测,材料将在自身重量下继续崩溃,形成一个无限的挤压点,一个体积为零、密度无限的地方,我们将其命名为奇点。 在奇异之处,时空不复存在。 我们所知道的物理定律崩溃了。 我们还没有物理理解或数学工具来描述奇点本身,甚至还没有奇点确实发生的情况。 但是,从外部看,基本黑洞(不旋转的黑洞)的整个结构可以描述为被事件视野包围的奇点。 与人类相比,黑洞实际上是非常简单的物体。
科学家们还计算了如果宇航员掉入黑洞会发生什么。 让我们占据一个距离事件视野很长而安全的距离的观测位置,看着这位宇航员向它坠落。 起初他从我们身边掉下来,移动得越来越快,就像他在接近任何一颗巨星一样。 但是,当他接近黑洞的事件视野时,情况发生了变化。 从我们的外部角度看,黑洞周围的强大引力场将使他的时钟运行得更慢。
如果当他接近事件视野时,他根据自己的时钟每秒发出一次信号,我们将看到他的信号之间的间隔越来越长,直到他到达事件视野时间隔变得无限长。 (回想一下我们对引力红移的讨论,我们可以说,如果坠落的宇航员每秒使用蓝光发送信号,我们将看到光线变得越来越红,直到其波长几乎是无限的。) 随着时钟刻度之间的间距接近无穷大,在我们看来,宇航员正在慢慢停下来,在事件视野中被时间冻结。
同样,在外部观察者看来,所有落入黑洞的物质也会停在事件视野上,冻结在原地,需要无限的时间才能从黑洞中掉下来。 但是不要以为落入黑洞的物质在事件视野中很容易看见。 巨大的红移将使人们很难观察到来自黑洞 “冰冻” 受害者的任何辐射。
但是,这只是我们在远离黑洞的地方看待事物的方式。 对宇航员来说,他的时间以正常速度发展,然后他直接穿过事件视野进入黑洞。 (请记住,这个地平线不是物理屏障,而只是太空中一个时空曲率使逃生无法逃脱的区域。)
你可能对你(从远处观看)和宇航员(掉进去)对所发生的事情有如此不同的看法感到困惑。 这就是爱因斯坦关于时空的观念被称为相对论的原因。 每个观察者对世界的衡量取决于(相对于)他或她的参考框架。 处于强重力状态的观察者测量时间和空间的方式与坐在较弱重力状态下的观察者不同。 当爱因斯坦提出这些想法时,许多科学家也难以理解对同一个事件的两种截然不同的看法可能是正确的,每种观点都在自己的 “世界” 中,他们试图在计算中找出一个错误。 没有错误:我们和宇航员看待他掉入黑洞的情况确实截然不同。
对于宇航员来说,没有回头路可走。 一旦进入事件视野,宇航员及其无线电发射机发出的任何信号将永远隐藏在外面的宇宙之外。 但是,当他接近黑洞时,他不会有很长时间(从他的角度来看)为自己感到难过。 假设他先掉了脚。 奇点对他脚施加的重力大于对他头部的重力,因此他会被稍微拉伸。 因为奇点是一个点,所以他身体的左侧会稍微向右拉,右侧稍微向左拉,使两侧都更接近奇点。 因此,宇航员将在一个方向上受到轻微挤压,然后向另一个方向伸展。 一些科学家喜欢将这种拉伸和缩小意大利面条的过程称为意大利面条化。 宇航员在什么时候变得如此紧张以至于死亡,取决于黑洞的大小。 对于质量是太阳质量数十亿倍的黑洞,例如在星系中心发现的黑洞,只有在宇航员穿过事件视野之后,意大利面条化才会显现出来。 对于质量只有几个太阳质量的黑洞,宇航员甚至在到达事件视野之前就会被拉伸和撕裂。
地球对进行太空行走的宇航员施加类似的潮汐力。 就地球而言,潮汐力量非常小,以至于它们不会对宇航员的健康和安全构成威胁。 在黑洞的情况下并非如此。 迟早,当宇航员接近黑洞时,潮汐力量会变得如此之大,以至于宇航员将被撕裂,最终沦为单个原子的集合,这些原子将继续不可阻挡地落入奇点。
从之前的讨论中,你可能会同意,跳入黑洞绝对是千载难逢的经历! 你可以看到尼尔·德格拉斯·泰森(Neil DeGrasse Tyson)对黑洞死亡的引人入胜的解释,他在其中解释了潮汐力量在人体被意大利面条化死亡之前对人体的影响。
在这段探索频道视频摘录中也可以看到类似的解释。
关键概念和摘要
理论表明,恒星核心在耗尽核燃料时质量超过太阳质量三倍的恒星将崩溃变成黑洞。 黑洞周围的表面(逃生速度等于光速)被称为事件视野,表面的半径称为施瓦茨柴尔德半径。 任何东西,甚至光线,都无法从黑洞中逃出事件视野。 在其中心,每个黑洞都被认为具有奇点,一个密度无限且体积为零的点。 从外部观察者看来,落入黑洞的物质似乎会在事件视野处冻结在原位。 但是,如果我们驾驭正在流入的物质,我们就会穿过事件视野。 当我们接近奇点时,甚至在我们达到奇点之前,潮汐力量就会使我们的身体分崩离析。
词汇表
- 黑洞
- 时空中的一个区域,重力如此强以至于任何东西,甚至光都无法逃脱
- 事件视野
- 时空中的边界,这样边界内部的事件就不会对其外部世界产生影响,也就是说,黑洞周围区域的边界,时空曲率不再提供任何出路
- 唯一
- 根据广义相对论,任何变成黑洞的物体都必须折叠到零体积和无限密度点


