19.2: 调查星星
- Page ID
- 202482
学习目标
在本节结束时,您将能够:
- 理解对距离遥远物体(包括恒星)的距离进行三角测量的概念
- 解释为什么天基卫星比地面方法提供更精确的距离
- 讨论天文学家为研究离太阳最近的恒星所做的努力
这是从行星到恒星迈出的巨大一步。 例如,我们的 Voyager 1 号探测器于 1977 年发射,现在距离地球的距离比任何其他航天器都要远。 正如 2016 年所写的那样,Voyager 1 距离太阳 134 AU。 1 但是,最近的恒星是距离地球数十万澳元。 即便如此,原则上我们可以使用与土木工程师测量到人迹罕至的山脉或树木的距离时使用的相同技术(三角测量方法)来测量与恒星的距离。
太空中的三角测量
三角测量的一个实际例子是你自己的深度感知。 正如你每天早晨照镜子时高兴地发现的那样,你的两只眼睛相距一定距离。 因此,你可以从两个不同的角度看待世界,正是这种双视角让你大致了解物体有多远。
要明白我们的意思,拿起一支笔,把它放在脸前几英寸处。 先用一只眼睛(闭上另一只眼睛)看着它,然后切换眼睛。 注意笔似乎是如何相对于房间里的物体移动的。 现在握住笔与笔保持一定距离:移位少了。 如果你玩移动笔一会儿,你会注意到你握得越远,它似乎移动得越少。 你的大脑会自动进行这样的比较,让你很好地了解附近的事物有多远。
如果你的手臂是用橡胶制成的,你可以将笔伸到离眼睛足够远的地方,这样移位就会变得难以察觉。 这是因为我们对几十米以上的物体的深度感知会失败。 为了看到物体在离你一个城市街区或更远的地方移动,你的眼睛需要分开得更远。
让我们看看测量师如何利用同样的想法。 假设你正在尝试测量一棵树穿过深河的距离(图\(\PageIndex{1}\))。 你设置了两个相隔一定距离的观测站。 该距离(图 AB 行\(\PageIndex{1}\))称为基线。 现在,可以从每个站点观察到相对于基线的树的方向(图中的 C)。 请注意,C 与两个站的出现方向不同。 由于观察者有利位置的变化而导致的远程物体方向的这种明显变化被称为视差。
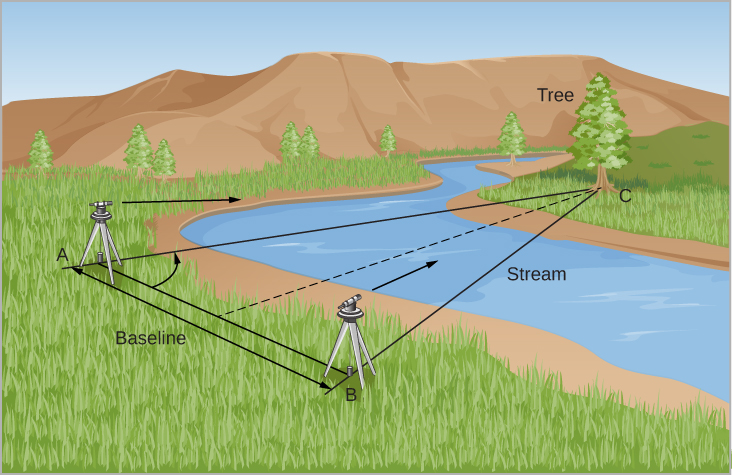
视差也是直线 AC 和 BC 构成的角度 —— 用数学术语来说,是基线所对应的角度。 了解 A 和 B 处的角度以及基线 AB 的长度,可以求解三角形 ABC 的任何维度,比如距离 AC 或 BC。 解决方案可以通过构造比例图或使用三角函数进行数值计算来实现。 如果树离得更远,整个三角形会更长更薄,视差角度会更小。 因此,我们有一个一般规则,即视差越小,我们测量的物体必须越远。
实际上,当我们尝试测量太空距离时,测量师用来测量地球距离的那种基线是完全没有用的。 天文物体离得越远,基线必须越长才能给我们合理的测量机会。 不幸的是,几乎所有的天体都很远。 要测量它们的距离,需要非常大的基线和高度精确的角度测量。 月球是唯一一个足够近的物体,通过在没有望远镜的情况下进行测量就能相当准确地找到其距离。 托勒密正确地确定了到月球的距离,在百分之几以内。 他使用转弯的地球本身作为基线,测量夜晚两个不同时间月球相对于恒星的位置。
在望远镜的帮助下,后来的天文学家得以使用地球的直径作为基线,测量到更近的行星和小行星的距离。 非盟最初就是这样建立的。 但是,要找到恒星,需要更长的基线进行三角测量和极其灵敏的测量。 这样的基线是由地球每年环绕太阳的旅行提供的。
到星星的距离
当地球从轨道的一侧移动到另一侧时,它慷慨地为我们提供了2 AU(约合3亿千米)的基线。 尽管这比地球的直径要大得多的基线,但恒星距离太远,以至于肉眼仍然看不见由此产生的视差偏移——即使是最近的恒星也是如此。
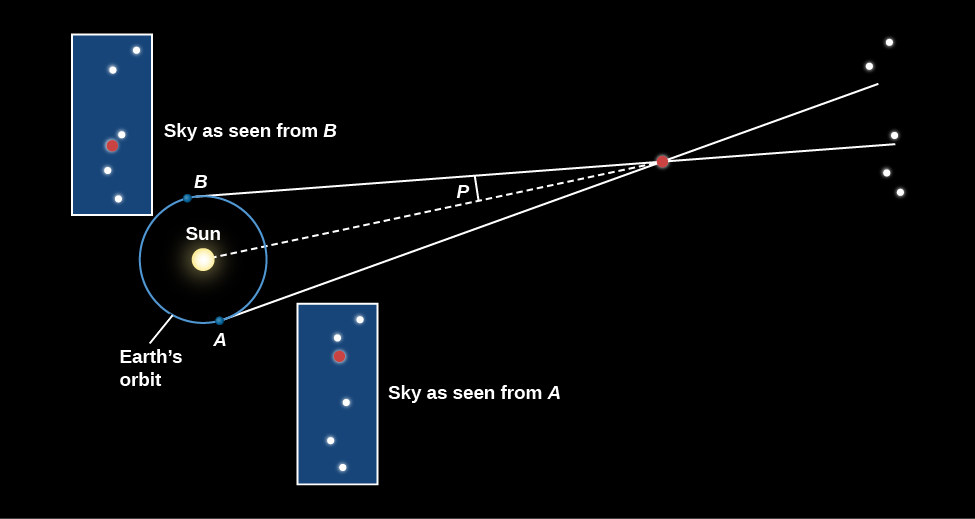
在 “观测天空:天文学的诞生” 一章中,我们讨论了这种困境如何使古希腊人感到困惑,其中一些人实际上暗示太阳可能是太阳系的中心,而地球在太阳系周围运动。 但是,亚里士多德和其他人认为,地球不可能绕太阳旋转。 他们说,如果是这样,当我们从地球轨道的不同部分观察天空时,我们一定会在更远的物体的背景下观察较近恒星的视差(图\(\PageIndex{3}\))。 第谷·布拉赫(1546—1601 年)在将近2000年后提出了同样的错误论点,当时他用肉眼仔细测量了恒星位置,发现没有这样的变化。
这些早期的观察者没有意识到恒星到底有多远,因此它们的位置变化有多小,即使以整个地球轨道为基线。 问题在于他们没有工具来测量视差偏移太小,人眼看不见。 到了十八世纪,当人们对地球的革命不再存在严重怀疑时,很明显,恒星一定非常遥远。 配备望远镜的天文学家开始设计出能够测量附近恒星相对于更远(因此不移动)天体背景的微小偏移的仪器。
这是一个重大的技术挑战,因为即使是最近的恒星,视差角度通常也只有弧线的几分之一秒。 回想一下,一秒的弧度(弧秒)是一个只有 1/3600 度的角度。 如果你从大约 5 千米(3 英里)的距离观看,像美国四分之一大小的硬币的直径似乎为 1 弧秒。 想想这个角度有多小。 难怪天文学家花了很长时间才测量出如此微小的变化。
首次成功探测到恒星视差是在 1838 年,当时德国的弗里德里希·贝塞尔(图\(\PageIndex{2}\))、在好望角工作的苏格兰天文学家托马斯·亨德森和俄罗斯的弗里德里希·斯特鲁夫独立测量了 61 Cygni、Alpha Centauri 恒星的视差分别是 Vega。 即使是最近的恒星半人马座阿尔法在一年中的总位移量也仅为1.5弧秒左右。

\(\PageIndex{3}\)该图显示了此类测量的工作原理。 从地球轨道的两侧看,与更远的恒星模式相比,附近的恒星会改变位置。 天文学家实际上将视差定义为从地球轨道的两侧观察恒星时所移动角度的一半(图中标有 P 的角度\(\PageIndex{3}\))。 这个定义的原因只是他们更喜欢处理 1 AU 而不是 2 AU 的基线。
恒星距离单位
如果基线为一个 AU,那么一颗恒星必须有多远才能有 1 弧秒的视差? 答案原来是206,265澳元,或3.26光年。 这等于 3.1 × 10 13 千米(换句话说,31 万亿千米)。 我们给这个单位起一个特殊的名字,parsec (pc),源自 “我们有一秒钟的标准差距距离”。 恒星的距离 (\(D\)) 以秒差距为单位只是其视差 (p) 的倒数(以弧秒为单位);也就是说,
\[D=\frac{1}{p} \nonumber\]
因此,视差为0.1弧秒的恒星将在10秒差距处找到,而视差为0.05弧秒的恒星将在20秒差距之外找到。
在我们的大部分距离来自视差测量的时代,差距是一个有用的距离单位,但它不像光年那样直观。 光年作为一个单位的一个优势是,它强调了这样一个事实,即当我们望向太空时,我们也在回顾时空。 我们从100光年以外的恒星上看到的光在100年前离开了那颗恒星。 我们研究的不是现在的恒星,而是过去的恒星。 今天从遥远的星系到达我们望远镜的光在地球存在之前就离开了它们。
在本文中,我们将使用光年作为距离单位,但是许多天文学家在撰写技术论文或在会议上互相交谈时仍然使用差距。 要在两个距离单位之间进行转换,请记住:1 parsec = 3.26 光年,1 光年 = 0.31 parsec。
示例\(\PageIndex{1}\):光年有多远?
光年是指光在 1 年内传播的距离。 鉴于光以 300,000 km/s 的速度传播,那么一光年中有多少千米?
解决方案
我们之前了解到速度 = 距离/时间。 我们可以重新排列这个方程式,这样\(\text{distance } = \text{ velocity } \times \text{ time }\)。 现在,我们需要确定一年中的秒数。
1 年中大约有 365 天。 要确定秒数,我们必须估计 1 天内的秒数。
我们可以按如下方式更改单位(注意时间单位是如何抵消的):
\[ 1 \text{ day } \times 24 \text{ hr/day } \times 60 \text{ min/hr } \times 60 \text{ s/min } = 86,400 \text{ s/day} \nonumber\]
接下来,要获得每年的秒数:
\[ 365 \text{ days/year } \times 86,400 \text{ s/day } = 31,536,000 \text{ s/year} \nonumber\]
现在,我们可以将光速乘以每年的秒数,得出光在 1 年内行驶的距离:
\[ \begin{aligned} \text{distance } & = \text{ velocity } \times \text{ time} \\ & = 300,000 \text{ km/s } \times 31,536,000 \text{ s} \\ & =9.46 \times 10^{12} \text{ km} \end{aligned} \nonumber\]
这相当于灯光在一年内覆盖了将近一万亿千米。 为了帮助你想象这个距离有多长,我们要提一下 1 光年长的绳子可以绕地球周长 2.36 亿次。
练习\(\PageIndex{1}\)
上面的数字真的很大。 如果我们用可能更容易理解的术语来表达,比如地球的直径,会发生什么? 地球的直径约为 12,700 千米。
- 回答
-
\[ \begin{aligned} 1 \text{ light-year } & = 9.46 \times 10^{12} \text{ km} \\ & =9.46 \times 10^{12} \text{ km } \times \frac{1 \text{ Earth diameter}}{12,700 \text{ km}} \\ & =7.45 \times 10^8 \text{ Earth diameters} \end{aligned} \nonumber\]
这意味着一光年大约是地球直径的7.45亿倍。
命名星星
你可能想知道为什么星星有这么混乱的名字。 看看测量视差的前三颗恒星:61 Cygni、Alpha Centauri 和 Vega。 这些名字中的每一个都来自不同的指定星星的传统。
最亮的恒星有源自古代的名字。 有些来自希腊语,例如小天狼星,意思是 “烧焦的那个”,指的是它的光彩。 一些来自拉丁语,但许多最著名的名字来自阿拉伯语,因为正如《观测天空:天文学的诞生》中所讨论的那样,黑暗时代之后,希腊和罗马的大部分天文学都是通过阿拉伯语翻译在欧洲 “重新发现” 的。 例如,Vega 的意思是 “猛扑之鹰”,而 Betelgeuse(发音为 “Beetle-Juice”)的意思是 “中间人的右手”。
1603 年,德国天文学家约翰·拜耳(1572-1625 年)引入了一种更系统的恒星命名方法。 对于每个星座,他给最亮的恒星分配了一个希腊字母,大致按亮度顺序排列。 例如,在猎户座星座中,Betelgeuse 是最亮的恒星,因此它有希腊字母中的第一个字母 alpha,被称为 Alpha Orionis。 (“猎户座” 是猎户座的所有格形式,所以 Alpha Orionis 的意思是 “猎户座的第一个”。) 一颗名为锐佳的恒星是该星座中第二亮的恒星,被称为 Beta Orionis(图\(\PageIndex{4}\))。 由于希腊字母表中有24个字母,因此该系统允许在每个星座中标记24颗恒星,但是星座的恒星比这个要多得多。
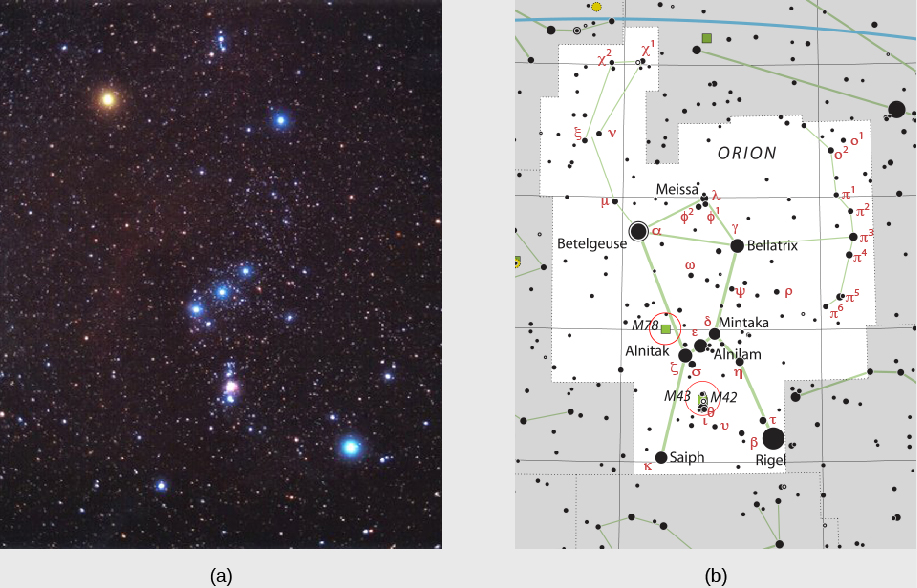
1725年,英国天文学家皇家约翰·弗拉姆斯蒂德(John Flamsteed)引入了另一个系统,在该系统中,较亮的恒星最终在每个星座中按其在天空中的位置或更确切地说是它们的右升顺序得到一个数字。 (地球、月球和天空中讨论了包括右升在内的天空坐标系。) 在这个系统中,Betelgeuse 被称为 58 Orionis,61 Cygni 是天鹅座天鹅星座中的第 61 颗恒星。
情况变得更糟了。 随着天文学家开始越来越了解恒星,他们起草了一系列专门的恒星目录,这些目录的爱好者开始用他们的目录号来称呼恒星。 如果你看一下附录一 —— 我们列出的最近的恒星清单(其中许多恒星太微弱了,无法获得古老的名字、拜耳字母或 Flamsteed 数字),你会看到其中一些目录的引用。 例如,一组标有 BD 编号的星星,代表 “Bonner Durchmusterung”。 这是 19 世纪 50 年代和 19 世纪 60 年代在波恩天文台整理的一系列天空区域中超过 32.4 万颗恒星的庞大目录。 请记住,这个目录是在摄影或计算机投入使用之前制作的,因此每颗恒星的位置必须用眼睛测量(至少两次),这是一项艰巨的任务。
还有一种完全不同的系统用于跟踪亮度不同的恒星,另一种系统用于在不可预测的时刻爆炸性变亮的恒星。 天文学家已经习惯了许多不同的恒星命名系统,但是学生们常常发现它们令人困惑,希望天文学家能够选择一个系统。 不要屏住呼吸:在天文学中,就像在人类思想的许多领域一样,传统具有强大的吸引力。 尽管如此,有了高速计算机数据库来帮助人类记忆,命名可能变得越来越不必要。 当今的天文学家通常根据恒星在天空中的精确位置来称呼恒星,而不是用它们的名字或各种目录号来称呼恒星。
最近的星星
没有一颗已知的恒星(太阳除外)距离地球 1 光年甚至 1 秒以内。 离太阳最近的恒星邻居是半人马座星座中的三颗恒星。 肉眼看来,这三颗恒星中最亮的是半人马座阿尔法,它距离南天极只有30○,因此在美国大陆看不见。 Alpha Centauri 本身就是一颗双星 —— 两颗相互革命的恒星 —— 距离太近,没有望远镜就无法区分。 这两颗恒星距离我们 4.4 光年。 附近还有第三颗微弱的恒星,叫做 Proxima Centauri。 Proxima 的距离为 4.3 光年,比其他两颗恒星稍微靠近我们。 如果 Proxima Centauri 是具有二进制 Alpha Centauri 的三星系统的一部分,那么它的轨道周期可能超过 500,000 年。
Proxima Centauri 是最常见的恒星类型的一个例子,也是我们最常见的恒星邻居类型(正如我们在《星星:天体普查》中看到的那样)。 低质量红矮星约占所有恒星的70%,在距离太阳 10 秒差距以内的恒星普查中占据主导地位。 对太阳邻域的最新调查显示,在10秒差距内有357颗恒星和褐矮星,其中248颗是红矮星。 但是,如果你想用肉眼看见 M 矮人,那你就不走运了。 这些恒星只产生太阳光的一小部分,而且几乎所有恒星都需要望远镜才能被探测。
在美国大部分地区,没有望远镜就能看到的最近的恒星是所有恒星中最亮的恒星小天狼星,它的距离略高于8光年。 它也是一个二进制系统,由一个绕蓝白色主序列恒星运行的微弱白矮星组成。 一个有趣的数字巧合是,光线在大约 8 分钟内从太阳传到我们,大约在 8 年内从天空中下一颗最亮的恒星到达我们。
示例\(\PageIndex{2}\):计算太阳的直径
对于附近的恒星,我们可以测量地球绕太阳运行时它们位置的明显变化。 我们之前写过,一个物体的距离必须是 206,265 AU 才能获得一秒弧的视差。 这个数字看起来一定很奇怪,但你可以弄清楚为什么这是正确的值。 我们将从估计太阳的直径开始,然后对视差为 1 弧秒的恒星应用同样的概念。 绘制一个带有圆圈代表太阳的草图,将地球放置在一定距离的地方,然后在上面放一个观察者。 从观察者站立的位置画两条线,一条到太阳的两侧。 绘制一个以地球为中心的圆圈,其周长穿过太阳的中心。 现在想想比例。 太阳在天空上跨度约半度。 一个完整的圆圈有 360○。 以地球为中心并穿过太阳的圆的周长由以下公式给出:
\[\text{circumference } =2 \pi \times 93,000,000 \text{ miles} \nonumber\]
那么,以下两个比率相等:
\[\frac{0.5^{\circ}}{360^{\circ}} = \frac{\text{diameter of Sun}}{2 \pi \times 93,000,000} \nonumber\]
计算太阳的直径。 你的答案与实际直径相比如何?
解决方案
为了求解太阳的直径,我们可以计算上面的表达式。
\ [\ begin {aligned}\ text {太阳直径} & =\ frac {0.5^ {\ circ}} {360^ {\ circ}}
\ times 2\ pi\ times 93,000,000\ text {miles}\ end {aligned}\ nonumber\]
这与大约 848,000 英里的真实价值非常接近。
练习\(\PageIndex{2}\)
现在应用这个想法来计算与视差为 1 弧秒的恒星的距离。 画一张类似于我们上面建议的图片,然后计算以澳大利亚为单位的距离。 (提示:请记住,视差角度由 1 AU 而不是 2 AU 定义,而 3600 弧秒 = 1 度。)
- 回答
-
206,265 AU
测量太空中的视差
1989年Hipparcos号航天器的发射彻底改变了恒星视差的测量,该航天器测量了数千颗恒星在大约300光年的距离,精度为10%至20%(见下图\(\PageIndex{5}\)和视差和太空天文学的专题报道)。 但是,即使是300光年也不到我们Galaxy主盘大小的1%。
2013年12月,欧洲航天局发射了希帕科斯的继任者盖亚。 盖亚正在测量近十亿颗恒星的位置和距离,精度为几百万分之一弧秒。 盖亚的距离限制将远远超出希帕科斯,研究恒星的距离可达30,000光年(比希帕科斯远100倍,覆盖银河盘的近1/3)。 盖亚还将能够测量银河系光环中成千上万颗恒星的正确运动 2,而目前只有最亮的恒星才能做到这一点。 在盖亚的任务结束时,我们不仅将拥有我们自己的银河系很大一部分的三维地图,而且还将在本章讨论的宇宙距离链中建立牢固的联系。 但是,要将这条链延伸到盖亚无法触及的范围并探索到附近星系的距离,我们需要一些全新的技术。
视差和太空天文学
精确测量视差偏离地球的微小角度最困难的事情之一是,你必须通过我们星球的大气层观察恒星。 正如我们在天文仪器中看到的那样,大气层的作用是将星光点分散成模糊的圆盘,这使得精确测量它们的位置变得更加困难。 天文学家长期以来一直梦想着能够从太空测量视差,现在有两个轨道观测站将这个梦想变为现实。
1989年由欧洲航天局发射的Hipparcos卫星的名称既是高精度视差采集卫星的缩写,也是对希腊先驱天文学家希帕丘斯的致敬,我们在《观测天空:天文学的诞生》中讨论了他的工作。 该卫星旨在从地球上空 36,000 公里处进行历史上最精确的视差测量。 但是,它的机载火箭发动机未能发射,这意味着它没有获得达到所需高度所需的助推力。 Hipparcos 最终在高度从 500 到 36,000 公里不等的椭圆轨道上度过了 4 年的寿命。 在这个轨道上,卫星每隔5个小时左右就会坠入地球的辐射带,这最终对为仪器提供能量的太阳能电池板造成了损失。
尽管如此,这次任务还是成功的,产生了两本目录。 一个给出12万颗星的位置,精度为千分之一弧秒,从欧洲看,大约相当于纽约高尔夫球的直径。 第二个目录包含超过一百万颗恒星的信息,这些恒星的位置已被测量到三万分之一弧秒。 现在,我们可以对距离大约 300 光年的恒星进行精确的视差测量。 (使用地面望远镜,只有大约 60 光年的精确测量才是可行的。)
为了在Hipparcos成功的基础上再接再厉,欧洲航天局于2013年发射了一颗名为 Gaia 的新卫星。 盖亚任务计划持续5年。 由于盖亚携带的望远镜比希帕科斯大,因此它可以观测更微弱的恒星,测量它们的位置的精确度提高200倍。 盖亚任务的主要目标是通过观测每颗10亿颗恒星70次,测量它们的位置以及视差和亮度,在大约30,000光年内绘制出银河系那一部分的精确三维地图。
很长一段时间以来,视差测量和精确的恒星位置一直是天文学研究的死水——主要是因为测量的精度在大约100年内没有太大提高。 但是,从太空进行测量的能力彻底改变了这个天文学领域,并将继续为我们的宇宙距离链提供关键环节。
欧洲航天局(ESA)维护着一个盖亚任务网站,您可以在其中了解有关盖亚任务的更多信息并获取有关盖亚观测的最新消息。
要了解有关 Hipparcos 的更多信息,请浏览欧洲航天局的这个网页,观看欧空局的 vodcast 《银河系图表——从希帕科斯到盖亚》。
摘要
对于相对较近的恒星,我们可以 “三角测量” 与地球每年绕太阳运动所产生的基线的距离。 从地球轨道的两侧看,附近恒星相对于非常遥远的背景恒星的位置偏移的一半被称为该恒星的视差,是衡量其距离的指标。 用于测量恒星距离的单位是光年、光在 1 年内传播的距离和差距(pc),即视差为 1 弧秒(1 parsec = 3.26 光年)的恒星的距离。 最近的恒星是红矮星,距离超过 1 秒差距。 1838 年首次报道了恒星视差的成功测量。 视差测量是宇宙距离链中的基本环节。 Hipparcos 卫星使我们能够精确测量出大约 300 光年的恒星的视差,而盖亚任务将产生高达 30,000 光年的视差。
脚注
1 为了进行比较,矮行星冥王星在距离太阳 40 AU 的平均距离处运行,而矮行星厄里斯目前距离太阳大约 96 AU。
2 正确的运动(如《分析星光》中所述,是恒星在天空中的运动(垂直于我们的视线)。
词汇表
- 视差
- 附近恒星的明显位移,是由地球绕太阳运动造成的
- parsec
- 天文学中的距离单位,等于 3.26 光年;在 1 秒差距时,恒星的视差为 1 弧秒


