5.6: 多普勒效应

Last updated
Save as PDF

Page ID: 202534

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

学习目标

在本节结束时，您将能够：

解释为什么我们从物体观察到的光子的光谱线会因为物体朝向或远离我们的运动而发生变化
描述我们如何使用多普勒效应来推断天文物体如何在太空中移动

最后两节向你介绍了许多新概念，我们希望通过这些概念，你已经看到了一个重要的想法浮出水面。天文学家可以通过解码光谱线中的信息来了解恒星和星系中的元素。但是，学习如何解码星光信息有一个复杂的因素。如果一颗恒星向我们移动或远离我们，它的线条在光谱中的位置将与它们在静止恒星中的位置略有不同。宇宙中的大多数物体确实有相对于太阳的运动。

运动会影响波浪

1842 年，克里斯蒂安·多普勒（Christian Doppler）首次通过聘请一群音乐家在敞篷轨道上行驶的轨道上演奏来测量运动对波浪的影响。然后，他将所学知识应用于包括光在内的所有波浪，并指出，如果光源正在接近或从观察者身上消失，光波将分别更紧密地聚集在一起或散开。一般原理，现在称为多普勒效应，如图所示\(\PageIndex{1}\)。

alt — 图\(\PageIndex{1}\)：多普勒效应。 (a) 源 S 产生波浪，其编号波峰（1、2、3 和 4）冲过静止的观察者。 (b) 现在，源 S 向观察点 A 移动，远离观察者 C。当光源位于 S4 位置时 Wave crest 1 发射，波峰 2 位于位置 S2，依此类推。观察者 A 看到波浪被这个动作压缩，然后看见蓝移（如果波浪很轻）。观察者 C 看见动作伸出的波浪，然后看到红移。观察者 B 的视线垂直于光源的运动，他看不到波浪的变化（而且感觉被排除在外）。

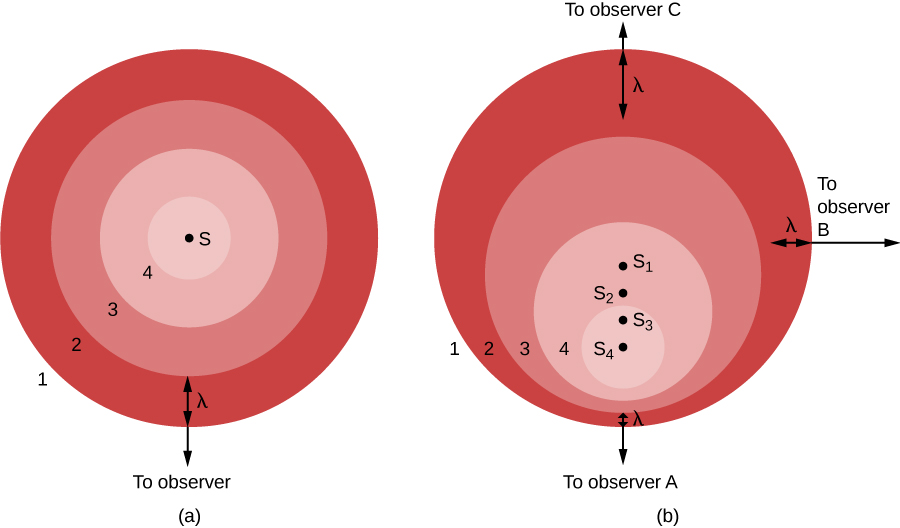
在图中\(\PageIndex{1a}\)，光源 (S) 相对于观察者处于静止状态。源头发出了一系列波浪，我们将其波峰标记为 1、2、3 和 4。光波向各个方向均匀分布，就像池塘里飞溅产生的波纹一样。波峰之间有一段距离 β，其中 β 是波长。观察者恰好位于图像底部的方向，他看到光波漂亮而均匀地传来，相隔一个波长。身处其他任何地方的观察者都会看到同样的东西。

另一方面，如果光源相对于观察者移动，如图所示\(\PageIndex{1b}\)，情况会更加复杂。从一个波峰发出到下一个波峰准备出来之间，源向页面底部移动了一点。从观察者 A 的角度来看，源头的这种运动缩短了波峰之间的距离——这位观察者可能会说，它正在将波峰挤在一起。

在图中\(\PageIndex{1b}\)，我们从三个观察者的角度展示了情况。可以在、、和 4 个位置看到声源\(S_1\)\(S_2\)\(S_3\)\(S_4\)，每个位置对应于一个波峰的发射。对观察者 A 来说，波浪似乎更紧密地相互跟踪，波长减小，频率也随之增加。（请记住，无论如何，所有光波都以光速穿过空旷的空间。这意味着运动不会影响速度，而只会影响波长和频率。随着波长的降低，频率必须增加。如果波浪较短，则每秒钟内将有更多波浪移动。）

对于其他观察者来说，情况并不相同。让我们从观察者 C 的角度来看情况，观察者位于图中观察者 A 的对面\(\PageIndex{1}\)。对她来说，消息来源正在远离她的所在地。因此，波浪不会被挤在一起，而是通过源的运动分散开来。波峰到达时波长增加，频率降低。对于观察者 B 来说，在与光源运动成直角的方向上，没有观察到任何效果。波长和频率与图 (a) 部分中的波长和频率相同。

从这个插图中我们可以看出，多普勒效应只能由朝向或远离观察者的运动产生，这种运动称为径向速度。侧身运动不会产生这样的效果。 A 和 B 之间的观察者会观察到光源沿其视线运动的那一部分的光波有所缩短。 B 和 C 之间的观察者会观察到他们视线上的光波在延长。

你可能听说过声波中的多普勒效应。当火车哨声或警笛接近你然后离开时，你会注意到声波的音高（这是人类感官解释声波频率的方式）有所降低。与静止的波浪相比，它们已经从向你冲来的频率稍高一些，变成了离开你时的频率稍低一些。

在沙滩男孩的专辑《Pet Sounds》中的经典歌曲 “Caroline，No” 的结尾处可以听到火车哨声变化的一个很好的例子。要听这个声音，请转到这首歌的 YouTube 版本。火车的声音大约在 2:20 开始。

颜色变化

当波源向你移动时，波长会稍微减小。如果涉及的波浪是可见光，则光的颜色会略有变化。随着波长的降低，它们会向光谱的蓝端移动：天文学家称之为蓝移（由于光谱的末端实际上是紫罗兰色，因此该术语可能应该是紫色偏移，但蓝色是更常见的颜色）。当光源从你身边移开并且波长变长时，我们将颜色的变化称为红移。由于多普勒效应最初是在天文学中的可见光下使用的，因此 “blueshift” 和 “redshift” 这两个术语已经很成熟。如今，天文学家用这些词来描述无线电波或 X 射线波长的变化，就像他们用它们来描述可见光的变化一样舒服。

朝向或远离我们的运动越大，多普勒偏移就越大。如果相对运动完全沿视线运动，则光的多普勒偏移公式为

\[\dfrac{\Delta λ}{λ}= \frac{v}{c} \nonumber\]

其中\(\lambda\)是光源发射的波长，\(\Delta \lambda\)是\(\lambda\)与观察者测量的波长之差，\(c\)是光速，\(v\)是观察者与光源在视线内的相对速度。如果速度\(v\)是衰退速度，则该变量被视为正值；如果是接近速度，则该变量被视为负值。求解这个速度方程，我们发现

\[ v = c \times \dfrac{\Delta \lambda}{\lambda}. \nonumber\]

如果一颗恒星接近我们或从我们身边消退，则其连续光谱中的光波长会相应缩短或延长，黑线的波长也是如此。但是，除非它的速度为每秒数万千公里，否则恒星看起来不会比平常更蓝或更红。因此，在连续频谱中不容易检测到多普勒偏移，也无法在这样的频谱中精确测量。但是，可以精确测量吸收线的波长，而且它们的多普勒偏移相对容易检测。

示例\(\PageIndex{1}\)：多普勒效应

如果我们知道三件事，我们可以使用多普勒效应方程来计算物体的径向速度：光速、发射光的原始（未移位）波长以及发射光的波长和我们观察到的波长之间的差异。对于特定的吸收线或发射线，我们通常确切地知道这条线在地球上的实验室中有什么波长，那里的光源没有移动。我们可以用望远镜上的仪器测量新的波长，因此我们知道多普勒偏移导致的波长差异。由于光速是一个通用常数，因此我们可以计算出恒星的径向速度。

一条特定的氢气发射线最初是从气云中发射波长为 656.3 nm 的。在我们的望远镜上，我们观察到发射线的波长为656.6 nm。这个气云向或远离地球的速度有多快？

解决方案

因为光线被转移到更长的波长（红移），所以我们知道气云正在远离我们。速度可以使用多普勒移位公式计算：

\[ν=c×\dfrac{\Delta \lambda}{\lambda}= \left(3.0 \times 10^8 ~ \text{m/s} \right) \left( \dfrac{0.3 ~ \text{nm}}{656.3 ~ \text{nm}} \right)= \left(3.0 \times 10^8 ~ \text{m/s} \right) \left(\dfrac{0.3 \times 10^{–9} ~ \text{m}}{656.3 \times 10^{–9} ~ \text{m}} \right)=140,000 ~ \text{m/s} =140 ~ \text{km/s} \nonumber\]

练习\(\PageIndex{1}\)

假设在恒星光谱中观察到的氢光谱线通常在 500 nm 处为 500.1 nm。恒星向或远离地球的速度有多快？

回答

因为光线被转移到更长的波长，所以恒星正在远离我们：

\[ν=c \times \dfrac{\Delta \lambda}{\lambda}= \left(3.0 \times 10^8 ~ \text{m/s} \right) \left(\dfrac{0.1 ~ \text{nm}}{500 ~ \text{nm}} \right)=\left( 3.0 \times 10^8 ~ \text{m/s} \right) \left(\dfrac{0.1 \times 10^{–9} ~ \text{m}}{500 \times 10^{–9} ~ \text{m}} \right)=60,000 ~ \text{m/s}\]

它的速度为 60,000 米/秒。

你现在可能会问：如果所有的恒星都在移动，运动改变了每条光谱线的波长，那么对于试图弄清楚恒星中存在哪些元素的天文学家来说，这不是一场灾难吗？毕竟，正是精确的波长（或颜色）告诉天文学家哪些线属于哪个元素。我们首先在实验室的气体容器中测量这些波长，这些容器不会移动。如果恒星光谱中的每条线现在都因其运动而转移到不同的波长（颜色），那么我们怎样才能确定我们在不知道速度的恒星中看到的是哪些线条和哪些元素？

振作起来。这种情况听起来比实际情况还要糟糕。天文学家很少用一条线来判断天文物体中是否存在元素。正是氢气或钙特有的线条图案使我们能够确定这些元素是我们正在观测的恒星或星系的一部分。多普勒效应不会改变来自给定元素的线条图案，它只会将整个图案稍微偏向更红色或更蓝的波长。转变后的模式仍然很容易识别。最重要的是，当我们识别出熟悉的元素的图案时，我们会得到奖励：图案的移动量可以使我们确定视线中物体的速度。

天文学家的培训包括许多学习解码光（和其他电磁辐射）的工作。熟练的 “解码器” 可以了解恒星的温度、恒星中有哪些元素，甚至是它朝向我们或远离我们的方向的速度。对于距离光年的恒星来说，这确实是令人印象深刻的大量信息。

摘要

如果当电子改变轨道并产生光谱线时，原子正在向我们移动，我们会看到该线在光谱中略微向其正常波长的蓝色移动。如果原子移开，我们就会看到这条线向红色移动。这种偏移被称为多普勒效应，可用于测量远处物体的径向速度。

词汇表

多普勒效应: 来自光源的辐射的波长或频率由于其远离或朝向观察者的相对运动而发生的明显变化

径向速度: 朝向或远离观察者的运动；位于视线内的相对速度分量