5.4: 原子的结构

学习目标

在本节结束时，您将能够：

• 描述原子的结构和原子核的组成部分
• 解释原子内电子的行为，以及电子如何与光相互作用以在能级之间移动

物质由称为原子的微小粒子组成的想法至少有25个世纪的历史了。 但是，直到二十世纪，科学家才发明出仪器，使他们能够在原子内部进行探测，发现原子并不像人们想象的那样艰难和不可分割。 相反，原子是一种复杂的结构，由更小的粒子组成。

探测原子

这些较小的粒子中的第一个是由英国物理学家詹姆斯（J.J.）发现的 1897 年的汤姆森。 这个被命名为电子的粒子是带负电荷的。 （无论是在闪电中还是在通往灯泡的电线中，都是这些颗粒的流动产生电流。） 由于处于正常状态的原子是电中性的，因此原子中的每个电子都必须由相同数量的正电荷来平衡。

下一步是确定正电荷和负电荷在原子中的位置。 1911年，英国物理学家欧内斯特·卢瑟福设计了一项实验，为这个问题提供了部分答案。 他用一束 alpha 粒子轰炸了一块极薄的金箔，厚度只有大约 400 个原子（图\(\PageIndex{1}\)）。 α粒子（α粒子）是氦原子，它们已经失去了电子，因此具有正电荷。 这些粒子中的大多数都穿过金箔，就好像金箔和金箔中的原子几乎是空白的空间一样。 但是，大约 8000 个 alpha 粒子中就有 1 个完全反转了方向并从铝箔向后反弹。 卢瑟福写道：“这是我一生中经历过的最不可思议的事件。 这几乎就像你向一张薄纸发射一枚 15 英寸的炮弹然后它又回来击中你一样不可思议。”

图\(\PageIndex{1}\)卢瑟福的实验。 (a) 当卢瑟福允许来自放射源的α粒子击中金箔目标时，他发现，尽管其中大多数是直接穿过的，但有些反弹回到了它们来自的方向。 (b) 根据这项实验，他得出结论，原子必须像微型太阳系一样构造，正电荷集中在原子核中，负电荷围绕原子核大体积运行。 请注意，这幅图不是按比例绘制的；相对于原子核的大小，电子轨道要大得多。

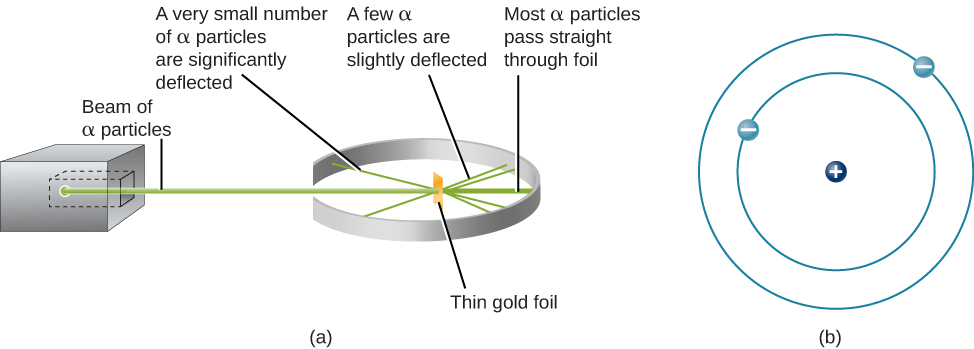
解释撞击金箔时方向反转的粒子的唯一方法是假设几乎所有的质量以及每个金原子中的所有正电荷都集中在一个很小的中心或原子核中。 当带正电荷的 alpha 粒子击中原子核时，它会反转方向，就像母球在击中另一个台球时会反转方向一样。 卢瑟福的模型将另一种类型的电荷——负电子——置于围绕这个原子核的轨道上。

卢瑟福的模型要求电子处于运动状态。 正电荷和负电荷相互吸引，因此静止的电子会落入正核。 此外，由于电子和原子核都非常小，因此大部分原子都是空的，这就是为什么卢瑟福几乎所有的粒子都能够在不与任何东西碰撞的情况下直接穿过金箔的原因。 卢瑟福的模型非常成功地解释了他进行的实验，尽管科学家最终会发现，即使是原子核本身也有结构。

原子核

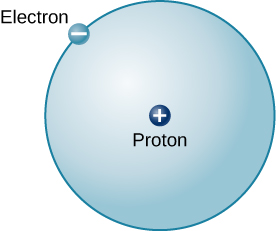
最简单的原子（也是太阳和恒星中最常见的原子）是氢气。 普通氢的原子核含有单个质子。 绕这个质子移动的是单个电子。 电子的质量比质子的质量小近2000倍；电子携带的电荷量与质子的电荷量完全相同，但符号相反（图\(\PageIndex{2}\)）。 相反的电荷相互吸引，因此它是将质子和电子保持在一起的电磁力，就像重力是保持行星绕太阳轨道运行的力一样。

图：\(\PageIndex{2}\)氢原子。 这是氢原子处于最低能量状态（也称为基态）的示意图。 质子和电子具有相等但相反的电荷，它们施加的电磁力将氢原子结合在一起。 在插图中，粒子的大小被夸大了，这样你就可以看见它们；它们不是按比例缩放的。 它们的显示距离也比实际要近得多，因为要显示它们的实际缩放距离需要不止一整页的时间。

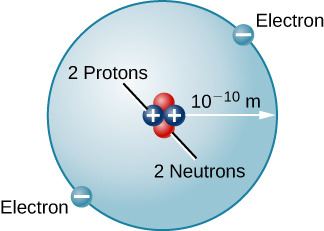
自然界中还有许多其他类型的原子。 例如，氦是太阳中第二丰富的元素。 氦的原子核中有两个质子，而不是表征氢气的单质子。 此外，氦核含有两个中子，这些粒子的质量与质子的质量相当，但没有电荷。 绕着这个原子核移动的是两个电子，所以氦原子的总净电荷也为零（图\(\PageIndex{3}\)）。

图\(\PageIndex{3}\) Helium Atom。 这里我们看到了氦原子处于最低能量状态的示意图。 所有氦原子的原子核中都存在两个质子。 在最常见的氦气品种中，原子核还含有两个中子，它们的质量与质子几乎相同，但不携带电荷。 两个电子绕原子核运行。

从对氢气和氦气的描述中，也许你已经猜到了我们在宇宙中发现的所有元素（不同类型的原子）的构建模式。 元素的类型由原子核中的质子数决定。 例如，任何具有六个质子的原子都是碳元素，八个质子是氧，26是铁，92是铀。 在地球上，典型的原子的电子数量与质子相同，这些电子在原子核周围遵循复杂的轨道模式。 但是，在恒星的深处，天气太热了，电子会从原子核中松开，（正如我们将看到的）过着分开但富有成效的生命。

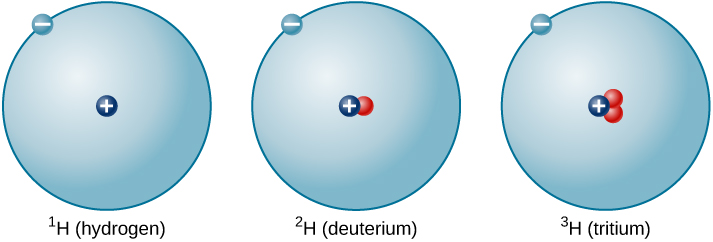
中子与质子的比例随着质子数量的增加而增加，但每个元素都是独一无二的。 给定元素的所有原子的中子数量不一定相同。 例如，大多数氢原子根本不含中子。 但是，有些氢原子包含一个质子和一个中子，而其他氢原子则包含一个质子和两个中子。 具有不同中子数量的各种类型的氢核被称为氢同位素（图\(\PageIndex{4}\)），所有其他元素也有同位素。 你可以将同位素视为同一个元素 “家族” 中的兄弟姐妹——密切相关，但具有不同的特征和行为。

图：氢的\(\PageIndex{4}\)同位素。 原子核中的单个质子将原子定义为氢气，但可能有零、一个或两个中子。 最常见的氢同位素是只有一个质子而没有中子的同位素。

要探索原子的结构，请前往 PhET Build a Atom 网站，在其中你可以向模型中添加质子、中子或电子，你创建的元素的名称就会出现。 你还可以看到净电荷、质量数、它是稳定的还是不稳定的，以及它是离子还是中性原子。

玻尔原子

卢瑟福的原子模型有一个严重的问题。 麦克斯韦的电磁辐射理论说，当电子改变速度或运动方向时，它们必须发射能量。 轨道电子不断改变其运动方向，因此它们应该发射持续的能量流。 将麦克斯韦的理论应用于卢瑟福的模型，所有电子在失去能量时都应该螺旋进入原子核，而这种崩溃应该很快发生，大约在10 ^-16 秒内。

正是丹麦物理学家尼尔斯·玻尔（Niels Bohr）（1885—1962 年）解开了电子如何留在轨道上的奥秘。 他正在尝试开发一个原子模型，该模型也可以解释在氢光谱中观察到的某些规律。 他建议，如果我们假设电子只能有一定大小的轨道，那么氢的光谱是可以理解的。 玻尔进一步假设，只要电子只在这些允许的轨道中的一个轨道上移动，它就不会辐射能量：只有当它从一个轨道移动到另一个轨道时，它的能量才会改变。

用科学史学家亚伯拉罕·派斯的话说，这个建议是 “物理学中有史以来最大胆的假设之一”。 如果在日常世界中有类似的东西在起作用，你可能会发现，当你上完天文课后去散步时，大自然允许你每分钟走两步，每分钟走五步，每分钟走十二步，但两者之间没有速度。 无论你尝试如何移动双腿，都只允许一定的步行速度。 为了让事情变得更奇怪，以任何一种允许的速度行走都不费吹灰之力，但是很难从一种速度转换为另一种速度。 幸运的是，这样的规则不适用于人类行为层面。 但是在原子的微观层面上，一个又一个的实验证实了玻尔这个奇怪想法的正确性。 玻尔的建议成为名为量子力学的亚原子世界新（也是更为复杂的）模型的基础之一。

在玻尔的模型中，如果电子从一个轨道移动到另一个更靠近原子核的轨道，它必须以电磁辐射的形式放弃一些能量。 但是，如果电子从内部轨道进入离原子核更远的轨道，则需要一些额外的能量。 获得必要能量的一种方法是吸收可能从外部来源流过原子的电磁辐射。

玻尔模型的一个关键特征是，每个允许的围绕给定原子的电子轨道都有一定的能量值；因此，我们可以将每个轨道视为一个能量水平。 要从一个轨道移动到另一个轨道（这将有自己的特定能量值），需要改变电子的能量，这种变化由两个能量值之间的差异决定。 如果电子升到较低的水平，则会释放出能量差；如果电子升至更高的水平，则必须从其他地方获得能量差。 每次跳跃（或过渡）到不同等级都有与之相关的固定和明确的能量变化。

这种情况的一个粗略的类比可能是生活在豪华公寓塔中，租金由视野质量决定。 这样的建筑物具有一定的、明确编号的楼层或楼层，公寓位于这些楼层上。 没有人可以住在 5.37 或 22.5 楼。 此外，当你上升到更高的楼层时，租金会更高。 如果你想将二十楼的公寓换成二楼的公寓，你就不会欠那么多租金。 但是，如果你想从三楼搬到二十五楼，你的租金会增加。 在原子中，电子存活的 “最便宜” 的地方也是尽可能低的水平，移动到更高的水平需要能量。

这里有一种情况是，更容易将电磁辐射视为粒子（光子）而不是波浪。 当电子从一个水平移动到另一个水平时，它们会释放或吸收少量能量。 当电子移动到更高的水平时，它会吸收能量恰到好处的光子（前提是有光子可用）。 当它移动到较低的水平时，它会发射一个光子，其能量与它在 “低成本生活环境” 中不再需要的能量完全相同。

光子和波浪视角必须相同：光就是光，不管我们怎么看。 因此，每个光子携带一定量的能量，该能量与它所代表的波的频率 (\(f\)) 成正比。 其能量 (\(E\)) 的值由公式给出

\[E=hf \nonumber\]

其中\(h\)，比例常数称为普朗克常数。

该常数以德国物理学家马克斯·普朗克命名，他是量子理论的创始人之一（图\(\PageIndex{5}\)）。 如果使用公制单位（即，如果能量以焦耳为单位测量，频率以赫兹为单位测量），则普朗克常数的值为\(h = 6.626 \times 10^{–34}\)焦耳秒 (J-s)。 能量较高的光子对应于较高频率的波（波长较短）；能量较低的光子是频率较低的波。

人物\(\PageIndex{5}\)尼尔斯·玻尔（1885—1962 年）和马克斯·普朗克（1858—1947 年）。 （a）玻尔，在这张 1935 年的照片中，他坐在办公桌前；（b）普朗克帮助我们了解了光子的能量行为。

举一个具体的例子，以太阳大气中的一个钙原子为例，其中电子从较低的水平跳到更高的水平。 要做到这一点，它需要大约 5×10 ^—19 焦耳的能量，它可以通过吸收来自太阳深处的能量的传递光子来方便地获得这些能量。 在可见光谱的深紫色部分中，该光子相当于频率约为7.5×10 ¹⁴ 赫兹、波长约为3.9×10 ^—7 米（393纳米）的光波。 尽管起初从将光描绘成光子（或能量包）切换到将其描绘成波浪可能看起来很奇怪，但这种切换已成为天文学家的第二天性，可以成为计算光谱的便捷工具。

示例\(\PageIndex{1}\)：光子的能量

既然我们知道如何计算光子的波长和频率，我们可以使用这些信息以及普朗克常数来确定每个光子携带的能量。 波长为 630 nm 的红色光子有多少能量？

解决方案

首先，正如我们之前了解到的那样，我们可以找到光子的频率：

\[f= \frac{c}{ \lambda} = \frac{3 \times 10^8 \text{ m/s}}{630 \times 10^{–9} \text{ m}} = 4.8 \times 10^{14} \text{ Hz} \nonumber\]

接下来，我们可以使用普朗克常数来确定能量（请记住，赫兹等于 1/s）：

\[E=hf= \left( 6.626 \times 10^{–34} \text{ J-s} \right) \left( 4.8 \times 10^{14} (1/\text{s}) \right)=3.2 \times 10^{–19} \text{ J} \nonumber\]

练习\(\PageIndex{1}\)

频率为 5.5×10 ¹⁴ Hz 的黄色光子的能量是多少？

回答

\[E=hf= \left(6.626 \times10^{–34} \right) \left(5.5 \times 10^{14} \right) = 3.6 \times 10^{–19} \text{ J} \nonumber\]

关键概念和摘要

原子由一个包含一个或多个带正电荷的质子的原子核组成。 除氢以外的所有原子也可以在原子核中包含一个或多个中子。 带负电荷的电子绕原子核运行。 质子的数量决定了原子的元素（氢有一个质子，氦有两个质子，依此类推）。 质子数量相同但中子数量不同的原子核是同一元素的不同同位素。 在玻尔原子模型中，允许轨道（或能量水平）上的电子不会发出任何电磁辐射。 但是，当电子从较低的水平升至更高的水平时，它们必须吸收能量恰到好处的光子，而当它们从更高的水平升至较低的水平时，它们会发出能量恰到好处的光子。 光子的能量与它用普朗克公式表示的电磁波的频率相关，\(E=hf\).

词汇表

能量水平

原子或离子所拥有的能量超过其在能量最低状态下所拥有的能量的特定水平或数量；也用于指电子在原子中可以具有的能量状态

同位素

原子具有相同质子数量但中子数量不同的两种或多种形式的相同元素中的任何一种

（原子的）核

原子的很大一部分，主要由质子和中子组成，电子围绕它旋转