3.1: 行星运动定律
- Page ID
- 202704
学习目标
在本节结束时,您将能够:
- 描述一下 Tycho Brahe 和 Johannes Kepler 如何帮助我们理解行星如何绕太阳移动
- 解释开普勒的三条行星运动定律
大约在伽利略开始对坠落物体进行实验的时候,另外两位科学家的努力极大地提高了我们对行星运动的理解。 这两位天文学家是观察者第谷·布拉赫和数学家约翰内斯·开普勒。 他们共同将哥白尼的猜测置于健全的数学基础上,为艾萨克·牛顿在下个世纪的工作铺平了道路。
第谷布拉赫的天文台
哥白尼的《革命报》出版三年后,第谷·布拉赫出生于一个丹麦贵族家庭。 他很早就对天文学产生了兴趣,并在年轻时进行了重要的天文观测。 其中包括仔细研究了我们现在所知道的是一颗爆炸的恒星,它在夜空中爆发得非常明亮。 他越来越高的声誉为他赢得了丹麦国王弗雷德里克二世的赞助,30岁时,布拉赫得以在北海的黑文岛上建立了一个精美的天文台(图\(\PageIndex{1}\))。 布拉赫是欧洲最后一位也是最伟大的望远镜前观察者。

在赫文,布拉赫连续记录了将近20年的太阳、月亮和行星的位置。 他广泛而精确的观察使他能够注意到,行星的位置与根据托勒密的研究结果公布的表格中给出的位置不同。 这些数据非常有价值,但是布拉赫没有能力对其进行分析,也没有能力开发出比托勒密发布的更好的模型。 他受到了进一步的抑制,因为他是个奢侈而残酷的家伙,而且他在政府官员中积聚了敌人。 当他的赞助人弗雷德里克二世于1597年去世时,布拉赫失去了政治基础,决定离开丹麦。 他在布拉格居住,在那里他成为了波希米亚皇帝鲁道夫的宫廷天文学家。 在他去世的前一年,布拉赫在那里找到了一位最有能力的年轻数学家约翰内斯·开普勒来帮助他分析大量的行星数据。
约翰内斯·开普勒
约翰内斯·开普勒出生于德国符腾堡省的一个贫困家庭,他一生的大部分时间都生活在三十年战争的动荡中(见图\(\PageIndex{1}\))。 他在图宾根大学就读并从事神学生涯。 在那里,他学习了哥白尼系统的原理,并转化为日心假说。 最终,开普勒去布拉格担任布拉赫的助手,布拉赫让他着手寻找令人满意的行星运动理论,这种理论与在赫文进行的一系列观测相吻合。 布拉赫在任何时候都不愿向开普勒提供太多材料,因为担心开普勒会自己发现环球运动的秘密,从而夺走布拉赫的一些荣耀。 直到 1601 年 Brahe 去世后,开普勒才完全掌握了这些无价的唱片。 他们的研究占据了开普勒20多年的大部分时间。
通过对行星运动的分析,开普勒提出了一系列原理,现在称为开普勒三定律,这些原理根据行星穿越太空的路径描述了行星的行为。 行星运动的前两个定律于 1609 年在《新天文学》上发表。 他们的发现是现代科学发展的重要一步。
行星运动的前两个定律
物体穿越空间的路径称为其轨道。 开普勒最初假设行星的轨道是圆形,但这样做使他无法找到与布拉赫观测结果一致的轨道。 通过研究火星的数据,他最终发现那颗行星的轨道呈现出一个有点扁平的圆或椭圆的形状。 在圆旁边,椭圆是最简单的闭合曲线,属于称为圆锥截面的一系列曲线(图\(\PageIndex{2}\))。
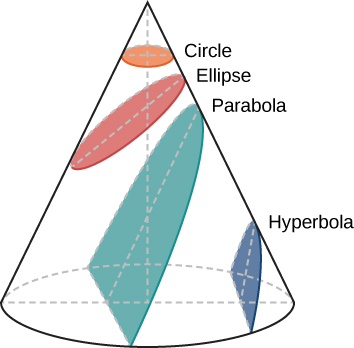
你可能还记得在数学课上,在圆圈中,中心是一个特殊的点。 从圆心到圆上任意位置的距离完全相同。 在椭圆中,从椭圆内部两个特殊点到椭圆上任一点的距离之和总是相同的。 椭圆内的这两个点被称为其焦点(单数:焦点),这是开普勒为此目的发明的词。
此属性建议了一种绘制椭圆的简单方法(图\(\PageIndex{3}\))。 我们将一圈绳子的末端缠绕在两根大头钉上,穿过一张纸推入画板上,这样绳子就会松弛。 如果我们将一支铅笔推到绳子上,拉紧绳子,然后将铅笔滑到大头钉周围的绳子上,由此产生的曲线就是椭圆。 无论铅笔在哪里,从铅笔到两根大头钉的距离之和都是恒定长度,即绳子的长度。 大头钉位于椭圆的两个焦点处。
椭圆的最宽直径称为其长轴。 这个距离(即从椭圆中心到一端的距离)的一半是长半轴,通常用于指定椭圆的大小。 例如,火星轨道的半长轴(也是行星与太阳的平均距离)为2.28亿千米。
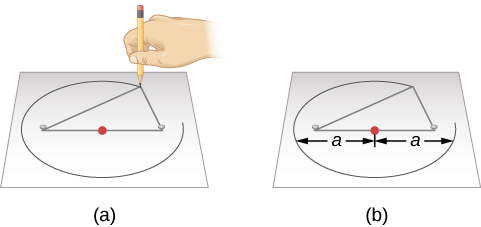
椭圆的形状(圆度)取决于两个焦点相对于长轴的距离有多近。 焦点与半长轴长度之间的距离之比称为椭圆的偏心率。
如果将焦点(或大头钉)移动到相同位置,则焦点之间的距离将为零。 这意味着偏心率为零,椭圆只是一个圆;因此,圆可以称为偏心率为零的椭圆。 在圆圈中,长半轴就是半径。
接下来,我们可以通过改变大头钉的间距(只要它们之间的距离不超过绳子的长度)来制作不同伸长度(或延伸长度)的椭圆。 偏心率越大,椭圆的长度就越长,最大偏心率为1.0,当椭圆变为 “平坦” 时,另一个极点是圆形。
椭圆的大小和形状完全由其长半轴和偏心率指定。 根据布拉赫的数据,开普勒发现火星有一个椭圆轨道,太阳位于一个焦点(另一个焦点是空的)。 火星轨道的偏心率仅为0.1左右;其轨道按比例绘制,实际上与圆圈没有区别,但事实证明,这种差异对于理解行星运动至关重要。
开普勒在他的第一定律中概括了这个结果,并说所有行星的轨道都是椭圆。 这是人类思想史上的一个决定性时刻:为了拥有一个可以接受的宇宙,没有必要只有圈子。 宇宙可能比希腊哲学家想要的要复杂一些。
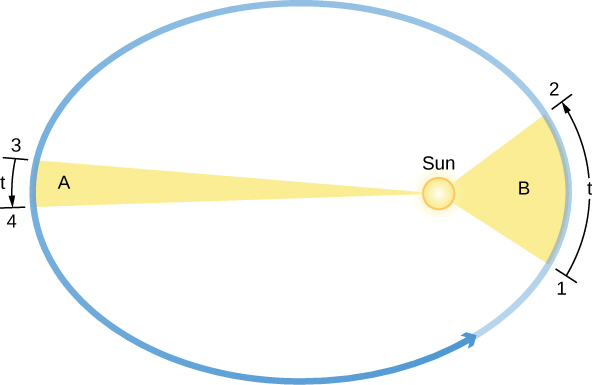
开普勒第二定律涉及每颗行星沿椭圆移动的速度,也称为轨道速度。 通过布拉赫对火星的观测,开普勒发现行星在靠近太阳时会加速,而在离开太阳时会减速。 他通过想象太阳和火星通过一条直的弹性线连接来表达这种关系的确切形式。 当火星离太阳更近时(图中的位置 1 和 2\(\PageIndex{4}\)),弹性线没有那么伸展,行星会快速移动。 离太阳更远,比如在位置3和4,这条线被拉伸了很多,行星移动得不那么快。 当火星在绕太阳的椭圆轨道上行驶时,弹性线在椭圆移动时会扫出椭圆的区域(我们图中的彩色区域)。 开普勒发现,在相等的时间间隔 (t) 中,这条虚线在空间中扫出的区域始终相等;也就是说,区域 B 从 1 到 2 的面积与区域 A 从 3 到 4 的面积相同。
如果行星在圆形轨道上移动,则弹性线的拉伸量始终相同,并且行星以恒定的速度绕其轨道移动。 但是,正如开普勒所发现的那样,在大多数轨道上,行星绕恒星运行(或月球绕其行星运行)的速度往往会有所不同,因为轨道是椭圆的。
开普勒第三定律
开普勒的前两个行星运动定律描述了行星轨道的形状,使我们能够计算出行星在轨道上任何点的运动速度。 开普勒很高兴发现了这样的基本规则,但这些规则并没有满足他全面理解行星运动的追求。 他想知道为什么行星的轨道是这样间隔的,并想在它们的运动中找到一种数学模式——他称之为 “球体的和谐”。 多年来,他一直在努力发现控制行星间距和每颗行星绕太阳运行所花费时间的数学关系。
1619 年,开普勒发现了一种基本关系,将行星的轨道与它们与太阳的相对距离联系起来。 我们将行星的轨道周期(\(P\))定义为行星绕太阳行驶一次所需的时间。 另外,回想一下,行星的半长轴 a 等于它与太阳的平均距离。 这种关系现在被称为开普勒第三定律,它表示行星的轨道周期平方与其轨道立方体的半长轴成正比,或者
\[P^2 \propto a^3 \nonumber\]
当\(P\)(轨道周期)以年为单位测量,并且 a 以称为天文单位(AU)的量表示时,公式的两面不仅成比例而且相等。 一个 AU 是地球和太阳之间的平均距离,大约等于 1.5×108 千米。 在这些单位中
\[P^2=a^3 \nonumber\]
开普勒第三定律适用于所有绕太阳运行的物体,包括地球,它提供了一种计算它们自进入轨道之时起与太阳的相对距离的方法。 让我们来看一个具体的例子来说明开普勒第三定律有多么有用。
例如,假设你计时火星绕太阳需要多长时间(以地球年为单位)。 然后可以使用开普勒的第三定律来计算火星与太阳的平均距离。 火星的轨道周期(1.88 地球年)的平方为 1.882 = 3.53,根据开普勒第三定律的方程,这等于其半长轴的立方程或\(a^3\)。\(P^2\) 那么必须将什么数字立方才能得出 3.53 呢? 答案是1.52(从那以后\(1.52 \times 1.52 \times 1.52 = 3.53\))。 因此,以天文单位表示的火星半长轴必须为 1.52 AU。 换句话说,要在不到两年的时间内绕太阳,火星离太阳的距离必须是地球的50%左右(再过一半)。
示例\(\PageIndex{1}\):计算周期
想象一下,一个物体正在绕太阳移动。 如果该物体的轨道的半长轴为 50 AU,其轨道周期将是多少?
解决方案
根据开普勒的第三定律,我们知道了这一点(当我们使用年和非盟单位时)
\[P^2=a^3 \nonumber\]
如果物体的轨道的半长轴为 4 AU(a = 50),我们可以立方体 50 然后取结果的平方根得出 P:
\[ \begin{array}{l} P = \sqrt{a^3} \\ P = \sqrt{50 \times 50 \times 50} = \sqrt{125,000} = 353.6 \text{ years} \end{array}\]
因此,该物体的轨道周期约为350年。 这将使我们假设的物体超出冥王星的轨道。
练习\(\PageIndex{1}\)
半长轴为 3 AU 的小行星(火星和木星之间的岩石块)的轨道周期是多少?
- 回答
-
\[P = \sqrt{3 \times 3 \times 3} = \sqrt{27} = 5.2 \text{ years}\]
开普勒的三条行星运动定律可以概括如下:
- 开普勒第一定律:每颗行星在椭圆的轨道上绕太阳移动,太阳位于椭圆的一个焦点上。
- 开普勒第二定律:连接行星和太阳的直线以相等的时间间隔扫出太空中的相等区域。
- 开普勒第三定律:行星轨道周期的平方与其轨道半长轴的立方成正比。
开普勒的三定律提供了哥白尼系统框架内行星运动的精确几何描述。 使用这些工具,可以大大提高精度来计算行星位置。 尽管如此,开普勒定律纯粹是描述性的:它们无法帮助我们理解哪些自然力量限制了行星遵循这套特定的规则。 这一步留给了艾萨克·牛顿。
示例\(\PageIndex{2}\):应用开普勒第三定律
使用此处提供的金星和地球的轨道周期和半长轴,计算\(P^2\)和\(a^3\),并验证它们是否遵守开普勒第三定律。 金星的轨道周期为0.62年,其半长轴为0.72 AU。 地球的轨道周期为 1.00 年,其半长轴为 1.00 AU。
解决方案
我们可以使用开普勒第三定律的方程式\(P^2 \propto a^3\)。 对于维纳斯来说,\(P^2 = 0.62 \times 0.62 = 0.38 \text{ years}\)和\(a^3 = 0.72 \times 0.72 \times 0.72 = 0.37 \text{ AU}\)(四舍五入的数字有时会导致这样的细微差异)。 轨道周期(0.38 年)近似于半长轴(0.37 AU)。
因此,金星遵守开普勒第三定律。 为了地球\(P^2 = 1.00 \times 1.00 = 1.00 \text{ year}\),还有\(a^3 = 1.00 \times 1.00 \times 1.00 = 1.00 \text{ AU}\)。 轨道周期(1.00 年)近似(在本例中等于)半长轴(1.00 AU)。 因此,地球遵守开普勒第三定律。
练习\(\PageIndex{1}\)
使用此处提供的土星和木星的轨道周期和半长轴,计算\(P^2\)和\(a^3\),并验证它们是否遵守开普勒第三定律。 土星的轨道周期为29.46年,其半长轴为9.54 AU。 木星的轨道周期为11.86年,其半长轴为5.20 AU。
- 回答
-
对于土星来说\(P^2 = 29.46 \times 29.46 = 867.9 \text{ years}\),还有\(a^3 = 9.54 \times 9.54 \times 9.54 = 868.3 \text{ AU}\)。 轨道周期(867.9 年)近似于半长轴(868.3 AU)。 因此,土星遵守开普勒第三定律。
为了纪念最初制定控制行星运动定律的科学家,建造第一艘航天器以寻找绕其他恒星运行的行星的团队决定将该探测器命名为 “开普勒”。 要了解有关约翰内斯·开普勒的生平及其行星运动定律的更多信息,以及有关开普勒任务的大量信息,请访问美国宇航局的开普勒网站并点击你感兴趣的链接。
关键概念和摘要
第谷·布拉赫对行星位置的精确观测为约翰内斯·开普勒得出行星运动的三个基本定律提供了数据。 开普勒定律将行星在其轨道上的行为描述如下:(1)行星轨道是椭圆,太阳处于同一个焦点;(2)在相等的间隔内,行星的轨道扫出相等的区域;(3)轨道周期(\(P\))和半长轴(\(a\))之间的关系轨道由\(P^2 = a^3\)(当以 AU\(a\) 为单位时,以地球年\(P\)为单位)给出。
词汇表
- 天文单位 (AU)
- 长度单位定义为地球和太阳之间的平均距离;该距离约为 1.5 × 108 千米
- 古怪
- 在椭圆中,焦点与长轴之间的距离之比
- 椭圆
- 一条闭合曲线,从椭圆上的任何一点到内部两个点(称为焦点)的距离之和始终相同
- 焦点
- (plural: foci)椭圆内两个固定点之一,从该点到椭圆上任一点的距离之和是恒定的
- 开普勒第一定律
- 每颗行星在椭圆的轨道上绕太阳移动,太阳位于椭圆的一个焦点上
- 开普勒第二定律
- 连接行星和太阳的直线在相等的时间间隔内扫除太空中相等的区域
- 开普勒第三定律
- 行星轨道周期的平方与其轨道半长轴的立方成正比
- 长轴
- 椭圆的最大直径
- 轨道
- 围绕另一个物体或点旋转的物体的路径
- 轨道周期 (P)
- 物体绕太阳传播一次所花费的时间
- 轨道速度
- 物体(通常是行星)绕另一个物体的质量运行的速度;如果是行星,则是指每颗行星沿其椭圆移动的速度
- 长半轴
- 圆锥截面(例如椭圆)长轴的一半


