5.7: 章节练习
- Page ID
- 204862
5.1 连续概率密度函数的属性
1。
该图说明了哪种分布类型?
图\(\PageIndex{23}\)
2。
该图说明了哪种分布类型?
图\(\PageIndex{24}\)
3。
该图说明了哪种分布类型?
图\(\PageIndex{25}\)
4。
阴影区域代表什么? \(P\)(___\(< x <\) ___)
图\(\PageIndex{26}\)
5。
阴影区域代表什么? \(P\)(___\(< x <\) ___)
图\(\PageIndex{27}\)
6。
对于连续概率分布,\(0 \leq x \leq 15\). 什么是\(P(x > 15)\)?
7。
\(f(x)\)如果函数是连续概率密度函数,则面积是多少?
8。
对于连续概率分布,\(0 \leq x \leq 10\). 什么是\(P(x = 7)\)?
9。
连续概率函数仅限于\(x = 0\)和之间的部分\(7\)。 什么是\(P(x = 10)\)?
10。
\(f(x)\)因为连续概率函数为\(\frac{1}{5}\),并且该函数仅限于\(0 \leq x \leq 5\)。 什么是\(P(x < 0)\)?
11。
\(f(x)\),一个连续概率函数,等于\(\frac{1}{12}\),并且该函数限制为\(0 \leq x \leq 12\)。 什么是\(P(0 < x < 12)\)?
12。
找出\(x\)落在阴影区域的概率。
图\(\PageIndex{28}\)
13。
找出\(x\)落在阴影区域的概率。
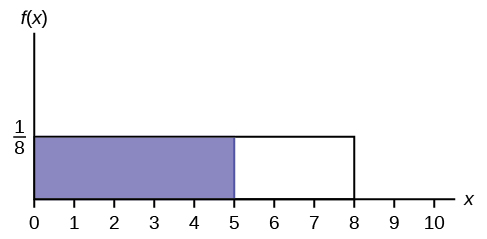.jpg)
图\(\PageIndex{29}\)
14。
找出\(x\)落在阴影区域的概率。
图\(\PageIndex{30}\)
15。
\(f(x)\),连续概率函数,\(\frac{1}{3}\)等于,函数限制为\(1 \leq x \leq 4\)。 描述一下\(P(x>\frac{3}{2})\)。
5.2 均匀分布
使用以下信息回答接下来的十个问题。 以下数据是28套房屋的平方英尺(以1,000平方英尺为单位)。
\ (\ pageIndex {2}\) “>| 1.5 | 2.4 | 3.6 | 2.6 | 1.6 | 2.4 | 2.0 |
| 3.5 | 2.5 | 1.8 | 2.4 | 2.5 | 3.5 | 4.0 |
| 2.6 | 1.6 | 2.2 | 1.8 | 3.8 | 2.5 | 1.5 |
| 2.8 | 1.8 | 4.5 | 1.9 | 1.9 | 3.1 | 1.6 |
样本均值 = 2.50,样本标准差 = 0.8302。
发行版可以写成\(X \sim U(1.5, 4.5)\)。
16。
这是什么类型的分发?
17。
在这种分布中,结果的可能性相同。 这是什么意思?
18。
连续概率分布的高\(f(x)\)度是多少?
19。
值的约束条件\(x\)是什么?
20。
图表\(P(2 < x < 3)\)。
21。
什么是\(P(2 < x < 3)\)?
22。
什么是\(P(x < 3.5 | x < 4)\)?
23。
什么是\(P(x = 1.5)\)?
24。
假设您已经知道房屋的面积超过2,000平方英尺,则找出随机选择的房屋面积超过3,000平方英尺的概率。
使用以下信息回答接下来的八个练习。 分布如下所示\(X \sim U(0, 12)\)。
25。
什么是\(a\)? 它代表什么?
26。
什么是\(b\)? 它代表什么?
27。
什么是概率密度函数?
28。
理论上的意思是什么?
29。
理论标准差是多少?
30。
绘制分布图\(P(x > 9)\)。
31。
查找\(P(x > 9)\)。
使用以下信息回答接下来的十一个练习。 郊区大学员工停车场的汽车使用寿命从六个月(0.5 年)统一分配到9.5年。
32。
这里测量的是什么?
33。
用文字来定义随机变量\(X\)。
34。
数据是离散的还是连续的?
35。
的值间隔\(x\)为 ______。
36。
的分布\(X\)是 ______。
37。
编写概率密度函数。
38。
绘制概率分布图。
- 绘制概率分布图。
图\(\PageIndex{31}\)
- 确定以下值:
- 的最低值\(\overline{x}\):_______
- 的最高值\(\overline{x}\):_______
- 矩形的高度:_______
- x 轴标签(单词):_____
- y 轴标签(单词):_____
39。
找出地段中汽车的平均车龄。
40。
找出地段中随机选择的汽车车龄不到四年的概率。
- 绘制图表并给感兴趣区域加上阴影。
图\(\PageIndex{32}\)
- 找出概率。 \(P(x < 4)\)= _______
41。
仅考虑车龄小于7.5年的汽车,可以得出该批次中随机选择的汽车车龄不到四年的概率。
- 绘制图形,为感兴趣区域添加阴影。
图\(\PageIndex{33}\)
- 找出概率。 \(P(x < 4 | x < 7.5) =\)_______
42。
前两个问题发生了什么变化,使解决方案有所不同?
43。
找出地段中汽车年龄的第三个四分位数。 这意味着你必须找到这样一个值\(\frac{3}{4}\),即75%的汽车最多(小于或等于)那个年龄。
- 绘制图表并给感兴趣区域加上阴影。
图\(\PageIndex{34}\)
- 找到\(k\)这样的值\(P(x < k) = 0.75\)。
- 第三个四分位数是 _______
5.3 指数分布
使用以下信息回答接下来的十个练习。 客户服务代表必须花不同的时间与每位客户交流,以解决各种问题。 与每位客户花费的时间可以通过以下分布进行建模:\(X \sim Exp(0.2)\)
44。
这是什么类型的分发?
45。
这种分布结果的可能性是否相同? 为什么或者为什么不呢?
46。
什么是\(m\)? 它代表什么?
47。
这是什么意思?
48。
标准差是多少?
49。
陈述概率密度函数。
50。
绘制分布图。
51。
查找\(P(2 < x < 10)\)。
52。
查找\(P(x > 6)\)。
53。
找到第 70 个百分位数。
使用以下信息回答接下来的七个练习。 分布如下所示\(X \sim Exp(0.75)\)。
54。
m 是什么?
55。
什么是概率密度函数?
56。
什么是累积分布函数?
57。
绘制分布。
58。
查找\(P(x < 4)\)。
59。
找到第 30 个百分位数。
60。
找到中位数。
61。
哪个更大,平均值还是中位数?
使用以下信息回答接下来的 16 个练习。 碳14是一种放射性元素,其半衰期约为5,730年。 据说碳14会呈指数级衰减。 衰减率为 0.000121。 我们从一克碳14开始。 我们对衰变碳14所需的时间(年)感兴趣。
62。
这里测量的是什么?
63。
数据是离散的还是连续的?
64。
用文字来定义随机变量\(X\)。
65。
衰减率 (\(m\)) 是多少?
66。
的分布\(X\)是 ______。
67。
找出持续时间少于 5,730 年的碳 14 含量(一克的百分比)。 这意味着,找到\(P(x < 5,730)\)。
- 绘制图表并给感兴趣区域加上阴影。
图\(\PageIndex{35}\)
- 找出概率。 \(P(x < 5,730) =\)__________
68。
找出持续时间超过 10,000 年的碳 14 百分比。
- 绘制图表并给感兴趣区域加上阴影。
图\(\PageIndex{36}\)
- 找出概率。 \(P(x > 10,000) =\)________
69。
百分之三十(30%)的碳14会在多少年内分解?
- 绘制图表并给感兴趣区域加上阴影。
图\(\PageIndex{37}\)
找到\(k\)这样的值\(P(x < k) = 0.30\)。


