Skip to main content
Global

10.3: 理性不平等

  1. Last updated
  2. Save as PDF
  • Page ID
    171341

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    求解有理不等式需要找到分子和分母的零，然后使用这些值调查数字线上的解集区域。

    示例 Template:Index

    求解不等式并用区间表示法写出解集：

    1. \(\dfrac{x − 1}{x + 1} ≥ 0\)
    2. \(\dfrac{2x − 3}{x + 1} ≤ 0\)
    3. \(\dfrac{x + 2}{x − 2} ≥ 0\)
    解决方案
    1. \(\begin{array} &&\dfrac{x − 1}{x + 1} ≥ 0 &\text{Example problem} \\ &\dfrac{x − 1}{x + 1} ≥ 0 &\text{The quotient must be greater than or equal to \(0\).}\\ &x − 1 = 0,\; x = 1 &\ text {找到分子的零}\\ &x + 1 = 0, x =\; −1 &\ text {找到分母的零}\ end {array}\)
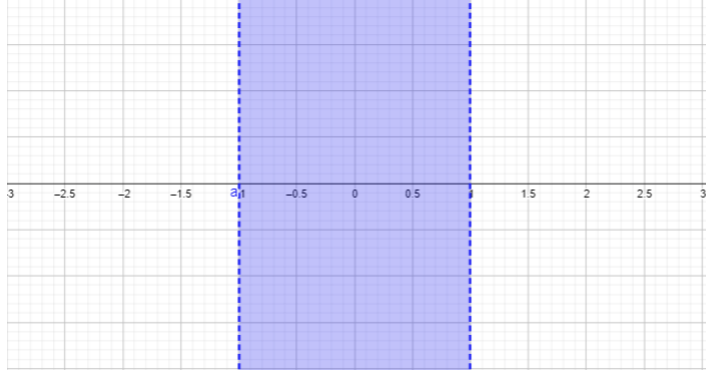
    clipboard_ec11760d50b919ddd83bc64d27535e4b7.png
    零将数字行划分为多个\(3\)区域，\(x < −1\)，\(−1 < x < 1\)，\(x > 1\)

    \(\begin{array} &&\text{For } x < −1, \text{ choose } x = −2. \;\;\dfrac{−2 − 1}{−2 + 1} = \dfrac{−3}{−1} = 3 ≥ 0 \\ &\text{Replacing \(-2\)表示答案中的\(x\)结果\(3\)，该结果大于或等于\(0\)。 \(x < −1\)该区域包含在解决方案集中。}\\ [0.25in] &\ text {For} −1 < x < 1，\ text {choose} x = 0。\;\ dfrac {0 − 1} {0 + 1} = −1 < 0\\ &\ text {替换\(0\)答案中的\(x\)结果\(-1\)，小于\(0\)，不满足问题中给定的不等式。}\\ &\ text {此区域\(−1 < x < 1\)不包括在解集中。}\\ [0.25in] &\ text {For} x > 1，\ text {choose} x = 2.\;\;\ dfrac {2 + 1} {2 + 1} =\ dfrac {1} ≥ 0\\ &\ text {替换\(2\)答案中的\(x\)结果\(\dfrac{1}{3}\)，哪个是大于或等于\(0\)。 \(x > 1\)该区域包含在解集中。}\\ [0.25in] & (−∞, −1) (1, ∞)\\ &\ text {用区间表示法书写的最终答案（有关更多详细信息，请参阅区间表示法部分）。} \ end {array}\)

    1. \(\begin{array} &&\dfrac{2x − 3}{x + 1} ≤ 0 &\text{Example problem} \\ &\dfrac{2x − 3}{x + 1} ≤ 0 &\text{The quotient must be less than or equal to \(0\).}\\ &2x − 3 = 0,\; x = 1.5 &\ text {找到分子的零}\\ &x + 1 = 0,\; x = −1 &\ text {找到分母的零}\ end {array}\)
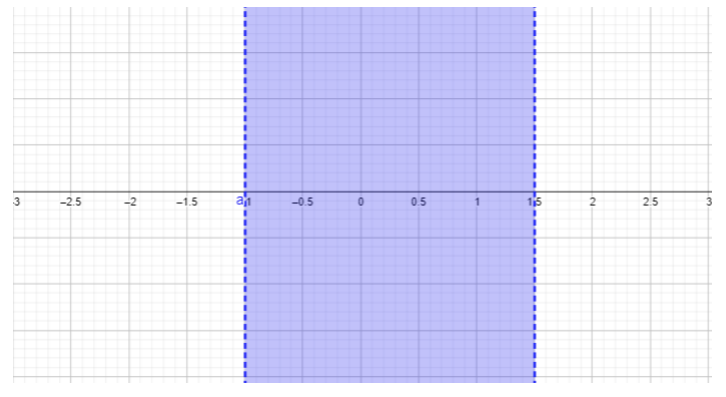
    clipboard_eb1a3fd2706ba7b03d6acdeb3ad51ec07.png
    零将数字行划分为多个\(3\)区域，\(x < −1\)，\(−1 < x < 1.5\)，\(x > 1.5\)

    \(\begin{array} &&\text{For } x < −1, \text{ choose } x = −2. \;\; \dfrac{2(−2) − 3}{−2 − 1} = \dfrac{−7}{−3} = \dfrac{7}{3} ≥ 0 \\ &\text{Replacing \(-2\)表示答案中的\(x\)结果大于\(\dfrac{7}{3}\)\(0\)，未满足问题中给定的不等式。}\\ &\ text {此区域\(x < −1\)不在解集合中。}\\ [0.25in] &\ text {For} −1 < x < 1.5，\ text {choose} x = 0。\;\ dfrac {2 (0) −3} {0 − 1} =\ dfrac {−3} {−1} = 3 ≥ 0\\ &\ text {替换\(0\)答案中的\(x\)结果\(3\)，大于或等于\(0\)，这不是问题所要求的。}\\ &\ text {解集中不包括该区域\(−1 < x < 1.5\)。}\\ [0.25in] &\ text {For} x > 1，\ text {choose} x = 2。\;\ dfrac {2 (2) − 3} {2 − 1} =\ dfrac {1} {1} = 1 ≥ 0\\ &\ text {替换\(2\)答案中的\(x\)结果\(1\)，大于或等于\(0\)。 该区域\(x > 1\)不包含在解决方案集中。}\\ [0.25in] &\\ &\ text {这个问题没有解决方案。 \(\dfrac{2x − 3}{x + 1}\)永远不会小于或等于\(0\)。} \ end {array}\)

    1. \(\begin{array} &&\dfrac{x + 2}{x − 2} ≥ 0 &\text{Example problem} \\ &\dfrac{x + 2}{x − 2} ≥ 0 &\text{The quotient must be greater than or equal to \(0\).}\\ &x + 2 = 0,\;\; x = −2 &\ text {找到分子的零}\\ &x − 2 = 0,\;\; x = 2 &\ text {找到分母的零}\ end {array}\)
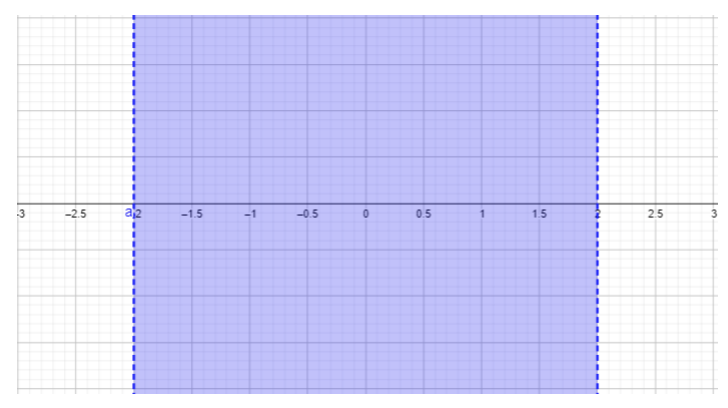
    clipboard_e3374fd2eab55feb8c3dfe2d5ebd8d557.png
    零将数字行划分为多个\(3\)区域，\(x < −2\)，\(−2 < x < 2\)，\(x > 2\)

    \(\begin{array} &&\text{For } x < −2, \text{ choose } x = −3. \dfrac{−3 + 2}{−3 − 2} = \dfrac{−1}{−5} = \dfrac{1}{5} ≥ 0 \\ &\text{Replacing \(-3\)表示答案中的\(x\)结果\(\dfrac{1}{5}\)，该结果大于或等于\(0\)。 \(x < −2\)该区域包含在解决方案集中。}\\ [0.25in] &\ text {For} −2 < x < 2，\ text {choose} x = 0。\;\ dfrac {0 + 2} {0 − 2} = −1 < 0\\ &\ text {替换\(0\)答案中的\(x\)结果\(-1\)，小于\(0\)，不满足问题中给定的不等式。}\\ &\ text {此区域\(−2 < x < 2\)不包含在解集中。}\\ [0.25in] &\ text {For} x > 2，\ text {choose} x = 3.\;\ dfrac {3 + 2} {3 − 2} =\ dfrac {5} {1} = 5 ≥ 0\\ &\ text {替换\(3\)\(x\)结果为回答\(5\)，它大于或等于\(0\)。 \(x > 2\)该区域包含在解集中。}\\ [0.25in] & (−∞, −2) (2, ∞)\\ &\ text {用区间表示法书写的最终答案（更多详情请参阅区间表示法部分）。} \ end {array}\)

    练习 Template:Index
    1. \(\dfrac{x + 3}{x − 2} ≥ 0\)
    2. \(\dfrac{x − 2}{x − 1} ≤ 0\)
    3. \(\dfrac{2x − 1}{x + 2} ≤ 0\)
    4. \(\dfrac{2x − 3}{x + 1} ≥ 0\)