10.2：求解和绘制不等式，以及用区间表示法写出答案
- Page ID
- 171328
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)要求解不等式并绘制图表：
- 使用上一节中的不等式属性求解不等式。
- 在数字线上绘制解决方案集合的图表。
- 用间隔表示法写出解集。
求解不等式，在数字线上绘制解集合图，并用区间表示法显示解集：
- \(−1 ≤ 2x − 5 < 7\)
- \(x^2 + 7x + 10 < 0\)
- \(−6 < x − 2 < 4\)
解决方案
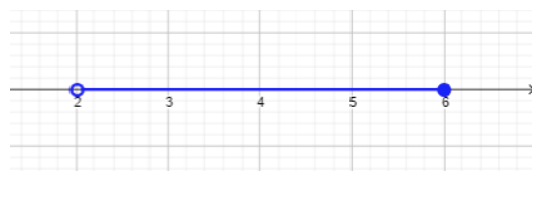
- \(\begin{array} &&−1 ≤ 2x − 5 < 7 &\text{Example problem} \\ &−1 + 5 ≤ 2x − 5 + 5 < 7 + 5 &\text{The goal is to isolate the variable \(x\)，所以首先将不等式中的所有三个区域相加\(5\)。}\\ &4 ≤ 2x < 12 &\ text {Simplify。}\\ &\ dfrac {4} {2} ≤ 2x^2 <\ dfrac {4} {2} &\ text {全部除\(2\)以分离变量\(x\)。}\\ &2 ≤ x < 6 &\ text {最终答案写于不等式/解决方案集合形式。}\\ & [2, 6) &\ text {用区间表示法写的最终答案（更多详情请参阅间隔符号部分）}\ end {array}\)
- \(\begin{array} &&x^2 + 7x + 10 < 0 &\text{Example problem} \\ &(x + 5)(x + 2) < 0 &\text{Factor the polynomial.} \\ &(x + 5)(x + 2) < 0 &\text{The product must be less than \(0\)，这意味着如果\((x + 5) > 0\)，那么\((x + 2) < 0\)。 同样，if\((x + 5) < 0\)，那么\((x + 2) > 0\)。}\\ & (x + 5) > 0 (x + 2) < 0 &\ text {Find the intersection of each of these inequalities.}\\ &x > −5 x < −2 &\ text {找出每个不等式的交点。} \ end {array}\)
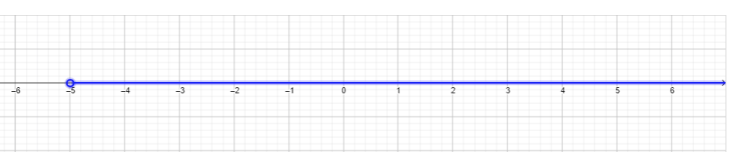
\(\begin{array} &&\;\;\;−5 < x < −2 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;&\text{Final answer written in inequality/solution set form.} \\ &\;\;\;(−5, −2) \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;&\text{Final answer written in interval notation (see section on Interval Notation for more details).} \end{array}\)
- \(\begin{array}&&−6 < x − 2 ≤ 4 &\text{Example problem} \\ &−6 + 2 < x − 2 + 2 ≤ 4 + 2 &\text{The goal is to isolate the variable \(x\)，所以首先将不等式中的所有三个区域相加\(2\)。}\\ &−4 < x ≤ 6 &\ text {以不等式/解集形式写的最终答案。}\\ & (−4, 6] &\ text {用区间表示法写的最终答案（更多详情请参阅间隔表示法部分）。} \ end {array}\)
求解不等式，在数字线上绘制解集合图，并用区间表示法显示解集：
- \(0 ≤ x + 1 ≤ 4\)
- \(0 < 2(x − 1) ≤ 4\)
- \(6 < 2(x − 1) < 12\)
- \(x^2 − 6x − 16 < 0\)
- \(2x^2 − x − 15 > 0\)