Skip to main content
Global

11.6: النموذج القياسي

  1. Last updated
  2. Save as PDF
  • Page ID
    196438

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    أهداف التعلم

    في نهاية هذا القسم، ستكون قادرًا على:

    • وصف النموذج القياسي من حيث القوى الأساسية الأربع وجسيمات التبادل
    • ارسم مخطط Feynman لتفاعل بسيط بين الجسيمات
    • استخدم مبدأ عدم اليقين الخاص بـ Heisenberg لتحديد نطاق القوى الموصوفة في النموذج القياسي
    • شرح الأساس المنطقي وراء نظريات التوحيد الكبرى

    النشاط الفكري الرئيسي لأي عالم هو تطوير ومراجعة النماذج العلمية. يسعى عالم فيزياء الجسيمات إلى تطوير نماذج لتفاعلات الجسيمات. يعتمد هذا العمل بشكل مباشر على العمل المنجز في مجال الجاذبية والكهرومغناطيسية في القرون السابع عشر والثامن عشر والتاسع عشر. الهدف النهائي للفيزياء هو «نظرية كل شيء» موحدة تصف جميع تفاعلات الجسيمات من حيث معادلة واحدة أنيقة وصورة. قد تكون المعادلة نفسها معقدة، لكن العديد من العلماء يشكون في أن الفكرة وراء المعادلة ستجعلنا نصرخ: «كيف يمكن أن نفوتها؟ كان الأمر واضحًا جدًا!»

    في هذا القسم، نقدم النموذج القياسي، وهو أفضل نموذج حالي لتفاعلات الجسيمات. وصفنا النموذج القياسي بالتفصيل من حيث القوى الكهرومغناطيسية والنووية الضعيفة والقوية. في نهاية هذا القسم، نستعرض نظريات التوحيد في فيزياء الجسيمات.

    مقدمة عن النموذج القياسي

    يحتوي النموذج القياسي لتفاعلات الجسيمات على فكرتين: نظرية الضعف الكهربائي وديناميكا الكروموديناميكا الكمومية (QCD) (القوة المؤثرة بين شحنات اللون). توحد نظرية الضعف الكهربائي نظرية الديناميكا الكهربائية الكمومية (QED)، المعادل الحديث للكهرومغناطيسية الكلاسيكية، ونظرية التفاعلات النووية الضعيفة. يجمع النموذج القياسي بين نظرية النسبية وميكانيكا الكم.

    في النموذج القياسي، تحدث تفاعلات الجسيمات من خلال تبادل البوزونات، «حاملات القوة». على سبيل المثال، يتم توصيل القوة الكهروستاتيكية بين جزيئين مشحونين بشكل إيجابي عن طريق إرسال واستقبال فوتونات عديمة الكتلة. يمكن أن يحدث هذا في نطاق نظري لا نهائي. نتيجة هذه التفاعلات هي تنافر كولوم (أو الجذب). وبالمثل، ترتبط الكواركات معًا من خلال تبادل الغلوونات عديمة الكتلة. تبعثر الليبتونات عن اللبتونات الأخرى (أو تتحلل إلى جزيئات أخف) من خلال تبادل البوزونات الضخمة W و Z. يوجد ملخص للقوى كما هو موضح في النموذج القياسي في الجدول\(\PageIndex{1}\). تمت إضافة قوة الجاذبية، بوساطة تبادل الجاذبية عديمة الكتلة، في هذا الجدول للتأكد من اكتمالها ولكنها ليست جزءًا من النموذج القياسي.

    الجدول\(\PageIndex{1}\): القوى الأربع والنموذج القياسي
    قوة القوة النسبية جسيم التبادل (البوزونات) الجسيمات التي تم العمل عليها النطاق
    قوي 1 غلوون الكواركات \(10^{-15}m\)
    كهرومغناطيسية 1/137 فوتون الجسيمات المشحونة \(\infty\)
    ضعيف \(10^{-10}\) \(W^+, \, W^-, \, Z\)البوزونات الكواركات والليبتونات والنيوترينوات \(10^{-18}m\)
    الجاذبية \(10^{-38}\) جرافيتون جميع الجسيمات \(\infty\)

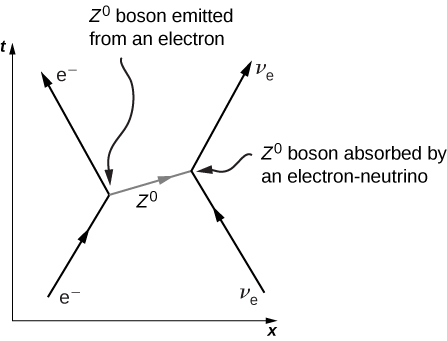
    يمكن التعبير عن النموذج القياسي من حيث المعادلات والرسوم البيانية. المعادلات معقدة وعادة ما يتم تناولها في دورة أكثر تقدمًا في الفيزياء الحديثة. ومع ذلك، يمكن التقاط جوهر النموذج القياسي باستخدام مخططات Feynman. مخطط فينمان، الذي ابتكره الفيزيائي الأمريكي ريتشارد فاينمان (1918-1988)، هو مخطط الزمكان الذي يصف كيفية تحرك الجسيمات وتفاعلها. يتم استخدام رموز مختلفة لجزيئات مختلفة. يتم عرض تفاعلات الجسيمات في بُعد واحد كرسم بياني للموضع الزمني (وليس رسمًا بيانيًا للموضع والوقت). على سبيل المثال، ضع في اعتبارك تشتت الإلكترون والإلكترون النيوترينو (الشكل\(\PageIndex{1}\)). يتحرك الإلكترون نحو القيم الموجبة لـ x (إلى اليمين) ويصطدم بنيوترينو إلكتروني يتحرك إلى اليسار. يتبادل الإلكترون بوزون Z (الشحنة صفر). ينتشر الإلكترون إلى اليسار وينتشر النيوترينو إلى اليمين. هذا التبادل ليس فوريًا. ينتقل بوزون Z من جسيم إلى آخر خلال فترة زمنية قصيرة. يقال إن تفاعل الإلكترون والنيوترينو يحدث عبر القوة النووية الضعيفة. لا يمكن تفسير هذه القوة بالكهرومغناطيسية الكلاسيكية لأن شحنة النيوترينو تساوي صفرًا. تتم مناقشة القوة النووية الضعيفة مرة أخرى لاحقًا في هذا القسم.

    الشكل عبارة عن رسم بياني لـ t مقابل x. يتحرك السهم المسمى e ناقص لأعلى ولليمين ويلتقي بقاعدة سهم آخر يحمل علامة e ناقص يتجه لأعلى ولليسار. يُطلق على الوصلة اسم z0 بوزون منبعث من الإلكترون. على يمين هذا يوجد سهم يتجه لأعلى ولليسار. يلتقي الطرف بقاعدة سهم آخر يتجه لأعلى ولليمين. كلاهما يحمل علامة v suncept e ويطلق على الوصلة اسم z0 بوزون يمتصه نيوترينو الإلكترون. يتم توصيل التقاطعين على الرسم البياني بواسطة شعاع يسمى z0. هذه تشير إلى اليمين وإلى الأعلى قليلاً.
    الشكل\(\PageIndex{1}\): في مخطط فينمان هذا،\(Z^0\) يحمل تبادل الافتراضي القوة النووية الضعيفة بين الإلكترون والنيوترينو.

    قوة كهرومغناطيسية

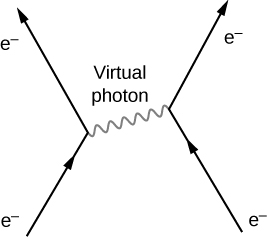
    وفقًا لـ QED، تنتقل القوة الكهرومغناطيسية بين الجسيمات المشحونة من خلال تبادل الفوتونات. تعتمد النظرية على ثلاث عمليات أساسية: ينتقل الإلكترون من مكان إلى آخر، وينبعث أو يمتص الفوتون، وينتقل من مكان إلى آخر مرة أخرى. عندما يتفاعل إلكترونان، يصدر إلكترون واحد الفوتون ويستقبله الآخر (الشكل\(\PageIndex{2}\)). تنقل الفوتونات الطاقة والزخم من إلكترون إلى آخر. النتيجة الصافية في هذه الحالة هي قوة مثيرة للاشمئزاز. الفوتونات المتبادلة افتراضية. الجسيم الافتراضي هو جسيم موجود لفترة قصيرة جدًا بحيث لا يمكن ملاحظته. نظرًا لأن وقت عبور الفوتون صغير\(\Delta t\) للغاية، فإن مبدأ عدم اليقين لهايزنبرغ ينص على أن عدم اليقين في طاقة الفوتون\(\Delta E\)، قد يكون كبيرًا جدًا.

    يوضح الشكل أربعة أسهم تحمل علامة e ناقص. يتجه أحدهما لأعلى ولليمين ويلتقي بقاعدة سهم آخر يتجه لأعلى ولليسار. على يمين هذا يوجد سهم يتجه لأعلى ولليسار. يلتقي الطرف بقاعدة سهم آخر يتجه لأعلى ولليمين. يتم توصيل التقاطعين على الرسم البياني بخط متموج يسمى الفوتون الافتراضي. هذه تشير إلى اليمين وإلى الأعلى قليلاً.
    الشكل\(\PageIndex{2}\): رسم فينمان التخطيطي لإلكترونين يتفاعلان من خلال تبادل الفوتون.

    لتقدير نطاق التفاعل الكهرومغناطيسي، افترض أن عدم اليقين بشأن الطاقة يمكن مقارنته بطاقة الفوتون نفسه، مكتوبًا

    \[\Delta E \approx E. \nonumber \]

    ينص مبدأ هايزنبرغ غير المؤكد على ذلك

    \[\Delta E \approx \frac{h}{\Delta t}. \nonumber \]

    بدمج هذه المعادلات، لدينا

    \[\Delta t \approx \frac{h}{E}. \nonumber \]

    يتم إعطاء طاقة الفوتون من خلال\(E = hf\)، لذلك

    \[\Delta t \approx \frac{h}{hf} \approx \frac{1}{f} = \frac{\lambda}{c}. \nonumber \]

    وبالتالي فإن المسافة التي يمكن أن يتحرك بها الفوتون في هذا الوقت هي

    \[d = c\Delta t \approx c\left(\frac{\lambda}{c}\right) = \lambda. \nonumber \]

    يمكن أن تكون طاقة الفوتون الافتراضي صغيرة بشكل تعسفي، لذلك يمكن أن يكون طوله الموجي كبيرًا بشكل تعسفي - من حيث المبدأ، حتى كبيرًا بشكل لا نهائي. لذلك فإن القوة الكهرومغناطيسية هي قوة بعيدة المدى.

    قوة نووية ضعيفة

    القوة النووية الضعيفة هي المسؤولة عن التحلل الإشعاعي. نطاق القوة النووية الضعيفة قصير جدًا (حوالي\(10^{-18}\) متر فقط) ومثل القوى الأخرى في النموذج القياسي، يمكن وصف القوة الضعيفة من حيث تبادل الجسيمات. (لا توجد وظيفة بسيطة مثل قوة كولوم لوصف هذه التفاعلات.) الجسيمات المتبادلة هي واحدة من ثلاثة بوزون:\(W^+\),\(W^-\) و\(Z^0\). يتنبأ النموذج القياسي بوجود جزيئات spin-1 هذه ويتنبأ أيضًا بكتلتها المحددة. وبالاقتران مع التجارب السابقة، كان من المتوقع أن تكون كتلة بوزونات W المشحونة\(81 \, GeV/c^2\) وأن تكون كتلة\(Z^0\) البوزونات\(90 \, GeV/c^2\). اكتشفت تجربة CERN الجسيمات في الثمانينيات بهذه الكتل على وجه التحديد - وهو انتصار مثير للإعجاب للنموذج.

    غالبًا ما ترتبط القوة النووية الضعيفة بتشتت وتحلل الجسيمات غير المستقرة إلى جزيئات ضوئية. على سبيل المثال، تتحلل النيوترونات إلى بروتونات من خلال القوة النووية الضعيفة. رد الفعل هذا مكتوب

    \[n \rightarrow p + e^- + \nu_e, \nonumber \]

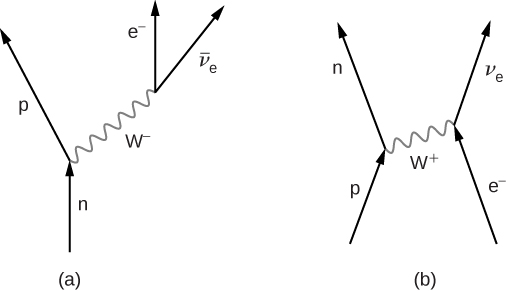
    حيث n هو النيوترون، p هو البروتون،\(e^-\) هو إلكترون، وهو نيوترينو الإلكترون عديم الكتلة تقريبًا.\(\nu_e\) هذه العملية، التي تسمى تحلل بيتا، مهمة في العديد من العمليات الفيزيائية. يوجد رسم تخطيطي لـ Feynman لانحلال بيتا في الشكل\(\PageIndex{3a}\). يصدر النيوترون بروتون\(W^-\) ويصبح بروتونًا، ثم\(W^-\) ينتج إلكترون ومضاد للنيوترينو. هذه العملية مشابهة لحدث التشتت

    \[e^- p \rightarrow n + \nu_e, \nonumber \]

    في هذه العملية، يصدر البروتون a\(W^+\) ويتم تحويله إلى نيوترون (الشكل\(\PageIndex{3b}\)). \(W^+\)ثم يتحد مع الإلكترون، مكونًا النيوترينو. يتم أخذ التفاعلات الكهربائية الضعيفة الأخرى في الاعتبار في التمارين.

    يوضح الشكل أ أربعة سهام. يشير أحد الأسهم، المسمى n، إلى الأعلى ويلتقي طرفه بقاعدة سهم آخر يتجه لأعلى ولليسار، يسمى p. على يمين هذا السهم يوجد سهم يحمل علامة e ناقص يشير لأعلى. قاعدتها متصلة بقاعدة سهم آخر يتجه لأعلى ولليمين. هذا يسمى v bar scropict e. يتم توصيل التقاطعين على الرسم البياني بخط متموج يسمى W ناقص. هذا يشير إلى الأعلى واليمين. يوضح الشكل (ب) أربعة سهام. يشير أحد الأسهم، المسمى p، إلى الأعلى واليمين. يلتقي طرفه بقاعدة سهم آخر يتجه لأعلى ولليسار، يسمى n. إلى يمين هذا السهم يوجد سهم يحمل علامة e ناقص يشير لأعلى ولليسار. يلتقي طرفه بقاعدة سهم آخر يتجه لأعلى ولليمين. هذا يسمى v subcept e. يتم توصيل التقاطعين على الرسم البياني بخط متموج يسمى W plus. هذا يشير إلى الأعلى واليمين.
    الشكل\(\PageIndex{3}\): رسم فينمان للجسيمات التي تتفاعل من خلال تبادل بوزون W: (أ) تحلل بيتا؛ (ب) تحويل بروتون إلى نيوترون.

    يمكن تقدير نطاق القوة النووية الضعيفة بحجة مماثلة لتلك السابقة. بافتراض أن عدم اليقين بشأن الطاقة يمكن مقارنته بطاقة جسيم التبادل\((E \approx mc^2)\)، لدينا

    \[\Delta t \approx \frac{h}{mc^2}. \nonumber \]

    وبالتالي فإن المسافة القصوى d التي يمكن أن يقطعها جسيم التبادل (على افتراض أنه يتحرك بسرعة قريبة من c) هي

    \[d \approx c\Delta t = \frac{h}{mc}. \nonumber \]

    نحصل على واحدة من البوزونات الناقلة المشحونة بـ\(mc = 4.27 \times 10^{-17} \, J \cdot s/m\).\(mc^2 \approx 80 BeV = 1.28 \times 10^{-8} J\) وبالتالي، فإن نطاق القوة التي توسط فيها هذا البوزون هو

    قوة نووية قوية

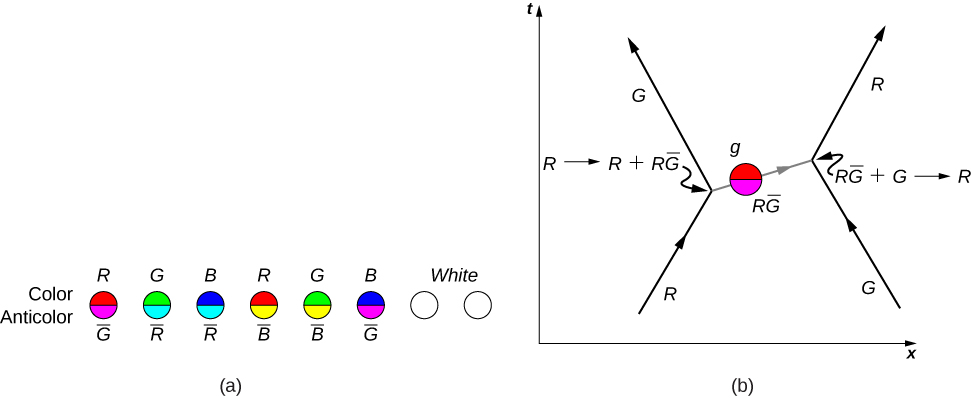
    تصف التفاعلات النووية القوية التفاعلات بين الكواركات. يتم وصف تفاصيل هذه التفاعلات بواسطة QCD. وفقًا لهذه النظرية، ترتبط الكواركات معًا عن طريق إرسال واستقبال الغلوونات. مثلما تحمل الكواركات شحنة كهربائية [تحدد إما قوة التفاعلات الكهرومغناطيسية بين الكواركات\((+2/3)e\) أو\((-1/3)e\) تلك التي تحدد قوة التفاعلات الكهرومغناطيسية بين الكواركات، تحمل الكواركات أيضًا «شحنة لونية» (إما حمراء أو زرقاء أو خضراء) تحدد قوة التفاعلات النووية القوية. كما تمت مناقشته من قبل، ترتبط الكواركات معًا في مجموعات في مجموعات ذات ألوان محايدة (أو «بيضاء»)، مثل الأحمر والأزرق والأخضر والأحمر الأحمر.

    ومن المثير للاهتمام أن الغلوونات نفسها تحمل شحنة ملونة. توجد ثمانية جلونات معروفة: ستة تحمل لونًا ومضادًا للون، واثنتان محايدة اللون (الشكل\(\PageIndex{4a}\)). لتوضيح التفاعل بين الكواركات من خلال تبادل الغلوونات المشحونة، ضع في اعتبارك مخطط فينمان في الشكل\(\PageIndex{4b}\). مع مرور الوقت، يتحرك كوارك أحمر إلى اليمين وكوارك أخضر غريب يتحرك يسارًا. (تظهر هذه في الحافة السفلية من الرسم البياني.) يتبادل الكوارك العلوي الغلوون الأحمر المضاد للأخضر مع الكوارك الغريب. (تظهر الألوان المضادة كألوان ثانوية. على سبيل المثال، يتم تمثيل الأحمر المضاد باللون السماوي لأن اللون السماوي يمتزج مع اللون الأحمر لتكوين ضوء أبيض.) وفقًا لـ QCD، يجب أن تكون جميع التفاعلات في هذه العملية - المحددة بالرؤوس - محايدة اللون. لذلك، يتحول الكوارك السفلي من الأحمر إلى الأخضر، ويتحول الكوارك الغريب من الأخضر إلى الأحمر.

    يوضح الشكل أ 8 دوائر على التوالي. الدائرتان الأخيرتان بيضاء. يختلف النصفان العلوي والسفلي لكل دائرة من الدوائر الست الأولى في اللون. يتم تسمية النصفين العلويين بالألوان ويتم تصنيف النصفين السفليين على أنهم مضادون للون. النصفان العلوي والسفلي لكل دائرة من اليسار إلى اليمين هما كما يلي: أولاً: أحمر يحمل علامة R وأرجواني مكتوب عليه G bar، وثانيًا: أخضر يحمل علامة G والسماوي المسمى R bar، ثالثًا: أزرق يحمل علامة B وشريط سماوي يحمل علامة R، رابعًا: أحمر يحمل علامة R وأصفر يحمل علامة B، وخامسًا: أخضر يحمل علامة G والأصفر يحمل علامة B، السادس: الأزرق المسمى B والأرجواني المسمى G bar. الشكل (ب) عبارة عن رسم بياني لـ t مقابل x. السهم المتجه لأعلى ولليمين يسمى R. يلتقي طرفه بقاعدة السهم G، الذي يشير لأعلى ولليسار. يتم تسمية التقاطع من R إلى R بالإضافة إلى شريط R G. على يمين هذين السهمين يوجد سهم G يشير لأعلى ولليسار. يلتقي طرفه بقاعدة السهم R. ويتم تسمية التقاطع من شريط RG بالإضافة إلى G إلى R. ويتم توصيل التقاطعين بواسطة سهم يشير إلى اليمين. على طول السهم توجد دائرة تسمى RG bar.
    الشكل\(\PageIndex{4}\): (أ) ثمانية أنواع من الغلوونات تحمل القوة النووية القوية. الغلوونات البيضاء عبارة عن مزيج من أزواج الألوان المضادة للألوان. (ب) التفاعل بين الكواركات من خلال تبادل الغلوون.

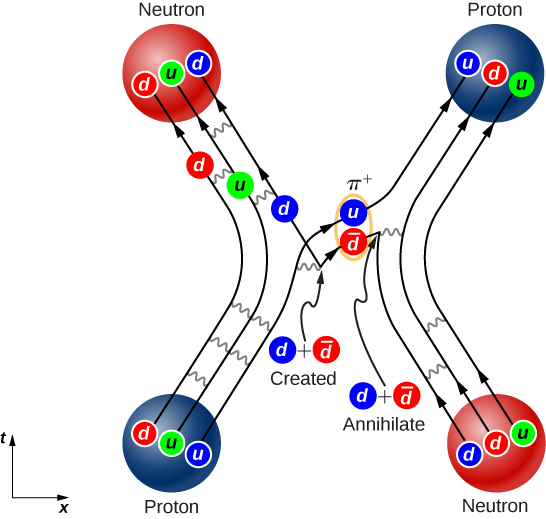
    كما اقترح هذا المثال، يمكن أن يكون التفاعل بين الكواركات في نواة الذرة معقدًا للغاية. \(\PageIndex{5}\)يوضِّح الشكل التفاعل بين بروتون ونيوترون. لاحظ أن البروتون يتحول إلى نيوترون ويتحول النيوترون إلى بروتون أثناء التفاعل. يشير وجود أزواج الكوارك-أنتيكوارك في التبادل إلى أن الترابط بين النيوكليونات يمكن تصميمه كتبادل للبيونات.

    في أعلى يسار الشكل توجد دائرة تسمى النيوترون. بداخلها ثلاث دوائر أصغر تسمى d و u و d. وفي الزاوية اليمنى العليا توجد دائرة تسمى البروتون. بداخلها ثلاث دوائر تحمل اسم u, d, u. في أسفل اليمين توجد دائرة تسمى النيوترون. بداخلها ثلاث دوائر تسمى d و d و u وفي أسفل اليسار توجد دائرة تسمى البروتون. بداخلها ثلاث دوائر تسمى d و u و u. خطوط من d و u في الجزء السفلي الأيسر من البروتون تتصل بـ d و u في أعلى النيوترون الأيسر. تتصل الخطوط من d و u في الجزء السفلي الأيمن من النيوترون بتلك الموجودة في البروتون العلوي الأيمن. يتصل خط من u في الجزء السفلي الأيسر من البروتون بـ u في أعلى البروتون الأيمن. في منتصف خط الاتصال هذا، يقترن u بدائرة أخرى تسمى d bar. هذا الزوج يسمى pi plus. يشير إلى الدائرة التي تحمل علامة d bar من اليسار سهم، تم إنشاء قاعدته بـ d plus d bar. يتصل خط من قاعدة السهم بـ d في أعلى النيوترون الأيسر. يوجد على يمين الدائرة التي تحمل علامة d bar خط، تُسمى نقطة نهايته d plus d bar elinadate. يربط الخط d في الجزء السفلي الأيمن من النيوترون به. تظهر الخطوط المتموجة بين جميع خطوط التوصيل.
    الشكل\(\PageIndex{5}\): مخطط فينمان الذي يصف التفاعل النووي القوي بين البروتون والنيوترون.

    من الناحية العملية، من الصعب إنتاج تنبؤات QCD. تنشأ هذه الصعوبة من القوة المتأصلة في القوة وعدم القدرة على إهمال المصطلحات في المعادلات. وبالتالي، غالبًا ما يتم إجراء حسابات QCD بمساعدة أجهزة الكمبيوتر العملاقة. يتم دعم وجود الجلوونات من خلال تجارب تشتت الإلكترون والنيوكليون. إن لحظات الكوارك المقدرة التي تنطوي عليها أحداث التشتت هذه أصغر بكثير مما نتوقعه بدون الجلوونات لأن الغلوونات تحمل بعضًا من زخم كل تصادم.

    نظريات التوحيد

    لقد عرف الفيزيائيون منذ فترة طويلة أن قوة التفاعل بين الجسيمات تعتمد على مسافة التفاعل. على سبيل المثال، يواجه جزيئان موجبان الشحنة قوة تنافر أكبر على مسافة قصيرة ثم على مسافة طويلة. في تجارب التشتت، تعتمد قوة التفاعل على طاقة الجسيم المتفاعل، لأن الطاقة الأكبر تعني تفاعلات أوثق وأقوى.

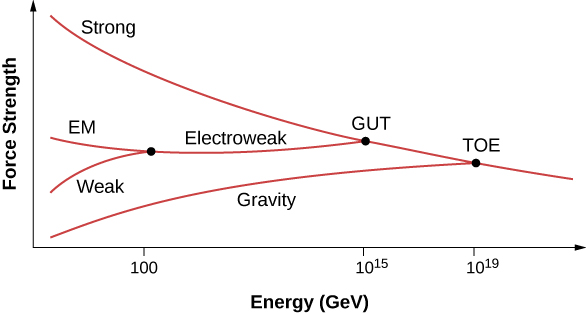
    رسم بياني لقوة القوة مقابل الطاقة في GeV. منحنى يسمى المنحدرات القوية لأسفل ولليمين. تُسمى النقطة الموجودة على المنحنى بقيمة x من 10 إلى القوة 19 باسم TOE. يتفرع منحنى يسمى الجاذبية من هنا، متجهًا نحو الأسفل واليسار. تُسمى النقطة الموجودة على المنحنى القوي بقيمة x من 10 إلى القوة 15 بـ GUT. منحنى يتجه إلى اليسار من هنا. يطلق عليه اسم Electroweak. يتفرع هذا إلى قسمين عند نقطة بقيمة x 100. يُطلق على الفرع المتجه إلى اليسار اسم EM والفرع المتجه إلى الأسفل واليسار يُصنف على أنه ضعيف.
    الشكل\(\PageIndex{6}\): توحيد كبير للقوى في الطاقات العالية.

    يشك علماء فيزياء الجسيمات الآن في أن قوة جميع تفاعلات الجسيمات (القوى الأربع) تندمج عند الطاقات العالية، ويمكن وصف تفاصيل تفاعلات الجسيمات في هذه الطاقات من حيث قوة واحدة (الشكل\(\PageIndex{6}\)). تصف النظرية الموحدة شكل هذه التفاعلات وتشرح سبب تفكك هذا الوصف في مقاييس الطاقة المنخفضة. النظرية الموحدة الكبرى هي نظرية تحاول وصف التفاعل القوي والضعيف كهربائيًا من حيث قوة واحدة فقط. تأخذ نظرية كل شيء (TOE) مفهوم التوحيد خطوة أخرى إلى الأمام. يجمع TOE بين جميع القوى الأساسية الأربعة (بما في ذلك الجاذبية) في نظرية واحدة.